Wave propagation analysis in functionally graded metal foam plates with nanopores

Abstract

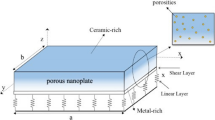
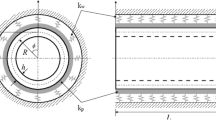
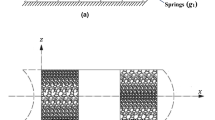
In this paper, the influence of the surface effect on wave propagation characteristics in functionally graded metal foam plates (FGMFPs) with nanopores is studied, where different porosity distribution patterns are taken in account. The surface effect between pore and matrix in FGMFP is considered by the Gurtin–Murdoch surface elasticity model. The plate is divided into finite thickness layers along the gradient, and each layer of porous material is homogenized using locally exact homogenization theory. On the basis of obtaining the effective modulus of each layer of porous material, the governing equations of the plates are obtained by Hamilton’s principle and different plate theories, upon which wave dispersion and phase velocity curves of FGMFP are obtained. The developed method is verified by comparing the wave dispersion curves against existing literature. Finally, the effects of different plate theories, porosity distribution, unit cell array, surface effect, pore radius and its distribution pattern, and graphene platelet weight fraction on the wave dispersion and phase velocity curves are systematically investigated. The results in this paper may provide guidance for the design of FGMFPs with nanopores.

Appendices

Appendix 1

By applying the G–M interface conditions (Eqs. (3–5)) and displacement continuity conditions, the relationship between the unknown coefficients $F_{nj}^{{}}$ and $G_{nj}^{{}}$(j = 1, 2, 3, 4) in the fiber phase and matrix phase is obtained, for n = 0,

$$\left[ {\begin{array}{*{20}l} {F_{{{01}}} } \\ {F_{{{02}}} } \\ \end{array} } \right]^{\left( m \right)} = \left[ {\begin{array}{*{20}l} {b_{{{01}}} + b^{\prime}_{{{01}}} } \\ {b_{{{02}}} + b^{\prime}_{{{01}}} } \\ \end{array} } \right]F_{{{01}}}^{\left( r \right)} + \left[ {\begin{array}{*{20}l} {c_{{{01}}} + c^{\prime}_{{{01}}} } \\ {c_{{{02}}} + c^{\prime}_{{{01}}} } \\ \end{array} } \right] {\mathbf{\bar{\varepsilon }}}_{{{33}}} + \left[ {\begin{array}{*{20}l} {d_{{{01}}} + d^{\prime}_{{{01}}} } \\ {d_{{{02}}} + d^{\prime}_{{{01}}} } \\ \end{array} } \right]\left( {{\mathbf{\bar{\varepsilon }}}_{{{11}}} + {\mathbf{\bar{\varepsilon }}}_{{{22}}} } \right),$$

(30)

where $b_{01} = \frac{{\left( {C_{11}^{\left( r \right)} + C_{12}^{\left( r \right)} } \right) + \left( {C_{11}^{\left( m \right)} + C_{12}^{\left( m \right)} } \right)}}{{2C_{12}^{\left( m \right)} }},c_{01} = \frac{{\left( {C_{13}^{\left( r \right)} - C_{13}^{\left( m \right)} } \right)}}{{2C_{11}^{\left( m \right)} }},d_{01} = - \frac{1}{2}b_{02} ,c_{02} = - c_{01} ,d_{02} = - d_{01} ,d_{01}^{\prime } = \frac{1}{2}d_{01}^{\prime }$_,$b_{02} = \frac{{\left( {C_{11}^{\left( r \right)} + C_{12}^{\left( r \right)} } \right) - \left( {C_{11}^{\left( m \right)} + C_{12}^{\left( m \right)} } \right)}}{{2C_{12}^{\left( m \right)} }},d_{01}^{\prime } = - \frac{{s^{\prime } }}{{C_{11}^{\left( m \right)} }},c_{01}^{\prime } = - \frac{{\lambda_{s} }}{{2C_{11}^{\left( m \right)} r}},d_{02}^{\prime } = - d_{01}^{\prime } ,c_{02}^{\prime } = - c_{01}^{\prime } ,d_{02}^{\prime } = - d_{01}^{\prime } ,s^{\prime } = - \frac{{\left( {\lambda_{s} + 2\mu_{s} } \right)}}{r}$.

For $n \ge {2},$

$$\begin{aligned} {\mathbf{A}}_{n}^{\left( m \right)} F_{n}^{\left( m \right)} & = \left( {{\mathbf{A}}_{n}^{\left( r \right)} + {\mathbf{A}}_{0n}^{\prime \left( r \right)} } \right){\mathbf{F}}_{n}^{\left( r \right)} + \delta_{n2} \left( {{\mathbf{A}}_{0}^{{}} + {\mathbf{A}}_{0}^{\prime } } \right)\left( {\overline{\varepsilon }_{11} - \overline{\varepsilon }_{22} } \right), \\ {\mathbf{A}}_{n}^{\left( m \right)} G_{n}^{\left( m \right)} & = \left( {{\mathbf{A}}_{n}^{\left( r \right)} + {\mathbf{A}}_{n}^{\left( r \right)} } \right){\mathbf{G}}_{n}^{\left( r \right)} + \delta_{n2} \left( {{\mathbf{A}}_{0}^{{}} + {\mathbf{A}}_{0}^{{}} } \right){\mathbf{2}}\overline{\varepsilon }_{12} ,\\ \end{aligned}$$

(31)

where ${\mathbf{F}}_{n}^{\left( m \right)} = \left[ {F_{{n{1}}}^{\left( m \right)} ,F_{{n{2}}}^{\left( m \right)} ,F_{{n{3}}}^{\left( m \right)} ,F_{{n{4}}}^{\left( m \right)} } \right]^{{\text{T}}}$,${\mathbf{G}}_{n}^{\left( m \right)} = \left[ {G_{{n{1}}}^{\left( m \right)} ,G_{{n{2}}}^{\left( m \right)} ,G_{{n{3}}}^{\left( m \right)} ,G_{{n{4}}}^{\left( m \right)} } \right]^{{\text{T}}}$${\mathbf{F}}_{n}^{\left( r \right)} = \left[ {\begin{array}{*{20}l} {F_{{n{1}}}^{\left( r \right)} } & {F_{{n{2}}}^{\left( r \right)} } \\ \end{array} } \right]^{{\text{T}}}$,${\mathbf{G}}_{n}^{\left( r \right)} = \left[ {\begin{array}{*{20}l} {G_{{n{1}}}^{\left( r \right)} } & {G_{{n{2}}}^{\left( r \right)} } \\ \end{array} } \right]^{{\text{T}}}$, and the superscripts r and m represent the ring and matrix phase, respectively.

$${\mathbf{A}}_{n}^{\left( m \right)} = \left[ {\begin{array}{*{20}l} {1} &\quad {1} &\quad {1} &\quad {1} \\ {\beta_{{n{1}}} } & \quad {\beta_{{n{2}}} } &\quad {\beta_{{n{3}}} } &\quad {\beta_{{n{4}}} } \\ {P_{{n{1}}} } &\quad {P_{{n{2}}} } &\quad {P_{{n{3}}} } &\quad {P_{{n{4}}} } \\ {R_{{n{1}}} } &\quad {R_{{n{2}}} } &\quad {R_{{n{3}}} } &\quad {R_{{n{4}}} } \\ \end{array} } \right]^{\left( m \right)} ,{\mathbf{A}}_{n}^{\left( f \right)} = \left[ {\begin{array}{*{20}l} {1} &\quad {1} \\ {\beta_{{n{1}}} } &\quad {\beta_{{n{2}}} } \\ {P_{{n{1}}} } &\quad {P_{{n{2}}} } \\ {R_{{n{1}}} } &\quad {R_{{n{2}}} } \\ \end{array} } \right],{\mathbf{A^{\prime}}}_{n}^{\left( f \right)} = \left[ {\begin{array}{*{20}l} 0 &\quad 0 \\ 0 &\quad 0 \\ {{{I_{{n{1}}}^{\left( r \right)} } \mathord{\left/ {\vphantom {{I_{{n{1}}}^{\left( r \right)} } r}} \right. \kern-\nulldelimiterspace} r}} &\quad {{{I_{{n{2}}}^{\left( r \right)} } \mathord{\left/ {\vphantom {{I_{{n{2}}}^{\left( r \right)} } r}} \right. \kern-\nulldelimiterspace} r}} \\ {{{nI_{{n{1}}}^{\left( r \right)} } \mathord{\left/ {\vphantom {{nI_{{n{1}}}^{\left( r \right)} } r}} \right. \kern-\nulldelimiterspace} r}} &\quad {{{nI_{{n{2}}}^{\left( r \right)} } \mathord{\left/ {\vphantom {{nI_{{n{2}}}^{\left( r \right)} } r}} \right. \kern-\nulldelimiterspace} r}} \\ \end{array} } \right],$$

$${\mathbf{A}}_{0}^{{}} = \frac{{1}}{{2}}\left[ {\begin{array}{*{20}l} 0 &\quad 0 &\quad {C_{{{11}}}^{\left( r \right)} - C_{{{12}}}^{\left( r \right)} - C_{{{11}}}^{\left( m \right)} + C_{{{12}}}^{\left( m \right)} } &\quad {C_{{{11}}}^{\left( r \right)} - C_{{{12}}}^{\left( r \right)} - C_{{{11}}}^{\left( m \right)} + C_{{{12}}}^{\left( m \right)} } \\ \end{array} } \right]^{T} ,{\mathbf{A^{\prime}}}_{0}^{{}} = \left[ {\begin{array}{*{20}l} 0 &\quad 0 &\quad {\frac{{s^{\prime}}}{{2}}} &\quad {s^{\prime}} \\ \end{array} } \right]^{T},$$

(32)

where $I_{{n{1}}}^{\left( r \right)} = \left( {\lambda_{s} + \mu_{s} } \right)\left( {{1} + n\beta_{nj}^{\left( r \right)} } \right)$.

Appendix 2

By substituting Eq. (19) and Eq. (20) into Eq. (23), the corresponding governing equation based on different plate theories is as follows

2.1 GPT

$$\begin{aligned} & A_{11} \frac{{\partial^{2} u_{0} }}{{\partial x^{2} }} + A_{66} \frac{{\partial^{2} u_{0} }}{{\partial y^{2} }} + \left( {A_{12} + A_{66} } \right)\frac{{\partial^{2} v_{0} }}{\partial x\partial y} - B_{11} \frac{{\partial^{3} v_{0} }}{{\partial x^{3} }} - \left( {B_{12} + 2B_{66} } \right)\frac{{\partial^{3} w_{0} }}{{\partial x\partial y^{2} }} = I_{0} \ddot{u}_{0} - I_{1} \frac{{\partial \ddot{w}_{0} }}{\partial x} \\ & A_{22} \frac{{\partial^{2} v_{0} }}{{\partial y^{2} }} + A_{66} \frac{{\partial^{2} v_{0} }}{{\partial x^{2} }} + \left( {A_{12} + A_{66} } \right)\frac{{\partial^{2} u_{0} }}{\partial x\partial y} - B_{22} \frac{{\partial^{3} w_{0} }}{{\partial y^{3} }} - \left( {B_{12} + 2B_{66} } \right)\frac{{\partial^{3} w_{0} }}{{\partial y\partial x^{2} }} = I_{0} \ddot{v}_{0} - I_{1} \frac{{\partial \ddot{w}_{0} }}{\partial y} \\ \end{aligned}$$

(33)

$$\begin{aligned} & B_{11} \frac{{\partial^{3} u_{0} }}{{\partial x^{3} }} + \left( {B_{12} + 2B_{66} } \right)\frac{{\partial^{3} u_{0} }}{{\partial x\partial y^{2} }} + \left( {B_{12} + 2B_{66} } \right)\frac{{\partial^{3} v_{0} }}{{\partial y\partial x^{2} }} + B_{22} \frac{{\partial^{3} v_{0} }}{{\partial y^{3} }} - D_{11} \frac{{\partial^{4} w_{0} }}{{\partial x^{4} }} - 2\left( {D_{12} + 2D_{66} } \right)\frac{{\partial^{4} w_{0} }}{{\partial y^{2} \partial x^{2} }} \\ & \quad - D_{22} \frac{{\partial^{4} w_{0} }}{{\partial y^{4} }} = I_{0} \ddot{w}_{0} + I_{1} \left( {\frac{{\partial \ddot{u}_{0} }}{\partial x} + \frac{{\partial \ddot{v}_{0} }}{\partial y}} \right) - I_{2} \left( {\frac{{\partial^{2} \ddot{w}_{0} }}{{\partial x^{2} }} + \frac{{\partial^{2} \ddot{w}_{0} }}{{\partial y^{2} }}} \right) \\ \end{aligned}$$

2.2 FSDT

$$A_{{{22}}} \frac{{\partial^{{2}} v_{0} }}{{\partial y^{{2}} }} + A_{{{66}}} \frac{{\partial^{{2}} v_{0} }}{{\partial x^{{2}} }} + \left( {A_{{{12}}} + A_{{{66}}} } \right)\frac{{\partial^{{2}} u_{0} }}{\partial x\partial y} - B_{{{22}}} \frac{{\partial^{{3}} w_{0} }}{{\partial y^{{3}} }} - \left( {B_{{{12}}} + {2}B_{{{66}}} } \right)\frac{{\partial^{{3}} w_{0} }}{{\partial y\partial x^{{2}} }} = I_{0} \ddot{v}_{0} + I_{{1}} \frac{{\partial^{{2}} \phi_{y} }}{{\partial t^{{2}} }}$$

$$A_{{{22}}} \frac{{\partial^{{2}} v_{0} }}{{\partial y^{{2}} }} + A_{{{66}}} \frac{{\partial^{{2}} v_{0} }}{{\partial x^{{2}} }} + \left( {A_{{{12}}} + A_{{{66}}} } \right)\frac{{\partial^{{2}} u_{0} }}{\partial x\partial y} - B_{{{22}}} \frac{{\partial^{{3}} w_{0} }}{{\partial y^{{3}} }} - \left( {B_{{{12}}} + {2}B_{{{66}}} } \right)\frac{{\partial^{{3}} w_{0} }}{{\partial y\partial x^{{2}} }} = I_{0} \ddot{v}_{0} + I_{{1}} \frac{{\partial^{{2}} \phi_{y} }}{{\partial t^{{2}} }}$$

$$\begin{aligned} & \kappa A_{44} \frac{{\partial^{2} w_{0} }}{{\partial x^{2} }} + \kappa A_{55} \frac{{\partial^{2} w_{0} }}{{\partial y^{2} }}\kappa A_{44} \frac{{\partial \phi_{x} }}{\partial x} + \kappa A_{55} \frac{{\partial \phi_{y} }}{\partial y} = I_{0} \ddot{w}_{0} \\ & B_{11} \frac{{\partial^{2} u_{0} }}{{\partial x^{2} }} + B_{66} \frac{{\partial^{2} u_{0} }}{{\partial y^{2} }} + \left( {B_{12} + B_{66} } \right)\frac{{\partial^{2} v_{0} }}{\partial x\partial y} + D_{11} \frac{{\partial^{2} \phi_{x} }}{{\partial x^{2} }} + D_{66} \frac{{\partial^{2} \phi_{x} }}{{\partial y^{2} }} + \left( {D_{12} + D_{66} } \right)\frac{{\partial^{2} \phi_{y} }}{\partial x\partial y} \\ & \quad - \kappa A_{44} \frac{{\partial w_{0} }}{\partial x} - \kappa A_{44} \phi_{x} = I_{1} \ddot{u}_{0} + I_{2} \frac{{\partial^{2} \phi_{x} }}{{\partial t^{2} }} \\ \end{aligned}$$

(B2)

$$\begin{aligned} & B_{22} \frac{{\partial^{2} v_{0} }}{{\partial y^{2} }} + B_{66} \frac{{\partial^{2} v_{0} }}{{\partial x^{2} }} + \left( {B_{12} + B_{66} } \right)\frac{{\partial^{2} u_{0} }}{\partial x\partial y} + D_{22} \frac{{\partial^{2} \phi_{y} }}{{\partial y^{2} }} + D_{66} \frac{{\partial^{2} \phi_{y} }}{{\partial x^{2} }} + \left( {D_{12} + D_{66} } \right)\frac{{\partial^{2} \phi_{x} }}{\partial x\partial y} - \kappa A_{55} \frac{{\partial w_{0} }}{\partial y} \\ & \quad - \kappa A_{44} \phi_{y} = I_{1} \ddot{v}_{0} + I_{2} \frac{{\partial^{2} \phi_{y} }}{{\partial t^{2} }} \\ \end{aligned}$$

2.3 TSDT

$$\begin{aligned} & A_{11} \frac{{\partial^{2} u_{0} }}{{\partial x^{2} }} + A_{66} \frac{{\partial^{2} u_{0} }}{{\partial y^{2} }} + \left( {A_{12} + A_{66} } \right)\frac{{\partial^{2} v_{0} }}{\partial x\partial y} - B_{11} \frac{{\partial^{3} w_{b} }}{{\partial x^{3} }} - \left( {B_{12} + 2B_{66} } \right)\frac{{\partial^{3} w_{b} }}{{\partial x\partial y^{2} }} \\ & \quad - \left( {B_{12}^{s} + 2B_{66}^{s} } \right)\frac{{\partial^{3} w_{s} }}{{\partial x\partial y^{2} }} - B_{11}^{s} \frac{{\partial^{3} w_{s} }}{{\partial x^{3} }} = I_{0} \ddot{u}_{0} - I_{1} \frac{{\partial \ddot{w}_{b} }}{\partial x} - J_{1} \frac{{\partial \ddot{w}_{s} }}{\partial x} \\ \end{aligned}$$

$$\begin{aligned} & A_{22} \frac{{\partial^{2} v_{0} }}{{\partial y^{2} }} + A_{66} \frac{{\partial^{2} v_{0} }}{{\partial x^{2} }} + \left( {A_{12} + A_{66} } \right)\frac{{\partial^{2} v_{0} }}{\partial x\partial y} - B_{22} \frac{{\partial^{3} w_{b} }}{{\partial y^{3} }} - \left( {B_{12} + 2B_{66} } \right)\frac{{\partial^{3} w_{b} }}{{\partial x^{2} \partial y}} \\ & \quad - \left( {B_{12}^{s} + 2B_{66}^{s} } \right)\frac{{\partial^{3} w_{s} }}{{\partial x^{2} \partial y}} - B_{22}^{s} \frac{{\partial^{3} w_{s} }}{{\partial y^{3} }} = I_{0} \ddot{v}_{0} - I_{1} \frac{{\partial \ddot{w}_{b} }}{\partial x} - J_{1} \frac{{\partial \ddot{w}_{s} }}{\partial y} \\ \end{aligned}$$

(35)

$$\begin{aligned} & B_{11} \frac{{\partial^{3} u_{0} }}{{\partial x^{3} }} + \left( {B_{12} + 2B_{66} } \right)\frac{{\partial^{2} u_{0} }}{{\partial x\partial y^{2} }} + \left( {B_{12} + 2B_{66} } \right)\frac{{\partial^{2} v_{0} }}{{\partial^{2} x\partial y}} + B_{22} \frac{{\partial^{3} v_{0} }}{{\partial y^{3} }} - D_{11} \frac{{\partial^{4} w_{b} }}{{\partial x^{4} }} \\ & \quad - 2\left( {D_{12} + 2D_{66} } \right)\frac{{\partial^{4} w_{b} }}{{\partial y^{2} \partial x^{2} }} - D_{22} \frac{{\partial^{4} w_{b} }}{{\partial y^{4} }} - D_{11}^{s} \frac{{\partial^{4} w_{s} }}{{\partial x^{4} }} - 2\left( {D_{12}^{s} + 2D_{66}^{s} } \right)\frac{{\partial^{4} w_{s} }}{{\partial y^{2} \partial x^{2} }} \\ & \quad - D_{22}^{s} \frac{{\partial^{4} w_{s} }}{{\partial y^{4} }} = I_{0} \left( {\ddot{w}_{s} + \ddot{w}_{b} } \right) - I_{1} \left( {\frac{{\partial \ddot{u}_{0} }}{\partial x} + \frac{{\partial \ddot{v}_{0} }}{\partial y}} \right) - I_{2} \nabla^{2} \ddot{w}_{b} - J_{2} \nabla^{2} \ddot{w}_{s} \\ \end{aligned}$$

$$\begin{aligned} & B_{11}^{s} \frac{{\partial^{3} u_{0} }}{{\partial x^{3} }} + \left( {B_{12}^{s} + 2B_{66}^{s} } \right)\frac{{\partial^{2} u_{0} }}{{\partial x\partial y^{2} }} + \left( {B_{12}^{s} + 2B_{66}^{s} } \right)\frac{{\partial^{2} v_{0} }}{{\partial x^{2} \partial y}} + B_{22}^{s} \frac{{\partial^{3} v_{0} }}{{\partial y^{3} }} - D_{11}^{s} \frac{{\partial^{4} w_{b} }}{{\partial x^{4} }} \\ & \quad - 2\left( {D_{12}^{s} + 2D_{66}^{s} } \right)\frac{{\partial^{4} w_{b} }}{{\partial y^{2} \partial x^{2} }} - D_{22}^{s} \frac{{\partial^{4} w_{b} }}{{\partial y^{4} }} - H_{11}^{s} \frac{{\partial^{4} w_{s} }}{{\partial x^{4} }} - 2\left( {H_{12}^{s} + 2H_{66}^{s} } \right)\frac{{\partial^{4} w_{s} }}{{\partial y^{2} \partial x^{2} }} \\ & \quad - H_{22}^{s} \frac{{\partial^{4} w_{s} }}{{\partial y^{4} }} + A_{55}^{s} \frac{{\partial^{2} w_{s} }}{{\partial x^{2} }} + A_{44}^{s} \frac{{\partial^{2} w_{s} }}{{\partial y^{2} }} = I_{0} \left( {\ddot{w}_{b} + \ddot{w}_{s} } \right) + J_{1} \left( {\frac{{\partial \ddot{u}_{0} }}{\partial x} + \frac{{\partial \ddot{v}_{0} }}{\partial y}} \right) - J_{2} \nabla^{2} \ddot{w}_{b} - K_{2} \nabla^{2} \ddot{w}_{s} \\ \end{aligned}$$

Appendix 3

The simplified stiffness and mass matrices $\left[ {\mathbf{K}} \right]_{i}$ and $\left[ {\mathbf{M}} \right]_{i}$ (i = GPT, FSDT, TSDT) read:

$$\begin{aligned} \left[ {\mathbf{K}} \right]_{{{\text{GPT}}}} & = \left[ {\begin{array}{*{20}l} {k_{{{11}}} } &\quad {k_{{{12}}} } &\quad {k_{{{13}}} } \\ {k_{{{12}}} } &\quad {k_{{{11}}} } &\quad {k_{{{13}}} } \\ { - k_{{{13}}} } &\quad { - k_{{{13}}} } &\quad {k_{{{33}}} } \\ \end{array} } \right],\left[ {\mathbf{M}} \right]_{{{\text{GPT}}}} = \left[ {\begin{array}{*{20}l} {m_{{{11}}} } &\quad {0} &\quad {m_{{{13}}} } \\ {0} &\quad {m_{{{11}}} } &\quad {m_{{{13}}} } \\ { - m_{{{13}}} } &\quad { - m_{{{13}}} } &\quad {m_{{{33}}} } \\ \end{array} } \right] \\ \left[ {\mathbf{K}} \right]_{{{\text{FSDT}}}} & = \left[ {\begin{array}{*{20}l} {k_{{{11}}} } &\quad {k_{{{12}}} } &\quad {0} &\quad {k_{{{14}}}^{F} } &\quad {k_{{{14}}}^{F} } \\ {k_{{{12}}} } &\quad {k_{{{11}}} } &\quad {0} &\quad {k_{{{14}}}^{F} } &\quad {k_{{{14}}}^{F} } \\ {0} &\quad {0} &\quad {k_{{{33}}}^{F} } &\quad {k_{{{34}}}^{F} } &\quad {k_{{{34}}}^{F} } \\ {k_{{{14}}}^{F} } &\quad {k_{{{14}}}^{F} } &\quad { - k_{{{34}}}^{F} } &\quad {k_{{{44}}}^{F} } &\quad {k_{{{45}}} } \\ {k_{{{14}}}^{F} } &\quad {k_{{{14}}}^{F} } &\quad { - k_{{{34}}}^{F} } &\quad {k_{{{45}}} } &\quad {k_{{{44}}}^{F} } \\ \end{array} } \right],\left[ {\mathbf{M}} \right]_{{{\text{GPT}}}} = \left[ {\begin{array}{*{20}l} {m_{{{11}}} } &\quad {0} &\quad {0} &\quad {m_{{{14}}}^{F} } &\quad {0} \\ {0} &\quad {m_{{{11}}} } &\quad {0} &\quad {0} &\quad {m_{{{14}}}^{F} } \\ {0} &\quad {0} &\quad {m_{{{33}}} } &\quad {0} &\quad {0} \\ {m_{{{14}}}^{F} } &\quad {0} &\quad {0} &\quad {m_{{{44}}}^{F} } &\quad {0} \\ {0} &\quad {m_{{{14}}}^{F} } &\quad {0} &\quad {0} &\quad {m_{{{44}}}^{F} } \\ \end{array} } \right] \\ \left[ {\mathbf{K}} \right]_{{{\text{GPT}}}} & = \left[ {\begin{array}{*{20}l} {k_{{{11}}} } &\quad {k_{{{12}}} } &\quad {k_{{{13}}} } &\quad {k_{{{14}}}^{T} } \\ {k_{{{12}}} } &\quad {k_{{{11}}} } &\quad {k_{{{13}}} } &\quad {k_{{{14}}}^{T} } \\ { - k_{{{13}}} } &\quad { - k_{{{13}}} } &\quad {k_{{{33}}} } &\quad {k_{{{34}}}^{T} } \\ { - k_{{{14}}}^{T} } &\quad { - k_{{{14}}}^{T} } &\quad {k_{{{34}}}^{T} } &\quad {k_{{{44}}}^{T} } \\ \end{array} } \right],\left[ {\mathbf{M}} \right]_{{{\text{GPT}}}} = \left[ {\begin{array}{*{20}l} {m_{{{11}}} } &\quad {0} &\quad {m_{{{13}}} } &\quad {m_{{{14}}}^{T} } \\ {0} &\quad {m_{{{11}}} } &\quad {m_{{{23}}} } &\quad {m_{{{14}}}^{T} } \\ { - m_{{{13}}} } &\quad { - m_{{{13}}} } &\quad {m_{{{33}}} } &\quad {m_{{{34}}}^{{}} } \\ { - m_{{{14}}}^{T} } &\quad { - m_{{{14}}}^{T} } &\quad {m_{{{34}}}^{{}} } &\quad {m_{{{44}}}^{T} } \\ \end{array} } \right] \\ \end{aligned}$$

(36)

$$\begin{aligned} k_{11} & = - k^{2} \left( {A_{11} + A_{66} } \right),k_{12} = - k^{2} \left( {A_{12} + A_{66} } \right),k_{13} = - ik^{3} \left( {B_{11} + B_{12} + 2B_{66} } \right) \\ k_{33} & = - k^{4} \left( {D_{11} + D_{22} + 2D_{12} + 4D_{66} } \right),k_{14}^{F} = - k^{2} \left( {B_{11} + B_{66} } \right),k_{33}^{F} = - \kappa k^{2} \left( {A_{44} + A_{55} } \right) \\ k_{34}^{F} & = i\kappa kA_{55} ,k_{44}^{F} = - \left( {k^{2} D_{66} + k^{2} D_{11} + \kappa A_{44} } \right),k_{45} = - k^{2} \left( {D_{12} + D_{66} } \right) \\ k_{14}^{T} & = - ik^{3} \left( {B_{11}^{s} + B_{12}^{s} + 2B_{66}^{s} } \right),k_{34}^{T} = - k^{4} \left( {D_{11}^{s} + D_{22}^{s} + 2D_{12}^{s} + 4D_{66}^{s} } \right) \\ k_{24}^{T} & = k_{14}^{T} ,k_{44}^{T} = - \left( {k^{4} H_{11}^{s} + k^{4} H_{22}^{s} + 2k^{4} \left( {H_{12}^{s} + H_{66}^{s} } \right) + \kappa k^{2} \left( {A_{44}^{s} + A_{55}^{s} } \right)} \right) \\ m_{11} & = - I_{0} ,m_{13} = iI_{1} k,m_{33} = - I_{0} - 2k^{2} I_{2} ,m_{14}^{F} = - I_{1} ,m_{33}^{F} = - I_{0} ,m_{44}^{F} = - I_{2} \\ m_{14}^{T} & = iJ_{1} k,m_{34} = - I_{0} - 2k^{2} J_{2} ,m_{44}^{T} = - I_{0} - 2k^{2} K_{2} \\ \end{aligned}$$

(37)