Abstract
In the present work, a spectral solver is developed for integration of certain differential equations of solid mechanics, namely static stress equilibrium in composite materials, described in cylindrical or spherical polar coordinates. The spectral approach is encompassed in approximating the displacement field using expansion into a series of Chebyshev polynomials in the radial coordinate and complex exponents in the angular direction. Consequently, differential operators in real space become algebraic operators in spectral space. The spatial heterogeneity and metric non-flatness pertinent to polar geometry are addressed by an iterative strategy, employing both second-order and first-order iterative solvers. The essence of the new contribution is in addressing the difficulty posed by the inherent nonsmoothness present in composite materials and the polar singularity. The interplay of the two produces instability, which is resolved in the proposed approach, specifically by using a new efficient linesearch algorithm, appropriate for the studied class of problems. The method is illustrated by analysis of 1D and 2D linear-elastic and linear-elastic–perfectly plastic response of composites to prescribed radial surface displacement. The developed method allows performing stress homogenization on polar representative volume elements, which has its conceptual advantages, while allowing similar runtime (for sufficient computing resources and an iterative strategy) to the one exhibited by spectral analysis in Cartesian coordinates.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The effort to obtain detailed description of deformation of loaded composite materials, especially in the inelastic regime, counts many decades. As a mathematical problem, the quasistatic inelastic analysis requires three components: kinematic relation between the total, elastic and plastic measures of deformation, an evolution equation for the measure of plastic deformation, and a constitutive relation, giving the stress (or energy) as a function of the elastic measure of deformation. For crystalline material, typically, the aforementioned kinematic relation is derived from symmetry considerations. The plastic part of the deformation gradient is discrete-time-integrated from an evolution law based on kinematic assumption of stress-induced lattice slips. The total deformation gradient is then determined by enforcing stress equilibrium and geometric compatibility, given a constitutive law, which enforces the deformation gradient to be the gradient of a deformation field satisfying appropriate boundary conditions.
One possible approach to the derivation of the deformation gradient is to incorporate it as a gradient of the deformation map into the equilibrium equation and solve a boundary-value problem for the displacement field, subsequently deriving the deformation gradient. For any objective non-degenerate free-energy functional such a problem would be nonlinear and could only be solved approximately. Dividing the physical domain into finite elements, in which stress and strain fields are approximated by polynomial functions of the coordinates, is a standard approach for analyzing homogeneous mechanical parts. Alternatively to this approach, essentially involving the solution of a set of second-order differential equations, there is a mixed-variable strategy, in which both stresses and displacements are incorporated as dependent variables and one aims at solving both equilibrium and the constitutive equations [1].
In contrast, one can use trigonometric, oscillatory shape functions. This is the approach used in spectral methods based on Fourier transforms [2].
In the field of study dedicated to establishing effective mechanical characteristics of composite materials, spectral methods, based on the Fourier transform, are, indeed, popular. In media with random microstructure, it is often sufficient to identify a Representative Volume Element (RVE), which extends to one or several characteristic lengths pertinent to the microstructure (in the case of periodic microstructure, the periodicity cell serves this purpose). The average mechanical response of the RVE (or periodicity cell) is then representative of the coarse-grained response of the medium itself. Furthermore, the RVE (or periodicity cell) is often characterized by the fact that it has periodic (or antiperiodic) boundary conditions. In Fourier space, periodic (or antiperiodic) boundary conditions translate to multiplication by a complex exponent. This means that the actual boundary conditions can be normalized out. Moreover, a discrete Fourier transform (DFT) operator can be constructed such that subsequent application of forward and backward DFT will be loss-free. Also, the DFT can be implemented using the FFT strategy [3], with complexity and memory usage of \({\mathcal {O}}(N\log {N})\) dependence on system size. In addition, it should also be mentioned that, for smooth physical profiles approximated by Fourier series, the number of Fourier coefficients required for convergence decays exponentially (see [4] for a comprehensive review).
One disadvantage of spectral methods and in particular as it pertains to the use of the discrete Fourier transform, is the requirement that the spatial grid be structured. This imposes a certain limitation on the RVE geometry, which thus should not be arbitrary. However, when the purpose is not to perform stress-analysis of a structure of arbitrary shape but rather to perform coarse-graining and find the effective response, this restriction can be tolerated. The standard approach has been to use an RVE in the form of a right rectangular prism.
The arbitrary-shape RVE (random shape, nonconvex, irregular polyhedron, etc.) may perhaps indeed be irrelevant for practical purposes, but one may opt to construct RVEs of other forms than a right rectangular prism. Noteworthy examples are the spherical or cylindrical RVEs. This form can have a structured associated mesh appropriate for use with the Fourier transform operator. The advantage of a spherical or a cylindrical RVE with respect to a right rectangular prism is the higher ratio of bulk-to-surface volume, which diminishes boundary effects. In addition, it may have a smaller effect of induced artificial anisotropy. Since it is not required from an RVE to have a space-filling shape, the spherical option is feasible. Indeed, the benefits of this choice were reported in [5,6,7], where a FEM solution was used for the determination of effective elastic properties of an example composite.
The study detailed in [5] shows two calculations of stress distribution in an RVE using FEM analysis, one with a cubic RVE and one with a spherical RVE. It further compares the convergence of Young’s modulus for the two RVEs with increase in resolution (number of elements). Subsequently, a measure of artificial RVE-induced anisotropy is shown, leading to the conclusion that the spherical RVE exhibits better performance both in terms of rate of convergence and measure of induced artificial anisotropy. Based on that, the present work assumes the advantage of a spherical RVE to be an established fact, taking as a task the development of a spectral method in polar coordinates, that will have the spatial advantages of a spherical RVE and the runtime typical for a spectral method (it is furthermore assumed, of course, that the advantage of a sphere over a cube implies also the advantage of a disk over a square).
It is important to mention several relevant works in the recent literature. In what concerns spectral solution of second-order PDEs in polar coordinates, noteworthy studies are given in [8, 9]. In [9], a hierarchy of Jacobi polynomials is employed to transform differential operators into algebraic ones, with examples form hydrodynamics, showing fine-detailed patterns. That strategy has however several disadvantages for homogenization of composites. On one hand, it treats smooth problems, whereas the inherently nonsmooth nature of composite micromechanics poses its own stability challenges when employing spectral description. On the other hand, the approach in [9] is essentially pseudospectral (see [10]), with the associated implications in terms of expected runtime. Both shortcomings are addressed by the present work.
A comprehensive review of various computational aspects related to spectral homogenization in the presence of nonlinearity and other multi-physical effects can be found in [11].
This work is conceived as a first step toward the development of 3D spherical RVEs, to be employed for coarse-grained analysis of polycrystalline metal undergoing finite plastic strains. Notwithstanding, it is an analysis method in its own right, allowing to obtain the displacement field in 1D and 2D composites with polar symmetry, in elastic and elastoplastic regimes of quasistatic deformation.
A known method of solution consists of finding the deformation gradient by solving for equilibrium in Fourier space using convolution with a Green function representing the (compatible) response of a linear reference material. This is a computationally efficient approach, which may be numerically superior to the Finite Element method, as reported in [12]. This efficiency can be (partly) attributed to the preconditioning in the iterative solution of the equilibrium equations, resulting from the use of the aforementioned Green function [13]. Indeed, in this approach, the compatibility of the obtained deformation gradient field can be guaranteed [14]. Thus far, this approach was tested in Cartesian coordinates.
An important question is that of the definition of a linear reference material. The definition has to be such that the corresponding effective stiffness would lead to appropriate preconditioning of the equilibrium equations in Fourier space, one that would guarantee stable numerical solution of the emergent large linear system. The standard approach employed in [12, 15], for example, is to use an arithmetic average of the minimum and maximum tangent moduli of the material. As noted in [16], this choice guarantees convergent solution for the so-called strain-based approach (which is a Banach method). For the optimal, so-called polarization-based approach suggested in [16] and employed in [13], no analytic estimate for the linear reference material modulus guaranteeing stability is available. However, a rigorous procedure for the determination of such reference material for the polarization-based approach is given in [17]. Partly due to this reason, the present work employs, for the 1D analysis, a general-purpose quasi-Newton solver, that can guarantee convergence. In order for the general-purpose solver to converge, the initial guess has to fall into its basin of attraction. To this end, a fixed-point iteration of the sort employed in [18, 19] is used for the first several iterations.
For the 2D setting, the present work employs, instead, a first-order (Cauchy-like) method, for which convergence can be guaranteed for phases with arbitrary elastic moduli contrast. For smooth and convex problems, one would usually prefer a second-order method, with its faster convergence. However, in a spectral iterative approach, in the 2D setting, a first-order method has the advantage that the two dimensions can be decoupled (no need for multiplication by the inverse of the Jacobian/Hessian), which may reduce the overall computational runtime (given a proper initialization strategy).
As aforementioned, this work is dedicated to the analysis of the deformation of a representative volume of a composite material in polar geometry, for which the advantages discussed above hold. An obvious challenge posed by polar description is the non-flatness of the metric, manifested in the fact that the equilibrium equations have non-uniform coefficients. Moreover, efficient spectral description requires the use of special orthogonal polynomials, such as Chebyshev polynomials, for example [20]. The associated spectral transforms in the polar description then become singular. The singularity has to be treated, for stable numerical solution. To this end various approaches have been suggested in the literature, with such tools as special pole conditions, collocation points, etc. [21, 22]. The present work also suggests a collection of tools to successfully deal with polar coordinates in the presence of nonsmoothness. In the 1D analysis case, filtering of nonsmooth interfaces is performed, to overcome the polar-singularity-related Gibbs instability. In the 2D analysis case, the polar singularity is removed altogether by introduction of a minimum radius, which renders the polar description conformal to the Cartesian one, and prevents resonances between radial and angular modes.
The following sections present the first cases solved by the proposed approach, namely that of a 1D (spherically symmetric) composite with two and three layers in linear-elastic deformation and a two-layer composite in linear-elastic–perfectly plastic deformation, and the case of a 2D (cylindrical) two-isotropic-phases composite in linear-elastic deformation.
2 The case of composites with isotropic linear-elastic phases—1D analysis for spherical symmetry (quasi-3D)
For homogeneous isotropic linear-elastic materials, the static equilibrium equation reads:
with the boundary conditions \(u_r(0)=0\) and \(u_r(b)=u_b\).
The radial stress is given by:
An additional stress component (representing the ‘hoop’ stress) can be defined as:
The equilibrium equation can then be written as:
2.1 Analytical solution for a core–shell composite under external pressure
For a core–shell composite, the analytical solution for the displacement field reads:
with
For typical values of compressibility and shear modulus, the solution is plotted in Figs. 1 and 2.
2.2 Numerical solution with a spectral method
Numerical solution of the equilibrium equation on a discrete grid of points is next sought in the form of a truncated expansion in Chebyshev polynomials of the first kind,
such that \(r_i/b=\frac{1}{2}+\frac{x_i}{2}\).
The points are chosen to be the Chebyshev nodes, for stability reasons. The first-kind nodes are:
This choice makes the expansion of the displacement field be a Fourier series, rendering the method a spectral one.
2.2.1 Solution of the homogeneous problem
For a homogeneous ball with prescribed surface displacement, a spectral solution of Eq. (1) is sought. Substituting Eq. (7) into Eq. (1), the following matrix form is obtained for the (approximate) equilibrium equation:
where the superscript ‘h’ means ‘homogeneous’ and the representative matrix W is constructed as follows [23]:
where \({\textbf {M}}_0\) is the identity matrix of rank N and
Since the system is homogeneous and the matrix \({\textbf {W}}\) is singular, regularization is needed. Here, the so-called \(\tau \)-method [24] is followed. The last two equations in Eq. (9) are substituted by the two Dirichlet boundary conditions for the displacements (Neumann BCs are unstable), so that Eq. (9) is replaced by the equations as follows:
where \(u_b\) is taken from the analytical solution in this case (the ball-sphere assemblage) and in the case of general homogenization from the applied effective strain and the RVE size. The homogeneous solution obtained by solving the system in Eq. (14) for the same parameters as used for the analytical solution is plotted in Fig. 1.
2.2.2 Solution of the inhomogeneous problem
Stress equilibrium is expressed in Eq. (4), which should hold for every r. Since this equation involves a derivative with respect to r of a linear function of the elastic constants, which jump across the boundary between the core and the shell, it turns out that Eq. (4) involves the Dirac Delta function, which does not have a stable spectral representation (this is a general problem when using spectral methods). To circumvent that, instead of solving Eqs. (4), we will opt to address its indefinite integral, namely:
The stress calculated for a smooth displacement field (as one produced by a Chebyshev expansion) calculated with elastic constants having a jump (proportional to the stiffness ratio between the phases), will also contain a jump. For the second term in \({\mathcal {I}}_1\), the jump will be lifted. However, the first term in \({\mathcal {I}}_1\) is still discontinuous, and thus cannot be treated in a stable manner by a spectral solver. To overcome this obstacle, we will perform a second integration along the polar coordinate r, and obtain the following equation:
The second term in \({\mathcal {I}}_2\) is a double integral of a function with a finite jump, and as such, it is smooth. Consequently, this term can be spectrally expanded with strong convergence and thus this term will not lead to round-off-errors-induced instability. However, the first term is an integral over a function with a finite jump, and as such is continuous, but nonsmooth. This nonsmoothness may lead to instability. Taking a third integral is not possible, since a second-order differential equation can only be solved with two integrations, or more unknown coefficients will emerge than the number of boundary conditions. Therefore, another regularization is needed to prevent possible instability due to weak convergence, for which a long convergence ‘tail’ may start ‘resonating’ with round-off errors. Here it is opted to use a filter, specifically for the first term. The following is suggested (with \({\bar{\sigma }}_*\) defined later):
2.2.3 The spectral-space equations
The inhomogeneous problem should be solved iteratively, starting from the following initialization:
For every iteration number n, the spectral-space (Fourier-transformed) strain components should be calculated by applying spectral operators as follows:
where [23]
Once the spectral coefficients of the two strains, namely \({\hat{\epsilon }}^{(n)}_{s}(k),{\hat{\epsilon }}^{(n)}_{r}(k)\), have been obtained for a given iteration number, n, the corresponding inverse Fourier transforms have to be computed.
At the Chebyshev nodes, the said inverse Fourier transforms would be:
(where \(\tau _i\) denote general real-space nodes in the radial direction).
Due to the definition of the Chebyshev polynomials of the first kind as rising-frequency cosines, and the choice of Chebyshev nodes, the inverse transforms above are in fact Fourier transforms. One could calculate them by the FFT algorithm. However, in the 1D setting the computational runtime is not particularly challenging, thus the expressions given above are suggested with no alteration. In the 2D setting addressed subsequently in this work, computational runtime may already become an issue and, therefore, it is there where the formulation is changed and Chebyshev transforms are expressed by use of the more efficient FFT algorithm.
Once having the relevant strain components in the real space at iteration n, the constitutive law is to be applied, to obtain the stress components. The following two real-space measures are relevant:
The medium characteristics are assumed to be encompassed in the elastic properties, which are the Lamé parameters in the considered case. Those should be defined over the entire computational domain, which means using step functions, for a regular composite:
where H(z) is the Heaviside function.
For the starred values, a filtering algorithm is suggested, as follows.
2.2.4 The smoothening filter
Filtering material properties in high-contrast composites to improve convergence in calculating Fourier transforms can be achieved by local simplified homogenization, as in [25]. Here, instead, a simple iterative algorithm is suggested.
The fields \(\xi _*=\lbrace \lambda _*,\mu _*\rbrace \) are obtained upon convergence of the following iterative smoothening algorithm. First, an iterative filter is initialized with the discontinuous moduli:
Then (and for every filter-iteration), the discrete gradient is defined as
Next, a typical maximal discretization-induced jump-slope is calculated:
Finally, the filter is updated as follows:
(in the expression for \({\tilde{z}}_i^{(m+1)}\), the second and third cases are mutually excluding: the jump is either at the current or the previous interval—the next interval is considered as the current when the filter is applied to the next node).
The filtering algorithm should run over i from 2 to \(N-1\) for several iterations m until converging at \(m=m^*\). Then, the filtered vector of stress values along the discrete grid should be given by:
The following relations are appropriate for a sufficient, conservative filter: \(\beta /\alpha \in [10,20], \alpha \in [1,2]\). For most of the examples solved in this work, the choice \(\beta =10\alpha \) was made unless specified otherwise. The value of the smoothening-intensity \(\alpha \) is determined by fast numerical optimization in each calculation. The effect of the filter is demonstrated in Fig. 4. Typically, \(m^*<20\).
2.2.5 Fourier–Chebyshev transforms
Once the two relevant real-space stress components \({{\tilde{\sigma }}},{\bar{\sigma }}_*\) are obtained for a given iteration n, the transforms \({\mathcal {F}}\lbrace {{{\tilde{\sigma }}}}\rbrace , \ {\mathcal {F}}\lbrace {r{\bar{\sigma }}_*}\rbrace \) should be calculated by forward Fourier–Chebyshev (FC) transform, as follows:
which for Chebyshev nodes becomes
upon using the Gauss–Chebyshev quadrature rule, and for the second stress component as follows:
Using the appropriate (two) Gauss–Chebyshev quadrature rules, one gets:
where \(k=1\ldots N\) and the second-kind Chebyshev nodes are specified by:
The obtained result implies that Eqs. (22–29), which are written for a general set of real-space nodes \(\tau _i\), should be implemented twice, once for \(x_i\), and once for \(y_i\). The calculation of the forward transforms should be performed recursively, for increasing values of the wave-number k, where the vector \(T_{k}(\tau _i)\) should be obtained using the recurrence relation, as follows:
Having at hand the FC transforms of the appropriate stress components, one can formally obtain the FC transform of Eq. (18) at iteration n, as follows:
where use is made of spectral operators representing real-space single and double anti-derivatives vanishing at \(x_i=x_1,y_i=y_1\), defined in matrix form as follows:
where \(\check{{\textbf {L}}}\) is a matrix of size \(N\times N\), defined as follows:
After obtaining the Fourier–Chebyshev expansion coefficients of the double integral (over the polar coordinate r) of the stress-equilibrium equations, one can acknowledge the fact that the double integration allows the addition or subtraction of a linear term in spatial coordinates. As the first two spectral coefficients allow to span a linear expression in real space, clearly, the first two spectral expansion coefficients of the twice-integrated equilibrium equations are of insignificant values. This means that two additional equations are needed to close the system of size N. Clearly, such equations are the boundary conditions. Borrowing from Eq. (15), the final set of the nonlinear equations in spectral space to be solve is as follows:
We now have a system of N equations of the form \({\textbf {f}}({\textbf {U}})=0\), which should be solved iteratively, using a general-purpose efficient numerical equation solver. The most appropriate candidate for a solver is the low-memory ‘good’ Broyden method, as was recently employed in [26]. In general, the idea is that a corrector for the spectral coefficients of the displacement field can be obtained according to the update formula below:
with the convergence criterion \(\Vert {{\textbf {f}}}^{(n)}\Vert <\epsilon _c\). Also,
The update of the approximate inverse Jacobian, \(\tilde{{\textbf {J}}}\), follows the closed-form relation below:
with
and
and with the initial condition \({\tilde{J}}_{kj}^{(1)}=\delta _{kj}\). Since \(U_k^{(n=1)}=U_k^h\), the remaining quantities required for the algorithm are \({\textbf {U}}^{(2)}\) (as \({\textbf {f}}^{(2)}\) then yields from Eq. (39)), and \(\tilde{{\textbf {U}}}^{(2)}\).
Regarding the nonlinear-iteration index, n, clarification may be in order. In fact, the update formula for the approximate inverse Jacobian matrix for general large enough n as employed here is the standard one for the good Broyden algorithm, and indeed, for \(\tilde{{\textbf {J}}}\), the overall iteration index is also the Broyden index and the consecutive-update iteration index. The quantity \(\tilde{{\textbf {J}}}\) is calculated after f, in the same iteration. However, in the update formula for the variable \({\textbf {U}}\), in the standard algorithm, Eq. (40) would have \({\tilde{J}}_{kj}^{(n-1)}\) and not \({\tilde{J}}_{kj}^{(n-2)}\). But in a standard algorithm, the iterations for \({\textbf {U}}\) and \({\textbf {f}}\) would start together with the Broyden iterations for \(\tilde{{\textbf {J}}}\). In contrast, here, the Broyden algorithm only starts from the second iteration, and thus the superscripts of \(\tilde{{\textbf {J}}}\) lag by 1, as the first iteration is performed not with the Broyden update but with another method (outlined below).
Also, of course, the deviation from the standard Broyden algorithm is encompassed in the separate equations for \(n=1,2,3\), as given by Eqs. (41, 43, 44). In fact, the Broyden algorithm starts from the third iteration of the nonlinear solution procedure, but the alternative method employed for the second iteration also produces an intermediate step for the third iteration. This intermediate step is encompassed in generating the value \(\tilde{{\textbf {U}}}^{(2)}\). The reason for this complexity is that the Broyden method converges fast when its first guess is close enough to the solution. To guarantee that, the approximate inverse Jacobian matrix has to be calibrated somehow. This is achieved by generating three initial values of \({\textbf {U}}\) by other methods. As aforementioned, \({{\textbf {U}}}^{(1)}\) is generated by the homogeneous solver, and the two subsequent values are generated by the method of Green function of Moulinec and Suquet [14] (which is a fixed-point-iteration-based method), as follows:
2.2.6 Derivation of the mapping \({\mathcal {G}}\)
For low heterogeneity (of material properties), it is possible to approximate the displacement field by iteratively solving the equilibrium equation using a fixed-point mapping, in which the left-hand side is a double spatial integral of the stress-equilibrium equation of a homogeneous medium (with the same displacements at the boundaries of the domain as for the full heterogeneous system). The right-hand side, in turn, is the correction, accounting for the heterogeneity. Using the quantities derived in the previous subsections, the following equation emerges:
The idea is to use the divergence of the excess stress produced strictly by material heterogeneity as a sort of a body-force, iteratively, assuming the heterogeneity-related fluctuating part of the displacement field will sharpen in each iteration, when the ‘body-force’ is calculated based on the previous, less-fluctuating, more homogeneous displacement field. Such an iterative fixed-point is known to converge for small-contrast composites. In our case, we do not assume necessarily small-contrast phases, although this assumption is not unreasonable for polycrystalline metals where the phases are different grains, more or less similar in properties (up to statistical differences related to different crystal orientations). In any case, we opt to use this method only for two iterations, and not till convergence is achieved. After two iterations, the solver should switch to the good Broyden algorithm.
Evidently, one observes that \(q_l^{(1)}\) can be calculated with \(\hat{{\mathcal {I}}}_l^{(1)}\), instead of \(\Delta \hat{{\mathcal {I}}}_l^{(1)}\), since the \({\textbf {W}}\) matrix is singular and \({\textbf {U}}^{(1)}\) has only two nonzero components (the first two), as corresponds to a spatially linear field and as such is an eigenfunction of the homogeneous equation, and there will be only the difference in the first two components, which will be eliminated by the boundary conditions. However, in the second iteration this will no longer be the case, and the actual excess heterogeneity-induced stress divergence is required for the update. Moreover, there is also the difference between \(\hat{{\mathcal {I}}}_l^{(1)}\) and \(\Delta \hat{{\mathcal {I}}}_l^{(1)}\) produced by numerical round-off errors in the homogeneous solution (numerical solution of a linear system). This additional noise activates instability in the iterative scheme, which is in fact stable when taking strictly the heterogeneity-induced excess-stress divergence on the right-hand side.
For the auxiliary spectral displacement field iteration, which is the initial point assumed by the first Broyden iteration, the following formula should be used:
(only the fluctuation changes), where
Now, \(\Delta \hat{{\mathcal {I}}}_l^{(n)}\) is calculated similarly to \(\hat{{\mathcal {I}}}_l^{(n)}\) but with difference expressions for the real-space stress fields. Instead of Eq. (23), the following expressions should be used:
for \(n=1,2\). The effective elastic properties are \(\bar{\lambda }^{(n)},\bar{\mu }\) and the effective longitudinal modulus is \({\bar{M}}_{(n)}=\bar{\lambda }^{(n)}+2\bar{\mu }\).
The reason for division by \({\bar{M}}\) in Eqs. (47, 49), is that the homogeneous equilibrium equation considered throughout this study is actually the homogeneous stress divergence divided by the longitudinal modulus.
The reason for using specifically the effective moduli here is as follows. For the solution of the homogeneous spherically symmetric linear-elastic problem with specified boundary displacement, the values of the elastic properties play no role. However, when (small) heterogeneity in the elastic properties is introduced, it is assumed to slightly perturb the basic displacement field. This basic displacement field corresponds to zero heterogeneity. It can also be viewed as an average, coarse-grained field corresponding to the average elastic properties of the medium. These are also termed the effective elastic properties. In this sense, the homogeneous baseline displacement field is perceived to be associated with corresponding equilibrium-stress, emerging from the homogeneous displacement field, when the effective elastic properties are considered. Therefore, for a convergent fixed-point iteration, as the one in Eqs. (46, 48), corresponding to small phase-contrast, the left-hand side (which is the homogeneous stress-equilibrium equation) is associated with the effective elastic properties. This, in turn, for the spherically symmetric case, is associated with multiplication of the left-hand side by the effective elastic longitudinal modulus—or division of the right-hand side by that modulus.
Even though taking specifically the effective elastic properties is essential for the convergence of the fixed-point iteration, and the convergence is only guaranteed for small phase-contrast [18, 19], we maintain this choice here. Even though the fixed-point iteration is not required to provide convergence in the present algorithm and the phase-contrast is not assumed to be small, still specifically the effective moduli are used in the formulae. The reason for this choice is the idea that it is appropriate to maintain the link to the traditional approach and make it a natural extension of the slightly perturbed case with flat Cartesian metric, where the scheme converges with no need for a general-purpose solver, such as the Broyden method. Next, the derivation of the effective elastic properties is outlined.
2.2.7 The effective elastic properties
The effective shear modulus for a spherically symmetric core–shell composite can be derived analytically, as follows. The composite has a circular axisymmetric cross section about any axis of rotation and thus simple torsional theory applies, and the effective shear modulus can be calculated by direct averaging of the torsional rigidity of ‘slices’ perpendicular to the axis of rotation (dividing by the diameter), if one assumes that the composite is welded at an infinitesimal area at the surface and is subjected to a torque around an axis coincident and normal with the welded area, and going through the center of the sphere. The constitutive law of torsion then relates the applied overall torque, \(\bar{{\mathcal {T}}}\), to the maximum angle of rotation of a plane normal to the axis of rotation, \(\theta \):
For a piecewise-constant shear modulus corresponding to a core and a shell, the effective value becomes:
The effective bulk modulus for the present case can be derived from the analytical solution, as given by Eqs. (5, 6). The derivation is as follows: the bulk modulus is defined as the outer pressure divided by the overall relative volume decrease:
(where \(\epsilon _v\) denotes hypoelastic volumetric strain).
Substituting Eq. (6), this yields:
2.2.8 Homogenization (numerical)
For the linear-elastic regime, homogenization consists in finding the effective elastic properties by performing numerical volume-averaging. For the spherically symmetric case, only the applied pressure and volumetric strain can change, and thus only the effective bulk modulus can be found by numerical homogenization. Therefore, we next describe the procedure of numerically determining the effective bulk modulus. Clearly, in view of the above, it has to be assumed that the effective shear modulus is known (since two effective Lamé coefficients are needed for the solution procedure). We will assume that the shear modulus is known from an external source. In practice, we will use the analytical formula derived above.
The task will now be to numerically determine the effective bulk modulus. We will achieve it by utilizing a formula similar to the one in Eq. (53). In other words, we will take a volume average of the volumetric strain, to obtain an estimate of the effective bulk modulus, as follows:
The iterative solver requires in Eq. (50) the values of the effective Lamé parameters. The effective shear modulus is already given in Eq. (52). The remaining Lamé parameters should be determined as follows:
(the last values are auxiliary and are only needed for the second and third iteration of the solver, before the Broyden method is called).
After the algorithm converges, the numerically homogenized bulk modulus should also converge, desirably to the value obtained analytically for the considered benchmark example.
In essence, the first guess for the numerically effective bulk modulus is obtained from the homogeneous displacement field. In this sense, the procedure can be employed for a general shell-assembly, the only problem would be to have an analytical estimate for the effective bulk modulus, to validate the numerical homogenization. The benchmark example with a core–shell composite is solved in the following subsection, where the radial displacement field and stress are shown for both the analytical and the numerical solution, along with convergence history and the obtained value of the effective bulk modulus, for the considered problem parameters.
This concludes the theory for the linear-elastic spherically symmetric case, as far as the numerical method is concerned.
2.3 Numerical example
The developed spectral solver was employed for a core–shell composite with the following parameters (where the subscript a refers to the core and b to the shell, and \(\epsilon _c\) is convergence-value of the residue of the equilibrium equations in Fourier space):
2.3.1 Stiffer core, ‘softer’ shell
The first example was solved for a stiffer (copper) core, and a more compliant (aluminum) shell, with the following parameters:
The value of \(\alpha \) should be above unity for smoothening to take place. In the considered example, stability was achieved already for \(\alpha =1.19\).
In the examples below, the number of spectral modes was set equal to the number of integration points (Chebyshev nodes of either kind). It is important to note that the radial coordinate is normalized (nondimensionalized).
Figure 1 shows the radial displacement profile in the composite, with the analytical solution, the homogeneous first guess and the converged spectral solution. Figure 2 shows the radial stress distribution of the analytical solution and selected points from the numerical solution. Figure 3 shows the convergence history of the norm of the equilibrium equations (their double spatial integral in spectral space). Figure 4 shows the effect of the smoothening filter on the spatial distribution of the elastic moduli profiles.
Radial displacement profile—analytic solution (solid red), homogeneous first guess—dash black and convergent spectral solution—dash blue(colour figure online)
The analytical and numerical effective bulk moduli as obtained in the considered example are:
One notes the resemblance of the derived profiles to those shown in [30].
Radial stress profile—analytic solution (solid red) and convergent spectral solution—blue circles(colour figure online)
Convergence history of the norm of the equilibrium equations
Effect of the smoothening filter on the spatial distribution of the elastic moduli profiles
2.4 A three-phase composite: core, intermediate shell and outer shell
This subsection complements the linear-elastic spherically symmetric composite problem by considering also a three-phase assemblage. We will not repeat here all the steps of the solution-algorithm as outlined above, only providing the additional, necessary, details.
2.4.1 Analytical solution for a core–shell–shell composite under external pressure
For a core–shell–shell composite, the analytical solution for the displacement field reads:
with
The effective shear modulus, obtained for the assumption of pure torsion, reads:
The bulk modulus, obtained analytically in the same manner as for the core–shell composite, is given by:
2.4.2 Numerical solution for a core–shell–shell composite under external pressure
The spectral solution can be obtained for this case similarly to the way it is done for the core–shell composite, with a few notes. In the homogenization formula in Eq. (55), one should replace b by the relevant outer surface radius, c. Also, everywhere, the normalization of quantities with the dimension of length, should be done with c, rather than b. The obtained results are as follows.
2.4.3 Copper core, aluminum filling, copper ‘jacket’
An example was solved for a copper core and ‘jacket’ and aluminum filling, with the following parameters:
Figure 5 shows the radial displacement profile in the composite, with the analytical solution, the homogeneous first guess and the converged spectral solution. Figure 6 shows the radial stress distribution of the analytical solution and selected points from the numerical solution. Figure 7 shows the convergence history of the norm of the equilibrium equations (their double spatial integral in spectral space). Figure 8 shows the effect of the smoothening filter on the spatial distribution of the elastic moduli profiles.
Radial displacement profile—analytic solution (solid red), homogeneous first guess—dash black and convergent spectral solution—dash blue(colour figure online)
Radial stress profile—analytic solution (solid red) and convergent spectral solution—blue circles (one notes that the stress distribution is harder to capture with the spectral method for a case with more phases, since it challenges interpolation with a fixed number of harmonics)(colour figure online)
Convergence history of the norm of the equilibrium equations
Effect of the smoothening filter on the spatial distribution of the elastic moduli profiles
The analytical and numerical effective bulk moduli as obtained in the considered example are:
3 The 1D spherically symmetric case—elastoplastic regime (linear elasticity, perfect plasticity)
In the 1D setting, there is the advantage that there are no rotations, and thus the hyperelastic formulation does not have the feature of correcting the representation of geometric nonlinearity. Its only benefit is thus correct description of large elastic stretches. However, large elastic stretches are only observed in elastomers, which usually do not exhibit plasticity. Therefore, we opt for treating the 1D-case plasticity with linear elasticity.
3.1 The yield-flow stress, kinematic assumption and constitutive law
For estimating the form of the scalar function of the stress tensor for which plastic flow may occur, we assume the well-known yield condition of linear-elastic material under spherical symmetry according to both the Tresca and von Mises models,
The assumption of perfect plasticity is encompassed in the postulate that the RSS at which material yields remains the flow stress as long as plastic strain accumulates.
The additive elastoplastic decomposition is assumed here to hold for the small-strain tensor, namely
Finally, linear Hooke’s law is assumed to relate the (Cauchy) stress to the elastic strain tensor.
3.2 Analytical solution for a (stiffer) linear-elastic core and a linear-elastic–perfectly plastic shell
For the case of a linear-elastic core–shell composite with different Lamé parameters (with \(\kappa _a>\kappa _b\)) and external pressure p, the critical pressure for onset of plasticity is:
For higher pressure, plasticity will emerge at the core–shell interface. For even higher pressure, the entire shell will become plastic. The core will remain elastic for any pressure within the framework of the linear-elastic model and the assumed pressure-independent \({\mathcal {J}}_2\)-plasticity (since then the stress deviator is identically zero).
The following solution would then hold for the displacement field, if we assume perfect plasticity, in which the flow stress is constant and equal to the yield stress:
and for the stress field:
(one notes that for \(a=0\) this stress field is indeed singular, as anticipated in the discussion given above, for slip-based plasticity in polar symmetry).
The stress distribution is found solving for the first-order stress-equilibrium equation directly. The displacement field is integrated subsequently using the spherical linear-elastic constitutive relation. To obtain the critical pressure value for yield of the entire shell, a kinematic assumption is needed.
Then, one derives the following (higher than \(p_{cr}^{(1)}\)) critical value of the pressure (by requiring \(|\epsilon _{rr}^{p}(r=b)|>0\)):
with the condition \(p>p_{cr}^{(2)}\).
The radial displacement and stress fields for the derived analytical solution for the linear-elastic–perfectly plastic model are plotted in Figs. 9 and 10 for appropriate parameter values.
3.3 Numerical (spectral) solution
Assuming linear-elastic response and additive strain decomposition (which follows from multiplicative elastoplastic decomposition for linear-elastic response), we can derive the expressions for the stresses defined in Eq. (22) to account for plastic strains. For linear-elastic response and standard \({\mathcal {J}}_2\)-plasticity, the plastic strain is deviatoric and thus the following condition holds:
where \(\epsilon _r^{p}, \ \epsilon _s^{p}\) are defined as the plastic counterparts of \(\epsilon _r\) and \(\epsilon _s\).
Then, the constitutive response becomes dependent on one internal variable only, and the relevant stress components (before filtering) become:
where \(\epsilon _r^{p}\) is given by the following explicit expression:
This is an example of nonsmooth (piecewise-smooth) constitutive response. This linear-elastic–perfectly plastic constitutive response was implemented in the framework of the spectral solver and the results were compared to the analytic solution, as discussed in the following section.
3.4 Numerical example—stiff core, ‘softer’ (entirely plastic) shell
An example was solved for a stiff (copper) core and a more compliant (aluminum) and moreover entirely ‘plastified’ shell, with the following parameters (here, uniquely, the value of \(\beta /\alpha \) was doubled to 20, to accommodate the perfect-plasticity-related nonsmoothness):
(and using Eq. (77)).
Radial displacement profile—analytic solution (solid red), homogeneous first guess—dash black and convergent spectral solution—dash blue (colour figure online)
Radial stress profile—analytic solution (solid red line) and convergent spectral solution—blue circles (colour figure online)
Convergence history of the norm of the equilibrium equations
Effect of the smoothening filter on the spatial distribution of the elastic moduli profiles
The resulting effective total strain is no higher than about \(1\%\), which renders the linear-elastic approximation and the additive strain-decomposition reasonable.
It is interesting to compare the displacement fields for the linear-elastic versus the linear-elastic–perfectly plastic solution for the same applied pressure.
Radial displacement profile—linear-elastic solution (dash red), linear-elastic–perfectly plastic solution—dash blue (colour figure online)
Figure 9 shows excellent agreement between the numerical-spectral and analytical solutions for the displacement field. Figure 10 covers the validation in terms of stress, complementing the validation by displacement, where the displacement is less sensitive to error. The radial stress is indeed nearly uniform, as the pressure is much higher than the yield stress and the geometry is pressure-dominated. Figures 11 and 12 are similar to their counterparts for the hyperelastic response. The iterative algorithm is terminated after reaching a plateau in the equation-norm error. The plateau is at a reasonable value to determine convergence. As for all the previous cases, the number of Chebyshev nodes used in the spectral approximation was taken as \(N=100\).
Figure 13 shows the radial displacement profile in the composite, with the reference solution for the linear-elastic limit (with the same displacement boundary conditions) and the converged spectral solution for the linear-elastic–perfectly plastic formulation. There is noticeable though limited deviation between the linear-elastic and elastoplastic response. The boundary displacement is larger in absolute value in the (weaker) elastoplastic composite for the same pressure (compared to unyielding material), whereas the core displacement is smaller in absolute value in the elastoplastic case, as the plastic shell takes on most of the displacement and provides some displacement-screening to the elastic core.
3.5 Homogenization
3.5.1 Analytical solution
One can compare the ambient bulk modulus with the tangent bulk modulus for pressures for which the entire shell has yielded. For the specified parameters, the two values, as can be obtained from the analytical solution, are as follows:
where the parameters were assumed to take the values specified in the previous section (\(a/b=0.7\), etc.).
Clearly, the effective tangent bulk compressibility after the yield of the entire shell can be obtained from the ambient effective bulk compressibility by setting \(\mu _b/\kappa _b\rightarrow 0\), which is expected, since perfect-plastic yield implies the decrease in sheer stiffness. For the chosen parameters, plastic yield of the entire aluminum shell corresponds only to about \(1\%\) reduction in the effective tangent bulk modulus. Indeed, with spherical symmetry, for realistic materials, plastic (deviatoric) yield has little effect on the (spherical) stress–strain relation.
For analytic estimation of the effective shear modulus, we cannot assume a combined torsion-compression stress state, but a reasonable estimate can be obtained if we assume pure torsion applied to a composite with an elastic core and a plastic shell—such that the torque is large enough for yield of the entire shell:
3.5.2 Numerical solution
Calculation of the tangent bulk modulus for the linear-elastic–perfectly plastic case using the spectral solution (through a numerical derivative) gives the following values (for the iterative solver still Eqs. (55–56) are employed, as plastic strain is isochoric and the elasticity is linear):
which correlates well with the analytical values.
This concludes the analysis for the 1D, spherically symmetric case. The next section presents the analysis for the 2D polar case—for a composite material occupying a domain on a disk punctured in the center.
4 Composites with isotropic linear-elastic phases—polar 2D analysis
4.1 Spectral solution for the homogeneous case
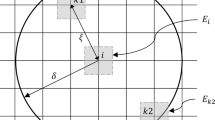
For homogeneous, isotropic, linear-elastic material, the static equilibrium equations in 2D polar coordinates (on a punctured disk with inner and outer radii \(r_0\) and c, respectively), read:
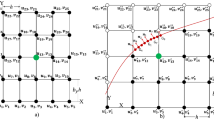
where \(u_r,u_{\theta }\) are radial and angular displacements, respectively, and \(\lambda ,\mu \) are the Lamè coefficients. In addition, appropriate boundary conditions should be specified: \(u_r(r=r_b,\theta )=u^{(r_b)}_r(\theta ),u_{\theta }(r=r_b,\theta )=u^{(r_b)}_{\theta }(\theta )\).
In order to solve the equilibrium equations above, the unknown displacement fields are expanded into truncated Fourier series in \(\theta \), as follows:
where the two Fourier-coefficient fields are given by:
and \(\theta _j=\frac{2\pi j}{N_{\theta }}\) are angular Fourier gridlines. One easily finds from the above equations that the Fourier coefficient of \(\partial {u_r}/\partial {\theta }\) is \(iqR_q\), and the same holds for \(u_{\theta }\). It is easier to solve second-order equations with positive-power coefficients, and thus the equations are multiplied by \(r^2\), which does not change the solution space. Also, to get convergence of the entries of the matrix representing the linear differential operator for high angular harmonics, it is instructive to perform double angular integration, which amounts to dividing by \(-q^2\). Hence, taking angular Fourier transforms of Eqs. (79–80), one obtains the following equations for \(R_q(r)\) and \(\Theta _q(r)\), when also dividing by the reference Lamè coefficients (and changing the sign):
for \(q=1,2,\ldots ,N_q-1\). For \(q=0\), separate equations are derived.
After solving Eqs. (83–84) on a grid of concentric circles \(r_i, i=1\ldots N_r\), one can obtain the displacements on the 2D grid by setting \(r\rightarrow r_i, \theta \rightarrow \theta _j\) in Eq. (81).
4.2 Solution of Eqs. (83–84) on a grid using Chebyshev polynomials
Numerical solution of the Fourier transforms of the equilibrium equations on a discrete grid of radial points is next sought in the form of a truncated expansion in Chebyshev polynomials:
such that
where \({{\hat{r}}}_0=r_0/c\).
The points \(x_i\) are chosen to be the Chebyshev nodes, for stability reasons. The nodes are:
As noted in the 1D analysis section, this choice makes the expansion of the displacement field be a Fourier series, rendering the method a spectral one.
For a homogeneous punctured disk with prescribed boundary displacements, spectral solution of Eqs. (83–84) is sought. Substituting Eq. (85) into Eqs. (83–84), the following matrix form is obtained for the (approximate) equilibrium equation:
and the representative matrix \({\textbf {W}}^{(q)}\) is constructed as follows:
and
where \({\textbf {M}}_0\) is the identity matrix of rank \(N_r\) and
Since the system is homogeneous and the matrix \({{\textbf {W}}}^{(q)}\) is singular, regularization is needed. Again, the \(\tau \)-method [24] is followed. Four equations in Eqs. (88) are substituted by four Dirichlet boundary conditions for the Fourier transforms of the punctured disk-boundaries displacements distributions (Neumann BCs are unstable), so that Eqs. (88) are replaced by the equations as follows:
The boundary conditions considered in the example solved in this section correspond to small radial, negative, angle-independent displacement on the perimeter, although more complex boundary conditions, as, say, those representing simple shear, could be addressed too. The angular Fourier transforms of the radial and angular boundary displacements for the assumed boundary conditions would be:
where \({\mathfrak {E}}_p\) is imposed radial strain, and \(r_b\) represents either \(r_0\) or c.
Computational efficiency considerations. It may be beneficial to solve the homogeneous system in Eq. (91) using a multigrid approach, that is, only actually solving it for small resolution and employing the corresponding double-spectral-transform coefficients for subsequent iterative solution of the inhomogeneous problem. In that case, the solution of the homogeneous problem would not contribute significantly to the overall CPU, since one would only need to solve a linear system of dimension \({\mathcal {O}}(\log {N})\), N being the convergence-providing number of 2D gridpoints.
After solving the homogeneous problem for \(\log {N}\) gridpoints, N being the eventual, convergent number of gridpoints, one would not even have to interpolate the results on a (twice-) finer grid, like in spatial methods (be it FE or finite difference, etc.). Instead, it would be sufficient to construct the initialization vector of double-Fourier coefficients for the inhomogeneous problem on a twice denser grid as follows:
It should be stressed, however, that the discussion above is at this stage rather hypothetical, as a multigrid strategy was not actually implemented in a specific example. The matter is noted merely to point a potential implementation rendering the Cartesian and polar spectral methods for composite materials (asymptotically) equivalent in terms of estimated runtime.
4.3 Solution of the inhomogeneous problem
After solving the homogeneous problem and employing the inverse Fourier transforms, one can obtain the displacements at the real-space gridpoints. From those displacements, the three 2D stress components can be readily computed using the following formulas:
The two equilibrium equations can then be (multiplied by \(r>0\) and) written as:
One can then take Fourier transforms in the angular direction of the two equilibrium equations to obtain the spectral-space equilibrium equations, as follows:
for \(q=0,1,\ldots ,N_q-1\).
Stress equilibrium is expressed in Eq. (100), which should hold for every r. Since these equations involve derivatives with respect to r of linear functions of the elastic constants, which jump across the boundary between different phases, it turns out that Eq. (100) involves the Dirac Delta function, which does not have a stable spectral representation (this is a general problem when using spectral methods). To circumvent that, instead of solving Eqs. (100), we will opt to address their indefinite integrals, namely:
The stress derived from a smooth displacement field (as the one produced by a Chebyshev expansion) calculated with elastic constants having a jump (proportional to the stiffness ratio between the phases), will also contain a jump. For the second and third terms in \({\mathcal {I}}_{11}\) and \({\mathcal {I}}_{21}\), the jump disappears. However, the first terms in \({\mathcal {I}}_{11}\) and \({\mathcal {I}}_{21}\) are still discontinuous, and thus cannot be treated in a stable manner by a spectral solver (the Gibbs phenomenon will lead to instability in an iterative solution). To overcome this obstacle, second integration along the polar coordinate r is performed, leading to the following equations:
Similarly to the case in the 1D analysis, the second and third terms in \({\mathcal {I}}_{21}\) and \({\mathcal {I}}_{22}\) here are double integrals of a function with a finite jump, and as such, they are smooth. Consequently, these terms can be spectrally expanded with strong convergence and they would not lead to instability or runtime increase. However, the first terms in \({\mathcal {I}}_{21}\) and \({\mathcal {I}}_{22}\) are integrals over functions with finite jumps, and as such they are continuous, but nonsmooth. Taking a third integral is not possible, since a second-order differential equation can only be solved with two integrations, or more unknown coefficients will emerge than the number of boundary conditions. In the 1D analysis, where a second-order solver was employed (due to its quadratic convergence and small memory requirement owing to the small amount of data in 1D), another regularization was needed to prevent possible instability due to weak convergence, for which a long convergence ‘tail’ may start ‘resonating’ with round-off errors. There, it was suggested to use a filter, specifically for the first terms in \({\mathcal {I}}_{11}\) and \({\mathcal {I}}_{21}\). In the 2D case, filtering does not seem to affect the result and the aforementioned instability is not manifested when using a first-order dissipative solver and removing the polar singularity in the center by puncturing the disk of the computational domain.
4.3.1 The spectral-space equations—inverse Fourier transforms
The inhomogeneous problem should be solved iteratively, with initialization from the solution of the homogeneous problem.
For every iteration number n, at the Chebyshev nodes, the inverse Fourier–Chebyshev transforms would be:
Due to the definition of the Chebyshev polynomials of the first kind as rising-frequency cosines, and the choice of Chebyshev nodes, the inverse transforms above are in fact Fourier transforms. Since \(T_m(z)=\cos (m\arccos (z))\), one has:
Also, at the Chebyshev nodes, one can calculate the derivative as follows:
Introducing the following definitions:
one can express the required displacements and strains as Fourier transforms allowing computation with the FFT algorithm:
where
are canonical-form forward and inverse discrete Fourier transforms, which can be implemented using the FFT algorithm in \({\mathcal {O}}(N_r\log N_r)\) time. Such transforms should be calculated for every angular harmonic q rendering the overall operation linear in \(N=N_rN_q\). However, if multiple cores are available, of the order of \(N_q\), then the inverse transforms can be calculated in parallel, making this part of the algorithm run in time of \({\mathcal {O}}(\sqrt{N})\) (in log-terms-suppressing notation).
The next step is calculation of the inverse angular Fourier transform of the relevant strain components, as follows:
where
The inverse transforms \(\tilde{\mathbb {F}}\) in Eq. (109) can be performed using the FFT algorithm in parallel computation, with a different processor for every l value. This is possible even for several hundreds of radial divisions, assuming a cluster with several hundreds of cores is available.
It is crucial to note that it is not suggested here to use a parallel, distributed, FFT algorithm. Instead, it is proposed to use a single-node FFT algorithm, albeit to run radial FFT algorithms simultaneously for different angles on the disk.
It should be noted that many standard FFT definitions often contain division by the number of Fourier harmonics in the inverse transform and no division in the forward transform, contrary to the choice made in this work, where the division is assumed in the forward transform, to reproduce uniform distributions by a single-term expansion.
The inverse Fourier transforms in the radial and angular directions should be done in a sequence, first the radial, then the angular, using simultaneous execution of single-node FFT code for every angular harmonic (for the radial transform) and then for every radial point (for the angular FFT). Then, the overall runtime of the double inverse transform could be \({\mathcal {O}}(\sqrt{N}\log {N})\) (or \({\mathcal {O}}(\sqrt{N})\) in the log-terms-suppressing notation as used in [27]).
Once having the relevant strain components in the real space at iteration n, the constitutive law in Eq. (98) is to be applied at each real-space gridpoint, to obtain the stress components’ arrays.
The medium characteristics are assumed to be encompassed in the elastic properties, which are the Lamé parameters in the considered case. Those should be defined over the entire computational domain, which means using step functions, for a typical composite.
If \(N_r\) parallel cores are available, then \(N_r\) parallel sequences of \(N_{\theta }\) consecutive computations in each can be performed, for the (local) calculation of stress from strain. The time required for this part of the computation would also be \({\mathcal {O}}(\sqrt{N})\).
4.3.2 Forward Angular Fourier transforms
After the calculation of the real-space stresses, angular Fourier transforms should be computed (for every angular harmonic). The following quantities emerge:
It is important to note that the above sums represent integrals, in the sense of a rectangular (Riemann) approximation, or, up to a correction in the end terms, also a trapezoidal approximation, which is equivalent to analytic integration over piecewise-linear interpolation. The high-frequency exponent, represented by the sine, can be approximated on a period using a piecewise-linear interpolation controlled by 3 points, with three linear segments. Therefore, in order to get correct integration, the number of integration points has to be at least 3 on the period of the highest-frequency Fourier term. In other words, it is required to have
where the choice \(N_{\theta } = 3N_q\) is found to be sufficient in the present work. Violation of the above condition leads to instability and inaccurate solution. In contrast, a Chebyshev polynomial of degree k has not 3k but only k special points (roots or extrema) on the range where it is defined, and thus \(N_r\) radial integration points are sufficient (and this is the choice made in what is shown below).
4.3.3 Forward Fourier–Chebyshev transforms
Once the three angular transforms are obtained for a given iteration n, forward Fourier–Chebyshev (FC) transforms in the radial direction should be calculated, as follows:
which for the Chebyshev nodes becomes:
where the Gauss–Chebyshev quadrature rule is employed.
It is also necessary to obtain the FC transform of the quantities \(r{\check{\sigma }}^{(q)}_{rr},r{\check{\sigma }}^{(q)}_{r\theta }\), for later use in the FC transform of Eq. (102). Unlike in the 1D case, where the center \(r=0\) was included in the computational domain, here a punctured disk is assumed, and multiplication by r does not change the type of singularity and does not require the use of Chebyshev polynomials of the second kind. Instead, direct calculation is employed:
which for the Chebyshev nodes becomes
The calculation of the forward transforms can be performed recursively, for increasing values of the radial wave-number k, where the vector \(T_{k}(x_l)\) should be obtained using the recurrence relation, as follows:
Alternatively, one can again employ the appropriate property of the Chebyshev polynomials that \(T_k(\cos (z))=\cos (kz)\) and the fact that \(x_i\) are Chebyshev nodes, to represent the FC transforms above as standard discrete Fourier transforms enabling calculation by the FFT algorithm:
and
where one defines
The four transforms as given above can be calculated on \(N_q\) cores in parallel, in which case the overall CPU would scale as \({\mathcal {O}}(N_r\log N_r)\), or, in log-term-suppressing notation, \({\mathcal {O}}(\sqrt{N})\) again, the same as the forward angular transforms, the inverse angular and radial transforms and the application of the constitutive law.
Having at hand the FC transforms in Eqs. (114) and (116) calculated efficiently according to Eqs. (118–120), one can formally obtain the FC transforms of Eq. (102) at iteration n, as follows:
where use is made of spectral operators representing real-space single and double anti-derivatives, defined in matrix form as follows:
where \(\check{{\textbf {L}}}\) is a matrix of size \(N_r\times N_r\), defined as follows:
Since the matrix \(\check{{\textbf {L}}}\) is two-banded, the complexity of multiplication of a vector (stress double transform) by this matrix is \({\mathcal {O}}(N_r)\). All six of such multiplications as given in Eq. (121) should be done at every iteration n in a separate computational core for every angular harmonic q, simultaneously (if \(N_q\) cores are available). Wherever double integration should take place, a factor of two would multiply the runtime (first multiplying the stress by \(\check{{\textbf {L}}}\) and then multiplying the result by \(\check{{\textbf {L}}}\) again). The overall runtime of the double integration in spectral space would then also be \({\mathcal {O}}(\sqrt{N})\).
After obtaining the Fourier–Chebyshev expansion coefficients of the double integrals (over the polar coordinate r) of the angular Fourier transforms of the stress-equilibrium equations (albeit multiplied by r), one can acknowledge the fact that the double integration in r allows the addition or subtraction of a linear term in spatial coordinates.
As the first two spectral coefficients allow to span a linear expression in r, clearly, the first two spectral expansion coefficients (for every value of q) of the twice-integrated-in-r angular Fourier transforms of the equilibrium equations are of insignificant value. This means that two additional equations are needed for every displacement vector, to close the system of size \(N_r\) for every q. Clearly, such equations are the boundary conditions.
The final form of the problem is finding, iteratively, the root of the function \(\hat{{\textbf {f}}}\) (defined below), as follows:
where the final equations are obtained after dividing by \(q^2\), to represent (minus) the double integration in the angular direction, necessary for stability, as mentioned earlier; dividing by the external radius c, to have units of displacement, and also dividing by the relevant reference elastic moduli, similarly to what was done for the homogeneous problem:
It is suggested here to solve these equations iteratively, using a first-order method as follows:
where the (small) stepsize \(t_n\) in every iteration n is determined by Armijo-Goldstein-kind linesearch [28], as follows:
where \(\Psi \) is the total energy of the system.
The following initialization holds:
(where \({\hat{V}}_{k}^{(q)}\) is the solution of the homogeneous problem described in Sect. 4.2).
An important feature of the approach is that the boundary conditions have to be imposed exactly and explicitly. For linear elasticity, this can be done analytically, as follows:
This means that if the boundary conditions are satisfied for the initial guess (the solution of the homogeneous problem)—and they are, then they are also satisfied for any iteration.
The iterative solution strategy using a first-order method allows updating the vector of variables independently and simultaneously for every angular harmonic, using Eq. (126), the only additional information required being the value of the scalar stepsize in each iteration n. The runtime of such parallel update is again \({\mathcal {O}}(\sqrt{N})\) (for every try of the stepsize). Fulfillment of the boundary conditions requires four summations over \(N_r\), which adds another task of complexity \({\mathcal {O}}(\sqrt{N})\) in each sub-iteration as suggested below.
4.3.4 The stepsize-determination algorithm
One of the advantages of function-minimization algorithms over equation solvers is the fact that it is easier to determine the stepsize when the goal is to minimize the value of a function. For a smooth function \(z({\textbf {x}})\), the following holds:
(where the iteration number is denoted here by k rather than n for generality—not to be confused with the radial harmonic index k from the previous subsections), which means that away from the solution any small-enough positive stepsize decreases the function value, and one can establish \(t_k\) using sub-iterations, as follows:
where strictly \(\tau \in (0,1)\) and typical values are \(\tau \in (0.5,0.99)\).
Since the stepsize increases exponentially in a finite range, the number of sub-iterations becomes logarithmic in the resolution, rendering the optimization problem tractable. Since it is always possible to find (quickly) the stepsize decreasing the objective function z, it is possible to always decrease it until the minimum is found, at which point the gradient of z vanishes, which corresponds to the solution of the system of equations. This is reminiscent of the tractability of integrable systems. When the function z, being the integral of the equations \(\nabla z=0\), exists, the solution deviates from the initial point logarithmically in time (effort). In contrast, when the integral does not exist, some initial points may lead to exponential deviation from the initial point and the solution, reminiscent of the exponential deviation of the state from a chaotic trajectory. In the optimization realm analogy, this can be seen as follows.
Without an integral, a weight function for the determination of the stepsize would usually be a squared norm of the equations, for which case the following will hold:
Such an algorithm will guarantee the decrease in the norm of the equations until its local minimum is found. The problem is that at the local minimum of the norm, it is not evident that \({\textbf {g}}={\textbf {0}}\), but rather a weaker condition is fulfilled, namely \((\nabla {\textbf {g}}^{\top }){\textbf {g}}={\textbf {0}}\). It is possible that \(\nabla {\textbf {g}}^{\top }\) be a singular matrix, in which case the solution might converge to a point which is not a root.
Another option is to use the following scheme:
But here again, if the gradient of the vector of equations becomes singular, it may happen that no small stepsize leads to a change, let alone a decrease in the norm of the equations.
Another way is to use the Newton step, for which the decrease in the value of the norm of the equations can be guaranteed with a quick linesearch,
however, if the gradient of the equations is singular, the solution will diverge.
For an arbitrary step,
a singular gradient of the equations will still lead to convergence to a point which is not a root, even for a strictly nonsingular matrix \({\textbf {A}}\). This is because the squared norm of the equations is an unreliable weight function for stepsize determination.
However, if the system is integrable, and a function \(z({\textbf {x}})\) exists such that \(\nabla z={\textbf {g}}\) and the matrix \({\textbf {A}}\) is nonsingular, then a possible optimization approach would be:
For a nonsingular \({\textbf {A}}\), the iterations would terminate only at the solution, as long as \(t_k\) is always nonzero. For any point except the exact solution, due to the nonsingularity of \({\textbf {A}}\), there would always be a nonzero stepsize \(t_k\), small enough in absolute value, for which the objective function z would be decreased by the specified step. Therefore, for a nonsingular matrix \({\textbf {A}}\), this last optimization method would be successful given a method to establish the nonzero stepsize logarithmically in time.
The relevance of this analysis to the studied problem lies in the fact that the equations to be solved, namely Eq. (124), can be expressed as the action of a linear operator on the spatial equilibrium equations, namely \(\hat{{\textbf {f}}}={\textbf {A}}\nabla \Psi \). The linear operator \({\textbf {A}}\) represents the consecutive action of double angular integration, angular Fourier transform, double radial integration, radial Fourier–Chebyshev transform and multiplication by a positive scalar (normalization by reference moduli). All those operations are obviously invertible. Therefore, for the studied case, \({\textbf {A}}\) is clearly nonsingular.
This is a crucial fact that enables efficient solution. The situation with a general nonsingular \({\textbf {A}}\) is more complex than with \({\textbf {A}}\) being the identity matrix, like the case of standard function minimization by the Cauchy steepest descent method. Here, in the studied problem, due to the intrinsic nonsmoothness of a composite material, spectral solution with the gradient descent method is unstable, and multiplication by a stabilizing nonsingular operator (with its spatial integrations) is required. The drawback is that \({\textbf {A}}\) although being nonsingular, is however not necessarily positive definite, and therefore the quadratic form \(\nabla ^{\top }{\Psi }{} {\textbf {A}}_k\nabla {\Psi }\) although nonzero away from the local extremum of \(\Psi \), can nevertheless be negative.
Therefore, the algorithm for the determination of the stepsize would consist of finding \(t_k\) for every k, such that it would be small enough in absolute value, yet nonzero, but its sign would have to be determined by trial and error.
The following algorithm is suggested:
The iterations l are performed until maximum descent is obtained, i.e., until getting \(\Psi _k^{(l+1)}>\Psi _k^{(l)}<\Psi _k^{(l-1)}\). In the examples solved in the present work, the following values were used: \(\zeta =0.9,t_{\text {max}}=3,t_{\text {min}}=10^{-6}\).
Concerning computational runtime, the following can be said: since the algorithm used to determine the stepsize is of Armijo-Goldstein type, i.e., it makes an exponential search, clearly, the number of required iterations is logarithmic in the energy resolution, since the stepsize is altered until energy is minimized. Now, the resolution of the energy is as high as the spatial resolution of the problem, which scales with N. Therefore, the number of required sub-iterations is expected to be logarithmic in N, which is neglected anyway in polynomial runtime analysis. Therefore, for runtime estimation, it is sufficient to check the complexity of a single calculation of the total energy in the domain.
The total energy of the system is calculated in real space by summing (over all the gridpoints) the local energy density, which for a linear-elastic material is given by the local elastic constants and the squares of the strain components (which are calculated anyway). When enough processors are available, one could run a loop of \(N_{\theta }\) parallel computations, in each of which calculation of the energy density at \(N_r\) different radial points is performed, followed by \(N_r\) operations of addition of pointwise values for the radial sum.
Once the \(N_{\theta }\) sums are computed (simultaneously), within a period of time which scales as \({\mathcal {O}}(N_r)\), further computation is performed, consistent of \(N_{\theta }\) additions of the radially summed energy contributions for every angle. Therefore, the overall runtime of the computation of the total energy would be \({\mathcal {O}}(N_r)+{\mathcal {O}}(N_{\theta })\), which is simply \({\mathcal {O}}(\sqrt{N})\). Therefore, the whole stepsize-determination algorithm (when sufficient computer power is available) would have the computational runtime of \({\mathcal {O}}(\sqrt{N}\log {N})\), or when suppressing log-term notation, again \({\mathcal {O}}(\sqrt{N})\).
Next, the derivation of the elastic properties \(\mathring{\lambda },\mathring{\mu }\) of the ‘reference-homogeneous-material’ is outlined.
4.3.5 The reference elastic properties
The reference elastic properties are calculated as weighted averages of the properties of the phases, with the weight being related to the areal fraction occupied by a phase:
where for the considered example, \(\sum \nolimits _{q}{S_q}=\pi c^2\).
4.3.6 The special case of \(q=0\)
For the \(q=0\) case, no double integration in the angular direction is needed for stabilization of the equilibrium equations, and the representative matrix \({\textbf {W}}^{(0)}\) is constructed as follows:
Also, the vector of equations to be solved is as follows:
(where Eqs. (129) still hold).
4.3.7 Homogenization
For the linear-elastic regime, homogenization consists in finding the effective elastic properties by relating the total force to the effective boundary displacement. We next describe the procedure of numerically determining the effective bulk modulus.
In case the radial displacement is specified on the surface, the following expression emerges:
where a reasonable value would be \(\eta _*=0.1\), representing angular parametrization of a fraction of the radial span of the computational domain, at which distance from the outer boundary the displacement is probed for approximating the boundary (radial) derivative by a finite difference. Approximating the radial derivative by a finite difference is equivalent to averaging it over several nodes’ range. This is crucial in view of the fact the derivative is highly noisy in spectral representation. Moreover, since the elastic moduli have spatial jumps, the resulting associated strains have jumps as well, which implies that their spectral representations are non-convergent Riemann-like series, which cannot be directly used for homogenization of the elastic moduli. A remedy is suggested here in the form of a finite difference. Using the finite difference leads to convergence of the effective elastic modulus (the compressibility) with increased spatial resolution (convergence which is otherwise absent).
The effective bulk modulus is obtained upon convergence in the iteration number n. The homogenization procedure has computational complexity of \({\mathcal {O}}(1)\) in terms of dependence on N, and thus does not change the overall runtime.
The effective shear modulus can be computed by applying shear loading, represented by appropriate boundary conditions, which is left here for future work.
4.3.8 Resultant overall-runtime analysis
Without multigrid strategy but with \({\mathcal {O}}(\sqrt{N})\) processor cores used simultaneously, the solution of the homogeneous problem requires at most \({\mathcal {O}}({N}^{1.1865})\) time [27]. The calculation of the vector of equations for the inhomogeneous problem requires inverse and forward angular Fourier transforms, which demand \({\mathcal {O}}(\sqrt{N}\log N)\) operations, and inverse and forward radial Fourier–Chebyshev transforms, which add another \({\mathcal {O}}(\sqrt{N}\log N)\) term. Calculation of stresses from strains in real space requires \({\mathcal {O}}(\sqrt{N})\) operations with parallel computing; spatial integration also has \({\mathcal {O}}(\sqrt{N})\) CPU in parallel computation. The update scheme is \({\mathcal {O}}(\sqrt{N})\) as well. The determination of the stepsize with the proposed algorithm, using adequate algorithm parameters requires \({\mathcal {O}}(\log N)\) sub-iterations, which can be omitted in polynomial complexity analysis.
The calculation of the energy for every sub-iteration also requires \({\mathcal {O}}(\sqrt{N})\) operations with parallel computing. As for the required number of the Nonlinear Gradient Descent steps, it is empirically observed to be \({\mathcal {O}}(N^{1/2})\), much like PCG (Preconditioned Conjugate Gradient) in the linear FEM formulation [29]. This is reasonable, since in fact the equations solved here are also linear and the matrix \({\textbf {A}}\) plays the role of a preconditioner (by encompassing the double integrations in space). Moreover, the matrix \({\textbf {A}}\) rotates the gradient, thus rendering the method no longer one of strict gradient descent. It can be argued that the Conjugate Gradient method is also rotated or projected gradient descent, and thus the employed method can be viewed as a variant of PCG, and as such should have the aforementioned computational complexity when applied to solving a linear system, as indeed observed numerically.
Another argument in favor of the estimation of the computational complexity as aforementioned, as related to the required number of iterations till convergence, can be made by appealing to the Saint-Venant Principle. Due to this principle, the strong coupling between angular and radial modes is localized to several modes necessary to represent the interfaces between the phases in the composite. It seems that strong radial fields variation is evident for lower frequencies. This is similar to how bending energy depends on Gaussian curvature (curvature in both dimensions), which is localized, being costly. Indeed, as shown in the profiles provided in the numerical examples section, radial profiles far from phases-interfaces do not strongly reflect the angular complexity, and angular profiles do not seem distorted by radial field variation, insofar as the displacement is concerned, in line with the Saint-Venant principle. Consequently, the multiplicity of complexity between \(N_q\) and \(N_r\) is limited, and the problem becomes closer to solving separately a system of size \(N_q\) and in addition a system of size \(N_r\), which requires \({\mathcal {O}}(N^{1/2})\) iterations.
Therefore, the overall complexity of the proposed method without multigrid strategy is \({\mathcal {O}}({N}^{1.1865})\) when \({\mathcal {O}}(\sqrt{N})\) processor cores are available simultaneously, which may be asymptotically superior to the complexity of the Finite Element Method employed from scratch (without multigrid), which is \({\mathcal {O}}({N}^{1.5})\), being encompassed in \(\sqrt{N}\) iterations of the PCG algorithm, each requiring \({\mathcal {O}}(N)\) operations on the sparse stiffness matrix, plus the time-linear incomplete Cholesky factorization required for convergence. In each iteration, N-linear time is required even in parallel computation due to communication cost, as there is coupling (unlike in the spectral method) [29].
When employing multigrid strategy, the proposed spectral method can (currently only hypothetically) run in CPU of \({\mathcal {O}}(\sqrt{N})\). This runtime is, of course, expected also for the Cartesian spectral method. The multigrid approach allows suppressing the higher complexity of the solution of the homogeneous problem that holds for the polar method. Moreover, it can render the required number of iterations in the solution of the inhomogeneous problem to be subpolynomial in the system size. Furthermore, the choice of Chebyshev nodes for the radial Fourier–Chebyshev transforms allows performing FFT in both dimensions. Therefore, with multigrid strategy, the proposed polar spectral solver has the same runtime (asymptotically in system size and suppressing log terms) as the Cartesian spectral method. Using multigrid approach and \(\sqrt{N}\) parallel processing cores, one could (theoretically) have sublinear computation time.
The standard FEM approach with adaptive multigrid PCG on parallel processors for stable elastic problems has typically linear runtime [30], the heaviest (time-linear) part being the incomplete Cholesky factorization, which is required for guaranteeing convergence (\(\sqrt{N}\) parallel cores performing \({\mathcal {O}}((\sqrt{N})^2)\) time-long factorizations [31]). The advantage of the spectral approach is that in spectral space instead of interpolation, the multigrid strategy allows obtaining the higher-resolution spectral-coefficient vectors simply by concatenation with additional zeros, which can be done in parallel for every angular harmonic, taking only \({\mathcal {O}}(\sqrt{N})\) time. In contrast, in the FE approach, incomplete Cholesky factorization matrices should be derived for every resolution (whereas in the spectral method there is the inherent a priori factorization in the spectral space). Of course, the spectral method can only be applied to a well-shaped domain, a circle in the present case. In contrast, FEA is suitable for arbitrary geometries. For homogenization purposes, an arbitrary-shape domain is not necessarily required, a square and a circle (in 2D) may be sufficient, and the spectral approach may be advantageous. Furthermore, the polar algorithm has the advantage of reduced artificial anisotropy and boundary error, as discussed in [5, 7].
It is therefore clarified how the spectral approach can theoretically have an advantage in CPU, wherever a structured (rectangular or punctured circular) computational domain is sufficient, under the condition that \({\mathcal {O}}(\sqrt{N})\) processor cores are available for parallel computation. The advantage is maximized if multigrid strategy is employed.
For sequential implementation of all the described operations, the computational complexity of the algorithm is dominated by that of the solution of the homogeneous problem. The solution of the homogeneous problem requires \({\mathcal {O}}({N}^{1.1865})\) time for each angular harmonic. Performing these operations sequentially for all the angular harmonics results in runtime of \({\mathcal {O}}({N}^{1.6865})\). For the inhomogeneous problem, the FFT in each dimension runs in \({\mathcal {O}}({N}\log N)\) for the entire space (\(\sqrt{N}\) calls to a 1D FFT algorithm with its \({\mathcal {O}}(\sqrt{N}\log N)\) complexity), and the same holds for the inverse FFT of the strains. Calculation of stresses and energy scales with the number of spatial nodes, or \({\mathcal {O}}(N)\). The number of sub-iterations for the determination of the stepsize is \({\mathcal {O}}(\log N)\), and thus every iteration of the gradient descent runs in \({\mathcal {O}}({N}\log ^2 N)\). The required number of gradient descent iterations is estimated to be \({\mathcal {O}}(N^{1/2})\).
Therefore, the overall complexity of the method is expected to be \({\mathcal {O}}({N}^{1.6865})\). This means that the runtime is dominated by the solution of the homogeneous problem. For applications in microstructural design or topology optimization, the homogeneous problem can be solved only once, such that the different designs would only require the solution of the inhomogeneous problem. For an efficient topology optimization algorithm the required number of function calls would scale with the number of gridpoints (design variables), N (see [32]), rendering the complexity of the optimization procedure to be \({\mathcal {O}}({N}^{1.6865})+{\mathcal {O}}({N}^{2.5}\log ^2 N)\), or simply \({\mathcal {O}}({N}^{2.5}\log ^2 N)\).
This means that with sequential programming in application to topological optimization of composite microstructure, the polar spectral solver would have (asymptotically) equivalent overall computational complexity to that of the Cartesian one. When keeping only powers of the system size, N, the computational complexity of the polar spectral method in topology optimization would be \({\mathcal {O}}({N}^{2.5})\). In comparison, the computational complexity of FE analysis without parallel computation or multigrid strategy is \({\mathcal {O}}({N}^{1.5})\). In efficient topology optimization the overall complexity with FE analysis would therefore be the same, \({\mathcal {O}}({N}^{2.5})\). This is to say that even in the simplest computing implementation, sequential without multigrid strategy, there is a typical application where the proposed algorithm is expected to have asymptotically the same runtime as standard methods.
This concludes the theory for the 2D polar isotropic linear-elastic case. In the following, numerical examples are given.
4.4 Numerical example 1: The case of three cyclo-symmetrically structured inclusions
4.4.1 Assignment of phases
To model a composite, the Lamé coefficients have to be defined on the real-space grid by cases. As an example, we assume three concentric annuli and six equal angular stripes, with two material phases, as follows:
Maps of the spatial distribution of the elastic constants are given in Fig. 14.
4.4.2 Loading, geometry and material parameters
The following parameters were used in the solved example:
the materials being Tungsten and aluminum, and the last value implying that an angular gridpoint was assigned to every degree (recall that \(N_q=N_{\theta }/3\)).
Lamé parameters’ maps, \(\mu \) (top) and \(\lambda \) (bottom)
4.4.3 Results
The obtained results, in the form of displacement maps and profiles at selected radial and angular cuts, as well as convergence plots for the energy, equations norm and effective bulk modulus, are presented in Figs. 15, 16, 17, 18 and 19. The equations’ norm is the square root of the sum of the squares of the residues of the spectral-space equilibrium equations divided by the number of equations (essentially—RMS), normalized by the boundary radial strain, in units of the expected resolution error for a given spatial resolution (which is the inverse of the number of equations):
Displacements maps, \(u_r\) (top) and \(u_{\theta }\) (bottom)
Radial (top) and angular (bottom) profiles of the radial displacement at radial mid-range, \(u_r\)
Radial (top) and angular (bottom) profiles of the angular displacement at angular mid-range, \(u_{\theta }\)
4.4.4 Discussion of Results
One notes the interesting occurrence of a maximum along r around \(r=c/2\) in the angular displacement, apparent in Figs. 15 (bottom) and 17 (top). Another noteworthy fact is the surprisingly small (periodic) angular variation of the radial displacement, as seen in Figs. 15 (top) and 16 (bottom). Figure 16 (top) is reminiscent of Fig. 9, reflecting the Saint-Venant principle.
Figure 17 (bottom) is noteworthy for its somewhat surprising saw-tooth-like nature. Figure 18 (top) is monotonically decreasing, as expected for the steepest descent method with energy-minimizing stepsize.
Convergence of the total elastic energy and the normalized spectral-equations norm
Convergence of the effective bulk modulus to the value \(\langle \kappa \rangle \approx 283\,\hbox {GPa}\)
4.5 Example 2—matrix with randomly distributed identical (stiffer) fibers
The case of a cylindrical composite with randomly distributed identical circular-section stiffer fibers is considered, as shown in Fig. 20.
Circular cross section of a composite (aluminum matrix) with 17 randomly distributed identical stiffening (Tungsten) fibers of circular cross section (denoted in red), with 18 angular and 18 radial points for every fiber cross section (colour figure online)
4.5.1 Loading, material and computational parameters
The following parameters were used in the solved example:
As in the first example, here too the radial boundary displacement was prescribed with a 1% negative uniform radial strain.
4.5.2 Results
The solution was obtained with sufficient convergence after 30 iterations. Figures 21 and 22 show the resultant (normalized) transversal-displacement and shear stress maps.
Transversal displacement map for the randomly fiber-reinforced composite, where \(u'_{\theta }=(u_{\theta }-u_{\theta }^{\text {min}})/(u_{\theta }^{\text {max}}-u_{\theta }^{\text {min}})\), where \(u_{\theta }^{\text {min}}/c=-5.4\times 10^{-4}\) and \(u_{\theta }^{\text {max}}/c=7.4\times 10^{-4}\)
Shear stress map in the randomly fiber-reinforced composite, where \(\sigma '_{r\theta }=(\sigma _{r\theta }-\sigma _{r\theta }^{\text {min}})/ (\sigma _{r\theta }^{\text {max}}-\sigma _{r\theta }^{\text {min}})\), where \(\sigma _{r\theta }^{\text {min}}=-330.72 \,\text {MPa} \) and \(\sigma _{r\theta }^{\text {max}}=292.95\,\text {MPa} \)
A radial profile of the radial displacement going leftward from the center (passing no fibers) is given in Fig. 23.
Radial profile of the radial displacement \(u_r\) for \(\theta =\pi \)
One notes the abrupt changes in slope, corresponding to discontinuity in strain, typical for composites where displacement and stress continuity are enforced.
Numerical homogenization for the random composite converges relatively quickly (compared to the three-structured-inclusions case), producing a convergence history plot for the coarse-grained bulk modulus as given in Fig. 24.
Convergence history of the coarse-grained bulk modulus resulting from numerical homogenization
The convergent value of the coarse-grained bulk modulus as obtained by numerical homogenization is
To validate the feasibility of the obtained result, we calculate the values of the Hashin–Shtrikman (HS) bounds [33] for cylindrical geometry for the chosen material phases:
For the assumed composite cross section as given in Fig. 20, the volume fraction amounts to \(\phi =17 (18/270)^2=0.0756\). The shear moduli are \(\mu _a\approx 25.94\; \text {GPA}, \mu _b\approx 121.21\;\text {GPa}\). Consequently, the Hashin–Shtrikman bounds are
The value obtained by numerical homogenization falls, therefore, into the (rather narrow) feasible range, as dictated by the HS bounds, which is a validation of the feasibility of the proposed algorithm. The proximity of the homogenized value to the lower HS bound is in correspondence with the third-order analysis discusses in [34], which discusses the so-called Beran–Molyneux bounds for the case of a small volume fraction of the stiffer material, both bounds being rather close to the HS lower bound.
4.6 Example 3—matrix with randomly distributed identical voids (missing fibers in a cylinder)
The first two examples were instrumental in validating the convergence of the algorithm, either to the analytical solution for a benchmark case—as in the first example, which is essentially close enough to the 1D problem to make it possible to validate convergence by comparing displacement profiles—or, as in the second example, by comparing the homogenized response to the theoretical (narrow) feasible range. Now that the algorithm can be considered validated, the third example aims to show that nontrivial stress field distributions can emerge when solving in polar coordinates.
Here the same geometry of the composite is assumed as in the previous example, with the same 17 randomly oriented circular domains occupied by the second-phase material. Only now the material is not Tungsten but rather void (the matrix still being aluminum). This can represent fibers that were drawn out of place in a cylindrical specimen. Figure 25 shows a cross section of the porous material.
Circular cross section of a composite (aluminum matrix) with 17 randomly distributed identical cylindrical voids of circular cross section (denoted in white), with 18 angular and 18 radial points for every void
Figure 26 shows the shear displacement field for the porous material subjected to negative radial displacement on the boundary. One observes how the voids determine the characteristic length of change in the stress field. Illustrating the richness of the shear stress field is the main reason for which the porous material example is considered, and hence no additional solution data is presented here.
Shear stress map in the porous aluminum, with \(\sigma '_{r\theta }=(\sigma _{r\theta }-\sigma _{r\theta }^{\text {min}})/ (\sigma _{r\theta }^{\text {max}}-\sigma _{r\theta }^{\text {min}})\), where \(\sigma _{r\theta }^{\text {min}}=-63.471\, \text {MPa} \) and \(\sigma _{r\theta }^{\text {max}}=64.585\,\text {MPa} \)
5 Conclusions
The main motivation of the present endeavor was to develop a tool for computational micromechanics, which would allow performing analysis and homogenization of elastoplastic response of multiple-phases composites. The spherical RVE in 3D (and a cylindrical one in 2D) has the advantage of higher bulk-to-surface volume, which enables taking a smaller RVE for the same material microstructure and getting the same homogenized response. Another advantage is lower numerical grid-induced material anisotropy, when compared to a cubic RVE.
Homogenization requires the availability of a stable and accurate solver, for establishing the displacement field in the composite. In this work, a new single-domain spectral solver was developed for stable integration of nonsmooth differential equations of solid mechanics in polar (cylindrical and spherical) coordinates. At a first instance, the one-dimensional case was considered, with full angular symmetry, considering both linear-elastic and linear-elastic–perfectly plastic response. The main result of that part of the work is the construction of a stable spectral integration scheme in the presence of polar singularity and nonsmoothness related to material properties, typical for solid mechanics of composites. Filtering of sharp interfaces was introduced, along with a second-order nonlinear solver (the Good Broyden method), using the Suquet scheme for the initial guess to fall inside the basin of attraction of the Broyden method. In the second instance, the 2D polar case was addressed. A matrix-with-inclusions composite with isotropic linear-elastic phases was considered. The singularity in the center was removed by puncturing. No interface-smoothening was employed. The equilibrium equations were solved by use of the Cauchy method, following the direction of the equations vector rotated by a stabilizing nonsingular matrix, with a stepsize determined by exponential linesearch minimizing total elastic energy.
The polar metrics was dealt with spectrally by employing Chebyshev polynomials on a grid of Chebyshev nodes, which rendered the Chebyshev transforms essentially Fourier transforms, making the approach a spectral one. Stability of the spectral formulation was achieved by matrix representation of the projection of the differential and (double) integral real-space operators on the space of Chebyshev polynomials. For the 2D case, the angular Fourier transform with (triple) oversampling was employed. Several typical examples were solved: the linear-elastic case was treated in both spherical and cylindrical symmetry. For spherical symmetry, both two-phase and three-phase composites were studied, with finite contrast between the elastic moduli of the phases. For the 1D case, plasticity was treated, under the simplified assumptions of linear-elastic response and perfect plasticity with flow stress equal to the yield stress. In all the considered cases the spectral method produced stable solutions for the displacement field. In all the 1D cases, analytical solutions were derived for validation of the developed spectral solver, and full validation was observed, to compensate for the stretched assumption that one Suquet step lands the state to within the basin of attraction of the Good Broyden method. For the 2D case, no analytical validation was performed. Instead, the fact of convergence to the solution was inferred from the robustness of the Cauchy method. In the 1D analysis, for all the linear-elastic cases, the effective bulk compressibility was derived. For the plastic case, since plastic flow was assumed to be isochoric, and the elastic response is linear, the tangent bulk modulus could be defined unambiguously, for a typical pressure for which in a core–shell composite the shell is entirely in the plastic regime. In the 2D analysis, stable homogenization of the bulk modulus was obtained by using a finite-difference scheme for approximating the strain.
A random fiber-reinforced composite was solved in the 2D cylindrical setting. Homogenization was performed numerically and the obtained coarse-grained bulk modulus was found to fall in the narrow range dictated by the Hashin–Shtrikman variational bounds.
A central contribution of the work is the algorithm for the determination of the stepsize for the Cauchy method in the 2D analysis. Standard exponential linesearch in a finite positive range fails, since the vector of equations to be solved is not aligned with the gradient of the energy, as the latter is unstable in spectral representation for a composite with sharp interfaces. The proposed algorithm guarantees maximum descent for a state-update direction represented by the vector of equations rotated by any nonsingular linear operator, with number of sub-iterations logarithmic in system size for the determination of the stepsize.
An important feature of the proposed method, apart from it allowing stable single-domain spectral solution of multi-phase composites with sharp interfaces, is the successful application of the FFT algorithm in two dimensions, which it enables, optimizing potential computation time.
Future work could address the 2D scenario with non-axially-symmetric boundary conditions, allowing to perform homogenization also for the shear modulus. Moreover, anisotropic and inelastic phases (in 2D) could be addressed. Finally, generalization to 3D would be of interest.
References
Chiumenti, M., Cervera, M., Moreira, C., Barbat, G.: Stress, strain and dissipation accurate 3-field formulation for inelastic isochoric deformation. Finite Elem. Anal. Des. 192, 103534 (2021)
Shanthraj, P., Diehl, M., Eisenlohr, P., Roters, F., Raabe, D.: Spectral Solvers for Crystal Plasticity and Multi-physics Simulations. In: Hsueh, C.H., et al. (eds.) Handbook of Mechanics of Materials. Springer, Singapore (2019)
Cooley, J.W., Tukey, J.W.: An algorithm for the machine calculation of complex Fourier series. Math. Comp. 19, 297–301 (1965)
Schneider, M.: A review of nonlinear FFT-based computational homogenization methods. Acta Mech. 232, 2051–2100 (2021)
Gl\(\ddot{\text{u}}\)ge, R., Weber, M., Bertram, A.: Comparison of spherical and cubical statistical volume elements with respect to convergence, anisotropy, and localization behavior. Comput. Mater. Sci. 63, 91–104 (2012)
Gl\(\ddot{\text{ u }}\)geund, R., Weber, M.: (2013). Numerical properties of spherical and cubical representative volume elements with different boundary conditions Technische Mechanik 97–103
Gl\(\ddot{\text{ u }}\)ge, R.: Generalized boundary conditions on representative volume elements and their use in determining the effective material properties Comput. Mater. Sci. 79, 408–416 (2013)
Townsend, A., Wilber, H., Wright, G.B.: Computing with functions in spherical and polar geometries I. The sphere. SIAM J. Sci. Comput. 38(4), C403–C425 (2016)
Vasil, G.M., Burns, K.J., Lecoanet, D., Olver, S., Brown, B.P., Oishi, J.S.: Tensor calculus in polar coordinates using Jacobi polynomials. J. Comput. Phys. 325, 53–73 (2016)
Boyd, J.P.: The choice of spectral functions on a sphere for boundary and eigenvalue problems: a comparison of Chebyshev, Fourier and associated Legendre expansions. Mon. Weather Rev. 106, 1184–1191 (1978)
Mianroodi, J.R., Shanthraj, P., Liu, C., et al.: Modeling and simulation of microstructure in metallic systems based on multi-physics approaches. NPJ Comput. Mater. 8(93), 1–15 (2022)
Eisenlohr, P., Diehl, M., Lebensohn, R.A., Roters, F.: A spectral method solution to crystal elasto-viscoplasticity at finite strains. Int. J. Plast. 46, 37–53 (2013)
Shanthraj, P., Eisenlohr, P., Diehl, M., Roters, F.: Numerically robust spectral methods for crystal plasticity simulations of heterogeneous materials. Int. J. Plast. 66, 31–45 (2015)
Lahellec N., Michel J.C., Moulinec H., Suquet ,P.: Analysis of inhomogeneous materials at large strains using fast Fourier transforms. In: Miehe, C. (eds.) IUTAM Symposium on Computational Mechanics of Solid Materials at Large Strains. Solid Mechanics and Its Applications, vol. 108. Springer, Dordrecht (2003)
Roters, F., Diehl, M., Shanthraj, P., Eisenlohr, P., Reuber, C., Wong, S.L., Maiti, T., Ebrahimi, A., Hochrainer, T., Fabritius, H.O., Nikolov, S., Friák, M., Fujita, N., Grilli, N., Janssens, K.G.F., Jia, N., Kok, P.J.J., Ma, D., Meier, F., Werner, E., Stricker, M., Weygand, D., Raabe, D.: DAMASK—The Düsseldorf advanced material simulation kit. Comput. Mater. Sci. 158, 420–478 (2019)
Monchiet, V., Bonnet, G.: A polarization-based FFT iterative scheme for computing the effective properties of elastic composites with arbitrary contrast. Int. J. Numer. Methods Eng. 89(11), 1419–1436 (2012)
Moulinec, H., Silva, F.: Comparison of three accelerated FFT-based schemes for computing the mechanical response of composite materials. Int. J. Numer. Methods Eng. 97, 960–985 (2014)
Sharma, L., Peerlings, R.H.J., Shanthraj, P., Roters, F., Geers, M.G.D.: An FFT-based spectral solver for interface decohesion modelling using a gradient damage approach. Comput. Mech. 65, 925–939 (2020)
Willot, F.: Fourier-based schemes for computing the mechanical response of composites with accurate local fields. C. R. Mechanique 343, 232–245 (2015)
Chebyshev, P.L.: Théorie des mécanismes connus sous le nom de parallélogrammes. Mémoires des Savants étrangers présentés à l’Académie de Saint-Pétersbourg 7, 539–586 (1854)
Su, Y.: Collocation spectral methods in the solution of Poisson equation. M.Sc. thesis, Department of Mathematics, University of British Columbia (1998)
Olver, S., Townsend, A.: A fast and well-conditioned spectral method. SIAM Rev. 55(3), 462–489 (2013)
Sezer, M., Kaynak, M.: Chebyshev polynomial solutions of linear differential equations. Int. J. Math. Educ. Sci. Technol. 27(4), 607–618 (1996)
Crisci, M.R., Russo, E.: An extension of Ortiz’ recursive formulation of the Tau method to certain linear systems of ordinary differential equations. Math. Comput. 41, 27–42 (1983)
Gélébart, L., Ouaki, F.,: Filtering material properties to improve FFT-based methods for numerical homogenization. J. Comput. Phys. 294, 90–95 (2015)
Perchikov, N., Aboudi, J.: Micromechanical analysis of hyperelastic composites with localized damage using a new low-memory Broyden-step-based algorithm. Arch. Appl. Mech. 90(1), 47–85 (2020)
Peng, R., Vempala, S.S.: Solving sparse linear systems faster than matrix multiplication. In: Proceedings of the 2021 ACM-SIAM Symposium on Discrete Algorithms, SODA (2021)
Armijo, L.: Minimization of functions having Lipschitz continuous first partial derivatives. Pac. J. Math. 16(1), 1–3
Botsch, M., Bommes, D., Kobbelt, L.: Efficient linear system solvers for mesh processing. In: Martin, R., Bez, H., Sabin, M. (eds.) Mathematics of Surfaces XI. Lecture Notes in Computer Science, vol. 3604. Springer, Berlin (2005)
Hu, Z., Haider, M.A.: Algebraic multigrid preconditioning for finite element solution of inhomogeneous elastic inclusion problems in articular cartilage. Adv. Appl. Math. Mech. 3(6), 729–744 (2011)
Kaporin, I.E., Kon’shin, I.N.: Parallel solution of symmetric positive definite systems based on decomposition into overlapping blocks. Zhurn. Vychisl. Matem. i Matem. Fiziki. 41(4), 515–528 (2001)
Teytaud, O., Gelly, S.: General lower bounds for evolutionary algorithms. In: Runarsson, T.P., Beyer, HG., Burke, E., Merelo-Guervós, J.J., Whitley, L.D., Yao, X. (eds) Parallel Problem Solving from Nature—PPSN IX. PPSN 2020. Lecture Notes in Computer Science, vol. 4193. Springer, Berlin (2006)
Hashin, Z.: On elastic behaviour of fibre reinforced materials of arbitrary transverse phase geometry. J. Mech. Phys. Solids 13(3), 119–134 (1965)
Torquato, S., Lado, F.: Effective properties of two-phase disordered composite media: II. Evaluation of bounds on the conductivity and bulk modulus of dispersions of impenetrable spheres. Phys. Rev. B 33(9), 6428–6435 (1986)
Acknowledgements
This work was funded by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation)—DI 1873/4-1 and GL 626/5-1.
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Perchikov, N., Diehl, M. A single-domain spectral solver for spatially nonsmooth differential equations of quasistatic solid mechanics in polar coordinates. Acta Mech 234, 599–647 (2023). https://doi.org/10.1007/s00707-022-03406-0
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00707-022-03406-0