1 Introduction

The tremendous progress in the field of material technology allows to increase the load-bearing capacity of the compressed elements while maintaining mass (cf. Goel et al. [13]). This process leads to the development of increasingly slender elements that are not resistant to buckling. In the case of bars with significant imperfections, it is quite difficult to notice the beginning of the loss of stability and determine the value of the critical force. Therefore, in the case of bars with a constant cross section, the Southwell method is commonly known and used to determine the critical load value (cf. Rykaluk [30] and Timoshenko and Goodier [38]). However, the problem arises as to whether this method can be used for non-prismatic bars.

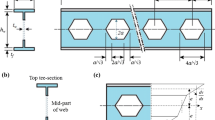
Before we settle this issue, let us take a closer look at the method itself and its evolution. In his publication published in 1932, Robert Southwell suggested a very effective method of experimental determination of the critical force corresponding to the bifurcation form of loss of stability of elastic bars (cf. Southwell [37]. The work highlighted the advantages of the suggested method while simultaneously pointing out some of its limitations. The method guarantees that the correct value of the critical force is obtained, provided that the values of transverse bending under the influence of the applied axial force are relatively small (assuming small curvatures), and the deformations are only of the linear-elastic type. In the derivations presented in Southwell's work [37] there is one more assumption: the moment of inertia of the bar and therefore its cross section is constant along its length.

The essence of the Southwell method is presented in Fig. 1. The experimental determination of the critical force leading to the bifurcation loss of stability of a compressed bar is based on the execution of a sequence of measurements of the transverse extreme defelection \((\delta )\) for successive values of gradually increasing P compressive force. The typical chart \(P=P(\delta )\) (see Fig. 1b) is far from the expected bifurcation path due to the existing geometric and load imperfections in the bar. Southwell justified mathematically (cf. Southwell [37]) that the chart \(\delta /P=f\left(\delta \right)\) is a straight line, and the inverse of the slope is the Pkr critical load value sought (see Fig. 1c). He also pointed out that the determined value of the critical force is the more precise the sequence of measurements Piδ is closer to the area adjacent to the critical force Pkr.

Fig. 1
figure 1

The idea of Southwell’s method

Full size image

Shortly after publication, Southwell's proposal attracted a lot of attention due to its simplicity. Of the works that have appeared after Southwell's publication, the following deserve special mentioning: Donnell [10], Wang [39]. In the following years, interest in the Southwell method continued, and this is evidenced not only by the monograph by Timoshenko and Gere [38], but also by the following works: Merchant [26], Murray [27], Trahair [35, 36], Ariaratnam [1]. Spencer and Walker, in their work Spencer and Walker [34], listed the circumstances in which the classical Southwell method may fail and suggested alternative solutions guaranteeing the correct value of the critical force.

One of the modifications to the classical Southwell method was put forward by Massey (cf. Massey [23]. His suggestion concerns the critical force causing the torsional buckling of the beams and is known as Massey's plot method (cf. Zirakian [42]. The same problem was addressed in Trahair's suggestion of 1969 (cf. Trahair [35]) and is called the modified plot method (cf. Zirakian [41, 42]).

Another modification of Southwell's method was suggested by Meck (cf. Meck [25]). His suggestion also concerned the determination of critical loads causing the torsion of beams (cf. Mandal and Calladine [18]). The method of determining the critical load in lateral buckling that he modified is known as the Meck method (cf. Zirakian [41, 42]).

Despite it having been developed ninety years ago, the Southwell method still enjoys widespread recognition among researchers involved in the experimental assessment of structure stability. It is used both in the education of trainee engineers as well as in serious scientific research, yet not all of its users remember the limitations listed by Southwell (cf. Blum and Rasmussen [4]).

Attempts to include elasto-plastic deformations in the modified Southwell method emerged quite early (cf. Wang [39], Ariaratnam [1], Singer [33]) and are still the subject of research by many authors. It should be mentioned that Ariaratnam was the first to draw attention to the possibility of applying the Southwell method also to compressed bars with different support conditions and bars with variable flexural stiffness (cf. Ariaratnam [1]). As for the stability of non-prismatic bars, the scholars' interest in this subject has also continued, and it does not seem to diminish. A lot of scientists have considered the issue of the stability of compressed bars with a cross section that changes along the axis. In his work, Dinnik [9], among other solutions, considers the eigenvalue problem for bars, the shape of which was defined by power functions up to the fourth degree inclusive. The work by Bo-Hao et al. (2013) describes the stability of tubular double steel conical columns. The study by Marcinowski and Sadowski [21] deals with the issue of optimization of the stability of non-prismatic bars with the use of complex functions, while their other work, namely Marcinowski and Sadowski [20], is concerned with the issue of optimization of the stability of non-prismatic bars with variable wall thickness. It should be noted, however, that there are no standardized and easily applicable algorithms to test the stability of this type of structural elements (cf. Marques et al. [22]), and those that do exist for individual cases are usually rather complicated (cf. Serna et al. [32]).

As for the Southwell method itself, the evidence of an unwavering interest in it is the contemporary work of a team of scientists from Ariel University in Israel: Blostotsky and Efraim [2], Blostotsky et al. [3]. The subject of the work of this team is the optimal selection of measurement data, as well as their skilful interpolation and extrapolation leading to a more accurate estimation of the critical forces.

This paper includes a strict solution of the differential equation of bar stability with a parabolic variable moment of inertia of the cross section and a parabolic form of initial geometric imperfections. The solution was obtained with the help of the Mathematica™ system (cf. Wolfram [40]. As in the classical approach, it was the basis for the construction of the Southwell plot, and the plot turned out to be a straight line with the slope being the inverse of the critical force sought. Thus, the correctness of the Southwell method for this special case of a bar was proved.

2 The subject of the work and its purpose

The subject of detailed considerations is a compressed bar made of elastic material (constant Young's modulus E) with the static diagram shown in Fig. 2. The bar is characterized by a monotonically variable cross section, and the distribution of the moment of inertia of its cross section (and thus of its bending stiffness) is parabolic in nature, as shown in Fig. 3a.

Fig. 2
figure 2

Static diagram of the system

Full size image
Fig. 3
figure 3

Distribution of flexural stiffness a and an example of technical implementation of the bar b

Full size image

The mathematical description of the variability of the moment of inertia is rendered by the relation:

$$I\left( x \right) = - \frac{{4I_{0} }}{{L^{2} }}x^{2} + \frac{{4I_{0} }}{L}x + I_{{p^{\prime } }}$$
(1)

where Ipis the moment of inertia of the bar cross section at its ends, while (Ip + I0) constitutes the moment of inertia of the bar cross section in its mid-length (see Fig. 3a); I(x) is the value of the moment of inertia in any cross section of the bar.

In Fig. 3b an example of technical implementation of a bar whose moment of inertia meets the dependence (1) is depicted. It is a bar with a variable b(x) section width and constant h cross-section height (thickness). The b(x) function is similar to the I(x) function defined by the relationship (1).

The main purpose of this paper is to show that Southwell's method of experimental determination of the critical force in a compressed bar is true not only for bars with constant stiffness, but also for bars with a variable cross section as defined in Fig. 3.

3 Differential equation of bar stability and its solution

The differential equation of the bar's stability may be obtained by equating the product of the curvature and bending stiffness of the bar with the bending moment in the bar initially bent according to the function:

$$w_{i} \left( x \right) = \frac{{4w_{0} }}{{L^{2} }}\left( {Lx - x^{2} } \right),$$
(2)

where w0 is the amplitude of the parabolic bow deflection (see Fig. 4a).

Fig. 4
figure 4

The initial shape of the bar a and its deflection when P force is applied b

Full size image

According to the classical theory of bar bending:

$${\text{EI}}\left( x \right)\frac{{{\text{d}}^{2} w}}{{{\text{d}}x^{2} }} = - M\left( x \right) = - P \cdot w_{c} (x),$$
(3)

or

$$\mathrm{EI}\left(x\right)\frac{{\mathrm{d}}^{2}w}{\mathrm{d}{x}^{2}}=-P\cdot \left[w\left(x\right)+{w}_{i}\left(x\right)\right],$$
(4)

where M(x) is the bending moment within the current x section.

Substituting the initial deflection function wi(x) according to (2) to the Eq. (4) leads to the following differential equation of the bar stability:

$$\mathrm{EI}\left(x\right)\frac{{\mathrm{d}}^{2}w}{\mathrm{d}{x}^{2}}+Pw=-P\frac{4{w}_{0}}{{L}^{2}}\left(Lx-{x}^{2}\right),$$
(5)

and after taking into account the relation (1) defining the moment of inertia I(x), it is expressed by the relation:

$$E\left(-\frac{4{I}_{0}}{{L}^{2}}{x}^{2}+\frac{4{I}_{0}}{L}x+{I}_{p}\right)\frac{{\mathrm{d}}^{2}w}{\mathrm{d}{x}^{2}}+Pw=-P\frac{4{w}_{0}}{{L}^{2}}\left(Lx-{x}^{2}\right).$$
(6)

Let us consider the homogeneous equation first:

$$E\left(-\frac{4{I}_{0}}{{L}^{2}}{x}^{2}+\frac{4{I}_{0}}{L}x+{I}_{p}\right)\frac{{\mathrm{d}}^{2}w}{\mathrm{d}{x}^{2}}+Pw=0.$$
(7)

In order to solve Eq. (7), an analysis using a linear change of the independent variable can be performed (cf. Pradeep [29]. Let

$$t=\frac{x-{x}_{2}}{{x}_{2}-{x}_{1}},$$
(8)

where

$$\begin{gathered} x_{1} = \frac{1}{{2I_{0} }}\left( {I_{0} L - \sqrt {L^{2} \left( {I_{0}^{2} + I_{0} I_{p} } \right)} } \right), \hfill \\ x_{2} = \frac{1}{{2I_{0} }}\left( {I_{0} L + \sqrt {L^{2} \left( {I_{0}^{2} + I_{0} I_{p} } \right)} } \right) \hfill \\ \end{gathered}$$
(9)

are the roots of the equation \(I\left(x\right)=0\).

In view of (8) we have

$$\frac{\mathrm{d}w}{\mathrm{d}x}=\frac{\mathrm{d}w}{\mathrm{d}t}\frac{\mathrm{d}t}{\mathrm{d}x}=\frac{1}{{x}_{2}-{x}_{1}}\frac{\mathrm{d}w}{\mathrm{d}t},$$
(10)
$$\frac{{\mathrm{d}}^{2}w}{\mathrm{d}{t}^{2}}=\frac{\mathrm{d}}{\mathrm{d}x}\left(\frac{\mathrm{d}w}{\mathrm{d}x}\right)=\frac{1}{{x}_{2}-{x}_{1}}\frac{\mathrm{d}}{\mathrm{d}t}\left(\frac{\mathrm{d}w}{\mathrm{d}x}\right)=\frac{1}{{\left({x}_{2}-{x}_{1}\right)}^{2}}\frac{{\mathrm{d}}^{2}w}{\mathrm{d}{t}^{2}}.$$
(11)

Substituting the last dependencies into the relationship (7), taking into account (9) and the inverse relation to (8), i.e., \(x=\left({x}_{2}-{x}_{1}\right)t+{x}_{2}\), we get:

$$E\left(-\frac{4{I}_{0}}{{L}^{2}}{x}^{2}+\frac{4{I}_{0}}{L}x+{I}_{p}\right)\frac{1}{{\left({x}_{2}-{x}_{1}\right)}^{2}}\frac{{\mathrm{d}}^{2}w}{\mathrm{d}{t}^{2}}+Pw=0,$$
(12)
$$E\left(-4t\left(t-1\right)\left({I}_{0}+{I}_{p}\right)\right)\frac{{I}_{0}}{{L}^{2}\left({I}_{0}+{I}_{p}\right)}\frac{{\mathrm{d}}^{2}w}{\mathrm{d}{t}^{2}}+Pw=0,$$
(13)
$$E\left(4t\left(1-t\right)\right)\frac{{I}_{0}}{{L}^{2}}\frac{{\mathrm{d}}^{2}w}{\mathrm{d}{t}^{2}}+Pw=0,$$
(14)

which ultimately leads to the equation:

$$t\left(1-t\right)\frac{{\mathrm{d}}^{2}w}{\mathrm{d}{t}^{2}}+\frac{{\mathrm{PL}}^{2}}{4{\mathrm{EI}}_{0}}w=0,$$
(15)

which can be identified with the hypergeometric Gaussian differential equation (cf. Palmer [28])Footnote 1:

$$t\left(1-t\right)\frac{{\mathrm{d}}^{2}w}{\mathrm{d}{t}^{2}}+\left[c-\left(a+b+1\right)t\right]\frac{\mathrm{d}w}{\mathrm{d}t}-ab w={0}^{(1)}.$$
(16)

The general solution of the homogeneous Eq. (7) is the relation

$$\begin{aligned} w_{j} \left( t \right) = & - C_{1} tF\left( {\frac{1}{2}\left( {1 - \frac{{\sqrt {{\text{EI}}_{0} \left( {{\text{PL}}^{2} + {\text{EI}}_{0} } \right)} }}{{{\text{EI}}_{0} }}} \right),\frac{1}{2}\left( {1 + \frac{{\sqrt {{\text{EI}}_{0} \left( {{\text{PL}}^{2} + {\text{EI}}_{0} } \right)} }}{{{\text{EI}}_{0} }}} \right),2,t} \right) \\ & + C_{2} G_{2,2}^{2,0} \left( {t|\begin{array}{*{20}c} {\frac{1}{2}\left( {3 - \sqrt {\frac{{{\text{PL}}^{2} + {\text{EI}}_{0} }}{{{\text{EI}}_{0} }}} } \right),\frac{1}{2}\left( {3 + \sqrt {\frac{{{\text{PL}}^{2} + {\text{EI}}_{0} }}{{{\text{EI}}_{0} }}} } \right)} \\ {0 , 1} \\ \end{array} } \right), \\ \end{aligned}$$
(17)

where F is the so-called hypergeometric function (cf. Derezinski, Karczmarczyk [7]), which is defined by hypergeometric series (cf. Gauss [11]):

$$F\left(a,b,c,z\right)=\sum_{n=1}^{\infty }\frac{{\left(a\right)}_{n}{\left(b\right)}_{n}}{{\left(c\right)}_{n}}\frac{{z}^{n}}{n!},$$
(18)

while the factor

$${\left(\xi \right)}_{n}=\prod_{i=0}^{n-1}\left(\xi +i\right)=\frac{\Gamma \left(\xi +n\right)}{\Gamma \left(\xi \right)},$$
(19)

used in relationship (18)(Footnote 2), is called the symbol of Pochhammer (see Diaz [8]).

Function:

$${G}_{p,q}^{m,n}\left(t|\begin{array}{c}{a}_{1}\dots {a}_{p}\\ {b}_{1}\dots {b}_{q}\end{array}\right)=\frac{1}{2\pi i}\int_{L}^{ }\frac{\prod_{j=1}^{m}\Gamma \left({b}_{j}-s\right)\prod_{j=1}^{n}\Gamma \left(1-{a}_{j}+s\right)}{\prod_{j=m+1}^{q}\Gamma \left(1-{b}_{j}+s\right)\prod_{j=n+1}^{p}\Gamma \left({a}_{j}-s\right)}{t}^{s}\mathrm{d}s,$$
(20)

occurring in (17), defined by the curvilinear integral on the complex plane, is called Meijer's G function(Footnote 3) (see Łydka [16], Karpa, Lopez [16]).

The expression (17) with the substitution (8) and formulas (9) is the general integral (\({w}_{j}\)) of the homogeneous Eq. (7). After taking into account the substitutions, however, \({w}_{j}={w}_{j}\left(x\right)\).

Solving the eigenvalue problem, and thus determining the exact formula for the critical force, is a very complicated task due to the complexity of the deflection function. Therefore, in the further part of the article, the general method of determining the critical force was indicated (see (29)), as well as the formula that gives an approximate value to it was listed (see (30)).

Due to Eq. (6), its particular integral is predicted in the form:

$${w}_{s}\left(x\right)={A}_{0}+{A}_{1}x+{A}_{2}{x}^{2},$$
(21)

the inclusion of which in the Eq. (6) allows to determine its coefficients:

$$\begin{array}{c}{A}_{0}=\frac{-8E{{I}_{p}w}_{0}}{{\mathrm{PL}}^{2}-8{\mathrm{EI}}_{0}},\\ {A}_{1}=-\frac{4\mathrm{PL}{w}_{0}}{{\mathrm{PL}}^{2}-8{\mathrm{EI}}_{0}},\\ {A}_{2}=\frac{4P{w}_{0}}{{\mathrm{PL}}^{2}-8{\mathrm{EI}}_{0}}.\end{array}$$
(22)

In view of recent relations:

$${w}_{s}\left(x\right)=\left(\frac{-8E{{I}_{p}w}_{0}}{P{L}^{2}-8E{I}_{0}}\right)+\left(-\frac{4PL{w}_{0}}{P{L}^{2}-8E{I}_{0}}\right)x+\frac{4P{w}_{0}}{P{L}^{2}-8E{I}_{0}}{x}^{2}.$$
(23)

Following the considerations, a general solution wo(x) of Eq. (6) is the sum of the relations (17) (including the substitution (8) and formulas (9)) and (23), i.e., \({w}_{\mathrm{o}}\left(x\right)={w}_{j}\left(x\right)+{w}_{\mathrm{s}}\left(x\right)\).

Boundary conditions of the considered bar case (see Fig. 2) are:

$$\begin{array}{c}{w}_{\mathrm{o}}\left(0\right)=0,\\ {w}_{\mathrm{o}}\left(L\right)=0,\end{array}$$
(24)

and further analysis allows to determine the integration constants (included in the relation (17)). They are expressed in the relationships:

$$C_{1} = \frac{{\alpha_{1} }}{{\alpha_{2} }}$$
(25)

wherein

$$\begin{aligned} \alpha_{1} =\, & 16ELI_{p} w_{0} \left( {I_{p} + I_{0} } \right) \\ & \quad \times \left[ {G_{2,2}^{2,0} \left( {\frac{1}{2}\left( {1 - \frac{{LI_{0} }}{{\sqrt {L^{2} I_{0} \left( {I_{p} + I_{0} } \right)} }}} \right)\left| {\begin{array}{*{20}c} {\frac{1}{2}\left( {3 - \sqrt {\frac{{PL^{2} + EI_{0} }}{{EI_{0} }}} } \right),\frac{1}{2}\left( {3 + \sqrt {\frac{{PL^{2} + EI_{0} }}{{EI_{0} }}} } \right)} \\ {0,1} \\ \end{array} } \right.} \right)} \right. \\ & \quad \left. { +\, G_{2,2}^{2,0} \left( {\frac{1}{2}\left( {1 + \frac{{LI_{0} }}{{\sqrt {L^{2} I_{0} \left( {I_{p} + I_{0} } \right)} }}} \right)\left| {\begin{array}{*{20}c} {\frac{1}{2}\left( {3 - \sqrt {\frac{{PL^{2} + EI_{0} }}{{EI_{0} }}} } \right),\frac{1}{2}\left( {3 + \sqrt {\frac{{PL^{2} + EI_{0} }}{{EI_{0} }}} } \right)} \\ {0 , 1} \\ \end{array} } \right.} \right)} \right], \\ \end{aligned}$$
(26)
$$\begin{aligned} \alpha_{2} = & \left( {FL^{2} - 8EI_{0} } \right) \times \left[ {\left( {\sqrt {L^{2} I_{0} \left( {I_{p} + I_{0} } \right)} + LI_{p} + LI_{0} } \right)} \right. \\ & \quad \times F\left( {\frac{1}{2}\left( {1 + \frac{{\sqrt {EI_{0} \left( {PL^{2} + EI_{0} } \right)} }}{{EI_{0} }}} \right),\frac{1}{2}\left( {1 - \frac{{\sqrt {EI_{0} \left( {PL^{2} + EI_{0} } \right)} }}{{EI_{0} }}} \right),2,\frac{1}{2}\left( {1 + \frac{{LI_{0} }}{{\sqrt {L^{2} I_{0} \left( {I_{p} + I_{0} } \right)} }}} \right)} \right) \\ & \quad \times G_{2,2}^{2,0} \left( {\frac{1}{2}\left( {1 - \frac{{LI_{0} }}{{\sqrt {L^{2} I_{0} \left( {I_{p} + I_{0} } \right)} }}} \right)\left| {\begin{array}{*{20}c} {\frac{1}{2}\left( {3 - \sqrt {\frac{{PL^{2} + EI_{0} }}{{EI_{0} }}} } \right),\frac{1}{2}\left( {3 + \sqrt {\frac{{PL^{2} + EI_{0} }}{{EI_{0} }}} } \right)} \\ {0, 1} \\ \end{array} } \right.} \right) \\ & \quad + \left( {\sqrt {L^{2} I_{0} \left( {I_{p} + I_{0} } \right)} + LI_{p} + LI_{0} } \right) \\ & \quad \times F\left( {\frac{1}{2}\left( {1 + \frac{{\sqrt {EI_{0} \left( {PL^{2} + EI_{0} } \right)} }}{{EI_{0} }}} \right),\frac{1}{2}\left( {1 - \frac{{\sqrt {EI_{0} \left( {PL^{2} + EI_{0} } \right)} }}{{EI_{0} }}} \right),2,\frac{1}{2}\left( {1 - \frac{{LI_{0} }}{{\sqrt {L^{2} I_{0} \left( {I_{p} + I_{0} } \right)} }}} \right)} \right) \\ & \quad \left. { \times G_{2,2}^{2,0} \left( {\frac{1}{2}\left( {1 + \frac{{LI_{0} }}{{\sqrt {L^{2} I_{0} \left( {I_{p} + I_{0} } \right)} }}} \right)\left| {\begin{array}{*{20}c} {\frac{1}{2}\left( {3 - \sqrt {\frac{{PL^{2} + EI_{0} }}{{EI_{0} }}} } \right),\frac{1}{2}\left( {3 + \sqrt {\frac{{PL^{2} + EI_{0} }}{{EI_{0} }}} } \right)} \\ {0, 1} \\ \end{array} } \right.} \right)} \right], \\ \end{aligned}$$
(27)

and

$${C}_{2}=\frac{{\beta }_{1}}{{\beta }_{2}} ,$$
(28)

where

$$\begin{aligned} \beta_{1} =\, & \frac{{C_{1} }}{{2L\left( {I_{p} + I_{0} } \right)}}\left( {\sqrt {L^{2} I_{0} \left( {I_{p} + I_{0} } \right)} + LI_{p} + LI_{0} } \right) \\ & \quad \times \left[ {F\left( {\frac{1}{2}\left( {1 + \frac{{\sqrt {EI_{0} \left( {PL^{2} + EI_{0} } \right)} }}{{EI_{0} }}} \right),\frac{1}{2}\left( {1 - \frac{{\sqrt {EI_{0} \left( {PL^{2} + EI_{0} } \right)} }}{{EI_{0} }}} \right),2,\frac{1}{2}\left( {1 + \frac{{LI_{0} }}{{\sqrt {L^{2} I_{0} \left( {I_{p} + I_{0} } \right)} }}} \right)} \right)} \right. \\ & \quad \left. { + \frac{{8EI_{p} w_{0} }}{{PL^{2} - 8EI_{0} }}} \right], \\ \end{aligned}$$
(29)
$${\beta }_{2}={G}_{\mathrm{2,2}}^{\mathrm{2,0}}\left(\frac{1}{2}\left(1+\frac{L{I}_{0}}{\sqrt{{L}^{2}{I}_{0}\left({{I}_{p}+I}_{0}\right)}}\right)|\begin{array}{c}\frac{1}{2}\left(3-\sqrt{\frac{P{L}^{2}+E{I}_{0}}{E{I}_{0}}}\right),\frac{1}{2}\left(3+\sqrt{\frac{P{L}^{2}+E{I}_{0}}{E{I}_{0}}}\right)\\ 0 , 1\end{array}\right).$$
(30)

A complete solution \(w(x)\) of the Eq. (6) with the boundary conditions (24) is the sum of functions (17) and (23), taking into account the relations (8) and (9) and the constants C1 and C2 as expressed by the formulas (25)–(30).

4 Bar deflection at half its length, critical force

The obtained exact solution of Eq. (6) will be analyzed in detail based on the example of a bar with the following material and geometric parameters:

  • bar length: \(L = 1000\, \mathrm{mm},\)

  • moment of inertia at bar ends: \({I}_{p}= 673\, {\mathrm{mm}}^{4},\)

  • moment of inertia in the middle of the bar length: \({I}_{p}+{I}_{0}= 911\, {\mathrm{mm}}^{4},\)

  • amplitude of the initial deflection: \({w}_{0} = 1\cdot {10}^{-3}\,\mathrm{ mm},\)

  • Young's modulus: \(E = 2\cdot {10}^{5}\,\mathrm{ MPa}.\)

Moments of inertia given above were obtained for the column of rectangular cross section of constant thickness t = 5 mm and the variable width from bp = 64.6 mm and bp + b0 = 87.5 mm (comp. Figure 3).

An example of a deflection function w(x) for \(P=1732.5\, \mathrm{N}\) is shown in Fig. 5. Maximum deflection (\(\delta\)) can be seen halfway along the rod's length:

Fig. 5
figure 5

An example of a bar deflection function w(x) for \(P=1732.5 \mathrm{N}\)

Full size image
$$\delta =w\left(\frac{L}{2}\right),$$
(31)

and this value is a function of the forcing load:

$$\delta =\delta \left(P\right).$$
(32)

The inverse relation, i.e., \(P={P}^{-1}\left(\delta \right)\), due to the complexity of the deflection function w(x), is impossible to determine. However, this relationship can be written as the equality:

$$\Phi \left(\delta ,P\right)=0,$$
(33)

which is an implicit equation and from which the value of the exciting force can be determined depending on the assumed deflection (or vice versa). A special case is the situation in which the deflection increases indefinitely.

Then, the corresponding load input is the desired value of the critical force:

$${\mathrm{lim}}_{\delta \to \infty }\left[\Phi \left(\delta ,P\right)=0\right]\Rightarrow P={P}_{\mathrm{kr}}.$$
(34)

Due to the considerable difficulty in finding the above limit, the value of the critical force can be determined on the basis of the relationship that was obtained by applying the Rayleigh quotient(Footnote 4) with the help of the Mathematica™ system (cf. Wolfram [40]:

$${P}_{\mathrm{kr}}\approx \frac{16E{I}_{0}^{3}}{{L}^{2}\left({I}_{0}^{2}-3{I}_{0}{I}_{P}+3{I}_{p}^{2}\sqrt{\frac{{I}_{0}}{{I}_{0}{+I}_{P}}}\mathrm{artgh}\sqrt{\frac{{I}_{0}}{{I}_{0}{+I}_{P}}}\right)}.$$
(35)

Due to the adopted buckling type (2), the above formula offers an overestimated result, but the error does not exceed 1%.

For the assumed geometrical and material parameters, the critical force is determined on the basis of the relation (34), assuming the valueFootnote 5:

$$P_{{{\text{kr}}}} = 1733.12 {\text{N}}{.}$$
(36)

The situation is illustrated in Fig. 6, and the deflection takes on enormous values, it even tends to infinity, while the force value tends to value Pkr.

Fig. 6
figure 6

The course of the bar deflection function w(x) at an almost critical inducement load

Full size image

5 Southwell’s method for compressed bars with parabolic variable bending stiffness

Based on the determined bar deflection function w(x), in Table 1 are the values of the compressive force (P) and the corresponding maximum deflection values (\(\delta\)) for a bar with geometrical and material parameters adopted in Chapter 4. The values provided in Table 1 were also used to plot the graph \(P=P\left(\delta \right)\) shown in Fig. 7.

Table 1 The values of the compressive force and the corresponding maximum deflections
Full size table
Fig. 7
figure 7

Equilibrium path of a compressed bar

Full size image

Ariaratnam, in his work (1961), noted that the characteristic \(P=f(\delta )\) is a hyperbola. The approximationFootnote 6 of data contained in Table 1 by means of the functionFootnote 7:

$${h}_{A}\left(\delta \right)=\frac{m}{\delta -p}+q$$
(37)

leads to the parameter values:

$$\begin{gathered} m = - 1776.861, \hfill \\ p = - 1.026, \hfill \\ q = 1732.340, \hfill \\ \end{gathered}$$
(38)

and its equations in this particular case (see Fig. 8):

Fig. 8
figure 8

The approximation of the equilibrium path by Ariaratnam’s hyperbola

Full size image
$${h}_{A}\left(\delta \right)=\frac{-1776.861}{\delta +1.026}+1732.340,$$
(39)

from which it follows that its horizontal asymptote is

$$q=1732.340.$$
(40)

Figure 9 shows the diagram of the Ariaratnam hyperbola for larger deflections. It is clearly visible that it has a horizontal asymptote, the value of which corresponds to the value of the critical force (cf. (34)).Footnote 8 Bearing in mind the above considerations, it can be concluded that the determination of the horizontal asymptote of the Ariaratnam hyperbola, approximating the bar deflection value and the corresponding exciting forces, may be one of the methods of determining the value of the critical force.

Fig. 9
figure 9

Ariaratnam’s hyperbola for larger deflections

Full size image

Critical forces obtained for columns of constant, rectangular cross section of thickness t = 5 mm and widths b = bp = 64.61 mm and b = bp + b0 = 87.46 mm were shown in Fig. 9 just for comparative purposes as well.

Let us now proceed to the Southwell method. The chart in Fig. 7 shall be presented in relation \(\delta /P=f(\delta )\). In Fig. 10, which illustrates this very situation, it can be noticed that the distribution of points is linearFootnote 9. This is also confirmed by the fact that Pearson's linear correlation coefficient (R) is equal to one, which indicates a full positive linear relationship between the values obtained.

Fig. 10
figure 10

Graphical equilibrium path of a compressed bar in a relation \(\delta /P=f(\delta )\) and the Southwell function

Full size image

The regression line, which is the Southwell function of the above data (the red line), is a straight line with the equation:

$$\frac{\delta }{P}\left(\delta \right)=577366\cdot {10}^{-9}\delta +591724\cdot {10}^{-12}.$$
(41)

The critical force, which is the inverse of the Southwell’s straight lineslope, has a value of.

$$P_{{{\text{kr}}}} { } = \left( {577366\cdot10^{ - 9} } \right)^{ - 1} = { }1733.0025{\text{ N}}{.}$$
(42)

Due to the value of the Pearson linear correlation coefficient, indicating a full positive linear relationship between the obtained values (which has already been mentioned above) and due to the analysis carried out, it can be concluded that Southwell's method is also correct for a bar with a parabolically variable stiffness and a parabolic, curved initial bow imperfection.

6 The proof of the Southwell method – the numerical approach

To check the correctness of the Southwell method in reference to compressed columns of variable cross section also the numerical approach based on FEM was adopted. To this end two different columns were considered. The first is shown in Fig. 11. It is a case of a pin ended column. Its thickness h is constant, and the width b(x) is described by the function:

Fig. 11
figure 11

Geometry, static scheme, and initial deflection of the column

Full size image
$$\frac{1}{2}b\left(x\right)=\frac{1}{2}{b}_{p}+\frac{1}{2}{b}_{0}\bullet \mathrm{sin}\frac{\pi \bullet x}{L} .$$
(43)

The following data were used in numerical simulations: E = 210 GPa,  = 0.3, L = 1000 mm, bp = 40 mm, b0 = 15 mm, h = 5 mm.

The initial deflection was defined as follows:

$${f}_{0}\left(x\right)={A}_{0}\bullet \mathrm{sin}\left(\frac{\pi \cdot x}{L}\right) , {A}_{0}=\frac{L}{1000} .$$
(44)

The Abaqus system based on finite element method was used, and due to symmetry only half of the column was discretised (comp. Figs. 11 and 12). The four nodes, shell finite elements of S4 family were used. Boundary conditions are shown in Fig. 12. Ui denote displacements in directions x, y, and z (1, 2, and 3, respectively) and URi– rotations with respect to axes x, y, and z (1, 2, and 3, respectively).

Fig. 12
figure 12

Discrete model of the column, nonlinear equilibrium path, and the Southwell plot

Full size image

In the first step of the analysis, the critical force for the column of ideal geometry was calculated as the result of the linear buckling analysis. The obtained value of the critical force was equal to \({P}_{cr}^{\mathrm{LBA}}= 1135.12 \mathrm{N}\).

Critical forces obtained for columns of constant, rectangular cross section of thickness t = 5 mm and widths b = bp = 40 mm and b = bp + b0 = 55 mm (comp. Figure 11) were shown in Fig. 12 for comparative purposes as well.

In the next step of the numerical simulations, the nonlinear equilibrium path of the initially deflected column (comp. Eq. (44)) was calculated. Geometrically nonlinear analysis (GNA) was carried out using the incremental Newton–Raphson method with the load control option. The load parameter was gradually increased, and the corresponding displacements were calculated analogously as it is done in laboratory tests. The obtained nonlinear equilibrium path P(f) is shown in Fig. 12 with the red line. On the same plot the relationship \(\frac{f}{P}(f)\) was presented. This Southwell’s plot was determined on the basis of calculation points taken from the nonlinear equilibrium path from the range [0, 4] of the deflection f. The inverse of the direction coefficient of this straight line is the searched critical force:

$${P}_{\mathrm{cr}}^{\mathrm{South}}= \frac{1}{8.80585\bullet {10}^{-4}}=1135.61 \mathrm{N} .$$
(45)

The difference in reference to \({P}_{\mathrm{cr}}^{\mathrm{LBA}}= 1135.12 \mathrm{N}\) is equal 0.05%. The other considered column is shown in Fig. 13.

Fig. 13
figure 13

Geometry, static scheme, and initial deflection of the column

Full size image

The variable width of the column was described by the function defined below:

$$\frac{1}{2}b\left(x\right)=\frac{1}{2}{b}_{p}+\frac{1}{2}{b}_{0}\bullet \frac{L-x}{L}\bullet \mathrm{cos}\frac{\pi \bullet (x+200)}{520} .$$
(46)

The following data were used in numerical simulations: E = 210 GPa,  = 0.3, L = 1000 mm, bp = 40 mm, b0 = 15 mm, h = 5 mm.

The initial deflection was defined as follows:

$${f}_{0}\left(x\right)={A}_{0}\bullet (2 {x}^{4}-5L{x}^{3}+3{L}^{2}{x}^{3} ), {A}_{0}=\frac{1}{500\bullet {L}^{3}} .$$
(47)

Results of numerical analyses analogous to those carried out in a case of the previously considered column are presented in Fig. 14.

Fig. 14
figure 14

Discrete model of the column, nonlinear equilibrium path, and the Southwell plot

Full size image

The Southwell’s straight line was determined on the basis of calculation points taken from the nonlinear equilibrium path from the range [0, 7] of the lateral deflection f. The inverse of the direction coefficient of this straight line is the searched critical force:

$${P}_{\mathrm{cr}}^{\mathrm{South}}= \frac{1}{5.70234\bullet {10}^{-4}}=1753.67 \mathrm{N} .$$
(48)

The difference in reference to \({P}_{\mathrm{cr}}^{\mathrm{LBA}}= 1750.56 \mathrm{N}\) is equal 0.18%.

Critical forces obtained for columns of constant, rectangular cross section of thickness t = 5 mm and widths b = bmin = 29.51 mm and b = bmax = 45.32 mm (comp. Fig. 13) were shown in Fig. 14 for comparative purposes as well.

Both examples presented in this Section confirm the correctness of the Southwell method also in a case of columns of different modes of section variabilities and different boundary conditions.

7 Recapitulation and conclusions

Due to technological advances, bars with variable cross sections are increasingly used in building structures and machine parts. To estimate their buckling capacity, it is necessary to know the critical force accompanying the bifurcation loss of stability of a bar subjected to a compressive force. The critical force can be determined experimentally, and the most effective way to experimentally determine its value is the Southwell method in its original version, derived and justified for elastic bars with cross sections unchanged along the length (cf. Southwell [37]. Before that, however, it would have to be decided whether the Southwell method can be applied to bars with cross sections of variable length. This question was positively resolved by Ariaratnam in his 1961 work. In a general way, applying the variation approach, he justified the correctness of Southwell's method also for bars with bending stiffness variable along the length (cf. Ariaratnam [1]).

In this work, the authors solved a differential equation of stability for a bar with parabolic variable bending stiffness and parabolic initial bow deflection of the bar axis with the help of the Mathematica™ system. The exact solution found enabled full verification of the correctness of the Southwell method for the examined rod case. The paper shows that the critical force can be determined by measuring the characteristics \(P(\delta )\) (it takes the form of a hyperbola as in the case of a bar with a constant cross section) and constructing a plot δ/P as a function of δ. The plot is a straight line, and the inverse of the slope of this line is the value of the critical force sought. Thus it was proved that for bars with the considered geometry the Southwell method is as correct as for bars with constant cross sections and can be successfully used in the experimental stability analyses of the considered elastic bars.

The correctness of the Southwell method was confirmed also numerically on the example of two other columns of variable cross section and different boundary conditions. The numerical analyses based on FEM have revealed that the buckling loads obtained as a result of linear buckling analysis were nearly exactly the same as buckling loads obtained from Southwell’s plots.