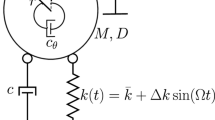Abstract
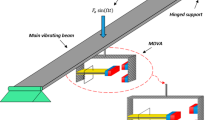
Structural nonlinearity for conventional double-end fixed beam MEMS resonators considerably restricts their performance because of large displacement instabilities and excessive frequency noise. To solve this problem, a new resonator design based on H-shaped structural beams is proposed to alleviate the axial force caused by a large deflection of the beam structure. An analytical expression for the nonlinear stiffness of the proposed beam is derived using the Rayleigh–Ritz energy method. Nonlinear vibration equations of the resonant system are then formulated and solved analytically via the method of multiple scales. The results show that the H-shaped beam design can effectively reduce the nonlinearity without significantly decreasing the linear stiffness. The solution to the nonlinear stiffness of a given electrically excited resonant system is quantitatively verified by finite element analysis. The analytical solution to the nonlinear vibration of the system is verified by numerical simulation. The obtained dynamic results indicate that the H-shaped beam design can effectively improve the stability of the resonant frequency and it can also depress the cross-sensitivity of the resonator.











Similar content being viewed by others
References
Ma, C., Chen, S., Guo, F.: Simultaneous determination of the mass and position of attached particles using a micro-beam resonant mass sensor with axial pre-tension. Acta Mech. 232(10), 4037–4055 (2021)
Khater, M.E.: On the sensitivity of bifurcation-based electrostatic MEMS sensors: cantilever with tip plate. Acta Mech. 232, 3033–3040 (2021)
Zou, X., Seshia, A.A.: The impact of damping on the frequency stability of nonlinear MEMS oscillators. J. Microelectromech. Syst. 24(3), 537–544 (2015)
Nguyen, C.T.-C.: MEMS technology for timing and frequency control. IEEE Trans. Ultrason., Ferroelectr., Freq. Control 54(2), 251–270 (2007)
Liu, R., Nilchi, J. N., Li, W.-C., Nguyen, C. T.-C.: Soft-impacting micromechanical resoswitch zero-quiescent power AM receiver. In: Proc. IEEE 29th Int. Conf. Micro Electro Mech. Syst., pp. 51–54 (2016)
Demirci, M.U., Nguyen C. T.-C.: A low impedance VHF micromechanical filter using coupled-array composite resonators. In: Proc. 13th Int. Conf. IEEE Solid-State Sens., Actuators Microsyst. (TRANSDUCERS) Dig. Tech. Papers, pp. 2131–2134 (2005)
Kaajakari, V., Mattila, T., Oja, A., Seppa, H.: Nonlinear limits for single-crystal silicon microresonators. J. Microelectromech. Syst. 13(5), 715–724 (2004)
Kaajakari, V., Koskinen, J.K., Mattila, T.: Phase noise in capacitively coupled micromechanical oscillators. IEEE Trans. Ultrason. Ferroelectr. Freq. Control. 52, 2322–2331 (2005)
Mestrom, R.M.C., Fey, R.R., Beek, J.T.M.V., Phan, T.: Modelling the dynamics of a MEMS resonator: simulations and experiments. Sens Actuators A Phys. 142(1), 306–315 (2008)
Mestrom, R.M.C., Fey, R.R., Phan, K., Nijmeijer, H.: Simulations and experiments of hardening and softening resonances in a clamped–clamped beam MEMS resonator. Sens. Actuators A Phys. 162(2), 225–234 (2010)
Braghin, F., Resta, F., Leo, E., Spinola, G.: Nonlinear dynamics of vibrating MEMS. Sens. Actuators A Phys. 134(1), 98–108 (2007)
Elshurafa, A.M., Khirallah, K., Tawfik, H.H., Emira, A., Aziz, A.K.S.A., Sedky, S.M.: Nonlinear dynamics of spring softening and hardening in folded-MEMS comb drive resonators. J. Microelectromech. Syst. 20(4), 943–958 (2011)
Ramini, A.H., Hennawi, Q.M., Younis, M.I.: Theoretical and experimental investigation of the nonlinear behavior of an electrostatically actuated in-plane MEMS arch. J. Microelectromech. Syst. 25(3), 570–578 (2016)
Li, L.L., Polunin, P.M., Dou, S., Shoshani, O., Strachan, B.S., Jensen, J.S., Shaw, S.W., Turner, K.L.: Tailoring the nonlinear response of MEMS resonators using shape optimization. Appl. Phys. Lett. 110, 081902 (2017)
Kenny, T.: Scaling of amplitude-frequency-dependence nonlinearities in electrostatically transduced microresonators. Appl. Phys. Lett. 102(7), 2682–2693 (2007)
Jaakkola, O., Kiihamäki, J., Lamminmäki, T., Mattila, T., Oja, A., Ruokonen, K., Seppä, H., Seppälä, P., Tittonen, I.: Electromechanical analysis of micromechanical SOI-fabricated RF resonators. In: Proc. 3rd Int. Conf. Modeling and Simulation of Microsyst., Semiconductors, Sensors and Actuators (San Diego), pp217–220 (2000)
Veijola, T., Mattila, T.: Modeling of nonlinear micromechanical resonators and their simulation with the harmonic-balance method. Int. J. RF Microw. Comput.-Aided Eng. 11(5), 310–321 (2001)
Zhang, W., Baskaran, R., Turner, K.L.: Effect of cubic nonlinearity on auto-parametrically amplified resonant MEMS mass sensor. Sens. Actuators A Phys. 102(1–2), 139–150 (2002)
Chen, D., Wang, Y., Guan, Y., Chen, X., Liu, X., Xie, J.: Methods for nonlinearities reduction in micromechanical beams resonators. J. Microelectromech. Syst. 27(5), 764–773 (2018)
Tilmans, H.A.C., Legtenberg, R.: Electrostatically driven vacuum-encapsulated polysilicon resonators: Part II. Theory and performance. Sens. Actuators A Phys. 45(1), 67–84 (1994)
Sobreviela, G., Zhao, C., Pandit, M.N., Do, C., Du, S., Zou, X., Seshia, A.: Parametric noise reduction in a high-order nonlinear MEMS resonator utilizing its bifurcation points. J. Microelectromech. Syst. 26(6), 1189–1199 (2017)
Nemov, A.S., Matikainen, M.K., Wang, T., Mikkola, A.: Analysis of electromechanical systems based on the absolute nodal coordinate formulation. Acta Mech. 233, 1019–1030 (2022)
Sharifnia, M.: A higher-order nonlinear beam element for planar structures by using a new finite element approach. Acta Mech. 233, 495–511 (2022)
Li, M., Tang, H.X., Roukes, M.L.: Ultra-sensitive NEMS-based cantilevers for sensing, scanned probe and very high-frequency applications. Nat. Nanotechnol. 2(2), 114–120 (2007)
Li, M., Bhiladvala, R.B., Morrow, T.J., Sioss, J.A., Lew, K.-K., Redwing, J.M., Keating, C.D., Mayer, T.S.: Bottom-up assembly of large-area nanowire resonator arrays. Nat. Nanotechnol. 3(2), 88–92 (2008)
Agarwal, M., Park, K., Candler, R., Hopcroft, M., Jha C., Melamud, R., Kim, B., Murmann, B., Kenny, T.W.: Non-linearity cancellation in MEMS resonators for improved power-handling. In: IEEE InternationalElectron Devices Meeting, 5–5 Dec. 2005, Washington, DC, USA.
Sobreviela, G., Vidal-Álvarez, G., Riverola, M., Uranga, A., Torres, F., Barniol, N.: Suppression of the A-f-mediated noise at the top bifurcation point in a MEMS resonator with both hardening and softening hysteretic cycles. Sens. Actuators A Phys. 256, 59–65 (2017)
Senturia, S.D.: Microsystem design. Springer, US (2001)
Landau, L.D., Lifshitz E.M.: Mechanics, 3rd edn: volume 1 of course of theoretical physics. Elsevier 1976.
Nayfeh, A.H., Mook, D.T.: Nonlinear oscillations. John Wiley and Sons, New York (1979)
Author information
Authors and Affiliations
Corresponding authors
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix
Appendix
1.1 Perturbation analysis of nonlinear response of the main resonance
For the main resonance, \({\omega }_{0}\approx \omega\). In order to analyze the response of system near natural frequency, it is necessary to specify the order of damping, nonlinearity and excitation so that they can appear simultaneously in the perturbation method [28]. If \({y}_{e}=\varepsilon \mathrm{cos}\left({\omega }_{0}t\right)\) is assumed, the nonlinearity will produce a term that is proportional to the \({\rm O}\left({\varepsilon }^{3}\right)\) order of \(\mathrm{cos}{\omega }_{0}t\). Therefore, if \({y}_{e}=\varepsilon u\) is assumed, then the order of \(\zeta {\omega }_{0}\dot{{y}_{e}}\) needs to be \({\varepsilon }^{2}\mu \dot{{y}_{e}}\), and the order of \(\left({f}_{0}/m\right)\mathrm{cos}\left(\omega t\right)\) is \({\varepsilon }^{3}f\mathrm{cos}\left(\omega t\right)\), the governing equation (26) in Sect. 2.2 becomes
where
The multiscale method is used to find the approximate solution to eq. (A.1).
Assume
then
Because the excitation is the order of \({\rm O}({\varepsilon }^{2})\), for the sake of consistency, we assume
In this paper, the problem is solved by quadratic approximation:
Substituting Eqs. (A.2) and (A.3) into Eq. (A.1), and making the coefficients of \(\varepsilon\), \({\varepsilon }^{2}\), \({\varepsilon }^{3}\) on both sides of the equation equal,
The general solution of Eq. (A.4) can be written as
In the formula, \(Q\left({T}_{1},{T}_{2}\right)\) is still an undetermined function, which will be determined by eliminating the long-term terms in \({u}_{1}\) and \({u}_{2}\). Substituting Eq. (A.7) into Eq. (A.5), we obtain.
where cc represents the conjugate complex number of the preceding items. By eliminating those items that cause \({u}_{1}\) to produce long-term terms, \({D}_{1}Q=0\) or \(Q=Q({T}_{2})\) will be obtained. Therefore, the solution of Eq. (A.8) is
Substituting Eqs. (A.7) and (A.9) into Eq. (A.6), we obtain.
where \(Q\mathrm{^{\prime}}\) represents the derivative of \({T}_{2}\), and NST represents those terms containing \({e}^{3i{\omega }_{0}{T}_{0}}\). If
the long-term terms in \({u}_{2}\) will be eliminated. To solve the Eq. (A.11), \(Q\) is expressed as
where \(\alpha\) and \(\beta\) are both real numbers, so the result is divided into real and imaginary parts.
where
The simultaneous equations (A.13) and (A.14) can eliminate \(\beta\), then
Substituting Eq. (A.12) into Eq. (A.7) and (A.9), and substituting the result into Eq. (A.3), the quadratic approximation is obtained:
When \({a}^{\mathrm{^{\prime}}}={\lambda }^{\mathrm{^{\prime}}}=0\), steady-state motion exists, corresponding to the singularities of Eqs. (A.13) and (A.16), where the amplitude and phase are unchanged, which is
The frequency response function can be obtained by adding the squares of the Eqs. (A.18) and (A.19), as follows.
which is
The phase response function can be obtained by comparing Eqs. (A.18) to (A.19),
The stability of different parts of the frequency response curve can be obtained by analyzing the properties of their motion in the neighborhood of each singular point.
Assuming \(\left({a}_{0},{\theta }_{0}\right)\) is the singularity of Eqs. (A.18) and (A.19), then
Combined with the Eqs. (A.23) and (A.24), the Taylor series expansion of the Eqs. (A.13) and (A.14) in the neighborhood of \(\left({a}_{0},{\theta }_{0}\right)\) is carried out, and the equation is retained to the linear term. If \(\left({a}_{0}+{a}_{1},{\theta }_{0}+{\theta }_{1}\right)\) is any point in this neighborhood, then there is
Therefore, the stability problem of steady-state motion is transformed into the eigenvalue problem of the coefficient matrix at the right end of the above equation. Using Eqs. (A.25) and (A.26), the following eigenvalue equation can be obtained:
which is
Thus,
where
If \(\Delta >0\), the eigenvalues are two unequal real roots. When \({\lambda }_{1}\) and \({\lambda }_{2}\) are both positive, the singularity is an unstable point. When \({\lambda }_{1}\) and \({\lambda }_{2}\) are both negative, the singularity is a stable point. When the signs of \({\lambda }_{1}\) and \({\lambda }_{2}\) are opposite, the singularity is an unstable saddle point. If \(\Delta =0\), the eigenvalues are two equal real roots. At this time, if the eigenvalue is less than 0, the node is stable, otherwise, it is unstable. If \(\Delta <0\), the eigenvalue is a conjugate complex. When the real part of the eigenvalue is less than 0, the singularity is a stable focus. When it is greater than 0, the singularity is an unstable point. When it is equal to 0, the singularity is called the center.
In summary, regardless of the value of \(\Delta\), the singularity is a stable point as long as the eigenvalue (or the real part of the eigenvalue) is less than zero. For this problem, the damping \(\mu\) is always positive, so for the case of \(\Delta \le 0\), the steady-state motion is stable. For \(\Delta >0\), only the relationship \(-\mu +\sqrt{\Delta }/2<0\) is satisfied, and the steady-state motion is stable. There is only one case in which steady-state motion is unstable, which is
Therefore, we can obtain
Therefore, when \(\Gamma <0\), the steady-state motion is unstable, otherwise it is stable. In a nonlinear system, if there are multiple steady-state solutions, the initial conditions determine which steady-state solution the system physically realizes.
Rights and permissions
Springer Nature or its licensor holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Zhou, C., Fu, Q., Zhang, X. et al. Nonlinearity reduction in MEMS resonators based on design of H-shaped beams. Acta Mech 233, 4903–4918 (2022). https://doi.org/10.1007/s00707-022-03340-1
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00707-022-03340-1