Propagation of SH-waves in inhomogeneous piezoelectric/piezomagnetic half-space with circular inclusion

Abstract

In this article, the dynamic characteristics of a circular inclusion in an inhomogeneous piezoelectric/piezomagnetic half-space with propagating anti-plane shear waves are studied. The exponential distribution of material parameters along the coordinate axis is considered. The Helmholtz equation includes variable coefficients due to inhomogeneity. First, the Helmholtz equation is transformed into standard form by introducing new variables. Next, integral equations with respective boundary conditions are composed and solved by orthogonal function expansion and effective truncation techniques. Obtained results enable to understand the influence on the dynamic stress concentration factor as well as the electric and magnetic field intensities under proper conditions. The conclusions of this article are verified by comparing the analytical solutions to the ones obtained by finite element method.

Appendix

1.1 Part I: Decoupling of governing equations

The constitutive equations for a piezoelectric/piezomagnetic material look as follows:

$$ \begin{aligned} \tau _{{xz}} & = c_{{44}} (x,y)\frac{{\partial u}}{{\partial x}} + e_{{15}} (x,y)\frac{{\partial \phi }}{{\partial x}} + h_{{15}} (x,y)\frac{{\partial \varphi }}{{\partial x}}, \\ \tau _{{yz}} & = c_{{44}} (x,y)\frac{{\partial u}}{{\partial y}} + e_{{15}} (x,y)\frac{{\partial \phi }}{{\partial y}} + h_{{15}} (x,y)\frac{{\partial \varphi }}{{\partial y}}, \\ D_{x} & = e_{{15}} (x,y)\frac{{\partial u}}{{\partial x}} - \kappa _{{11}} (x,y)\frac{{\partial \phi }}{{\partial x}} - t_{{11}} (x,y)\frac{{\partial \varphi }}{{\partial x}}, \\ D_{y} & = e_{{15}} (x,y)\frac{{\partial u}}{{\partial y}} - \kappa _{{11}} (x,y)\frac{{\partial \phi }}{{\partial y}} - t_{{11}} (x,y)\frac{{\partial \varphi }}{{\partial y}}, \\ B_{x} & = h_{{15}} (x,y)\frac{{\partial u}}{{\partial x}} - t_{{11}} (x,y)\frac{{\partial \phi }}{{\partial x}} - \mu _{{11}} (x,y)\frac{{\partial \varphi }}{{\partial x}}, \\ B_{y} & = h_{{15}} (x,y)\frac{{\partial u}}{{\partial y}} - t_{{11}} (x,y)\frac{{\partial \phi }}{{\partial y}} - \mu _{{11}} (x,y)\frac{{\partial \varphi }}{{\partial y}}. \\ \end{aligned} $$

(33)

Here, $\sigma _{{xz}}$ and $\sigma _{{yz}}$ are stress tensor components;$D_{x}$ and $D_{y}$ are electric displacement tensor components;$B_{x}$ and $B_{y}$ are magnetic induction components;$w$, $\phi$, and $\varphi$ are displacement, electric potential, and magnetic potential, respectively.

Taking into account the absence of body forces and free charges for the dynamic problem, the equilibrium equations of the piezoelectric/piezomagnetic medium are written as follows:

$$ \begin{aligned} \frac{{\partial \tau _{{xz}} }}{{\partial x}} + \frac{{\partial \tau _{{yz}} }}{{\partial y}} & = \rho \frac{{\partial ^{2} u}}{{\partial t^{2} }}, \\ \frac{{\partial D_{x} }}{{\partial x}} + \frac{{\partial D_{y} }}{{\partial y}} & = 0, \\ \frac{{\partial B_{x} }}{{\partial x}} + \frac{{\partial B_{y} }}{{\partial y}} & = 0. \\ \end{aligned} $$

(34)

Employing Eqs. (34) into (33), the following governing equations are obtained:

$$ \begin{aligned} \frac{{\partial c_{{44}} (x,y)}}{{\partial x}}\frac{{\partial u}}{{\partial x}} + c_{{44}} (x,y)\frac{{\partial ^{2} u}}{{\partial x^{2} }} + \frac{{\partial e_{{15}} (x,y)}}{{\partial x}}\frac{{\partial \phi }}{{\partial x}} + e_{{15}} (x,y)\frac{{\partial ^{2} \phi }}{{\partial x^{2} }} + \frac{{\partial h_{{15}} (x,y)}}{{\partial x}}\frac{{\partial \varphi }}{{\partial x}} + h_{{15}} (x,y)\frac{{\partial ^{2} \varphi }}{{\partial x^{2} }} + \frac{{\partial c_{{44}} (x,y)}}{{\partial y}}\frac{{\partial u}}{{\partial y}} + c_{{44}} (x,y)\frac{{\partial ^{2} u}}{{\partial y^{2} }} + \frac{{\partial e_{{15}} (x,y)}}{{\partial y}}\frac{{\partial \phi }}{{\partial y}} + e_{{15}} (x,y)\frac{{\partial ^{2} \phi }}{{\partial y^{2} }} + \frac{{\partial h_{{15}} (x,y)}}{{\partial y}}\frac{{\partial \varphi }}{{\partial y}} + h_{{15}} (x,y)\frac{{\partial ^{2} \varphi }}{{\partial y^{2} }} = \rho (x,y)\frac{{\partial ^{2} u}}{{\partial t^{2} }} \\ \,,\end{aligned} $$

$$ \begin{aligned} & \frac{{\partial e_{{15}} (x,y)}}{{\partial x}}\frac{{\partial u}}{{\partial x}} + e_{{15}} (x,y)\frac{{\partial ^{2} u}}{{\partial x^{2} }} - \frac{{\partial \kappa _{{11}} (x,y)}}{{\partial x}}\frac{{\partial \phi }}{{\partial x}} \\ & \quad - \kappa _{{11}} (x,y)\frac{{\partial ^{2} \phi }}{{\partial x^{2} }} - \frac{{\partial t_{{11}} (x,y)}}{{\partial x}}\frac{{\partial \varphi }}{{\partial x}} - t_{{11}} (x,y)\frac{{\partial ^{2} \varphi }}{{\partial x^{2} }} \\ & \quad + \frac{{\partial e_{{15}} (x,y)}}{{\partial y}}\frac{{\partial u}}{{\partial y}} + e_{{15}} (x,y)\frac{{\partial ^{2} u}}{{\partial y^{2} }} - \frac{{\partial \kappa _{{11}} (x,y)}}{{\partial y}}\frac{{\partial \phi }}{{\partial y}} \\ & \quad - \kappa _{{11}} (x,y)\frac{{\partial ^{2} \phi }}{{\partial y^{2} }} - \frac{{\partial t_{{11}} (x,y)}}{{\partial y}}\frac{{\partial \varphi }}{{\partial y}} - t_{{11}} (x,y)\frac{{\partial ^{2} \varphi }}{{\partial y^{2} }} = 0 \\ \,,\end{aligned} $$

$$ \begin{aligned} \frac{{\partial h_{{15}} (x,y)}}{{\partial x}}\frac{{\partial u}}{{\partial x}} + h_{{15}} (x,y)\frac{{\partial ^{2} u}}{{\partial x^{2} }} - \frac{{\partial t_{{11}} (x,y)}}{{\partial x}}\frac{{\partial \phi }}{{\partial x}} \\ & \quad - t_{{11}} (x,y)\frac{{\partial ^{2} \phi }}{{\partial x^{2} }} - \frac{{\partial \mu _{{11}} (x,y)}}{{\partial x}}\frac{{\partial \varphi }}{{\partial x}} - \mu _{{11}} (x,y)\frac{{\partial ^{2} \varphi }}{{\partial x^{2} }} \\ & \quad + \frac{{\partial h_{{15}} (x,y)}}{{\partial y}}\frac{{\partial u}}{{\partial y}} + h_{{15}} (x,y)\frac{{\partial ^{2} u}}{{\partial y^{2} }} - \frac{{\partial t_{{11}} (x,y)}}{{\partial y}}\frac{{\partial \phi }}{{\partial y}} \\ & \quad - t_{{11}} (x,y)\frac{{\partial ^{2} \phi }}{{\partial y^{2} }} - \frac{{\partial \mu _{{11}} (x,y)}}{{\partial y}}\frac{{\partial \varphi }}{{\partial y}} - \mu _{{11}} (x,y)\frac{{\partial ^{2} \varphi }}{{\partial y^{2} }} = 0 \,.\\ \end{aligned} $$

(35)

By substituting Eqs. (1) into (35), the governing equations can be described as follows:

$$ \begin{aligned} c_{{440}} \nabla ^{2} u + 2c_{{440}} \left( {p\frac{{\partial u}}{{\partial x}} + q\frac{{\partial u}}{{\partial y}}} \right) + e_{{150}} \nabla ^{2} \phi + 2e_{{150}} \left( {p\frac{{\partial \phi }}{{\partial x}} + q\frac{{\partial \phi }}{{\partial y}}} \right) + h_{{150}} \nabla ^{2} \varphi + 2h_{{150}} \left( {p\frac{{\partial \varphi }}{{\partial x}} + q\frac{{\partial \varphi }}{{\partial y}}} \right) = \rho _{0} \frac{{\partial ^{2} u}}{{\partial t^{2} }} \\ \,,\end{aligned} $$

$$ \begin{aligned} e_{{150}} \nabla ^{2} u + 2e_{{150}} \left( {p\frac{{\partial u}}{{\partial x}} + q\frac{{\partial u}}{{\partial y}}} \right) - \kappa _{{110}} \nabla ^{2} \phi - 2\kappa _{{110}} \left( {p\frac{{\partial \phi }}{{\partial x}} + q\frac{{\partial \phi }}{{\partial y}}} \right) - t_{{110}} \nabla ^{2} \varphi - 2t_{{110}} \left( {p\frac{{\partial \varphi }}{{\partial x}} + q\frac{{\partial \varphi }}{{\partial y}}} \right) = 0 h_{{150}} \nabla ^{2} u + 2h_{{150}} \left( {p\frac{{\partial u}}{{\partial x}} + q\frac{{\partial u}}{{\partial y}}} \right) - t_{{110}} \nabla ^{2} \phi - 2t_{{110}} \left( {p\frac{{\partial \phi }}{{\partial x}} + q\frac{{\partial \phi }}{{\partial y}}} \right) - \mu _{{110}} \nabla ^{2} \varphi - 2\mu _{{110}} \left( {p\frac{{\partial \varphi }}{{\partial x}} + q\frac{{\partial \varphi }}{{\partial y}}} \right) = 0 \\ \,,\end{aligned} $$

(36)

where $\nabla ^{2}$ represents the two-dimensional Laplace operator.

1.2 Part I: Calculation of unknown coefficients

According to the boundary conditions (11) on the boundary $B_{{in}}$, the integral equations with unknown coefficients $A_{n}$,$B_{n}$,$C_{n}$,$D_{n}$,$E_{n}$,$R_{n}$,$L_{n}$,$T_{n}$,$U_{n}$ and $V_{n}$ are established as follows:

$$ \sum\limits_{{n = - \infty }}^{{ + \infty }} {A_{n} \xi _{n}^{{(11)}} + } \sum\limits_{{n = - \infty }}^{{ + \infty }} {R_{n} \xi _{n}^{{(16)}} } = \xi ^{{(1)}} \,,$$

$$ \begin{gathered} \sum\limits_{{n = - \infty }}^{{ + \infty }} {A_{n} \xi _{n}^{{(21)}} + } \sum\limits_{{n = 1}}^{{ + \infty }} {B_{n} \xi _{n}^{{(22)}} + \sum\limits_{{n = 1}}^{{ + \infty }} {C_{n} \xi _{n}^{{(23)}} + } \sum\limits_{{n = 1}}^{{ + \infty }} {D_{n} \xi _{n}^{{(24)}} + } } \sum\limits_{{n = 1}}^{{ + \infty }} {E_{n} \xi _{n}^{{(25)}} } + \sum\limits_{{n = - \infty }}^{{ + \infty }} {R_{n} \xi _{n}^{{(26)}} } \hfill \\ + \sum\limits_{{n = - \infty }}^{{ + \infty }} {L_{n} \xi _{n}^{{(27)}} + } \sum\limits_{{n = - \infty }}^{{ + \infty }} {T_{n} \xi _{n}^{{(28)}} } + \sum\limits_{{n = - \infty }}^{{ + \infty }} {U_{n} \xi _{n}^{{(29)}} + } \sum\limits_{{n = - \infty }}^{{ + \infty }} {V_{n} \xi _{n}^{{(210)}} } = \xi ^{{(2)}} \,,\hfill \\ \end{gathered} $$

$$ \begin{gathered} \sum\limits_{{n = - \infty }}^{{ + \infty }} {A_{n} \xi _{n}^{{(31)}} + } \sum\limits_{{n = 1}}^{{ + \infty }} {B_{n} \xi _{n}^{{(32)}} + \sum\limits_{{n = 1}}^{{ + \infty }} {C_{n} \xi _{n}^{{(33)}} + } \sum\limits_{{n = 1}}^{{ + \infty }} {D_{n} \xi _{n}^{{(34)}} + } } \sum\limits_{{n = 1}}^{{ + \infty }} {E_{n} \xi _{n}^{{(35)}} } + \sum\limits_{{n = - \infty }}^{{ + \infty }} {R_{n} \xi _{n}^{{(36)}} } \hfill \\ + \sum\limits_{{n = - \infty }}^{{ + \infty }} {L_{n} \xi _{n}^{{(37)}} + } \sum\limits_{{n = - \infty }}^{{ + \infty }} {T_{n} \xi _{n}^{{(38)}} } + \sum\limits_{{n = - \infty }}^{{ + \infty }} {U_{n} \xi _{n}^{{(39)}} + } \sum\limits_{{n = - \infty }}^{{ + \infty }} {V_{n} \xi _{n}^{{(310)}} } = \xi ^{{(3)}} \hfill \,,\\ \end{gathered} $$

$$\sum\limits_{{n = 1}}^{{ + \infty }} {B_{n} \xi _{n}^{{(42)}} + \sum\limits_{{n = 1}}^{{ + \infty }} {C_{n} \xi _{n}^{{(43)}} + } } \sum\limits_{{n = - \infty }}^{{ + \infty }} {L_{n} \xi _{n}^{{(47)}} + } \sum\limits_{{n = - \infty }}^{{ + \infty }} {T_{n} \xi _{n}^{{(48)}} } = \xi ^{{(4)}}\,, $$

$$ \begin{gathered} \sum\limits_{{n = - \infty }}^{{ + \infty }} {A_{n} \xi _{n}^{{(51)}} + } \sum\limits_{{n = 1}}^{{ + \infty }} {B_{n} \xi _{n}^{{(52)}} + \sum\limits_{{n = 1}}^{{ + \infty }} {C_{n} \xi _{n}^{{(53)}} + } \sum\limits_{{n = 1}}^{{ + \infty }} {D_{n} \xi _{n}^{{(54)}} + } } \sum\limits_{{n = 1}}^{{ + \infty }} {E_{n} \xi _{n}^{{(55)}} } + \sum\limits_{{n = - \infty }}^{{ + \infty }} {R_{n} \xi _{n}^{{(56)}} } \hfill \\ + \sum\limits_{{n = - \infty }}^{{ + \infty }} {L_{n} \xi _{n}^{{(57)}} + } \sum\limits_{{n = - \infty }}^{{ + \infty }} {T_{n} \xi _{n}^{{(58)}} } + \sum\limits_{{n = - \infty }}^{{ + \infty }} {U_{n} \xi _{n}^{{(59)}} + } \sum\limits_{{n = - \infty }}^{{ + \infty }} {V_{n} \xi _{n}^{{(510)}} } = \xi ^{{(5)}} \hfill \,,\\ \end{gathered} $$

$$ \sum\limits_{{n = 1}}^{{ + \infty }} {D_{n} \xi _{n}^{{(64)}} + } \sum\limits_{{n = 1}}^{{ + \infty }} {E_{n} \xi _{n}^{{(65)}} } + \sum\limits_{{n = - \infty }}^{{ + \infty }} {U_{n} \xi _{n}^{{(69)}} + } \sum\limits_{{n = - \infty }}^{{ + \infty }} {V_{n} \xi _{n}^{{(610)}} } = \xi ^{{(6)}} $$

(37)

where: $\xi _{n}^{{(11)}} = \sum\limits_{{j = 1}}^{4} {S_{n}^{{(j)}} }$,$\xi _{n}^{{(16)}} = - J_{n} (k_{{03}} \left| {\eta ^{\prime}} \right|)\left[ {{{\eta ^{\prime}} \mathord{\left/ {\vphantom {{\eta ^{\prime}} {\left| {\eta ^{\prime}} \right|}}} \right. \kern-\nulldelimiterspace} {\left| {\eta ^{\prime}} \right|}}} \right]^{n} e^{{ - p_{3} (\frac{{\eta ^{\prime} + \bar{\eta }^{\prime}}}{2}) - q_{3} (\frac{{\eta ^{\prime} - \bar{\eta }^{\prime}}}{{2i}})}}$,

$\xi _{n}^{{(21)}} = \frac{{k_{1} M_{{\text{1}}}^{{\text{I}}} }}{2}\left[ {\sum\limits_{{j = 1}}^{4} {\chi _{n}^{{(j)}} } \exp (i\theta ) + \sum\limits_{{j = 1}}^{4} {\gamma _{n}^{{(j)}} } \exp ( - i\theta )} \right]$,$\xi _{n}^{{(22)}} = M_{2}^{{\text{I}}} \left[ {\sum\limits_{{j = 1}}^{2} {\varsigma _{n}^{{(j)}} \exp (i\theta )} + \sum\limits_{{j = 1}}^{2} {\vartheta _{n}^{{(j)}} \exp ( - i\theta )} } \right]$,

$\xi _{n}^{{(23)}} = M_{2}^{{\text{I}}} \left[ {\sum\limits_{{j = 1}}^{2} {\upsilon _{n}^{{(j)}} \exp (i\theta )} + \sum\limits_{{j = 1}}^{2} {\psi _{n}^{{(j)}} \exp ( - i\theta )} } \right]$,$\xi _{n}^{{(24)}} = {{(M_{3}^{{\text{I}}} } \mathord{\left/ {\vphantom {{(M_{3}^{{\text{I}}} } {M_{2}^{{\text{I}}} }}} \right. \kern-\nulldelimiterspace} {M_{2}^{{\text{I}}} }})\xi _{n}^{{(22)}}$,$\xi _{n}^{{(25)}} = {{(M_{3}^{{\text{I}}} } \mathord{\left/ {\vphantom {{(M_{3}^{{\text{I}}} } {M_{2}^{{\text{I}}} }}} \right. \kern-\nulldelimiterspace} {M_{2}^{{\text{I}}} }})\xi _{n}^{{(23)}}$,

$\xi _{n}^{{(26)}} = - \frac{{k_{{03}} M_{{\text{1}}}^{{{\text{III}}}} }}{2}\left[ {\iota _{1} \exp (i\theta ) + \nu _{1} \exp ( - i\theta )} \right]$,$\xi _{n}^{{(27)}} = - M_{2}^{{{\text{III}}}} \left[ {\iota _{2} \exp (i\theta ) + \nu _{2} \exp ( - i\theta )} \right]$,

$\xi _{n}^{{(28)}} = - M_{2}^{{{\text{III}}}} \left[ {\iota _{3} \exp (i\theta ) + \nu _{3} \exp ( - i\theta )} \right]$,$\xi _{n}^{{(29)}} = {{(M_{3}^{{{\text{III}}}} } \mathord{\left/ {\vphantom {{(M_{3}^{{{\text{III}}}} } {M_{2}^{{{\text{III}}}} }}} \right. \kern-\nulldelimiterspace} {M_{2}^{{{\text{III}}}} }})\xi _{n}^{{(27)}}$,$\xi _{n}^{{(210)}} = {{(M_{3}^{{{\text{III}}}} } \mathord{\left/ {\vphantom {{(M_{3}^{{{\text{III}}}} } {M_{2}^{{{\text{III}}}} }}} \right. \kern-\nulldelimiterspace} {M_{2}^{{{\text{III}}}} }})\xi _{n}^{{(28)}}$,

$\xi _{n}^{{(31)}} = a_{{\text{1}}}^{{\text{I}}} \xi _{n}^{{(11)}}$, $\xi _{n}^{{(32)}} = b_{{\text{1}}}^{{\text{I}}} \sum\limits_{{j = 1}}^{4} {\varphi _{{1n}}^{{(j)}} }$,$\xi _{n}^{{(33)}} = b_{{\text{1}}}^{{\text{I}}} \sum\limits_{{j = 1}}^{4} {\varphi _{{2n}}^{{(j)}} }$,$\xi _{n}^{{(34)}} = {\text{ }}(c_{1}^{I} /b_{1}^{I} )\xi _{n}^{{(32)}}$,$\xi _{n}^{{(35)}} = ({{c_{{\text{1}}}^{{\text{I}}} } \mathord{\left/ {\vphantom {{c_{{\text{1}}}^{{\text{I}}} } {b_{{\text{1}}}^{{\text{I}}} }}} \right. \kern-\nulldelimiterspace} {b_{{\text{1}}}^{{\text{I}}} }})\xi _{n}^{{(33)}}$,

$\xi _{n}^{{(36)}} = a_{{\text{1}}}^{{{\text{III}}}} \xi _{n}^{{(16)}}$,$\xi _{n}^{{(37)}} = - b_{{\text{1}}}^{{{\text{III}}}} e^{{ - p_{3} (\frac{{\eta ^{\prime} + \bar{\eta }^{\prime}}}{2}) - q_{3} (\frac{{\eta ^{\prime} - \bar{\eta }^{\prime}}}{{2i}})}} H_{n}^{{(1)}} (ik^{\prime}_{3} \left| {\eta ^{\prime}} \right|)\left[ {{{\eta ^{\prime}} \mathord{\left/ {\vphantom {{\eta ^{\prime}} {\left| {\eta ^{\prime}} \right|}}} \right. \kern-\nulldelimiterspace} {\left| {\eta ^{\prime}} \right|}}} \right]^{n}$,

$\xi _{n}^{{(38)}} = - b_{{\text{1}}}^{{{\text{III}}}} e^{{ - p_{3} (\frac{{\eta ^{\prime} + \bar{\eta }^{\prime}}}{2}) - q_{3} (\frac{{\eta ^{\prime} - \bar{\eta }^{\prime}}}{{2i}})}} H_{n}^{{(2)}} (ik^{\prime}_{3} \left| {\eta ^{\prime}} \right|)\left[ {{{\eta ^{\prime}} \mathord{\left/ {\vphantom {{\eta ^{\prime}} {\left| {\eta ^{\prime}} \right|}}} \right. \kern-\nulldelimiterspace} {\left| {\eta ^{\prime}} \right|}}} \right]^{n}$,$\xi _{n}^{{(39)}} = ({{c_{{\text{1}}}^{{{\text{III}}}} } \mathord{\left/ {\vphantom {{c_{{\text{1}}}^{{{\text{III}}}} } {b_{{\text{1}}}^{{{\text{III}}}} }}} \right. \kern-\nulldelimiterspace} {b_{{\text{1}}}^{{{\text{III}}}} }})\xi _{n}^{{(37)}}$,$\xi _{n}^{{(310)}} = ({{c_{{\text{1}}}^{{{\text{III}}}} } \mathord{\left/ {\vphantom {{c_{{\text{1}}}^{{{\text{III}}}} } {b_{{\text{1}}}^{{{\text{III}}}} }}} \right. \kern-\nulldelimiterspace} {b_{{\text{1}}}^{{{\text{III}}}} }})\xi _{n}^{{(38)}}$,

$\xi _{n}^{{(42)}} = {{(1} \mathord{\left/ {\vphantom {{(1} {M_{2}^{{\text{I}}} }}} \right. \kern-\nulldelimiterspace} {M_{2}^{{\text{I}}} }})\xi _{n}^{{(22)}}$,$\xi _{n}^{{(43)}} = {{(1} \mathord{\left/ {\vphantom {{(1} {M_{2}^{{\text{I}}} }}} \right. \kern-\nulldelimiterspace} {M_{2}^{{\text{I}}} }})\xi _{n}^{{(23)}}$, $\xi _{n}^{{(47)}} = {{(1} \mathord{\left/ {\vphantom {{(1} {M_{2}^{{{\text{III}}}} }}} \right. \kern-\nulldelimiterspace} {M_{2}^{{{\text{III}}}} }})\xi _{n}^{{(27)}}$,$\xi _{n}^{{(48)}} = {{(1} \mathord{\left/ {\vphantom {{(1} {M_{2}^{{{\text{III}}}} }}} \right. \kern-\nulldelimiterspace} {M_{2}^{{{\text{III}}}} }})\xi _{n}^{{(28)}}$,

$\xi _{n}^{{(51)}} = ({{a_{2}^{{\text{I}}} } \mathord{\left/ {\vphantom {{a_{2}^{{\text{I}}} } {a_{{\text{1}}}^{{\text{I}}} }}} \right. \kern-\nulldelimiterspace} {a_{{\text{1}}}^{{\text{I}}} }})\xi _{n}^{{(31)}}$, $\xi _{n}^{{(52)}} = ({{b_{2}^{{\text{I}}} } \mathord{\left/ {\vphantom {{b_{2}^{{\text{I}}} } {b_{{\text{1}}}^{{\text{I}}} }}} \right. \kern-\nulldelimiterspace} {b_{{\text{1}}}^{{\text{I}}} }})\xi _{n}^{{(32)}}$,$\xi _{n}^{{(53)}} = ({{b_{2}^{{\text{I}}} } \mathord{\left/ {\vphantom {{b_{2}^{{\text{I}}} } {b_{{\text{1}}}^{{\text{I}}} }}} \right. \kern-\nulldelimiterspace} {b_{{\text{1}}}^{{\text{I}}} }})\xi _{n}^{{(33)}}$,$\xi _{n}^{{(54)}} = ({{c_{2}^{{\text{I}}} } \mathord{\left/ {\vphantom {{c_{2}^{{\text{I}}} } {b_{2}^{{\text{I}}} }}} \right. \kern-\nulldelimiterspace} {b_{2}^{{\text{I}}} }})\xi _{n}^{{(52)}}$,$\xi _{n}^{{(55)}} = ({{c_{2}^{{\text{I}}} } \mathord{\left/ {\vphantom {{c_{2}^{{\text{I}}} } {b_{2}^{{\text{I}}} }}} \right. \kern-\nulldelimiterspace} {b_{2}^{{\text{I}}} }})\xi _{n}^{{(53)}}$,$\xi _{n}^{{(56)}} = ({{a_{2}^{{{\text{III}}}} } \mathord{\left/ {\vphantom {{a_{2}^{{{\text{III}}}} } {a_{{\text{1}}}^{{{\text{III}}}} }}} \right. \kern-\nulldelimiterspace} {a_{{\text{1}}}^{{{\text{III}}}} }})\xi _{n}^{{(36)}}$,$\xi _{n}^{{(57)}} = ({{b_{2}^{{{\text{III}}}} } \mathord{\left/ {\vphantom {{b_{2}^{{{\text{III}}}} } {b_{{\text{1}}}^{{{\text{III}}}} }}} \right. \kern-\nulldelimiterspace} {b_{{\text{1}}}^{{{\text{III}}}} }})\xi _{n}^{{(37)}}$, $\xi _{n}^{{(58)}} = ({{b_{2}^{{{\text{III}}}} } \mathord{\left/ {\vphantom {{b_{2}^{{{\text{III}}}} } {b_{{\text{1}}}^{{{\text{III}}}} }}} \right. \kern-\nulldelimiterspace} {b_{{\text{1}}}^{{{\text{III}}}} }})\xi _{n}^{{(38)}}$,$\xi _{n}^{{(59)}} = ({{c_{2}^{{{\text{III}}}} } \mathord{\left/ {\vphantom {{c_{2}^{{{\text{III}}}} } {b_{2}^{{{\text{III}}}} }}} \right. \kern-\nulldelimiterspace} {b_{2}^{{{\text{III}}}} }})\xi _{n}^{{(57)}}$, $\xi _{n}^{{(510)}} = ({{c_{2}^{{{\text{III}}}} } \mathord{\left/ {\vphantom {{c_{2}^{{{\text{III}}}} } {b_{2}^{{{\text{III}}}} }}} \right. \kern-\nulldelimiterspace} {b_{2}^{{{\text{III}}}} }})\xi _{n}^{{(58)}}$, $\xi _{n}^{{(64)}} = \xi _{n}^{{(42)}}$,$\xi _{n}^{{(65)}} = \xi _{n}^{{(43)}}$,$\xi _{n}^{{(69)}} = \xi _{n}^{{(64)}}$,$\xi _{n}^{{(610)}} = \xi _{n}^{{(65)}}\,,$.

$\chi _{n}^{{(1)}} = H_{{n - 1}}^{{(1)}} (k_{1} \left| {\eta ^{\prime}} \right|)\left[ {{{\eta ^{\prime}} \mathord{\left/ {\vphantom {{\eta ^{\prime}} {\left| {\eta ^{\prime}} \right|}}} \right. \kern-\nulldelimiterspace} {\left| {\eta ^{\prime}} \right|}}} \right]^{{n - 1}}$, $\chi _{n}^{{(2)}} = - H_{{n + 1}}^{{(1)}} (k_{1} \left| {\eta ^{\prime}_{1} } \right|)\left[ {{{\eta ^{\prime}_{1} } \mathord{\left/ {\vphantom {{\eta ^{\prime}_{1} } {\left| {\eta ^{\prime}_{1} } \right|}}} \right. \kern-\nulldelimiterspace} {\left| {\eta ^{\prime}_{1} } \right|}}} \right]^{{ - n - 1}}$, $\chi _{n}^{{(3)}} = ( - 1)^{n} H_{{n - 1}}^{{(1)}} (k_{1} \left| {\eta ^{\prime}_{2} } \right|)\left[ {{{\eta ^{\prime}_{2} } \mathord{\left/ {\vphantom {{\eta ^{\prime}_{2} } {\left| {\eta ^{\prime}_{2} } \right|}}} \right. \kern-\nulldelimiterspace} {\left| {\eta ^{\prime}_{2} } \right|}}} \right]^{{n - 1}}$,$\chi _{n}^{{(4)}} = - ( - 1)^{n} H_{{n + 1}}^{{(1)}} (k_{1} \left| {\eta ^{\prime}_{3} } \right|)\left[ {{{\eta ^{\prime}_{3} } \mathord{\left/ {\vphantom {{\eta ^{\prime}_{3} } {\left| {\eta ^{\prime}_{3} } \right|}}} \right. \kern-\nulldelimiterspace} {\left| {\eta ^{\prime}_{3} } \right|}}} \right]^{{ - n - 1}}$,

$\gamma _{n}^{{(1)}} = - H_{{n + 1}}^{{(1)}} (k_{1} \left| {\eta ^{\prime}} \right|)\left[ {{{\eta ^{\prime}} \mathord{\left/ {\vphantom {{\eta ^{\prime}} {\left| {\eta ^{\prime}} \right|}}} \right. \kern-\nulldelimiterspace} {\left| {\eta ^{\prime}} \right|}}} \right]^{{n + 1}}$, $\gamma _{n}^{{(2)}} = H_{{n - 1}}^{{(1)}} (k_{1} \left| {\eta ^{\prime}_{1} } \right|)\left[ {{{\eta ^{\prime}_{1} } \mathord{\left/ {\vphantom {{\eta ^{\prime}_{1} } {\left| {\eta ^{\prime}_{1} } \right|}}} \right. \kern-\nulldelimiterspace} {\left| {\eta ^{\prime}_{1} } \right|}}} \right]^{{ - n + 1}}$.

$\gamma _{n}^{{(3)}} = - ( - 1)^{n} H_{{n + 1}}^{{(1)}} (k_{1} \left| {\eta ^{\prime}_{2} } \right|)\left[ {{{\eta ^{\prime}_{2} } \mathord{\left/ {\vphantom {{\eta ^{\prime}_{2} } {\left| {\eta ^{\prime}_{2} } \right|}}} \right. \kern-\nulldelimiterspace} {\left| {\eta ^{\prime}_{2} } \right|}}} \right]^{{n + 1}}$,$\gamma _{n}^{{(4)}} = ( - 1)^{n} H_{{n - 1}}^{{(1)}} (k_{1} \left| {\eta ^{\prime}_{3} } \right|)\left[ {{{\eta ^{\prime}_{3} } \mathord{\left/ {\vphantom {{\eta ^{\prime}_{3} } {\left| {\eta ^{\prime}_{3} } \right|}}} \right. \kern-\nulldelimiterspace} {\left| {\eta ^{\prime}_{3} } \right|}}} \right]^{{ - n + 1}}$,

$\varsigma _{n}^{{(1)}} = - n\eta ^{{\prime - n - 1}}$,$\varsigma _{n}^{{(2)}} = - ( - 1)^{n} n(\eta ^{\prime} - 2d - 2hi)^{{ - n - 1}}$, $\vartheta _{n}^{{(1)}} = - n(\bar{\eta }^{\prime} + 2hi)^{{ - n - 1}}$,$\vartheta _{n}^{{(2)}} = - ( - 1)^{n} n(\bar{\eta }^{\prime} - 2d)^{{ - n - 1}}$,

$\upsilon _{n}^{{(1)}} = - n(\eta ^{\prime} - 2hi)^{{ - n - 1}}$,$\upsilon _{n}^{{(2)}} = - n( - 1)^{n} (\eta ^{\prime} - 2d)^{{ - n - 1}}$,$\psi _{n}^{{(1)}} = - n\bar{\eta }^{{\prime - n - 1}}$,$\psi _{n}^{{(2)}} = - ( - 1)^{n} n(\bar{\eta }^{\prime} - 2d + 2hi)^{{ - n - 1}}$,

$$ \iota _{1} = e^{{p_{3} \left( {\frac{{\eta ^{\prime} + \bar{\eta }^{\prime}}}{2}} \right) + q_{3} \left( {\frac{{\eta ^{\prime} - \bar{\eta }^{\prime}}}{{2i}}} \right)}} \left[ {\frac{{k_{{03}} }}{2}J_{{n - 1}}^{{(1)}} (k_{{03}} \left| {\eta ^{\prime}} \right|)\left[ {{{\eta ^{\prime}} \mathord{\left/ {\vphantom {{\eta ^{\prime}} {\left| {\eta ^{\prime}} \right|}}} \right. \kern-\nulldelimiterspace} {\left| {\eta ^{\prime}} \right|}}} \right]^{{n - 1}} - \frac{1}{2}(p_{3} - q_{3} i)J_{n}^{{(1)}} (k_{{03}} \left| {\eta ^{\prime}} \right|)\left[ {{{\eta ^{\prime}} \mathord{\left/ {\vphantom {{\eta ^{\prime}} {\left| {\eta ^{\prime}} \right|}}} \right. \kern-\nulldelimiterspace} {\left| {\eta ^{\prime}} \right|}}} \right]^{n} } \right], $$

$$ \nu _{1} = e^{{p_{3} \left( {\frac{{\eta ^{\prime} + \bar{\eta }^{\prime}}}{2}} \right) + q_{3} \left( {\frac{{\eta ^{\prime} - \bar{\eta }^{\prime}}}{{2i}}} \right)}} \left[ { - \frac{{k_{{03}} }}{2}J_{{n + 1}}^{{(1)}} (k_{{03}} \left| {\eta ^{\prime}} \right|)\left[ {{{\eta ^{\prime}} \mathord{\left/ {\vphantom {{\eta ^{\prime}} {\left| {\eta ^{\prime}} \right|}}} \right. \kern-\nulldelimiterspace} {\left| {\eta ^{\prime}} \right|}}} \right]^{{n + 1}} - \frac{1}{2}(p_{3} + q_{3} i)J_{n}^{{(1)}} (k_{{03}} \left| {\eta ^{\prime}} \right|)\left[ {{{\eta ^{\prime}} \mathord{\left/ {\vphantom {{\eta ^{\prime}} {\left| {\eta ^{\prime}} \right|}}} \right. \kern-\nulldelimiterspace} {\left| {\eta ^{\prime}} \right|}}} \right]^{n} } \right], $$

$$ \iota _{3} = e^{{p_{3} \left( {\frac{{\eta ^{\prime} + \bar{\eta }^{\prime}}}{2}} \right) + q_{3} \left( {\frac{{\eta ^{\prime} - \bar{\eta }^{\prime}}}{{2i}}} \right)}} \left[ {\frac{{ik^{\prime}_{3} }}{2}H_{{n - 1}}^{{(1)}} (ik^{\prime}_{3} \left| {\eta ^{\prime}} \right|)\left[ {{{\eta ^{\prime}} \mathord{\left/ {\vphantom {{\eta ^{\prime}} {\left| {\eta ^{\prime}} \right|}}} \right. \kern-\nulldelimiterspace} {\left| {\eta ^{\prime}} \right|}}} \right]^{{n - 1}} - \frac{1}{2}(p_{3} - q_{3} i)H_{n}^{{(1)}} (ik^{\prime}_{3} \left| {\eta ^{\prime}} \right|)\left[ {{{\eta ^{\prime}} \mathord{\left/ {\vphantom {{\eta ^{\prime}} {\left| {\eta ^{\prime}} \right|}}} \right. \kern-\nulldelimiterspace} {\left| {\eta ^{\prime}} \right|}}} \right]^{n} } \right], $$

$$ \nu _{3} = e^{{p_{3} \left( {\frac{{\eta ^{\prime} + \bar{\eta }^{\prime}}}{2}} \right) + q_{3} \left( {\frac{{\eta ^{\prime} - \bar{\eta }^{\prime}}}{{2i}}} \right)}} \left[ { - \frac{{ik^{\prime}_{3} }}{2}H_{{n + 1}}^{{(1)}} (ik^{\prime}_{3} \left| {\eta ^{\prime}} \right|)\left[ {{{\eta ^{\prime}} \mathord{\left/ {\vphantom {{\eta ^{\prime}} {\left| {\eta ^{\prime}} \right|}}} \right. \kern-\nulldelimiterspace} {\left| {\eta ^{\prime}} \right|}}} \right]^{{n + 1}} - \frac{1}{2}(p_{3} + q_{3} i)H_{n}^{{(1)}} (ik^{\prime}_{3} \left| {\eta ^{\prime}} \right|)\left[ {{{\eta ^{\prime}} \mathord{\left/ {\vphantom {{\eta ^{\prime}} {\left| {\eta ^{\prime}} \right|}}} \right. \kern-\nulldelimiterspace} {\left| {\eta ^{\prime}} \right|}}} \right]^{n} } \right], $$

$$ \iota _{2} = e^{{p_{3} \left( {\frac{{\eta ^{\prime} + \bar{\eta }^{\prime}}}{2}} \right) + q_{3} \left( {\frac{{\eta ^{\prime} - \bar{\eta }^{\prime}}}{{2i}}} \right)}} \left[ {\frac{{ik^{\prime}_{3} }}{2}H_{{n - 1}}^{{(2)}} (ik^{\prime}_{3} \left| {\eta ^{\prime}} \right|)\left[ {{{\eta ^{\prime}} \mathord{\left/ {\vphantom {{\eta ^{\prime}} {\left| {\eta ^{\prime}} \right|}}} \right. \kern-\nulldelimiterspace} {\left| {\eta ^{\prime}} \right|}}} \right]^{{n - 1}} - \frac{1}{2}(p_{3} - q_{3} i)H_{n}^{{(2)}} (ik^{\prime}_{3} \left| {\eta ^{\prime}} \right|)\left[ {{{\eta ^{\prime}} \mathord{\left/ {\vphantom {{\eta ^{\prime}} {\left| {\eta ^{\prime}} \right|}}} \right. \kern-\nulldelimiterspace} {\left| {\eta ^{\prime}} \right|}}} \right]^{n} } \right], $$

$$ \nu _{2} = e^{{p_{3} \left( {\frac{{\eta ^{\prime} + \bar{\eta }^{\prime}}}{2}} \right) + q_{3} \left( {\frac{{\eta ^{\prime} - \bar{\eta }^{\prime}}}{{2i}}} \right)}} \left[ { - \frac{{ik^{\prime}_{3} }}{2}H_{{n + 1}}^{{(2)}} (ik^{\prime}_{3} \left| {\eta ^{\prime}} \right|)\left[ {{{\eta ^{\prime}} \mathord{\left/ {\vphantom {{\eta ^{\prime}} {\left| {\eta ^{\prime}} \right|}}} \right. \kern-\nulldelimiterspace} {\left| {\eta ^{\prime}} \right|}}} \right]^{{n + 1}} - \frac{1}{2}(p_{3} + q_{3} i)H_{n}^{{(2)}} (ik^{\prime}_{3} \left| {\eta ^{\prime}} \right|)\left[ {{{\eta ^{\prime}} \mathord{\left/ {\vphantom {{\eta ^{\prime}} {\left| {\eta ^{\prime}} \right|}}} \right. \kern-\nulldelimiterspace} {\left| {\eta ^{\prime}} \right|}}} \right]^{n} } \right], $$

$$ \begin{aligned} \xi ^{{(1)}} & = - (w^{i} + w^{r} ),\xi ^{{(2)}} = - (\tau _{{\theta z}}^{i} + \tau _{{\theta z}}^{r} ),\xi ^{{(3)}} = - (\phi ^{i} + \phi ^{r} ), \\ \xi ^{{(4)}} & = - (D_{\theta }^{i} + D_{\theta }^{r} ),\xi ^{{(5)}} = - (\varphi ^{i} + \varphi ^{r} ),\xi ^{{(6)}} = - (B_{\theta }^{i} + B_{\theta }^{r} ). \\ \end{aligned} $$

In order to solve Eq. (37), we multiply both sides of these equations by the coefficient $\exp ( - im\theta ^{\prime})$ and integrate the variable $\theta ^{\prime}$ in the known coefficient of Eq. (37) in the range of $( - \pi ,\pi )$. Such operation enables to simplify Eq. (37) into linear algebraic equations.

1.3 Part II: Green’s function

Green’s function method is also called point source method.

Firstly, the piezoelectric/piezomagnetic half-space is divided into two right angle regions along the vertical interface $B_{V}$, and the unit point source load $\delta (\eta - \eta _{0} ){\kern 1pt}$,$\eta _{0} = yi(y \le h)$ is applied on the boundary $B_{V}$ as the incident wave source, as shown in Fig. 

Fig. 15

Point source load

15.

The displacement function also satisfies the governing Eq. (6) and the boundary conditions (10), (11) on the boundaries $B_{H}$ and $B_{{in}}$. Unlike the boundary conditions on the vertical boundary $B_{H} {\kern 1pt}$ in Sect. 4.1, here it becomes:

$$ {\kern 1pt} {\kern 1pt} \left. {\tau _{{xz}}^{{\text{I}}} } \right|_{{x = 0}} = \delta (\eta - \eta _{0} ) \,,$$

(38)

Since Medium I is homogeneous, the displacement function $G_{{w1}}^{i}$ can be expressed as follows according to [15]:

$$ G_{{w1}}^{i} = H_{0}^{{(1)}} (k_{1} \left| {\eta - \eta _{0} } \right|) + H_{0}^{{(1)}} (k_{1} \left| {\eta - \bar{\eta }_{0} - 2hi} \right|)\,, $$

(39)

Taking into account that Medium II is inhomogeneous, the displacement function $G_{{w2}}^{i}$ can be expressed in the following form:

$$ G_{{w2}}^{i} = e^{{ - \frac{{p_{2} (\eta + \bar{\eta })}}{2}}} \left[ {H_{0}^{{(1)}} (k_{{02}} \left| {\eta - \eta _{0} } \right|) + H_{0}^{{(1)}} (k_{{02}} \left| {\eta - \bar{\eta }_{0} - 2hi} \right|)} \right]\,, $$

(40)

The displacement field $G_{{w1}}^{{( \bullet )}}$,$G_{{w2}}^{{( \bullet )}}$, electric field $G_{{\phi 1}}^{{( \bullet )}}$,$G_{{\phi 2}}^{{( \bullet )}}$, and magnetic field $G_{{\varphi 1}}^{{( \bullet )}}$,$G_{{\varphi 2}}^{{( \bullet )}}$ are obtained by means of the same procedure as used for calculating SH-wave (Note that the superscript $( \bullet )$ refers to I, II, III).

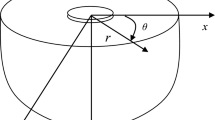
To make the calculations more convenient, the polar coordinate system $(r^{\prime\prime},\theta ^{\prime\prime})$ is set at the origin of the right-angle plane, and the respective complex variables are $\eta ^{\prime\prime} = r^{\prime\prime}e^{{i\theta ^{\prime\prime}}}$ and $\bar{\eta ^{\prime\prime}} = r^{\prime\prime}e^{{ - i\theta ^{\prime\prime}}}$.

Then pairs of unknown external force $f_{1} (r^{\prime\prime},\theta ^{\prime\prime})$,$f_{2} (r^{\prime\prime},\theta ^{\prime\prime})$, external electric field $f_{3} (r^{\prime\prime},\theta ^{\prime\prime})$,$f_{4} (r^{\prime\prime},\theta ^{\prime\prime})$, and external magnetic field $f_{5} (r^{\prime\prime},\theta ^{\prime\prime})$,$f_{6} (r^{\prime\prime},\theta ^{\prime\prime})$ are applied on the boundary $B_{V}$ as the amplitude function of $\delta (\eta - \eta _{0} ){\kern 1pt}$, as shown in Fig. 

Fig. 16

Systems of external force

16. Note that unknown parameters in each pair introduced above have equal values and opposite directions.

Finally, these unknown coefficients above are obtained with the aid of the continuous conditions (15) on the boundary $B_{V}$:

$$ \begin{aligned} & w^{{\text{I}}} + w^{{f1}} = w^{{{\text{II}}}} + w^{{f2}} ,\phi ^{{\text{I}}} + \phi ^{{f3}} = \phi ^{{{\text{II}}}} + \phi ^{{f4}} , \\ & \varphi ^{{\text{I}}} + \varphi ^{{f5}} = \varphi ^{{{\text{II}}}} + \varphi ^{{f6}} \,,\\ \end{aligned} $$

(41)

where:

$w^{{f1}} = \int_{0}^{{ + \infty }} {f_{1} (r^{\prime\prime}_{0} ,\beta _{1} )G_{w}^{{\text{I}}} (r^{\prime\prime}_{0} ,\beta _{1} ;r^{\prime\prime},\theta ^{\prime\prime})} dr^{\prime\prime}_{0}$,$w^{{f2}} = - \int_{0}^{{ + \infty }} {f_{2} (r^{\prime\prime}_{0} ,\beta _{1} )G_{w}^{{{\text{II}}}} (r^{\prime\prime}_{0} ,\beta _{1} ;r^{\prime\prime},\theta ^{\prime\prime})} dr^{\prime\prime}_{0}$,

$\phi ^{{f1}} = \int_{0}^{{ + \infty }} {f_{3} (r^{\prime\prime}_{0} ,\beta _{1} )G_{\phi }^{{\text{I}}} (r^{\prime\prime}_{0} ,\beta _{1} ;r^{\prime\prime},\theta ^{\prime\prime})} dr^{\prime\prime}_{0}$,$\phi ^{{f2}} = - \int_{0}^{{ + \infty }} {f_{4} (r^{\prime\prime}_{0} ,\beta _{1} )G_{\phi }^{{{\text{II}}}} (r^{\prime\prime}_{0} ,\beta _{1} ;r^{\prime\prime},\theta ^{\prime\prime})} dr^{\prime\prime}_{0}$,

$\varphi ^{{f1}} = \int_{0}^{{ + \infty }} {f_{5} (r^{\prime\prime}_{0} ,\beta _{1} )G_{\varphi }^{{\text{I}}} (r^{\prime\prime}_{0} ,\beta _{1} ;r^{\prime\prime},\theta ^{\prime\prime})} dr^{\prime\prime}_{0}$,$\varphi ^{{f2}} = - \int_{0}^{{ + \infty }} {f_{6} (r^{\prime\prime}_{0} ,\beta _{1} )G_{\varphi }^{{{\text{II}}}} (r^{\prime\prime}_{0} ,\beta _{1} ;r^{\prime\prime},\theta ^{\prime\prime})} dr^{\prime\prime}_{0}$,

$\beta _{1} = - {\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-\nulldelimiterspace} 2}$ and physical variable $( \bullet )^{{fi}}$ is produced by $f_{i} (r^{\prime\prime},\theta ^{\prime\prime})$, $(i = 1,2,3,4)$.

The scattering wave has no effect on the boundary $B_{V}$. According to Eq. (15), the continuity conditions for stress, electric displacement, and magnetic induction must be satisfied as follows:

$f_{1} (r^{\prime\prime}_{0} ,\beta _{1} ) = f_{2} (r^{\prime\prime}_{0} ,\beta _{1} )$, $f_{3} (r^{\prime\prime}_{0} ,\beta _{1} ) = f_{4} (r^{\prime\prime}_{0} ,\beta _{1} )$,$f_{5} (r^{\prime\prime}_{0} ,\beta _{1} ) = f_{6} (r^{\prime\prime}_{0} ,\beta _{1} )$,

$$ \begin{aligned} & \int_{0}^{{ + \infty }} {f_{1} (r^{\prime\prime}_{0} ,\beta _{1} )\left[ {G_{w}^{{\text{I}}} (r^{\prime\prime}_{0} ,\beta _{1} ;r^{\prime\prime},\theta ^{\prime\prime}) + } \right.} \left. {G_{w}^{{{\text{II}}}} (r^{\prime\prime}_{0} ,\beta _{1} ;r^{\prime\prime},\theta ^{\prime\prime})} \right]{\text{d}}r^{\prime\prime}_{0} = - w^{s} , \\ & \int_{0}^{{ + \infty }} {f_{3} (r^{\prime\prime}_{0} ,\beta _{1} )\left[ {G_{\phi }^{{\text{I}}} (r^{\prime\prime}_{0} ,\beta _{1} ;r^{\prime\prime},\theta ^{\prime\prime}) + } \right.} \left. {G_{\phi }^{{{\text{II}}}} (r^{\prime\prime}_{0} ,\beta _{1} ;r^{\prime\prime},\theta ^{\prime\prime})} \right]{\text{d}}r^{\prime\prime}_{0} = - \phi ^{s} , \\ & \int_{0}^{{ + \infty }} {f_{5} (r^{\prime\prime}_{0} ,\beta _{1} )\left[ {G_{\varphi }^{{\text{I}}} (r^{\prime\prime}_{0} ,\beta _{1} ;r^{\prime\prime},\theta ^{\prime\prime}) + } \right.} \left. {G_{\varphi }^{{{\text{II}}}} (r^{\prime\prime}_{0} ,\beta _{1} ;r^{\prime\prime},\theta ^{\prime\prime})} \right]{\text{d}}r^{\prime\prime}_{0} = - \varphi ^{s} . \\ \end{aligned} $$

(42)

Equations (42) are Fredholm equations of the first kind. By selecting different coordinate points, they can be solved by the interpolation method.

1.4 Part III: Relationship between different parameters of SH-waves

Based on the continuity of displacement as well as electric potential and magnetic potential on the vertical boundary in Eq. (15), the following relationship can be known:

$$ k_{1} \sin \alpha _{0} = k_{2} \sin \alpha _{2} \,,$$

(43)

For mathematical simplicity, the following parameters are introduced:

$\lambda _{1} = \cos \alpha _{0}$,$\lambda _{2} = \cos \alpha _{2}$,$c_{1} = c_{{{\text{440}}}}^{{\text{I}}}$,$c_{2} = c_{{{\text{440}}}}^{{{\text{II}}}}$,$e_{1} = e_{{{\text{150}}}}^{{\text{I}}}$,$e_{2} = e_{{{\text{150}}}}^{{{\text{II}}}}$,$h_{1} = h_{{{\text{150}}}}^{{\text{I}}}$,$h_{2} = h_{{{\text{150}}}}^{{{\text{II}}}}$,$d_{1} = \kappa _{{{\text{110}}}}^{{\text{I}}}$,$d_{2} = \kappa _{{{\text{110}}}}^{{{\text{II}}}}$,$t_{1} = t_{{{\text{110}}}}^{{\text{I}}}$,$t_{2} = t_{{{\text{110}}}}^{{{\text{II}}}}$,$\mu _{1} = \mu _{{{\text{110}}}}^{{\text{I}}}$,$\mu _{2} = \mu _{{{\text{110}}}}^{{{\text{II}}}}$.

Combining with Eq. (15), the following equations are obtained:

$$ \left\{ \begin{gathered} w_{0} c_{1} (ik_{1} \lambda _{1} ) - w_{1} c_{1} (ik_{1} \lambda _{1} ) + \phi _{0} e_{1} (ik_{1} \lambda _{1} ) - \phi _{1} e_{1} (ik_{1} \lambda _{1} ) + \varphi _{0} h_{1} (ik_{1} \lambda _{1} )_{1} - \varphi _{1} h_{1} (ik_{1} \lambda _{1} ) \hfill \\ = w_{2} c_{2} (ik_{{02}} \lambda _{2} - p_{2} ) + \phi _{2} e_{2} (ik_{{02}} \lambda _{2} - p_{2} ) + \varphi _{2} h_{2} (ik_{{02}} \lambda _{2} - p_{2} ) \hfill \\ w_{0} e_{1} (ik_{1} \lambda _{1} ) - w_{1} e_{1} (ik_{1} \lambda _{1} )_{1} - \left[ {\phi _{0} d_{1} (ik_{1} \lambda _{1} ) - \phi _{1} d_{1} (ik_{1} \lambda _{1} )} \right] - \left[ {\varphi _{0} t_{1} (ik_{1} \lambda _{1} ) - \varphi _{1} t_{1} (ik_{1} \lambda _{1} )} \right] \hfill \\ = w_{2} e_{2} (ik_{{02}} \lambda _{2} - p_{2} ) - \phi _{2} d_{2} (ik_{{02}} \lambda _{2} - p_{2} ) - \varphi _{2} t_{2} (ik_{{02}} \lambda _{2} - p_{2} ) \hfill \\ w_{0} h_{1} (ik_{1} \lambda _{1} ) - w_{1} h_{1} (ik_{1} \lambda _{1} ) - \left[ {\phi _{0} t_{1} (ik_{1} \lambda _{1} ) - \phi _{1} t_{1} (ik_{1} \lambda _{1} )} \right] - \left[ {\varphi _{0} \mu _{1} (ik_{1} \lambda _{1} ) - \varphi _{1} \mu _{1} (ik_{1} \lambda _{1} )} \right] \hfill \\ = w_{2} h_{2} (ik_{{02}} \lambda _{2} - p_{2} ) - \phi _{2} t_{2} (ik_{{02}} \lambda _{2} - p_{2} ) - \varphi _{2} \mu _{2} (ik_{{02}} \lambda _{2} - p_{2} ). \hfill \\ \end{gathered} \right. $$

(44)

Note that $w_{0}$, $\phi _{0}$, and $\varphi _{0}$ in Eq. (44) are known quantities, so Eq. (44) can be transformed into the following form:

$$ \left\{ \begin{gathered} w_{1} c_{1} (ik_{1} \lambda _{1} ) + w_{2} c_{2} (ik_{{02}} \lambda _{2} - p_{2} ) + \phi _{1} e_{1} (ik_{1} \lambda _{1} ) + \phi _{2} e_{2} (ik_{{02}} \lambda _{2} - p_{2} ) + \varphi _{1} h_{1} (ik_{1} \lambda _{1} ) + \varphi _{2} h_{2} (ik_{{02}} \lambda _{2} - p_{2} ) \hfill \\ = w_{0} c_{1} (ik_{1} \lambda _{1} ) + \phi _{0} e_{1} (ik_{1} \lambda _{1} ) + \varphi _{0} h_{1} (ik_{1} \lambda _{1} ) \hfill \\ w_{1} e_{1} (ik_{1} \lambda _{1} ) + w_{2} e_{2} (ik_{{02}} \lambda _{2} - p_{2} ) - \phi _{1} d_{1} (ik_{1} \lambda _{1} ) - \phi _{2} d_{2} (ik_{{02}} \lambda _{2} - p_{2} ) - \varphi _{1} t_{1} (ik_{1} \lambda _{1} ) - \varphi _{2} t_{2} (ik_{{02}} \lambda _{2} - p_{2} ) \hfill \\ = w_{0} e_{1} (ik_{1} \lambda _{1} ) - \phi _{0} d_{1} (ik_{1} \lambda _{1} ) - \varphi _{0} t_{1} (ik_{1} \lambda _{1} ) \hfill \\ w_{1} h_{1} (ik_{1} \lambda _{1} ) + w_{2} h_{2} (ik_{{02}} \lambda _{2} - p_{2} ) - \phi _{1} t_{1} (ik_{1} \lambda _{1} ) - \phi _{2} t_{2} (ik_{{02}} \lambda _{2} - p_{2} ) - \varphi _{1} \mu _{1} (ik_{1} \lambda _{1} ) - \varphi _{2} \mu _{2} (ik_{{02}} \lambda _{2} - p_{2} ) \hfill \\ = w_{0} h_{1} (ik_{1} \lambda _{1} ) - \phi _{0} t_{1} (ik_{1} \lambda _{1} ) - \varphi _{0} \mu _{1} (ik_{1} \lambda _{1} ). \hfill \\ \end{gathered} \right. $$

(45)

For mathematical simplicity, the parameters $\gamma _{1} = ik_{1} \lambda _{1}$ and $\gamma _{2} = ik_{{02}} \lambda _{2} - p_{2}$ are introduced. In Eq. (45),$w_{0}$, $\phi _{0}$, and $\varphi _{0}$ are regarded as known coefficients. Cramer’s Rule can be used to find the unknown coefficients $w_{1}$,$w_{2}$,$\phi _{1}$,$\phi _{2}$,$\varphi _{1}$, and $\varphi _{2}$.