Abstract
In this work, we investigate the behaviour of liquids in symmetric open microgrooves and give a criterion for spontaneous capillary flow. To that end, we use a two-dimensional model and analyse the liquid morphologies minimizing the Gibbs energy of the system. We find that the condition of a flat liquid surface, which was hitherto assumed, is indeed the solution minimizing the Gibbs energy, so that it can safely be accepted to investigate whether open capillaries fill spontaneously. Furthermore, we find a condition for spontaneous capillary flow that depends on the cross-section of the channel alone. We use the findings to derive the critical contact angle, below which spontaneous capillary flow happens, for three examples including V-grooves, Gaussian grooves, and lenticular grooves.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Since the first investigations on capillary flows [1], liquid flow into open microchannels has been used in various fields ranging from biology [2,3,4], medicine [5,6,7] up to the fabrication of electronic devices [8,9,10,11,12,13]. The question of whether capillaries spontaneously fill with fluid is easy to answer: when it is energetically favourable. For closed microfluidics it follows that a liquid will wet a channel without the need of applying an external pressure if the contact angle is below a critical value. For round tubes this happens for contact angles \(\theta \) if [1]
For nonuniform channels a similar equation holds if we take the average contact angle, the generalized Cassie angle [14], instead. It is defined as weighted sum of the contact angles \(\theta _i\) of each component of the considered microchannel,
with the weights \(f_i\) being the corresponding area fraction per component. Therefore, the surface weighted contact angle has to be below a critical angle before spontaneous capillary flow can occur:
Put differently, if the contact angle of the liquid is smaller than \(\pi /2\) for most of the round tube, spontaneous capillary flow will happen.
In contrast to closed microfluidic channels, liquids in open microfluidic systems have a free interface. Thus, when looking at a cross section of the microchannel, it’s surface is not necessarily flat and can bulge freely giving rise to complex morphologies. For example, in rectangular grooves the liquid shape depends strongly on the exact geometry and the contact angle, giving rise to a zoo of possible morphologies [15].
For open microchannels not only the liquid morphologies, but also the condition of spontaneous capillary flow are both strongly dependent on the channel geometry itself [14]. The generalized Cassie angle has been used successfully to predict the onset of fluid flow [16,17,18,19] when assuming that the open surface is flat and the contact angle to the gaseous surroundings is \(\theta _\text {gas}=\pi \) in Eq. (3) [14].
One problem is imminent: Eq. (3) does tell, whether an open microchannel fills or not, but does not give information about what the cross section of the liquid filling the channel looks like. It has been argued that this curvature may be neglected for most cases [20]. However, as shown in the case of V-grooves [21], in some geometries the top surface cannot equilibrate to a state without curvature, due to a restriction stemming from the geometry and the contact angle itself.
This discrepancy is the starting point of our work, i.e. we want to investigate how an additional curvature in the top surface affects the condition of spontaneous capillary flow to derive a more general criterion for open grooves and relate it to the generalized contact angle in Eq. (3). Further, we derive a condition for minimal energy cross sections and try to understand up to which liquid level smooth grooves fill spontaneously.
It is known that the condition of whether microchannels fill or not has to do with the Laplace pressure; however, we are not aware of a precise derivation of this empirical knowledge. An extensive theoretical description of liquids on cylindrical surfaces was done by Roy and Schwartz [22], who used perturbation theory on three-dimensional energy functionals. With our work, we not only want to formulate the same approach with a two-dimensional model, but also show how the condition on spontaneous capillary flow can be applied by three examples. By the derivation we will find that we can drop the restriction on the microgrooves to be symmetric, so that we can really obtain the same results and formulate a critical contact angle for capillary filling by using a simple two-dimensional model of a symmetric microgroove.
Our work focuses on open capillary systems, with only taking surface energies into account, i.e. we neglect temperature changes, electromagnetic fields, changes in chemical composition, and gravity. We investigate microchannels coupled to an infinite reservoir for which we assume that the reservoir provides a zero pressure source of liquid. As with any other thermodynamic reservoir, it does neither cost energy to supply nor to uptake an additional amount of the liquid volume into the channel or backfilling into the reservoir. For the case of a finite volume, our approach will reversely yield the filling length L, provided it is huge against edge effects. In experiments, that condition is typically fulfilled if we look at micrometre sized channels so that gravity can be neglected, and large reservoirs to minimize the Laplace pressure arising from them.
We start by recapitulating the derivation of Young’s equation for the cross section of microgrooves, which is typically derived for flat substrates [23, 24] or fibres [25], but not microgrooves. Even though typical derivations of Young’s equation argue with surface forces hinting that this model works for arbitrarily shaped surfaces, we deliberately chose to focus on derivations based on energy considerations. A recent discussion supporting this choice has been done by Makkonen [26].
After establishing Young’s equation, we investigate the conditions for spontaneous capillary flow for a given microchannel layout and fixed contact angle between the substrate and the liquid. Since the liquid is only entering the groove when it is energetically favourable, i.e. when the energy of the system is lowered for a groove of finite wetting height, this breaks down to the problem of finding minimal energy states for a given contact angle that follows Young’s law. In other words, we minimize the Gibbs energy per length to draw conclusions about what morphology a system of infinite length will take.
Finally, we apply our findings to three model systems, being V-grooves, Gaussian grooves, and lenticular grooves.
2 Two-dimensional model
In the following, we are investigating the minimal energy states of liquids inside microgrooves. We look at the cross section of the microgroove filled with liquid and investigate the Gibbs energy to find the minimal energy states. We want to prove that states having zero curvature—flat liquid surfaces—always correspond to extreme points of the Gibbs energy, independent of the exact shape of the groove.
For a given cross section the function describing the liquid surface has to be a function of constant curvature to minimize its surface energy given that additional terms in Gibbs energy (e.g. potential energy due to weight) can be neglected. (see Proof 1 in Appendix). For larger droplets radius, where gravity contributes, the reader is referred to Tamanini [27] and Roura et al. [28]. Thus, we can assume that the liquid shapes are always part of a circle or straight lines since these are the only shapes in two dimensions having constant curvature and thus fulfilling the Young–Laplace equation. Any other liquid shape with varying mean radius will induce Laplace pressure differences along its surface such that the liquid itself is not in equilibrium, inducing internal flows. Thus, since we are only interested in minimal energy states, we can safely focus on circular or straight cross sections for two-dimensional calculations being the only states of constant curvature in two dimensions.
Since the problem is stated with the goal to find wetting solutions \(\theta <90^\circ \), we neglect morphologies with trapped air on the bottom of the grooves. Even though we build our model around symmetric microgrooves, we will find that this restriction can be dropped, since only the contact angle at the liquid level and the curvature of the surface at this point are relevant.
The situation in thermodynamic equilibrium is governed by Gibbs free energy G, and this quantity depends, as it is known for gaseous systems, at least on temperature T and pressure p. But for solids as well as liquids additional terms can arise, which are due to any other energy contribution present in the system as well as the reservoir, e.g. binding energy represented by the atomic chemical potential. Here, we disregard the temperature change, pressure change, any electrical or magnetic fields, and reactions leading to a change in chemical potential.
Since we will focus on liquid in micrometre sized capillaries, the contribution of gravity can be neglected. The contribution of gravity is multiple orders of magnitudes below the surface energies. Only for length scales near the capillary length [24], which is typically in the millimetre range for the system under consideration, gravity does influence the system. It follows that the Gibbs free energy of the system is virtually described solely by its surface energies.
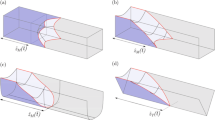
We assume that the total Gibbs energy is composed of a contribution scaling with the length of the groove \(G_{2D}L\) and additional parts stemming from the front of the liquid meniscus \(G_{\text {front}}\) independent on the length of the groove, as shown in Fig. 1. In this case one can write
where we have introduced the surface energies between the solid and the liquid phase \(\gamma _{sl}\), the liquid and the gaseous phase \(\gamma _{lg}\), and the solid and gaseous phase \(\gamma _{sg}\) with corresponding surface areas \(A_{sl}\), \(A_{lg}\), and \(A_{sg}\).
Spontaneous capillary flow is linked to whether the Gibbs energy is decreased or increased when filling the capillary, i.e. when L is increasing. This condition then corresponds to finding the sign of \(G_{2D}\), since for large lengths L
For negative (positive) \(G_{2D}\) the Gibbs energy of the system is decreasing (increasing) for increasing length L, allowing (prohibiting) spontaneous capillary flow. Thus, knowing the exact behaviour of the liquid for the cross section of the microchannel is sufficient to predict its filling behaviour.
Similarly, one can also argue that, for sufficiently long filling length L, the contributions of the front of the liquid can safely be neglected, so that the problem of finding the energy of a groove with unit length L for an arbitrary liquid volume can be simplified to finding the minimal energy configuration of its cross section per unit length.
Liquid in open Gaussian groove with contact angle \(\theta =30^\circ \). For large wetted lengths L the contribution of the Gibbs energy of the front of the groove \(G_\text {front}\) can be neglected compared to the contribution \(G_\text {2D} L\) scaling with the wetted length. Figure created with Surface Evolver [29]
In summary, we can describe the system shown in Fig.1 with the Gibbs free energy per unit length L and find minimal energy states by investigating:
2.1 Liquid in a symmetrical infinite groove
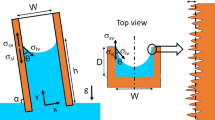
Similar to the derivation of Young’s equation for a droplet sitting on a flat surface [23] (see Proof 2 in Appendix), we can now focus on finding minimal energy solutions of infinitely long microgrooves. Assume a straight microchannel with its cross section defined by a function f(x) being strictly monotonically increasing and twice differentiable for \(x>0\). We create a symmetric microgroove by mirroring this function along the \(x=0\) plane and assume the created microchannel to be filled with a liquid up to a point \(x_0=R\sin \vert \alpha \vert \) as shown in Fig. 2. The angle between the liquid and the surface will be denoted as \(\theta \) and the radius of the circular liquid shape R, as in the previous Section. Here, we also point out that for channels with some non-differentiable cross sections bistability conditions can exist [30] which are not treated in this work.
The Gibbs free energy of the system is given by Eq. (9) with variation
where we have used that \(dA_{sl}=- dA_{sg}\).
We investigate the problem of finding the liquid morphology of minimal energy sitting in this groove. Further, we assume that the liquid is wetting with a contact angle of \(\theta <90^{\circ }\) in order to avoid solutions where it is favourable to have air trapped in the bottom of the grooves.
We find the angle between the horizontal and the function f(x) as \({\epsilon =\arctan {f'\left( x_0\right) }}\) which yieldsFootnote 1
The wetted lengths are given by
and the cross-sectional area by
with variation
Note that we can set the value of \(A_0\) equal to zero in Eq. (15), since this only gives a constant offset to the Gibbs free energy and is not affecting the physics. In fact, this choice sets the Gibbs free energy to zero when there is no liquid present.
To find minimal energy configurations for a given contact angle \(\theta \) and given groove shape \(f\left( x\right) \) we minimize the energy by variation of R and \(\alpha \). For the conservation of the cross-sectional area \(\phi \) we introduce the Lagrange parameter \(\lambda \) and minimize \(G_\text {2D}/L-\lambda \left( \phi -\phi _0\right) \) which yields (see Proof 3 in Appendix))
which is exactly Young’s equation for flat surfaces [31]. Thus, the contact angle follows Young’s equation, independent of the grooves shape. As found for liquid droplets sitting on flat surfaces, the Lagrange multiplier \(\lambda \) is found to be equal to the Laplace pressure [23].
As seen in the example of the three-dimensional droplet, the same derivation can be performed with \(\lambda =0\) such that the volume is not conserved. By performing the same manipulations, it can be shown that even in this case Young’s equation is recovered. Thus, we have proven that Young’s equation also holds for cross sections of infinitely long microgrooves regardless of the exact cross section. Furthermore, we have recovered the Laplace pressure in the case when the liquid volume is conserved.
2.2 Minimal energy cross section
After recovering Young’s equation for the cross section of symmetric grooves, we can investigate up to which point a microgroove wants to fill when connected to an infinite reservoir. To this end, we rewrite the Gibbs energy in terms of \(x_0=R\sin \vert \alpha \vert \), and search for minima for any cross-sectional area with \(x_0\) as the only independent variable. Analoguovsly to Eqs. (13)–(15) we are evaluating the wetted areas,
and formulate the condition of the minimal Gibbs energy,
where we have introduced the short-hand notation \(\alpha (x_0)=\arctan f'(x_0)-\theta \). Thus, there is an extremal point in the Gibbs free energy when the large parentheses of Eq. (23) vanish. There is no obvious solution to this equation due to the dependence on both, \(f'(x_0)\) and \(f''(x_0)\). However, when drawing the limit \(x_0 \rightarrow z\) with z such that \(f'(z)=\tan \theta \) carefully, one can see that \(f'(x_0)=\tan \theta \) is a solution, being the state when \(\alpha =0\), i.e. when the liquid surface is flat. It can be inferred that a flat liquid surface complying with Young’s equation is always an extremal point of the Gibbs free energy. We can even get information about the type of the extremal point by looking at the second derivative at this point:
We can see that the second derivative is positive, i.e. implying a minimum of the Gibbs free energy for \(f''(x_0)<0\), i.e. if the groove has a negative curvature at the point \(x_0\). Thus, \(\alpha =0\) indicates the filling level of minimal energy for grooves having a negative curvature at this point.
For positive curvature \(f''(x_0)>0\), the sign of Eq. (24) is not determined without further information about the function f(x).
In summary, Young’s equation holds for the cross section of liquids inside infinitely long grooves. If the groove is connected to an infinite amount of liquid, the state where the liquid surface is flat describes an extremal point of the Gibbs energy. This extremal point describes the cross section with minimal Gibbs energy if the groove has negative curvature. Thus, Eq. (3) is fulfilled if the cross section of the groove is concave at the filling point \(x_0\).
On the other hand, this statement neither implies that the global energy minimum for arbitrary volume lies at \(\alpha =0\), nor that this state is reachable for all geometries. As we will see from the example of V-grooves, restricting the contact angle to a certain value by predefined surface energies restricts the contact angle and thus \(\alpha \) to a value which is not necessarily zero. The condition of \(\alpha =0\) is not always achievable for this geometry and the minimal energy states are either at infinite filling height (\(x_0\rightarrow \infty \)), or zero filling height (\(x_0 \rightarrow 0\)).
This derivation also shows that for the minimization of Gibbs energy in two-dimensional systems only the value of \(f'(x_0)\), \(f''(x_0)\) and the contact point \(x_0\) are determining the points of minimal energy. We can deduce that the system is memory-less in the sense that already wetted areas do not influence the minimal energy states. Thus, even the common derivation of Young’s contact angle found in textbooks [23, 32] based on the minimization of the Gibbs free energy around the contact line can be applied to cross sections of microgrooves. Furthermore, the result on the generalized contact angle in Eq. (3) is true for the cases when the second derivative in Eq. (24) is positive.
We summarize these findings into the following condition for capillary filling:
Assume that a symmetric function f(x) mirrored around \(x=0\) describes the cross section of a microgroove. Spontaneous capillary flow for liquids with contact angle \(\theta <\pi /2\) happens when:
There exists a morphology where the surface of the liquid is flat or concave with both sides fulfilling Young’s equation at the contact points \(x_0\) with the second derivative of the Gibbs free energy given in Eq. (24) being positive. The latter is always fulfilled when the curvature of the surface at the contact point is negative, \(f''(x_0)<0\).
We will see in the following how these conditions can help us decide when open capillaries will fill spontaneously and the liquid flows along the channel direction. We investigate three morphologies: V-grooves, Gaussian grooves, and lenticular grooves.
3 Examples
3.1 V-grooves
We focus on liquid morphologies inside infinitely long V-grooves with opening angle \(2\beta \) and contact angle \(\theta <\pi /2\) that is solely defined by the surface energies between the liquid and the surface. The definition of lengths can be seen in Fig. 3. As before, we do not consider states where air is trapped beneath the liquid, thus we have to restrict the contact angle to \(\theta <90^{\circ }\).
From geometry it can be seen that \(\alpha \) is completely determined by the opening angle of the groove and the contact angle
with the total Gibbs energy of this system being
with a cross-sectional area \(\phi \) of
Thus, for this system a surface with zero curvature (as assumed for the Cassie angle) and following Young’s equation is not always achievable. However, as derived before, \(\alpha =0\) can be used to obtain a critical contact angle for capillary filling,
which is in accordance with the literature [14, 21, 33,34,35].
An exemplary plot of the energy given in Eq. (27) for a V-groove with opening angle \(2\beta =50^\circ \) for different \(\theta \) and cross sections \(\phi \) (see Fig. 4) shows how this critical contact angle (drawn as thick black line) separates two distinct regimes in the plot. For the lower half, labelled “I”, the energy per length is smaller than zero and decreases further for increasing liquid cross section. The Gibbs energy per length being negative is exactly the condition for the existence of spontaneous capillary flow—it is energetically favourable for the liquid to enter the capillary. Additionally, since the Gibbs energy per unit length is decreasing for increasing cross section it can be inferred that the liquid will wet the channel up to the maximal cross section and thus maximal filling height \(x_0\). In contrast, section “II” above the critical contact angle shows a positive Gibbs energy per length. Thus, it is energetically unfavourable for the liquid to wet the capillary.
For a contact angle below (above) the critical contact angle, the global maxima and minima are at minimal (maximal) and maximal (minimal) cross section, respectively (see Proof 4 in Appendix). Thus, a V-groove, connected to an infinite liquid reservoir, will show spontaneous capillary filling if and only if the contact angle between the fluid and the surface is below the critical contact angle determined by \(\alpha =0\).
Gibbs energy of liquid in an infinitely long V-groove with opening angle \(2\beta =50^\circ \). Critical contact angle \(\theta _{\mathrm{crit}}=65^\circ \) drawn as thick black horizontal line. Only for small contact angles below the critical contact angle the energy is decreasing for larger cross sections
3.2 Gaussian grooves
Another interesting test case are Gaussian grooves, since they were not treated in the literature before and occur naturally when laser-writing microchannels [36]. We investigate the Gibbs energy of a liquid sitting in a non-normalized Gaussian groove defined by the function
We find the area of the cross section of the liquid to be
with erf denoting the error function. Evaluation of the Gibbs energy yields
If we consider the liquid to be connected to an infinite reservoir, we can use the condition of a flat liquid surface and find (see Proof 5 in Appendix)
A plot of \(\theta _{\mathrm{crit}}\) can be found in Fig. 5. Note that the critical contact angle is always below \(\pi /2\) and decreases for increasing channel width \(\sigma \).
An exemplary plot of the Gibbs energy for a Gaussian groove of fixed width \(\sigma =1\) for different contact angles and cross sections in Fig. 9 shows that the critical contact angle separates two distinct regions. Above the critical contact angle (region I), only solutions with \(\alpha >0\) exist as plotted in Fig. 6, with the energy minimum at minimal cross section. Thus, in this region it is energetically unfavourable for the liquid to be inside the channel, and spontaneous capillary flow will not arise (Fig. 7).
Below the critical contact angle, there are three distinct regions separated by the two possible solutions to \(\alpha =0\) as shown in Fig. 8. Starting from a low liquid cross section and a fixed contact angle \(\theta <\theta _{\mathrm{crit}}\) (region IV), the fluid shows \(\alpha >0\) with increasing energy for increased fill level. At a certain point, it reaches its cross section with maximal energy at \(\alpha =0\). After this point the fluid surface is convex with \(\alpha <0\) (region III) with decreasing Gibbs free energy for higher fill level. The minimum of the Gibbs free energy is found at the second solution of \(\alpha =0\). Above this level, the energy is increasing again such that the previous minimum is indeed a global minimum of the Gibbs free energy. At the critical contact angle, the two solutions of \(\alpha =0\) coincide as shown in Fig. 7 and Fig. 9.
Knowing the energy landscape of the liquid inside Gaussian channels, we can conclude that below the critical contact angle there exists a minimal energy state for a finite filling height. Thus, the condition for spontaneous capillary filling is met if \(\theta <\theta _{\mathrm{crit}}\) which distinguishes the case when spontaneous capillary flow happens, to the case when it is not present. However, due to the increase of Gibbs energy at a smaller cross section, there is an energy barrier to overcome beforehand.
Liquid morphologies in Gaussian channel with \(\sigma =1\) and contact angle \(\theta =50^\circ \) being above the critical contact angle \(\theta _{\mathrm{crit}}=40.6^\circ \) (region I). The minimal energy surfaces for different cross sections are colour-coded depending on their Gibbs energy. All possible liquid surfaces for contact angles above the critical contact angle are concave and increase in energy for increasing cross section
Liquid in Gaussian channel with \(\sigma =1\) at the critical contact angle \(\theta =\theta _{\mathrm{crit}}=40.6^\circ \). The minimal energy surfaces for different cross sections are colour-coded depending on their Gibbs energy. At a single point, the morphology is showing a flat surface, whereas being concave for all other cross sections above (region II) and below (region IV) the critical cross section. The minimal energy is achieved for the minimal cross section
Liquid in Gaussian channel with \(\sigma =1\) and contact angle \(\theta =30^\circ \) below the critical contact angle \(\theta _{\mathrm{crit}}=40.6^\circ \). The minimal energy surfaces for different cross sections are colour-coded depending on their Gibbs energy. In region IV, for small cross sections, the surface is concave with increasing energy for increasing cross section. At the first critical filling height where \(\alpha =0\) the energy reaches its maximum, followed by region III having a convex shape. The minimal energy is achieved by the second point where \(\alpha =0\). For higher cross sections (region IV), the morphology is convex again with the energy increasing for increasing cross sections
Gibbs energy of liquid in infinitely long Gaussian-groove with FWHM \(\sigma =1\). Critical contact angle drawn as thick black horizontal line. The condition \(\alpha =0\) is drawn as dashed black line. Only for small contact angles below the critical contact angle the energy is decreasing for larger cross sections
3.3 Lenticular grooves
As last example we are investigating lenticular grooves being defined by
with \(-R<x<R\) as drawn in Fig. 10. The condition \(\alpha =0\) yields
Due to the shape of the right hand side of this equality, approaching infinity for small \(x_0\) and zero for \(x_0\) close to R, there exists a solution to \(\alpha =0\) for each contact angle \(\theta <90^\circ \). Additionally, since the curvature of this function is always negative \(f''(x)<0\), those solutions are always minimal energy solutions. This is the reason why lenticular grooves of any radius R are ideal for spontaneous capillary flow. They allow for minimal energy solutions and thus allow spontaneous capillary flow for all contact angles below the critical contact angle,
4 Summary
With this work we have shown how minimal energy calculations can be used to find a condition for spontaneous capillary flow of open symmetric microgrooves. We started by introducing a two-dimensional model for the Gibbs energy of a microgroove and retraced Young’s equation for the cross section since this derivation is typically only done for liquids on flat surfaces. We found that the Laplace pressure is conserving the liquid volume in the form of a Lagrange parameter. By using these results in our model, we were able to derive conditions for minimal Gibbs energy, being a flat liquid surface with the curvature of the substrate at the contact point to the liquid being negative. This is in accordance with previous works, and justifies a simplified calculation using the Cassie angle for most cases.
Finally, we tested the theory for three different groove geometries and derived the critical contact angle for spontaneous capillary flow for each of them.
Notes
Note that \(\alpha \) can have both positive or negative values. In the latter case, the circle drawn in Fig. 2 will be mirrored along the horizontal plane making the liquid surface bulge out.
References
Washburn, E.W.: The dynamics of capillary flow. Phys. Rev. 17(3), 273 (1921)
Mao, S., Zhang, Q., Li, H., Zhang, W., Huang, Q., Khan, M., Lin, J.-M.: Adhesion analysis of single circulating tumor cells on a base layer of endothelial cells using open microfluidics. Chem. Sci. 9(39), 7694–7699 (2018). https://doi.org/10.1039/C8SC03027H
Torabi, S., Li, L., Grabau, J., Sands, M., Berron, B.J., Xu, R., Trinkle, C.A.: Cassie–Baxter surfaces for reversible, barrier-free integration of microfluidics and 3d cell culture. Langmuir 35(32), 10299–10308 (2019). https://doi.org/10.1021/acs.langmuir.9b01163
Liu, L., Veerappan, V., Pu, Q., Cheng, C., Wang, X., Lu, L., Allen, R.D., Guo, G.: High-resolution hydrodynamic chromatographic separation of large DNA using narrow, bare open capillaries: a rapid and economical alternative technology to pulsed-field gel electrophoresis? Anal. Chem. 86(1), 729–736 (2014). https://doi.org/10.1021/ac403190a
Dak, P., Ebrahimi, A., Swaminathan, V., Duarte-Guevara, C., Bashir, R., Alam, M.A.: Droplet-based biosensing for lab-on-a-chip, open microfluidics platforms. Biosensors 6(2), 14 (2016). https://doi.org/10.3390/bios6020014
Yu, J., Berthier, E., Craig, A., de Groot, T.E., Sparks, S., Ingram, P.N., Jarrard, D.F., Huang, W., Beebe, D.J., Theberge, A.B.: Reconfigurable open microfluidics for studying the spatiotemporal dynamics of paracrine signaling. Nat. Biomed. Eng. 3(10), 830–841 (2019). https://doi.org/10.1038/s41551-019-0421-4
Tung, C.-K., Krupa, O., Apyadin, E., Liou, J., Diaz-Santana, A., Kim, B.J., Wu, M.: A contact line pinning based microfluidic platform for modelling physiological flows. Lab Chip 13(19), 3876–3885 (2013). https://doi.org/10.1039/c3lc50489a
Lone, S., Zhang, J.M., Vakarelski, I.U., Li, E.Q., Thoroddsen, S.T.: Evaporative lithography in open microfluidic channel networks. Langmuir 33(11), 2861–2871 (2017). https://doi.org/10.1021/acs.langmuir.6b03304
Hyun, W.J., Secor, E.B., Bidoky, F.Z., Walker, S.B., Lewis, J.A., Hersam, M.C., Francis, L.F., Frisbie, C.D.: Self-aligned capillarity-assisted printing of top-gate thin-film transistors on plastic. Flex. Print. Electron. 3(3), 035004 (2018). https://doi.org/10.1088/2058-8585/aad476
Mahajan, A., Hyun, W.J., Walker, S.B., Rojas, G.A., Choi, J.-H., Lewis, J.A., Francis, L.F., Frisbie, C.D.: A self-aligned strategy for printed electronics: exploiting capillary flow on microstructured plastic surfaces. Adv. Electr. Mater. 1(9), 1500137 (2015). https://doi.org/10.1002/aelm.201500137
Pierre, A., Sadeghi, M., Payne, M.M., Facchetti, A., Anthony, J.E., Arias, A.C.: All-printed flexible organic transistors enabled by surface tension-guided blade coating. Adv. Mater. 26(32), 5722–5727 (2014). https://doi.org/10.1002/adma.201401520
Horváth, B., Křivová, B., Schift, H.: Nanoimprint meets microfluidics: development of metal wires from nanoparticle ink filled capillaries. Micro Nano Eng. 3, 22–30 (2019). https://doi.org/10.1016/j.mne.2019.02.004
Lade, R.K., Jochem, K.S., Macosko, C.W., Francis, L.F.: Capillary coatings: flow and drying dynamics in open microchannels. Langmuir 34(26), 7624–7639 (2018). https://doi.org/10.1021/acs.langmuir.8b00811
Berthier, J., Brakke, K.A., Berthier, E.: Open Microfluidics. Wiley, Hoboken (2016)
Seemann, R., Brinkmann, M., Herminghaus, S., Khare, K., Law, B.M., McBride, S., Kostourou, K., Gurevich, E., Bommer, S., Herrmann, C., Michler, D.: Wetting morphologies and their transitions in grooved substrates. J. Phys.: Condens. Matter 23(18), 184108 (2011). https://doi.org/10.1088/0953-8984/23/18/184108
Lee, J.J., Berthier, J., Theberge, A.B., Berthier, E.: Capillary flow in open microgrooves: bifurcations and networks. Langmuir 35(32), 10667–10675 (2019). https://doi.org/10.1021/acs.langmuir.9b01456
Khare, K., Herminghaus, S., Baret, J.-C., Law, B.M., Brinkmann, M., Seemann, R.: Switching liquid morphologies on linear grooves. Langmuir 23(26), 12997–13006 (2007). https://doi.org/10.1021/la701899u
Berthier, J., Brakke, K.A., Furlani, E.P., Karampelas, I.H., Poher, V., Gosselin, D., Cubizolles, M., Pouteau, P.: Whole blood spontaneous capillary flow in narrow v-groove microchannels. Sens. Actuators B: Chem. 206, 258–267 (2015). https://doi.org/10.1016/j.snb.2014.09.040
Berthier, E., Dostie, A.M., Lee, U.N., Berthier, J., Theberge, A.B.: Open microfluidic capillary systems. Anal. Chem. 91(14), 8739–8750 (2019). https://doi.org/10.1021/acs.analchem.9b01429
Berthier, J., Brakke, K.A., Berthier, E.: A general condition for spontaneous capillary flow in uniform cross-section microchannels. Microfluid. Nanofluid. 16(4), 779–785 (2014). https://doi.org/10.1007/s10404-013-1270-1
Herminghaus, S., Brinkmann, M., Seemann, R.: Wetting and dewetting of complex surface geometries. Ann. Rev. Mater. Res. 38(1), 101–121 (2008). https://doi.org/10.1146/annurev.matsci.38.060407.130335
Roy, R.V., Schwartz, L.W.: On the stability of liquid ridges. J. Fluid Mech. 391, 293–318 (1999)
Bruus, H.: Theoretical Microfluidics. Oxford Master Series in Physics. Oxford University Press, Oxford (2007)
Butt, H.-J., Graf, K., Kappl, M.: Physics and Chemistry of Interfaces. Wiley, Weinheim (2013)
Klatte, J., Haake, D., Weislogel, M., Dreyer, M.: A fast numerical procedure for steady capillary flow in open channels. Acta Mech. 201(1), 269–276 (2008). https://doi.org/10.1007/s00707-008-0063-1
Makkonen, L.: Young’s equation revisited. J. Phys.: Condens. Matter 28(13), 135001 (2016). https://doi.org/10.1088/0953-8984/28/13/135001
Tamanini, I.: On the sphericity of liquid droplets. Astérisque 118, 235–241 (1984)
Roura, P., Fort, J.: Local thermodynamic derivation of Young’s equation. J. Colloid Interface Sci. 272(2), 420–429 (2004)
Brakke, K.A.: The surface evolver. Exp. Math. 1(2), 141–165 (1992). https://doi.org/10.1080/10586458.1992.10504253
Seemann, R., Brinkmann, M., Kramer, E.J., Lange, F.F., Lipowsky, R.: Wetting morphologies at microstructured surfaces. Proc. Natl. Acad. Sci. USA 102(6), 1848 (2005). https://doi.org/10.1073/pnas.0407721102
Schrader, M.E.: Young–Dupre revisited. Langmuir 11(9), 3585–3589 (1995). https://doi.org/10.1021/la00009a049
Berthier, J.: Micro-Drops and Digital Microfluidics. William Andrew, Norwich (2012)
Dokowicz, M., Nowicki, W.: Morphological transitions of droplets wetting a series of triangular grooves. Langmuir 32(28), 7259–7264 (2016). https://doi.org/10.1021/acs.langmuir.6b01275
Langbein, D.W.: Capillary surfaces: shape-stability-dynamics. In: Particular Under Weightlessness. Springer Tracts in Modern Physics, vol. 178. Springer, Berlin (2002)
Rye, R.R., Mann, J.A., Yost, F.G.: The flow of liquids in surface grooves. Langmuir 12(2), 555–565 (1996). https://doi.org/10.1021/la9500989
Snakenborg, D., Klank, H., Kutter, J.P.: Microstructure fabrication with a CO\(_2\) laser system. J. Micromech. Microeng. 14(2), 182–189 (2003). https://doi.org/10.1088/0960-1317/14/2/003
Corless, R.M., Gonnet, G.H., Hare, D.E.G., Jeffrey, D.J., Knuth, D.E.: On the Lambert W function. Adv. Comput. Math. 5(1), 329–359 (1996). https://doi.org/10.1007/BF02124750
Funding
Open access funding provided by Johannes Kepler University Linz. This work has been supported by the COMET-K2 “Center for Symbiotic Mechatronics” of the Linz Center of Mechatronics (LCM) funded by the Austrian Federal Government and the Federal State of Upper Austria and by the Austrian Research Promotion Agency (FFG) Project AUTOMATE under project number 890068.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors have no competing interests to declare that are relevant to the content of this article.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix
Appendix
1.1 Proof 1
We want to prove that functions g(x) spanning a fixed cross-sectional area A between two points p and q with \(g(p)=g(q)=0\) are functions of constant curvature.
Proof
The area is described by
whereas the length of the curve is given by
We want to minimize this length under the requirement of constant curvature being introduced by a Lagrangian multiplier \(\lambda \). Thus, we can minimize the Lagrangian
which leads to
where the left-hand side can be identified as the curvature of the function. \(\square \)
1.2 Proof 2
We want to derive Young’s equation for a droplet sitting on a flat surface. We assume that the solution has to be spherical (see Proof 1) with a radius R and makes an (still unknown) contact angle \(\theta \) with surface (Fig. 11).
Proof
We start by writing down the differential associated with the minimization of the Gibbs energy G under the constraint of a fixed droplet volume \(V_0\) ensured by the Lagrange parameter \(\lambda \),
where we have used that \(dA_{sl}=- dA_{sg}\). Each of the three parentheses of the last line has to vanish independently, thus one can express
by setting the second summand (variation of \(\theta \)) equal to zero and plug the result into the third summand (variation of R), which yields:
This factor is only zero if
\(\square \)
1.3 Proof 3
We want to find the minimal energy state for symmetric infinite microchannels with a cross-sectional area fixed to \(\phi _0\) as given in Eq. (16). The surface areas are taken from Eqs. (13) to (15), whereas the Gibbs energy is given by Eq. (11).
Proof
The differential corresponding to the minimization can be equated to
Since \(\alpha \) and R are independent variables, both expressions in the square parentheses must vanish independently. We can set both parentheses to zero and simplify the equations further by multiplying the first parenthesis with \(\sin \vert \alpha \vert \), the second with \(-\cos (\alpha )\) and adding the results, giving
Thus, we have two cases \(\lambda =-\text {sgn}(\alpha )\gamma _{lg}/R\) and \(\alpha =0\), whereas the latter is illegitimate due to the previous multiplication with \(\sin (\vert \alpha \vert )\). Plugging the first case into the square parenthesis of Eq. (A.14) yields
where we have used Eq. (18) for the last equality. In summary, we find that
which is exactly Young’s equation for flat surfaces along with \(\phi =\phi _0\). \(\square \)
1.4 Proof 4
It is to prove that the total energy of a liquid in a V-shaped groove with an opening angle of \(2 \beta \) and contact angle of the liquid to the walls of \(\theta \) under the constraint \(\alpha <0\) (\(\alpha >0\)) is decreasing (increasing) with increasing filling length.
Proof
As found in Eq. (35), the Gibbs energy per length can be formulated as
where we replaced \(\alpha \) by \(\alpha =\frac{\pi }{2}-\beta -\theta \). Since the first factors are always positive (negative) for positive (negative) \(\alpha \), it remains to show that
under the constraints \(\theta \in \left[ 0,\frac{\pi }{2}-\beta \right] \) and \(\beta \in \left( 0,\frac{\pi }{2}\right) \).
The extreme points can be found by setting
The derivative with regard to \(\theta \) can be written as
with n being an integer number. Due to the valid ranges of \(\beta \) and \(\theta \), the only possibility that is just outside of the valid values is \(n=0\) leading to
Considering the derivative with regard to \(\beta \) leads to
which is always zero under the constraint of Eq. (A.26). To check whether the found extreme points are a minimum or maximum, we are taking an epsilon environment around the variables at this point
with \(\vert \epsilon \vert \ll 1\). This leads to an epsilon environment around the condition in Eq. (A.26) as:
Thus, for creating an epsilon environment around the condition (A.22), it is sufficient to use one variable \(\epsilon \) that can be split into individual contributions of \(\epsilon _\theta \) and \(\epsilon _\beta \),
where we have used Taylor series up to first order in \(\epsilon \) in the third line. The last line is always true due to the cotangents being larger than zero in the definition range of \(\beta \). With that proven, we showed that the energy of a liquid in a V-shaped groove is indeed minimized with increasing filling length if and only if \(\alpha <0\). \(\square \)
1.5 Proof 5
We want to find the critical contact angle of Gaussian grooves.
Proof
We start by drawing the limit \(\vert \alpha \vert \rightarrow 0\) in Eq. (33) carefully. Note that \(R\vert \alpha \vert \) cannot be disregarded, since it will converge to a finite value in the limit. Evaluation of the limit leads to:
A graphical representation of this equation is found in Fig. 12 where the straight lines represent the left side of the equation. From this Figure, it can easily be seen that this equation can have two, one, or zero solutions in \(x_0/\sigma \) depending on the value of \(\sigma \tan {\theta }\).
Graphical representation of Eq. (A.36) where the red curves depict the left hand side, whereas the thick black curve represents the right hand side. Depending on the value of \(\sigma \tan {\theta }\) there might be none, one or two solutions in \(x_0/\sigma \). There is a critical contact angle \(\theta _{\mathrm{crit}}\) below which two solutions exist. For any contact angle above \(\theta _{\mathrm{crit}}\) the equation does not have a solution
We can cast Eq. (A.36) into the Lambert W relation [37],
by identifying \(z=-\left( \sigma \tan {\theta }\right) ^2/2\) and \(W(z)=-2\left( x_0/\sigma \right) ^2\). As before, depending on the value of z, this equation can have two or no solutions. To be more specific, a solution only exists for \(-1/e\le z<0\). In our variables, this yields the condition
where we have identified the critical contact angle \(\theta _{\mathrm{crit}}\). Ultimately, this yields that the Gibbs free energy has extremal points only in the range where the contact angle between the liquid and the surface is below a critical contact angle, depending on the groove width \(\sigma \). From the curvature of the groove it can be found that the first zero at lower \(x_0\) is the state of a maximum of the Gibbs energy, whereas the second zero point gives the cross section of minimal energy. \(\square \)
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Mitteramskogler, T., Hingerl, K. & Jakoby, B. A condition for spontaneous capillary flow in open microgrooves. Acta Mech 233, 3923–3939 (2022). https://doi.org/10.1007/s00707-022-03289-1
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00707-022-03289-1