1 Introduction

The present paper concerns turbulent free-surface flow over a wavy bottom. The ensemble-averaged flow is assumed to be steady and plane (two-dimensional). Considered are small slopes of the bottom, which implies very large Reynolds numbers, provided the flow differs but slightly from fully developed flow. More details concerning the deviations from fully developed flow will be given in Sect. 2. With regard to the Froude numbers, the investigation focuses on Froude numbers that are very close to the critical value 1.

Although the inviscid flow over a wavy bottom is a classical problem, there are still open questions that deserve investigation. An example is [23], where a potential-flow theory for subcritical and supercritical flow is presented. Solutions are given for Froude numbers Fr = 0.33 and Fr = 4.4, i.e., not close to the critical value.

Concerning turbulent flow, the recent paper [2] is of particular interest as it gives a survey of the literature on open-channel flow over wavy bottoms with a particular emphasis on practical applications, beginning with early investigations. The authors of [2] themselves treated the Reynolds averaged Navier–Stokes equations. Application of assuming hydrostatic pressure distribution is discussed, but cf. also the monograph [7]. The turbulent diffusivity concept (Boussinesq hypothesis) was applied in [2] for modeling the Reynolds shear stress, and numerical solutions for subcritical (Fr = 0.79) and supercritical (Fr = 1.69) flows, respectively, were given. In contrast to the present work, the bottom elevations are relatively large, and the nonlinearities that are characteristic of near-critical flow are not considered in [2]. Although the Reynolds numbers in the experiments described in [30] are of the order of a few thousands, i.e., too low to be of value for comparison with the present analysis, the results are of general interest as two different wave regimes were observed.

The present paper is related to previous work on near-critical turbulent open-channel flow. In particular, the foundations for dealing with turbulent flow without applying a turbulence model were already laid down in [12]. Problems associated with selecting and applying various turbulence models, cf. [20], are thereby avoided. The basic idea is to compare the actual flow with a fully developed reference flow that is assumed to be known. This path was further pursued in [25,26,27, 33, 34, 37, 40, 41], among others. The analyses lead to steady-state versions of a Korteweg–deVries (KdV) equation with various extensions, depending on the particular problem. The present analysis is complimentary to [37], where stationary solitary waves over slightly uneven bottoms were considered. It remained an open question whether uneven bottoms of suitable shapes can support not only stationary solitary waves but also stationary periodic waves, presumably described by Jacobian Elliptic Functions that are known as solutions of the classical KdV equation [9] as well as of extended KdV equations [31, 39]. A partial answer was given in [24], where periodic solutions of the extended KdV equation according to [37] were obtained. However, those solutions are limited to a very narrow parameter regime. To provide a more general description of steady, spatially periodic flow, is the aim of the present work.

The structure of the paper is the following. After formulating the problem and defining appropriate non-dimensional quantities, the analysis due to [37] is modified to obtain an extended KdV equation that leads to a periodic solution, which is more general than the solutions known previously. The new solution is then applied to determine the local Froude number and the effective bottom friction force. Finally, limiting cases, including inviscid flow, are discussed, and conclusions are presented.

2 Formulation of the problem

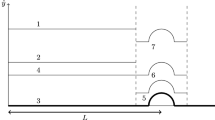
Steady plane (two-dimensional) turbulent open-channel flow over an inclined bottom of constant roughness is considered (Fig. 1). The flow is driven by the gravity force, with \({\text{g}}\) as the acceleration due to gravity. Surface tension is neglected, which implies that the Weber number defined in terms of the turbulent kinetic energy near the free surface is very large. This condition is commonly satisfied for turbulent flows in nature as well as in hydraulic engineering; cf. [5].

Fig. 1
figure 1

Steady near-critical turbulent free-surface flow over a wavy bottom (schematic)

Full size image

The channel bottom is basically a plane with small slope \(\alpha\), apart from small perturbations of characteristic length l and elevation b. The latter may vary in longitudinal direction. A Cartesian coordinate system is chosen such that the x-axis is in the bottom plane, while the y-axis points upwards. The flow velocity components in the x,y-coordinate system are u and v, respectively. Ensemble or time averaged quantities will be denoted by an overbar, e.g., \(\overline{h }\) stands for the averaged surface height.

It is assumed that the flow would be fully developed, i.e., invariant with respect to x, if the bottom were exactly plane. For a bump of finite length, as considered in [37], this implies that the flow is indeed fully developed far upstream and far downstream. However, for a spatially periodic bottom unevenness that extends to infinity in both directions, the fully developed flow over the plane bottom is an artifact that is introduced as a reference state. It serves not only for defining non-dimensional parameters and variables, but also plays an important role in the analysis, cf. below.

3 Non-dimensional parameters, coordinates and variables

In what follows, the subscript r refers to the fully developed flow over a plane bottom with slope \(\alpha\) as the reference state. Thus, the averaged surface height above bottom of the fully developed flow, \({\overline{h} }_{\mathrm{r}}\), serves as reference length, cf. Figure 1. For the purpose of serving as reference velocity, the volumetric mean velocity \({\overline{u} }_{\mathrm{r}}=\dot{V}/{\overline{h} }_{\mathrm{r}}\) is introduced, where \(\dot{V}\) denotes the volume flow rate per unit width in the direction normal to the x, y plane. Note that the units of \(\dot{V}\) are m2/s. Based on these reference quantities, the Froude number and the Reynolds number are defined as

$$Fr = \overline{u}_{{\text{r}}} /\sqrt {{\text{g}}\overline{h}_{{\text{r}}} }$$
(1)

and

$$Re = \overline{h}_{{\text{r}}} \overline{u}_{{\text{r}}} /\nu = \dot{V}/\nu ,$$
(2)

respectively, where \(\nu\) is the constant kinematic viscosity of the liquid.

As the present analysis concerns near-critical flow, a small parameter \(\varepsilon\) is introduced by the relation

$$Fr = 1 + \frac{3}{2}\varepsilon\qquad (0 < \varepsilon \ll 1),$$
(3)

where the coefficient \(3/2\) just serves to obtain the results in a convenient form.

The reference quantities are also used to define non-dimensional coordinates and variables. It is natural to refer the y-coordinate to \(\overline{h}_{r}\). The x-coordinate, however, is contracted with a small parameter \(\delta\). Following [12], or [37], \(\delta\) is defined as

$$\delta = 3\sqrt \varepsilon .$$
(4)

Thus, the non-dimensional Cartesian coordinates X, Y and the non-dimensional bottom elevation B are introduced as follows:

$$X = \delta x/\overline{h}_{{\text{r}}},\quad Y = y/\overline{h}_{{\text{r}}} ,\quad B = b/\overline{h}_{{\text{r}}} .$$
(5)

Furthermore, the non-dimensional variables

$$\overline{H} = \overline{h}/\overline{h}_{{\text{r}}},\quad \overline{U} = \overline{u}/\overline{u}_{{\text{r}}}$$
(6)

are introduced. For other non-dimensional variables, e.g., pressure and Reynolds stresses, see [37].

4 Asymptotic expansion for near-critical flow over a slightly uneven, in particular wavy, bottom

The asymptotic expansion for a slightly uneven bottom, as presented below, essentially follows [37]. However, modifications are required in order to comprise periodic solutions.

Fully developed flow with very small slopes requires very large Reynolds numbers. It follows from the asymptotic theory of turbulent shear flows [32] that the flow field can be divided into a turbulent defect layer, which comprises almost the whole flow field, and a very thin viscous wall (bottom) layer. Concerning the latter, a universal solution is known to exist for steady flow, cf. [10], or [32]. Thus, it suffices to consider the defect layer. The system of basic equations consists of the continuity equation and the Reynolds equations of motion, supplemented by kinematic and dynamic boundary conditions at the free surface and by the tangential-flow condition at the bottom; see [37] for details, and for justification of the latter condition see [19]. Matching to the viscous bottom layer is accomplished by applying the logarithmic overlap law (“law of the wall”) in a form proposed in [32], p. 536. The applicability of the logarithmic law was verified in [37] for the flow over bumps and ramps. It will be seen below that the bottom elevations according to the present analysis are slightly larger than those considered in [37], but the justification of applying the logarithmic law as given in Appendix A of [37] remains valid for the present case.

For completeness, we note that for rather large amplitudes separation at the bottom may occur, leading to deviations from the logarithmic law, see, for instance, [8]. According to [38], separated, recirculatory flow may lead to drag reduction, in contrast to the present results.

To describe flows with Froude numbers very close to the critical value 1, the basic equations are expanded for \(\varepsilon \to 0\), with \(\varepsilon\) defined in (3). In general, the small parameter \(\varepsilon\) is independent of the slope \(\alpha\) that has been introduced above as a small parameter. However, it was shown in previous work, beginning with [12], that the analysis can be kept free of turbulence modeling if \(\alpha\) is assumed to be of the order of \(\varepsilon^{2}\). This assumption is also suitable for comparing the theoretical results with experimental findings, cf. [12, 16, 17, 35] for undular jumps and [36, 37] for solitary waves. Thus, the relationship

$$\alpha = \text{O}({\varepsilon^{2} })$$
(7)

is retained in the present analysis.

Another problem concerns the small unevenness of the bottom. Principally, one is rather free in choosing the order of magnitude of the small height of the bottom elevation. The choice proposed in [37] is perfectly suited for describing bumps and ramps of finite length. However, it leads to inconsistencies in case of periodic bottom elevations that, of course, extend to infinity. For the latter case, a suitable choice can be written as follows:

$$B = 3\varepsilon^{2} \psi \left( X \right),\quad \psi = {\text{O}}\left( 1 \right).$$
(8)

This is half an order of magnitude, i.e., by a factor of the order of \(\varepsilon^{ - 1/2}\), larger than in [37], but still much smaller than the free-surface elevation, which will turn out to be of the order of \(\varepsilon\).

Having fixed the orders of magnitude, the dependent variables are expanded for \(\varepsilon \to 0\), following [33] and [37]. The main results can be written as follows, with three dots indicating higher-order terms:

$$\overline{H}\left( X \right) = 1 + \varepsilon H_{1} \left( X \right) + \ldots ,$$
(9)
$$\overline{U}\left( {X,Y} \right) = 1 + \sqrt \alpha {\Delta }U\left( Y \right) - \varepsilon H_{1} \left( X \right) + \ldots ,$$
(10)

where the free-surface elevation \(H_{1} \left( X \right)\) has to satisfy the following ordinary differential equation:

$$H_{1}^{\prime \prime \prime} + \left( {H_{1} - 1} \right)H_{1}^{\prime } = \beta H_{1} - \psi^{\prime } ,$$
(11)

with

$$\beta = \frac{1}{3}\alpha \varepsilon^{ - 3/2} .$$
(12)

Primes denote derivations with respect to X.

According to the asymptotic expansions given in [37], the perturbations of other flow quantities, in particular the pressure and the lateral velocity component, can be expressed in terms of the free-surface elevation \({H}_{1}\left(X\right)\). The same is true for the local Froude number and the bottom friction force, as will be shown in Sects. 6 and 7, respectively.

Note that the differential Eq. (11) is inhomogeneous if \(\psi\) is a given, non-vanishing function of X, i.e., for a given bottom elevation. The case \(\psi \equiv\) 0 is of no interest here, as a plane bottom permits only damped stationary waves, e.g., the undular jumps investigated previously [12, 16, 17, 39,40,41].

The number 1 on the right-hand side of (9) represents the surface height in the fully developed flow, whereas the non-dimensional velocity distribution in the fully developed flow is equal to \(1+\sqrt{\alpha }\Delta U(Y)\), with \(\Delta U(Y)=\mathrm{O}(1)\) and \(\sqrt{\alpha }\Delta U(Y)\) representing the small velocity defect in the fully developed flow. This quantity can be considered as known. Based on dimensional analysis, a boundary condition at the free surface of fully developed flow was derived [34], leading to the following velocity defect, written in the present notation:

$${\Delta }U = \left( {1/\kappa } \right)\left( {{\text{ln}}Y + 1} \right),$$
(13)

where \(\kappa\) is von Kármán’s universal constant. The logarithmic velocity distribution according to (13) was found to be in good agreement with measurements [18] and direct numerical simulations [28]. Note that \({\Delta }U\) does not appear in (11), i.e., it does not affect the first-order perturbation of the free surface. Note also that, according to (7), the second term and the third term on the right-hand side of (10) are of the same order of magnitude.

The ordinary differential Eq. (11) can be identified as the steady-state version of an extended KdV equation. The extension of the KdV equation consists of two parts, i.e., the linear term \(\beta H_{1}\), which is due to friction, and the “forcing” term \(- \psi ^{\prime}\), which is due to the bottom elevation. Taking (7) into account, it follows from (12) that \(\beta = {\text{O}}( {\sqrt \varepsilon })\). Thus, as in [37], the friction term is half an order of magnitude smaller than the leading terms in the extended KdV Eq. (11). This is a consequence of choosing the relative orders of magnitude of \(\alpha\) and \(\varepsilon\) according to (7), i.e., such that turbulence modeling can be avoided. The bottom elevation, however, is chosen in the present analysis such that the forcing term is half an order of magnitude larger than the term due to friction, whereas both terms are of the same order of magnitude in [37].

The parameter \(\beta\) is a similarity parameter of near-critical turbulent free-surface flow that satisfies the relation (7). For different values of slope and Froude number, the effects of friction are the same if the values of \(\beta\) are equal. In the absence of a forcing term, e.g., for undular jumps over a plane bottom with constant roughness [12], \(\beta\) characterizes the damping of the surface undulations and may, therefore, be called damping parameter.

It ought to be mentioned that linear dissipation terms in extended KdV equations have already been discussed in the investigations [4, 6, 14, 22, 31].

In previous work on solitary waves, e.g., [33, 36, 37], integral relations played an important role. They were obtained by integrating the extended KdV equation from \(X\to -\infty\) to \(X\to +\infty\). Apart from a limiting case considered in Sect. 8.1, spatially periodic waves are of interest in the present paper. Therefore, (11) is integrated over one wave length, denoted by \(\lambda\). Accounting for the periodicity of \(H_{1}\) and \(\psi\), one obtains

$$\mathop \int \limits_{{X_{0} }}^{{X_{0} + \lambda }} H_{1} {\text{d}}X = 0,$$
(14)

where \(X_{0}\) is an arbitrary value of X.

5 An exact periodic solution

An exact solution of a steady-state extended KdV equation similar to (11) was found in [37] by setting both the left-hand side and the right-hand side equal to zero. A stationary solitary wave above a ramp of a particular shape was obtained. The same idea was pursued in [24] to obtain periodic solutions. It turned out, however, that those periodic solutions have the disadvantage of being restricted to a very narrow parameter regime. In what follows it will be shown that a small, but essential, modification of the original idea leads to periodic solutions that cover the whole parameter space of the functions appearing in the solutions.

First, we consider functions \(\tilde{H}_{1} \left( X \right)\) that make the left-hand side of (11) zero, i.e., \(\tilde{H}_{1}\) has to satisfy the equation

$$\tilde{H}_{1}^{\prime \prime \prime } + \left( {\tilde{H}_{1} - 1} \right)\tilde{H}_{1}^{\prime } = 0.$$
(15)

Equation (15) is the steady-state version of the classical KdV equation, which is known to possess periodic solutions (see, for instance, [21] or [42], p. 470). The periodic solutions are written here according to [9], pp. 27 and 28, after performing a few algebraic substitutions, as follows:

$$\tilde{H}_{1} = {\Gamma } + 12\gamma^{2} m {\text{cn}}^{2} (\gamma X|m),$$
(16)

with

$${\Gamma } = 1 + 4\gamma^{2} \left( {1 - 2m} \right)$$
(17)

and cn as the Jacobian Elliptic Function Cosinus Amplitudinis with parameter m, \(0 < m < 1\), cf. [1], pp. 569–575. The parameter \(\gamma\) characterizes the wave number according to the following relation for the wavelength \(\lambda\):

$$\lambda = 2K\left( m \right)/\gamma ,$$
(18)

where \(K\left( m \right)\) is the Complete Elliptic Integral of the First Kind.

In the second step, we set

$$H_{1} = \tilde{H}_{1} - D,$$
(19)

with D as a constant that is to be determined such that \(H_{1}\) satisfies (11). Taking (15) into account, (11) reduces to

$$\psi^{\prime} = D\tilde{H}_{1}^{\prime} + \beta \left( {\tilde{H}_{1} - D} \right).$$
(20)

Integrating (20) gives

$$\psi = D\tilde{H}_{1} + \beta \left( {\int \tilde{H}_{1} {\text{d}}X - DX} \right).$$
(21)

Integrating (16), one obtains for the integral in (21) the expressionFootnote 1

$$\int \tilde{H}_{1} {\text{d}}X = 12\gamma Z\left( {\gamma X{|}m} \right) + \left\{ {1 + 4\gamma^{2} \left[ {3E\left( m \right)/K\left( m \right) + m - 2} \right]} \right\}X,$$
(22)

where a constant of integration has been omitted. As the constant of integration is multiplied by the small parameter \(\beta\) in (21), taking it into account would just lead to a negligibly small vertical shift of the bottom. \(K\left( m \right)\) has already been introduced above as the Complete Elliptic Integral of the First Kind, and \(E\left( m \right)\) is the Complete Elliptic Integral of the Second Kind. \(Z\left( {\gamma X{|}m} \right)\) denotes Jacobi’s Zeta Function with variable \(\gamma X\) and parameter m, see [1], pp. 595, and [29], pp. 562–563 with Fig. 22.16.3. By definitions, \(Z\left( {\gamma X{|}m} \right)\) and \({\text{cn}}(\gamma X|m)\) are periodic functions of X. It follows from (16) that \(\tilde{H}_{1}\) is also periodic in X. Thus, when (22) is inserted into (21) to obtain the unknown function \(\psi\), two periodic terms are obtained. However, within the parentheses, there also appear two linear terms. These terms must cancel for a periodic solution. Thus, the value of D becomes

$$D = 1 + 4\gamma^{2} \left[ {3E\left( m \right)/K\left( m \right) + m - 2} \right].$$
(23)

The constant D is of relevance not only for the relation (19), but also for the shape of the bottom unevenness to be given below. A plot of lines of constant values of D in an (\(m,\gamma\))-diagram is therefore shown in Fig. 2.

łFig. 2
figure 2

Dependence of the constant D on the parameters m and \(\gamma\)

Full size image

The special case \(D=0\) was considered in [24]. For \(D=0\), (23) becomes a relationship for \(\gamma\) as a function of m. For \(D=1\), both \(\gamma\) and the amplitude of \({H}_{1}\) are singular. Lines of constant values of D, with \(D\ne 1\), approach the line \(D=1\) as an asymptote in the \(m,\gamma\) -diagram, see Fig. 2. It follows from (23) that \(D=1\) for \(m={m}_{s}\approx 0.9611\), i.e., \({m=m}_{s}\) is the equation of the asymptote in the (\(m,\gamma\))-diagram. Thus, the solutions given in [24] exist only in the narrow parameter range \({m}_{s}<m<1\).

Inserting (22) and (23) into (21), the following result for \(\psi \left( X \right)\), which describes the shape of the periodic bottom elevation, is obtained:

$$\psi = 12\gamma [D\gamma m {\text{cn}}^{{2}} (\gamma X|m) + \beta Z\left( {\gamma X{|}m} \right)] + D{\Gamma ,}$$
(24)

with \({\Gamma }\) as defined in (17).

Finally, inserting (16) and (23) into (19) shows that the surface elevation can be expressed in the following form:

$$H_{1} /12\gamma^{2} = m {\text{cn}}^{2} \left( {\gamma X{|}m} \right) - G,$$
(25)

with

$$G = m - 1 + E\left( m \right)/K\left( m \right) > 0 {\qquad\text{for} \qquad} 0 < m < 1.$$
(26)

Note that the right-hand side of (25) is a function of \(\gamma X\) only, with m as a parameter, see Fig. 3.

Fig. 3
figure 3

The non-dimensional elevation of the free surface, \({H}_{1}\), referred to the parameter \(12{\gamma }^{2}\), as a function of the coordinate \(\gamma X\), with m as parameter

Full size image

According to (25) and (26), the function \(H_{1} \left( X \right)/12\gamma^{2}\) varies between

$${\text{min}}\left( {H_{1} /12\gamma^{2} } \right) = 1 - m - E\left( m \right)/K\left( m \right)$$
(27)

and

$${\text{max}}\left( {H_{1} /12\gamma^{2} } \right) = 1 - E\left( m \right)/K\left( m \right).$$
(28)

Thus, the amplitude of the surface elevation \(H_{1} \left( X \right)\) is \(12\gamma^{2} m\). Furthermore, it follows from (25) and (24) that the periodic free-surface elevation and the periodic bottom elevation have the same wavelength \(\lambda\), as given in (18). Figure 4 shows three examples. As can be expected, there is a phase shift between \(H_{1} \left( X \right)\) and \(\psi \left( X \right)\). However, comparing (24) with (25) shows that the phase shift is proportional to the damping parameter \(\beta\). As realistic \(\beta\)-values are rather small, cf. [37], the phase shifts in the examples shown in Fig. 4 are so small that they are barely visible. To improve the visibility of the phase shift and the shape difference between \(H_{1}\) and \(\psi\), Fig. 5 has been added. This figure shows the results for one parameter set in a scale that permits a direct comparison of the results for the free-surface elevation and the bottom elevation. The numerically determined phase shift of the wave crests at X = 0 is 0.04.

Fig. 4
figure 4

Elevation of the free surface, \({H}_{1}\), and elevation of the bottom surface, \(\psi\), as functions of the non-dimensional coordinate X. The blue, red and green curves correspond to the blue, red and green dots, respectively, in Fig. 2. Parameter values: All curves \(D=2\), \(\beta =0.3\); blue \(m=0.3\), \(\gamma =0.55\); red \(m=0.6\), \(\gamma =0.65\); green \(m=0.9\), \(\gamma =1.16\). The scale of \({\text{Fr}}_{\mathrm{loc}}\) on the right-hand side of the diagram is for the reference Froude number \(\mathrm{Fr}=1.06\)

Full size image
Fig. 5
figure 5

Reduced values of the free-surface elevation, \({H}_{1}\), solid line, and the bottom-surface elevation, \(\psi\), dashed line, as functions of the non-dimensional coordinate X. Parameter values: \(\beta =0.3\), \(m=0.9\), \(\gamma =1.16\), corresponding to the green curves in Fig. 4

Full size image

In closing this section, we make the following remarks concerning the damping term. It might be tempting to drop the \(\beta\)-term in (24), as \(\beta =\mathrm{O}(\sqrt{\varepsilon })\), whereas the first term in the brackets is, at least formally, of order 1. This term, however, vanishes for \(D\to 0\), i.e., the case considered in [24], with interesting results; cf. above. In order to include this limiting case in the present analysis, the \(\beta\)-term is retained in (24). Remarkably, an anonymous reviewer provided the following, additional argument why the \(\beta\)-terms must not be dropped: “The value of D is determined from the terms of the order of \(\beta\). If inviscid flow would be assumed right away, i.e., with \(\beta\) set zero in the analysis, only the first term on the right-hand side in Eq. (21) would have been kept. Then, however, D could take any value independent of m and \(\gamma\) with (25, 21) satisfying Eq. (11). Obviously, this regime of inviscid solutions is more general and clearly distinct to the turbulent regime.” For a further discussion of the inviscid flow as a limiting case of the present analysis and a comparison of the results see Sect. 8.3.

6 Local Froude number

A quantity of considerable interest is the local Froude number, which is defined as

$$\text{Fr}_{{{\text{loc}}}} = \overline{u}_{m} /\sqrt {{\text{g}}\overline{h}} ,$$
(29)

with \(\overline{u}_{m}\) as the volumetric mean of \(\overline{u}\). Introducing non-dimensional variables according to (6), expanding according to (9) and (10), and observing that the mean value of \({\Delta }U\) vanishes per definition, one obtains the following relation, which was already given in [16]:

$$\text{Fr}_{{{\text{loc}}}} = 1 + \frac{3}{2}\varepsilon \left[ {1 - H_{1} \left( X \right)} \right].$$
(30)

This equation shows that the critical state occurs wherever \(H_{1} = 1\), independently of the value of the reference Froude number Fr. The maximum and minimum values of the local Froude number are obtained by inserting (27) and (28), respectively, into (30). The distribution of the local Froude number, i.e., \(1 - H_{1} \left( X \right)\), can be seen in Fig. 4 for a reference Froude number \(\text{Fr} = 1.06\).

7 Bottom friction force

It appears possible that the flow resistance is changed as a consequence of the waviness of the bottom surface [11]. Thus, the friction force acting at one wavelength \(\lambda\) of the wavy bottom is compared with the friction force acting at the same distance of the plane reference bottom. The difference of the two forces is denoted by \({\Delta F}_{\mathrm{f}}\). To determine the friction force, the friction coefficient \({c}_{f}\) is introduced. Since, in steady flow, the volume flow rate \(\dot{V}\) does not change with X for continuity reasons, irrespective of flow disturbances, the Reynolds number \(Re=\dot{V}/\nu\) remains constant, and \({c}_{\mathrm{f}}={c}_{\mathrm{f}}\,(Re)\) also remains constant, provided the roughness of the bottom surface is constant over the whole bottom. Since \({\text{d}}x=({\overline{h} }_{r}\text{/3}\sqrt{\varepsilon }\text{)d}X\) according to (5) with (4), \({\Delta F}_{\mathrm{f}}\) becomes

$${\Delta }F_{{\text{f}}} = \frac{{c_{{\text{f}}} \rho }}{2}\frac{{\overline{h}_{{\text{r}}} }}{{{3}\sqrt \varepsilon }}\mathop \int \limits_{{X_{0} }}^{{X_{0} + \lambda }} \left( {\overline{u}_{{\text{m}}}^{2} - \overline{u}_{{\text{r}}}^{2} } \right){\text{d}}X,$$
(31)

where \(\rho\) is the constant density of the liquid, \(\lambda\) is the wavelength and, as above, \(\overline{u}_{{\text{m}}}\) and \(\overline{u}_{{\text{r}}}\) are the volumetric mean and the reference value, respectively, of \(\overline{u}\). Again, \(X_{0}\) is an arbitrary value of X. Expanding as described above for the local Froude number, one obtains

$${\Delta }F_{{\text{f}}} = - \frac{1}{3}\sqrt \varepsilon c_{{\text{f}}} \rho \overline{u}_{{\text{r}}}^{2} \overline{h}_{{\text{r}}} \mathop \int \limits_{{X_{0} }}^{{X_{0} + \lambda }} H_{1} {\text{d}}X.$$
(32)

According to (14), the integral in (32) vanishes, and the result is

$${\Delta }F_{{\text{f}}} = 0,$$
(33)

i.e., there is no first-order effect of the bottom waviness on the flow resistance. The same result is obtained, as it ought to be, when the solution (25) is inserted into (32) and the integration is performed, using (18) for \(\lambda\).

8 Limiting cases

8.1 Limit \({m} \to 1\): Solitary wave

As \(m \to 1\), \(K\left( m \right) \to \infty\), \(E\left( m \right) \to 1\), \({\text{cn}}(\gamma X|m) \to {\text{sech}}\left( {\gamma X} \right)\), and \({\text{Z}}(\gamma X|m) \to {\text{tanh}}\left( {\gamma X} \right)\), cf. [1], pp. 569–575 and 590–595. Thus, (25) gives

$$H_{1} = 12\gamma^{2} {\text{sech}}^{{2}} \left( {\gamma X} \right) {\qquad\text{as}\qquad} m \to 1.$$
(34)

For \(\gamma = 1/2\), (34) leads to

$$H_{1} = 3{\text{sech}}^{{2}} \left( {X/2} \right),$$
(35)

which is the solitary-wave solution considered in [37]. Furthermore, with \(\gamma = 1/2\) one obtains from (24)

$$\psi = 6\beta {\text{tanh}}\left( {X/2} \right)$$
(36)

as the shape of the bottom ramp that gives rise to the solitary wave. Accounting for the different definitions of \(\psi\), (36) is in accord with [37].

8.2 Limit \({m} \to 0\): Trivial solution

The limiting case \(m \to 0\) is of little interest. It is true that \({\text{cn}}(\gamma X|m) \to {\text{cos}}\left( {\gamma X} \right)\) as \(m \to 0\), cf. [1], p. 571. But (25) gives \(H_{1} \equiv 0\), and (24) shows that \(\psi\) approaches a constant as \(m \to 0\), so that the extended KdV Eq. (11) is satisfied trivially.

8.3 Limit \(\beta \to 0\): Inviscid flow

For \(\beta \to 0\) with fixed \(\varepsilon\), (12) gives \({\alpha } \to 0\). Since in the presence of bottom friction a fully developed flow requires a non-zero slope, the limit \(\beta \to 0\) leads to inviscid flow. This is in accord with the discussion of the extended KdV Eq. (11) in Sect. 4. In this limit, only the forcing term remains on the right-hand side of (11). As the solution (25) for \(H_{1}\) is free of \(\beta\), it remains valid, whereas the \(\beta\)-term in (24) for the bottom elevation has to be dropped in case of inviscid flow.

The limit \({\alpha } \to 0\) with fixed \(\varepsilon\) violates the order-of-magnitude relation (7). However, according to the reasoning leading to (7), the relation is introduced only for properly describing the effect of turbulence. Thus, (7) is not of relevance for the inviscid flow, and the extended KdV Eq. (11) remains valid for vanishing \(\beta\).

For the applicability of the KdV equation and its modifications or extensions to inviscid flow cf. the survey articles [13, 15]. Novel periodic solutions of the KdV equation with a small forcing term were given in [3]. A comparison with the present solutions is not feasible, as the forcing term in (11) is of the order of 1.

9 Conclusions

The analysis presented above is valid for Froude numbers that differ from the critical value 1 by a small value that is written as \((3/2)\varepsilon\). The analysis, which does not require the application of a turbulence model, shows that stationary, spatially periodic perturbations of the free surface can be obtained with a suitably shaped periodic unevenness of the bottom surface. The free-surface elevation is described by the steady-state version of an extended KdV equation. In contrast to previous investigations on solitary waves [37] and periodic solutions of limited applicability [24], the extension terms are now of different orders of magnitude. The term due to wall friction remains to be of the order of \(\beta =\mathrm{O}(\sqrt{\varepsilon })\), whereas the forcing term, which is due to the periodic bottom unevenness, is a term of the order 1 in the KdV equation.

It is remarkable that the height of the bottom elevation is as small as \({{\text{O}}(\varepsilon }^{2})\) in comparison with the height of the free surface above bottom, and also much smaller than the free-surface elevation, which is of the order of \(\varepsilon\). This reflects the sensitivity of near-critical flows to perturbations that are associated with changes of the cross-sectional area. From the point of view of considering the KdV equation irrespective of a fluid mechanical background, the present finding may be interpreted as a resonance effect [3].

By a proper manipulation of the extended KdV equation, it was possible to find a periodic solution that can be expressed in terms of Jacobian Elliptic Functions and Complete Elliptic Integrals. The part of the solution that describes the surface elevation is independent of the parameter \(\beta\), but the part describing the bottom elevation consists of a term of the order of 1 and a term that is proportional to \(\beta\). The consideration of limiting cases indicates that the \(\beta\)-term, though half an order of magnitude smaller than the term of order 1, must not be dropped if the solution ought to be valid in the whole parameter regime of the Elliptic Functions.

Integrating the extended KdV equation over one period gives an integral relation that can be applied to show that the bottom friction force, averaged over one wavelength, is the same as for the reference flow over a plane bottom, i.e., there is neither an effective reduction nor an effective enlargement of the flow resistance due to the waviness of the bottom.