1 Introduction

We want to derive bounds to the overall incremental stiffness of heterogeneous hyperelastic media without voids, cracks, or rigid inclusions. (Remarks on voids can be found in Sect. 7. An extension to rigid inclusions is given in the author’s book on the theory of materials [1].) Constraints like incompressibility are also not taken into account. In order to make the notion of overall stiffness precise, we restrict our intention to any one of the following two types of problems.

  • Type 1: The heterogeneous body is finite and its boundary undergoes a homogeneous deformation.

  • Type 2: The heterogeneous body is infinite and has a periodic structure. Only periodic fields of stress and strain are admitted.

Our results will be valid simultaneously for each of these two types of problems. We recall the following classical results (cf. e.g. the review article of Willis [2]). Remarks on the notation can be found in Appendix A.

Consider a linear hyperelastic body with the local constitutive relation

$$\begin{aligned} \mathbf{T } ={\textsf {C}}:\mathbf{E } \end{aligned}$$
(1)

(\(\mathbf{T }\): stress, \({\mathbf{E }}\): small strain) and let a bar denote the volume average taken over the whole finite body (type 1) or over a typical cell of the periodic infinite body (type 2). The overall stiffness \(\tilde{\textsf {C}}\) is then defined as the linear mapping between the average values

$$\begin{aligned} {{\bar{\mathbf{T }}}} =\frac{1}{V}\int \mathbf{T }\,\mathrm{d}V\,,\qquad {\bar{\mathbf{E }}} =\frac{1}{V}\int \mathbf{E }\,\mathrm{d}V \end{aligned}$$
(2)

of stress and strain, i.e.

$$\begin{aligned} {\bar{\mathbf{T }}} ={\tilde{\textsf {C}}}: {\bar{\mathbf{E }}}. \end{aligned}$$
(3)

If the local stiffness \({\textsf {C}}\) is positive-definite throughout the body, then the following bounds exist:

$$\begin{aligned} \overline{\mathbf{E }: {\textsf {C}}: \mathbf{E }} \ge {\bar{\mathbf{E }}}:{\tilde{\textsf {C}}}:{\bar{\mathbf{E }}}\ge 2\,{\bar{\mathbf{T }}}:{\bar{\mathbf{E }}}-\overline{\mathbf{T }: {\textsf {C}}^{-1}: \mathbf{T }}. \end{aligned}$$
(4)

On the left-hand side, \({\mathbf{E }}\) is any compatible strain field, while, on the right-hand side, \({\mathbf{T }}\) is any equilibrium stress field.

We are interested in the behaviour of a prestressed body. Therefore we replace the finite relation (1) between stress and strain by the incremental relation

$$\begin{aligned} {\mathbf{S }} = {\textsf {A}}:\mathbf{L }= {\textsf {C}}:\mathbf{D }+\mathbf{L }\cdot \mathbf{T } \end{aligned}$$
(5)

between the rate of nominal stress \({\mathbf{S }}\) and the velocity gradient \({\mathbf{L }}\). This formula is elaborated in Eq. (163) of Appendix A. The second-order tensors \({\mathbf{S }}\) and \({\mathbf{L }}\) are, in general, not symmetric. The overall incremental stiffness \({\tilde{\textsf {A}}}\) relates the average values of these tensors by

$$\begin{aligned} {\bar{\mathbf{S }}} =\tilde{\textsf {A}}:{\bar{\mathbf{L }}}. \end{aligned}$$
(6)

If \({\textsf {A}}\) is positive-definite throughout the body, then the following bounds can be constructed along the classical line:

$$\begin{aligned} \overline{\mathbf{L }: {\textsf {A}}: \mathbf{L }} \ge {\bar{\mathbf{L }}}:\tilde{\textsf {A}}:\bar{\mathbf{L }}\ge 2\,\bar{\mathbf{S }}:\bar{\mathbf{L }}-\overline{\mathbf{S }: {\textsf {A}}^{-1}: \mathbf{S }}. \end{aligned}$$
(7)

On the left-hand side, \(\mathbf{{L} }\) is any admissible velocity gradient field, while, on the right-hand side, \(\mathbf{S }\) is any admissible solenoidal field (cf. Eqs. (164), (165) of Appendix A).

This result is not satisfactory. Positive-definiteness of the local incremental stiffness \({\textsf {A}}\) means

$$\begin{aligned} \mathbf{L }:{\textsf {A}}:\mathbf{L } = \mathbf{D }:{\textsf {C}}:\mathbf{D }+\mathbf{T }:\mathbf{L }^T\cdot \mathbf{L } >0\qquad \mathrm{if}\qquad \mathbf{L }\ne \mathbf{0 }. \end{aligned}$$
(8)

There are cases where \({\textsf {A}}\) is indeed positive-definite everywhere, but there are also important cases where it is not and therefore the bounds (7) are not valid.

  • Case 1: The second-order tensor \(\mathbf{T }\) and the fourth-order tensor \({\textsf {C}}\) are positive-definite everywhere. So there are only tensile principal stresses in the whole body. Then \({\textsf {A}}\) is obviously positive-definite.

  • Case 2: Let

    $$\begin{aligned} \mathbf{T } =t_1 \mathbf{e }_1\otimes \mathbf{e }_1+t_2 \mathbf{e }_2\otimes \mathbf{e }_2+t_3 \mathbf{e }_3\otimes \mathbf{e }_3\,,\qquad \mathbf{L }=\mathbf{e }_3\times \mathbf{1 }=\mathbf{e }_2\otimes \mathbf{e }_1-\mathbf{e }_1\otimes \mathbf{e }_2. \end{aligned}$$
    (9)

    Then

    $$\begin{aligned} \mathbf{L }:{\textsf {A}}:\mathbf{L } =\mathbf{T }:\mathbf{L }^T\cdot \mathbf{L }=t_1+t_2. \end{aligned}$$
    (10)

    If there are compressive stresses at some point such that the sum of two principal stresses is negative, then \({\textsf {A}}\) is obviously not positive-definite at that point.

  • Case 3: There is no prestress (\(\mathbf{T }=\mathbf{0 }\)) and \({\textsf {C}}\) is indefinite at some point and so is \({\textsf {A}}\).

The aim of this paper is the construction of upper and lower bounds to the incremental stiffness even in such cases where \({\textsf {A}}\) is not positive-definite throughout the body. This is achieved by using a modified local stiffness \({\textsf {A}}^{*}\) instead of \({\textsf {A}}\).

Some of the theoretical results were presented in a lecture at the XVIth International Congress of Theoretical and Applied Mechanics, Lyngby, Denmark, 1984. The emphasis of this paper is on the elaboration of some applications of the method and the demonstration of its benefits.

The article is organized as follows. The connection between the micro- and macrobehaviour of a composite is explained in Sect. 2. Section 3 introduces the concept of a pseudo-stiffness which allows the construction of upper and lower bounds in Sects. 4 and 5. The constitutive assumptions on which the existence of a pseudo-stiffness is based are investigated in Sect. 6. Some remarks on the treatment of cavities can be found in Sect. 7. Our construction of bounds is detailed in the context of a special geometry in Sect. 8: reinforcement in one direction. Finally, Sect. 9 presents the numerical evaluation of various examples.

2 The microfields

We need the following definitions.

  • \({\mathscr {S}}\) is the set of solenoidal tensor fields \(\mathbf{S }\) (cf. Eqs. (164), (165) of Appendix A). In case of a problem of type 2, these fields must additionally be periodic.

  • \({\mathscr {U}}\) is the set of continuous and piecewise continuously differentiable vector fields \(\mathbf{{u} }\). In case of a problem of type 1, \(\mathbf{{u} }\) must vanish on the boundary of the body. In case of a problem of type 2, \(\mathbf{{u} }\) must be periodic.

We study velocity fields

$$\begin{aligned} \mathbf{v } =\bar{\mathbf{L }}\cdot \mathbf{r } +\mathbf{u }\qquad \mathbf{u }\in {{\mathscr {U}}}, \end{aligned}$$
(11)

where \(\mathbf{{r} }\) denotes the position vector, and their gradients—note \(\mathbf{r }\otimes \nabla =\mathbf{1 }\)—

$$\begin{aligned} \mathbf{L }\equiv \mathbf{v }\otimes \nabla =\bar{\mathbf{L }} +\mathbf{u }\otimes \nabla . \end{aligned}$$
(12)

It follows from Eq. (168) of Appendix B that \(\bar{\mathbf{L}}\) is indeed the mean value of the velocity gradient field.

The velocity field induces the following rate of nominal stress field according to Eq. (5).

$$\begin{aligned} \mathbf{S } = {\textsf {C}}:\mathrm{sym}\,\big [\bar{\mathbf{L }} +\mathbf{u }\otimes \nabla \big ] + (\bar{\mathbf{L }} +\mathbf{u }\otimes \nabla )\cdot \mathbf{T }. \end{aligned}$$
(13)

The exact microfields \(\mathbf{u }_e\) and \(\mathbf{S }_e\) are obtained if the field \(\mathbf{S }\) is solenoidal, i.e.

$$\begin{aligned} \mathbf{0 } = \mathbf{S }_e\cdot \nabla = \Big ({\textsf {C}}:\mathrm{sym}\,\big [\bar{\mathbf{L }} +\mathbf{u }_e\otimes \nabla \big ]\Big )\cdot \nabla +\Big ( (\bar{\mathbf{L }} +\mathbf{u }_e\otimes \nabla )\cdot \mathbf{T }\Big )\cdot \nabla . \end{aligned}$$
(14)

Since we postulate \(\mathbf{T }\) to be solenoidal, we obtain \(\mathbf{u }_e\) from the differential equation

$$\begin{aligned} \Big ( {\textsf {C}}(\mathbf{r }):\mathrm{sym}\,[\mathbf{u }_e\otimes \nabla ]\Big )\cdot \nabla +\mathbf{u }_e\otimes \nabla \otimes \nabla :\mathbf{T } = -\mathrm{sym}[\bar{\mathbf{L }}]:\big ({\textsf {C}}(\mathbf{r })\cdot \nabla \big ) = -\bar{\mathbf{D }}:\big ({\textsf {C}}(\mathbf{r })\cdot \nabla \big ). \end{aligned}$$
(15)

We notice that the field \(\mathbf{u }_e\) is a linear function of \(\bar{\mathbf{D }}\). Therefore, averaging (5) and noting (171) of Appendix B, we can define the overall incremental stiffnesses \(\tilde{\textsf {A}}\) and \(\tilde{\textsf {C}}\) by

$$\begin{aligned} \bar{\mathbf{S }}_e= & {} \overline{ {\textsf {A}}:\mathbf{L }_e}=\tilde{\textsf {A}}:\bar{\mathbf{L }}\nonumber \\= & {} \overline{{\textsf {C}}:\mathbf{D }_e+\mathbf{L }_e\cdot \mathbf{T }} = \tilde{\textsf {C}}:\bar{\mathbf{D }}+\bar{\mathbf{L }}\cdot \bar{\mathbf{T }}. \end{aligned}$$
(16)

3 The pseudo-stiffness

The construction of bounds is only possible with a fourth-order tensor that is positive-definite everywhere in the body. If the stiffness \({\textsf {A}}\) does not satisfy this requirement, we replace it by a pseudo-stiffness \({\textsf {A}}^{*}\), defined by

$$\begin{aligned} {\textsf {A}}^{*} :\mathbf{L } \equiv {\textsf {A}} :\mathbf{L }-\frac{1}{2}\big (\mathbf{Y }\cdot \mathbf{L }^T+\mathbf{L }^T\cdot \mathbf{Y } -\mathbf{1 }:\mathbf{L }\;\mathbf{Y }-\mathbf{Y }:\mathbf{L }\;\mathbf{1 }\big ), \end{aligned}$$
(17)

where \(\mathbf{{Y} }\) is any second-order tensor. We hope to find a \(\mathbf{{Y} }\) that makes the quadratic form

$$\begin{aligned} \mathbf{L }: {\textsf {A}}^{*} :\mathbf{L } = \mathbf{L }:{\textsf {A}} :\mathbf{L }-\mathbf{Y }: \big (\mathbf{L }^2 -\mathbf{1 }:\mathbf{L }\;\mathbf{L }\big )= \mathbf{D }:{\textsf {C}} :\mathbf{D } +\mathbf{T }:\mathbf{L }^T\cdot \mathbf{L } -\mathbf{Y }: \big (\mathbf{L }^2 -\mathbf{1 }:\mathbf{L }\;\mathbf{L }\big ) \end{aligned}$$
(18)

positive-definite.

If \(\mathbf{{Y} }\) is constant throughout the body and \({\mathbf{L}}=\mathbf{v }\otimes \nabla \) is any velocity gradient field then

$$\begin{aligned}&\big (\mathbf{Y }\cdot \mathbf{L }^T+\mathbf{L }^T\cdot \mathbf{Y } -\mathbf{1 }:\mathbf{L }\;\mathbf{Y }-\mathbf{Y }:\mathbf{L }\;\mathbf{1 }\big )\cdot \nabla \nonumber \\&\quad = (\mathbf{Y }\cdot \nabla \otimes \mathbf{v })\cdot \nabla -\mathbf{Y }\cdot \nabla (\mathbf{v }\cdot \nabla )+\nabla \otimes \mathbf{v }\cdot \mathbf{Y }\cdot \nabla -\nabla (\mathbf{Y }:\mathbf{v }\otimes \nabla )=\mathbf{0 }. \end{aligned}$$
(19)

This has an important consequence: If \(\mathbf{v }=\mathbf{v }_e\) is the exact velocity field, then not only the nominal stress rate \(\mathbf{S }_e\) but also the pseudo-stress rate

$$\begin{aligned} \mathbf{S }_e^{*} = {\textsf {A}}^{*} :\mathbf{L }_e = \mathbf{S }_e-\frac{1}{2}\big (\mathbf{Y }\cdot \mathbf{L }_e^T+\mathbf{L }_e^T\cdot \mathbf{Y } -\mathbf{1 }:\mathbf{L }_e\;\mathbf{Y }-\mathbf{Y }:\mathbf{L }_e\;\mathbf{1 }\big ) \end{aligned}$$
(20)

is solenoidal.

$$\begin{aligned} \mathbf{S }_e\cdot \nabla =\mathbf{0 }\qquad \Longleftrightarrow \qquad \mathbf{S }_e^{*}\cdot \nabla =\mathbf{0 }. \end{aligned}$$
(21)

The overall pseudo-stiffness \(\tilde{\textsf {A}}^{*}\) is defined by

$$\begin{aligned} \overline{\mathbf{S }_e^{*}} = \tilde{\textsf {A}}^{*} :\bar{\mathbf{L }} = \overline{{\textsf {A}}^{*} :\mathbf{L }_e} = \overline{{\textsf {A}} :\mathbf{L }_e}-\frac{1}{2}\big (\mathbf{Y }\cdot \bar{\mathbf{L }}^T+\bar{\mathbf{L }}^T\cdot \mathbf{Y } -\mathbf{1 }:\bar{\mathbf{L }}\;\mathbf{Y }-\mathbf{Y }:\bar{\mathbf{L }}\;\mathbf{1 }\big ) \end{aligned}$$
(22)

and we have

$$\begin{aligned} \bar{\mathbf{L }}:\tilde{\textsf {A}}^{*}:\bar{\mathbf{L }} = \bar{\mathbf{D }} : \tilde{\textsf {C}}:\bar{\mathbf{D }}+ \bar{\mathbf{T }}: \bar{\mathbf{L }}^T\cdot \bar{\mathbf{L }}-\mathbf{Y }:(\bar{\mathbf{L }}^2-\mathbf{1 }:\bar{\mathbf{L }}\; \bar{\mathbf{L }}). \end{aligned}$$
(23)

Our incremental stiffnesses enjoy the symmetries

$$\begin{aligned} {\textsf {C}}:\mathbf{D } =\mathbf{D }:{\textsf {C}}\,,\qquad {\textsf {A}}:\mathbf{L } =\mathbf{L }:{\textsf {A}}\,,\qquad {\textsf {A}}^{*}:\mathbf{L } =\mathbf{L }:{\textsf {A}}^{*}. \end{aligned}$$
(24)

4 Construction of the upper bound

An arbitrary kinematically admissible velocity field can be written as

$$\begin{aligned} \mathbf{v } = \mathbf{v }_e +\mathbf{z }, \end{aligned}$$
(25)

where \(\mathbf{z }\in {{\mathscr {U}}}\) is the deviation from the exact velocity field \(\mathbf{v }_e\). Then we have

$$\begin{aligned} \overline{\mathbf{L }:{\textsf {A}}^{*} :\mathbf{L }} = \overline{(\mathbf{L }_e+\mathbf{z }\otimes \nabla ):{\textsf {A}}^{*} :(\mathbf{L }_e+\mathbf{z }\otimes \nabla )} = \overline{\mathbf{L }_e:{\textsf {A}}^{*} :\mathbf{L }_e} +2\,\underbrace{ \overline{\mathbf{z }\otimes \nabla :{\textsf {A}}^{*} :\mathbf{L }_e}} + \overline{\mathbf{z }\otimes \nabla :{\textsf {A}}^{*} :\mathbf{z }\otimes \nabla }.\nonumber \\ \end{aligned}$$
(26)

The underbraced term vanishes because of Eq. (167) of Appendix B since it can be rewritten as

$$\begin{aligned} \overline{\mathbf{z }\otimes \nabla :{\textsf {A}}^{*} :\mathbf{L }_e}= \overline{\mathbf{S }^{*}_e : \mathbf{z }\otimes \nabla }. \end{aligned}$$
(27)

The first term can be expanded as follows:

$$\begin{aligned} \overline{\mathbf{L }_e:{\textsf {A}}^{*} :\mathbf{L }_e} =\overline{\mathbf{L }_e:\mathbf{S }^{*}_e} =\overline{(\bar{\mathbf{L }}+\mathbf{u }_e\otimes \nabla ):\mathbf{S }^{*}_e} =\bar{\mathbf{L }}:\overline{\mathbf{S }^{*}_e} +\underbrace{\overline{(\mathbf{u }_e\otimes \nabla ):\mathbf{S }^{*}_e}} =\bar{\mathbf{L }}:\tilde{\textsf {A}}^{*}:\bar{\mathbf{L }}. \end{aligned}$$
(28)

The underbraced term vanishes again. We arrive at the upper bound

$$\begin{aligned} \bar{\mathbf{L }}\cdot \tilde{\textsf {A}}^{*}:\bar{\mathbf{L }}\le \overline{\mathbf{L }:{\textsf {A}}^{*} :\mathbf{L }} \end{aligned}$$
(29)

if the last term in (26) cannot be negative. This is achieved if a \(\mathbf{{Y} }\) can be found so that \({\textsf {A}}^{*}\) is positive-definite everywhere in the body. The simplest choice would be \(\mathbf{Y }=\mathbf{0 }\), but it is only admissible if \({\textsf {A}}\) is positive-definite everywhere. The inequality is expanded with the help of (18) and (23):

$$\begin{aligned} \bar{\mathbf{D }}:\tilde{\textsf {C}}:\bar{\mathbf{D }}+\bar{\mathbf{T }}:\bar{\mathbf{L }}^T\cdot \bar{\mathbf{L }}-\mathbf{Y }:(\bar{\mathbf{L }}^2-\mathbf{1 }:\bar{\mathbf{L }}\,\,\bar{\mathbf{L }})\le \overline{\mathbf{D }:{\textsf {C}}:\mathbf{D }+\mathbf{T }:\mathbf{L }^T\cdot \mathbf{L }-\mathbf{Y }:(\mathbf{L }^2-\mathbf{1 }:\mathbf{L }\,\,\mathbf{L })}. \end{aligned}$$
(30)

Noting Eqs. (172) and (173) of Appendix B, we finally arrive at an upper bound to the overall incremental stiffness \(\tilde{\textsf {C}}\):

$$\begin{aligned} \bar{\mathbf{D }}:\tilde{\textsf {C}}:\bar{\mathbf{D }}\le \overline{\mathbf{D }:{\textsf {C}}:\mathbf{D }+\mathbf{T }:(\nabla \otimes \mathbf{u })\cdot (\mathbf{u }\otimes \nabla )}. \end{aligned}$$
(31)

The existence of a tensor \(\mathbf{{Y} }\) was necessary for the validity of this statement, but its value does not enter the inequality. If a tensor \(\mathbf{{Y} }\) cannot be found, then the right-hand side is surely an approximation of the left-hand side but not necessarily an upper bound.

Equation (26) reveals that the error of the bound is quadratic in the deviation field \(\mathbf{{z} }\).

The simplest assumption \(\mathbf{u }\equiv \mathbf{0 }\) yields the Voigt bound

$$\begin{aligned} \bar{\mathbf{D }}:\tilde{\textsf {C}}:\bar{\mathbf{D }}\le \bar{\mathbf{D }}:\bar{\textsf {C}}:\bar{\mathbf{D }}. \end{aligned}$$
(32)

It does not depend on the stress field \(\mathbf{T }\) and is hence identical with the classical expression of the unstressed state.

5 Construction of the lower bound

If \({\textsf {A}}^{*}\) is positive-definite, then (20) can be inverted:

$$\begin{aligned} \mathbf{L }_e ={\textsf {A}}^{*-1}:\mathbf{S }_e^{*}. \end{aligned}$$
(33)

An arbitrary dynamically admissible (i.e. solenoidal) pseudo-stress rate field can be written as

$$\begin{aligned} \mathbf{S }^{*} =\mathbf{S }^{*}_e +\mathbf{S }_z, \end{aligned}$$
(34)

where \(\mathbf{S }_z\in {{\mathscr {S}}}\) is the deviation from the exact field \(\mathbf{S }^{*}_e \). Then we study

$$\begin{aligned}&2\,\bar{\mathbf{L }}:\overline{\mathbf{S }^{*}} -\overline{\mathbf{S }^{*}:{\textsf {A}}^{*-1} :\mathbf{S }^{*}} = 2\,\bar{\mathbf{L }}:\overline{(\mathbf{S }^{*}_e+\mathbf{S }_z)} -\overline{(\mathbf{S }^{*}_e+\mathbf{S }_z):{\textsf {A}}^{*-1} :(\mathbf{S }^{*}_e+\mathbf{S }_z)}\nonumber \\&\quad =2\,\bar{\mathbf{L }}:\overline{\mathbf{S }^{*}_e} -\overline{\mathbf{S }^{*}_e:{\textsf {A}}^{*-1} :\mathbf{S }^{*}_e} +2\,\underbrace{\overline{(\bar{\mathbf{L }}-{\textsf {A}}^{*-1} :\mathbf{S }^{*}_e):\mathbf{S }_z}}-\overline{\mathbf{S }_z:{\textsf {A}}^{*-1} :\mathbf{S }_z}. \end{aligned}$$
(35)

The underbraced term vanishes since we have

$$\begin{aligned} \overline{(\bar{\mathbf{L }}-{\textsf {A}}^{*-1} :\mathbf{S }^{*}_e):\mathbf{S }_z} = \overline{(\bar{\mathbf{L }}-\mathbf{L }_e):\mathbf{S }_z}= -\,\overline{(\mathbf{u }_e\otimes \nabla ):\mathbf{S }_z}=0. \end{aligned}$$
(36)

The first and the second term can be rewritten by means of (28) and (33),

$$\begin{aligned} \overline{\mathbf{S }^{*}_e:{\textsf {A}}^{*-1} :\mathbf{S }^{*}_e}= \overline{\mathbf{L }_e:\mathbf{S }^{*}_e} =\bar{\mathbf{L }}:\overline{\mathbf{S }^{*}_e}=\bar{\mathbf{L }}:\tilde{\textsf {A}}^{*}:\bar{\mathbf{L }}. \end{aligned}$$
(37)

The last term cannot be negative since \({\textsf {A}}^{*-1} \) is positive-definite if \({\textsf {A}}^{*} \) is. So we arrive at the lower bound

$$\begin{aligned} 2\,\bar{\mathbf{L }}:\overline{\mathbf{S }^{*}} -\overline{\mathbf{S }^{*}:{\textsf {A}}^{*-1} :\mathbf{S }^{*}}\le \bar{\mathbf{L }}:\tilde{\textsf {A}}^{*}:\bar{\mathbf{L }}. \end{aligned}$$
(38)

Equation (35) reveals that the error of the bound is quadratic in the deviation field \(\mathbf{S }_z\).

A lower bound to the overall incremental stiffness \(\tilde{\textsf {C}}\) is obtained by means of (23):

$$\begin{aligned} 2\,\bar{\mathbf{L }}:\overline{\mathbf{S }^{*}} -\overline{\mathbf{S }^{*}:{\textsf {A}}^{*-1} :\mathbf{S }^{*}} -\bar{\mathbf{T }}:\bar{\mathbf{L }}^T\cdot \bar{\mathbf{L }}+\mathbf{Y }:(\bar{\mathbf{L }}^2-\mathbf{1 }:\bar{\mathbf{L }}\,\,\bar{\mathbf{L }})\le \bar{\mathbf{D }}:\tilde{\textsf {C}}:\bar{\mathbf{D }}. \end{aligned}$$
(39)

In contrast to the upper bound, this lower bound depends on the choice of the tensor \(\mathbf{Y }\), not only explicitly but also hidden in \({\textsf {A}}^{*-1} \). The simplest assumption \(\mathbf{S }^{*}={\text {const.}}\) yields the Reuss bound

$$\begin{aligned} 2\,\bar{\mathbf{L }}:\mathbf{S }^{*} -\mathbf{S }^{*}:\overline{{\textsf {A}}^{*-1}} :\mathbf{S }^{*} -\bar{\mathbf{T }}:\bar{\mathbf{L }}^T\cdot \bar{\mathbf{L }}+\mathbf{Y }:(\bar{\mathbf{L }}^2-\mathbf{1 }:\bar{\mathbf{L }}\,\,\bar{\mathbf{L }})\le \bar{\mathbf{D }}:\tilde{\textsf {C}}:\bar{\mathbf{D }}. \end{aligned}$$
(40)

Given some \(\bar{\mathbf{L }}\), the left-hand side is maximal if we have

$$\begin{aligned} 2\,\bar{\mathbf{L }}:\delta \mathbf{S }^{*} -2\,\mathbf{S }^{*}:\overline{{\textsf {A}}^{*-1}} :\delta \mathbf{S }^{*}=0 \end{aligned}$$
(41)

or

$$\begin{aligned} \overline{{\textsf {A}}^{*-1}} : \mathbf{S }^{*} = \bar{\mathbf{L }}\qquad \Longleftrightarrow \qquad \mathbf{S }^{*}= \Big (\overline{{\textsf {A}}^{*-1}}\Big )^{-1} : \bar{\mathbf{L }} \end{aligned}$$
(42)

and the bound becomes

$$\begin{aligned} \bar{\mathbf{L }}:\Big (\overline{{\textsf {A}}^{*-1}}\Big )^{-1} :\bar{\mathbf{L }} -\bar{\mathbf{T }}:\bar{\mathbf{L }}^T\cdot \bar{\mathbf{L }}+\mathbf{Y }:(\bar{\mathbf{L }}^2-\mathbf{1 }:\bar{\mathbf{L }}\,\,\bar{\mathbf{L }})\le \bar{\mathbf{D }}:\tilde{\textsf {C}}:\bar{\mathbf{D }}. \end{aligned}$$
(43)

The left-hand side depends not only on \(\bar{\mathbf{D }}\) but also on the spin \(\bar{\mathbf{W }}\) which should be chosen so that the left-hand side assumes its maximum value. This task is performed in Sect. 8.2.

6 Examination of the constitutive requirement

The constitutive requirement on which the construction of our bounds is based deserves further inspection. Actually, it consists of two distinct parts:

  1. 1.

    A local inequality that reads: A tensor \(\mathbf{{Y} }\) can be found such that

    $$\begin{aligned} \mathbf{L }: {\textsf {A}}^{*} :\mathbf{L } = \mathbf{L }:{\textsf {A}} :\mathbf{L }-\mathbf{Y }: \big (\mathbf{L }^2 -\mathbf{1 }:\mathbf{L }\;\mathbf{L }\big )>0 \qquad \mathrm{if}\qquad \mathbf{L }\ne \mathbf{0 }. \end{aligned}$$
    (44)
  2. 2.

    A global statement concerning the inhomogeneous body as a whole. It reads: The tensor \(\mathbf{{Y} }\) must be the same for all points. So it is a constant and not a field. Note that the fulfilment of this condition depends on the set \({\mathscr {A}}\) of the local stiffnesses \({\textsf {A}}\) of all the material elements but not on their geometric distribution. On the other hand, the geometry must be taken into account to obtain this set \({\mathscr {A}}\) itself.

The local inequality is intimately related to the concept of polyconvexity introduced by Ball [3] into the theory of finite elasticity. If the strain energy of a hyperelastic material element is polyconvex (at least with respect to the actual state), then the weakened form (with \(\ge \) instead of > ) of (44) , which may be called infinitesimal polyconvexity, is satisfied. So our constitutive requirement is the strengthened form of uniform infinitesimal polyconvexity.

An important implication of the local inequality is revealed if we choose \(\mathbf{{L} }\) in the form of a rank-1 tensor.

$$\begin{aligned}&\mathbf{L } = \mathbf{a }\otimes \mathbf{b }\quad \Longrightarrow \quad \mathbf{L }^2 -\mathbf{1 }:\mathbf{L }\;\mathbf{L }=\mathbf{0 }\quad \Longrightarrow \nonumber \\&\mathbf{a }\otimes \mathbf{b }: {\textsf {A}}^{*} :\mathbf{a }\otimes \mathbf{b } = \mathbf{a }\otimes \mathbf{b }:{\textsf {A}} :\mathbf{a }\otimes \mathbf{b }>0\qquad \mathrm{if}\qquad |\mathbf{a }||\mathbf{b }|\ne 0. \end{aligned}$$
(45)

This is the condition of strong ellipticity (S-E) which is thus seen to be valid throughout the body. If it is violated anywhere in the body, then there exists no tensor \(\mathbf{{Y} }\) to satisfy our local inequality. In special cases of symmetry the S-E condition is not only necessary but also sufficient for the existence of a local \({\mathbf{Y}}\). Anyhow, the validity of the S-E condition at each point is generally insufficient to ensure that \(\mathbf{{Y} }\) be the same throughout the body.

We learn from Eq. (28) that the constitutive requirement implies the overall incremental stiffness \(\tilde{\textsf {A}}^{*}\) to be positive-definite. Therefore the global constitutive law satisfies the S-E condition, too.

Moreover, the validity of the constitutive requirement implies the uniqueness of the microfield \(\mathbf{u }_e\) (in case of a problem of type 2 only up to a constant field). To show this, we assume the existence of two such fields. Their difference \(\mathbf{{z} }\) is an element of \({\mathscr {U}}\), and the corresponding pseudo-stress rate \(\mathbf{S }^{*}_z={\textsf {A}}^{*}:\mathbf{z }\otimes \nabla \) is an element of \({\mathscr {S}}\). Hence, according to equations (167) and (169) of Appendix B, we have

$$\begin{aligned} 0=\overline{\mathbf{S }^{*}_z:\mathbf{z }\otimes \nabla }=\overline{\mathbf{z }\otimes \nabla :{\textsf {A}}^{*}:\mathbf{z }\otimes \nabla }=\overline{\mathbf{z }\otimes \nabla :{\textsf {A}}:\mathbf{z }\otimes \nabla }. \end{aligned}$$
(46)

But this implies \(\mathbf{z }\equiv \)const. if \({\textsf {A}}^{*}\) is positive-definite everywhere. The same argument has previously been used by Hill [4] to establish uniqueness in special cases. The uniqueness of \(\mathbf{u }_e\) means that internal buckling (i.e. a bifurcation) of the body is prevented. It cannot, however, exclude finite snapthrough.

We obtained the following hierarchy of statements:

figure a

The thin symbol of implication (\(\longleftarrow \)) means that a strict inequality (>) implies a non-strict inequality (\(\ge \)). The theorem of van Hove [5] establishes the equivalence of local infinitesimal quasiconvexity and the Hadamard condition. Truesdell and Noll [6] (Eq. 68.b.18) even present a stronger result: If a homogeneous body is in a homogeneously strained configuration, the S-E condition is satisfied and the boundary is fixed, then only the trivial solution \(\mathbf{u }\equiv \mathbf{0 }\) exists. (They call such a state infinitesimally superstable. If only the weaker Hadamard condition is satisfied, they call it infinitesimally stable.) This implies that internal buckling is impossible at least with our problem of type 1.

The situation is surely not so simple with composites. When a global \(\mathbf{{Y} }\) can be found, then the global S-E condition is guaranteed and internal buckling prevented. If such a \(\mathbf{{Y} }\) cannot be found, however, we do not know whether a loss of global strong ellipticity will happen at all or when and the same is the case with internal buckling.

7 Treatment of cavities

We idealize the cavity as a component with a small stiffness and a small tensile stress:

$$\begin{aligned} {\textsf {C}}_c=\mu _c\, {\textsf {I}}\,,\qquad \mathbf{T }_c = \sigma _c\mathbf{1 }. \end{aligned}$$
(47)

The local inequality reads

$$\begin{aligned} \mu _c\, \mathbf{D }:\mathbf{D } +\sigma _c\,\mathbf{1 }:\mathbf{L }^T\cdot \mathbf{L } -\mathbf{Y }:(\mathbf{L }^2-\mathbf{1 }:\mathbf{L }\,\,\mathbf{L })>0. \end{aligned}$$
(48)

We use an orthonormal basis and discuss two choices:

$$\begin{aligned} \mathbf{L } = \mathbf{e}_1\otimes \mathbf{e }_2+ { \mathbf{e}}_2\otimes \mathbf{e }_1\quad \Longrightarrow \quad 2\mu _c +2 \sigma _c -y_{11}-y_{22}>0, \end{aligned}$$
(49)
$$\begin{aligned} \mathbf{L } = { \mathbf{e}}_1\otimes \mathbf{e }_2- { \mathbf{e}}_2\otimes \mathbf{e }_1\quad \Longrightarrow \quad 2 \sigma _c +y_{11}+y_{22}>0. \end{aligned}$$
(50)

This implies

$$\begin{aligned} -2\sigma _c<y_{11}+y_{22}< 2\mu _c +2 \sigma _c \end{aligned}$$
(51)

for any orthonormal basis. Since \(\mu _c\) and \(\sigma _c\) may be arbitrarily small, only \(\mathbf{Y }=\mathbf{0 }\) is possible. Our bounds are then applicable if \(\mathbf{Y }=\mathbf{0 }\) is admissible at all points, i.e. only in the special case where \({\textsf {A}}\) is positive-definite everywhere in the solid body.

The construction of a Reuss bound makes no sense since the only admissible constant solenoidal field is \(\mathbf{S }=\mathbf{0 }\).

8 A special geometry: reinforcement in one direction

8.1 Constitutive requirements

The material behaviour of both the matrix and the reinforcement—called component \(\#1\) and component \(\#2\), respectively—is assumed to be isotropic:

$$\begin{aligned} {\textsf {C}}_j = 2\mu _j{\textsf {I}}+\lambda _j \mathbf{1 }\otimes \mathbf{1 }\qquad j=1,2. \end{aligned}$$
(52)

The reinforcement consists of cylindrical fibres of various radii in the direction \(\mathbf{{e} }\) with total volume fraction c. The prestress is assumed to be constant in each of the two components. The fields

$$\begin{aligned} \mathbf{T }_j = t_0 \mathbf{1 } + {\check{t}}_j\,\mathbf{e }\otimes \mathbf{e }\qquad j=1,2 \end{aligned}$$
(53)

satisfy the condition of equilibrium. A suitable form of \(\mathbf{{Y} }\) is then

$$\begin{aligned} \mathbf{Y }=y_0\mathbf{1 } +{\check{y}} \,\mathbf{e }\otimes \mathbf{e }. \end{aligned}$$
(54)

The overall behaviour of the composite will be transversely isotropic. Therefore we need a special decomposition of our tensors. We introduce the identity in the plane normal to \(\mathbf{{e} }\)

$$\begin{aligned} \mathbf{1 }_p = \mathbf{1 }-\mathbf{e }\otimes \mathbf{e } \end{aligned}$$
(55)

and the plane parts of \(\mathbf{{D} }\) and of the symmetric part of \(\mathbf{S }^{*}\) and their plane deviators,

$$\begin{aligned} \mathbf{D }_p =\mathbf{1 }_p\cdot \mathbf{D }\cdot \mathbf{1 }_p = \hat{\mathbf{D }}_p +\frac{1}{2}\,\mathbf{1 }:\mathbf{D }_p\;\mathbf{1 }_p \qquad \mathrm{with}\qquad \mathbf{1 }:\hat{\mathbf{D }}_p =0, \end{aligned}$$
(56)
$$\begin{aligned} \mathbf{S }_p =\frac{1}{2}\mathbf{1 }_p\cdot \big ( \mathbf{S }^{*}+\mathbf{S }^{*\,T} \big )\cdot \mathbf{1 }_p = \hat{\mathbf{S }}_p +\frac{1}{2}\,\mathbf{1 }:\mathbf{S }_p\;\mathbf{1 }_p \qquad \mathrm{with}\qquad \mathbf{1 }:\hat{\mathbf{S }}_p =0. \end{aligned}$$
(57)

The decompositions are

$$\begin{aligned} \mathbf{L } = \mathbf{D }+\mathbf{W } = \hat{\mathbf{D }}_p+\frac{1}{2}\,\mathbf{1 }:\mathbf{D }_p\;\mathbf{1 }_p+d\,\mathbf{e }\otimes \mathbf{e } +\mathbf{d }\otimes \mathbf{e }+\mathbf{e }\otimes \mathbf{d } +w\,\mathbf{e }\times \mathbf{1 }+\mathbf{w }\otimes \mathbf{e }-\mathbf{e }\otimes \mathbf{w } \end{aligned}$$
(58)

with \(\mathbf{d }\cdot \mathbf{e }=0\) and \(\mathbf{w }\cdot \mathbf{e }=0\) and

$$\begin{aligned} \mathbf{S }^{*}=\hat{\mathbf{S }}_p +\frac{1}{2} \mathbf{1 }:\mathbf{S }_p\;\mathbf{1 }_p +s\,\mathbf{e }\otimes \mathbf{e }+\mathbf{p }\otimes \mathbf{e }+\mathbf{e }\otimes \mathbf{p } +\omega \,\mathbf{e }\times \mathbf{1 }+\mathbf{q }\otimes \mathbf{e }-\mathbf{e }\otimes \mathbf{q } \end{aligned}$$
(59)

with \(\mathbf{p }\cdot \mathbf{e }=0\) and \(\mathbf{q }\cdot \mathbf{e }=0\).

Noting (5) and (17) we arrive at the local constitutive law and its inverse:

$$\begin{aligned} \mathbf{S }^{*} = {\textsf {A}}^{*}:\mathbf{L }= & {} \alpha _1\,\hat{\mathbf{D }}_p +\big (\alpha _2\,\mathbf{1 }:\mathbf{D }_p +\alpha _3\,d\big )\;\mathbf{1 }_p+\big (\hat{\alpha _3}\,\mathbf{1 }:\mathbf{D }_p+\alpha _4\, d \big ) \,\mathbf{e }\otimes \mathbf{e }\nonumber \\&+\,\alpha _5\,\mathbf{d }\otimes \mathbf{e } + \alpha _6\,\mathbf{e }\otimes \,\mathbf{d }+\alpha _7\,w\,\mathbf{e }\times \mathbf{1 } +\alpha _8\,\mathbf{w } \otimes \mathbf{e } +\alpha _9\,\mathbf{e }\otimes \,\mathbf{w } \end{aligned}$$
(60)

with

$$\begin{aligned} \alpha _1=2 \mu +t_0-y_0\,,\qquad \alpha _2= \frac{1}{2}(2 \mu +2\lambda +t_0+y_0)\,,\qquad \alpha _3 ={\hat{\alpha }}_3=\frac{1}{2}( 2\lambda +2y_0+{\check{y}}), \end{aligned}$$
(61)
$$\begin{aligned} \alpha _4 = 2\mu +\lambda +t_0+{\check{t}}\,,\qquad \alpha _5 = \frac{1}{2}(4\mu +2t_0-2y_0-{\check{y}}+2{\check{t}})\,,\qquad \alpha _6 = \frac{1}{2}(4\mu +2t_0-2y_0-{\check{y}}), \end{aligned}$$
(62)
$$\begin{aligned} \alpha _7=t_0+y_0\,,\qquad \alpha _8 = \frac{1}{2}(2t_0+2y_0+{\check{y}}+2{\check{t}}) \,,\qquad \alpha _9 = -\,\frac{1}{2}(2t_0+2y_0+{\check{y}}) \end{aligned}$$
(63)
$$\begin{aligned} \Longrightarrow \quad \alpha _5-\alpha _6 = \alpha _8+\alpha _9 ={\check{t}} \end{aligned}$$
(64)

and

$$\begin{aligned} \mathbf{L } = {\textsf {A}}^{*-1}:\mathbf{S }^{*}= & {} \beta _1\,\hat{\mathbf{S }}_{p} + \big (\beta _2\,\mathbf{1 }:\mathbf{S }_{p}+\beta _3\,s\big )\;\mathbf{1 }_p +\big ({\hat{\beta }}_3\, \mathbf{1 }:\mathbf{S }_{p}+\beta _4 \,s\big )\mathbf{e }\otimes \mathbf{e } \nonumber \\&+ \beta _5\,\mathbf{p }\otimes \mathbf{e } + \beta _6\,\mathbf{e }\otimes \, \mathbf{p }+\beta _7\,\omega \,\mathbf{e }\times \mathbf{1 } +\beta _8\,\mathbf{q }\otimes \mathbf{e }+\beta _9\,\mathbf{e }\otimes \, \mathbf{q } \end{aligned}$$
(65)

with

$$\begin{aligned} \beta _1=\frac{1}{\alpha _1}\,,\qquad \beta _2=\frac{\alpha _4}{\Delta _1}\,,\qquad \beta _3 = -\,\frac{2\alpha _3}{\Delta _1}\,,\qquad {\hat{\beta }}_3 = -\,\frac{2{\hat{\alpha }}_3}{\Delta _1} \,,\qquad \beta _4 = \frac{4\alpha _2}{\Delta _1}, \end{aligned}$$
(66)
$$\begin{aligned} \beta _5 = -\,\frac{4 \alpha _9}{\Delta _2}\,,\qquad \beta _6 = \frac{4 \alpha _8}{\Delta _2}\,,\qquad \beta _7=\frac{1}{\alpha _7}\,,\qquad \beta _8 = \frac{4 \alpha _6}{\Delta _2}\,,\qquad \beta _9 = -\,\frac{4 \alpha _5}{\Delta _2}, \end{aligned}$$
(67)

and

$$\begin{aligned} \Delta _1 = 4 (\alpha _2\alpha _4-\alpha _3{\hat{\alpha }}_3)= \frac{1}{\beta _2\beta _4-\beta _3{\hat{\beta }}_3} \,,\qquad \Delta _2 = 2(\alpha _6\alpha _8-\alpha _5\alpha _9)=\frac{8}{\beta _6\beta _8-\beta _5\beta _9}. \end{aligned}$$
(68)

The distinction between \(\alpha _3\) and \({\hat{\alpha }}_3\) will only be needed later. Here we get

$$\begin{aligned} \mathbf{L }: {\textsf {A}}^{*} :\mathbf{L }= & {} \alpha _1\hat{\mathbf{D }}_p:\hat{\mathbf{D }}_p +\alpha _2(\mathbf{1 }:\mathbf{D }_p)^2 +2\,\alpha _3 \, \mathbf{1 }:\mathbf{D }_p\,d +\alpha _4\,d^2\nonumber \\&+\,(\alpha _5+\alpha _6)\mathbf{d }\cdot \mathbf{d }+2\,\alpha _7 \,w^2+(\alpha _5-\alpha _6+\alpha _8+\alpha _9)\mathbf{d }\cdot \mathbf{w } +(\alpha _8-\alpha _9)\mathbf{w }\cdot \mathbf{w }\nonumber \\= & {} \alpha _1\hat{\mathbf{D }}_p:\hat{\mathbf{D }}_p +\alpha _2\Big (\mathbf{1 }:\mathbf{D }_p +\frac{\alpha _3}{\alpha _2}\,d\Big )^2 + \frac{\Delta _1}{4\alpha _2}\,d^2+2\alpha _7 w^2 +(\alpha _8-\alpha _9) \Big (\mathbf{w } +\frac{\alpha _8+\alpha _9}{\alpha _8-\alpha _9}\,\mathbf{d }\Big )^2 +\frac{\Delta _2}{\alpha _8-\alpha _9}\,\mathbf{d }\cdot \mathbf{d }.\nonumber \\ \end{aligned}$$
(69)

Positive-definiteness of \({\textsf {A}}^{*}\) requires

$$\begin{aligned} \alpha _1>0\,,\qquad \alpha _2>0\,,\qquad \frac{\Delta _1}{4}=\alpha _2\alpha _4-\alpha _3^2>0\,,\qquad \alpha _7>0\,,\qquad \alpha _8-\alpha _9>0\,,\qquad \frac{\Delta _2}{2}=\alpha _6\alpha _8-\alpha _5\alpha _9>0.\nonumber \\ \end{aligned}$$
(70)

The restrictions on \(\alpha _1, \alpha _2, \alpha _7\) yield upper and lower bounds to \(y_0\). The third condition describes a region in the \(y_0,{\check{y}}\)-plane that is bounded by the following parabola branches:

$$\begin{aligned} {\check{y}} = -2 \lambda -2 y_0 \pm \sqrt{ 2(2\mu +\lambda +t_0+{\check{t}})y_0 +4(\mu +\lambda )(2\mu +\lambda +{\check{t}})+2(4\mu +3\lambda +t_0+{\check{t}})t_0}. \end{aligned}$$
(71)

The sixth condition describes a region in the \(y_0,{\check{y}}\)-plane that is bounded by the following two parallel lines:

$$\begin{aligned} {\check{y}} = -2 t_0-2 y_0 +2\Big (\mu +t_0 \pm \sqrt{ (\mu +t_0)(\mu +t_0 +{\check{t}})}\Big ). \end{aligned}$$
(72)

Both components must also satisfy the S-E conditions:

$$\begin{aligned} \mathbf{a }\otimes \mathbf{b } :{\textsf {A}}: \mathbf{a }\otimes \mathbf{b } = \mu \, \mathbf{a }\cdot \mathbf{a }\,\mathbf{b }\cdot \mathbf{b }+(\mu +\lambda ) (\mathbf{a }\cdot \mathbf{b })^2 +\mathbf{a }\cdot \mathbf{a }\,\big (t_0\,\mathbf{b }\cdot \mathbf{b }+{\check{t}}\, (\mathbf{b }\cdot \mathbf{e })^2\big )>0. \end{aligned}$$
(73)

We choose \(|\mathbf{a }|=|\mathbf{b }|=1\) and call \(\gamma \) the angle between \(\mathbf{{b} }\) and \(\mathbf{{a} }\) and \(\epsilon \) the angle between \(\mathbf{{b} }\) and \(\mathbf{{e} }\). Then

$$\begin{aligned} \mu +(\mu +\lambda ) \cos ^2\gamma +t_0+{\check{t}} \cos ^2\epsilon >0. \end{aligned}$$
(74)

This implies four inequalities,

$$\begin{aligned} \mu +t_0>0\,,\qquad 2\mu +\lambda +t_0>0\,,\qquad \mu +t_0+{\check{t}}>0\,,\qquad 2\mu +\lambda +t_0+{\check{t}} >0. \end{aligned}$$
(75)

Due to the first condition of (75) the fifth condition of (70) may be disregarded since it can never be more rigorous than the sixth condition.

Inequalities (70) and (75) must be satisfied for each of the two components separately. If it turns out that a contradiction exists between the conditions of the two components, then a tensor \(\mathbf{{Y} }\) cannot be found and our construction of bounds is not applicable. An example will be discussed in Sect. 9.1.

8.2 Voigt and Reuss bounds

We note

$$\begin{aligned} \bar{\mathbf{D }}:\bar{\mathbf{ D }} = {\hat{\bar{\mathbf{D }}}}_p:{\hat{\bar{\mathbf{D }}}}_p+\frac{1}{2} (\mathbf{1 }: \bar{\mathbf{D }}_p)^2+{\bar{d}}^2+2\,\bar{\mathbf{d }}\cdot \bar{\mathbf{d }} \,,\qquad \mathbf{1 }:\bar{\mathbf{ D }} = \mathbf{1 }: \bar{\mathbf{D }}_p+{\bar{d}}. \end{aligned}$$
(76)

The Voigt bound (32) is easily evaluated.

$$\begin{aligned} \bar{\mathbf{D }}:\tilde{\textsf {C}}:\bar{\mathbf{D }}\le & {} 2{\bar{\mu }}\bar{\mathbf{D }}:\bar{\mathbf{D }} +{\bar{\lambda }}(\mathbf{1 }:\bar{\mathbf{D }})^2 \nonumber \\= & {} \tau _1^{\mathrm{V}}{\hat{\bar{\mathbf{D }}}}_p:{\hat{\bar{\mathbf{D }}}}_p + \tau _2^{\mathrm{V}}(\mathbf{1 }:\bar{\mathbf{D }}_p)^2 + \tau _3^{\mathrm{V}}\, \mathbf{1 }:\bar{\mathbf{D }}_p\,{\bar{d}} + \tau _4^{\mathrm{V}}\,{\bar{d}}^2 + \tau _5^{\mathrm{V}}\bar{\mathbf{d }}\cdot \bar{\mathbf{d }} \end{aligned}$$
(77)

with

$$\begin{aligned} \tau _1^{\mathrm{V}}= 2{\bar{\mu }}\,,\qquad \tau _2^{\mathrm{V}}= {\bar{\mu }}+{\bar{\lambda }}\,,\qquad \tau _3^{\mathrm{V}}=2\,{\bar{\lambda }} \,,\qquad \tau _4^{\mathrm{V}} =2{\bar{\mu }}+{\bar{\lambda }}\,,\qquad \tau _5^{\mathrm{V}} =4{\bar{\mu }} \end{aligned}$$
(78)

and

$$\begin{aligned} {\bar{\mu }}=(1-c)\mu _1+ c\,\mu _2\,,\qquad {\bar{\lambda }}= (1- c)\lambda _1+ c\,\lambda _2. \end{aligned}$$
(79)

The Reuss bound (43) gives

$$\begin{aligned} \bar{\mathbf{D }}:\tilde{\textsf {C}}:\bar{\mathbf{D }}\ge & {} \epsilon {\hat{\bar{\mathbf{D }}}}_p:{\hat{\bar{\mathbf{D }}}}_p + \zeta \,(\mathbf{1 }:\bar{\mathbf{D }}_p)^2 +\eta \,\mathbf{1 }:\bar{\mathbf{D }}_p\,{\bar{d}} +\theta \,{\bar{d}}^2 \nonumber \\&+\,2 \underline{\big (\bar{\beta _7}^{-1}-t_0-y_0\big )} {\bar{w}}^2 +\phi \,\bar{\mathbf{d }}\cdot \bar{\mathbf{d }}+\chi \,\bar{\mathbf{d }}\cdot \bar{\mathbf{w }}+\psi \,\bar{\mathbf{w }}\cdot \bar{\mathbf{w }} \end{aligned}$$
(80)

with

$$\begin{aligned} \varepsilon =\bar{\beta _1}^{-1}-t_0+y_0 \end{aligned}$$
(81)

,

$$\begin{aligned} \zeta =\frac{1}{4}\Big (\bar{\beta _4}/(\bar{\beta _2}\bar{\beta _4}-{\bar{\beta }}_3\bar{{\hat{\beta }}}_3)-2 t_0-2y_0\Big ), \end{aligned}$$
(82)
$$\begin{aligned} \eta =-\frac{1}{2} \Big (({\bar{\beta }}_3+\bar{{\hat{\beta }}}_3)/(\bar{\beta _2}\bar{\beta _4}-{\bar{\beta }}_3\bar{{\hat{\beta }}}_3)+4y_0+2{\check{y}}\Big ), \end{aligned}$$
(83)
$$\begin{aligned} \theta =\bar{\beta _2}/(\bar{\beta _2}\bar{\beta _4}-{\bar{\beta }}_3\bar{{\hat{\beta }}}_3)-t_0-\bar{{\check{t}}}, \end{aligned}$$
(84)
$$\begin{aligned} \phi \equiv 2\big (\bar{\beta _8} -\bar{\beta _9}\big ) /(\bar{\beta _6}\bar{\beta _8}-\bar{\beta _5}\bar{\beta _9})-2t_0-\bar{{\check{t}}}+2y_0+{\check{y}}, \end{aligned}$$
(85)
$$\begin{aligned} \chi \equiv 2\big (-\bar{\beta _8} -\bar{\beta _9}+\bar{\beta _6} -\bar{\beta _5}\big ) /(\bar{\beta _6}\bar{\beta _8}-\bar{\beta _5}\bar{\beta _9})-2\bar{{\check{t}}}, \end{aligned}$$
(86)
$$\begin{aligned} \psi \equiv 2\big (\bar{\beta _5} +\bar{\beta _6}\big ) /(\bar{\beta _6}\bar{\beta _8}-\bar{\beta _5}\bar{\beta _9})-2t_0-\bar{{\check{t}}}-2y_0-{\check{y}}, \end{aligned}$$
(87)

and

$$\begin{aligned} \bar{{\check{t}}} = (1-c) {\check{t}}_1 +c\, {\check{t}}_2. \end{aligned}$$
(88)

The expression does not only depend on \(\bar{\mathbf{D }}\) but also on \(\bar{\mathbf{W }}\). The underlined term vanishes, however. The maximum is achieved if we choose \(\chi \,\bar{\mathbf{d }}+2 \psi \,\bar{\mathbf{w }}=\mathbf{0 }\). Then the last three terms of (80) become

$$\begin{aligned} \Big (\phi -\frac{\chi ^2}{4\psi }\Big )\,\bar{\mathbf{d }}\cdot \bar{\mathbf{d }}. \end{aligned}$$
(89)

This expression is indefinite in the case \({\check{t}}\equiv \)const. which implies \(\chi =\psi =0\). This is especially irritating if we want to investigate the stress-free state \(\mathbf{T }\equiv \mathbf{0 }\). The problem is easily avoided if we apply a slightly modified \({\check{t}}\).

So we arrive at

$$\begin{aligned} \bar{\mathbf{D }}:\tilde{\textsf {C}}:\bar{\mathbf{D }} \ge \tau _1^{\mathrm{R}}{\hat{\bar{\mathbf{D }}}}_p:{\hat{\bar{\mathbf{D }}}}_p + \tau _2^{\mathrm{R}}(\mathbf{1 }:\bar{\mathbf{D }}_p)^2 + \tau _3^{\mathrm{R}}\, \mathbf{1 }:\bar{\mathbf{D }}_p\,{\bar{d}} + \tau _4^{\mathrm{R}}\,{\bar{d}}^2 + \tau _5^{\mathrm{R}}\bar{\mathbf{d }}\cdot \bar{\mathbf{d }} \end{aligned}$$
(90)

with

$$\begin{aligned} \tau _1^{\mathrm{R}}= \epsilon \,,\qquad \tau _2^{\mathrm{R}}= \zeta \,,\qquad \tau _3^{\mathrm{R}}=\eta \,,\qquad \tau _4^{\mathrm{R}} =\theta \,,\qquad \tau _5^{\mathrm{R}} =\phi -\frac{\chi ^2}{4\psi }. \end{aligned}$$
(91)

8.3 The kinematic approach

Now we allow a microdisplacement \(\mathbf{{u} }\):

$$\begin{aligned} \mathbf{L } =\mathbf{D }+\mathbf{W }= \bar{\mathbf{L }}+\mathbf{u }\otimes \nabla =\bar{\mathbf{D }}+ \bar{\mathbf{W }}+\mathbf{u }\otimes \nabla . \end{aligned}$$
(92)

We first consider one single cylindrical wire of radius R in an infinite matrix and use cylindrical co-ordinates with local basis \(\mathbf{e }_r, \mathbf{e }_{\phi },\mathbf{e }\). The deformation of the matrix shall be influenced by the reinforcement within a cylinder of radius \(\xi R\). We are interested in the case where the reinforcement is very stiff. It cannot but undergo an extension in the direction of \(\mathbf{{e} }\) accompanied by a lateral contraction characterized by Poisson’s ratio

$$\begin{aligned} \nu =\frac{\lambda _2}{2(\mu _2+\lambda _2)}. \end{aligned}$$
(93)

This means

$$\begin{aligned} \mathbf{u } =\frac{f(r)}{r} \mathbf{K }\cdot \mathbf{r }\quad \mathrm{with}\quad \mathbf{K } = -(\mathbf{1 }+\mathbf{e }\otimes \mathbf{e })\cdot \bar{\mathbf{D }}\cdot \mathbf{1 }_p -\nu \, \mathbf{e }\cdot \bar{\mathbf{D }}\cdot \mathbf{e }\;\mathbf{1 }_p = \,-\,\bigg ({\hat{\bar{\mathbf{D }}}}_p +\Big (\frac{1}{2}\mathbf{1 }:\bar{\mathbf{D }}_p +\nu {\bar{d}} \Big )\,\mathbf{1 }_p+2\mathbf{e }\otimes \bar{\mathbf{d }}\bigg )\nonumber \\ \end{aligned}$$
(94)

and

$$\begin{aligned} \mathbf{u }\otimes \nabla= & {} \frac{f(r)}{r}\mathbf{K }\cdot (\mathbf{r }\otimes \nabla )+ \mathbf{K }\cdot \mathbf{r }\otimes \nabla \Big (\frac{f(r)}{r}\Big ) = \frac{f(r)}{r}\mathbf{K }+\mathbf{K }\cdot \mathbf{e }_r\otimes \mathbf{e }_r \;r \Big (\frac{f(r)}{r}\Big )'\nonumber \\= & {} \mathbf{K }\cdot \Big (f'\mathbf{e }_r\otimes \mathbf{e }_r +\frac{f}{r}\mathbf{e }_{\phi }\otimes \mathbf{e }_{\phi }\Big ). \end{aligned}$$
(95)

We choose

$$\begin{aligned} f(r)=\left\{ \begin{array}{l l l} r &{} : &{}\quad 0\le r\le R \quad (\mathrm{wire\, zone}),\\ R\Big (\frac{\xi R -r}{\xi R -R}\Big )^2&{} : &{}\quad R\le r\le \xi R \quad (\mathrm{transition\, zone}),\\ 0&{} : &{}\quad \xi R\le r\quad (\mathrm{far\, zone}). \end{array}\right. \end{aligned}$$
(96)

Within the wire we have

$$\begin{aligned} \mathbf{u }\otimes \nabla =\mathbf{K }\,,\qquad \mathbf{D } = \bar{\mathbf{D }} +\mathrm{sym}\,[\mathbf{K }]= {\bar{d}}\Big ( \mathbf{e }\otimes \mathbf{e }-\nu \,\mathbf{1 }_p\Big ), \end{aligned}$$
(97)

and far away

$$\begin{aligned} \mathbf{D }=\bar{\mathbf{D }}. \end{aligned}$$
(98)

We want to evaluate the upper bound according to (31):

$$\begin{aligned} \bar{\mathbf{D }}:\tilde{\textsf {C}}:\bar{\mathbf{D }}\le & {} \overline{\mathbf{D }:{\textsf {C}}:\mathbf{D } + \mathbf{T }: (\nabla \otimes \mathbf{u })\cdot (\mathbf{u }\otimes \nabla )}\nonumber \\= & {} \overline{2\mu \,\mathbf{D }:\mathbf{D } +\lambda (\mathbf{1 }:\mathbf{D })^2+ \mathbf{T }: (\nabla \otimes \mathbf{u })\cdot (\mathbf{u }\otimes \nabla )}\nonumber \\= & {} 2\,{\bar{\mu }}\,\bar{\mathbf{D }}:\bar{\mathbf{D }} +4\,\bar{\mathbf{D }}:\overline{\mu \, \mathrm{sym}[\mathbf{u }\otimes \nabla ]} +2\,\overline{\mu \, \mathrm{sym}[\mathbf{u }\otimes \nabla ]:\mathrm{sym}[\mathbf{u }\otimes \nabla ]}\nonumber \\&+\, {\bar{\lambda }}(\mathbf{1 }:\bar{\mathbf{D }})^2+2 (\mathbf{1 }:\bar{\mathbf{D }})\overline{\lambda \, \mathbf{1 }:\mathrm{sym}[\mathbf{u }\otimes \nabla ]} +\overline{\lambda \,(\mathbf{1 }:\mathrm{sym}[\mathbf{u }\otimes \nabla ])^2}\nonumber \\&+\,\overline{ \mathbf{T }: (\nabla \otimes \mathbf{u })\cdot (\mathbf{u }\otimes \nabla )}. \end{aligned}$$
(99)

Consider a cross section normal to \(\mathbf{{e} }\) with total area A. The areas of the wire zones, the transition zones, and the far zone are

$$\begin{aligned} \sum A_w = c\, A\,,\qquad \sum A_t =(\xi ^2-1)\, c\, A\,,\qquad A_f = (1-c\,\xi ^2) A. \end{aligned}$$
(100)

The mean value of some function \(\Phi \) can be composed of the mean values of the three zones,

$$\begin{aligned} {\bar{\Phi }} = c\, {\bar{\Phi }}_w+(\xi ^2-1)\,c \,{\bar{\Phi }}_t +(1-c\,\xi ^2){\bar{\Phi }}_f. \end{aligned}$$
(101)

The condition \(A_f > 0\) requires \(c\,\xi ^2<1\). In the special case of a regular hexagonal arrangement of wires with identical radius we even have \(c\xi ^2 <\pi /(2\sqrt{3})\). We will later on perform our examples with \(\xi =2.5\). This value is applicable if the volume fraction c of the reinforcement is not much greater than \(10\%\).

We make use of the results of Appendix C and find

$$\begin{aligned} \overline{\mu \, \mathrm{sym}[\mathbf{u }\otimes \nabla ]} =-\,c\big (\mu _1-\mu _2\big )\mathrm{sym}\,[\mathbf{K }], \end{aligned}$$
(102)
$$\begin{aligned} \mathbf{1 }:\overline{\lambda \, \mathrm{sym}[\mathbf{u }\otimes \nabla ]} =-\,c\big (\lambda _1-\lambda _2\big )\mathbf{1 }:\mathbf{K }, \end{aligned}$$
(103)
$$\begin{aligned} \overline{\mu \, \mathrm{sym}[\mathbf{u }\otimes \nabla ]:\mathrm{sym}[\mathbf{u }\otimes \nabla ]}= -c(\mu _1-\mu _2)\mathrm{sym}\,[\mathbf{K }]:\mathrm{sym}\,[\mathbf{K }]+c\mu _1 k(\xi )\frac{1}{8}\big (5\mathbf{K }:\mathbf{K } +\mathbf{K }^T:\mathbf{K }+(\mathbf{1 }_p:\mathbf{K })^2\big ),\nonumber \\ \end{aligned}$$
(104)
$$\begin{aligned} \overline{\lambda \,\big (\mathbf{1 }: \mathrm{sym}[\mathbf{u }\otimes \nabla ]\big )^2}=-c(\lambda _1-\lambda _2)(\mathbf{1 }_p:\mathbf{K })^2 +c\lambda _1 k(\xi )\frac{1}{4}\Big (2\mathrm{sym}\,[\mathbf{K }]:\mathrm{sym}\,[\mathbf{K }] +(\mathbf{1 }_p:\mathbf{K })^2\Big ), \end{aligned}$$
(105)
$$\begin{aligned} \overline{ \mathbf{T }: (\nabla \otimes \mathbf{u })\cdot (\mathbf{u }\otimes \nabla )}= & {} t_0 \;\overline{ (\mathbf{u }\otimes \nabla ):(\mathbf{u }\otimes \nabla )}\nonumber \\&= c\, t_0\,k(\xi )\mathbf{K }:\mathbf{K }. \end{aligned}$$
(106)

Noting the representation (94) of \(\mathbf{{K} }\) we finally arrive at the upper bound

$$\begin{aligned} \bar{\mathbf{D }}:\tilde{\textsf {C}}:\bar{\mathbf{D }} \le \tau _1^{\mathrm{K}}{\hat{\bar{\mathbf{D }}}}_p:{\hat{\bar{\mathbf{D }}}}_p + \tau _2^{\mathrm{K}}(\mathbf{1 }:\bar{\mathbf{D }}_p)^2 + \tau _3^{\mathrm{K}}\, \mathbf{1 }:\bar{\mathbf{D }}_p\,{\bar{d}} + \tau _4^{\mathrm{K}}\,{\bar{d}}^2 + \tau _5^{\mathrm{K}}\bar{\mathbf{d }}\cdot \bar{\mathbf{d }}. \end{aligned}$$
(107)

with

$$\begin{aligned}&\tau _1^{\mathrm{K}}=2\mu _1+\frac{1}{2} c k(\xi )(3\mu _1+\lambda _1+2t_0\big )\,,\quad \tau _2^{\mathrm{K}}=\mu _1+\lambda _1+\frac{1}{2} ck(\xi )(2\mu _1+\lambda _1+t_0\big ),\nonumber \\&\tau _3^{\mathrm{K}}=2\lambda _1 +2\nu c k(\xi )(2\mu _1+\lambda _1+t_0), \end{aligned}$$
(108)
$$\begin{aligned} \tau _4^{\mathrm{K}}=(1-c)(2\mu _1+\lambda _1)+c(2\mu _2+\lambda _2)+4 \nu c(\lambda _1-\lambda _2) +2 \nu ^2 c\big ( k(\xi )(2\mu _1+\lambda _1+t_0)+2(\mu _2+\lambda _2-\mu _1-\lambda _1)\big ),\nonumber \\ \end{aligned}$$
(109)
$$\begin{aligned} \tau _5^{\mathrm{K}}=4 \mu _1 +ck(\xi )\big (5 \mu _1+\lambda _1+4 t_0\big ). \end{aligned}$$
(110)

We see that smaller values of \(k(\xi )\) produce better bounds. Good results are obtained with \(\xi =2.5\),  \(k(\xi )=2.468\). (If \(\xi >2.5\), then \(k(\xi )\) is only slightly decaying and reaches its minimum \(k(4.69)=2.19\), but large values of \(\xi \) require very small volume fractions c.)

8.4 The dynamic approach

We remember the first two terms of (39):

$$\begin{aligned} \Psi \equiv 2\,\bar{\mathbf{L }}:\overline{\mathbf{S }^{*}}-\overline{\mathbf{S }^{*}:{\textsf {A}}^{*-1} :\mathbf{S }^{*}}. \end{aligned}$$
(111)

We introduce the following solenoidal field:

$$\begin{aligned} \mathbf{S }_1^{*}=\mathbf{Z }={\text {const.}}\,,\qquad \mathbf{S }_2^{*}=\mathbf{Z }+\sigma \mathbf{e }\otimes \mathbf{e }={\text {const.}} \end{aligned}$$
(112)

and find

$$\begin{aligned} \Psi =2\,\bar{\mathbf{L }}:\mathbf{Z } -\mathbf{Z }:\overline{{\textsf {A}}^{*-1}} :\mathbf{Z }+2 c \sigma {\bar{d}}-2c\sigma \mathbf{e }\otimes \mathbf{e }:{\textsf {A}}_2^{*-1} :\mathbf{Z }-c \sigma ^2 \mathbf{e }\otimes \mathbf{e }:{\textsf {A}}_2^{*-1} :\mathbf{e }\otimes \mathbf{e }. \end{aligned}$$
(113)

The maximum is achieved if we choose

$$\begin{aligned} \sigma = \frac{1}{N} \Big ( {\bar{d}}-\mathbf{e }\otimes \mathbf{e }:{\textsf {A}}_2^{*-1} :\mathbf{Z }\Big )\qquad \mathrm{with}\qquad N = \mathbf{e }\otimes \mathbf{e }:{\textsf {A}}_2^{*-1} :\mathbf{e }\otimes \mathbf{e }. \end{aligned}$$
(114)

It becomes

$$\begin{aligned} \Psi = 2\,\bar{\mathbf{L }}:\mathbf{Z } -\mathbf{Z }:\overline{{\textsf {A}}^{*-1}} :\mathbf{Z }+c \frac{1}{N} \Big ( {\bar{d}}-\mathbf{e }\otimes \mathbf{e }:{\textsf {A}}_2^{*-1} :\mathbf{Z }\Big )^2. \end{aligned}$$
(115)

Now varying \(\mathbf{{Z} }\), the maximum of this expression is found if we have

$$\begin{aligned} \bar{\mathbf{L }} -\overline{{\textsf {A}}^{*-1}} : \mathbf{Z } -c \frac{1}{N}\Big ( {\bar{d}}-\mathbf{e }\otimes \mathbf{e }:{\textsf {A}}_2^{*-1} :\mathbf{Z }\Big )\mathbf{e }\otimes \mathbf{e }:{\textsf {A}}_2^{*-1} =\mathbf{0 }. \end{aligned}$$
(116)

We perform a double contraction with \(\mathbf{{Z} }\) and subtract the result from (115) to find a simpler form of the maximum value:

$$\begin{aligned} \Psi = \bar{\mathbf{L }}:\mathbf{Z } +c\frac{1}{N}\Big ({\bar{d}}- \mathbf{e }\otimes \mathbf{e }:{\textsf {A}}_2^{*-1}:{\mathbf{Z }}\Big ){\bar{d}}.\nonumber \\ \end{aligned}$$
(117)

The representation (65) implies

$$\begin{aligned} {\textsf {A}}^{*-1}:\mathbf{e }\otimes \mathbf{e }=\beta _3\, \mathbf{1 }_p+\beta _4 \,\mathbf{e }\otimes \mathbf{e }, \end{aligned}$$
(118)
$$\begin{aligned} N= \mathbf{e }\otimes \mathbf{e }:{\textsf {A}}^{*-1}:\mathbf{e }\otimes \mathbf{e }=\beta _4, \end{aligned}$$
(119)
$$\begin{aligned} \mathbf{e }\otimes \mathbf{e }:{\textsf {A}}^{*-1}:\mathbf{Z }=\beta _3 \,\mathbf{1 }:\mathbf{Z }_p + \beta _4 \,\mathbf{e }\cdot \mathbf{Z }\cdot \mathbf{e }, \end{aligned}$$
(120)
$$\begin{aligned} \mathbf{1 }_p:{\textsf {A}}^{*-1}:\mathbf{Z }= 2 \,\beta _2 \,\mathbf{1 }_p:\mathbf{Z }+2\,{\hat{\beta }}_3\, \mathbf{e }\cdot \mathbf{Z }\cdot \mathbf{e }. \end{aligned}$$
(121)

We write \(\beta _{j (1)}\) or \(\beta _{j (2)}\) in order to discern the \(\beta \)-values of the two components.

The double contraction of (116) with \(\mathbf{e }\otimes \mathbf{e }\) yields

$$\begin{aligned} {\bar{d}} =\beta _{3(1)} \mathbf{1 }:\mathbf{Z }_p +\beta _{4(1)} \mathbf{e }\cdot \mathbf{Z }\cdot \mathbf{e }. \end{aligned}$$
(122)

Then (116) becomes

$$\begin{aligned} \bar{\mathbf{L }} =\Big ((1-c){\textsf {A}}_1^{*-1}+c{\textsf {A}}_2^{*-1}\Big ):\mathbf{Z } +c\Big (\frac{\beta _{3(2)}}{\beta _{4(2)}} \mathbf{1 }_p+\mathbf{e }\otimes \mathbf{e }\Big )\Big (\big (\beta _{3(1)}-\beta _{3(2)}\big ) \mathbf{1 }:\mathbf{Z }_p + \big (\beta _{4(1)}-\beta _{4(2)}\big ) \mathbf{e }\cdot \mathbf{Z }\cdot \mathbf{e }\Big ).\nonumber \\ \end{aligned}$$
(123)

Making use of (65) we can write

$$\begin{aligned} \bar{\mathbf{L }}= & {} \beta ^{\dagger }_1\,\hat{\mathbf{Z }}_{p} + \big (\beta ^{\dagger }_2\,\mathbf{1 }:\mathbf{Z }_{p}+\beta _3^{\dagger }\,\mathbf{e }\cdot \mathbf{Z }\cdot \mathbf{e }\big )\;\mathbf{1 }_p \nonumber \\&+\,\big ({\hat{\beta }}^{\dagger }_3\, \mathbf{1 }:\mathbf{Z }_{p}+\beta _4^{\dagger } \,\mathbf{e }\cdot \mathbf{Z }\cdot \mathbf{e }\big )\mathbf{e }\otimes \mathbf{e } + \beta _5^{\dagger }\,\mathbf{p }\otimes \mathbf{e } + \beta _6^{\dagger }\,\mathbf{e }\otimes \, \mathbf{p }+\beta _7^{\dagger }\,\omega \,\mathbf{e }\times \mathbf{1 } +\beta _8^{\dagger }\,\mathbf{q }\otimes \mathbf{e }+\beta _9^{\dagger }\,\mathbf{e }\otimes \, \mathbf{q }.\nonumber \\ \end{aligned}$$
(124)

with

$$\begin{aligned}&\beta _1^{\dagger }={\bar{\beta }}_1\,,\qquad \beta _2^{\dagger }={\bar{\beta }}_2+ c\frac{\beta _{3(2)}}{\beta _{4(2)}}\big (\beta _{3(1)}-\beta _{3(2)}\big ) \,,\qquad \beta _3^{\dagger }={\bar{\beta }}_3+ c\frac{\beta _{3(2)}}{\beta _{4(2)}}\big (\beta _{4(1)}-\beta _{4(2)}\big ),\nonumber \\&\qquad {\hat{\beta }}_3^{\dagger }=\bar{{\hat{\beta }}}_3+ c\big (\beta _{3(1)}-\beta _{3(2)}\big )=\beta _{3(1)}, \end{aligned}$$
(125)
$$\begin{aligned} \beta _4^{\dagger }={\bar{\beta }}_4 + c\big (\beta _{4(1)}-\beta _{4(2)}\big )=\beta _{4(1)}\,,\qquad \beta _5^{\dagger }={\bar{\beta }}_5\,,\qquad \beta _6^{\dagger }={\bar{\beta }}_6\,,\qquad \beta _7^{\dagger }={\bar{\beta }}_7\,,\qquad \beta _8^{\dagger }={\bar{\beta }}_8\,,\qquad \beta _9^{\dagger }={\bar{\beta }}_9.\nonumber \\ \end{aligned}$$
(126)

We also need

$$\begin{aligned} \frac{1}{2}\mathbf{1 }:\bar{\mathbf{D }}_p =\beta ^{\dagger }_{2} \mathbf{1 }:\mathbf{Z }_p + \beta ^{\dagger }_{3} \mathbf{e }\cdot \mathbf{Z }\cdot \mathbf{e }, \end{aligned}$$
(127)

and, together with (122), find

$$\begin{aligned} \mathbf{1 }:\mathbf{Z }_p = \Delta _1^{\dagger }\Big (-\beta _3^{\dagger }{\bar{d}}+\frac{1}{2}\beta ^{\dagger }_{4}\mathbf{1 }:\bar{\mathbf{D }}_p \Big ). \end{aligned}$$
(128)
$$\begin{aligned} \mathbf{e }\cdot \mathbf{Z }\cdot \mathbf{e } = \Delta _1^{\dagger }\Big (\beta _2^{\dagger }{\bar{d}}-\frac{1}{2}{\hat{\beta }}^{\dagger }_{3}\mathbf{1 }:\bar{\mathbf{D }}_p \Big ). \end{aligned}$$
(129)

with

$$\begin{aligned} \Delta _1^{\dagger }=\frac{1}{ \beta _2^{\dagger }\beta ^{\dagger }_{4}-\beta _3^{\dagger }{\hat{\beta }}^{\dagger }_{3}}. \end{aligned}$$
(130)

We introduce this into the second term of (117) and arrive at

$$\begin{aligned} \Psi = \bar{\mathbf{L }}:\mathbf{Z }+\frac{c}{2}\Delta _1^{\dagger }\Big ({\hat{\beta }}_3^{\dagger }- \frac{\beta _{3(2)}}{\beta _{4(2)}}\beta _4^{\dagger }\Big )\mathbf{1 }:\bar{\mathbf{D }}_p{\bar{d}} +c \bigg (\frac{1}{\beta _{4(2)}}+ \Delta _1^{\dagger }\Big (\frac{\beta _{3(2)}}{\beta _{4(2)}}\beta _3^{\dagger }-\beta _2^{\dagger }\Big )\bigg ){\bar{d}}^2. \end{aligned}$$
(131)

The first term is that of the Reuss bound with \(\mathbf{S }^{*}\equiv \mathbf{Z }\), cf. (42), (43). The values \({\bar{\beta }}\) have only to be replaced by \(\beta ^{\dagger }\). We define

$$\begin{aligned} \zeta ^{\dagger }=\frac{1}{4}\Big (\Delta _1^{\dagger }{\beta _4}^{\dagger }-2 t_0-2y_0\Big ), \end{aligned}$$
(132)
$$\begin{aligned} \eta ^{\dagger }=-\frac{1}{2} \Delta _1^{\dagger }({\beta }_3^{\dagger }+{\hat{\beta }}_3^{\dagger }) -2y_0-{\check{y}} +\frac{c}{2}\Delta _1^{\dagger }\Big ({\hat{\beta }}_3^{\dagger }- \frac{\beta _{3(2)}}{\beta _{4(2)}}\beta _4^{\dagger }\Big ), \end{aligned}$$
(133)
$$\begin{aligned} \theta ^{\dagger }=\Delta _1^{\dagger }{\beta _2^{\dagger }}-t_0-\bar{{\check{t}}} +c \bigg (\frac{1}{\beta _{4(2)}}+ \Delta _1^{\dagger }\Big (\frac{\beta _{3(2)}}{\beta _{4(2)}}\beta _3^{\dagger }-\beta _2^{\dagger }\Big )\bigg ), \end{aligned}$$
(134)

and arrive at the lower bound

$$\begin{aligned} \bar{\mathbf{D }}:\tilde{\textsf {C}}:\bar{\mathbf{D }} \ge \tau _1^{\mathrm{D}}{\hat{\bar{\mathbf{D }}}}_p:{\hat{\bar{\mathbf{D }}}}_p + \tau _2^{\mathrm{D}}(\mathbf{1 }:\bar{\mathbf{D }}_p)^2 + \tau _3^{\mathrm{D}}\, \mathbf{1 }:\bar{\mathbf{D }}_p\,{\bar{d}} + \tau _4^{\mathrm{D}}\,{\bar{d}}^2 + \tau _5^{\mathrm{D}}\bar{\mathbf{d }}\cdot \bar{\mathbf{d }}. \end{aligned}$$
(135)

with

$$\begin{aligned} \tau _1^{\mathrm{D}}= \epsilon \,,\qquad \tau _2^{\mathrm{D}}= \zeta ^{\dagger }\,,\qquad \tau _3^{\mathrm{D}}=\eta ^{\dagger } \,,\qquad \tau _4^{\mathrm{D}} =\theta ^{\dagger }\,,\qquad \tau _5^{\mathrm{D}} =\phi -\frac{\chi ^2}{4\psi }. \end{aligned}$$
(136)

9 Examples

We construct upper and lower bounds for several values of stiffness and stress. The coefficients \(\tau _1\) to \(\tau _5\) are not appropriate for a comparison of the bounds. We make use of the proper numbers, derived from \(\tau _2\), \(\tau _3\), and \(\tau _4\), instead, and define

$$\begin{aligned} {\tilde{\varrho }}_1 = \frac{1}{2}\bigg (\tau _2+\tau _4+\sqrt{(\tau _2-\tau _4)^2+\tau _3^2}\bigg )\,,\qquad {\tilde{\varrho }}_2 = \frac{1}{2}\bigg (\tau _2+\tau _4-\sqrt{(\tau _2-\tau _4)^2+\tau _3^2}\bigg )\,,\qquad {\tilde{\varrho }}_3=\tau _1\,,\qquad {\tilde{\varrho }}_4=\tau _5.\nonumber \\ \end{aligned}$$
(137)

These coefficients depend on the volume fraction c of the reinforcement. They are better understood if we refer them to the values at \(c=0\):

$$\begin{aligned} \varrho _j (c)= \frac{{\tilde{\varrho }}_j (c)}{|{\tilde{\varrho }}_j (0)|}\qquad j=1\ldots 4. \end{aligned}$$
(138)

The first two coefficients describe the behaviour under combinations of the stretchings \(\mathbf{1 }:\bar{\mathbf{D }}_p\;\mathbf{1 }_p\) and \({\bar{d}}=\mathbf{e }\cdot \bar{\mathbf{D }}\cdot \mathbf{e }\) and the last two the behaviour under the shearings \({\hat{\bar{\mathbf{D }}}}_p\) and \(\bar{\mathbf{d }}\otimes \mathbf{e }+\mathbf{e }\otimes \bar{\mathbf{d }}\), respectively.

9.1 Uniaxial stress

We choose

$$\begin{aligned} 20 \mu _1 =10\lambda _1 = \lambda _2=2\mu _2. \end{aligned}$$
(139)

So the stiffness of the reinforcement is ten times the stiffness of the matrix and Poisson’s ratio of the two components—cf. (93)—is the same,

$$\begin{aligned} \nu _1=\nu _2 =\frac{1}{3}. \end{aligned}$$
(140)

We assume the existence of a normal stress in the direction of \(\mathbf{e }\), proportional to the local stiffness:

$$\begin{aligned} t_0=0\,,\qquad {\check{t}}_1 =\varepsilon \mu _1\,,\qquad {\check{t}}_2 =\varepsilon \mu _2\quad \Longrightarrow \quad \bar{\mathbf{T }} = \varepsilon {\bar{\mu }}\mathbf{e }\otimes \mathbf{e }. \end{aligned}$$
(141)

We infer from (72)

$$\begin{aligned} \mu _2\big (1-\sqrt{1+\varepsilon }\big )<y0+{\check{y}}/2<\mu _1\big (1+\sqrt{1+\varepsilon }\big ). \end{aligned}$$
(142)

This implies

$$\begin{aligned} \sqrt{1+\varepsilon }>\frac{\mu _2-\mu _1}{\mu _2+\mu _1}\quad \Longrightarrow \quad \varepsilon >-\frac{4\mu _2/\mu _1}{(1+\mu _2/\mu _1)^2}=-0.3305. \end{aligned}$$
(143)

If the uniaxial stress \({\check{t}}\) is compressive, then a tensor \(\mathbf{Y}\) can only exist if \(\epsilon \) is not smaller than this critical value. Otherwise internal buckling cannot be excluded as we have seen in Sect. 6 and the construction of our bounds is not applicable.

We consider the critical case and infer from (71)

$$\begin{aligned}&y_0+{\check{y}}/2 = \mu _1\big (1+\sqrt{1+\epsilon }\big )=1.818\mu _1 \nonumber \\&\quad <-\lambda _1+\sqrt{(\mu _1(1+\epsilon /2)+\lambda _1/2)(2\mu _1+2\lambda _1+y_0)}=\Big (-2+\sqrt{1.8348(6+y_0/\mu _1)}\Big )\mu _1. \end{aligned}$$
(144)

which, together with the condition \(\alpha _1=2\mu _1-y_0>0\) according to (70) and (61), limits \(y_0\) to the narrow range

$$\begin{aligned} 1.945<y_0/\mu _1<2.0. \end{aligned}$$
(145)

We choose a fixed \(\mathbf{{Y} }\) that satisfies (144) and (145), namely

$$\begin{aligned} y_0/\mu _1 = 1.99\,,\qquad {\check{y}}/\mu _1 = -0.345, \end{aligned}$$
(146)

and want to investigate the influence of the stress level \(\epsilon \) on the bounds. So we compare \(\varrho _j\) of \(\epsilon =-\,0.33\) and \(\epsilon =+\,0.33\). The data of Table 1 are based on a volume fraction \(c=0.1\) of the reinforcement. The labels V, K, D, R refer to the bounds of Voigt, of the kinematic and the dynamic approach, and of Reuss.

Table 1 Bounds in case of uniaxial stress with a fixed \(\mathbf{{Y} }\)
Full size table

We see that only the first two Reuss bounds depend on the stress \({\check{t}}\).

Next we want to study the influence of various \(\mathbf{{Y} }\) on the bounds. Therefore we consider a tensile stress, namely \(\epsilon =+\,0.33\). If we had \(t_0>0\), then the stiffness \({\textsf {A}}\) would be positive-definite and \(\mathbf{Y }=\mathbf{0 }\) a possible choice. Since we have \(t_0=0\) we must allow an arbitrarily small \(y_0>0\). The conditions \(\alpha _1>0\) and \(\alpha _7>0\) according to (70), (61), and (63) give

$$\begin{aligned} 0<y_0/\mu _1<2.0. \end{aligned}$$
(147)

Conditions (71) and (72) yield

$$\begin{aligned}&-0.153\mu _1= \mu _1\big (1-\sqrt{1+\epsilon }\big )<y_0+{\check{y}}/2 \nonumber \\&\quad <-\lambda _1+\sqrt{(\mu _1(1+\epsilon /2)+\lambda _1/2)(2\mu _1+2\lambda _1+y_0)}=\Big (-2+\sqrt{2.165(6+y_0/\mu _1)}\Big )\mu _1. \end{aligned}$$
(148)

This implies

$$\begin{aligned} y_0/\mu _1 =0.01\quad&\Longrightarrow&\quad -0.326<{\check{y}}/\mu _1<3.194,\nonumber \\ y_0/\mu _1 =1.99\quad&\Longrightarrow&\quad -4.286<{\check{y}}/\mu _1 <0.338. \end{aligned}$$
(149)

The results can be found in Table 2, which again uses \(c=0.1\).

Table 2 Bounds in case of uniaxial tension, influence of the choice of \(\mathbf{{Y} }\)
Full size table

We arrive at the conclusion: If the stresses are positive, then the lower bounds can be computed with \(\mathbf{Y }\approx \mathbf{0 }\). We see, however, that the first two lower bounds become better when computed with \(y_0/\mu _1\approx 2\), whereas the third one is worse. In addition, the first Reuss bound increases if \({\check{y}}\) increases, while the second Reuss bound increases if \({\check{y}}\) decreases.

9.2 Prestress

We choose the stiffness coefficients of (139), a volume fraction \(c=0.1\), and the following stresses:

$$\begin{aligned} t_0=0\,,\qquad {\check{t}}_1 =-0.4 \mu _1\,,\qquad {\check{t}}_2 =0.36 \mu _2\quad \Longrightarrow \quad \bar{\mathbf{T }}=\mathbf{0 }. \end{aligned}$$
(150)

Now \(\mathbf{Y }\approx \mathbf{0 }\) is not allowed because of the compressive stress in the matrix. The overall stress of the composite is zero, while there was an overall tension in the foregoing example. Nevertheless, most of the results are identical. The only deviations occur with the first two Reuss bounds and can be found in Table 3.

Table 3 Prestress, influence of the choice of \(\mathbf{{Y} }\) on two Reuss bounds
Full size table

9.3 Matrix with negative modulus of compression

We introduce the deviator \(\hat{\mathbf{D }}\) of \(\mathbf{{D} }\) and the modulus of compression \(\kappa \). Then the isotropic material behaviour can be characterized by

$$\begin{aligned} {\textsf {C}}:\mathbf{D } = 2 \mu \mathbf{D }+\lambda \mathbf{1 }:\mathbf{D }\;\mathbf{1 } = 2 \mu \hat{\mathbf{D }}+\kappa \mathbf{1 }:\mathbf{D }\;\mathbf{1 }. \end{aligned}$$
(151)

with

$$\begin{aligned} \kappa = \frac{1}{3}(2\mu +3\lambda ). \end{aligned}$$
(152)

We assume a stress-free state so that S-E conditions (75) reduce to

$$\begin{aligned} \mu>0\,,\qquad 2\mu +\lambda>0\quad \Longrightarrow \quad \kappa >-\frac{4}{3} \mu . \end{aligned}$$
(153)

We are interested in the range \(0>\kappa >-\frac{4}{3} \mu \) where the S-E conditions are satisfied, but \({\textsf {C}}\) is indefinite. The classical approach is not applicable since it is based on the assumption of a positive-definite \({\textsf {C}}\). So we construct bounds with the help of suitable values of \(\mathbf{{Y} }\).

We choose

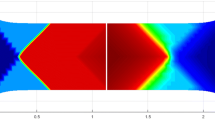
$$\begin{aligned} \lambda _2=2\mu _2=20\mu _1 \,,\quad \lambda _1=-\frac{3}{4}\mu _1 \quad \Longrightarrow \quad \kappa _2=\frac{8}{3}\mu _2>0\,,\quad \kappa _1=-\frac{1}{12}\mu _1<0\,,\qquad \nu _2=\frac{1}{3}\,,\quad \nu _1 = -\frac{3}{2},\nonumber \\ \end{aligned}$$
(154)

and \(t_0=0\), \({\check{t}}_j = \mu _j/1000\) and \(c=0.1\). The region of allowable values in the \(y_0,{\check{y}}\) plane can be seen in Fig. 1. It is limited by conditions (70) of the matrix material. The results are given in Table 4.

Fig. 1
figure 1

Negative modulus of compression. Allowable range of \(\mathbf{{Y} }\) (\(\mu _1=1\))       A: \(\;\alpha _7=0\),    B: \(\;\alpha _1=0\),   C: \(\;\Delta _1=0\),    D: \(\;\Delta _2=0\)

Full size image
Table 4 Negative modulus of compression
Full size table

The Voigt bounds and the first two Reuss bounds are not useful. The largest values of the first two bounds of the dynamic approach are obtained with \(y_0\approx 2\). If , in contrast, \(y_0\approx 0\) is chosen, then the second one is useless.

Next we are interested in the dependence of the overall stiffness \(\tilde{\textsf {C}}\) on the volume fraction c. The negative value of \(\kappa \) causes \(\varrho _2\) to be negative if c is small, while the other three coefficients are positive with any c. Figure 2 gives the dependence of \(\varrho _2\) on c with \(y_0=1.99\). We see that positive-definiteness of the overall stiffness \(\tilde{\textsf {C}}\) is guaranteed if \(c>0.026\). The matrix alone is not stable under free boundary conditions, but this is repaired by a rather small reinforcement.

Fig. 2
figure 2

Negative modulus of compression. Dependence of \(\varrho _2\) on c      K:   Kinematic approach,   D:   Dynamic approach

Full size image

9.4 Soft inclusions

We choose

$$\begin{aligned} 2 \mu _1 =\lambda _1 = 10\lambda _2=20\mu _2. \end{aligned}$$
(155)

So the stiffness of the matrix is ten times the stiffness of the component \(\#\)2 and Poisson’s ratio of the two components is the same. The behaviour of the component \(\#\)2 is now not that of a reinforcement but resembles more that of cavities. The composite shall be free of stress everywhere. Nevertheless we choose \(t_0=0\) and \({\check{t}}_j=\mu _j/1000\) to avoid the problem described after Eq. (89). We omit the kinematic approach. (Our velocity field (94) is inappropriate here.) The results in Table 5 are again based on \(c=0.1\).

Table 5 Soft inclusions
Full size table

The choice \(\mathbf{Y }\approx \mathbf{0 }\) yields acceptable results. If we choose \(y_0/\mu _1\approx 2\), then the third bound is no longer useful, while the first two bounds become better: the bounds of the dynamic approach and the first Reuss bound with any value of \({\check{y}}\), the second Reuss bound, however, only if \({\check{y}}\) is as small as possible, i.e. \({\check{y}}/\mu _1\approx -4\).

9.5 Different Poisson’s ratio

We choose

$$\begin{aligned} \mu _1 =\mu _2=\mu \,,\qquad \lambda _1 = 8\mu \,,\qquad \lambda _2=2\mu \end{aligned}$$
(156)

and find

$$\begin{aligned} \nu _1=\frac{4}{9}\,,\qquad \nu _2=\frac{1}{3}. \end{aligned}$$
(157)

The composite shall be free of stress everywhere. Nevertheless we choose \(t_0=0\) and \({\check{t}}_1=\mu /500\) and \({\check{t}}_2=\mu /1000\) to avoid the problem described after Eq. (89). We omit the kinematic approach again. Table 6 is based on the volume fraction \(c=0.3\).

The choice \(\mathbf{Y }\approx \mathbf{0 }\) yields reasonable results. But if we choose \(y_0/\mu \approx 2\), then the first two bounds become better. Since we consider a stress-free state and \({\textsf {C}}\) is positive-definite, the bounds that correspond to the choice \(\mathbf{Y }\approx \mathbf{0 }\) could also be obtained with the classical results according to (4) without recourse to \({\textsf {A}}\) or \({\textsf {A}}^{*}\). However, if we introduce a suitable \(\mathbf{{Y} }\), then the Reuss bounds are even better than the bounds of the more sophisticated dynamic approach based on \(\mathbf{Y }\approx \mathbf{0 }\).

Table 6 Different Poisson’s ratio
Full size table

10 Conclusions

We succeeded in constructing upper and lower bounds to the incremental stiffness of a hyperelastic composite even in cases where a simple extension of the classical approach is not applicable. This is especially the case if the material is under essential compression stresses or if the modulus of compression is not positive somewhere. The remedy is to find some tensor \(\mathbf{{Y} }\) that makes a pseudo-stiffness positive-definite. Then it is not only possible to construct the bounds, but we also can be sure that the overall stiffness satisfies the S-E conditions and that internal buckling of the composite is not possible. The existence of a \(\mathbf{Y}\) does only depend on the material properties of the body, while phenomena like internal buckling are surely influenced by the geometry of the composite. In general, the tensor \(\mathbf{{Y} }\) will not be uniquely determined and a suitable choice can improve the bounds as our examples demonstrate.

The concept of a pseudo-stiffness, based on the availability of some tensor \(\mathbf{{Y} }\), allows new insight into the behaviour of composites. This is obvious with the examples of Sect. 9. The application of the method to very complex composites, however, although possible in principle, may be limited due to practical difficulties.