Effects of parameter uncertainties on the forecasted behavior of thermomechanically loaded thick-walled functionally graded spherical structures

Abstract

The subject of the investigation is an elastic functionally graded hollow spherical device under internal pressure and homogeneous heating. Since in reality uncertain parameter values are to be expected with respect to both basic material data and influences of the manufacturing process, the effects of these uncertainties are in the focus of the present study. For the numerical results, specifically a container or pressure vessel of steel-aluminum functionally graded material is considered. Essentially, the largest possibly occurring von Mises stress is taken as an assessment criterion. It is demonstrated that uncertainty ranges of the system inputs may cause much larger scattering ranges (in percentages) of the predicted maximum stresses. Moreover, the sensitivity of the results to variations of different individual parameter values is discussed, and it is shown that an application of sophisticated and computationally expensive homogenization schemes to the functionally graded material is meaningful only if the basic data can be determined with quite high accuracy.

1 Introduction

Functionally graded materials (FGMs) and their applications find ever-growing interest in engineering, from both a theoretical and a practical point of view. This is due to the possibility of achieving increased strength and/or reduced weight of an FGM-structure as well as high resistance against thermal or chemical influences. As is well known, in such structures the physical properties like density, Young’s modulus, Poisson’s ratio, etc. vary–in principle–continuously in one or more direction(s); manufacturing methods are discussed, e.g., in the review articles [1, 2].

Hence, because of the beneficial characteristics mentioned above, using FGMs has been proposed also for spherical devices like containers and pressure vessels. There exists a number of studies on this topic, considering various types of loads and grading laws. Both analytical and numerical approaches have been applied, and comprehensive references to earlier papers can be found, e.g., in the recent articles [3,4,5,6].

However, in the large majority of studies on FGM hollow spheres an autonomous variation of each physical property with radius is presupposed. For example, in the frequently considered power law grading the exponents in the equations for all the material properties are chosen independently of each other. Based thereon, valuable theoretical insights may be obtained, of course, but the feasibility of manufacturing such an FGM remains an open question. Indeed, there also exist some studies on functionally graded spherical devices taking homogenization method(s) into account, see, e.g., [5, 7,8,9,10,11]. The commonly used method is based on the Voigt scheme (rule of mixtures), but i.a. also the Mori-Tanaka scheme [7, 9,10,11], the self-consistent scheme [11], and the Reuss scheme [5] have been applied.

Nevertheless, whereas the consideration of homogenization methods for an FGM structure certainly is an approach closer to physical reality, the question for the ‘correct’ or ‘best’ scheme(s) has quite generally been a broadly discussed issue in literature. In fact, an appropriate choice will depend on several features like the chemical composition of the FGM, the microstructure, the grading characteristics, etc. With respect to functionally graded spherical containers or pressure vessels, comparative results can be found in [5, 9, 11], and particularly in the comprehensive study [12]. Particularly the latter investigation reveals that some homogenization schemes yield quite similar results for the calculated stress distributions, but some others predict even qualitatively different behavior.

Indeed, one may argue that–for an already manufactured FGM device–the physical properties could be determined experimentally, and then either the relevant homogenization scheme(s) could be found or the values of (pseudo-)autonomously varying parameters could be determined with high accuracy. In this reasoning two points should however not be disregarded. First, it is quite generally not an easy task to measure the effective properties of an FGM structure [13]. Second, and even more important, one should take account of the fact that usually the primary objective in engineering is not to recalculate the behavior of an already existing structure but to reasonably forecast the characteristics of some newly designed one. For the latter task, one should bear in mind that in general the production process will cause (at least minor) deviations of the spatial distribution of the constituents and the microstructure of an FGM device from the design [14] (and will give rise to some scattering even within the same batch of objects). What is more, the values of the basic physical parameters of the constituents will frequently be subject to some uncertainties, too.

Hence, since at least for predictive purposes in engineering the application of homogenization methods seems adequate, one should find an appropriate balance between sophistication of the homogenization schemes and computational and/or experimental effort. In view of the above-mentioned deviations and uncertainties, this raises the question for both the meaningful complexity of the homogenization method(s) and–of particular importance–the extremum stresses which may occur within the range of possible parameter values: appropriate methods to clarify this issue are uncertainty/sensitivity studies.

However, whereas there exists a huge amount of papers on the problem of homogenization for various functionally graded materials and in different contexts (see, e.g., the review article [15]), the question for uncertainty/sensitivity has been addressed to a noticeably lesser extent; this was pointed out also in [16, 17]. Indeed, there exist some recent studies on this topic for the statics and dynamics of FGM beams and frame-structures [16, 18,19,20,21,22], of FGM plates [17, 23,24,25,26], and of FGM shells [27]; earlier investigations for functionally graded thick hollow cylinders can be found in [28, 29]. Distantly related studies on the sensitivity of large deformations of FGM hyperelastic spherical pressure vessels were given in [30, 31], but – to the authors’ best knowledge – the influence of material and/or grading uncertainties and scattering on the forecasted strength of thermomechanically loaded metal based thick-walled spherical FGM structures has not been in the focus of previous analyses.

Hence, it is the aim of the present paper to discuss this issue for an internally pressurized and homogeneously heated steel-aluminum FGM hollow sphere with power-law grading [5], taking the radial variation not only of Young’s modulus but also of Poisson’s ratio and the coefficient of thermal expansion into account. Since for Young’s modulus the Voigt rule and the Reuss rule represent the upper and lower bound, respectively, both of them are considered. The other material parameters are presumed to follow the rule of mixtures. The resulting boundary value problem for the governing differential equation for the radial displacement is solved numerically; based thereon, the stress distribution can be calculated. In the core of the study are then the predicted maximum stresses in the device for different values of the basic material parameters – given even in quite recent sources! – and the grading index for the considered steel-aluminum FGM. It is shown that there may occur significant differences in the forecasted maximum stresses, which even may superimpose the question for the most meaningful homogenization scheme(s).

A further important point is the following one. In many of the hitherto performed uncertainty studies on FGM structures, a random/probabilistic approach is followed (e.g., [18, 19, 24, 26,27,28]). However, as emphasized in [20,21,22], the underlying statistical information about the scattering of the relevant system inputs is generally difficult to obtain and frequently not available in practice; hence, in the latter references an interval analysis is adopted. Such an analysis requires only the knowledge of the possible upper and lower bounds of the parameter values, and the present study is also based on these data only. What is more, a reliable safety assessment of a pressure vessel, e.g., should be based rather on the definite largest stresses which might occur during operation than on just an – even very high – probability of working well. Hence, the present contribution also aims at showing which combination of upper or lower bounds of the parameter values leads to the highest possible stresses in an FGM spherical container or pressure vessel.

The paper is organized as follows. In Sect. 2, the mathematical formulation of the problem is given. In Sect. 3, first the grading law and the applied homogenization schemes are introduced, then the numerical solution procedure is discussed. Next, based on data found in literature, in Sect. 4 the uncertainty ranges of the parameter values are estimated. Then, in Sect. 5, numerical results for the scattering ranges of the largest predicted stresses are given. Finally, in Sect. 6, the conclusions from the preceding investigation are drawn.

2 Statement of the problem and governing equations

The mathematical formulation of the problem is as follows. An elastic functionally graded hollow sphere with $a\le r\le b$ is presumed to be subject to internal pressure P and stress-free outer surface, that is,

$$\begin{aligned} r=a:\ \ \sigma _{r}=-P,\qquad \ \ \ \ \ r=b:\ \ \sigma _{r}=0. \end{aligned}$$

(1)

Moreover, spherical symmetry is presupposed, hence in the spherical coordinate system ($r,\theta ,\phi$) the relations $\sigma _{\theta }=\sigma _{\phi }$ and $\epsilon _{\theta }=\epsilon _{\phi }$ hold. Then, the equation of equilibrium in radial direction reads

$$\begin{aligned} \frac{\mathrm{d}\sigma _{r}}{\mathrm{d}r}+\frac{2}{r}\left( \sigma _{r}-\sigma _{\theta }\right) =0, \end{aligned}$$

(2)

and within the geometrically linear theory the strains are related to the radial displacement u by

$$\begin{aligned} \epsilon _{r}=\frac{\mathrm{d}u}{\mathrm{d}r},\text { \ \ }\epsilon _{\theta }=\frac{u}{r}. \end{aligned}$$

(3)

In the absence of thermal shocks, for containers and pressure vessels in general slow and hence–essentially–homogeneous heating during operation can be presumed. Furthermore, if only moderate temperatures occur, the material properties may be considered temperature-independent. (It shall be recalled that homogeneous heating – without additional mechanical load – would not lead to stresses in a homogeneous hollow sphere but on the contrary in a functionally graded one, due to the spatially varying thermal expansion!). Thus, taking nevertheless a radial variation of Young’s modulus E, of Poisson’s ratio $\nu$, and also of the coefficient of thermal expansion $\alpha$ into account, the generalized Hooke’s law reads

$$\begin{aligned} \epsilon _{r}&=\frac{1}{E\left( r\right) }\left[ \sigma _{r}-2\nu \left( r\right) \sigma _{\theta }\right] +\alpha \left( r\right) T, \end{aligned}$$

(4)

$$\begin{aligned} \epsilon _{\theta }&=\frac{1}{E\left( r\right) }\left[ \sigma _{\theta }-\nu \left( r\right) \left( \sigma _{r}+\sigma _{\theta }\right) \right] +\alpha \left( r\right) T. \end{aligned}$$

(5)

Using Eqs. (3)–(5) and denoting the derivative of a quantity with respect to r by a bar, the stresses can be expressed in terms of u and $u^{\prime }$ as

$$\begin{aligned} \sigma _{r}&=\frac{E\left( r\right) }{\left[ 1+\nu \left( r\right) \right] \left[ 1-2\nu \left( r\right) \right] r}\left\{ 2\nu \left( r\right) u+\left[ 1-\nu \left( r\right) \right] ru^{\prime }-\left[ 1+\nu \left( r\right) \right] r\alpha \left( r\right) T\right\} , \end{aligned}$$

(6)

$$\begin{aligned} \sigma _{\theta }&=\frac{E\left( r\right) }{\left[ 1+\nu \left( r\right) \right] \left[ 1-2\nu \left( r\right) \right] r}\left\{ u+\nu \left( r\right) ru^{\prime }-\left[ 1+\nu \left( r\right) \right] r\alpha \left( r\right) T\right\} . \end{aligned}$$

(7)

Insertion of Eqs. (6) and (7) into the equation of equilibrium (2) then leads to a differential equation for the radial displacement,

$$\begin{aligned}&r^{2}u^{\prime \prime }+ru^{\prime }\left\{ 2+\frac{rE^{\prime }\left( r\right) }{E\left( r\right) }+\frac{2r\left[ 2-\nu \left( r\right) \right] \nu \left( r\right) \nu ^{\prime }\left( r\right) }{\left[ 1-\nu \left( r\right) \right] \left[ 1+\nu \left( r\right) \right] \left[ 1-2\nu \left( r\right) \right] }\right\} \nonumber \\&\qquad -\frac{2u}{1-\nu \left( r\right) }\left\{ 1-\nu \left( r\right) \left[ 1+\frac{rE^{\prime }\left( r\right) }{E\left( r\right) }\right] -\frac{r\left[ 1+2\nu ^{2}\left( r\right) \right] \nu ^{\prime }\left( r\right) }{\left[ 1+\nu \left( r\right) \right] \left[ 1-2\nu \left( r\right) \right] }\right\} \nonumber \\&\quad =\frac{r^{2}T\left[ 1+\nu \left( r\right) \right] }{1-\nu \left( r\right) }\left\{ \alpha ^{\prime }\left( r\right) +\alpha \left( r\right) \left[ \frac{E^{\prime }\left( r\right) }{E\left( r\right) }+\frac{2\nu ^{\prime }\left( r\right) }{1-2\nu \left( r\right) }\right] \right\} \text { .} \end{aligned}$$

(8)

This equation is valid for all functions $E\left( r\right)$, $\nu \left( r\right)$, and $\alpha \left( r\right)$. After specifying these functions by some homogenization scheme(s), the boundary value problem based on the differential equation (8) can be solved, which requires – except in a few special cases [5] – numerical means (see Sect. 3.3). Simultaneously, considering Eqs. (6) and (7), also the stresses in the hollow sphere are obtained.

Checking whether the structure still is in the elastic range is performed by von Mises’ yield criterion (which here is equivalent to Tresca’s criterion [32]), i.e., that plasticization will occur if at some radius

$$\begin{aligned} \sigma _{M}=\sigma _{y}\left( r\right) \qquad \text {with}\qquad \sigma _{M}=\left| \sigma _{\theta }-\sigma _{r}\right| \end{aligned}$$

(9)

where $\sigma _{y}\left( r\right)$ denotes the uniaxial yield limit.

3 Grading, homogenization schemes, and numerical procedure

3.1 Grading

As already mentioned in the Introduction, power law grading of the spherical container or pressure vessel is presumed. Moreover, it is taken into account that at the inner surface either pure constituent 1 or an alloy of both constituents may occur and that at the outer surface either pure constituent 2 or an alloy of both constituents may occur. Hence, the relations for the volume fractions read

$$\begin{aligned} V_{1}(r)&=\frac{\left[ \left( \frac{b}{a}\right) ^{m}-\left( \frac{r}{a}\right) ^{m}\right] V_{1a}+\left[ \left( \frac{r}{a}\right) ^{m}-1\right] V_{1b}}{\left( \frac{b}{a}\right) ^{m}-1}, \end{aligned}$$

(10)

$$\begin{aligned} V_{2}(r)&=1-V_{1}(r) \end{aligned}$$

(11)

Fig. 1

Examples of volume fraction distributions (of constituent 1) in a hollow sphere with $b/a=1.5$; a $V_{1a}=1.0$, $V_{1b}=0$, b $V_{1a}=0.6$, $V_{1b}=0$, c $V_{1a}=1.0$, $V_{1b}=0.3$, d $V_{1a}=0.8$, $V_{1b}=0.2$

where $V_{1a}$ and $V_{1b}$ mean the volume fractions of constituent 1 at $r=a$ and $r=b$, respectively. The grading index m can be chosen in a (theoretically arbitrarily) wide range of negative and positive values, thus enabling the consideration of different forms of the volume fraction variations. Examples thereof are provided in Fig.1; there and in the following Figures, the radial coordinate is non-dimensionalized by r/a .

3.2 Homogenization schemes

The Voigt model–denoted by the index V and equivalent to the linear rule of mixtures–states for the homogenized Young’s modulus that

$$\begin{aligned} E_{V}(r)=E_{1}V_{1}(r)+E_{2}V_{2}(r), \end{aligned}$$

(12)

which together with Eqs. (10), (11) yields

$$\begin{aligned} E_{V}(r)=\frac{E_{1}-E_{2}}{\left( \frac{b}{a}\right) ^{m}-1}\left\{ \left[ \left( \frac{b}{a}\right) ^{m}-\left( \frac{r}{a}\right) ^{m}\right] V_{1a}+\left[ \left( \frac{r}{a}\right) ^{m}-1\right] V_{1b}\right\} +E_{2}. \end{aligned}$$

(13)

If the Reuss model (denoted by the index R) is applied, the homogenized Young’s modulus is presumed to obey the basic relation

$$\begin{aligned} E_{R}(r)=\left[ \frac{V_{1}\left( r\right) }{E_{1}}+\frac{1-V_{1}\left( r\right) }{E_{2}}\right] ^{-1}, \end{aligned}$$

(14)

and therefore in the present case

$$\begin{aligned} E_{R}(r)=\frac{\left[ \left( \frac{b}{a}\right) ^{m}-1\right] E_{1}E_{2} }{\left( E_{2}-E_{1}\right) \left\{ \left[ \left( \frac{b}{a}\right) ^{m}-\left( \frac{r}{a}\right) ^{m}\right] V_{1a}+\left[ \left( \frac{r}{a}\right) ^{m}-1\right] V_{1b}\right\} +\left[ \left( \frac{b}{a}\right) ^{m}-1\right] E_{1}}. \end{aligned}$$

(15)

The derivative of $E_{R}(r)$– occurring in Eq. (8) – reads

$$\begin{aligned} E_{R}^{\prime }(r)=\frac{\left( a^{m}-b^{m}\right) \left( E_{1} -E_{2}\right) \left( V_{1a}-V_{1b}\right) E_{1}E_{2}mr^{-1+m}}{\left\{ b^{m}\left[ E_{1}-V_{1a}\left( E_{1}-E_{2}\right) \right] -a^{m}\left[ E_{1}-V_{1b}\left( E_{1}-E_{2}\right) \right] +r^{m}\left( E_{1} -E_{2}\right) \left( V_{1a}-V_{1b}\right) \right\} ^{2}}. \end{aligned}$$

(16)

Although occasionally for the other material properties (e.g., for the coefficient of thermal expansion in [33]) some more sophisticated schemes were applied, too, the effective homogenized values of $\nu \left( r\right)$, $\alpha \left( r\right) ,$ and $\sigma _{y}\left( r\right)$ are calculated in accordance with most studies on FGM structures by the rule of mixtures (12). Thus, taking again Eqs. (10) and (11) into account, one obtains

$$\begin{aligned} \text {Pr}_\mathrm{eff}(r)=\frac{\Pr _{1}-\Pr _{2}}{\left( \frac{b}{a}\right) ^{m} -1}\left\{ \left[ \left( \frac{b}{a}\right) ^{m}-\left( \frac{r}{a}\right) ^{m}\right] V_{1a}+\left[ \left( \frac{r}{a}\right) ^{m}-1\right] V_{1b}\right\} +\text {Pr}_{2} \end{aligned}$$

(17)

where Pr$_{j}=\nu _{j}$, $\alpha _{j},\sigma _{y,_{j}}$ with $j=1,2$, and the derivative (corresponding also to $E_{V}^{\prime }(r)$) reads

$$\begin{aligned} \text {Pr}_\mathrm{eff}^{\prime }(r)=\frac{\left( \Pr _{1}-\Pr _{2}\right) \left( V_{1a}-V_{1b}\right) mr^{-1+m}}{a^{m}-b^{m}}. \end{aligned}$$

(18)

3.3 Numerical procedure

The necessary numerical solution of the boundary value problem is accomplished by the solver bvp4c, which is a fast and reliable solver for ordinary differential equations in the MATLAB program. The Tutorial [34], which introduces the function bvp4c, was used during the preparation of the algorithm. The numerical method of bvp4c is based on the Simpson method (with residual control for MATLAB), which is implemented into the collocation method with a $C^{1}$ piecewise cubic polynomial or an implicit Runge–Kutta formula with a continuous extension [35].

Fig. 2

Comparison of analytical results given in [5], Fig.8] - based on $\nu =const.$- with the present numerical solution for a steel-aluminum pressure vessel with $b/a=1.3$ and an internal pressure of 40 MPa (for the other parameter values see [5])

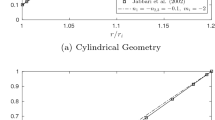
The accuracy of the numerical solution was checked i.a. by a comparison with analytical results for a steel-aluminum pressure vessel given in [5], Fig.8], where $\nu =const.$ was presumed; the underlying parameter values can be found in [5]. As one can see from Fig. 2, the coincidence of the results is excellent, and it should be pointed out that for an internal pressure of 40 MPa the maximum stress difference occurring for the Voigt scheme is only $4.664\times 10^{-4}$ MPa, and $4.676\times 10^{-3}$ MPa for the Reuss scheme.

It already was emphasized in the Introduction that the subsequent investigation is based on–realistic–upper (ub) and lower (lb) bounds of the basic data for the FGM structure and not on statistical information. Hence, for the determination of the relevant stresses the following procedure was applied. For each uncertain parameter $D_{j}$ with $D_{j,lb}$ $\le D_{j}\le D_{j,ub}$ in the interval $\left[ D_{j,lb},D_{j,ub}\right]$ an appropriately large number of equally spaced data points was considered. Then, the respective maximum von Mises stress in the hollow sphere was calculated for each combination of all data points of all uncertain parameters, i.e., $E_{j}$, $\nu _{j}$, $\alpha _{j}$ ($j=1,2$), and -partially- m. Of course, also specific analyses were performed keeping some of the parameter values constant. Remarkably, it turned out that the predicted largest von Mises stresses always are connected with bounds of all the parameter values; this will be discussed in detail in Sect. 5.

4 Material data

In practice, functionally graded spherical containers or pressure vessels can be composed of various constituent pairs. Their choice depends on the intended purpose of use and the possibilities of manufacturing. For a metal-metal FGM, in [5] a steel-aluminum graded material was proposed; for a specific production method of such an FGM see, e.g., [36]. Hence, the subsequent discussion is based on this type of functionally graded material.

Whereas it seems quite natural that the published values of some properties of steel (like the uniaxial yield limit) differ considerably for different kinds thereof, it is remarkable that the published material data of other properties – even of pure iron and pure aluminum – are not unambiguous, too; thus, there arises the question for their effects on predicted stress distributions.

For steel at room temperature, recently reported values of (static) Young’s modulus are, e.g., 206.1 GPa [37], 214.9 GPa [38], and $200-240$ GPa [39]; further values (e.g., in [40]) lie within the interval given in [39]. As for Poisson’s ratio, reported data vary from $\nu =0.27$ in [41] and $\nu =0.275$ in [38] to $\nu =0.29$ in [42], e.g.; since a common rounded value is $\nu =0.3$, this value is considered as upper bound. The coefficient of thermal expansion is quoted, e.g., as $\alpha =10-12\times 10^{-6}$/K in [43], as $\alpha =12.3\times 10^{-6}$/K in [37], and a still higher value of $\alpha =14.9\times 10^{-6}$/C is reported in [44]. Summing up, for the present investigation the values given in Table 1 are considered as upper and lower bounds of the above material parameters. It must however be emphasized that these bounds just shall provide an estimation of realistic scattering/uncertainty ranges of material data and should not be understood as some strict physical limits; moreover, all of the parameters show – even at moderately elevated temperatures – at least a minimal temperature dependence. Since the present study is focussed on the elastic behavior of the spherical device, the uniaxial yield limit is only required to check whether the maximum von Mises stress is sufficiently lower than the elastic limit, and a (rather low) value of $\sigma _{y}=200$ MPa is presumed.

Table 1 Lower and upper bounds of the material parameters considered in the present study, and percentage deviation of upper bound from lower bound for each parameter

For Young’s modulus of aluminum, in [21] the considered bounds are 66.5 GPa and 73.5 GPa, other recent studies are based on intermediate values, e.g., on 69 GPa in [45] or on 73 GPa in [10]. Thus, depending (also) on the purity of the specific aluminum, the published data vary within a comparatively large range, and the bounds given in [21] are presumed in the present investigation as well. As for Poisson’s ratio of aluminum, a common rounded value in literature is $\nu =0.3$, too, but more specific references give values of $\nu =0.33$ ([10]), of $\nu =0.32$ to $\nu =0.35$ ([43]), and an online publication for material scientists quotes as maximum value $\nu =0.36$ ([46]). The coefficient of thermal expansion is reported as $\alpha =22.2\times 10^{-6}$/K in [47], but in several references higher values are given, e.g., in [48] $\alpha =23.8\times 10^{-6}$/K or in [49] $\alpha =24\times 10^{-6}$/K . Hence, the bounds for the material data of aluminum considered in the present study are the ones also shown in Table 1. Of course, the remarks in the previous paragraph apply here, too, and to be at the safe side for checking the elastic behavior a very small uniaxial yield limit of $\sigma _{y}=40$ MPa is taken [50].

5 Forecasted stresses: numerical results

To assess now the effects of both the parameter uncertainties and the uncertainty introduced by deviations in the manufacturing process – modelled by varying the grading index m – a hollow steel-aluminum sphere with $b/a=1.5$ subject to an internal pressure of $P=15$ MPa and a (moderate) temperature rise by 50 K is considered. Furthermore, grading from $V_{1a}=0.8$ to $V_{1b}=0.2$ is presumed (see Fig. 1(d)). For such a sphere and material data within the bounds given in Table 1, the scattering ranges (see Appendix) of the homogenized parameters $E\left( r\right)$, $\nu \left( r\right)$, and $\alpha \left( r\right)$ are shown in Fig. 3 for two different values of the grading index m.

Fig. 3

Scattering ranges of the homogenized parameters $E\left( r\right)$, $\nu \left( r\right)$, and $\alpha \left( r\right)$ for material data within the bounds given in Table 1 for $m=-10$ and $m=10$, respectively

Next, to begin with, by the procedure described in Sect. 3.3 the combined effects of all the material parameter uncertainties are analyzed for the fixed values of m given in Fig. 3. As already mentioned, the numerical calculations have shown that the predicted extremum von Mises stresses always occur if each parameter takes a boundary value of its interval. Since $\max \left( \sigma _{M}\left( r\right) \forall r\right)$ is decisive for the strength test of the device, in the following Figures the ‘Max Mises Case’ (MaxMC) corresponds to the parameter combination yielding the highest $\max \left( \sigma _{M}\left( r\right) \forall r\right)$, whereas the ‘Min Mises Case’ (MinMC) is related with the parameter combination yielding the lowest $\max \left( \sigma _{M}\left( r\right) \forall r\right)$. Of course, from the engineering point of view, the MaxMC is the worst case to be expected, the MinMC the best one.

Fig. 4

Stress distributions for the MinMC and the MaxMC for $m=-10$ and the Voigt scheme: a von Mises stresses, b circumferential stresses, c radial stresses (note the ordinate scale), d corresponding material parameter values

For $m=-10$ and the Voigt scheme, Fig. 4a–c shows the von Mises stresses for the MinMC and the MaxMC and the corresponding radial and circumferential stresses. Whereas both the absolute values and the differences of $\sigma _{r}$ are small, the deviations of $\sigma _{\theta }$ and hence of $\sigma _{M}$ near the inner surface are significant, and the largest predicted stresses are by almost $70\%$ higher than the smallest ones! As one observes from Fig. 4d, the MaxMC corresponds to the upper limits of all the parameter intervals with one exception: the lower bound of $\alpha _{1}=\alpha _{Steel}$. On the contrary, the MinMC is connected with the lower bounds of the parameter intervals, except for $E_{2}=E_{Al}$ and $\alpha _{1}=\alpha _{Steel}$. As a supplement, Fig. 5 demonstrates by the ratio of the forecasted von Mises stresses to the yield limit that the device would remain in the elastic state even in the MaxMC; this was checked also in the subsequently discussed cases, of course, but referring to this further plots are omitted.

Fig. 5

Ratio of von Mises stresses to yield limit for $m=-10$ and the Voigt scheme

Fig. 6

Stress distributions for the MinMC and the MaxMC for $m=-10$ and the Reuss scheme: a von Mises stresses, b circumferential stresses, c radial stresses (note the ordinate scale), d corresponding material parameter values

Figure 6 presents for $m=-10$ and the Reuss scheme the same comparisons as before. Whereas the general trends in the predicted stress distributions are similar, the maxima are somewhat lower than for the Voigt rule. Nevertheless, at the inner surface the highest forecasted stress differs from the lowest one by almost 60%. Remarkably, the correlations of the MinMC and the MaxMC with the bounds of the parameter intervals are the same as for the Voigt scheme, with only one exception: the MinMC is connected with the lower bound of $E_{2}=E_{Al}$.

Fig. 7

Stress distributions for the MinMC and the MaxMC for $m=10$ and the Voigt scheme: a von Mises stresses, b circumferential stresses, c radial stresses (note the ordinate scale), d corresponding material parameter values

For a different grading with $m=10$ and the Voigt scheme, Fig. 7 shows analogous comparisons. As one can see, for this kind of grading the predicted stress distributions are also qualitatively different. Whereas the highest von Mises stresses still are forecasted at the inner surface (with a difference of about 40% between MaxMC and MinMC), the largest deviation of the MaxMC from the MinMC is observed at the outer surface. The bounds of the parameter values corresponding to the MaxMC are just the same as for $m=-10$ and the Voigt rule (see Fig. 4), the MinMC is however predicted for the lower bound of $E_{2}=E_{Al}$.

Fig. 8

Stress distributions for the MinMC and the MaxMC for $m=10$ and the Reuss scheme: a von Mises stresses, b circumferential stresses, c radial stresses (note the ordinate scale), d corresponding material parameter values

Corresponding results for $m=10$ and the Reuss scheme are depicted in Fig. 8. Again, the largest von Mises stresses are forecasted at the inner surface, with a difference of more than 30% to the smallest ones; however, while at a lower absolute level, the uncertainty at the outer surface is even larger. As one observes by a comparison of Figs. 7d and 8d, the upper/lower bounds of the material data corresponding to the minMC and the maxMC are the same as for $m=10$ and the Voigt rule.

Analysing now the above results, on the whole four main features with respect to uncertainties can be noticed. First, the MaxMC always is connected with the upper bounds of Young’s modulus for both steel and aluminum; this may be explained by the form of Hooke’s law. Second, the same holds true for the upper bounds of Poisson’s ratios. Third, as for the coefficient of thermal expansion, the MaxMC is associated with the largest possible difference of $\alpha _{2}=\alpha _{Al}$ and $\alpha _{1}=\alpha _{Steel}$, i.e., with the upper bound for aluminum and the lower bound for steel. This observation is in accordance with the expectation that a more inhomogeneous thermal expansion field in the device will lead to higher self-stresses. Fourth, although the largest possible MaxMC always is predicted if the Voigt rule is applied, there is a broad overlapping of the expectation ranges of $\sigma _{M}\left( a\right)$ for the Voigt scheme and the Reuss scheme (see Table 2); the implications thereof will be discussed in Sect. 6.

Of course, there now also arises the question for the influence of each individual parameter on the MaxMC, i.e., the question for the sensitivity of the results. To clarify this issue, as a starting point a spherical container with the same dimensions and under the same load as stated above (and $m=-10$) was considered. Moreover, as bases for the material parameter values, the average values shown in Fig. 9 (bottom) were considered. Then, in each case five of the six parameters were kept fixed and the sixth one was varied within the bounds given in Table 1.The results of this procedure are presented in Fig. 9. As one observes, the influence of $E_{1}=E_{Steel}$ on the largest predicted von Mises stress is significant and more pronounced than that of $E_{2}=E_{Al}$ (notwithstanding that the abscissa scales are different). As compared to this, the uncertainties of Poisson’s ratios of both constituents have a minor effect only. On the contrary, the largest effect can however be attributed to both coefficients of thermal expansion, even in the moderate temperature range under consideration.

Finally, there remains to analyse the influence of uncertainties caused by the manufacturing process. Of course, the primary deviations from the design – and hence from the intended properties - may occur with respect to the volume fraction distributions of the constituents, but, as already was mentioned, also the microstructure of an FGM-device may depend to a certain degree on the specific production process; however, the latter effect is hardly quantifiable. For the spherical pressure vessel under consideration (with the load data given above) the manufacturing uncertainty can be estimated from Fig. 10. In this Figure, the predicted largest von Mises stresses are shown for the MaxMC and the MinMC vs. the grading index in the interval $-10\le m\le 10$. If volume fraction uncertainties are roughly estimated by a deviation of about $\pm 10\%$ from the intended distribution and hence in the present model from the design $m-$value, the effect of this kind of production uncertainty may be considered moderate.

Fig. 9

Effects of the uncertainty of each individual material parameter on $\sigma _{M}\left( a\right)$ (= largest von Mises stress) for the MaxMC

Fig. 10

Effect of the grading index m on $\sigma _{M}\left( a\right)$ (= largest von Mises stress) for the MaxMC and the MinMC, respectively: a for the Voigt scheme, b for the Reuss scheme

6 Conclusions

In the present investigation, the scattering of the maximum predicted stresses in a thermomechanically loaded thick-walled hollow FGM-sphere caused by both the basic material parameter uncertainties and by deviations in the manufacturing process has been studied. Specifically, numerical results have been given for a steel-aluminum pressure vessel. Summarizing the above findings and focusing primarily on the largest von Mises stresses that might occur, in essence the subsequent conclusions can be drawn.

• (i) With respect to uncertainties of the material data, Young’s moduli as well as the coefficients of thermal expansion of both FGM-constituents have a significant influence on the predicted stresses; on the contrary, there is a minor effect of Poisson’s ratios only. Hence, from the engineering point of view, special attention should be paid to obtain values as accurate as possible of $E_{1},E_{2}$ and particularly also of $\alpha _{1},\alpha _{2}$.

• (ii) Remarkably, both the MaxMC case and the MinMC case always are found to be related with bounds of the individual uncertainty range of all the material parameter values. Generally, the upper bounds of Young’s moduli are relevant for the largest stresses which might occur. With respect to the coefficients of thermal expansion, the largest possible difference of $\alpha _{1}$ and $\alpha _{2}$ is related with the largest forecasted stresses.

• (iii) As compared to the above results, the effects of uncertainties caused by a (careful!) manufacturing process – which are particularly difficult to be quantified – appear not to be of outstanding influence.

• (iv) In quantitative terms, uncertainty ranges of the material parameters may cause about two- to three-times as large expectation ranges (in percentages) for the maximum von Mises stresses.

• (v) As one would expect, the largest von Mises stresses may be forecasted if the Voigt homogenization scheme is applied. However, considering the comparisons given in Table 2, one observes that there are broad overlapping uncertainty ranges–roughly speaking, depending on the reference value ranges by about $65\!-\!90\%$–for the Voigt scheme and the Reuss scheme, respectively. Since these two schemes represent the upper and the lower limit for an assessment of the strength of the device, other homogenization schemes will lead to some intermediate results. Hence, taking the overlaps and also the issue addressed in point (iv) into account, from the engineering point of view it seems as a priority to determine the basic material data very accurately before looking for more sophisticated and computationally expensive homogenization schemes.

Table 2 Largest predicted von Mises stresses, uncertainty ranges, and overlaps with each other

Whereas the above results are based on a steel-aluminum FGM spherical pressure vessel under a specific type of thermomechanical load, they nevertheless clearly demonstrate the least amount of uncertainty that may occur in predicting the behavior of the device, particularly if the material data cannot be determined with sufficiently high accuracy. Indeed, the temperature dependence of the material parameters, the occurrence of inhomogeneous and/or strong heating, and the microstructural uncertainties due to the manufacturing process, e.g., will most likely increase the actual scattering ranges of the results further. Hence, the present investigation might also be seen as a suggestion to pay quite generally more attention to this issue in further studies on all kinds of thermo-/mechanically loaded FGM-devices.

Appendix

As can be assured by elementary inequalities, the lower and upper limit curves of the scattering ranges of the homogenized values of $E\left( r\right)$, $\nu \left( r\right)$, and $\alpha \left( r\right)$ shown in Fig. 3 are governed by the lower and upper bounds, respectively, of the material data of both constituents.

   To begin with, the rule of mixtures (Voigt rule) and an uncertain—arbitrary—pair of parameters $D_{j}$ with $D_{j,lb}\le D_{j}\le D_{j,ub}$ $\left( j=1,2\right)$ is considered. To verify the above statement, it first is asserted that for the lower limit $\Pr _{\mathrm{eff,low}\lim }\left( r\right)$ of the homogenized property $\Pr _\mathrm{eff}$ there holds the inequality

$$\begin{aligned} \text {Pr}_{\mathrm{eff,low}\lim }\left( r\right) \le \text {Pr}_\mathrm{eff}\left( r\right) \text { for all }D_{j}\text { }\left( j=1,2\right) . \end{aligned}$$

(A.1)

Taking Eqs. (11) and (12) into account, this is equivalent to the relation

$$\begin{aligned} \left( D_{1,lb}-D_{2,lb}\right) V_{1}(r)+D_{2,lb}\le \left( D_{1} -D_{2}\right) V_{1}\left( r\right) +D_{2}, \end{aligned}$$

(A.2)

which can be reformulated as

$$\begin{aligned} 0\le \left( D_{1}-D_{1,lb}\right) V_{1}\left( r\right) +\left( D_{2}-D_{2,lb}\right) \left[ 1-V_{1}\left( r\right) \right] . \end{aligned}$$

(A.3)

Since $D_{j}\ge D_{j,lb}$ $\left( j=1,2\right)$ and both $V_{1}\left( r\right) \ge 0$ and $1-V_{1}\left( r\right) =V_{2}\left( r\right) \ge 0$, the inequality (A.3) and thus also the assertion (A.1) hold true.

   Otherwise, if for Young’s modulus the Reuss rule (Eq. (14)) is applied, the assertion analogous to the inequality (A.2) reads

$$\begin{aligned} \frac{E_{1,lb}E_{2,lb}}{E_{1,lb}\left[ 1-V_{1}\left( r\right) \right] +E_{2,lb}V_{1}\left( r\right) }\le \frac{E_{1}E_{2}}{E_{1}\left[ 1-V_{1}\left( r\right) \right] +E_{2}V_{1}\left( r\right) } \end{aligned}$$

(A.4)

or equivalently

$$\begin{aligned} 0\le E_{1}E_{1,lb}\left( E_{2}-E_{2,lb}\right) \left[ 1-V_{1}\left( r\right) \right] +E_{2}E_{2,lb}\left( E_{1}-E_{1,lb}\right) V_{1}\left( r\right) . \end{aligned}$$

(A.5)

Since all of the multipliers at the right-hand side of relation (A.5) are non-negative, this inequality and hence also assertion (A.1) hold true, again.

    Analogous considerations can then be applied to the upper bounds of the uncertain material data, and this finally verifies the initial statement about the limit curves in Fig.3.