1 Introduction

Engineering materials may contain branched or intersecting cracks as a result of manufacturing or use. When the material is loaded, the crack surfaces may come into contact. Usually, the contact area and the traction distribution are unknown as they depend on the body and cracks geometries and boundary conditions. Closing cracks affects the stress distribution, material strength and stiffness. Due to the complexity of the problem, cracked plates are most often analysed using numerical methods.

Usually, in the literature, single branched or intersecting cracks in finite or infinite plates subjected to static loads are presented. Cheung et al. [1] used the stress functions for the analysis of crucifix cracks, two perpendicular cracks and star-shaped cracks in finite plates. Isida and Noguchi [2] applied the body force method and the perturbation procedure to compute stress intensity factors (SIFs) for various symmetrical and unsymmetrical branched cracks in infinite domains. Chen and Hasebe [3] formulated a singular integral equation to solve the branch crack problem. The method was applied to star-shaped cracks, symmetrical branched cracks and two intersecting cracks. Daux et al. [4] presented the extended finite element method (X-FEM) for the analysis of cracks with multiple branches and cracks emanating from holes. Tan et al. [5] developed the hybrid boundary node method and the displacement discontinuity method for the analysis of a branched crack and a star-shaped crack in a finite plate. Borovik [6] determined the effective elastic properties of a sintered material with branched cracks. A unit cell containing the halves of two adjacent cracks was modelled using the FEM. The influence of different dimensions of crack branches on the effective elastic properties was investigated. For the same material and the computer model, Borovik [7] analysed the effect of crack branch lengths on SIF.

Straight cracks can be partially or completely closed by specific loads and branched or intersecting cracks are frequently closed by any load. Melville [8] presented analytical expressions for the SIF of an embedded straight crack in an infinite medium subjected to uniform compressive stress. Several researchers have used the boundary element method (BEM) for closure of single cracks. Karami and Fenner [9] used the multi-domain BEM to analyse crack closure of straight edge crack and internal slanted crack in a plate. Lee [10] analysed crack closure problems using the dual BEM. The influence of crack size, angle and friction coefficient on SIF for plates with internal and edge cracks subjected to compressive and bending loads was analysed. Tuhkuri [11] used the dual BEM to analyse SIF for plates with a straight crack and a radial crack emanating from a circular hole in an infinite plate. The load that causes propagation of wing cracks was compared with the experimental results. Phan et al. [12] used the symmetric-Galerkin BEM for SIF analysis of a single straight crack, two-wing crack and T-crack in unbounded domains under compression. Zhang et al. [13] determined experimentally the critical stress for a branch crack in a cement mortar specimen subjected to compression. In order to explain the influence of the angle between the crack branches on the critical stress, numerical computations using the FEM and photoelastic test were performed. However, the study did not take into account the contact of crack surfaces. Tofique and Hallback [14] used the distributed dislocation dipole technique and Bueckner’s principle to analyse straight, kinked and branched cracks in plates, where cracks may close under the influence of external load. SIF computed by the proposed method were compared with FEM solutions.

Cracks have a great influence on the elastic properties of materials. Usually, overall properties of cracked materials are analysed by analytical methods, assuming that the cracks are straight and separated. Kachanov [15] considered frictional sliding of randomly oriented penny-shaped cracks in compressed rock. The material compliance was investigated for various axial to radial compression ratios for the case of an axisymmetric load. Kachanov [16, 17] defined the parameters that properly describe the influence of the microstructure on the effective elastic properties by considering the elastic potential. Cracks constrained against the normal opening (sliding cracks) were analysed. Nemat-Nasser and Hori [18] investigated the effect of crack density, friction coefficient and load conditions on the effective bulk modulus and shear modulus using the self-consistent method. More complex homogenization problems are analysed by various computational methods. Yin and Ehrlacher [19] applied the displacement discontinuity BEM to study the effect of crack discretization, size and density on the overall moduli of cracked solids. Huang et al. [20] used the BEM and the unit cell method to calculate the effective properties of solids with randomly distributed and parallel cracks. Renaud et al. [21] applied the indirect BEM to compute effective moduli of brittle materials with cracks of different size, location and orientation. Su et al. [22] applied the FEM in the generalized self-consistent method (GSCM) to compute the effective elastic properties of plates with straight cracks. The influence initial load, crack density, crack orientation and contact of crack surfaces with friction were considered. Grechka and Kachanov [23] analysed the effective elastic properties of solids with interacting and intersecting circular cracks. They showed a good agreement of the FEM results obtained with the use of RVEs with small number of cracks with the non-interaction approximation solutions. Sevostianov et al. [24] studied the influence of the microstructure of sintered metal fibres on elastic properties. Analytical methods were used to calculate the effective properties. The influence of the volume and shape of pores as well as the length of crack branches, which depend on the temperature of sintering, was analysed. Liu and Graham-Brady [25] calculated the compliance of periodically distributed wing cracks under compression. The influence of the number of cracks, their size and orientation as well as the friction coefficient was studied. Analytical results were compared with FEM solutions.

The BEM was applied by Fedelinski [26] to analyse representative volume elements (RVE) with randomly distributed and separated straight cracks. The influence of crack density on effective elastic properties and SIF was studied. The same approach was used by Fedelinski [27] to model sintered metal fibres, which contained regularly distributed voids and branched cracks at the fibre corners. The influence of void shapes and the dimensions of the crack branches on the SIF and elastic properties was investigated. A preliminary analysis of simple plates with cracks subjected to static compression was presented by Fedelinski [28]. The influence of load direction and crack orientation on contact forces, SIF and effective elastic properties for a single inclined crack in an infinite plate, a branched crack in a rectangular plate and multiple parallel inclined cracks in a square plate was studied. Holek and Fedelinski [29] applied finite and the boundary element method to analyse a single inclined crack in an infinite plate, a branched crack in a rectangular plate and a RVE with randomly distributed cracks. The contact pressures between crack surfaces, computed by the two methods, were compared.

The present paper shows the boundary integral equations and the numerical implementation of the BEM for cracked plates. An iterative procedure for determining the contact forces between crack surfaces is described. The original contribution of the work is the application of BEM to closed branched or interesting cracks to analyse contact forces, stress intensity factors and effective elastic properties for various loading conditions.

2 Boundary element method for a plate with cracks

Portela et al. [30] presented the dual boundary element method (DBEM) for traction-free surfaces of straight or kinked cracks. In that paper, contact of crack surfaces was not considered. In the present work, the computer code is further developed and the crack surfaces can be loaded with contact forces. The formulation shown by Portela et al. [30] is briefly described to make the paper self-contained.

Consider a linearly elastic, homogeneous and isotropic plate with a single crack. The two crack surfaces coincide before loading. The boundary of the body Γ can be divided into the external boundary Γe and two crack surfaces Γ+ and Γ−. On the part of the boundary, time-independent in-plane tractions and on the remaining boundary, displacements are prescribed.

The displacement of internal point or a point on the external boundary x′ can be computed using the following boundary integral equation (Aliabadi [31]):

$$ c_{{{\text{ij}}}} ({\text{x}}^{\prime } )u_{{\text{j}}} ({\text{x}}^{\prime } ) = \int\limits_{\Gamma } {U_{{{\text{ij}}}} ({\text{x}}^{\prime } ,{\text{x}})} t_{{\text{j}}} ({\text{x}})d\Gamma ({\text{x}}) - \int\limits_{\Gamma } {T_{{{\text{ij}}}} ({\text{x}}^{\prime } ,{\text{x}})u_{{\text{j}}} } ({\text{x}})d\Gamma ({\text{x}}), $$
(1)

where x is the boundary point, cij is a constant, which depends on the position of the point x′ (for the boundary point it depends on the shape and orientation of the boundary), uj is the displacement component, tj is the traction component, and Uij and Tij are the Kelvin fundamental solutions of elastostatics [31]. For two-dimensional problems, the indices are i, j = 1,2.

The displacements of two coincident points x′ and x″ on the opposite smooth crack surfaces can be expressed by the boundary integral equation (Portela et al. [30]):

$$\frac{1}{2}u_{{\text{i}}} ({\text{x}}^{\prime }) + \frac{1}{2}u_{{\text{i}}} ({\text{x}}^{\prime \prime }) = \int\limits_{\Gamma } {U_{{{\text{ij}}}} ({\text{x}}^{\prime },{\text{x}})} t_{{\text{j}}} ({\text{x}})d\Gamma ({\text{x}}) - \int\limits_{\Gamma } {T_{{{\text{ij}}}} ({\text{x}}^{\prime },{\text{x}})u_{{\text{j}}} } ({\text{x}})d\Gamma ({\text{x}}).$$
(2)

Similarly, the tractions for the same points x′ and x″ can be expressed by the boundary integral equation [30]:

$$\frac{1}{2}t_{{\text{j}}} ({\text{x}}^{\prime }) - \frac{1}{2}t_{{\text{j}}} ({\text{x}}^{\prime \prime }) = n_{{\text{i}}} ({\text{x}}^{\prime })\left\{ {\int\limits_{\Gamma } {U_{{{\text{kij}}}} ({\text{x}}^{\prime },{\text{x}})} t_{{\text{k}}} ({\text{x}})d\Gamma ({\text{x}}) - \int\limits_{\Gamma } {T_{{{\text{kij}}}} ({\text{x}}^{\prime },{\text{x}})u_{{\text{k}}} } ({\text{x}})d\Gamma ({\text{x}})} \right\},$$
(3)

where Ukij and Tkij are the fundamental solutions of elastostatics [31] and ni is an component of the outward normal unit vector at the point x′.

In order to obtain numerical solution, the boundary Γ of the body is divided into boundary elements. Quadratic boundary elements having three nodes are used in the present approach. The displacement equation (1) is applied for collocation nodes along the external boundary, the displacement equation (2) and the traction equation (3) simultaneously for coincident nodes on both crack surfaces. As a result, the following matrix equation is obtained:

$$\left[ {\begin{array}{*{20}c} {{\bf {H}}^{ee} } & {{\bf H}^{e + } } & {{\bf H}^{e - } } \\ {{\bf H}^{ + e} } & {{\bf H}^{ + + } } & {{\bf H}^{ + - } } \\ {{\bf H}^{ - e} } & {{\bf H}^{ - + } } & {{\bf H}^{ - - } } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {{\bf u}^{e} } \\ {{\bf u}^{ + } } \\ {{\bf u}^{ - } } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {{\bf G}^{ee} } & {{\bf G}^{e + } } & {{\bf G}^{e - } } \\ {{\bf G}^{ + e} } & {{\bf G}^{ + + } } & {{\bf G}^{ + - } } \\ {{\bf G}^{ - e} } & {{\bf G}^{ - + } } & {{\bf G}^{ - - } } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {{\bf t}^{e} } \\ {{\bf t}^{ + } } \\ {{\bf t}^{ - } } \\ \end{array} } \right],$$
(4)

where ue, u+, u− and te, t+, t− contain nodal values of displacements and tractions along the external and opposite crack surfaces, respectively. The submatrices H and G depend on the fundamental solutions of elastostatics and quadratic interpolating functions. The columns of matrices H and G and elements of matrices u and t are reordered according to the boundary conditions.

The matrix equation is solved, and unknown displacements and tractions along boundaries of the body are obtained. The stress intensity factors (SIF) are computed using the path-independent J-integral [30]. In a similar way, the method can be applied to multiple branched or intersecting cracks.

3 Contact of crack surfaces

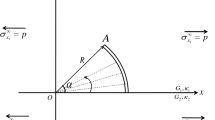
When a cracked plate is loaded, especially with branched or intersecting cracks, the crack surfaces can come into contact. In order to analyse contact tractions, two arbitrary coincident nodes x′ and x″ on opposite crack surfaces are selected (Fig. 1a). The local coordinate axes xt-xn are introduced at nodes x′ and x″, where xt is parallel and xn is perpendicular to crack surfaces. The relative displacements of nodes x′ and x″ in the local crack coordinate axes xt-xn are denoted by Δut and Δun (Fig. 1b).

Fig. 1
figure 1

Arbitrary coincident nodes x′ and x″ on crack surfaces: a local crack coordinate system, b relative displacements, c contact tractions

Full size image

Possible contact tractions in the local coordinate axes xt-xn at nodes x′ and x″ are denoted, by: tt′, tn′ and tt″, tn″, respectively (Fig. 1c). The contact tractions satisfy the following equilibrium equations: tt′ = tt″ and tn′ = tn″.

In the present work, frictionless contact between the crack surfaces is assumed. In this case, there can be two different modes of contact:

  • (a) separation mode: Δun > 0.

    tt′ = 0, tn′ = 0, the unknowns are: Δut, Δun.

  • (b) slip mode: Δun = 0.

    tt′ = 0, the unknowns are: Δut, tn′.

The boundary displacements and tractions along the crack surfaces should satisfy these contact conditions.

In order to satisfy the contact conditions, the following iterative procedure has been developed. For each iteration, the relative displacements in the normal Δun (crack opening) and tangential directions Δut (crack sliding) of each pair of coincident nodes on opposite crack surfaces are computed. If the opening is negative, it means that the penetration of crack surfaces occurs. In this case, the pair of nodes is subjected to small normal tractions, which reduce overlapping of the crack surfaces. The computations are repeated with the load on the crack surfaces. In the next iteration, the crack opening is analysed, and if it is negative, the normal tractions on crack surfaces are increased. If the crack opening is positive and the crack is loaded, the tractions are reduced. The iterative process is repeated until the crack overlapping Δun is less than the prescribed tolerance. The tolerance depends on the initial maximum absolute value of the crack opening Δumax. The change of the normal crack tractions Δtn is constant, and it is taken as a fraction of the applied external traction.

The algorithm of determining crack tractions is as follows:

  • (1) Assume traction-free crack surfaces.

  • (2) Compute crack opening and sliding for each pair of coincident crack nodes.

  • (3) If the crack opening is positive or zero with a specified tolerance, then finish computations.

  • (4) If the crack opening is negative, then increase normal tractions on the crack surfaces.

  • (5) If crack opening is positive and the crack is loaded, then reduce normal tractions on crack surfaces.

  • (6) Go to step 2.

The stress intensity factors for cracks are computed using the path-independent J-integral. The J-integrals for cracks without contact and with frictionless contact have the same forms (Tuhkuri [11]).

4 Numerical examples

Three numerical examples are analysed. The first example shows a single star-shaped crack in a square plate, which is subjected to different tractions. An influence of the load conditions on the contact of the crack surfaces is studied. The second example—multiple interacting cracks in an infinite plate—is used to verify accuracy of the BEM by comparison with the available solutions. Two different crack configurations are considered—loose and tight. The last example shows randomly distributed cracks in a square plate. The plate, which contains intersecting cracks, is subjected to various tractions in order to obtain effective elastic properties. Stress intensity factors are computed for each numerical example.

4.1 Star-shaped crack in a square plate

A square plate of width 2w and height 2 h (w = h) contains in the centre a star-shaped crack having six branches, as shown in Fig. 2. The length of the branches is a, and the angle between the branches is α = 1/3π. The branches emanate from a small hole having the radius r. The proportions of dimensions are a/w = 0.5 and r/a = 0.05. The Poisson ratio is v = 0.3, and the plate is in plane strain conditions. Four different load cases are considered: (a) horizontal tension t1 = p, (b) horizontal compression t1 = − p, (c) vertical tension t2 = p and (d) vertical compression t2 = − p.

Fig. 2
figure 2

Star-shaped crack in a square plate

Full size image

The plate boundaries are divided into 206 boundary elements (80 elements for the external boundary, 20 elements for each crack branch and 6 elements for the hole). The relative load increment Δtn/p = 0.005 and the displacement tolerance Δun/Δumax = 0.001 are assumed. The initial and deformed shapes of the crack for the different load cases are shown in Fig. 3. If the crack is subjected to horizontal tension, the four inclined branches B are opened. If the crack is subjected to vertical tension, two horizontal branches A are opened. The horizontal branches A are in contact without sliding along whole surfaces when the crack is subjected to horizontal tension or vertical compression. In these cases, the material along the surfaces behaves like a continuous material. In order to verify accuracy of results, the normal contact pressure is compared to the normal stress in the continuous material. Normal stresses are obtained by analysing crack with four inclined branches B. The comparison is shown in Fig. 4. The agreement of the results is good.

Fig. 3
figure 3

Star-shaped crack in a square plate—initial shape (dashed lines) and deformed shape (continuous lines): a horizontal tension, b horizontal compression, c vertical tension and d vertical compression

Full size image
Fig. 4
figure 4

Comparison of normalized contact pressure along the horizontal branch A with normalized normal stress of the continuous material: a horizontal tension, b vertical compression

Full size image

The maximum values of pressure for vertical compression are greater than for horizontal tension. Normal pressure for horizontal tension has a maximum for about x1/a = 0.35.

It follows from the equilibrium equation that average normal stress along the entire horizontal line of symmetry for horizontal tension is tn/p = 0, and for vertical compression is tn/p = 1.05. Non-fractured material along the horizontal line of symmetry is subjected to tension in case of horizontal tension and compressed by vertical compression.

If the contact of crack surfaces is not taken into account, overlapping occurs in case: (a) for horizontal branches A, (b) inclined branches B, (c) inclined branches B, and (d) horizontal branches A. In general, when a branched crack is subjected to tension, there is overlap with branches whose direction is close to the applied load, and in compressed cracks for branches whose direction is close to the direction perpendicular to the applied load.

The normalized stress intensity factors K/Ko, where Ko = p(πa)1/2, are given in Table 1.

Table 1 Normalized stress intensity factors K/Ko
Full size table

4.2 Multiple interacting cracks in an infinite plate

An infinite plate contains four cracks: two straight inclined cracks, a kinked crack and a branched crack, as shown in Fig. 5. The length of crack branches is a = 1; the coordinates of crack centres and the crack branch angles are given in Fig. 5. The plate is subjected in infinity to biaxial tension t1 = 0.50 and t2 = 1.00 and shear load t12 = 0.25. Two crack configurations are considered: loose (Fig. 5a) and tight (Fig. 5b). The Poisson ratio is v = 0.3, and the plate is in plane stress conditions. The problem was formulated, and the SIFs were computed by Yavuz et al. [32]. The infinite plate is modelled as a large square plate with edge dimensions equal to 100. The plate boundaries are divided into 280 boundary elements (100 elements for the external boundary and 20 elements for each crack branch). The load increment is assumed as Δtn = 0.005 and the relative displacement tolerance Δun/Δumax = 0.001.

Fig. 5
figure 5

Multiple interacting cracks in an infinite plate—geometry and tractions: a loose configuration, b tight configuration

Full size image

The deformed crack shapes for the loose configuration are presented in Fig. 6. The stress intensity factors computed by BEM, the results published by Yavuz et al. [32] and the relative differences between them ΔK/Ko, where Ko = t2(πa)1/2 are given in Table 2. The maximum normalized differences are ΔKI/Ko = 0.32% and ΔKII/Ko = 0.24%. The results agree very well.

Fig. 6
figure 6

Deformed shapes of the cracks for the loose configuration

Full size image
Table 2 Stress intensity factors for loose configuration of multiple interacting cracks
Full size table

The deformed crack shapes for the tight configuration are presented in Fig. 7. The stress intensity factors computed by BEM, the results published by Yavuz et al. [32] and the relative differences between them ΔK/Ko are given in Table 3. The maximum normalized differences are ΔKI/Ko = 0.55% and ΔKII/Ko = 0.25%. The results agree very well. As can be seen in Table 3 and Fig. 7, KI for the crack tip Q is negative and there is an overlapping of the crack edges, because in (Yavuz et al. [32]) and in the present solution, the contact of crack surfaces was not taken into account.

Fig. 7
figure 7

Deformed shapes of the cracks for the tight configuration—contact ignored

Full size image
Table 3 Stress intensity factors for tight configuration of multiple interacting cracks—contact ignored
Full size table

The problem was reanalysed by considering contact of crack surfaces. The deformed shapes of the cracks are shown in Fig. 8, and the SIFs are given in Table 4. The SIF for the crack tip Q is now positive. Table 4 shows the relative differences in solutions ΔK/Ko when contact is considered and ignored. The greatest differences are for the crack tips P, Q and R of the branched crack and the nearby crack tips D and F.

Fig. 8
figure 8

Deformed shapes of the cracks for the tight configuration—contact considered

Full size image
Table 4 Stress intensity factors for tight configuration of multiple interacting cracks—contact considered
Full size table

4.3 Randomly distributed cracks in a square plate

A computer code for generation of randomly distributed cracks was developed. The straight cracks of length 2a are situated in a rectangular domain of width 2w and height 2 h, as shown in Fig. 9. It is assumed that the minimum distance between the cracks and the outer boundary of the domain is d. The computer code generates randomly the coordinates of the crack centre and its angle with respect to the global coordinate system. In the case of intersection of cracks, the computer code calculates the coordinates of intersection point, the angle between the cracks and the number of intersection points in the whole structure.

Fig. 9
figure 9

Randomly distributed cracks in a rectangular plate

Full size image

The computer code is used to generate 20 cracks. Four different lengths of the cracks are considered a/w = 0.05, 0.10, 0.15 and 0.20. The following dimensions are assumed: w = h and d/w = 0.05. One million of structures are considered to obtain statistical representation of the results. The number of intersection points depends on the length of cracks, as shown in Table 5.

Table 5 Total number of intersection points in one million structures
Full size table

In Fig. 10, the histogram shows the number of structures having a specific number of intersections for different lengths of cracks. For small cracks (a/w = 0.05, 0.10) most structures have only one intersection point. For a/w = 0.15, the largest part of the structures has 3 intersection points and for a/w = 0.20–6 intersection points.

Fig. 10
figure 10

Histogram of number of intersections

Full size image

One of the plates with randomly generated cracks for a/w = 0.2 has been selected for the numerical analysis.

The density of cracks can be defined as (Kachanov [17]):

$$\rho = \frac{{na^{2} }}{A},$$
(5)

where n is the number of cracks and A is the RVE area. For the considered cracked plate, the density is ρ = 0.2.

The plate is shown in Fig. 11. The plate contains cracks with four intersection points, which are denoted by A, B, C and D in Fig. 11. The relative coordinates of crack tips are given in Table 6, and the relative coordinates of intersection points and the angles α between the cracks are presented in Table 7. The Poisson ratio is v = 0.3, and the plate is in plane strain conditions.

Fig. 11
figure 11

Square plate with 20 randomly distributed cracks

Full size image
Table 6 Coordinates of crack tips
Full size table
Table 7 Geometry of intersecting cracks
Full size table

The plate is subjected to three different boundary conditions shown in Fig. 12—tension t1 = p or compression t1 = − p in the horizontal direction, tension t2 = p or compression t2 = − p in the vertical direction and shear load in two different directions t12 = p and t12 = − p. The plate is simply supported at the centres of the lower and upper edge of the plate.

Fig. 12
figure 12

Boundary conditions for the square plate with 20 randomly distributed cracks: a tension in the horizontal direction, b tension in the vertical direction, c shear load

Full size image

The cracked plate is divided into 480 boundary elements (80 elements for the outer boundary of the plate and 20 elements for each crack). The increment of contact forces in each iteration is assumed to be 0.01 Δtn/p and the tolerance of cracks penetration—0.01 Δun/Δumax.

The plate is analysed without contact and with contact of crack edges. Figures 13–16 show initial and deformed shapes of cracked plate for different boundary conditions.

Fig. 13
figure 13

Square plate with 20 randomly distributed cracks under the horizontal tension—initial shape (dashed lines) and deformed shape (continuous line): a tension without contact, b tension with contact of crack surfaces

Full size image
Fig. 14
figure 14

Square plate with 20 randomly distributed cracks under the horizontal compression—initial shape (dashed lines) and deformed shape (continuous lines): a compression without contact, b compression with contact of crack surfaces

Full size image
Fig. 15
figure 15

Square plate with 20 randomly distributed cracks under the shear load—case 1—initial shape (dashed lines) and deformed shape (continuous line): a shear load without contact, b shear load with contact of crack surfaces

Full size image
Fig. 16
figure 16

Square plate with 20 randomly distributed cracks under the shear load—case 2—initial shape (dashed lines) and deformed shape (continuous line): a shear load without contact, b shear load with contact of crack surfaces

Full size image

The normalized stress intensity factors for all crack tips are given in Tables 8 and 9, where the normalized SIF is Ko = p(πa)1/2. SIFs are not given for compressive and shear load 2 without contact because they have exactly the same absolute values as for the tensile and shear load 1 without contact, respectively, but the opposite sign. After applying the contact procedure, some crack tips have negative KI, but the absolute values are smaller compared to SIF for other cracks. The overlapping of crack edges can be further reduced by using smaller load increments and smaller overlap tolerance.

Table 8 Normalized stress intensity factors – horizontal load
Full size table
Table 9 Normalized stress intensity factors—shear load
Full size table

Average strains are computed using the RVE boundary displacements:

$$\overline{\varepsilon }_{{{\text{ij}}}} = \frac{1}{2A}\int\limits_{\Gamma } {(u_{{\text{i}}} n_{{\text{j}}} + u_{{\text{j}}} n_{{\text{i}}} )d\Gamma } ,$$
(6)

where Γ is RVE boundary and ni is the component of the normal outward unit vector to the boundary.

Average stresses are computed using the tractions along the RVE external boundaries:

$$\overline{\sigma }_{{{\text{ij}}}} = \frac{1}{A}\int\limits_{\Gamma } {t_{{\text{i}}} x_{{\text{j}}} d\Gamma } ,$$
(7)

The average strains and stresses are used to compute effective elastic properties.

The normalized effective properties for different loads are given in Tables 10 and 11. The properties are normalized with respect to properties of the plate without cracks. In the case of tension, the contact of crack surfaces slightly increases the Young moduli E. The significant overlapping is for intersecting cracks, which are in the direction to the applied load, as can be seen in Fig. 13a. This overlapping has small influence on strains in the direction of applied load and the Young modulus. The application of the contact procedure reduces overlapping and strains in the perpendicular direction. Therefore, the Poisson ratios decrease when the contact is taken into account, as can be seen in Table 10.

Table 10 Normalized effective elastic properties—Young’s modulus and Poisson’s ratio
Full size table
Table 11 Normalized effective elastic properties—shear Kirchhoff’s modulus
Full size table

The Young moduli of the cracked plate subjected to compression are significantly greater than that of the plate subjected to tension. The average absolute value of crack angles relative to the x1 axis is 39.6°. Since this angle is smaller than the angle relative to the x2 axis, the crack opening is smaller and the effective Young modulus in the horizontal direction is greater than in the vertical direction. The Poisson ratio v is reduced by cracks when the plate is in tension and increased in compression. The increase in the Poisson ratio was shown by Kachanov [15] for axisymmetric compressed rocks. Similar normalized values of the Young moduli and Poisson ratios in tension without contact mean that the Poisson ratios decrease, mainly due to increased strains in the direction of the load. The contact of crack surfaces increases the shear Kirchhoff moduli G.

Su et. al [22] analysed separated straight cracks using the GSCM combined with the FEM. The analysed plates were in plane stress state, and the Poisson ratio was v = 1/3. For the same crack density ρ = 0.2, as in the present example, randomly oriented cracks, initially stress-free state, they obtained E/Eo = 0.530 for tension, E/Eo = 0.850 for compression and G/Go = 0.701 for shear load with contact of crack surfaces without friction. These values are similar to the results obtained in the present work.

5 Conclusions

The computer method and code were developed for plates with multiple randomly distributed cracks, including intersecting cracks, using the boundary element method. Possible contact tractions between crack surfaces are computed using an iterative procedure. Three numerical examples are analysed to show the accuracy of the method and possible applications. The first example—a star-shaped crack in a square plate, shows that the contact of crack surfaces can occur when the crack is subjected to tension. The example demonstrates the accuracy of the contact tractions between crack surfaces. The second example—multiple interacting cracks in an infinite domain—shows a very good agreement of the stress intensity factors with the available results presented in the literature for a loose and tight configurations. Additionally, the influence of contact forces on SIF is presented. The third example—randomly distributed cracks in a square plate—shows the behaviour of the plate under different types of loads. Effective elastic properties—the Young moduli, the Poisson ratios and the shear Kirchhoff moduli—are computed for the cracked plate. Cracks reduce the effective Young modulus of a stretched material more than a compressed material. The application of the contact procedure has small influence on the effective Young modulus of a material subjected to tension. The Poisson ratio is lower in the stretched material and greater in the compressed material than the Poisson ratio of the material without cracks. Stress intensity factors are computed for each considered structure.