Experimental and numerical investigation of the flow in a cylindrical cavity with an unsteady rotating lid

Abstract

In this paper, we analyse the flow in a cylindrical cavity of aspect ratio H/R = 2, with a top lid rotating with a sinusoidal time-varying speed. The Reynolds numbers, based on the time-averaged rotating speed and the radius of the cavity (Re = $\Omega _0 R^2/\nu$) are 2800, 3500 and 4100. Particle Image velocimetry measurements and numerical simulations are performed to determine the effect on the flow of different imposed frequencies on the rotating lid. The acceleration and deceleration of the lid produce a marked pulsatile flow behaviour. It is found that at low Reynolds numbers the frequencies measured in the flow coincide with the frequency imposed on the rotating lid, while at the largest Re considered the flow frequencies are significantly lower, especially when the frequency of the disk is large. The fluctuations induced in the vertical velocity component are about 100% of the instantaneous values while for the angular component the fluctuations are of the same order as the instantaneous values.

1 Introduction

Swirling flows or rotating flow in an enclosure replicates many natural phenomena such as tornadoes, water circulation in oceans, meteorological movements, as mentioned by Childs [1] in his book called “Rotating flow”. The swirling flow in a cylindrical cavity has been studied for more than 50 years by Escudier [2], Lopez et al. [3], Westergaard et al. [4], Sørensen et al. [5], Gelfgat et al. [6] and others. The cylinder with the rotating lid being the most straightforward configuration has been extensively used for understanding the transitions and instability in the rotating flow, both experimentally and numerically. One of the earliest experimental investigations on the lid-driven cavity was initiated by Vogel [7] and Ronnenberg [8] using Laser-Doppler measurements. Escudier [2] identified the re-circulating bubbles at the cylindrical cavity axis and described as the vortex breakdown. This vortex breakdown was further investigated this phenomenon by Westergaard et al. [4] using PIV techniques. Spohn et al. [9] used fluorescent dye & electrolytic precipitation to study the vortex breakdown bubbles. They described the appearance of vortex breakdown this phenomenon bubbles for a range of Reynolds numbers using several sets of flow structures. They also reported the origin of the asymmetries, spiral-shaped structures, and the separation lines near the sidewall boundary layer of the cylinder.

Sotiropoulos et al. [10] numerically reproduced the asymmetries of the flow observed by Spohn et al. [9]. The numerical simulations were carried out in transient mode even the low Reynolds numbers were considered. The Lagrangian tracking of fluid particles near the vortex breakdown revealed that asymmetries are notable at the very early stages of the vortex breakdown with an uneven distribution of the fluid particles along with the vortex bubble’s structure. They have also shown the stability loss in the sidewall boundary layer of three-dimensional disturbances in the form of counter-rotating pairs of spiral vortices [11, 12].

Many researchers extensively studied the cavity flows for the advection and convection in the vortex breakdown, also mentioned as Chaotic advection or convection. The chaotic nature of the flow in the interior of the vortex breakdown bubble mechanism helps to enhance mixing in non-turbulent flows. This phenomenon manifests itself in the trajectories of passive Lagrangian markers that are advected by a flow field of very simple Eulerian structure [13, 14]. The Lagrangian transport within the bubbles was studied by using PLIF experimental means and show that the spatial distribution of the dye tracer varies continuously in a random manner even though the flow fields are steady from the Eulerian standpoint [7]. This finding is consistent with the arbitrarily long šil’nikov transients of upstream-originating orbits documented numerically by Sotiropoulos et al. [15].

Romano et al. [16, 17] carried out similar studies in the cylindrical cavity with partially filled fluid to understand the liquid–gas interface and studied that the Chaotic advection is caused by a breakup of a degenerate heteroclinic connection between the two saddle foci when the flow becomes three-dimensional. The Froude number and capillary number extinct at the limits of increasing Reynold’s numbers. The chaotic mixing in lid-driven cavities has been analysed by [18, 19]. They found that in general terms, at lower Reynolds number the chaotic mixing can be more important than higher Reynolds numbers. The studies by Ottino et al. [20, 21] have some similar convection behaviour and studied the flow for mixing based on the chaotic nature of the flow. However, the experiments were analysed for the rotating cylinder, which slightly different from our case having a rotating lid. Still, some flow phenomena were similar, as mentioned by Sortipoulas [10,11,12,13, 15]; this could be due to the cylindrical cavity. The turbulence in the rotating flow is studied by Gollub et al. [22].

Based on the height-to-radius aspect ratio and the lid’s rotation rate, the flow may be subjected to complicated transitions with three-dimensional unsteadiness causing re-circulation, meridional circulation, fluctuations, and azimuthal waves of the flow. Fluctuations in the fluid flow that propagate along the azimuth direction due to the angular velocity component in the cavity are called azimuthal waves. Sørensen et al. [5] mapped the flow behaviour at several aspect ratios of the cylindrical cavity with azimuthal modes of different wave numbers (K). Each aspect ratio has a different number of waves with respect to Reynolds numbers ${\mathrm {Re} = \Omega _0 R^2/\nu }$. For instance, the aspect ratio H/R = 3 at Re = 2800 causes fluctuations in the flow results in wave number K = 4, K = 0 at Re = 2900 and K = 5 at Re = 4100. The above-referred H/R = 3, the fluctuation causing the flow having the first wave corresponding to K = 4 appears at Re = 2800, called a critical Reynolds number.

Similarly, the critical Reynolds number for H/R = 3.5 is Re = 2100 with K = 3 for the first wave. The critical Reynolds numbers to the aspect ratios were tabulated and plotted, respectively, in Sørensen et al. [5] and Gelfgat et al. [6]. The flow behaviours were also studied using computational techniques. Daube and Sørense [23, 24] solved the Navier–Stokes equations for unsteady axisymmetric cases and wrote them as vorticity-stream functions. They simulated the flow in a cylindrical tank with a rotating bottom. Lopez et al. [25] have shown that the flow remains axisymmetric over a broad range of governing parameters and Reynolds numbers and used Navier–Stokes formulation to solve the time accurate, explicit finite difference equations. Other authors [26,27,28,29,30,31] described the vortex breakdown mechanism; they also computed the negative azimuthal component for the vorticity, using a simple, steady, inviscid, axisymmetric equation of motion. Lopez and Perry [32] described the swirling motion in the meridional circulation, explaining the vortex bubble’s formation in the centre axis as Escudier [4] explained, the separation of the bubbles regarding a range of Reynolds numbers and the vortex bubble’s disappearances. The vortex bubble and its influence in the flow were numerically reconfirmed by Mullin [33,34,35]; Kobine and Mullin [36, 37].

Sørensen and Christensen [38] investigated the flow behaviour with an experiment that involved a periodical insertion of particles in the flow. They identified the squeezing and folding structures on the centre axis of the vortex core region. These phenomena might be a consequence of the dynamical fluid flow in the unsteady domain as conjectured by them. Hence these structures could also be considered as the effects of the hysteretic jump of azimuthal modes. They also reported the vortex breakdown and the divergence in the swirling flow due to the fluid’s inertial rebound to the cavity walls. Brøns et al. [39] analysed the topological streamlines of vortex breakdown in the co-rotating and counter-rotating lids and concluded that the cylinder flow is sensitive to the rotation rate. Watson et al. studied the evolution of the vortex breakdown numerically [40].

As many authors have described, the rotating cavity flow chiefly depends on two factors: (a) the aspect ratio and (b) the Reynolds number. The flow within the cylindrical cavity can be categorized as follows: (a) steady, laminar, axisymmetric without separation (Peres et al. [41, 42]) (b) steady laminar, axisymmetric with vortex breakdown composed of two bubbles in the axis of symmetry (Gelfgat et al. [6]) (c) periodic laminar unsteady axisymmetric and non-axisymmetric flow with several azimuthal waves (fluctuations) depending on the aspect ratio and Reynolds number (Sørensen et al. [5], Peres et al. [41]) (d) transitional unsteady flow (Sørensen et al. [5]) and (e) fully turbulent flow (Sørensen et al. [5], Gelfgat et al. [6]).

The rotating lid induces a radial motion due to the centrifugal force. When the Reynolds number increases, the flow’s topology suddenly changes from steady to unsteady regime. For the cylindrical cavity with a top rotating lid, the studies have been carried out only for cases having constant rotating velocities. In this paper, we analyse the lid-driven cylindrical cavity’s flow behaviour for different Reynolds numbers under various sinusoidal rotations of the lid apart from the lid’s constant rotating condition. The results of the investigation for steady axisymmetric and unsteady non-axisymmetric structures are presented. The temporal and spatial dynamics of the flow are reported.

Fig. 1

Basic design and monitor points: $(r, z) = 1(3R/4, H/4), 2(R/2, H/4),$ 3(R/4, 3H/4), 4(3R/4, H/2),  5(R/2, H/2), 6(R/4, H/2),  7(3R/4, 3H/4), 8(R/2, 3H/4), 9(R/4, 3H/4)

Fig. 2

Schematic diagram of experimental setup and instrumentation

2 Experimental model

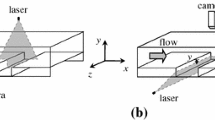
A cylindrical container made of plexiglass with an inner diameter of 209 mm is used for the experiments (Fig. 1). The top lid of the cavity is connected to a stepper motor with an encoder linked to a computer to control the rotation speed. The lid and motor are connected using a rod for the lifting flexibility to vary the height (H) of the domain, which allows the cylindrical cavity to adjust the aspect ratio (H/R) between 0 and 2. The gap between the rotating disk and the cylinder’s wall is $\sim$ 1 mm. The working fluid is a 70% glycerine–water mixture. The Schematic diagram of experimental setup and instrumentation is shown in Fig. 2.

The cylindrical cavity is enclosed with a cubical transparent plexiglass box with dimensions 300 $\times$ 300 $\times$ 300 mm. The space between the cylinder and the box is filled with the same working fluid to minimize optical deviations. The density of the fluid ($\sim$ 1201 kg/m$^3$) and the viscosity ($\sim$ $2.9045\times 10^{-5}$ m$^2/$s) are maintained constant and measured before each experiment. For PIV measurements polyamide beads with an average diameter of $\sim$10 $\mu$m were used as seeding particles.

The experiments were carried out with a cylinder height of H = 209 mm. The error in the aspect ratio is less than 0.1%. The maximum Reynolds number, based on the radius of the cylinder and the maximum linear velocity of the lid, was 4100 and it corresponds to a rotation rate of 113.81 ± 0.02 RPM. Since the viscosity of the fluid is sensitive to temperature, it is maintained constant to avoid variations in the Reynolds number during each experiment. The total error of the Reynolds number did not exceed ± 0.05%.

The 2D Particle Image Velocimetry (PIV) was performed using a 5W green laser (532 nm) for illumination and the high-speed camera (Photron mini UX) triggered using a pulse generator. The optical system is composed of two lenses. One forms the beam and the other generates a light sheet of about 1 mm of thickness. Two images of an illuminated plane with a resolution of 1280 $\times$ 1024 pixels were captured at every 0.1 s with an interval of 0.004 s. This time interval produces maximum displacements of about 20 pixels. Each image was taken with an exposure time of 1/1000 s. The images were saved in the computer and processed with an in-house PIV code. The interrogation area was 32 $\times$ 32 pixels and the overlapping was 16 pixels. The error of the PIV technique used has been estimated by analysing synthetic images of particles displaced according to a solid body rotation. It has been found that the error obtained using the same PIV parameters as those used in the experiments is about 3% for the maximum velocities.

Time histories of angular radial and axial velocity were computed at various planes and points in the flow field using the PIV data. The data were collected at the eight points as indicated in Fig. 1. They were located at the horizontal planes z = 3H/4, z = H/2, z = H/4 and at the vertical plane y = 0. The flow velocities and the time histories were recorded and used to determine the frequency applying spectral analysis, and the results were compared to the predictions of Sørensen et al. [5] and Gelfgat et al. [6].

In this work, two different conditions of the lid rotation were considered: constant and sinusoidal variation of the rotation rate. The sinusoidal variation of the rotation rate is achieved by controlling the motor using an encoder. A 20% amplitude variation in angular velocity was adopted as

$$\begin{aligned} \Omega _{\omega _k} = \Omega _0 (1 + 0.2 sin ( \omega _k \Omega _0 t)), \end{aligned}$$

(1)

where the non-dimensional frequency is $\omega _k=2\pi f\Omega _0$, following the notation by Sørense et al. [5]. f is the dimensional frequency (Hz) and $\Omega _0$ (rad/s) is the dimensional rotating speed.

The flow is also governed by three non-dimensional parameters (a) the aspect ratio of the cavity H/R, (b) the non-dimensional amplitude $A^*=\frac{\Omega _\mathrm{max}}{\Omega _0}$ where $\Omega _\mathrm{max}$ is $\Omega _0$ + 0.2$\Omega _0$, and (c) the Reynolds number ${\mathrm {Re} = \Omega _0 R^2/\nu }$.

The effects of the sinusoidal rotation of the lid are analysed for Re = 2800, 3500 and 4100 at H/R = 2. The selected values of the non-dimensional frequency were $\omega _k$ = 0.236, 0.098 and 0.084 according to the values reported by Sørensen et al. [5] to investigate the flow at the same Reynolds numbers (refer Table 1 from [5]) in which Sørensen et al. tabulated the neutral and critical Reynolds numbers, and associated non-dimensional frequencies, as functions of wave number and aspect ratio.

3 Computational model

The cylindrical cavity is filled with an incompressible Newtonian fluid and the flow is driven by a rotating lid. The governing continuity and momentum equations can be written as

$$\begin{aligned}&\overrightarrow{\bigtriangledown } . \overrightarrow{v} = 0, \end{aligned}$$

(2)

$$\begin{aligned}&\rho \left( \frac{\partial \overrightarrow{v}}{\partial t} + (\overrightarrow{v}.\overrightarrow{\bigtriangledown }) \overrightarrow{v} \right) = - \overrightarrow{\bigtriangledown } p + \mu {\bigtriangledown }^2 \overrightarrow{v}. \end{aligned}$$

(3)

The non-slip boundary conditions are imposed on the walls of the cavity. The cylindrical wall and the bottom wall are at rest. At the top rotating lid the local azimuthal velocity component is set to be proportional to the radial position with the instantaneous rotation rate (i.e. $v_\theta (r,\theta ,t)=\Omega (t) r$ and $\Omega (t) = \Omega _0 (1 + 0.2 \hbox {sin} ( \omega _k \Omega _0 t))$. The discontinuity of the velocity boundary condition at the edge of the rotating lid did not produce any observable numerical instability [17].

The flow inside the cylindrical cavity was computed numerically using a cylindrical design with a rotating lid at the top and a stationary wall at the bottom, as shown in Fig. 1. A structured-nonuniform mesh was used for the numerical study. After the mesh independency test, the mesh with 0.7 million nodes was selected, since results with a mesh of 1.9 million nodes were very similar. The governing equations were solved numerically with the finite volume code ANSYS-Fluent R12.

The simulation was initialized with density- based, transient condition. The solution was computed until the flow reached the statistically fully developed condition with a non-dimensional time step $\varDelta t$* = 0.3 ($\varDelta t$* = $t\Omega _0$). An user-defined function was used to define and impose the sinusoidal rotation of the lid.

A central-differencing third-order MUSCL spatial discretization was used for flow, while the second-order implicit formulation was used for the transient temporal discretization. Gradient reconstruction was accomplished by Least-Squares cell-based algorithm.

4 Results

In this study, we analyse the flow behaviour in a cylindrical cavity with aspect ratio H/R = 2 for lid rotation rates corresponding to Re = 2800, 3500, and 4100. Both constant rotation rates and sinusoidal time evolution of the velocity of the lid are considered.

Table 1 shows the cases analysed. It indicates the Reynolds number, the non-dimensional frequencies imposed to the lid, the non-dimensional periods associated with the corresponding frequencies and the non-dimensional measured frequencies of the flow and the wave numbers. The time scale for the definition of the dimensionless quantities is the inverse of the time-averaged rotation rate of the lid.

The flow field for the constant rotation is used to validate our results with those reported by S$\phi$rensen et al. [5], Peres et al. [41], Gelfgat et al. [6]. Depending on the Reynolds number and aspect ratio the flow has vortex bubbles at the centre of the cavity along the vertical plane, as reported by Escudier [4]and Peres et al. [41]. Simulations of the flow at steady state carried out under the same flow conditions (Re = 1000, 1850 and aspect ratio $H/R = 2$) as those used by Peres et al. [41] are found to be in agreement. For the constant rotating condition, at Re =2800, the flow in the cavity is unsteady and shows a fluctuation wave with a wave number K = 0 associated with the non-dimensional frequency $\omega _k$ = 0.236, according to the experiments of Sørensen et al. [5] and the simulations of Gelfgat et al. [6]. Our simulation predicts a non-dimensional frequency $\omega _k$ = 0.23 while from the experiment the frequency obtained is $\omega _k$ = 0.26, as indicated in Table 1. Similarly, at Re =3500, we obtain, experimentally, low-intensity velocity fluctuations with K = 1 at a frequency $\omega _k$ = 0.0819. According to Sørensen et al. [5], the flow has a second fluctuation wave K = 1 at Re = 3200 with a frequency (${\omega _k}$ = 0.84 ). At Re = 4100, the flow exhibits perturbations with wave numbers K = 0, 1, 2 and 3.

Table 1 Flow conditions and frequencies

When the sinusoidal variation of the rotation rate of the lid is imposed, the positive acceleration generated causes the fluid to flow downwards near the wall and raise at the centre of the cavity. While the deceleration of the lid causes the fluid to reduce the radial motion. This reduction in rotation causes the deceleration of the flow near the wall and near the central region of the cavity. The alternance of these positive and negative accelerations imposes marked periodic fluctuations of the flow within the cavity.

4.1 Unsteady sinusoidal rotation at Re = 2800

As shown in Table 1, for this case we used two frequencies for the perturbation of the rotation rate of the disk, $\omega _k =0.236$ and $\omega _k = 0.084$.

For the cases with sinusoidal rotation, the periodic flow is phase averaged using the flow frequencies indicated in Table 1, which have been obtained from the power spectra of the measured velocity signals. Between 40 and 50 individuals are used for averaging. It can be seen that at Re = 2800 the frequencies imposed to the disk are very similar to those measured within the flow.

Figure 3 illustrates the comparison of the experimental and numerical power spectra of the angular velocity signal at the radial position 3R/4 and height H/4 (see point 1 Fig. 1). It can be seen as an excellent agreement between the simulations and the measurements. The spectral plot shows a peak at $\omega _k$ = 0.239 and harmonics.

Fig. 3

Comparison of experimental and numerical results for the sinusoidal rotation ($\Omega _{\omega k}$) at the point 1 in Fig. 1 (3R/4, H/4) having Re = 2800, H/R = 2 with a 20% increased amplitude and the non-dimensional frequency $\omega _k = 0.236$

Figure 4 compares the numerical and experimental phase-averaged results during a complete cycle. Figure 4a shows the instantaneous and fluctuating angular velocities at z = H/4. The comparison of the instantaneous angular velocities at point 1 (3R/4, H/4) is shown in Fig. 4b. Figure 4c shows the instantaneous and fluctuating axial velocities at the vertical plane y = 0 of the cavity. In Fig. 4b the snapshots corresponding to Fig. 4a, c are indicated with letters.

Fig. 4

Re = 2800, H/R = 2 with a 20% increased amplitude for $\Omega _{\omega K}$= 0.236 (a) instantaneous and fluctuations of the angular velocity at z = H/4 [horizontal plane] (b) phase averaged instantaneous angular velocity at (3R/4, H/4) for a period and (c) instantaneous and fluctuations of the axial velocity at y = 0 [vertical plane]

Figure 4a reveals that the angular velocity component near the wall reaches a maximum at non-dimensional time of about 5 (see Fig. 4b) and progressively decreases until time 26, which corresponds to the period of the cycle. Simultaneously, the angular velocity component near the axis of the cavity follows the opposite trend (i.e. at time about 5 it is minimal). The fluctuations obtained numerically are axisymmetric during the whole period and their intensities are of the same order of magnitude as the instantaneous values. In the experimental measurements of the instantaneous vertical velocity component a certain degree of non-axisymmetry is observed, as well as in the time-averaged flow field not shown here for sake of brevity. This non-axisymmetry can be attributed to small vertical and horizontal misalignments of the axis of rotation of the rotating lid as reported in [43, 44].

Similarly, the axial velocity contours along the vertical plane (Fig. 4c). The instantaneous axial velocity shows that the fluid flows downward near the wall and raises around the vortex bubble located at the axis of the cavity. It can be seen that this vortex bubble, characterized by low axial velocities, moves vertically during the flow cycle. This upward and downward motion of the vortex bubble is known as the undulation of the vortex bubble.

The axial velocity fluctuations near the sidewall have periodic changes between positive and negative values which correspond to the acceleration changes of the rotation rate of the lid. The flow at the centre of the cavity below the disk exhibits the same alternates between positive and negative fluctuations.

At Re = 2800 the influence of an additional frequency of $\omega _k$ = 0.084 is analysed and the phase averaged flow for the simulations and measurements are shown in Fig. 5.

Fig. 5

Re = 2800, H/R = 2 with a 20% increased amplitude for $\Omega _{\omega K}$= 0.084 (a) instantaneous and fluctuations of the angular velocity at plane H/4 [horizontal plane] (b) phase averaged instantaneous angular velocity at (3R/4, H/4) for a period and (c) instantaneous and fluctuations of the axial velocity at y = 0 [vertical plane]

In Fig. 5b, the flow gradually increases from A and reaches its maximum velocity at B and C. The flow slowly decreases from C to H and falls back to its initial state at I. The velocity contours in Fig. 5a also have the above-described variations.

The instantaneous contours of the angular velocity component (Fig. 5a) show a similar behaviour than for the previous frequency. That is, according to the numerical simulations, the velocity increases near the wall when it decreases near the centre following an axisymmetric fluctuation with a wave number of K = 0.

The axial velocity contours and fluctuations are plotted on the vertical plane and are shown in Fig. 5c. The comparison between this case, corresponding to a perturbation at a lower frequency ($\omega _k$ = 0.084) and that shown in Fig. 4 ($\omega _k$ = 0.236) reveals that the near wall fluctuations have a larger spatial extension, in agreement with the lower frequency of the rotation rate of the lid. Also, the same trend is observed for the fluctuations at the central region of the cavity.

It should be noted that the sinusoidal variation of the rotation rate of the lid generates fluctuations of the vertical velocity component with larger intensities, of about 100%, than those imposed in the rotating disk (20%). These fluctuations are distributed along with all the cavity height. The intensities for the fluctuations of the angular velocity component at z = H/4 are of the same order as the instantaneous values (see Figs. 4a or 5a).

4.2 Unsteady sinusoidal rotation at Re = 3500

Results at Re = 3500 were obtained from PIV measurements along the central vertical plane of the cavity and at two different heights (z = 3H/4 and z = H/4). As shown in Table 1 at this Reynolds number three cases were analysed. Similarly to Re = 2800 the imposed frequencies are very similar to those found in the fluid (see Table 1). These are used to compute the phase averaged time evolutions shown in Figs. 6 and 7.

Fig. 6

Re = 3500, H/R = 2 with a 20% increased amplitude for $\Omega _{\omega K}$= 0.084. a Instantaneous and fluctuations of the angular velocity at plane z = 3H/4. b Phase averaged instantaneous angular velocity at (3R/4, H/4) for a period. c Instantaneous and fluctuations of the angular velocity at H/4. d Instantaneous and fluctuations of the axial velocity at the vertical plane y = 0

Fig. 7

Re = 3500, H/R = 2 with a 20% increased amplitude for $\Omega _{\omega K}$= 0.098. a Instantaneous and fluctuations of the angular velocity at plane z = 3H/4. b Phase averaged instantaneous angular velocity at (3R/4, H/4) for a period. c Instantaneous and fluctuations of the angular velocity at H/4. d Instantaneous and fluctuations of the axial velocity at the vertical plane y = 0

Fig. 8

Re = 4100, H/R = 2 with a 20% increased amplitude for $\Omega _{\omega K}$= 0.236 (a) instantaneous and fluctuations of the angular velocity at plane z = 3H/4 and (c) H/4 [horizontal plane] (b) phase averaged instantaneous angular velocity at (3R/4, H/4) for a period and (d) instantaneous and fluctuations of the axial velocity at y = 0 [vertical plane]

Fig. 9

Re = 4100, H/R = 2 with a 20% increased amplitude for $\Omega _{\omega K}$ = 0.084 (a) instantaneous and fluctuations of the angular velocity at plane z = 3H/4 and (c) H/4 [horizontal plane] (b) phase averaged instantaneous angular velocity at (3R/4, H/4) for a period and (d) instantaneous and fluctuations of the axial velocity at y = 0 [vertical plane]

Fig. 10

Re = 4100, H/R = 2 with a 20% increased amplitude for $\Omega _{\omega K}$= 0.098 (a) instantaneous and fluctuations of the angular velocity at plane z = 3H/4 and (c) H/4 [horizontal plane] (b) phase averaged instantaneous angular velocity at (3R/4, H/4) for a period and (d) instantaneous and fluctuations of the axial velocity at y = 0 [vertical plane]

Figures 6a, c and 7a, c show that, at Re = 3500, the spatial distributions of the fluctuations of the angular velocity component are non-axisymmetric. This feature is more evident at height z = H/4 than in plane K = 3H/4. In this plane located near the rotating disk (Figs. 6a and 7a), the fluctuations display an structure with a wave number close to K = 0 with some deformations along the angular direction. Farther from the disk the fluctuations near the cylindrical walls show an alternance of wave-numbers from K=3–0 and to K = 4. Note that these flow structures are not obtained for the constant rotation rate of the disk. As shown in Table 1, in this case the fluctuations exhibit wave-numbers K = 0 and K = 1.

The fluctuations of the vertical velocity component (Figs. 6d and 7d) show a periodic and axisymmetric behaviour in the region near the axis of the cavity. Similar to Re = 2800, at Re =3500, the fluctuations near the cylindrical wall show an alternance between negative and positive values. This alternance is more evident for marked for $\omega _k$ = 0.084 than for $\omega _k$ = 0.098. Also, at this Reynolds number the sinusoidal rotation of the disk produced fluctuations of the vertical velocity component with intensities of the same order of magnitude as the instantaneous values.

Similarly to Re = 2800, at Re = 3500 the intensities of the fluctuations of the angular velocity components are of the same order of magnitude as the instantaneous values and the fluctuations of the vertical velocity component are about twice the instantaneous values.

4.3 Unsteady sinusoidal rotation at Re = 4100

At Re = 4100 we analysed the steady case and the sinusoidal variation of the rotating rate with three different frequencies $\omega _k$ = 0.084, $\omega _k$ = 0.098 and $\omega _k$ = 0.236. As shown in Table 1, the measured flow frequencies, used to compute the phase averaged fields, are between 20 and 30% smaller than the imposed frequencies on the lid.

Figures 8 ($\omega _k$ = 0.084), 9 ($\omega _k$ = 0.098) and 10 ($\omega _k$ = 0.236) show the time evolution during one period of the angular and axial velocity components and their fluctuations at the three different frequencies, respectively.

The spatial distribution of fluctuations of the angular velocity component near the rotating disk (z = 3H/4) shown in Figs. 8a, 9a and 10a reveal the predominance of a fluctuation along the periphery of the cylindrical wall with a wave number K = 4, independently of the frequency imposed. Contrary, the wave numbers of the fluctuations observed at the lower plane (z = H/4) (Figs. 8c, 9c and 10c) are different for each frequency. At ($\omega _k$ = 0.084) (Fig. 8c) two different wave numbers are found, K = 3 (see for example Fig. 8cA, cB or cC) and K = 4 (see for example Fig. 8cD, cE or cF). At ($\omega _k$ = 0.098) (Fig. 9c) the number of different wave numbers observed is larger. We found K = 2 (Fig. 9cA), K = 3 (Fig. 9cB and cI), K = 4 (see for example Fig. 9cF, cG) and K = 5 (Fig. 9cD or cE). At ($\omega _k$ = 0.236) (Fig. 10c) there is no clear spatial organization of the fluctuations of the angular velocity component, probably because the relatively large value of the frequency inhibits the formation of clear flow structures associated with particular values of wave numbers.

The time evolutions of the fluctuations of the vertical velocity component are shown in Figs. 8d, 9d and 10d. It can be seen that at low frequencies (Figs. 8d and 9d) the fluctuations along the axis of the cavity exhibit a single lobe that changes sign along the period. At higher frequency (Fig. 10d) the fluctuation in this central part appears as two or three lobes of opposite sign which progressively evolve along the axis of the cavity. For the three frequencies analysed, the intensity of the fluctuations of the vertical velocity component are about twice times the corresponding instantaneous values.

5 Conclusion

The unsteady axisymmetric and non-axisymmetric flow behaviour in a lid-driven cylindrical cavity with aspect ratio H/R = 2 has been analysed at Re = 2800, 3500 and 4100. A sinusoidal time-varying rotation has been imposed on the lid with different frequencies. The flow has been measured using a two-dimensional PIV technique, and numerical simulations at low Reynolds numbers have been performed.

At Re = 2800 and Re = 3500, the frequencies measured in the flow coincide with the frequency imposed on the rotating lid. In contrast, at Re = 4100, the flow frequencies are significantly lower, especially when the frequency of the disk is significant. For example, at Re = 4100 and an imposed non-dimensional frequency of $\Omega _{\omega K}$ = 0.084, the observed flow frequency is $\omega _K$=0.066, while, at this Reynolds number, for $\Omega _{\omega K}$ = 0.236, $\omega _K$ = 0.16. The phase averaged time evolutions of the angular velocity component for Re = 2800 show an axisymmetric pulsatile behaviour with a wave number of fluctuations K = 0 along all the period. At more significant Reynolds numbers (Re = 3500 and Re = 4100), the more complex spatial organization of the fluctuations appears with associated wave numbers of K = 3 and K = 4, which are observed alternatively and combined with K = 0 along the period.

The fast and slow rotation of the disk produces a pulsatile behaviour in the vertical velocity component, with flow descending near the lateral wall and the ascending flow along the axis of the cavity. This time evolution shows two different dynamics. At low frequencies, $\Omega _{\omega K}$ = 0.084 and 0.098, the positive and negative fluctuations extend along with all the height of the cavity, while at more significant frequencies, the fluctuations appear alternatively distributed along with the cavity height because of the relatively short time between the fast and slow rotation of the velocity of the disk.

Fig. 11

Radial velocity component along the radial direction

Fig. 12

Radial velocity component along the vertical direction

The sinusoidal variation of the rotation rate of the lid generates fluctuations of the vertical velocity component with large intensities, of about 100%, than those imposed in the rotating disk (20%). The intensities for the fluctuations of the angular velocity component are of the same order as the instantaneous values.

Appendix

1.1 Grid convergence

A mesh independence test was carried out for a constant rotation rate of the lid at Re = 1500. Figures 11 and 12 show the comparison of the velocity profiles with two different meshes. Figure 11 corresponds to the profile of the non-dimensional radial velocity component along the non-dimensional radial direction at z = H/2 and Fig. 12 to the radial velocity component along the vertical (z) direction at a radial position of r = 3R/4. The Mean Absolute Errors for the profiles of Figs. 11 and 12 with the two meshes are 2% and 0.7%, respectively.

The non-dimensional time step of the simulations at Re = 2800 was set to 0.3. This corresponds to 17 time steps per revolution of the rotating lid. Simulations with half of this time step gave very similar time evolutions of the velocity in the points indicated in Fig. 1.