1 Introduction

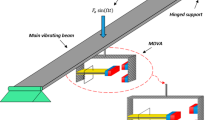
The emerging field of soft robotics offers the prospect of applying soft actuators as artificial muscles in robots, replacing traditional actuators based on hard materials such as electric motors and piezoceramic actuators. Dielectric elastomer transducers (DET) are one class of soft actuators that can deform in response to voltage and substitute biological muscles in the aspects of large deformation, high energy density, and fast response [1,2,3]. All that is required is an elastic and soft dielectric surrounded by two flexible electrodes with layer thicknesses in the lower micrometer range and electrical field strengths up to \(E = 60\,\mathrm {\frac{V}{\mu m}}\), as shown in Fig. 1. This enables low weight and, due to the small dimensions, high energy density. The DET’s operation can be described as a deformable capacitor, and its principle of operation is based on electrostatic pressure, being able to offer a large amount of deformation by applying sufficient voltage [4]. Due to their deformation under the influence of an electric field, they are suitable for certain actuator applications, e. g. proportionally controlled valves, haptic displays, and soft robotics applications [5, 6].

Fig. 1
figure 1

Schematic representation of a dielectric elastomer transducer comprising an elastic dielectric (yellow) and compliant electrodes (gray) in undeformed (left) and deformed shape (right) after applying an electric voltage \(v_{\mathrm {DE}}\) (Color figure online)

Full size image

Many research groups have recently focused on the modeling and design of soft robotics actuators based on dielectric elastomer transducers (DET) and are promising in the emerging field of soft robotics due to the advantages of light weight, high deformation, high energy density, inherent soft nature, shape control and self-sensing capabilities [7, 8]. For example, humanoid robots have been developed and consider the antagonistic arrangement of DETs to mimic the function of human muscles [9, 10]. DET-driven walking robots have been designed using stacked DETs [11]. A soft gripper based on bistable DET has been designed that is capable of grasping various objects with various sizes and shapes [12]. Thus, DETs have been coupled with various structures and mechanisms to achieve certain mechanical characteristics such as bistability, amplified stroke, minimum energy structures, and low energy consumption.

There are various methods and approaches for modeling DET systems combined with different structures. Models have already been developed and published describing the static [13, 14] as well as transient behavior [15, 16] of either the DE material in general or a certain transducer design. Advanced dynamic nonlinear continuum models have been developed taking into account the electromechanical coupling of the DET, which leads to a set of partial differential equations, and therefore, they are solved numerically using the finite element method [17, 18]. This novel modeling approach is applicable for a detailed analysis and design of the transducer’s coupled behavior, although it is difficult to use in control applications. For various types of DE transducers, different control-orientated modeling approaches have been previously presented by describing the DET as a lumped parameter system or using energy methods. A positioning control system based on a DE membrane [19] and a self-sensing control for a DE stack transducer [20] have been developed describing the DE actuator by a lumped parameter system. A soft robotic module actuated by rolled DET and a multi degree-of-freedom soft robot based on a double cone DET have been modeled using the Lagrange equations for a rigid body considering the DET as an external force acting on the system [21]. In addition, a thermodynamic model has been developed to describe the viscoelastic, electromechanical and dynamic response of a DET [22]. In this context, the dynamic modeling of DETs coupled with elastic structures has rarely been studied and mostly replaced by concentrated elements to model the dynamic behavior of DET systems, which have ultimately been used in design and control applications.

Within this contribution, we present an energy-based nonlinear modeling approach for DET systems combined with a flexible structure using the Hamilton principle for electromechanical systems [23,24,25]. The interactions between DE transducers and flexible structures connected with mechanical interfaces are investigated, taking into account the nonlinear and dynamic behavior of both the deformation of the elastic structure and the DETs. The approach comprises the electrical domain of the DET and is combined with the mechanical model by considering a lumped electrical circuit. In addition, multiple DETs are coupled with the structure, and different measurement points are concluded in the model, resulting in a MIMO System. The deformation of the elastic structures generally depends on the coordinate system and leads to a set of partial differential equations. In order to exclude the coordinate dependencies, the field variables are discretized with assumed elastic field shapes using the Rayleigh–Ritz formulation, where the geometric deformation of the soft actuator is guessed by polynomial functions. Thus, we obtain a state space model for the coupled DET system that reflects the actuator dynamics. As an predestinated example to demonstrate the modeling approach, a state space is developed for a buckled beam actuated by a multilayer DET.

Therefore, the remainder of this paper is structured as follows. In Sect.  2, we will present the Lagrange function, define the conservative energies and the corresponding virtual works of the mechanical and electrical domains for the DET system. The energy and work expression are approximated using the Rayleigh–Ritz method. After defining the generalized coordinates of the electromechanical system, the Hamilton principle is applied to derive the governing Lagrange equations, which can be easily transformed into a nonlinear state space model. The method is finally applied to a buckled beam structure actuated by a multilayer DET in Sect.  3. The novel concept uses elastic and dynamic instabilities of the buckled beam, while the DET provides the actuation. The actuation characteristics are investigated in Sect.  4 based on analytical solutions and numerical simulations, before finally Sect.  5 summarizes the findings.

2 Energy-based modeling for DET systems

A sophisticated approach for modeling the DET system is offered by the Lagrange formalism, also called the Hamilton principle, based on the calculus of variations. By using the generalized energy and power variables, the dynamic equations for mechatronic systems can be obtained. One important modeling decision is the choice of generalized physical coordinates. In the case of mechanical systems, the displacements \(\mathbf {q}_\mathrm {m}\) are commonly chosen as the generalized coordinates (for the continuous system, the coefficients of the Ritz approach are used), and for the electrical system we choose the charge \(\mathbf {q}_\mathrm {p}\) of the dielectric polymer [23]. Applying the Hamilton principle and variational calculus, the resulting system of equations leads to a set of nonlinear differential equations in terms of the generalized minimal coordinates \(\mathbf {q}_\mathrm {m}\) and \(\mathbf {q}_\mathrm {p}\). Table 1 provides the definitions of variables and quantities used in this Section.

Table 1 List of variables and quantities
Full size table
Fig. 2
figure 2

Schematic representation of a DET system coupled with an elastic structure considering lumped mass, spring and damping elements

Full size image

The following steps are carried out to derive the dynamic model of a DET system:

  1. 1.

    Definition of the Lagrangian and corresponding conservative energy terms

  2. 2.

    Definition of the nonconservative virtual works of the mechanical and electrical domain

  3. 3.

    Field variables approximation using Rayleigh–Ritz method and definition of generalized coordinates for the electromechanical system

  4. 4.

    Applying Hamilton’s principle and formulation of the nonlinear Lagrange equations

2.1 Lagrange functional

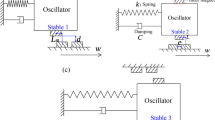
In the following, we will derive the electromechanical model of DETs coupled with an elastic flexible structure considering the system presented in Fig. 2. The DET system comprises an elastic structure  \(\varOmega \), DE materials \(\varOmega _{\mathrm {DE}}\), and concentrated mass, spring and damper elements. External forces and electrical voltages through the DEs can act on the system. Furthermore, multiple DETs are coupled with elastic structures with voltage inputs \(\mathbf {u}\), and different deflection points \(\mathbf {y}\) are concluded in the model, resulting in a MIMO System. Finally, boundary conditions are also defined, which will be later considered by the Rayleigh–Ritz approximation.

The Lagrangian \(\mathcal {L}\) for a DET system is given by:

$$\begin{aligned} \begin{aligned} \mathcal {L}&= \mathcal {T}-\mathcal {U}_\mathrm {s}-\mathcal {U}_{\mathrm {DE}}, \end{aligned} \end{aligned}$$
(1)

where \(\mathcal {T}\), \(\mathcal {U}_\mathrm {s}\), and \(\mathcal {U}_\mathrm {DE}\) are the kinetic energy, the elastic structure energy (in addition nonlinear spring elements), and free energy of the DET, respectively. The kinetic energy comprises the energies of the concentrated mass elements, the elastic structures and DETs:

$$\begin{aligned} \begin{aligned} \mathcal {T}&= \sum _{k=1}^{n_\mathrm {m}}\frac{1}{2}m_k\dot{\mathbf {x}}_{\mathrm {m},k}^2 + \frac{1}{2}\int _{\varOmega } \rho \left( \dot{u}_1^2 + \dot{u}_2^2 +\dot{u}_3^2 \right) \mathrm {d}V\\&\quad +\sum _{i=1}^{n_\mathrm {p}}\frac{1}{2}\int _{\varOmega _{\mathrm {DE},i}} \rho _{_\mathrm {DE}}\left[ (\dot{\lambda }_{x,i}x_{_\mathrm {DE}})^2 + (\dot{\lambda }_{y,i}y_{_\mathrm {DE}})^2 +(\dot{\lambda }_{z,i}z_{_\mathrm {DE}})^2 \right] \mathrm {d}V_\mathrm {DE}. \end{aligned} \end{aligned}$$
(2)

The kinetic energy of the DETs is formulated depending on the constant stretches \(\lambda _{x,i}\), \(\lambda _{y,i}\), and \(\lambda _{z,i}\) for each DET, where \(x_{_\mathrm {DE}}\), \(y_{_\mathrm {DE}}\), and \(z_{_\mathrm {DE}}\) are the coordinates of the DET in the undeformed state. It should be noted that the volume integrals \(\mathrm {d}V=\mathrm {d}x\mathrm {d}y\mathrm {d}z\) and \(\mathrm {d}V_\mathrm {DE}=\mathrm {d}x_{_\mathrm {DE}}\mathrm {d}y_{_\mathrm {DE}}\mathrm {d}z_{_\mathrm {DE}}\) are evaluated in the reference configuration and therefore do not depend on time.

Next, the energy of an elastic structure is given by

$$\begin{aligned} \begin{aligned} \mathcal {U}_{\mathrm {s}}&= \frac{1}{2}\int _{\varOmega } C_{ijkl}\varepsilon _{ij}\varepsilon _{kl}\mathrm {d}V+\sum _{i=1}^{n_\mathrm {s}}\int _{0}^{x_{\mathrm {s},i }}F_\mathrm {s}(x)\mathrm {d}x, \end{aligned} \end{aligned}$$
(3)

with the elasticity tensor \(C_{ijkl}\) and the strain tensor \(\varepsilon _{ij}\) depending on the displacement field \(u_1\), \(u_2\), and \(u_3\),

$$\begin{aligned} \begin{aligned} \varepsilon _{ij}&= \frac{1}{2}\left( \frac{\partial u_i}{\partial x_j}+\frac{\partial u_j}{\partial x_i}+\frac{\partial u_k}{\partial x_i}\frac{\partial u_k}{\partial x_j}\right) , \end{aligned} \end{aligned}$$
(4)

considering geometric nonlinearities of the elastic body. The Einstein summation convention is used to calculate the first term in \(\mathcal {U}_\mathrm {s}\) and the strain tensor. The components of the elastic strain energy can be simplified and adapted to the corresponding model depending on the actuator application. Therefore, Eqs. (3) and (4) can be simplified for well-known structures such as bar, beam, plate, and shell elements as applied in Sect.  3 for a buckled beam model. The second term in Eq. (3) corresponds to the external nonlinear spring elements as illustrated in Fig. 2. Finally, the free energy of the DET is introduced:

$$\begin{aligned} \begin{aligned} \mathcal {U}_{\mathrm {DE}}&= \sum _{i=1}^{n_\mathrm {p}}\int _{\varOmega _{\mathrm {DE},i}}\left( \psi \left( I_1(\mathbf {C}),I_2(\mathbf {C}),I_3(\mathbf {C})\right) +\frac{D_i^2}{2\varepsilon _0\varepsilon _{\mathrm {r}}}\right) \mathrm {d}V_{\mathrm {DE}}, \end{aligned} \end{aligned}$$
(5)

which comprises a hyperelastic material model described by the Helmholtz free energy function \(\psi \) and the electrical field energy conserved in the DET per unit reference volume. The strain energy function is expressed in terms of the principle invariants of the right Cauchy–Green tensor \(\mathbf {C}\) [26] by

$$\begin{aligned} \begin{aligned} I_1&=\mathrm {tr}(\mathbf {C})=\lambda _x^2+\lambda _y^2+\lambda _z^2,\\ I_2&=\mathrm {tr}(\mathbf {C}^{-1})\mathrm {det}(\mathbf {C})=\lambda _x^2\lambda _y^2+\lambda _x^2\lambda _z^2+\lambda _y^2\lambda _z^2,\\ I_3&=\mathrm {det}(\mathbf {C})=\lambda _x^2\lambda _y^2\lambda _z^2, \end{aligned} \end{aligned}$$
(6)

and it is valid for isotropic hyperelastic materials, where the eigenvalues of \(\mathbf {C}\) are the squares of the principle stretches \(\lambda _x^2,\lambda _y^2,\lambda _z^2\). Thus, we may consider \(\psi (\lambda _x,\lambda _y,\lambda _z)\) as a function of the principle stretches. Generally used hyperelastic material models are Neo-Hooke, Mooney–Rivlin, Yeoh, Gent and Ogden [27,28,29]. A uniform distribution is considered for the charges \(q_{\mathrm {p},i}\) over the area of the DET so that the true electric displacement field distribution can be written as

$$\begin{aligned} \begin{aligned} D_i&=\frac{q_{\mathrm {p},i}}{A_i}=\frac{q_{\mathrm {p},i}}{A_{0,i}\lambda _{x,i}\lambda _{y,i}}&\text {for}~i=1,\dots ,n_\mathrm {p}, \end{aligned} \end{aligned}$$
(7)

where \(A_i\) and \(A_{0,i}\) are the area of the i-th DET in the deformed and undeformed state, respectively Altogether, Eq. (5) can be rewritten as

$$\begin{aligned} \begin{aligned} \mathcal {U}_{\mathrm {DE}}&= \sum _{i=1}^{n_\mathrm {p}}\int _{\varOmega _{\mathrm {DE},i}}\left( \psi \left( \lambda _{x,i},\lambda _{y,i},\lambda _{z,i}\right) +\frac{q_{\mathrm {p},i}^2}{2\varepsilon _0\varepsilon _{\mathrm {r}}A_{0,i}^2\lambda _{x,i}^2\lambda _{y,i}^2}\right) \mathrm {d}V_{\mathrm {DE}}. \end{aligned} \end{aligned}$$
(8)

In this paper, we will assume homogenous constant stretches, so that the integral in Eq. (8) can be replaced by the DET volume \(V_\mathrm {DE}\). The well-known electrostatic pressure for an incompressible material \(\sigma _{\mathrm {e}}=\varepsilon _0\varepsilon _\mathrm {r}E^2\) can be recovered considering the energy of the DET shown in Fig. 1. The stored electric field energy is given by

$$\begin{aligned} \begin{aligned} \mathcal {U}_{\mathrm {e}}&=\frac{q_{\mathrm {p}}^2}{2\varepsilon _0\varepsilon _{\mathrm {r}}A_{0}^2\lambda _{x}^2\lambda _{y}^2}V_\mathrm {DE}=\frac{q_{\mathrm {p}}^2\lambda _z^2}{2\varepsilon _0\varepsilon _{\mathrm {r}}A_{0}^2}V_\mathrm {DE} \end{aligned} \end{aligned}$$
(9)

assuming an incompressible material \(\lambda _x\lambda _y\lambda _z=1\). The electrostatic force in the thickness direction \(F_\mathrm {e}\) can be calculated as

$$\begin{aligned} \begin{aligned} \delta \mathcal {U}_\mathrm {e}&=F_\mathrm {e}\delta d=\sigma _\mathrm {e}\lambda _x\lambda _yA_0d_0\delta \lambda _z\\&=\frac{\sigma _\mathrm {e}}{\lambda _z}V_\mathrm {DE}\delta \lambda _z = \frac{\partial \mathcal {U}_\mathrm {e}}{\partial \lambda _z}\delta \lambda _z. \end{aligned} \end{aligned}$$
(10)

Thus, the electrostatic pressure can be finally obtained using the electric field relation \(D=\varepsilon _0\varepsilon _{\mathrm {r}}E\):

$$\begin{aligned} \begin{aligned} \sigma _\mathrm {e} = \frac{\lambda _z}{V_\mathrm {DE}} \frac{\partial \mathcal {U}_\mathrm {e}}{\partial \lambda _z}=\frac{q_{\mathrm {p}}^2\lambda _z^2}{\varepsilon _0\varepsilon _{\mathrm {r}}A_{0}^2}=\frac{D^2}{\varepsilon _0\varepsilon _{\mathrm {r}}}=\varepsilon _0\varepsilon _{\mathrm {r}}E^2. \end{aligned} \end{aligned}$$
(11)

2.2 Nonconservative virtual works

The mechanical virtual work acting on the DET system is given by

$$\begin{aligned} \begin{aligned} \delta \mathcal {W}_\mathrm {m}&= \sum _{i=1}^{n_\mathrm {F}}\mathbf {F}_i\cdot \delta \mathbf {x}_{\mathrm {F},i}-\sum _{i=1}^{n_\mathrm {d}}d_i\dot{x}_{\mathrm {d},i}\delta x_{\mathrm {d},i}-\int _{\varOmega }D_{ijkl}\dot{\varepsilon }_{ij}\delta \varepsilon _{kl}\mathrm {d}V+\sum _{i=1}^{n_\mathrm {p}}\underbrace{\int _{\varOmega _{\mathrm {DE},i}}\delta w_{\mathrm {v,DE},i}\,\mathrm {d}V_{\mathrm {DE}}}_{V_{\mathrm {DE},i}\,\delta w_{\mathrm {v,DE},i}}, \end{aligned} \end{aligned}$$
(12)

which comprises the external forces, the damping elements, the inner dissipation of the structure, and viscose losses of DETs as depicted in Fig. 3.

Fig. 3
figure 3

Equivalent circuit diagram of a DET with lumped parameters to model the electrical behavior under consideration of losses (left). Viscoelastic behavior of the DET considering a Kelvin-Maxwell model (right)

Full size image

The Einstein summation convention is also used to calculate the dissipation of the structure \(\varOmega \) and can be simplified for the mentioned well-known elements. Within this contribution, the virtual work density \(\delta w_\mathrm {v,DE}\) of a DET is described by the viscosity \(\eta _\mathrm {v}\) and the Maxwell element in parallel comprising a spring \(E_{_\mathrm {M}}\) and dashpot \(\eta _{_\mathrm {M}}\) (creeping material) as experimentally proven in [15]:

$$\begin{aligned} \begin{aligned} \delta w_\mathrm {v,DE}=-E_{_\mathrm {M}}\varepsilon _{_\mathrm {E}}\delta \varepsilon _{_\mathrm {E}}-\eta _{_\mathrm {M}}\dot{\varepsilon }_{\mathrm {\eta }}\delta \varepsilon _{\mathrm {\eta }}-\eta _{\mathrm {v}}\dot{\varepsilon }_{z}, \end{aligned} \end{aligned}$$
(13)

where \(\varepsilon _{_\mathrm {E}}\), \(\varepsilon _{\eta }\), and \(\varepsilon _{z}=\lambda _z-1\) are the strains of the Maxwell spring element, the dashpot, and the strain in thickness direction. Due to the connection in series of \(E_\mathrm {M}\) and \(\eta _{_\mathrm {M}}\), the tension is the same for both elements,

$$\begin{aligned} \begin{aligned} E_{_\mathrm {M}}\varepsilon _{_\mathrm {E}}=\eta _{_\mathrm {M}}\dot{\varepsilon }_{\mathrm {\eta }}, \end{aligned} \end{aligned}$$
(14)

and the sum of the strains is described by the strain of the DET in z-direction,

$$\begin{aligned} \begin{aligned} \varepsilon _{z}=\varepsilon _{_\mathrm {E}}+\varepsilon _{\mathrm {\eta }}. \end{aligned} \end{aligned}$$
(15)

Inserting Eqs. (14) and (15) into Eq. (13), the virtual work density \(\delta w_\mathrm {v,DE}\) depends only on \(\varepsilon _{_\mathrm {E}}\) and \(\varepsilon _{z}\),

$$\begin{aligned} \begin{aligned} \delta w_\mathrm {v,DE}=\left[ \eta _{_\mathrm {M}}\left( \dot{\varepsilon }_z-\dot{\varepsilon }_{_\mathrm {E}}\right) -E_{_\mathrm {M}}\varepsilon _{_\mathrm {E}}\right] \delta \varepsilon _{_\mathrm {E}}-\left[ E_{_\mathrm {M}} \varepsilon _{_\mathrm {E}}+\eta _{\mathrm {v}}\dot{\varepsilon }_{z}\right] \delta \varepsilon _{z}. \end{aligned} \end{aligned}$$
(16)

The Maxwell strain \(\varepsilon _{_\mathrm {E}}\) will be defined as an additional generalized coordinate modeling the creep behavior of the DET.

Next, we will describe the electrical virtual work for the lumped circuit as illustrated in Fig. 3. According to the simplified approach in [30], the electrical model comprises a series resistance \(R_\mathrm {s}\) representing losses of the electrode, a parallel resistance \(R_\mathrm {p}\) of the non-ideally insulating polymer, and its capacitance \(C_\mathrm {p}\), which is already considered in the energy function \(\mathcal {U}_{\mathrm {DE}}\). Beside material and design parameters of the DET, these electrical parameters generally depend on the current deformation state. The resistances \(R_\mathrm {s}\) and \(R_\mathrm {p}\) are assumed to be constant and should not depend on the deformation. The electrical virtual work for \(n_{\mathrm {p}}\) DET elements under consideration of the input voltage \(v_{_\mathrm {DE}}\) is described by

$$\begin{aligned} \begin{aligned} \delta \mathcal {W}_\mathrm {e}&= \sum _{i=1}^{n_\mathrm {p}}\left( v_{_{\mathrm {DE},i}}-R_{\mathrm {s},i}\dot{q}_{_{\mathrm {DE},i}}\right) \delta q_{_{\mathrm {DE},i}}-R_{\mathrm {p},i}\dot{q}_{{{R_\mathrm {p}},i}}\delta q_{{R_\mathrm {p}},i}. \end{aligned} \end{aligned}$$
(17)

According to Kirchhoff’s current law, we obtain:

$$\begin{aligned} \begin{aligned} i_{R_\mathrm {p}}=i_{_\mathrm {DE}}-i_\mathrm {p} \Leftrightarrow \dot{q}_{R_\mathrm {p}}&=\dot{q}_{_\mathrm {DE}}-\dot{q}_{\mathrm {p}}. \end{aligned} \end{aligned}$$
(18)

The current relation (18) is inserted into Eq. (17), resulting in

$$\begin{aligned} \begin{aligned} \delta \mathcal {W}_\mathrm {e}&= \sum _{i=1}^{n_\mathrm {p}}V_{\mathrm {p},i}\delta q_{\mathrm {p},i}+V_{\mathrm {e},i}\delta q_{_{\mathrm {DE},i}}, \end{aligned} \end{aligned}$$
(19)

with the generalized voltages

$$\begin{aligned}&V_{\mathrm {p},i} =R_{\mathrm {p},i}\left( \dot{q}_{\mathrm {DE},i}-\dot{q}_{\mathrm {p},i}\right) , \end{aligned}$$
(20.1)
$$\begin{aligned}&V_{\mathrm {e},i} = v_{_{\mathrm {DE},i}}-\left( R_{\mathrm {s},i}+R_{\mathrm {p},i}\right) \dot{q}_{_{\mathrm {DE},i}}+R_{\mathrm {p},i}\dot{q}_{\mathrm {p},i}. \end{aligned}$$
(20.2)

2.3 Rayleigh–Ritz method

The Rayleigh–Ritz method is an approximation enabling a transformation of a partial differential equation (PDE) into a set of ordinary differential equations (ODEs). It allows us to represent a continuous system by a discrete approximation, which is expected to approximate the behavior of the continuous system. To achieve this, it is assumed that all distributed field variables (\(u_1,u_2,u_3\)) can be approximated by a general function

$$\begin{aligned} \begin{aligned} f\left( x,y,z,t\right) \approx \sum _{j=1}^{N}a_j(t)\phi _{j}\left( x,y,z\right) , \end{aligned} \end{aligned}$$
(21)

where \(\phi _j\) is a set of assumed modes, which are continuous. The coefficients \(a_j(t)\) are reduced by applying the geometric boundary conditions, which leads to a reduced function approximation,

$$\begin{aligned} \begin{aligned} f\left( x,y,z,t\right)&\approx \sum _{m=1}^{n_\mathrm {r}}q_m(t)\psi _{m}\left( x,y,z\right) ,&\text {with}~n_\mathrm {r}<N. \end{aligned} \end{aligned}$$
(22)

The \(n_\mathrm {r}\) functions of time \(q_m(t)\) are defined as the generalized coordinates of the continuous mechanical system, and \(\psi _m\) are the reduced modes. If the set of assumed modes is complete, the approximation converges toward the exact solution as their number \(n_\mathrm {r}\) increases. In this paper, we will approximate the modes \(\psi _{m}\left( x,y,z\right) \) with power series transforming the problem into a finite number \(n_\mathrm {r}\) degrees of freedom. The geometric deformation and kinematic assumptions of actuators are usually known for many applications so that we can approximate the field variables by a few sets of generalized coordinates. By the volume integral in the Lagrangian formulation, the field dependency of the distributed variables can be eliminated. This yields an ordinary differential equation in time describing the dynamical model by a few time-dependent state variables similar to those of discrete systems. There are different discretization methods (e.g. finite elements, finite difference, etc.) to derive an ODE system from a PDE and apply this for control systems. However, this leads to a very large ODE order and considers higher shape components in the system, which are mostly not excited by the actuation of the DE. Using the Ritz approach, the number of states can be significantly reduced by selecting only the most significant excitable modes of the solution and at the same time including the boundary conditions. A requirement for this is obviously the prior knowledge of the solution form or rather the geometric deformation of the structure, which is usually known for actuator applications.

Thus, the electromechanical system can be fully characterized by \(n_\mathrm {r}\) mechanical variables \(q_{m}\) \((m=1,\dots ,n_\mathrm {r})\), \(n_\mathrm {p}\) Maxwell strains \(\varepsilon _{E,j}\), and \(n_\mathrm {p}\) electric charges \(q_{\mathrm {p},j}\) \(\left( j=1,\dots ,n_\mathrm {p}\right) \) introducing the state vector of generalized coordinates of the mechanical domain,

$$\begin{aligned} \begin{aligned} \mathbf {q}_\mathrm {m}=\left[ q_1,\dots ,q_{n_\mathrm {r}}\right] ^\mathrm {T},&\mathbf {q}_\mathrm {\varepsilon }=\left[ \varepsilon _{E,1},\dots ,\varepsilon _{E,n_\mathrm {p}}\right] ^\mathrm {T}, \end{aligned} \end{aligned}$$
(23)

and the state vector of generalized charges for the electrical domain

$$\begin{aligned} \begin{aligned} \mathbf {q}_\mathrm {p}=\left[ q_{\mathrm {p},1},\dots ,q_{\mathrm {p},n_\mathrm {p}}\right] ^\mathrm {T}. \end{aligned} \end{aligned}$$
(24)

Considering Eqs. (23) and (24), the variables \(u_1,u_2,u_3,\mathbf {x}_{\mathrm {m}},\mathbf {x}_{\mathrm {F}},x_{\mathrm {s}},x_{\mathrm {d}},\varepsilon _{z}, \varepsilon _{ij}\), \(\lambda _x,\lambda _y,\lambda _z\) and their time derivatives that appear in the energy and work expressions can be described as functions of \(\mathbf {q}_\mathrm {m}\) and \(\dot{\mathbf {q}}_\mathrm {m}\) using the kinematic assumptions and constraints of the overall system. Hence, the Lagrangian functional in Eq. (1) is formulated as a function of \(\mathbf {q}_\mathrm {m}\), \(\dot{\mathbf {q}}_\mathrm {m}\), and \(\mathbf {q}_\mathrm {p}\),

$$\begin{aligned} \begin{aligned} \mathcal {L}\left( \mathbf {q}_\mathrm {m},\dot{\mathbf {q}}_\mathrm {m},\mathbf {q}_\mathrm {p}\right) =\mathcal {T}\left( \mathbf {q}_\mathrm {m},\dot{\mathbf {q}}_\mathrm {m}\right) -\mathcal {U}_\mathrm {s}\left( \mathbf {q}_\mathrm {m}\right) -\mathcal {U}_{\mathrm {DE}}\left( \mathbf {q}_\mathrm {m},\mathbf {q}_\mathrm {p}\right) . \end{aligned} \end{aligned}$$
(25)

Furthermore, the virtual works of the mechanical and electrical part are also described by the generalized coordinates and charges. Therefore, the virtual position vectors \(\delta \mathbf {x}_{\mathrm {F},k}\), coordinates \(\delta x_{\mathrm {d},l}\), strain \(\delta \varepsilon _z\), and strain tensor \(\delta \varepsilon _{kl}\) are described by the virtual generalized coordinates \(\delta q_m\),

$$\begin{aligned} \delta \mathbf {x}_{\mathrm {F},k}&=\sum _{m=1}^{n_\mathrm {r}}\frac{\partial \mathbf {x}_{\mathrm {F},k}}{\partial q_m}\delta q_m, \end{aligned}$$
(26.1)
$$\begin{aligned} \delta x_{\mathrm {d},l}&=\sum _{m=1}^{n_\mathrm {r}}\frac{\partial x_{\mathrm {d},l}}{\partial q_m}\delta q_m,\end{aligned}$$
(26.2)
$$\begin{aligned} \delta \varepsilon _{kl}&=\sum _{m=1}^{n_\mathrm {r}}\frac{\partial \varepsilon _{kl}}{\partial q_m}\delta q_m,\end{aligned}$$
(26.3)
$$\begin{aligned} \delta \varepsilon _{z}&=\sum _{m=1}^{n_\mathrm {r}}\frac{\partial \varepsilon _{z}}{\partial q_m}\delta q_m. \end{aligned}$$
(26.4)

Thus, the virtual work \(\delta \mathcal {W}_\mathrm {m}\) can be described by the virtual generalized coordinates \(\delta q_m\) by substituting Eqs. (26.1) in  (12),

$$\begin{aligned} \begin{aligned} \delta \mathcal {W}_\mathrm {m}&= \sum _{m=1}^{n_\mathrm {r}}\left[ Q_{\mathrm {F},m}-Q_{\mathrm {d},m}-Q_{\mathrm {s},m}-Q_{\mathrm {v},m}\right] \delta q_m + \sum _{i=1}^{n_\mathrm {p}}Q_{\varepsilon ,i}\delta \varepsilon _{\mathrm {E},i}, \end{aligned} \end{aligned}$$
(27)

with the generalized forces

$$\begin{aligned} Q_{\mathrm {F},m}&=\sum _{k=1}^{n_\mathrm {F}}\mathbf {F}_k\cdot \frac{\partial \mathbf {x}_{\mathrm {F},k}}{\partial q_m},\end{aligned}$$
(28.1)
$$\begin{aligned} Q_{\mathrm {d},m}&=\sum _{l=1}^{n_\mathrm {d}}d_l\dot{x}_{\mathrm {d},l} \frac{\partial x_{\mathrm {d},l}}{\partial q_m},\end{aligned}$$
(28.2)
$$\begin{aligned} Q_{\mathrm {s},m}&=\int _{\varOmega }D_{ijkl}\dot{\varepsilon }_{ij}\frac{\partial \varepsilon _{kl}}{\partial q_m}\mathrm {d}V,\end{aligned}$$
(28.3)
$$\begin{aligned} Q_{\mathrm {v},m}&=\sum _{i=1}^{n_\mathrm {p}}V_{\mathrm {DE},i}\left[ E_{\mathrm {M},i} \varepsilon _{\mathrm {E},i}+\eta _{\mathrm {v},i}\dot{\varepsilon }_{z,i}\right] \frac{\partial \varepsilon _{z,i}}{\partial q_m},\end{aligned}$$
(28.4)
$$\begin{aligned} Q_{\varepsilon ,i}&=V_{\mathrm {DE},i}\left[ \eta _{\mathrm {M},i}\left( \dot{\varepsilon }_{z,i}-\dot{\varepsilon }_{\mathrm {E},i}\right) -E_{\mathrm {M},i}\varepsilon _{E,i}\right] , \end{aligned}$$
(28.5)

where the latter two expressions (28.4) and (28.5) are determined using Eq. (16). Finally, the virtual work in Eq. (27) can be rewritten in vector form as follows:

$$\begin{aligned} \begin{aligned} \delta \mathcal {W}_\mathrm {m}&= \left( \mathbf {Q}_{\mathrm {F}}-\mathbf {Q}_{\mathrm {d}}-\mathbf {Q}_{\mathrm {s}}-\mathbf {Q}_{\mathrm {v}}\right) \delta \mathbf {q}_\mathrm {m}+\mathbf {Q}_{\varepsilon }\delta \mathbf {q}_\varepsilon =\mathbf {Q}\delta \mathbf {q}_\mathrm {m}+\mathbf {Q}_{\varepsilon }\delta \mathbf {q}_\varepsilon , \end{aligned} \end{aligned}$$
(29)

with the general virtual force vectors

$$\begin{aligned} \begin{aligned} \mathbf {Q}_\mathrm {F}&=\left[ Q_{\mathrm {F},1},\dots ,Q_{\mathrm {F},n_\mathrm {r}}\right] ,\\ \mathbf {Q}_\mathrm {d}&=\left[ Q_{\mathrm {d},1},\dots ,Q_{\mathrm {d},n_\mathrm {r}}\right] ,\\ \mathbf {Q}_\mathrm {s}&=\left[ Q_{\mathrm {s},1},\dots ,Q_{\mathrm {s},n_\mathrm {r}}\right] ,\\ \mathbf {Q}_\mathrm {v}&=\left[ Q_{\mathrm {v},1},\dots ,Q_{\mathrm {v},n_\mathrm {r}}\right] ,\\ \mathbf {Q}_\varepsilon&=\left[ Q_{\varepsilon ,1},\dots ,Q_{\varepsilon ,n_\mathrm {p}}\right] . \end{aligned} \end{aligned}$$
(30)

The electrical virtual work in Eq.(19) is independent of \(\mathbf {q}_\mathrm {m}\) and is also presented in vector form,

$$\begin{aligned} \begin{aligned} \delta \mathcal {W}_\mathrm {e}&=\mathbf {V}_\mathrm {p}\delta \mathbf {q}_\mathrm {p}+\mathbf {V}_\mathrm {e}\delta \mathbf {q}_\mathrm {DE}, \end{aligned} \end{aligned}$$
(31)

with the generalized voltage vectors

$$\begin{aligned} \begin{aligned} \mathbf {V}_\mathrm {p}&=\left[ V_{\mathrm {p},1},\dots ,V_{\mathrm {p},n_\mathrm {p}}\right] ,&\mathbf {V}_\mathrm {e}&=\left[ V_{\mathrm {e},1},\dots ,V_{\mathrm {e},n_\mathrm {p}}\right] . \end{aligned} \end{aligned}$$
(32)

It should be noted that the structure of the equations remains the same if one uses the Ritz approach since the shape function and its derivatives appear as integrals over the volume and generate constant values. Therefore, the structure of the equations only changes by the corresponding order of the Ritz approach or number of independent generalized coordinates. From the perspective of systems theory, unknown system parameters can be determined by an identification procedure without selecting a specific mode or shape of the solution and hence can be determined by experimental data.

2.4 Hamilton principle

The derivation of the electromechanical system can be obtained from a variational principle applied to the action of the Lagrange energy function considering the electrical and mechanical virtual works and the Rayleigh–Ritz approximation of the field quantities [31]. Thus, the Hamilton principle for the coupled electromechanical system is given by

$$\begin{aligned} \begin{aligned} \delta \mathcal {S}&= \int _{t_0}^{t_{\mathrm {e}}}\delta \mathcal {L}\mathrm {d}t + \int _{t_0}^{t_{\mathrm {e}}}\delta \mathcal {W}_{\mathrm {m}}+ \delta \mathcal {W}_{\mathrm {e}}\mathrm {d}t. \end{aligned} \end{aligned}$$
(33)

Inserting Eq. (25), (29), and (31) into Eq. (33), we obtain

$$\begin{aligned} \begin{aligned} \delta \mathcal {S}&= \int _{t_0}^{t_{\mathrm {e}}}\delta \mathcal {L}\left( \mathbf {q}_\mathrm {m},\dot{\mathbf {q}}_\mathrm {m},\mathbf {q}_\mathrm {p}\right) \mathrm {d}t + \int _{t_0}^{t_{\mathrm {e}}}\mathbf {Q}\delta \mathbf {q}_\mathrm {m}+\mathbf {Q}_{\varepsilon }\delta \mathbf {q}_\varepsilon +\mathbf {V}_\mathrm {p}\delta \mathbf {q}_\mathrm {p}+\mathbf {V}_\mathrm {e}\delta \mathbf {q}_\mathrm {DE}\mathrm {d}t. \end{aligned} \end{aligned}$$
(34)

Performing variation calculus to Eq.(34), we finally obtain the equation of the coupled electro mechanical DET system (Lagrange equations),

$$\begin{aligned}&\frac{\mathrm {d}}{\mathrm {d}t}\frac{\partial \mathcal {L}}{\partial \dot{\mathbf {q}}_\mathrm {m}}-\frac{\partial \mathcal {L}}{\partial \mathbf {q}_\mathrm {m}}=\mathbf {Q}=\mathbf {Q}_{\mathrm {F}}-\mathbf {Q}_{\mathrm {d}}-\mathbf {Q}_{\mathrm {s}}-\mathbf {Q}_{\mathrm {v}}, \end{aligned}$$
(35.1)
$$\begin{aligned}&\underbrace{\frac{\mathrm {d}}{\mathrm {d}t}\frac{\partial \mathcal {L}}{\partial \dot{\mathbf {q}}_\varepsilon }}_{=0}-\underbrace{\frac{\partial \mathcal {L}}{\partial \mathbf {q}_\varepsilon }}_{=0}=\mathbf {Q}_\varepsilon , \end{aligned}$$
(35.2)
$$\begin{aligned}&\underbrace{\frac{\mathrm {d}}{\mathrm {d}t}\frac{\partial \mathcal {L}}{\partial \dot{\mathbf {q}}_\mathrm {p}}}_{=0}-\frac{\partial \mathcal {L}}{\partial \mathbf {q}_\mathrm {p}}=\mathbf {V}_\mathrm {p}=\mathbf {R}_{\mathrm {p}}\left( \dot{\mathbf {q}}_{\mathrm {DE}} -\dot{\mathbf {q}}_{\mathrm {p}}\right) , \end{aligned}$$
(35.3)
$$\begin{aligned}&\underbrace{\frac{\mathrm {d}}{\mathrm {d}t}\frac{\partial \mathcal {L}}{\partial \dot{\mathbf {q}}_\mathrm {DE}}}_{=0}-\underbrace{\frac{\partial \mathcal {L}}{\partial \mathbf {q}_\mathrm {DE}}}_{=0}=\mathbf {V}_\mathrm {e}=\mathbf {v}_{\mathrm {DE}}-\left( \mathbf {R}_{\mathrm {s}}+\mathbf {R}_{\mathrm {p}}\right) \dot{\mathbf {q}}_{\mathrm {DE}}+\mathbf {R}_{\mathrm {p}}\dot{\mathbf {q}}_{\mathrm {p}}. \end{aligned}$$
(35.4)

Equation (with \(n_\mathrm {r}\) equations) (35.1) describes the motion of the mechanical system, and it is a set of nonlinear second-order differential equations. The equation set (\(n_\mathrm {p}\) equations) (35.2) describes the creep behavior of the DET material. Equation sets (35.3) and (35.4) with \(2n_\mathrm {p}\) equations represent the electrical model of the coupled DET system and correspond to Kirchhoff’s voltage law. The terms \(\frac{\mathrm {d}}{\mathrm {d}t}\frac{\partial \mathcal {L}}{\partial \dot{\mathbf {q}}_\mathrm {p}}\), \(\frac{\mathrm {d}}{\mathrm {d}t}\frac{\partial \mathcal {L}}{\partial \dot{\mathbf {q}}_\mathrm {DE}}\), \(\frac{\partial \mathcal {L}}{\partial \mathbf {q}_\mathrm {DE}}\), \(\frac{\mathrm {d}}{\mathrm {d}t}\frac{\partial \mathcal {L}}{\partial \dot{\mathbf {q}}_\varepsilon }\), and \(\frac{\partial \mathcal {L}}{\partial \mathbf {q}_\varepsilon }\) are zero, since \(\mathcal {L}\) does not depend on \(\dot{\mathbf {q}}_\mathrm {p}\), \(\mathbf {q}_\mathrm {DE}\), \(\dot{\mathbf {q}}_\mathrm {DE}\) or \(\mathbf {q}_\varepsilon \). The equations of the electrical system are reduced to \(n_\mathrm {p}\) equations by eliminating the current \(\dot{\mathbf {q}}_\mathrm {DE}\) resolving \(\mathbf {V}_{\mathrm {e}}\) according to \(\dot{\mathbf {q}}_\mathrm {DE}\) and substituting it in \(\mathbf {V}_{\mathrm {p}}\). The resistance matrices \(\mathbf {R}_\mathrm {p}\) and \(\mathbf {R}_\mathrm {s}\) are diagonal matrices with the elements \(R_{\mathrm {p},i}\) and \(R_{\mathrm {s},i}\) while \(\mathbf {v}_{\mathrm {DE}}\), \(\dot{\mathbf {q}}_{\mathrm {DE}}\), \(\mathbf {q}_{\mathrm {p}}\), and \(\dot{\mathbf {q}}_{\mathrm {p}}\) are the corresponding vectors. The electromechanical coupling appears in the expressions \(\frac{\partial \mathcal {L}}{\partial \mathbf {q}_\mathrm {m}}\) and \(\frac{\partial \mathcal {L}}{\partial \mathbf {q}_\mathrm {p}}\), which includes the free energy of the DET \(\mathcal {U}_\mathrm {DE}\). Using the state definition

$$\begin{aligned} \begin{aligned} \mathbf {x}&=\begin{bmatrix} \mathbf {q}_\mathrm {m}\\ \dot{\mathbf {q}}_\mathrm {m}\\ \mathbf {q}_\varepsilon \\ \mathbf {q}_\mathrm {p} \end{bmatrix},&\mathbf {u}=\mathbf {v}_\mathrm {DE},&\mathbf {y}=\mathbf {g}(\mathbf {q}_\mathrm {m}) \end{aligned} \end{aligned}$$
(36)

with \(n=2\left( n_\mathrm {q}+n_\mathrm {p}\right) \) states, \(p=n_\mathrm {p}\) inputs and q outputs, this can be easily transformed into a state space model of the form

$$\begin{aligned} \begin{aligned} \dot{\mathbf {x}}&=\mathbf {f}\left( \mathbf {x},\mathbf {u}\right) ,\\ \mathbf {y}&=\mathbf {g}\left( \mathbf {x},\mathbf {u}\right) . \end{aligned} \end{aligned}$$
(37)

Equation (37) can be finally used to design and control a complex DET actuator system suspended with flexible elastic structures. The proposed method includes various nonlinear and dynamical effects for both a DET and elastic structure, which leads to a complex high order nonlinear system. The model can be reduced, if for example we assume that the dynamic behavior of the elastic structure dominates the dynamic behavior of DETs. Thus, the creep losses of the DET can be neglected, and therefore, the Maxwell strain vector \(\mathbf {q}_\varepsilon \) can be eliminated. In this context, when modeling DET systems, not all energy or work terms have to be considered. Depending on the application, some physical effects can be neglected in order to generate simplified reasonable models that are suitable for further investigations avoiding complex incomprehensible systems.

3 Example: modeling DET coupled with a flexible buckled beam structure

In this Section, the general method derived in the previous Section is applied to a DET, coupled with a buckled beam as depicted in Fig. 4. The electromechanical system comprises a DET with n layers, two symmetric bending beams, and a mechanical interface connecting the elastic structure with the DET. Material and geometric parameters are listed in Table 2. The DET is stretched in such a way that the beam reaches a buckled state with a maximum deflection q. By applying a voltage to the DET, the actuator moves in vertical direction. Thus, the voltage \(v_{\mathrm {DE}}\) is defined as the input and the vertical displacement y as the output, resulting in a SISO System. Furthermore, two different mechanical interface configurations are examined and compared with each other, which can be easily considered by various boundary conditions. We will consider a simply supported beam and a fixed beam evaluated for the DE actuator system.

Fig. 4
figure 4

Schematic representation of a DET combined with a buckled beam structure and considering different boundary conditions, simply supported beam (left) and fixed beam (right)

Full size image

In the first step, before starting to derive the model equations, we will introduce the kinematic assumptions applied to the system. Energy and virtual work expressions are formulated for the DET material and beam elements considering the mechanical and electrical behavior of the model. The Rayleigh–Ritz approximation is performed, which accounts for different boundary conditions and in addition defines the generalized coordinate. Finally, the Hamilton principle is applied to the electromechanical system, resulting in a nonlinear ODE system that can be easily transformed into a state space model and utilized for further investigation. Geometric nonlinearities are considered to accurately describe the instable buckling behavior of the beam elements and therefore induce multiple equilibrium solutions [32], which appear in our actuator concept.

Table 2 Geometric and material parameters of DET and beam element under investigation
Full size table

3.1 Kinematic assumptions

3.1.1 Beam element assumption

The Euler–Bernoulli beam theory is considered, which provides a simple means of calculating the load and deflection characteristics of beams by introducing the kinematic assumption that a cross-sectional plane does not deform and thus only undergoes rigid displacements and rotation. This assumption is equivalent to neglecting the shear deformation of the material. A beam of length l, mass density \(\rho \), and a cross-section area A is considered. The transverse displacement on it is uniform and limited to the transverse displacement in the xz-plane,

$$\begin{aligned} \begin{aligned} u_2 = v&= 0,&u_3&= w(x,t), \end{aligned} \end{aligned}$$
(38)

which depends on the coordinate x, and time t. The axial displacement component results from the rotation of the cross section such that it remains orthogonal to the neutral axis,

$$\begin{aligned} \begin{aligned} u_1=u(x,z,t)&= -z\arcsin \left( \frac{\partial w}{\partial x}\right) , \end{aligned} \end{aligned}$$
(39)

and depends on the coordinate x, z, and time t. With Eq. (39), large rotations can be considered, which is necessary for an accurate characterization of the buckled beam structure [33]. The linearized time derivative

$$\begin{aligned} \begin{aligned} \dot{u}(x,z,t)&= -z\frac{ \dot{w}^{\prime }(x,t)}{\sqrt{1-w^{\prime }(x,t)^2}}\approx -z \dot{w}^{\prime }(x,t) \end{aligned} \end{aligned}$$
(40)

is considered when the rotatory inertia of the beam cross section is included. Based on the small strain assumption, the nonlinear strain terms in Eq. (4) are neglected,

$$\begin{aligned} \begin{aligned} \varepsilon _{ij}&= \frac{1}{2}\left( \frac{\partial u_i}{\partial x_j}+\frac{\partial u_j}{\partial x_i}\right) . \end{aligned} \end{aligned}$$
(41)

Considering the assumption of the Euler–Bernoulli beam, the strain tensor is reduced to the strain in x-direction:

$$\begin{aligned} \begin{aligned} \varepsilon _{11} = \frac{\partial u}{\partial x} = -z\frac{ w^{\prime \prime }(x,t)}{\sqrt{1-w^{\prime }(x,t)^2}}=-z\kappa (x,t). \end{aligned} \end{aligned}$$
(42)

\(\kappa (x,t)\) is the physical curvature of the deformed beam, and it is a function of w only. It is valid for small strains and does not contain any restriction on the magnitude of rotations, which is necessary for an accurate consideration of the buckling behavior [33]. A linearized form of the curvature \(\kappa \) is also necessary,

$$\begin{aligned} \begin{aligned} \varepsilon _{11} \approx -zw^{\prime \prime }(x,t), \end{aligned} \end{aligned}$$
(43)

which will be used for the small dissipation resulting in the beam elements. Finally, for isotropic material behavior with a uniaxial stress state, the elastic strain energy simplifies to

$$\begin{aligned} \begin{aligned} \frac{1}{2}\int _{\varOmega } C_{ijkl}\varepsilon _{ij}\varepsilon _{kl}\mathrm {d}V=\frac{1}{2}\int _{\varOmega } E\varepsilon ^2\mathrm {d}V. \end{aligned} \end{aligned}$$
(44)

3.1.2 DET assumption

An n-layer DET with length \(l_0\), area \(A_0\), and thickness \(d_0\) is considered. Within this contribution, the Neo-Hooke model

$$\begin{aligned} \begin{aligned} \psi (I_1(\mathbf {C}))=\psi (\lambda _x,\lambda _y,\lambda _z)=\frac{Y}{6}\left( \lambda _x^2+\lambda _y^2+\lambda _z^2-3\right) \end{aligned} \end{aligned}$$
(45)

is used for modeling the static mechanical behavior of the DET. Due to the incompressibility of the elastomers considered, on the one hand the volume

$$\begin{aligned} \begin{aligned} V_{\mathrm {DE}}=nA_0d_0 \end{aligned} \end{aligned}$$
(46)

is constant. On the other hand, a planar deformation in the x-direction occurs due to the design of the DE transducer considered, i.e., the stretch \(\lambda _y\) is equal to one, and \(\lambda _x\) directly depends on the stretch in the z-direction \(\lambda _z\):

$$\begin{aligned} \begin{aligned} \lambda _x\lambda _y\lambda _z=\lambda _{x}\lambda _z=1\rightarrow \lambda _z=\frac{1}{\lambda _{x}}. \end{aligned} \end{aligned}$$
(47)

The stretches are assumed to be constant and do not depend on the coordinates \(x_{\mathrm {DE}}\), \(y_{\mathrm {DE}}\), \(z_{\mathrm {DE}}\). Finally, the kinetic energy and viscose losses are assumed to be small compared to those of the beam elements, and therefore, they are neglected. Nonetheless, the viscose losses of the DE material are considered in the calculations, which induces an additional internal state variable \(q_{\varepsilon }=\varepsilon _{\mathrm {E}}\).

3.2 Energy functions and virtual works of the coupled DET beam structure

We will start by calculating the Lagrangian of the DET system, which comprises the kinetic energy, the strain energy of the symmetric buckled beam, and the free energy of the n-layer DET.

3.2.1 Kinetic energy

The kinetic energy \(\mathcal {T}\) is determined for the mechanical interface as a concentrated mass element m, and the kinetic energy for the two beam elements \(\mathcal {B}_1=\mathcal {B}_2=\mathcal {B}\) is simplified considering Eq. (2) and the assumptions of the Euler–Bernoulli beam theory:

$$\begin{aligned} \begin{aligned} \mathcal {T}&= \frac{1}{2}m\dot{y}^2 + \frac{1}{2}\int _{\mathcal {B}_1} \rho \left( \dot{u}^2 + \dot{w}^2 \right) \mathrm {d}V+\frac{1}{2}\int _{\mathcal {B}_2} \rho \left( \dot{u}^2 + \dot{w}^2 \right) \mathrm {d}V\\&= \frac{1}{2}m\dot{y}^2 + \int _{\mathcal {B}} \rho \left( \dot{u}^2 + \dot{w}^2 \right) \mathrm {d}V. \end{aligned} \end{aligned}$$
(48)

Inserting Eqs.(40) into (48), the kinetic energy of the beam can be written depending on w:

$$\begin{aligned} \begin{aligned} \mathcal {T}&= \frac{1}{2}m\dot{y}^2 + \int _{0}^l\int _A \rho \left( z^2\dot{w}^{\prime ^2} + \dot{w}^2 \right) \mathrm {d}A\mathrm {d}x\\&= \frac{1}{2}m\dot{y}^2 + \int _{0}^l \rho \left( I\dot{w}^{\prime ^2} + A\dot{w}^2 \right) \mathrm {d}x, \end{aligned} \end{aligned}$$
(49)

where \(I=\int _Az^2\mathrm {d}A\) is the geometric moment of inertia of the cross-section area A. The first term in the integral describes the kinetic energy for the rotation of the cross sections, while the second is the translational kinetic energy.

3.2.2 Strain energy

Given Eq.(42), the strain energy \(\mathcal {U}_\mathrm {s}\) of the system is written in terms of w and its derivative \(w^{\prime }\), \(w^{\prime \prime }\):

$$\begin{aligned} \begin{aligned} \mathcal {U}_\mathrm {s}&= \frac{1}{2}\int _{\mathcal {B}_1}E\varepsilon _{11}^2\mathrm {d}V+\frac{1}{2}\int _{\mathcal {B}_2}E\varepsilon _{11}^2\mathrm {d}V=\int _{\mathcal {B}}E\varepsilon _{11}^2\mathrm {d}V\\&= \int _{0}^l\int _{A}Ez^2w^{{\prime \prime }^2}\frac{1}{1-w^{{\prime }^2}}\mathrm {d}A\mathrm {d}x. \end{aligned} \end{aligned}$$
(50)

The expression \(\frac{1}{1-w^{{\prime }^2}}\) is typically approximated by a second-order Taylor series to simplify the calculation of a beam structure [34], resulting in

$$\begin{aligned} \begin{aligned} \mathcal {U}_\mathrm {s}&= \int _{0}^lEIw^{{\prime \prime }^2}\left( 1+w^{{\prime }^2}\right) \mathrm {d}x, \end{aligned} \end{aligned}$$
(51)

where EI represents the bending stiffness of the cross-section.

3.2.3 Free energy of DET

Finally, the free energy \(\mathcal {U}_{\mathrm {DE}}\) of the n-layer DET is given, taking into account the Neo-Hooke model and a uniform distributed charge over the DE area \(A_0\):

$$\begin{aligned} \begin{aligned} \mathcal {U}_{\mathrm {DE}}&= \int _{\varOmega _{\mathrm {DE}}}\frac{Y}{6}\left( \lambda _x^2+\lambda _y^2+\lambda _z^2-3\right) +\frac{q_{\mathrm {p}}^2}{2\varepsilon _0\varepsilon _{\mathrm {r}}n^2A_{0}^2\lambda _{x}^2\lambda _{y}^2}\mathrm {d}V_{\mathrm {DE}}. \end{aligned} \end{aligned}$$
(52)

Substituting the assumptions (46) and (47) into Eq. (52), the free energy is simplified:

$$\begin{aligned} \begin{aligned} \mathcal {U}_{\mathrm {DE}}&= \int _{\varOmega _{\mathrm {DE}}}\frac{Y}{6}\left( \lambda _x^2+\frac{1}{\lambda _x^2}-2\right) +\frac{q_{\mathrm {p}}^2}{2\varepsilon _0\varepsilon _{\mathrm {r}}n^2A_{0}^2\lambda _{x}^2}\mathrm {d}V_{\mathrm {DE}},\\&=V_{\mathrm {DE}}\left[ \frac{Y}{6}\left( \lambda _x^2+\frac{1}{\lambda _x^2}-2\right) +\frac{q_{\mathrm {p}}^2}{2\varepsilon _0\varepsilon _{\mathrm {r}}n^2A_{0}^2\lambda _{x}^2}\right] . \end{aligned} \end{aligned}$$
(53)

3.2.4 Mechanical virtual work

We will consider the dissipation of the beam and the viscose losses of the DE material as a mechanical virtual work acting on the DET system (see Eq. (12)), which can be expressed by:

$$\begin{aligned} \begin{aligned} \delta \mathcal {W}_\mathrm {m}&= \underbrace{-\int _{\mathcal {B}}2\eta \dot{\varepsilon }_{11}\delta \varepsilon _{11}\mathrm {d}V}_{\text {beam losses}} + \underbrace{V_{\mathrm {DE}}\left[ \eta _{\mathrm {M}}\left( \dot{\varepsilon }_{z}-\dot{\varepsilon }_{\mathrm {E}}\right) -E_{\mathrm {M}}\varepsilon _{E}\right] \delta \varepsilon _{\mathrm {E}} - V_{\mathrm {DE}}\left[ E_{\mathrm {M}} \varepsilon _{\mathrm {E}}+\eta _{\mathrm {v}}\dot{\varepsilon }_{z}\right] \delta \varepsilon _{z}}_{\text {DE losses}} \end{aligned} \end{aligned}$$
(54)

where \(\eta \), \(\eta _\mathrm {v}\), \(\eta _\mathrm {M}\) represent the damping coefficients of the beam and DE material (viscose losses, Maxwell element) and \(E_\mathrm {M}\) the elasticity modulus of the Maxwell element. By substituting the linearized expression (43) into the first expression of Eq. (54), the mechanical work is given depending on w(x, t), \(\varepsilon _z=\lambda _z-1\) and \(\varepsilon _\mathrm {E}\):

$$\begin{aligned} \begin{aligned} \delta \mathcal {W}_\mathrm {m}&= -\int _{0}^l2\eta I\dot{w}^{\prime \prime }\delta w^{\prime \prime }\mathrm {d}x + V_{\mathrm {DE}}\left[ \eta _{\mathrm {M}}\left( \dot{\lambda }_{z}-\dot{\varepsilon }_{\mathrm {E}}\right) -E_{\mathrm {M}}\varepsilon _{E}\right] \delta \varepsilon _{\mathrm {E}} - V_{\mathrm {DE}}\left[ E_{\mathrm {M}} \varepsilon _{\mathrm {E}}+\eta _{\mathrm {v}}\dot{\lambda }_{z}\right] \delta \lambda _{z}. \end{aligned} \end{aligned}$$
(55)

3.2.5 Electrical virtual work

The electrical virtual work is simply rewritten for the single electrical circuit with one mesh,

$$\begin{aligned} \begin{aligned} \delta \mathcal {W}_\mathrm {e}&= V_{\mathrm {p}}\delta q_{\mathrm {p}}+V_{\mathrm {e}}\delta q_{\mathrm {DE}}, \end{aligned} \end{aligned}$$
(56)

having the generalized voltages

$$\begin{aligned} \begin{aligned}&V_{\mathrm {p}} =R_{\mathrm {p}}\left( \dot{q}_{\mathrm {DE}}-\dot{q}_{\mathrm {p}}\right) ,\\&V_{\mathrm {e}} = v_{\mathrm {DE}}-\left( R_{\mathrm {s}}+R_{\mathrm {p}}\right) \dot{q}_{\mathrm {DE}}+R_{\mathrm {p}}q_{\mathrm {p}}. \end{aligned} \end{aligned}$$
(57)

3.3 Rayleigh–Ritz approximation and generalized coordinate

In the following, the Rayleigh–Ritz approximation is applied to the suspended DET beam system which allows us to represent the continuous system by a discrete approximation. The single field variable appearing in the equations above is w(x, t), which is approximated by the mentioned approach. Thus, the one-dimensional displacement field w(x, t) can be written as a polynomial function,

$$\begin{aligned} \begin{aligned} w\left( x,t\right)&\approx \sum _{j=0}^{N}a_j(t)\phi _j(x),&\phi _j(x)=x^j. \end{aligned} \end{aligned}$$
(58)

As previously mentioned, we will consider two different mechanical interfaces in Fig. 4, which leads to a different approximation of w(x, t) and therefore two different sets of equations with the same structure. In order to describe the beam deflection by only one general coordinate, the simply supported beam model will be approximated by a third-order polynomial,

$$\begin{aligned} \begin{aligned} w\left( x,t\right)&= a_3(t)x^3 + a_2(t)x^2 + a_1(t)x + a_0(t), \end{aligned} \end{aligned}$$
(59)

while the fixed beam model is described by a fourth-order polynomial,

$$\begin{aligned} \begin{aligned} w\left( x,t\right)&= a_4(t)x^4 + a_3(t)x^3 + a_2(t)x^2 + a_1(t)x + a_0(t). \end{aligned} \end{aligned}$$
(60)

Both defined functions (59) and (60) result in one degree of freedom models by satisfying the following geometric boundary conditions for both cases as follows:

  • simply supported beam model of Fig. 4:

    $$\begin{aligned} \begin{aligned} w\left( x=0,t\right)&= 0,&w^\prime \left( x=0,t\right) =0,&\\ w\left( x=\frac{2}{3}l,t\right)&= q(t),&w^\prime \left( x=\frac{2}{3}l,t\right) =0. \end{aligned} \end{aligned}$$
    (61)

  • fixed beam model of Fig. 4:

    $$\begin{aligned} \begin{aligned} w\left( x=0,t\right)&= 0,&w^\prime \left( x=0,t\right) =0,&w^\prime (x=\frac{l}{2},t)=q(t),\\ w\left( x=l,t\right)&= 0,&w^\prime \left( x=l,t\right) =0. \end{aligned} \end{aligned}$$
    (62)

Inserting the geometric boundary conditions (61) and (62) into the corresponding approximations (59) and (60), the field variable can be simplified by only one generalized coordinate q(t) regarding the simply supported beam,

$$\begin{aligned} \begin{aligned} w\left( x,t\right)&= q(t)\left[ -\frac{27}{4}\left( \frac{x}{l}\right) ^3+\frac{27}{4}\left( \frac{x}{l}\right) ^2\right] =q(t)S_{\mathrm {s}}(x), \end{aligned} \end{aligned}$$
(63)

and the fixed beam,

$$\begin{aligned} \begin{aligned} w\left( x,t\right)&= q(t)\left[ 16\left( \frac{x}{l}\right) ^4-32\left( \frac{x}{l}\right) ^3+16\left( \frac{x}{l}\right) ^2\right] =q(t)S_{\mathrm {f}}(x). \end{aligned} \end{aligned}$$
(64)

Thus, all kinematic variables appearing in the energy and work terms can be described by just one generalized mechanical coordinate \(q\, (n_\mathrm {r}=1)\), and the corresponding shape function S(x) (S(x) represents \(S_\mathrm {s}(x)\) or \(S_\mathrm {f}(x)\)), leading to a one degree of freedom motion as aimed before. The vertical deflection y that appears in the kinetic energy of the mass m,

$$\begin{aligned} \begin{aligned} y&= \int _0^l\frac{1}{2}\left( w^\prime (x,t)\right) ^2\mathrm {d}x=q^2 \underbrace{\int _0^l\frac{1}{2}\left( S^\prime (x)\right) ^2\mathrm {d}x}_{\text {const}} \end{aligned}, \end{aligned}$$
(65)

can be written depending on w and consequently as a function of q using the Rayleigh–Ritz approximation [35]. As we will see later, Eq. (65) represents the measured output of the system, and it is a nonlinear (quadratic) function of q. The assumed constant stretch \(\lambda _x\) is also introduced as a function of q describing the ratio between the actual deformed length \(l-y\) and the initial length of the DET \(l_0\) by:

$$\begin{aligned} \begin{aligned} \lambda _x&= \frac{l-y(q)}{l_0},&\lambda _z&=\frac{1}{\lambda _x(q)}. \end{aligned} \end{aligned}$$
(66)

Finally, the virtual mechanical work in Eq. (55) is rewritten depending on \(\delta q\) and \(\delta \varepsilon _\mathrm {E}\) according to:

$$\begin{aligned} \begin{aligned} \delta \mathcal {W}_\mathrm {m}&=\left( -\int _{0}^l2\eta I\dot{w}^{\prime \prime }\frac{\partial w^{\prime \prime }}{\partial q}\mathrm {d}x - V_{\mathrm {DE}}\left[ E_{\mathrm {M}} \varepsilon _{\mathrm {E}}+\eta _{\mathrm {v}}\dot{\lambda }_{z}\right] \frac{\partial \lambda _z}{\partial q}\right) \delta q + V_{\mathrm {DE}}\left[ \eta _{\mathrm {M}}\left( \dot{\lambda }_{z}-\dot{\varepsilon }_{\mathrm {E}}\right) -E_{\mathrm {M}}\varepsilon _{E}\right] \delta \varepsilon _{\mathrm {E}},\\&=-\left( Q_\mathrm {s}+Q_\mathrm {v}\right) \delta q + Q_\mathrm {\varepsilon }\delta \varepsilon _\mathrm {E},\\ \text {with}\\ Q_\mathrm {s}&=\int _{0}^l2\eta I\dot{w}^{\prime \prime }\frac{\partial w^{\prime \prime }}{\partial q}\mathrm {d}x=\dot{q}\underbrace{\int _{0}^l2\eta I\left( S^{\prime \prime }(x)\right) ^2\mathrm {d}x}_{\text {const}},\\ Q_\mathrm {v}&=V_{\mathrm {DE}}\left[ E_{\mathrm {M}} \varepsilon _{\mathrm {E}}+\eta _{\mathrm {v}}\dot{\lambda }_{z}(q)\right] \frac{\partial \lambda _z(q)}{\partial q},\\ Q_\mathrm {\varepsilon }&=V_{\mathrm {DE}}\left[ \eta _{\mathrm {M}}\left( \dot{\lambda }_{z}(q)-\dot{\varepsilon }_{\mathrm {E}}\right) -E_{\mathrm {M}}\varepsilon _{E}\right] , \end{aligned} \end{aligned}$$
(67)

where \(Q_\mathrm {s}\) and \(Q_\mathrm {v}\) comprises the generalized damping force of the beam and DE material, respectively. The generalized force \(Q_\mathrm {\varepsilon }\) represents the viscose losses caused by the Maxwell element, and it adds a new internal generalized coordinate \(\varepsilon _{\mathrm {E}}\) to the system. In summary, the Lagrange function and the virtual works of the holistic electromechanical model are represented by the generalized coordinate q, the internal coordinate \(\varepsilon _\mathrm {E}\), and the generalized charge \(q_\mathrm {p}\). The final step is to derive the dynamical model of the electromechanical system using the Hamilton principle, which leads to a set of nonlinear differential equations (Lagrange equations).

3.4 Hamilton principle and Lagrange equations

The Hamilton principle is applied to the DET beam model, resulting in the following variational equation (see Eq. (34)):

$$\begin{aligned} \begin{aligned} \delta \mathcal {S}&= \int _{t_0}^{t_{\mathrm {e}}}\delta \mathcal {L}\mathrm {d}t + \int _{t_0}^{t_{\mathrm {e}}}-\left( Q_\mathrm {s}+Q_\mathrm {v}\right) \delta q + Q_\mathrm {\varepsilon }\delta \varepsilon _\mathrm {E}+ V_\mathrm {p}\delta q_\mathrm {p}+V_\mathrm {e}\delta q_\mathrm {DE}\mathrm {d}t, \end{aligned} \end{aligned}$$
(68)

where \(Q_\mathrm {s}\), \(Q_\mathrm {v}\), \(V_\mathrm {p}\), and \(V_\mathrm {e}\) are determined from Eqs. (67) and  (57). The Lagrange function of the electromechanical system is summarized by the following expression:

$$\begin{aligned} \begin{aligned} \mathcal {L}\left( q,\dot{q},q_\mathrm {p}\right)&= \mathcal {T}\left( q,\dot{q}\right) -\mathcal {U}_\mathrm {s}\left( q\right) -\mathcal {U}_{\mathrm {DE}}\left( q,q_\mathrm {p}\right) , \end{aligned} \end{aligned}$$
(69)

using Eq. (49), (51), and (53) with

$$\begin{aligned} \begin{aligned} \mathcal {T}&= \frac{1}{2}m\dot{y}^2 + \int _{0}^l \rho \left( I\dot{w}^{\prime ^2} + A\dot{w}^2 \right) \mathrm {d}x= \frac{1}{2}m\dot{y}^2(q) + \dot{q}\underbrace{\int _{0}^l \rho \left( IS^{\prime ^2} + AS^2 \right) \mathrm {d}x}_{\mathrm {const}},\\ \mathcal {U}_\mathrm {s}&= \int _{0}^lEIw^{{\prime \prime }^2}\left( 1+w^{{\prime }^2}\right) \mathrm {d}x= q^2\underbrace{\int _{0}^lEIS^{{\prime \prime }^2}\mathrm {d}x}_{\mathrm {const}}+q^4\underbrace{\int _{0}^lEI\left( S^{{\prime \prime }}S^{{\prime }}\right) ^2\mathrm {d}x}_{\mathrm {const}},\\ \mathcal {U}_{\mathrm {DE}}&=V_{\mathrm {DE}}\left[ \frac{Y}{6}\left( \lambda _x^2(q)+\frac{1}{\lambda _x^2(q)}-2\right) +\frac{q_{\mathrm {p}}^2}{2\varepsilon _0\varepsilon _{\mathrm {r}}n^2A_{0}^2\lambda _{x}^2(q)}\right] . \end{aligned} \end{aligned}$$
(70)

It should be noted that the structure of the equation is not changed by the choice of the shape function S(x), except the constant terms in the above equation. Using Eqs. (63)–(66) in Eq. (70), the Lagrange function \(\mathcal {L}\left( q,\dot{q},q_\mathrm {p}\right) \) is represented by the generalized coordinates q, \(\dot{q}\), and \(q_\mathrm {p}\). According to Eq. (35), we finally attain the Lagrange equations of the DET beam model:

$$\begin{aligned} \begin{aligned}&\frac{\mathrm {d}}{\mathrm {d}t}\frac{\partial \mathcal {L}}{\partial \dot{q}}-\frac{\partial \mathcal {L}}{\partial q}=-\left( Q_\mathrm {s}+Q_\mathrm {v}\right) ,\\[0.1in]&\quad Q_\varepsilon =0\rightarrow V_{\mathrm {DE}}\left[ \eta _{\mathrm {M}}\left( \dot{\lambda }_{z}(q)-\dot{\varepsilon }_{\mathrm {E}}\right) -E_{\mathrm {M}}\varepsilon _{E}\right] =0\\&\quad -\frac{\partial \mathcal {L}}{\partial q_\mathrm {p}}=R_{\mathrm {p}}\left( \dot{q}_{\mathrm {DE}}-\dot{q}_{\mathrm {p}}\right) ,\\&\quad \dot{q}_{\mathrm {DE}}=\frac{1}{\left( R_{\mathrm {s}}+R_{\mathrm {p}}\right) }v_{\mathrm {DE}}+\frac{R_{\mathrm {p}}}{\left( R_{\mathrm {s}}+R_{\mathrm {p}}\right) }\dot{q}_{\mathrm {p}}, \end{aligned} \end{aligned}$$
(71)

where the fourth equation of (71) is substituted into the third equation to eliminate the variable \(\dot{q}_{\mathrm {DE}}\). The second equation represents the viscose losses of the DE due to the Maxwell element, and it is specified by the inner generalized coordinate \(\varepsilon _\mathrm {E}\). The calculations were performed and lead to the following set of equations:

$$\begin{aligned} \begin{aligned}&M\ddot{q}+a\,m\left( q^2\ddot{q}+2q\dot{q}^2\right) +d\dot{q}+c_1q+c_3q^3-\frac{bV_{\mathrm {DE}}}{\left( l-c_2q^2\right) ^3}\left[ \frac{Y}{3}\left( \frac{q\left( l-c_2q^2\right) ^4}{l_0^2}-l_0^2q\right) -\frac{l_0^2qq_\mathrm {p}^2}{A_0^2\varepsilon _0\varepsilon _\mathrm {r}n^2}\right] \\&\quad +V_{\mathrm {DE}}\left( E_\mathrm {M}\varepsilon _\mathrm {E}+\eta _\mathrm {v}\frac{2l_0c_2q\dot{q}}{\left( l-c_2q^2\right) ^2}\right) \frac{2l_0c_2q}{\left( l-c_2q^2\right) ^2}=0,\\&\quad \dot{\varepsilon }_{\mathrm {E}}=\frac{2l_0c_2q\dot{q}}{\left( l-c_2q^2\right) ^2}-\frac{E_{\mathrm {M}}}{\eta _\mathrm {M}}\varepsilon _{E},\\&\quad \dot{q}_\mathrm {p}=\frac{1}{R_{\mathrm {s}}}v_{\mathrm {DE}}-\left( \frac{1}{R_\mathrm {s}}+\frac{1}{R_\mathrm {p}}\right) \frac{l_0^2q_\mathrm {p}}{C_0\left( c_2q^2-l\right) ^2}. \end{aligned} \end{aligned}$$

The Maxwell element and the viscosity of the DE actuator can be neglected since these losses are generally smaller than those of the beam elements. Accordingly, the equations simplify to

$$\begin{aligned} \begin{aligned}&M\ddot{q}+a\,m\left( q^2\ddot{q}+2q\dot{q}^2\right) +d\dot{q}+c_1q+c_3q^3-\frac{bV_{\mathrm {DE}}}{\left( l-c_2q^2\right) ^3}\left[ \frac{Y}{3}\left( \frac{q\left( l-c_2q^2\right) ^4}{l_0^2}-l_0^2q\right) -\frac{l_0^2qq_\mathrm {p}^2}{A_0^2\varepsilon _0\varepsilon _\mathrm {r}n^2}\right] =0,\\&\quad \dot{q}_\mathrm {p}=\frac{1}{R_{\mathrm {s}}}v_{\mathrm {DE}}-\left( \frac{1}{R_\mathrm {s}}+\frac{1}{R_\mathrm {p}}\right) \frac{l_0^2q_\mathrm {p}}{C_0\left( c_2q^2-l\right) ^2}, \end{aligned} \end{aligned}$$

with

$$\begin{aligned} \begin{aligned} a&=\frac{59049}{1600}\frac{1}{l^2},&b&= \frac{243}{40}\frac{1}{l},&d&= \frac{729}{2}\frac{I\eta }{l^3},&M&= \frac{243}{280}\rho \left( Al+14\frac{I}{l}\right) ,\\ C_0&=\frac{\varepsilon _0\varepsilon _\mathrm {r}A_0n}{d_0} ,&c_1&= \frac{729}{2}\frac{EI}{l^3},&c_2&= \frac{243}{80}\frac{1}{l},&c_3&= \frac{708588}{70}\frac{EI}{l^5}, \end{aligned} \end{aligned}$$
(72)

when considering the simply supported beam model and

$$\begin{aligned} \begin{aligned} a&=\frac{262144}{11025}\frac{1}{l^2},&b&= \frac{512}{105}\frac{1}{l},&d&= \frac{2048}{5}\frac{I\eta }{l^3},&M&= \frac{256}{315}\rho \left( Al+12\frac{I}{l}\right) ,\\ C_0&=\frac{\varepsilon _0\varepsilon _\mathrm {r}A_0n}{d_0} ,&c_1&= \frac{2048}{5}\frac{EI}{l^3},&c_2&= \frac{256}{105}\frac{1}{l},&c_3&= \frac{2097152}{1155}\frac{EI}{l^5}, \end{aligned} \end{aligned}$$
(73)

for a fixed beam boundary condition. Notice that the structure of the equations remains the same for both boundary conditions and thus does not depend on the Rayleigh–Ritz approximation. The coefficients of the discrete model include the geometry and material parameters of the beam elements as well as the parameters of the DET. Finally, the electromechanical coupled behavior can be presented as a state space model used in system theory,

$$\begin{aligned} \begin{aligned} \dot{\mathbf {x}}&=\mathbf {f}(\mathbf {x})+\mathbf {b}u,\\ y&=g(\mathbf {x})=c_2q^2=c_2x_1^2, \end{aligned} \end{aligned}$$
(74)

with

$$\begin{aligned} \begin{aligned} \mathbf {x}&=\left[ \begin{array}{ccc} x_1&x_2&x_3\end{array}\right] ^T=\left[ \begin{array}{ccc} q&\dot{q}&q_\mathrm {p}\end{array}\right] ^T,~~~~ u=v_\mathrm {DE}, ~~~~\mathbf {b}=\left[ \begin{array}{ccc} 0&0&\frac{1}{R_\mathrm {s}}\end{array}\right] ^T,\\ \mathbf {f}&=\left[ \begin{array}{c} x_2 \\ [0.05in] -\frac{2amx_1x_2^2+dx_2+c_1x_1+c_3x_1^3}{M+amx_1^2}+\frac{bV_{\mathrm {DE}}}{\left( M+amx_1^2\right) \left( l-c_2x_1^2\right) ^3}\left[ \frac{Y}{3}\left( \frac{x_1\left( l-c_2x_1^2\right) ^4}{l_0^2}-l_0^2x_1\right) -\frac{l_0^2x_1x_3^2}{A_0^2\varepsilon _0\varepsilon _\mathrm {r}n^2}\right] \\ [0.15in] -\left( \frac{1}{R_\mathrm {s}}+\frac{1}{R_\mathrm {p}}\right) \frac{l_0^2x_3}{C_0\left( c_2x_1^2-l\right) ^2}\end{array}\right] . \end{aligned} \end{aligned}$$
(75)

4 Analysis of the coupled DET beam model

In order to validate the coupled DET beam model, analytical and numerical analyses have been performed considering the static and dynamic behavior of the soft actuator system. The investigations are carried out based on parameters listed in Table 2, which are chosen based on realistic data. In order to examine the mechanical buckling response of the coupled DET beam actuator, the steady-state solution of (75),

$$\begin{aligned} \begin{aligned} 0{\mathop {=}\limits ^{!}}\mathbf {f}(\mathbf {x})+\mathbf {b}u, \end{aligned} \end{aligned}$$
(76)

is calculated according to the unknown beam deflection q, where the beam length l is varied at voltages of \(v_{\mathrm {DE}}=0\,\mathrm {V}\) and \(v_{\mathrm {DE}}=v_\mathrm {max}=3\,\mathrm {kV}\). The initial geometry of the DET is kept constant: \(l_0,d_0,A_0\,=~\mathrm {const}\). Figure  5 a) and b) illustrates the equilibrium states depending on the pre-strain

$$\begin{aligned} \begin{aligned} \varepsilon _{\mathrm {b}}=\frac{l-l_0}{l_0} \end{aligned} \end{aligned}$$
(77)

of the DET for the two different boundary conditions. Considering the blue curves (\(v_{\mathrm {DE}}=0\,\mathrm {V}\)), the initial vertical state of the beam equilibrium is stable when \(\varepsilon _{\mathrm {b}}<\varepsilon _{\mathrm {b,min}}\), and it remains vertical up to \(\varepsilon _{\mathrm {b}}=\varepsilon _{\mathrm {b,min}}\), which corresponds to point A on the equilibrium paths. When increasing this value, the initial vertical equilibrium state becomes unstable, and any arbitrarily small disturbance definitely brings both beams out of the vertical state.

Fig. 5
figure 5

a, b: Equilibrium states of the DET beam actuator depending on the pre-strain \(\varepsilon _{\mathrm {b}}\) at voltages of \(v_{\mathrm {DE}}=0\,\mathrm {V}\) (blue line) and \(v_{\mathrm {DE}}=v_\mathrm {max}=3\,\mathrm {kV}\) (red line). c and d show the potential energy function for certain \(\varepsilon _\mathrm {b}\) with and without actuation, while e and f illustrate the vertical displacement \(\varDelta y=y_0-y(q)\) of the actuator system due to switching

Full size image

Since we have a stable deflected equilibrium state in the vicinity of point A, the beam will switch to a new stable state to either the right-hand \(q^+\) (convex shape) or left-hand \(q^-\) (concave shape), depending on the disturbance. At this bifurcation point, the solution splits into several, here two, paths. For \(\varepsilon _{\mathrm {b}}>\varepsilon _{\mathrm {b,min}}\), the DET beam actuator has two stable equilibrium points \(\mathrm {B}\) and \(\overline{\mathrm {B}}\) beside the unstable point at \(q=0\). The stability can be analyzed considering the total potential energy of the system,

$$\begin{aligned} \begin{aligned} \mathcal {U}_\mathrm {pot}(q,q_\mathrm {p})=\mathcal {U}_\mathrm {s}(q)+ \underbrace{\mathcal {U}_\mathrm {DE,m}(q)+\mathcal {U}_\mathrm {DE,e}(q,q_\mathrm {p})}_{\mathcal {U}_\mathrm {DE}(q,q_\mathrm {p})}+\mathcal {U}_\mathrm {DE,pre}-v_\mathrm {p}q_\mathrm {p}, \end{aligned} \end{aligned}$$
(78)

which comprises the potential energies of the beams \(\mathcal {U}_\mathrm {s}\), the DET’s energy \(\mathcal {U}_\mathrm {DE}\), the constant initial pre-strain \(\mathcal {U}_\mathrm {DE,pre}=\frac{Y}{6}\left( \lambda _{x,\mathrm {pre}}^2+\frac{1}{\lambda _{x,\mathrm {pre}}^2}-2\right) \) with \(\lambda _{x,\mathrm {pre}}=\frac{l}{l_0}\), and the driving voltage source \(v_\mathrm {p}q_\mathrm {p}\). The potential energy depends on the coordinate q and charge \(q_\mathrm {p}\) stored as electrical energy in \(\mathcal {U}_\mathrm {DE,e}(q,q_\mathrm {p})\). The energy expression in Eq. (78) is appropriate if the charge \(q_p\) is controlled in the system. In our case, we adjust voltages to deform the actuator, and therefore \(\mathcal {U}_\mathrm {pot}(q,q_\mathrm {p})\) is reformulated depending on the polymer voltage \(v_\mathrm {p}\) using the Legendre transformation

$$\begin{aligned} \begin{aligned} \mathcal {U}_\mathrm {pot}(q,v_\mathrm {p})&=\mathcal {U}_\mathrm {s}(q)+ \mathcal {U}_\mathrm {DE,m}(q)+\underbrace{v_\mathrm {p}q_\mathrm {p}-\mathcal {U}_\mathrm {DE,e}(q,v_\mathrm {p})}_{\mathrm {Legendre-transformation} }+\mathcal {U}_\mathrm {DE,pre}-v_\mathrm {p}q_\mathrm {p}\\&=\mathcal {U}_\mathrm {s}(q)+ \mathcal {U}_\mathrm {DE,m}(q)-\mathcal {U}_\mathrm {DE,e}(q,v_\mathrm {p})+\mathcal {U}_\mathrm {DE,pre}. \end{aligned} \end{aligned}$$
(79)

The energy \(\mathcal {U}_\mathrm {DE,e}(q,v_\mathrm {p})\) describes the electric co-energy of the DET, and it is calculated for a homogenous field by

$$\begin{aligned} \begin{aligned} \mathcal {U}_{\mathrm {DE,e}}&=\int _{\varOmega _{\mathrm {DE}}} \frac{1}{2}\varepsilon _0\varepsilon _{\mathrm {r}}E^2\mathrm {d}V_{\mathrm {DE}}=\frac{1}{2}nA_0d_0\varepsilon _0\varepsilon _{\mathrm {r}}\frac{v_\mathrm {p}^2}{d_0^2\lambda _z^2}=\frac{1}{2}C_0v_\mathrm {p}^2\lambda _x^2, \end{aligned} \end{aligned}$$
(80)

where \(\lambda _x\) is determined using Eq. (66) and \(C_0=n\varepsilon _0\varepsilon _{\mathrm {r}}\frac{A_0}{d_0}\) is the capacitance of the DET in the initial state. At steady state, the polymer voltage \(v_\mathrm {p}\) is related to the input voltage \(v_\mathrm {DE}\) considering the electric circuit in Fig. 3 for this case:

$$\begin{aligned} \begin{aligned} v_\mathrm {p}=\frac{R_\mathrm {p}}{R_\mathrm {p}+R_\mathrm {s}}v_\mathrm {DE}\approx v_\mathrm {DE}. \end{aligned} \end{aligned}$$
(81)

The normalized energy function

$$\begin{aligned} \begin{aligned} \mathcal {U}_\mathrm {pot,n}(q,v_\mathrm {p}) =\frac{\mathcal {U}_\mathrm {pot}(q,v_\mathrm {p})-\mathcal {U}_\mathrm {min}}{\mathcal {U}_\mathrm {max}-\mathcal {U}_\mathrm {min}} \end{aligned} \end{aligned}$$
(82)

is illustrated in Fig. 5c and d for the three chosen pre-strains \(\varepsilon _\mathrm {b}\). The minimum points \(\mathrm {B}\), \(\overline{\mathrm {B}}\) indicate the stable equilibrium points, and the maximum point at \(q=0\) corresponds to the unstable one A. By increasing the voltage up to \(v_\mathrm {DE}=3\,\mathrm {kV}\), the stable states move from point \(\mathrm {B}\) to \(\mathrm {C}\) and from point \(\overline{\mathrm {B}}\) to \(\overline{\mathrm {C}}\), respectively, as presented in Fig. 5a–d. The dashed lines between \(\overline{\mathrm {C}}\) and \(\mathrm {C}\) in Fig. 5 describe the unstable regions and therefore cannot be actuated within the voltage range \(0\le v_\mathrm {DE} \le v_\mathrm {max}\). However, it is possible to jump between the two stable states if the actuation force momentum is sufficiently large, enabling a bistable operation of the DET beam system between the convex and concave shapes, and vice versa. Figure 5e and f demonstrates the vertical displacement of the DET beam actuator, which is defined as the difference between the initial vertical displacement due to the pre-strain \(y_0\) at \(v_\mathrm {DE}=0\) and the actual displacement \(y=g(\mathbf {x})\) according to Eq. (74) due to the actuation \(v_\mathrm {DE}\ne 0\) by:

$$\begin{aligned} \begin{aligned} \varDelta y=y_0-y. \end{aligned} \end{aligned}$$
(83)

Hence, the DET beam actuator has two operation modes, namely in the vertical direction with the variable \(\varDelta y\) and the horizontal direction q. Comparing different mechanical interfaces, the horizontal deflection q as well as the vertical displacement \(\varDelta y\) of the fixed-end beam (right half of Fig. 5) are larger than those of the simply supported beam shown on the left half in Fig. 5. Furthermore, the bifurcation point is reached at a higher pre-strain because the motion is hindered by the fixed clamping. While both actuator designs strongly differ considering the horizontal displacement q at different pre-strains, the vertical deflections \(\varDelta y\) hardly differ from each other, as shown in Fig. 5e and f.

The dynamic behavior of the actuator is studied using the step responses illustrated in Fig. 6. The simulations are performed for the aforementioned pre-strains by different beam lengths. Figure 6a and b shows the evolution of the beam deflection q with respect to time t.

Fig. 6
figure 6

Step responses of both DET beam models for different mechanical interfaces for \(v_\mathrm {DE} = 0\,\mathrm {kV}\) and \(v_\mathrm {DE} = 3\,\mathrm {kV}\): a ,  b transient behavior of the beam deflection q, c,  d transient behavior of the vertical displacement \(\varDelta y\), e ,  f normalized vertical displacement \(\varepsilon _y=\frac{\varDelta y}{l_y}\)

Full size image

The transient behavior for \(t<1.5\,\mathrm {s}\) without input voltage appears due to the pre-strain of the DET. Oscillations increase with increased pre-strain. After a short settling time, the steady states are reached, where the actuator can be adjusted with input voltages. At time \(t=1.5\,\mathrm {s}\), the actuator is excited with the maximum voltage \(v_{\mathrm {DE}}=v_{\mathrm {max}}=3\,\mathrm {kV}\) as depicted in Fig. 6a and b for the simply supported and fixed-end beam. Due to the momentum of the beam, the actuator switches from the state \(q^+\) (\(\mathrm {B}\)) to \(q^-\) (\(\overline{\mathrm {C}}\)) for \(\varepsilon _\mathrm {b}=0.15,~0.2\) and moves toward (\(\overline{\mathrm {B}}\)) within \(3<t<4.5\,\mathrm {s}\) when the input voltage is switched off. Thus, the actuator can switch between the two equilibrium states depending on the actuation, which demonstrates the bistable characteristic of the system. However, considering a large pre-strain (\(\varepsilon _\mathrm {b}=0.25\)), the instability range between \(\mathrm {C}\) and \(\overline{\mathrm {C}}\) is too large to cross the maximum energy at \(q=0\) with \(v_\mathrm {DE}=3\,\mathrm {kV}\), and therefore, it remains in the same path \(q^+\) or needs much higher voltage momentum to jump into the concave state at \(\overline{\mathrm {C}}\).

In order to investigate the vertical deflection of the actuator, the displacement \(\varDelta y = y_0-y\) is investigated, which leads to the graphs shown in Fig. 6c and d. In addition, the actuation strain is defined as

$$\begin{aligned} \begin{aligned} \varepsilon _y=\frac{\varDelta y}{l_y}, \end{aligned} \end{aligned}$$
(84)

where \(l_y=l-y_0\) is the length of the actuator in the initial state without actuation, as shown in Fig. 6e and f. The vertical deflection of the simply supported beam actuator is about \(\varepsilon _y\approx 6.5\,\%\), while the vertical deflection of the fixed-end beam is approximately \(\varepsilon _y\approx 8\%\). It can be observed that the fixed-end beam performs much better than the simply supported beam. Nevertheless, the vertical motion is independent from the shape of the beams. Both the convex (\(q^+\)) and the concave (\(q^-\)) beam shapes result in the same values for \(\varDelta y\) and \(\varepsilon _y\). However, compared to actuators with poor DE films the deflection of DET beam structures increases the strain \(\varepsilon _y\).

Within this Section, we have demonstrated the functionality of a novel actuator concept that uses the instability of flexible structures to improve the actuator performance by significantly amplifying the deformations of DET systems. Besides the application in soft robotics, the actuator can be used for example as a valve in fluidic applications, which ensures a safe operation due to the supporting beam elements preventing fatigue of the DET. Furthermore, an energy efficient operation is possible due to the bistable characteristics of the DET beam actuator. Another example is to utilize the DET beam system as a sensor to measure pressures in fluids or perhaps forces within its stable operation region.

Further configurations of a beam-supporting DET structure are feasible offering more degrees of freedom in motion. Here, two beam elements are buckled by one DET in the concave and convex shape, respectively. For example, when two DETs are connected outside to a T-shape beam, a rotation of the structure is obtained in addition to the longitudinal deflection, also making use of buckling to amplify its deflections, as illustrated by certain configurations in Fig. 7. In general, the introduced buckling concepts can be multifariously combined to generate more complex kinematic motions, and in particular they are suited for soft robotic applications. The proposed modeling approach is predestined to analyze and optimize such MIMO-DET configurations in future work.

Fig. 7
figure 7

Examples of buckling beam configurations utilizing two DETs to generate more degrees of freedom, e.g., for soft robotics applications

Full size image

5 Conclusions

In this paper, an energy-based modeling approach has been presented to model the nonlinear dynamic behavior of soft material structures comprising dielectric elastomer transducers (DET) suspended with flexible elastic structures. For this purpose, the Hamilton principle was applied considering Lagrange energies and virtual works of both DETs and elastic structures as well as electrical and mechanical inputs. Thus, the overall electromechanical dynamics of the coupled DET structure were derived without the need to consider the inner dynamics and forces of the system. In order to obtain a set of nonlinear differential equations for the soft suspended DET structure, the Rayleigh–Ritz formulation was used to approximate the continuous field variables appearing in the system by generalized coordinates under consideration of defined boundary condition. The modeling approach is predestined for multiple-input–multiple-output (MIMO) systems. Nonlinear ODEs obtained by this approach can be easily utilized to design and control the soft transducer systems based on DETs. The method was successfully applied to a buckled beam structure actuated by a multilayer DET, resulting in complex nonlinear equations. As analyzed in detail based on analytical and numerical investigations, the soft actuator system shows structural instabilities and nonlinear characteristics of the DET. The behavior obtained significantly improves the actuated deflection of the soft actuator in two directions of motion and offers an energy efficient operation due to the bistability of the buckling beams. In the future, we will perform experimental results to prove the actuator’s performance and will further extend the work by designing and optimizing more complex DET beam systems with multi-degree-of-freedom motions, e.g., for soft robotic applications.