1 Introduction

In the area of offshore engineering and more specifically offshore wind, large-diameter monopiles comprise the most dominant type of substructure used as a foundation for offshore wind turbines [1]. Monopile installation is customarily performed by mounting a hammer on the top of the pile and exerting a forcing, either by impact or vibratory motion [2], adequate enough to drive the pile up to the predefined embedment depth. The analysis of this dynamic problem is traditionally conducted in practice by one-dimensional models [3, 4], representing the pile as an elastic rod supported by nonlinear springs and dashpots, a local soil reaction analogue, subjected to the hammer forcing. However, the aforementioned models cannot capture some physical characteristics, inherent to the system, namely the non-local soil reaction [5] and the dispersion of the stress waves propagating in the pile, which can be assumed to cause inaccurate pile drivability predictions [5, 6].

In this paper, the main objective is the introduction of a mode-matching method that can analyse the motion of two linear elastic rods in frictional contact. The mechanical system under consideration represents a pile driving model that addresses, even though in a simplistic manner, non-local soil reaction. In terms of modelling the frictional force exerted at the contact surfaces between bodies in dynamical systems, there are plentiful options of static and dynamic friction models [7, 8]. From a computational perspective, a comparative study of static and dynamic friction models was presented by Marques et al. [9]. Awrejcewicz and Olejnik [10] studied the complex nonlinear dynamic behaviour, including bifurcations and chaotic motions, for various friction laws. Further considerations, such as the stochastic nature of friction in modelling may also be advantageous for certain applications [11]. In the present model, the non-smooth character of the frictional force and the potential stick-slip behaviour can be adequately represented by the Coulomb friction model, which is predominantly applied in vibration problems dealing with friction.

Similar systems to the one presented have been formulated and studied in various applications [12,13,14,15,16]. Berger et al. [12] presented a mixed differential algebraic method for the analysis of problems with partial slip conditions, for the general case of a rate and state-dependent friction law. Therefore, a combination of numerical schemes is employed for the problem, both for detection of stick-slip transitions and for numerical integration of the equations of motion. In a relevant work by Quinn and Segalman [13], an elastic rod on a frictional foundation was studied to investigate further the influence of microslip in the dynamic behaviour of mechanical joints, by employing a regularization of Coulomb friction [17] in conjunction with numerical integration of the equations of motion by the Runge–Kutta method. Cigeroglu et al. [14] studied a similar system to further improve the one-dimensional microslip model by Menq et al. [15, 18], by introducing the inertia of the damper. The solution approach regarded specific stick-slip configurations, specifically two and three regions of stick-slip, while the solution was analytical, by examining a steady-state response in a single mode. Wang and Zhang [19] formulated a four-parameter model to predict the stick-slip behaviour of a lap-type bolted joint, based on microscale contact mechanics.

In general, advanced computational methods and dedicated algorithms have been developed in contact mechanics such as the mortar method, originally used in domain decomposition problems [20, 21]. McDevitt and Laursen [22] proposed a finite element formulation in which the contact interface was discretized into mortar elements, in one of the early applications of the mortar method in frictional problems. The penalty formulation was employed together with the mortar method for two-dimensional problems involving large deformations and frictional contact [23]. Further developments in the mortar method have been realized, including its use in three-dimensional problems with finite deformation contact and frictional sliding by Popp et al. [24].

To the knowledge of the authors, the solution of this class of problems necessitates the concurrent employment of advanced numerical schemes. Simpler alternatives without compromising the numerical accuracy and reforming the original problem are not available. Spatial discretization of the whole system is commonly accompanied by complex computational algorithms, specified for non-smooth dynamical systems [25, 26], to solve the temporal equations of the problem, since the discontinuous nature of friction gives rise to numerical issues in standard numerical integration techniques [17]. Alternatively, regularized forms of the Coulomb’s law can be used [9, 17, 27,28,29], which do not preserve the original multivalued friction force structure at zero relative velocity, in order to facilitate the numerical treatment of Coulomb friction in standard algorithms. Elasto-plastic friction models also possess similar computational structure to the regularized friction models. However, the former are formulated accordingly to address additional effects which cannot be captured by Coulomb friction model [30]. Evidently in the aforementioned cases, such a problem requires a combination of various complex schemes and can be computationally intensive. To this end, the method presented herein alleviates the need for the aforementioned schemes.

In the present paper, a space–time piecewise linear solution procedure is proposed for the case of two linear homogeneous elastic rods in frictional contact, in a manner similar to works in which piecewise linear solutions have been obtained for the case of a single oscillator [31,32,33,34]. The same principle holds in the case of any discretized system and this leads to the presented solution. Consecutively, the vibration problem of the two rods in frictional contact is solved by a mode-matching method and approximation of the convolution integral obtained, with a numerical quadrature method. The continuous description of the second restrained rod is preserved, while sliding is permitted by translation of the kinetic friction forces into multiple distributed loads, rendering the problem of both rods solvable by means of modal analysis in a hybrid manner.

The present paper is comprised of five sections. In Sect. 2, the problem statement is formulated. The method of solution of the problem at hand is presented in Sect. 3, divided into two parts, a first part in which the analytical derivations leading to the final mathematical statement are considered and a second part in which the mode-matching algorithm to obtain the response of the system is developed. Subsequently, in Sect. 4 a validation case is presented, along with a collection of further results and a convergence study, to showcase the potential of the method. Conclusively, in Sect. 5 the merit of the present method is outlined, related to computational efficiency, potential treatment of relevant vibration problems and possible extensions that this procedure can address.

Fig. 1
figure 1

Two rods in frictional interaction

Full size image

2 Model description and governing equations

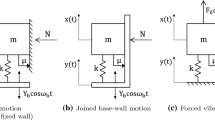
The problem analysed is shown in Fig. 1. The dynamical system consists of two linear homogeneous elastic rods, occupying the domains \( 0 \le z_1 \le L_1 \) and \( 0 \le z_2 \le L_2 \), respectively. The two rods are jointed partially and the interaction is described by Coulomb friction. The equations of motion of the coupled system read:

$$\begin{aligned} \rho _{1} A_{1} {\ddot{u}}_1(z_1, t)= & {} E_1 A_1 u_1 ''(z_1, t) + f + b_1(z_1), \end{aligned}$$
(1)
$$\begin{aligned} \rho _2 A_2 {\ddot{u}}_2(z_2, t)= & {} E_2 A_2 u_2 ''(z_2, t) - f + b_2(z_2). \end{aligned}$$
(2)

In Eqs. (1) and (2), \( E_i \), \( A_i \), \( \rho _i \), with \(i=1,2\), are the modulus of elasticity, the area of the cross section and the mass density per unit length of the two rods. The functions \(u_i(z_i, t)\) denote the axial displacements of the rods and \(b_i(z_i)\) are the distributed external loads. Hereafter, the prime stands for spatial differentiation, i.e. \((\cdot )' = \partial (\cdot ) / \partial z_i\), and the overdot denotes temporal differentiation, i.e. \( \dot{(\cdot )} = \partial (\cdot ) / \partial t\). As can be seen in Fig. 1, rod 1 is unrestrained and in case of full sliding along the interface it admits rigid body motion. The displacement \(u_1\) is constituted by a rigid body displacement term, \(u_1^R(t)\), superimposed by the term \(u_1^{Fl}(z_1,t)\), denoting the small flexible body displacement of rod 1, i.e. \(u_1(z_1,t)=u_1^R(t)+u_1^{Fl}(z_1,t)\). Given that the rigid body term can be large, the position of a point \(z_1\) of rod 1 in the coordinate system of rod 2 reads:

$$\begin{aligned} \displaystyle {{\overline{z}}_2 = z_1 + u_1(z_1,t) - l_1 }, \end{aligned}$$
(3)

where \({\overline{z}}_2\) denotes the instantaneous position of point \(z_1\) of rod 1 in the coordinate system \(z_2\) and \(l_1\) is the initial length of rod 1 not in contact with rod 2. Equation 3 implies that the adjacency of the material points between the two rods is determined by their respective initial undeformed positions and varies along the problem based on the value of \(u_1(z_1, t)\), which can be large due to the large rigid body component; the flexible body displacements of both rods are small and do no affect the relation of adjacency of material points.

During stick, the friction force is equal to the sum of forces acting at the point, while \({\ddot{u}}_1(z_1,t)= {\ddot{u}}_2({\overline{z}}_2,t)\) and \({\dot{u}}_1(z_1,t)={\dot{u}}_2({\overline{z}}_2,t)\) hold. In principle, the friction force f can be expressed for both stick and slip regions as follows:

$$\begin{aligned} f = \left\{ \begin{array}{ll} - \mu _k N_F {{\,\mathrm {sgn}\,}}\left( {\dot{u}}_1(z_1, t) - {\dot{u}}_2({\overline{z}}_2,t) \right) \left( {{\,\mathrm {H}\,}}({\overline{z}}_2) - {{\,\mathrm {H}\,}}(z_2 - l_2 - u_1(L_1,t))\right) , \quad {\dot{u}}_1(z_1, t) \ne {\dot{u}}_2({\overline{z}}_2,t), \\ \\ - (E_1 A_1 u_1 ''(z_1, t) + b_1(z_1) - \rho _1 A_1 {\ddot{u}}_1(z_1,t)) \left( {{\,\mathrm {H}\,}}({\overline{z}}_2) - {{\,\mathrm {H}\,}}(z_2 - l_2 - u_1(L_1,t))\right) , \quad {\dot{u}}_1(z_1, t) = {\dot{u}}_2({\overline{z}}_2,t). \end{array} \right. \nonumber \\ \end{aligned}$$
(4)

In Eq. (4), \( \mu _k \) is the kinetic friction coefficient, \( N_F \) is the uniformly distributed normal load, \(l_2\) is the initial contact length as shown in Fig. 1, while \({{\,\mathrm{sgn}\,}}(\cdot ) \) and \( {{\,\mathrm{H}\,}}(\cdot ) \) denote the signum and Heaviside functions, respectively. It is remarked that in Eq. (4) the friction force for a slipping point is given explicitly (as long as the slip holds), while the friction force for a sticking point is based on the overall coupled response of the system (see Sect. 3). Conclusively, the boundary conditions read as follows:

$$\begin{aligned} N_1 (0, t)= & {} - P(t), \quad N_1 (L_1, t) = 0, \end{aligned}$$
(5)
$$\begin{aligned} N_2 (0, t)= & {} 0, \quad u_2(L_2, t) = 0, \end{aligned}$$
(6)

where \(N_1(z_1,t)\) and \(N_2(z_2,t)\) denote the axial forces of rods 1 and 2, respectively, and P(t) is the external force at the top of rod 1. Eqs. (1) to (6) constitute the mathematical statement of the problem in the time domain. Coulomb friction yields nonlinear and non-smooth dynamical response, i.e. segments of the two rods can either stick or slip relative to each other.

3 Method of solution

The solution approach is based on the following steps:

  1. (i)

    spatial discretization of rod 1 and mapping of friction to discrete points (Sect. 3.1). Rod 2 maintains its continuous description;

  2. (ii)

    eigensolutions of the two rods and modal decomposition per time interval in which the problem remains linear. It is remarked that the eigensolutions for rod 1 are time-dependent and change per time interval, depending on the regions in stick or slip phase (Sect. 3.2);

  3. (iii)

    determination of the modal coordinates for the computed eigensolutions of the time interval defined in (ii) above (Sect. 3.2);

The method proposed tackles the problem in a piecewise linear manner and the time intervals mentioned in steps (ii) and (iii) above are identified by means of an iterative process.

3.1 Analytical derivations

The spatial discretization of rod 1 (Fig. 1) is accomplished by the central finite difference method of accuracy \( {\mathcal {O}} (h^2) \). Upon discretization, the nodes \( z_{1,i} \) are given by:

$$\begin{aligned} \displaystyle { z_{1,i} = (i - 1) \cdot h , \ \ i = 1, \dots , N \ \ \text {and} \ \ h =\frac{L_1}{N-1} ,} \end{aligned}$$
(7)

in which h and N, denote the spatial discretization step and the number of nodes, respectively. The discretized equation of motion of rod 1 takes the following form:

$$\begin{aligned} \begin{aligned} \displaystyle { \rho _1 A_1 {\ddot{u}}_{1,i} + \frac{E_1 A_1}{h^2} \left( 2 u_{1,i} - u_{1,i+1} - u_{1,i-1} \right) = f_{i} + b_{1, i}. } \end{aligned} \end{aligned}$$
(8)

The equations of motion of the first and the last node involve the terms \( u_{1, 0}\), \(u_{1, N + 1} \), corresponding to fictitious nodes [35, 36], which are eliminated by means of substitution of the central difference approximation into Eqs. (5) and (6):

$$\begin{aligned} \begin{aligned} u_1^{\prime } (z_1, t)\big |_{z_1=0}&\approx \frac{u_{1,2} - u_{1,0}}{2h} = - \frac{P(t)}{E_1 A_1} \Rightarrow \ u_{1,0} = u_{1,2} + \frac{2h P(t) }{E_1 A_1}, \end{aligned} \end{aligned}$$
(9)
$$\begin{aligned} \begin{aligned} u_1^{\prime } (z_1, t)\big |_{z_1=L_1}&\approx \frac{u_{1, N+1} - u_{1, N-1}}{2h} =0 \Rightarrow \ u_{1, N+1} = u_{1, N-1}. \end{aligned} \end{aligned}$$
(10)

Eqs. (8), (9) and (10) are subsequently combined into the following matrix equation:

(11)

in which \( {\mathbf {M}} \) and \( {\mathbf {K}} \) are the mass and stiffness matrices, respectively, and \({\mathbf {u}}_1\) is the displacement vector of length N. The vector \(\varvec{\hat{f}}\) denotes the Coulomb friction forces given by Eq. (4) upon discretization, at the nodes defined by Eq. (7). Finally, \( \varvec{\hat{p}} (t) \) is the external force vector, while \(b_1(z_1)\) and \(b_2(z_2)\) are henceforth considered zero as they do not affect the solution method.

Given the discretized representation of rod 1, the distributed friction force on rod 2 can be written as:

$$\begin{aligned} \displaystyle { f = \sum \limits _{i=1}^N {\tilde{f}}_i = \sum _{k=1}^{\Lambda _k} {\tilde{f}}_k + \sum _{s=1}^{\Lambda _s} {\tilde{f}}_s \ ,} \end{aligned}$$
(12)

in which \({\tilde{f}}_k\) and \({\tilde{f}}_s\) are the kinetic and static friction forces, respectively, with \(k=1,\ldots , \Lambda _k\) and \(s=1,\ldots , \Lambda _s\). The friction force applied by the ith node of the discretized rod 1 to rod 2 (Fig. 2), in the segment \( {\overline{z}}_{2,i}^l(t) \, \le \, z_2 \, \le \, {\overline{z}}_{2,i}^r (t)\), can be approximated by:

$$\begin{aligned} \displaystyle { {\tilde{f}}_i = \left( {{\,\mathrm{H}\,}}(z_2- {\overline{z}}_{2,i}^l(t) ) - {{\,\mathrm{H}\,}}(z_2 - {\overline{z}}_{2,i}^r(t) ) \right) \, \frac{\hat{f}_i}{h} }, \end{aligned}$$
(13)

in which \( {\overline{z}}_{2,i}^l(t) \), \( {\overline{z}}_{2,i}^r(t) \) are derived in correspondence with Eq. (3):

$$\begin{aligned} \displaystyle { {\overline{z}}_{2,i}^{l,r} (t) = z_{1,i} \mp \frac{h}{2} + u_{1,i}(t) - l_1 }. \end{aligned}$$
(14)
Fig. 2
figure 2

Friction forces acting along the two rods

Full size image

Therefore, \( {\overline{z}}_{2,i}^l(t) \), \( {\overline{z}}_{2,i}^r(t) \) comprise the coordinates of the moving boundaries of stick/slip regions (limited by discretization). Given Eqs. (13) and (14), it is noted that the slipping nodes are translated into kinetic forces, each one being distributed along a length equal to h and with magnitude \( \mu _k N_F \). Regarding the sticking nodes, their motion follows the motion of their adjacent points in rod 2, based on the kinematic relations given in Sect. 2. Therefore, the sticking nodes act as added mass and stiffness to rod 2 and are treated as pseudo-forces leading to modal coupling [37]. Substitution of Eq. (12) into Eq. (2) yields:

$$\begin{aligned} \displaystyle { \rho _2 A_2 \, {\ddot{u}}_2(z_2,t) = E_2 A_2 \,u_2''(z_2,t) - \left( \sum _{k=1}^{\Lambda _k} {\tilde{f}}_k + \sum _{s=1}^{\Lambda _s} {\tilde{f}}_s \right) } \end{aligned}$$
(15)

For the vibration of single-degree-of-freedom oscillators on a frictional surface exact solutions do exist [31,32,33,34]. All of these solutions are based on the piecewise linearity of the Coulomb friction model. In the approach described in Sect. 3.2 the piecewise linearity is further exploited to solve Eqs. (11) and (15).

3.2 Mode-matching algorithm

The present system admits a linear piecewise solution, which is valid for a time interval at which all the degrees of freedom of the system remain in the same state, being either stick or slip. Each time interval is terminated at the time moment at which the first state transition occurs. This specific time moment is determined by means of matrix \({\mathbf {C}}\), the elements of which are given as:

$$\begin{aligned} C_{ij} = \delta _{ij} \displaystyle { {\left\{ \begin{array}{ll} 1, \ \ \displaystyle { {\dot{u}}_{1,i} (t) \ne {\dot{u}}_2({\overline{z}}_{2,i},t) } \quad \text{ or } \quad \big |- \rho _1 A_1 h \, {\ddot{u}}_{1,i} (t) - {\mathbf {K}}_i {\mathbf {u}}_1(t) + \hat{p}_i(t) \big |\ge \mu _s N_F h, \\ \\ 0, \ \ \displaystyle { {\dot{u}}_{1,i} (t) = {\dot{u}}_2({\overline{z}}_{2,i},t) } \quad \text{ and } \quad \big |- \rho _1 A_1 h \, {\ddot{u}}_{1,i} (t) - {\mathbf {K}}_i {\mathbf {u}}_1(t) + \hat{p}_i(t) \big |< \mu _s N_F h, \end{array}\right. } } \end{aligned}$$
(16)

in which \(\delta _{ij}\) is the Kronecker delta, \({\mathbf {K}}_i\) is the ith row of the stiffness matrix \({\mathbf {K}}\) and \(j=1,\ldots ,N\). At the start of each time interval, the mass and stiffness matrices are pre-multiplied by the \({\mathbf {C}}\) matrix, i.e. \(\widetilde{{\mathbf {M}}} = {\mathbf {C}} \, {\mathbf {M}}\) and \(\widetilde{{\mathbf {K}}} = {\mathbf {C}} \, {\mathbf {K}} \). Upon application of \({\mathbf {C}}\), any possible state can be categorized in the three states shown in Fig. 3.

Fig. 3
figure 3

Global states and corresponding modified matrices: a a fully sticking system, b a fully non-sticking system and c a system with an arbitrary configuration of alternating sticking and non-sticking parts

Full size image

In terms of solution method, cases a) and b) correspond to linear problems per time interval. Case c) can be seen as a combination of a) and b), i.e. each subsystem (sticking or not) can be treated separately. In view of the above, the equation of motion of a single non-sticking series reads:

(17)

The subscript \(s=1,\dots ,S\) in Eq. (17) denotes the sth subsystem from the S identified subsystems in the respective time interval. Accordingly, \({\mathbf {M}}_s\), \({\mathbf {K}}_s\), \({\mathbf {u}}_{1s}\), \(\varvec{\hat{p}}_s(t)\) and \(\varvec{\hat{f}}_s\) denote the mass matrix, stiffness matrix, displacement vector, external force vector and friction forces vector of the sth subsystem. Since Eqs. (15) and (17) are both linear for a time interval \(t_{r-1} \, \le \, t \, \le \, t_r\), with \(r=1,..,R\) and \(t_R\) being the final time moment of the analysis, the response of the two rods can be sought for in the modal domain:

$$\begin{aligned} {\mathbf {u}}_{1s}=&{} \sum \limits _{n=1}^{N_s} \pmb {\phi }_{s,n} \, q_{s,n}(t), \end{aligned}$$
(18)
$$\begin{aligned} u_2(z_2,t)=&{} \sum \limits _{m=1}^{\infty } \psi _m(z_2) \, \eta _m(t). \end{aligned}$$
(19)

In Eqs. (18) and (19), \( \pmb {\phi }_{s,n} \) and \(\psi _n (z_2)\) are the mass-normalized modes of the generalized eigenvalue problem for the S identified subsystems and rod 2, respectively, while \(q_{s,n}(t)\) and \(\eta _m(t)\) denote the respective modal coordinates. Equation (18) retains this form for all the subsystems during a time interval, albeit each subsystem, e.g. the sth, is described in terms of its respective modes \(\pmb {\phi }_{s,n}\) and modal coordinates \(q_{s,n}(t)\). Substitution of Eqs. (18) and (19) into Eqs. (17) and (15) and linear transformation to the their respective modal domains yields the ordinary differential equations (ODEs) of the associated modal coordinates:

$$\begin{aligned} \ddot{q}_{s,n} (t) + \omega _{s,n}^2 \, q_{s,n} (t)&= \pmb {\phi }_{s,n} \cdot \left( \varvec{\hat{p}}_s(t) + \varvec{\hat{f}}_s \right) ,\quad n=1, \dots , N_s \end{aligned}$$
(20)
$$\begin{aligned} \ddot{\eta }_{m}(t)+ \omega _{m}^{2} \, \eta _{m} (t)&= \sum \limits _{k=1}^{\Lambda _k} - {\tilde{f}}_k \int \limits _{{\overline{z}}_{2,k}^l(t)}^{{\overline{z}}_{2,k}^r(t)} \! \psi _m(z_2) \mathrm {~d}z_2 + \sum \limits _{s=1}^{\Lambda _s} - {\tilde{f}}_s (t) \int \limits _{{\overline{z}}_{2,s}^l}^{{\overline{z}}_{2,s}^r} \! \psi _m(z_2) \mathrm {~d}z_2 , \quad m=1, \dots , N_m. \end{aligned}$$
(21)

In Eqs. (20) and (21), \(\omega _{s,n}\), \(\omega _m\) denote the eigenfrequencies and \(N_s\), \(N_m\) denote the number of modes of the respective modal set, defined by the related subscript. It is remarked that, due to numerical implementation, the infinite summation is truncated at \(N_m\) modes, which are adequate in number to analyse the exerted frequencies and achieve convergence of the solution. The modal forces in the right-hand side of Eq. (20) have the form of dot product of the associated vectors. Equations (20) and (21) comprise a set of linear ODEs. Thus, at each time interval their respective solutions can be written in the following exact closed form:

$$\begin{aligned} q_{s,n}(t)= & {} q_{s,n} (t_{r - 1} ) \, \cos \! \left( \omega _{s,n} (t - t_{r - 1}) \right) + \frac{\dot{q}_{s,n}(t_{r - 1} )}{\omega _{s,n}} \, \sin \! \left( \omega _{s,n} (t - t_{r - 1}) \right) \\&+ \frac{1}{\omega _{s,n}} \int \limits _{t_{r-1}}^t \! \pmb {\phi }_{s,n} \cdot \left( \varvec{\hat{p}}_s(\tau ) + \varvec{\hat{f}}_s \right) \, \sin \! \left( \omega _{s,n} (t - \tau ) \right) \mathrm {~d} \tau ,\nonumber \end{aligned}$$
(22)
$$\begin{aligned} \eta _m(t)= & {} \eta _m(t_{r-1}) \cos (\omega _m (t - t_{r-1})) + \frac{{\dot{\eta }}_m(t_{r-1})}{\omega _m} \sin (\omega _m (t - t_{r-1})) \\&+ \frac{1}{\omega _m} \int \limits _{t_{r-1}}^t \! \left( \sum \limits _{k=1}^{\Lambda _k} - {\tilde{f}}_k \int \limits _{{\overline{z}}_{2,k}^l(\tau )}^{{\overline{z}}_{2,k}^r(\tau )} \! \psi _m(z_2) \mathrm {~d}z_2 \right) \sin ( \omega _m (t - \tau )) \mathrm {~d} \tau \nonumber \\&+ \frac{1}{\omega _m} \int \limits _{t_{r-1}}^t \! \left( \sum \limits _{s=1}^{\Lambda _s} - {\tilde{f}}_s (\tau ) \int \limits _{{\overline{z}}_{2,s}^l}^{{\overline{z}}_{2,s}^r} \! \psi _m(z_2) \mathrm {~d}z_2 \right) \sin ( \omega _m (t - \tau )) \mathrm {~d} \tau .\nonumber \end{aligned}$$
(23)

By \(q_{s,n} (t_{r - 1} )\), \(\dot{q}_{s,n}(t_{r - 1} )\), \(\eta _m(t_{r-1})\) and \({\dot{\eta }}_m(t_{r-1})\) the initial conditions of the modal coordinates are denoted, for the time interval r, with initial time moment \(t_{r-1}\).

In principle, the convolution integrals associated with the friction forces do not admit analytical solutions. Thus, to acquire the response of rod 2, we resort to numerical approximation of the convolution integral by the composite trapezoidal rule, at time \( t= t_A \), as follows:

$$\begin{aligned} t_a&= t_{r - 1} + a \cdot \Delta t, \quad \ a = 1,2, \ldots , A, \end{aligned}$$
(24)
$$\begin{aligned} D_k (t)&= \int \limits _{t_{r-1}}^{t} \! \left( \sum \limits _{k=1}^{\Lambda _k} - {\tilde{f}}_k \! \int \limits _{{\overline{z}}_{2,k}^l(\tau )}^{{\overline{z}}_{2,k}^r(\tau )} \! \psi _m(z_2) \mathrm {~d}z_2 \right) \sin ( \omega _m (t - \tau )) \mathrm {~d} \tau \nonumber \\&= \frac{\Delta t}{2} \left[ \sum \limits _{a=1}^A \sum \limits _{k=1}^{\Lambda _k} - {\tilde{f}}_k \! \int \limits _{{\overline{z}}_{2,k}^l(t_a)}^{{\overline{z}}_{2,k}^r(t_a)} \! \psi _m(z_2) \mathrm {~d}z_2 \sin ( \omega _m (t - t_a)) + \sum \limits _{a=1}^A \sum \limits _{k=1}^{\Lambda _k} - {\tilde{f}}_k \! \int \limits _{{\overline{z}}_{2,k}^l(t_{a - 1})}^{{\overline{z}}_{2,k}^r(t_{a - 1})} \! \psi _m(z_2) \mathrm {~d}z_2 \sin ( \omega _m (t - t_{a - 1})) \right] . \end{aligned}$$
(25)

Conclusively, a method is now available to compute the response of the system, relying on the successive application of a mode-matching technique with time-dependent modal sets, distinct per time interval. Subsequent step is the definition of the routine of interchange of states in the system. A time interval is terminated by identification of the time moment at which the first state transition occurs. Thus, a change of state in the present problem is defined as the time moment t at which

$$\begin{aligned} {\mathbf {C}}(t) \ne {\mathbf {C}}(t_{r - 1}). \end{aligned}$$
(26)

At this point, one specifies a predetermined tolerance, regarding the accuracy of detecting the time moment of the change of state. Either in a stick-to-slip or slip-to-stick transition, to identify the time moment of the transition, a transcendental equation needs to be solved numerically, by marching forward temporally using a suitable algorithm [12]. Additional merit of the present method is that the evaluation of \( {\mathbf {C}} \) is achieved without the concurrent numerical integration of the equations of motion. Thus, the error of the present method per time interval is solely relied on the numerical approximation of the convolution integral associated with the friction forces. The latter treatment of the evolution of frictional slip permits a continuous and exact tracking of the slipping points along rod 2, which retains its continuous form, employing in total a spatially semi-discrete system.

In general, the applicability of the method extends over linear visco-elastic systems, given that the two bodies possess modes in vacuo, e.g. a Kelvin–Voigt visco-elastic rod. Furthermore, the interface may also incorporate a linear contact stiffness term. In these cases the mode-matching technique can be applied successfully and the procedure is identical with the presented one, with sole discrepancy the modified expressions of modal coordinates and the state matrix \({\mathbf {C}}\). However, it is evident that nonlinear material laws (e.g. nonlinear elasticity) and/or nonlinear interface behaviour (e.g. nonlinear contact stiffness in rough contacts [38]) that do not possess a multi-linear structure impose limitations on the present method. The framework presented can be easily extended to treat beams performing stick-slip vibrations and motions with contact separation, as the main principle of piecewise linearity can be exploited in all aforementioned cases. In the case of systems that attain large displacements, the current formulation is not applicable and different numerical methods, such as the mortar method may be used. Systems with frictional components may exhibit chaotic response [39] and the method presented can be used effectively to capture such regimes in the current or other systems, that are amenable to analysis by the mode-matching method.

Table 1 Parameters of numerical examples
Full size table

4 Numerical results

In Sect. 4.1 a validation case for the system considered herein under harmonic excitation is presented. Furthermore, in Sect. 4.2 numerical examples are presented for harmonic and short square pulse loading cases. For all following numerical examples, the static and kinetic friction coefficients are considered equal, i.e. \(\mu _s = \mu _k\).

4.1 Validation of the solution method

The properties of the two rods for the validation case considered are given in Table 1, while the excitation frequency is set to \(\Omega _1 = 20\) rad/s and the friction force per unit length is set to \(\mu _k N_f=0.6\) kN/m. The response obtained is compared with the numerical results by an established method for numerical integration of equations of motion in structural dynamics, namely the explicit Runge–Kutta method of accuracy \({\mathcal {O}}(\Delta t^4)\) (RK45) [40]. Due to the non-smooth nature of friction, in order to compare the results of the presented piecewise linear method with a respective method that accounts properly for stick-slip, an internal event detection routine is incorporated in the Runge–Kutta method, with a zero-crossing detection function to track transitions and assign a state to the system accordingly. For the numerical simulations with the Runge–Kutta algorithm, a time step of \(\Delta t = \frac{0.02h}{c} = 0.33 \cdot 10^{-5}\) s is chosen (\(\delta =0.02\)), according to standard criteria for the choice of time step size in nonlinear problems [41].

Fig. 4
figure 4

Displacement field \(u_1(z_1,t)\) for the validation case

Full size image
Fig. 5
figure 5

Displacement \(u_1(z_1,t)\) for the validation case at a \(z_1 = 0\), b \(z_1 = L_1/3\), c \(z_1 = 2 L_1 / 3\) and d \(z_1 = L_1\)

Full size image

In Fig. 4 predictions of the mode-matching method (MMM) are compared to those obtained by the Runge–Kutta method in a space–time plot. The displacement fields depicted in Fig. 4 are in good agreement qualitatively and quantitatively. To further examine the quantitative agreement of the two methods, in Fig. 5 the displacement \(u_1(z_1,t)\) at \(z_1=0, \, L_1/3, \, 2L_1/3, \, L_1\) is depicted as a function of time.

Evidently, the significance of an accurate response capture is more pronounced in the area where the stick-slip transitions are repetitive and the duration of stick intervals is large. Additionally, this is also the area within which numerical issues arise with standard techniques. In order to deal with those issues extremely small time steps would have to be used. Excellent quantitative agreement is observed between the mode-matching method and the Runge–Kutta method, for all the points shown in Fig. 5. For larger time steps than the ones used herein, the present analyses would give inaccurate predictions in the regions where stick-slip occurs. Regarding the computational efficiency, the computational time for the case of the Runge–Kutta method (\(\delta =0.02\)) was 6.67 times larger than the computational time of the proposed method, providing a significant computational gain in the analysis of stick-slip vibrations. Generally, for analyses similar to the presented one multiple zero-crossings can occur during a time step, some of which may not be detected, depending on the time step size in conjunction with the numerical error introduced by the approximate nature of the solution due to the numerical integration in standard techniques.

4.2 Numerical examples

Onwards, six numerical examples are presented to showcase the potential combinations of loads and parameters that can be analysed according to the proposed method. Specifically, three different types of external excitation are considered, namely a low-frequency (\({\mathrm {\Omega }}_1\)) and a high-frequency (\({\mathrm {\Omega }}_2\)) harmonic excitation and a short square pulse as depicted in Fig. 6. Furthermore, two cases A and B of different ratios \(P_0/(\mu _k N_F)\) of the external force (constant amplitude) to the sliding friction force per unit length are considered to examine the influence of the magnitude of frictional forces. The parameters used are summarized in Table 1 and the displacement \(u_1\) refers to the total displacement, including both rigid body and flexible body terms. In all analyses the rods are considered to be in contact along half of their length at \(t=0\). By considering these types of excitation, the presented method is shown to be effective not only for harmonic excitations that may lead the system to a stationary regime, but also when shock waves are excited in the system resulting in purely transient dynamics of the system.

Fig. 6
figure 6

External excitations P(t) at \(z_1=0\)

Full size image

For the first case of low-frequency harmonic excitation, (\({\mathrm {\Omega }}_1\)), applied at \(z_1=0\), the displacement \(u_1\) is visualized in terms of time signatures at specific cross sections of rod 1 in Fig. 7. One can clearly see in Fig. 7a, b that the rod experiences a rigid body displacement already during the first half period of the excitation. Thereafter the vibrations in the considered cross sections take place about the displaced position. For high \(P_0/(\mu _k N_F)\) ratio in Fig. 7a, all the considered cross sections almost always slide and sticking occurs only at the tip of the rod, \(z_1=L_1\). In case of purely rigid body motion, all cross sections would be experiencing identical displacement, which is not the case in Fig. 7a. This small deviation is due to the excitation of the flexible modes of rod 1 in vacuo and the frictional interaction, albeit the rigid body motion is clearly dominant. On the other hand, in Fig. 7b (low \(P_0/(\mu _k N_F)\)), the stick-slip vibrations of rod 1 are more eminent, especially at the cross sections that are closer to the tip of the rod, where plateaus are observed in \(u_1\) at positions \(z_1=2L_1/3\) and \(z_1=L_1\). These plateau-type intervals in displacement \(u_1\) comprise the most well-known characteristic of stick-slip motion, resulting from the transition of nodes into stick phase for a relatively long duration. Specifically in Fig. 7b, the tip of rod 1 remains in stick phase for approximately half the duration of the motion, as a result of the increased \(P_0/(\mu _k N_F)\) ratio.

Fig. 7
figure 7

Displacement \(u_1(z_1,t)\) for harmonic excitation with \({\Omega }_1 = 20\) rad/s

Full size image

Figure 7 is complemented by Fig. 8, in which the displacement  fields \(u_1\)  for  the  two  different  ratios of \(P_0/(\mu _k N_F)\) are displayed in combined space–time plots. From this graph the displacement \(u_1\) of any point can be extracted, as the vertical axis represents the material coordinates of rod 1, which may translate in time due to rigid body motion. As stated above, if in case A (high \(P_0/(\mu _k N_F)\)) the motion was purely of the rigid body type, then in Fig. 8a regions of different greyscale intensity would be separated by vertical lines. The deviation from such a graph is due to the activation of flexible dynamics in the system, for the above-said reasons. On the contrary, in Fig. 8b (low \(P_0/(\mu _k N_F)\)) the contribution of the flexible body dynamics is much more visible as the deviation from a graph of vertical greyscale regions is further enhanced. Thus, the contribution of flexible body dynamics is more eminent. In more detail, the frictional interaction takes place for \(z_1/L_1 > 0.5\) and the corresponding region in Fig. 8b displays much smaller displacements in terms of both amplitude and dynamic variation. The latter is a consequence of the higher friction forces present, which result in finite duration stick phases of nodes along the contact length.

Fig. 8
figure 8

Displacement fields \(u_1(z_1,t)\) for harmonic excitation with \({\mathrm {\Omega }}_1\,=\,20\) rad/s

Full size image
Fig. 9
figure 9

Relative velocity \({\dot{u}}_1(z_1,t) - {\dot{u}}_2({\overline{z}}_2,t) \) for harmonic excitation with \({\mathrm {\Omega }}_1\) = 20 rad/s

Full size image

To further assess the effect of the force to friction ratio (\(P_0/(\mu _k N_F)\)) for the case of excitation frequency \({\mathrm {\Omega }}_1\), the relative velocity for the points \(z_1= 2L_1/3, \, L_1\) (along the interface) is shown in Fig. 9. It is apparent that the increased friction (Fig. 9b) yields much lower relative velocities than those depicted in Fig. 9a, due to the prolonged sticking intervals. An important remark that further showcases the strength of the mode-matching method is the numerical stability during stick for the relevant nodes. In the relative velocity patterns, the higher frequency components triggered by the nonlinearity are also more visible than in the displacement plots.

In Figs. 10 and 11, the cases of high-frequency, \({\mathrm {\Omega }}_2\), harmonic excitation are considered. Specifically in Fig. 10a (high \(P_0/(\mu _k N_F)\)), as in the cases studied in Fig. 7 the considered cross sections of rod 1 perform oscillations around a displaced position, due to rigid body displacement. None of the cross sections can be seen to transition to stick phase after rod 1 is set in motion, meaning that rigid body motion can take place. The displacement \(u_1\) of the different cross sections can be seen to be not in-phase during the motion and with different amplitudes. These facts indicate that flexible dynamics are dominant in the response of the system, which is expectable as the excitation frequency, \({\mathrm {\Omega }}_2\), is between the 2nd and the 3rd flexible modes of rod 1 in vacuo. Therefore, the rigid body contribution in this case is much lower compared with the low-frequency, \({\mathrm {\Omega }}_1\), excited system (Fig. 8a). Along the previous line of thinking, Fig. 11a supplements this observation, as the regions of similar greyscale intensity in the graph under discussion are bounded by inclined lines along almost the whole graph. The latter fact is a result of stronger presence of flexible body than rigid body motion in the system, as remarked previously.

Fig. 10
figure 10

Displacement \(u_1(z_1,t)\) for harmonic excitation with \({\mathrm {\Omega }}_2\) = 150 rad/s

Full size image
Fig. 11
figure 11

Displacement fields \(u_1(z_1,t)\) for harmonic excitation with \({\mathrm {\Omega }}_2\) = 150 rad/s

Full size image
Fig. 12
figure 12

Relative velocity \({\dot{u}}_1(z_1,t) - {\dot{u}}_2({\overline{z}}_2, t)\) for harmonic excitation with \({\mathrm {\Omega }}_2\) = 150 rad/s

Full size image

The last case of harmonic excitation considered is characterized by high-frequency (\({\mathrm {\Omega }}_2\)) excitation and low force to friction ratio (\(P_0/(\mu _k N_F)\)). In Fig. 10b, the dynamic behaviour is similar to Fig. 10a (high \(P_0/(\mu _k N_F)\)) except that a permanent rigid body displacement does not occur due to the higher frictional forces. Additionally, the tip of rod 1 in Fig. 10b, \(z_1=L_1\), experiences sticking for intervals of small duration and obtains smaller amplitude of vibration compared with the other cross sections. As in Fig. 10a, also for this graph the flexible dynamics govern the behaviour of the system. These conclusions are supported by Fig. 11b, in which the inclined boundaries between regions of different greyscale intensity are smoother than in Fig. 11a, approaching an inclined straight line shape. Finally, a general conclusion for the case of higher frequency, \({\mathrm {\Omega }}_2\), is that contribution of rigid body motion diminishes and the flexible modes together with the frictional interaction dictate the response, for both low and high friction forces.

Fig. 13
figure 13

Numerical convergence study based on the spatial discretization, i.e. number of nodes N for rod 1 and number of modes \(N_m\) for rod 2

Full size image
Fig. 14
figure 14

Displacement \(u_1(z_1,t)\) for short pulse excitation

Full size image
Fig. 15
figure 15

Displacement fields \(u_1(z_1,t)\) for short pulse excitation

Full size image

The discussion of the results for the harmonic excitation (\({\mathrm {\Omega }}_2\)) cases is completed with Fig. 12, in which the relative velocities for the points experiencing friction are shown. For the low friction force (Fig. 10a), rod 1 appeared to be almost fully sliding, which as can be seen in Fig. 12a is the case, as only the rod tip experiences stick for a trivial duration. On the other hand, in Fig. 12b the rod tip sticks for a more appreciable duration due to the higher friction forces, compared to Fig. 12a. Overall, it is remarked that a comparison between Figs. 9 and 12 clearly demonstrates the effectiveness of high-frequency excitations to eliminate the stick phase in systems that perform stick-slip vibrations.

Overall, the results presented were obtained after convergence analyses for the different cases. As convergence criterion, a difference of \(1\%\) between the \(L^2\) displacement norms of any analysis and the final converged one is used. The tip of rod 1 (\(z_1=L_1\)) was chosen as control point, as it experiences sticking for larger time intervals than the rest of the nodes, and thus provides a good indication for the accuracy of the stick-slip predictions. The convergence ratio was denoted as \(R_i=L^2_i/L^2_f\), where \(L^2_i\) is the displacement norm of the ith analysis and \(L^2_f\) is the displacement norm of the converged analysis. The result of the convergence analyses for the various harmonic loading cases is shown in Fig. 13. The first remark is that the cases with high friction forces (\(\mu _k N_f=1.0\) kN/m) converged much slower than the two low-friction cases (\(\mu _k N_f=0.6\) kN/m). The latter converged quite quickly independently of the excitation frequency (even from the second analysis of the study as shown in Fig. 13). For the more computationally demanding cases with high friction, the analysis with the low-frequency excitation converged at slower rate. That can be understood in light of the relative velocity profiles shown in Fig. 9b, where the low-frequency/high-friction case showcased sticking intervals of significant duration for the tip of rod 1. Therefore, the low-frequency excitation in the case of high friction cannot eliminate the stick phase and prominent stick-slip vibrations occur, which in turn require refined mesh to be resolved accurately (e.g. at the tip of rod 1). From the aforementioned, it is evident that in stick-slip vibrations convergence can be affected and even dictated by the force to friction ratio and the occurring stick-slip vibrations, which were the dominant factor in the analyses presented.

Shock-type excitations can be also analysed with the present method and the results for the considered cases are shown in Figs. 14 and 15. First, Fig. 14 is examined, in which the displacements \(u_1\) of the selected cross sections are depicted. In both cases, rod 1 obtains an offset compared to its initial position and the vibrations are suppressed after a finite time leading essentially to a permanent rigid body displacement. The ratio \(P_0/(\mu _k N_F)\) is the sole factor of the dissimilar behaviour in the considered cases of impact excitation. For high \(P_0/(\mu _k N_F)\) ratio (Fig. 14a), the final rigid body displacement increases even after the external loading vanishes, which is a consequence of the low friction forces. The propagating stress wave attenuates because of friction along the region \(z_1/L_1 > 0.5\), though not significantly, resulting in a second abrupt increase of \(u_1\), due to the wave reflection at the free tip (\(z_1=L_1\)). During the stress wave passage through the region \(z_1/L_1 >0.5\), reflections at the cross sections that separate stick and slip regions are generated at the nodes along the contact length. These reflections in the case of Fig. 14b have larger amplitude, leading to a smaller permanent displacement of rod 1 and also to a different trend from the one observed in Fig. 14a.

To conclude with the impact excitation cases, in Fig. 15 the evolution of the displacement fields \(u_1\) are displayed. In Fig. 15a and b, the white triangular region of both figures at the bottom left corner corresponds to zero displacement. This visual observation is related to the first downward propagating wave and the absence of disturbance in the domain that this wave has yet to reach, clearly implying that the modal solution adopted can successfully account for a sharp wavefront. Furthermore, the dissimilarity of the two cases observed above, due to the different \(P_0/(\mu _k N_F)\) ratio, can be seen in more detail. In the case of low frictional forces (Fig. 15a), the most notable reflection occurs at the tip of rod 1, in contrast to Fig. 15b in which the primary reflection occurs at the first node of interaction at \(z_1/L_1=0.5\). An extreme example can be considered when friction forces are large enough, such that the two rods are essentially jointed and not a single node slips; thus, the system would behave as a stepped rod of two different segments. Back to the examined case, reflections naturally continue to arise at the stick-slip transitions along the contact length and the reflection at the tip is also apparent in Fig. 15b, albeit much weaker than in Fig. 15a. The lines bounding the different intensities of the greyscale spectrum in both graphs remain constant and are the well-known characteristics related to the dispersionless wave propagation in rod 1.

5 Conclusions

In this paper, a method for computation of the dynamic response of two rods in Coulomb frictional contact is developed. The method employs a semi-discrete spatial formulation together with a mode-matching algorithm. From computational perspective, the method offers multiple advantages. First, it provides great flexibility as to the discretization scheme of one system, while it preserves the continuous description of the other. This comes with the advantage of computational speed and accuracy. It is noted that in this paper the finite difference scheme is employed; however, any other suitable spatial discretization scheme is permissible. Second, the need for a regularization of Coulomb’s friction law is mitigated. The piecewise linear character of Coulomb friction is exploited which permits a solution in the form of a modal decomposition scheme. Given that, in the solution method presented, the need for numerical integration of the resulting equations of motion is altogether avoided, instead the numerical evaluation of convolution integrals is performed. Third, the generic framework of the solution permits the analysis of various vibration problems involving friction between one-dimensional elastic bodies in an efficient manner. Given the discussion above, additional forms of damping can be incorporated in the solution approach with minor modifications. Most importantly, the method of solution can be generalized for problems involving stick-slip vibrations of three-dimensional elastic bodies.