Abstract
The present paper investigates the static equilibrium of a thin elastic structure with concave sidecut pressed against a flat rigid surface, as an idealization of a ski or snowboard undergoing the conditions of a carved turn. An analytical model is derived to represent the contact behaviour and provide an explanation for concentrated loads occurring at the sidecut extremities. The deformations are prescribed assuming tied contact along the sidecut line and neglecting torsional deformations. The loading conditions leading to this ideal deformed state are then sought, in order to better understand the mechanics of the turn. The results are illustrated with different sidecut geometries and compared with finite element computations for validation purposes. Depending on the function describing the sidecut line, concentrated force and moment are found to take place at the sidecut extremities.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
1.1 Background
In the 1990s, influenced by snowboard designs, the classical ski geometry was replaced by a deep sidecut ski, the carving ski [1]. The term “sidecut” refers to the shape of the edge line running along the ski or snowboard, the interface between the skier and the mountain during a turn. If it is established that the sidecut geometry strongly influences the carving behaviour [2, 3], the kinematics of a ski or snowboard undergoing a carved turn are, to date, still not fully understood [4]. In particular, the assessment of the contact pressure along the sidecut line remains an open point.
An early investigation of a ski undergoing the conditions of a carved turn was made in 1989 by Renshaw and Mote [5], representing the ski as an Euler–Bernoulli beam. The free boundary problem was solved by setting free-end boundary conditions at the ski tips, assuming a zero transverse shear force at the sidecut extremities (the third derivative of the bending deflection was assumed to vanish at the beam ends). This approach, used in various studies ever since [6, 7], seems to be in contradiction with more recent measurements and simulation results, where the presence of contact forces at the sidecut extremities is suggested [8, 9].
Previous investigations on contact problems already reported local reaction forces at the contact boundaries. In the problem of a convex beam pressed on a flat surface [10], the contact stress distribution asymptotically approached a concentrated force at the edge of contact. Depending on the choice of the boundary conditions, the contact load was reported to be supported by a moment at the ends of the beams. Similarly, in the studies of adhesive stresses of a beam bonded to an elastic plane, asymptotic behaviour of the stress field was reported at the beam ends [11, 12]. Furthermore, a beam to beam contact representation of a train moving on a bridge has shown a concentrated force and moment acting at the front of the train, where the curvature and third derivatives of the deflection of the bridge did not vanish [13].
The objective of this paper is to investigate the kinematics of a ski or snowboard undergoing the conditions of a carved turn in an idealized framework. A relationship between the sidecut geometry and the loading environment is sought, in order to better understand the mechanics of the turn.
1.2 Paper content
This work describes the general static representation of a thin elastic structure with concave sidecut pressed on a flat surface. The structure is tilted on its edge and deformations are sought, such that the deformed sidecut line entirely comes in contact with a flat surface representing the ground. The problem can be formulated as follows: given a sidecut geometry, which external loading is required to achieve this ideal state of deformation, and can it be reached under realistic physical conditions?
In Sect. 2, the problem is set and the basis for the beam representation is defined under pure-bending conditions. In Sect. 3, the deformations required to bring the sidecut coincident with the running surface are assessed, and the related internal bending moment thereby determined. The external loading conditions leading to this deformed state are then sought, following the Euler–Bernoulli beam theory. The outcome is illustrated in Sect. 4 with three case studies, where different sidecut functions are investigated. The results are finally compared with those of corresponding finite element analysis for the purpose of validation. In the last section, the practical feasibility of the results is discussed and some conclusions are drawn.
2 Problem formulation
2.1 Model geometry
Throughout this paper, coordinate systems are defined as Cartesian and denoted by a bold capital letter. Their definition is given between curly brackets by the origin followed by the three basis vectors, mutually orthogonal. Vectors are denoted by a bold lowercase letter (e.g. \({}^{{\varvec{O\!}}} {{\varvec{x}}}={}^{{\varvec{O\!}}} [1 0 0]^T)\), where the upper left index indicates the coordinate system in which the vector is expressed. Planes are described between curly brackets by a point lying in the plane followed by the two vectors spanning it.
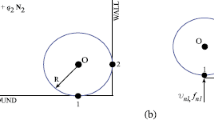
The initial geometry is represented in the local coordinate system \({\varvec{O}}=\{O{\varvec{xyz}}\}\), such that the sidecut line can be described in the plane \(\{O{\varvec{xy}}\}\) by a continuous function \(y=-h(x)\) (see Fig. 1). The sidecut line extends from point T to point N and passes through the mid-point M, with
The radius R of the circle passing through T, N and M is denoted as average sidecut radius. The opposite sidecut line is mirrored such that \(\overrightarrow{Ox}\) is an axis of symmetry of the structure.
2.2 Running surface
The flat surface representing the ground (denoted as running surface) is idealized by the plane \(\{M{\varvec{uv}}\}\). No contact interaction such as friction is considered. The running surface is tilted at an angle \(\theta \) with the plane \(\{O{\varvec{xy}}\}\), \({\varvec{u}}\) and \({\varvec{x}}\) being colinear (see Fig. 2).
The global coordinate system refers to the running surface and is denoted by \({\varvec{M}}=\{M{\varvec{uvw}}\}\). The transformation matrix \({}^{{\varvec{MO\!}}} {{\varvec{A_x}}}(\theta )\) corresponding to a positive rotation around the \({\varvec{x}}\)-axis by an angle \(\theta \), used for coordinate system transformation from \({\varvec{O}}\) to \({\varvec{M}}\), as given by:
2.3 Beam representation
The structure is represented by a one-dimensional inextensible beam running along the \({\varvec{x}}\)-axis, assumed to be subject only to bending deformations around the local \({\varvec{y}}\)-axis. As per [14], the deformed beam mid-line is described on \(\mathcal {D}=[x_T;x_N]\) (see Eq. (1)) by the vector function \({\varvec{r_0}}\):
where s refers to the arc-length of the beam mid-axis in the deformed configuration, and the components \(r_x(s)\) and \(r_z(s)\) are the unknowns of the problem.
Likewise, the deformed sidecut line is represented on \(\mathcal {D}=[x_T;x_N]\) (see Eq. (1)) by the vector function \({\varvec{r_s}}\). Since only bending deformations are considered, the beam mid-line is not subject to any twist, and the deformed sidecut line \({\varvec{r_s}}\) can be retrieved from the deformed beam mid-line position:
The mid-point M is taken as reference, since it is assumed to be coincident with the running surface in the initial configuration. Therefore, it is fixed in space and the following deformations are null:
3 Bending deformation
A bending angle distribution \(\beta (s)\) is sought such that a rotation around the local \({\varvec{y}}\)-axis of the beam by an angle \(\beta \) (see Fig. 3) brings the sidecut line coincident with the running surface (tied contact is assumed between the sidecut line and the running surface, see Fig. 2). The constraint can therefore be expressed such that the tangential vector to the deformed sidecut line \({\varvec{r_s}}\) lies within the plane \(\{M{\varvec{uv}}\}\).
The bending angle \(\beta \) is represented in Fig. 3 according to the sign convention defined in [15] (positive counterclockwise rotation). Let’s express the tangential vector to the deformed beam mid-axis \({\varvec{r_0'}}\), where the apostrophe denotes the function derivative with respect to the arc-length parameter s:
Because of the zero stretch condition, the vector quantity \({\varvec{r'_0}}(s)\) can be replaced by a scalar function \(\beta (s)\), such that
3.1 Bending rotation
In this section, the bending angle distribution \(\beta (s)\) required to bring the sidecut coincident with the running surface is assessed. The constraint is expressed such that the tangential vector to the deformed sidecut must lie within the running surface (see Fig. 2). The tangential vector to the deformed sidecut line \({\varvec{r_s'}}\) is derived from Eq. (4) with the use of Eq. (7):
The tangential vector is expressed in the global coordinate system:
In order for \({\varvec{r_s'}}\) to lie in the plane \(\{M{\varvec{uv}}\}\), its coordinate along the \({\varvec{w}}\)-axis must be null, and therefore:
3.2 Deformed sidecut
In this section, the deformed sidecut \({\varvec{r_s}}\) is expressed in the local coordinate system \({\varvec{O}}\). Since M is considered as the reference point, see Eq. (5), the deformed sidecut can be retrieved by integrating Eq. (8) on the interval [0, s]:
Replacing the bending rotation \(\beta (s)\) determined in Eq. (10), one obtains after simplification:
The deformed sidecut can therefore be expressed in the local coordinate system \({\varvec{O}}\):
3.3 Deformed sidecut curvature
The curvature distribution along the deformed sidecut is of particular interest and can be easily retrieved by expressing the deformed sidecut as a plane curve within the running surface (\(\{M{\varvec{uv}}\}\)-plane). The vector function \({\varvec{r_s}}\) describing the deformed sidecut line is expressed in the global coordinate system \({\varvec{M}}\) with the following transformation:
The derivatives of the deformed sidecut \({}^{{\varvec{M\!}}} {{\varvec{r_s}}}\) with respect to the parameter s are:
The signed curvature \(\kappa (s)\) along the deformed sidecut \({\varvec{r_s}}\) is [16]:
Remark: To obtain a constant curvature distribution along the deformed sidecut, the differential equation (16) can be rewritten with \(\kappa (s)=-\kappa _0\) (constant) and therefore leads to the differential equation
with the initial conditions
The solution of Eq. (17) is an elliptic integral, which cannot be expressed in terms of elementary functions. It can be solved by parametric equations [17] or evaluated by numerical means.
3.4 Bending moment
In this section, the internal bending moment relating to the prescribed deformations is expressed according to the Euler–Bernoulli beam theory. The bending curvature of a curve parametrized along its arc-length corresponds to the negative of the derivative of the bending angle, according to the sign convention defined in [15]. For the bending curvature \(\kappa _y\) of the beam mid-line, it holds:
Following the Euler–Bernoulli beam theory with a linear material constitutive law, the bending moment \(M_y\) is related to the bending curvature \(\kappa _y\) by the bending stiffness \(EI_y\):
with E the Young’s modulus and \(I_y\) the area moment of inertia of the beam cross section.
From Eq. (10) follows:
and the internal bending moment can be expressed as:
Remark: If the first derivative \(h'(s)\) is small enough to be neglected, the denominator in Eq. (22) approaches 1 and the bending moment can be approximated by
with \(r_z(s)\) being the bending deflection. Equation (23) reflects the expression of the bending moment according to the linear beam theory [15].
3.5 Contact forces
In this section, the external loads leading to a bending moment distribution as expressed in Eq. (22) are sought. According to the linear beam theory [15], the bending moment induces intern transverse shear forces \(Q_z(s)\) along the local \({\varvec{z}}\)-direction, with:
The transverse shear is related to the external applied transverse load \(p_z(s)\) along the \({\varvec{z}}\)-direction:
The external transverse load \(p_z(s)\) therefore relates to the second derivative of the bending moment:
The external transverse load \(p_z(s)\) can be interpreted as a contact force distribution. Since tied contact is assumed, the contact load can be positive or negative, depending on the force required to bring the sidecut coincident with the running surface. It will be noted that, since no torsion is considered, the external transverse load can be applied equivalently along the beam mid-line or along the sidecut line Fig. 4.
The equation of equilibrium of forces in the z-direction implies the existence of reaction forces to counterbalance the effect of the external applied transverse load \(p_z\). These reaction forces can only apply at the beam extremities, since \(p_z(s)\) is a continuous function (see Eqs. (26) and (22)). Let \(R_T\) and \(R_N\) be the reaction forces in the z-direction at point T and point N, respectively. According to the sign convention used [15]:
Likewise, the equation of equilibrium of moments implies the existence of reaction moments at the beam extremities, where the internal bending moment \(M_y(s)\) is not necessarily null (see Eq. (23)). Note that no other punctual moments can occur along the beam mid-axis, since \(M_y(s)\) is a continuous function (see Eq. (22)). Let \(M_T\) and \(M_N\) be the reaction moments at point T and point N, respectively:
It is acknowledged that a concentrated force or moment is not achievable in practice for the considered contact case. However, it is shown in Sect. 4 that there exist particular sidecut functions for which these concentrated loads vanish, and a tied contact between the sidecut line and the running surface can be foreseen.
4 Results validation
In order to illustrate the analytical results obtained in Sect. 3.5 and discuss their practical feasibility, three particular case studies were considered and set under investigation in Sect. 4.1 and 4.2. For validation purposes, the three case studies were idealized in 3D finite element models (see Sect. 4.3) and the numerical results are compared to the analytical solutions in Sect. 4.4.
4.1 Case studies
Three case studies were considered based on the specimen described in [8]. The geometrical proportions were identical for all cases and are reported in Table 1. Only the sidecut function h(s) passing through the points T, N, M was changed (see Fig. 1).
In all three cases, the structure features a constant thickness t and Young’s modulus E throughout. The geometry is defined such that the structure exhibits two axes of symmetry \(\overrightarrow{Ox}\) and \(\overrightarrow{Oy}\). The area moment of inertia of the beam cross section \(I_y\) an therefore be expressed as:
Replacing \(I_y\) in Eq. (22), the bending moment and its derivative can be expressed as:
4.1.1 Sidecut A
The first case consists in an initial sidecut line describing the arc of a circle of radius R. This case is frequently used in practice and reported in the literature, and therefore was set under investigation. It an be described on \(\mathcal {D}=[x_T;x_N]\) by the function \(h_A\):
The first and second derivatives of the sidecut function \(h_A\) are given for information:
4.1.2 Sidecut B
The second case is intended to show the effects of a vanishing bending moment at the sidecut extremities. According to Eq. (22), these conditions are achieved if the second derivative of the sidecut function also vanishes:
A fourth order polynomial sidecut line fulfilling these conditions can be described on \(\mathcal {D}=[x_T;x_N]\) by the function \(h_B\):
The first and second derivatives of the sidecut function \(h_B\) are given for information:
4.1.3 Sidecut C
The third case is intended to show the effects of a vanishing transverse shear force at the sidecut extremities. According to Eq. (30), these conditions are fulfilled if the second and the third derivatives of the sidecut function also vanish:
A sixth order polynomial sidecut line fulfilling these conditions can be described on \(\mathcal {D}=[x_T;x_N]\) by the function \(h_C\):
The first, second and third derivatives of the sidecut function \(h_C\) are given for information purposes:
4.2 Analytical results
In the three case studies presented in Sect. 4.1, only the function h(s) describing the sidecut line was varied. The sidecut functions investigated are shown in Fig. 5 along with their corresponding curvature distributions in Fig. 6.
The distribution of the internal and external forces is assessed for all three cases. The internal bending moment according to Eq. (22) is presented in Fig. 7, transverse shear forces according to Eq. (24) are shown in Fig. 8 and the external transverse load (or contact load) according to Eq. (26) is shown in Fig. 9.
Bending moment distributions \(M_y(s)\) according to Eq. (22)
Transverse shear force distributions Q(s) according to Eq. (24)
External transverse load distributions \(p_z(s)\) according to Eq. (26)
The reaction forces in Eq. (27) and reaction moments in Eq. (28) occurring at the sidecut extremities T and N are computed for all three cases and shown in Table 2. The linearized values (resulting from the computation of a linearized bending moment according to Eq. (23)) are shown for comparative purposes, together with the error made by considering a linearized model.
4.3 FEM representation
The analytical outputs presented in Sect. 4.2 were verified by comparing with the results of 3D finite element analysis representing the three case studies, whose geometrical and structural properties are reported in Table 1. The basis for the finite element models (FEM) is described in [8]. The structure was represented by general-purpose shell elements (4 nodes) accounting for finite membrane strain. The shell sections consisted of one orthotropic ply with a constant thickness. In order to simulate a rigid torsional and transverse bending behaviour, all shear moduli and transverse Young’s modulus were set to very high values (1e6 MPa) in order to idealize substantial stiff behaviour, and Poisson’s ratio was set to zero to avoid coupling of deformations. The material properties used for the analysis are summarized in Table 3. A representation of the FEM is shown in Fig. 10, where the approximate element size was \(10 \times 10\) mm.
A displacement-driven analysis was set up where the tilt angle \(\theta \) was imposed to the mid-line nodes. Additionally, the vertical displacement of each node along the sidecut line was constrained, such that the nodes lie coincident with the running surface. Displacements and reaction forces along the sidecut nodes were extracted to compute the numerical results described in Sect. 4.4.
4.4 Numerical results
The three case studies described in Sect. 4.1 were investigated by means of finite element analysis, according to the methodology described in Sect. 4.3. The deformed curvature distributions along the sidecut line were computed from the extracted displacements and compared with the analytical results of \(\kappa (s)\), see Eq. (16). The results are shown in Fig. 11. The vertical reaction forces were extracted for each node along the deformed sidecut and converted into a distributed load by dividing by the inter-node longitudinal distance. The finite element results were compared to the analytical results of \(p_z(s)\), see Eq. (26), and are shown in Fig. 11.
Comparison between analytical and finite element results for the three cases considered. On the left: deformed curvature distributions \(\kappa (s)\) along the sidecut line. On the right: external transverse load distributions \(p_z(s)\). Note: the oscillations observed on the FEM results of \(p_z(s)\) reach a maximum amplitude of \(330\,\mathrm{N.mm}^{-1}\) for Sidecut A and \(17\,\mathrm{N.mm}^{-1}\) for Sidecut B
The analytical and numerical results show a good overall correlation. The deformed sidecut curvatures are matching well within the numerical approximations of the finite element results. The external transverse loads obtained are in good agreement, though significant deviations are observed at the sidecut extremities, where some oscillations of the contact forces are observed on the numerical results. A direct comparison of the reaction forces and moments at the sidecut extremities could therefore not be made. In the finite element model, since no reaction moment can occur (only nodal displacements of the sidecut nodes were constrained), a numerical approximation is possibly obtained by the solver by alternating positive and negative reaction forces. It will be observed that the oscillations fade away for Sidecut C, where the curvature and the derivative of the bending moment vanish at the sidecut extremities.
5 Conclusions
In this work, we studied the loading environment of a concave sidecut line deformed on a flat surface, as an idealization of a ski or snowboard undergoing a carved turn. In addition to a contact pressure distribution required to achieve tie contact with the running surface, concentrated force and moment were found to take place at the sidecut extremities. It was shown that these concentrated loads can vanish for particular sidecut functions.
The magnitude of these concentrated forces was, depending on the sidecut function considered, in the order of the weight of a skier, and therefore shall not be neglected. In particular, when solving for the analytical deformation of a ski or snowboard, attention must be paid to the boundary conditions chosen at the sidecut extremities. The impact of these local forces onto the structural vibrations during a carved turn is a relevant concern that could be investigated in a follow-up work.
A sidecut describing the arc of a circle was shown to deform in a non-constant curvature radius, for a structure featuring constant thickness throughout. In order to achieve the tied contact, concentrated forces and moments must occur at the sidecut extremities, which is not achievable in practice. The tied contact condition can be practically foreseen if the internal bending moment and the transverse shear force vanish at the sidecut extremities. A polynomial function fulfilling these conditions was proposed in Eq. (38).
A formulation of the “exact” bending moment required to deform a concave sidecut line on a flat surface was given in Eq. (22). The linear beam theory led to an error of about \(2\%\) on the reaction forces calculations. Additionally, a differential equation to solve for a constant curvature along the deformed sidecut was given in Eq. (17). The results were validated by the means of finite element representations of three case studies.
While the hypothesis of pure-bending deformations is relevant for slender structures such as skis, it becomes questionable for snowboards featuring wider geometries. The model could be extended to include torsional deformations in the future.
References
Howe, J.: Skiing Mechanics. Poudre Press, Laporte, US-CO (1983)
Lind, D., Sanders, S.: The Physics of Skiing: Skiing at the Triple Point. Springer, New York (2004)
Jentschura, U., Fahrbach, F.: Physics of skiing: the ideal-carving equation and its applications. Can. J. Phys. 82, 4–10 (2003). https://doi.org/10.1139/p04-010
Sahashi, T., Ichino, S.: Carving-turn and edging angle of skis. Sports Eng. 4, 135–145 (2001). https://doi.org/10.1046/j.1460-2687.2001.00079.x
Renshaw, A., Mote, C.D.: A model for the turning snow ski. Int. J. Mech. Sci. 31, 721–736 (1989). https://doi.org/10.1016/0020-7403(89)90040-4
Kaps, P., Mössner, M., Nachbauer, W., Stenberg, R.: Pressure Distribution Under a Ski During Carved Turns. Science and Skiing, pp. 180-202. Dr. Kovac-Verlag, Hamburg (2001)
Heinrich, D., Mössner, M., Kaps, P., Nachbauer, W.: Calculation of the contact pressure between ski and snow during a carved turn in Alpine skiing. Scand. J. Med. Sci. Sports 20, 485–492 (2009). https://doi.org/10.1111/j.1600-0838.2009.00956.x
Caillaud, B., Winkler, R., Oberguggenberger, M., Luger, M., Gerstmayr, J.: Static model of a snowboard undergoing a carved turn: validation by full-scale test. Sports Eng. 22, 15 (2019). https://doi.org/10.1007/s12283-019-0307-4
Petrone, N.: The use of an edge load profile static bench for the qualification of alpine skis. Procedia Eng. 34, 385–390 (2012). https://doi.org/10.1016/j.proeng.2012.04.066
Block, J.M., Keer, L.M.: Partial plane contact of an elastic curved beam pressed by a flat surface. J. Tribol. 129, 60–64 (2007). https://doi.org/10.1115/1.2401212
Lanzoni, L., Radi, E.: A loaded Timoshenko beam bonded to an elastic half plane. Int. J. Solids Struct. 92–93, 76–90 (2016). https://doi.org/10.1016/j.ijsolstr.2016.04.021
Shan, Z.W., Su, R.K.L.: Improved uncoupled closed-form solution for adhesive stresses in plated beams based on Timoshenko beam theory. Int. J. Adhes. Adhes. (2019). https://doi.org/10.1016/j.ijadhadh.2019.102472
Cojocaru, E.C., Irschik, H., Gattringer, H.: Dynamic response of an elastic bridge due to a moving elastic beam. Comput. Struct. 82, 931–943 (2004). https://doi.org/10.1016/j.compstruc.2004.02.001
Irschik, H., Gerstmayr, J.: A continuum mechanics based derivation of Reissner’s large-displacement finite-strain beam theory: the case of plane deformations of originally straight Bernoulli-Euler beams. Acta Mech. (2009). https://doi.org/10.1007/s00707-008-0085-8
Mang, H.A., Hofstetter, G.: Festigkeitslehre, pp. 178-199. Springer Vieweg, Berlin (2013)
Gerstmayr, J., Irschik, H.: On the correct representation of bending and axial deformation in the absolute nodal coordinate formulation with an elastic line approach. J. Sound Vib 318, 461–487 (2008). https://doi.org/10.1016/j.jsv.2008.04.019
Anakhaev, K.N.: Elliptic integrals in nonlinear problems of mechanics. Dokl. Phys. 65, 142–146 (2020). https://doi.org/10.1134/S1028335820040011
Acknowledgements
The support of the author B. Caillaud by the TWF-Tiroler Science Fund within the project ZAP850003, “Optimal Sidecut Geometry of flexible Structures under Contact”, is gratefully acknowledged.
Open Access
This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
Funding
Open access funding provided by University of Innsbruck and Medical University of Innsbruck. The support of the author B. Caillaud by the TWF-Tiroler Science Fund within the project ZAP850003, “Optimal Sidecut Geometry of flexible Structures under Contact”, is gratefully acknowledged.
Author information
Authors and Affiliations
Ethics declarations
Conflicts of interest
No conflicts of interest, financial or otherwise, are declared by the authors.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Caillaud, B., Gerstmayr, J. On the kinematics of a concave sidecut line deformed on a flat surface. Acta Mech 232, 4919–4932 (2021). https://doi.org/10.1007/s00707-021-03080-8
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00707-021-03080-8