Experimental verification of theoretical approaches for radial gravity currents draining from an edge

Abstract

We present an experimental study of inertial gravity currents (GCs) propagating in a cylindrical wedge under different drainage directions (inward/outward), lock-release (full/partial gate width) and geometry (annulus/full cylinder). We investigate the following combinations representative of operational conditions for dam-break flows: (i) inward drainage, annular reservoir, full gate; (ii) outward drainage, full reservoir, full gate; and (iii) outward drainage, full reservoir, partial gate. A single-layer shallow-water (SW) model is used for modelling the first two cases, while a box model interprets the third case; the results of these approximations are referred to as “theoretical”. We performed a first series of experiments with water as ambient fluid and brine as intruding fluid, measuring the time evolution of the volume in the reservoir and the velocity profiles in several sections; in a second series, air was the ambient and water was the intruding fluid. Careful measurements, accompanied by comparisons with the theoretical predictions, were performed for the behaviour of the interface, radial velocity and, most important, the volume decay ${\mathcal {V}}(t)/{\mathcal {V}}(0)$. In general, there is good agreement: the theoretical volume decay is more rapid than the measured one, but the discrepancies are a few percent and the agreement improves as the Reynolds number increases. Velocity measurements show a trend correctly reproduced by the SW model, although often a delay is observed and an over- or under-estimation of the peak values. Some experiments were conducted to verify the role of inconsistencies between experimental set-up and model assumptions, considering, for example, the presence or absence of a top lid, wedge angle much less than $2\pi$, suppression of the viscous corner at the centre, reduction of disturbances in the dynamics of the ambient fluid: all these effects resulted in negligible impacts on the overall error. These experiments provide corroboration to the simple models used for capturing radial drainage flows, and also elucidate some effects (like oscillations of the radial flux) that are beyond the resolution of the models. This holds also for partial width lock-release, where axial symmetry is lost.

1 Introduction

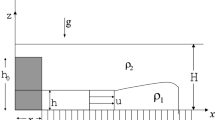
Gravity currents originate from a density difference within a fluid or between two fluids, one of which is called the ambient fluid. Here, we analyse the case of gravity currents generated by the collapse of a boundary in a cylindrical reservoir, filled with a fluid of density $\rho _c$, in equilibrium at rest under ordinary conditions. The collapse enables the excess hydrostatic pressure to drive fluid motion across the removed boundary within the ambient fluid of density $\rho _a < \rho _c$. The initial excess hydrostatic pressure $(\rho _c - \rho _a) g (h_0-z)$, where z is the vertical direction measured from the bottom, depends on $h_0$, which represents the initial depth of the heavier fluid. The originating current has a variable top interface whose slope and decreasing height change in time. In this context, the inertial–buoyancy regime holds for large initial Reynolds numbers, while the ambient fluid has a dynamic which may be eventually considered by employing two-layer models (for more details, see Ungarish [21]).

The scenario of a lock-release with a cylindrical geometry is of interest in many industrial applications, and may also be related to environmental contamination issues [18]. The impact, consequent to the dispersion of the fluid in the surrounding environment, is primarily linked to the fluid volume spilled from the reservoir at a given time after the collapse (see, for example, Ciriello et al. [4]).

A vast literature on lock-release and constant or time-varying inflow rate is available for different case studies, in viscous–buoyancy and in inertial–buoyancy regimes.

Axisymmetric gravity currents of a power-law fluid, with the nose advancing on an infinite plane, have been analysed theoretically and experimentally in Sayag and Worster [17] for two cases: lock-release and constant influx rate. In the lock-release case, inertia dominates the early stage of the current, immediately after the removal of the cylindrical wall, while, in the case of constant influx rate, viscosity balances buoyancy in most of the domain and far from the inflow boundary. In both cases, the radial spread of the current is time varying.

A large set of contributions is available for radial gravity-driven currents in the viscous–buoyancy regime. Didden and Maxworthy [6] measured their spreading rates for constant inflow rate, with measurements in good agreement with theory. Free surface viscous Newtonian gravity currents in inward radial flow and showing second kind self-similarity were analysed theoretically and experimentally by Diez et al. [7]; further experiments were conducted by Diez et al. [8]. Concerning non-Newtonian fluids, radial gravity currents of power-law behaviour were examined by Longo et al. [11]; non-Newtonian propagation in porous media is illustrated in Di Federico et al. [5] and Longo et al. [12]. As to porous media flow, axisymmetric gravity currents were also analysed in Zheng et al. [24] for inward propagation, finding again that a self-similarity of the second kind arises during the radial advancement of the front of the current, until the current reaches the internal fence.

The typical lock-release configuration is associated with drainage from the reservoir over a horizontal boundary at the same level of the bottom. As a consequence, the fluid volume turns into a thin two-dimensional or axisymmetric gravity current, as described in Simpson [18] and Ungarish [21]. Eventually, if the horizontal boundary over which the current flows is porous, the propagating volume decreases, although this effect has been proved to have little impact on the drainage process [1, 22].

Fig. 1

a Sketch of a cylindrical reservoir filled with fluid with a greater density than the ambient, up to a depth of $h_0$, and placed on a tripod above the ground level; the outward drainage configuration is shown with the lifting of the outer cylinder triggering the flow; b same as a but the inward drainage configuration is shown and the inner cylinder is lifted; c same as a but a partial gate is removed from the lateral wall of the reservoir

In real scenarios, one has to consider that the reservoir bottom may be placed on a platform, grid or tripod above the ground level as sketched in Fig. 1. This complicates the case under examination of a “drainage from the edge” type of flow, as compared to a classical lock-release scenario. In the literature, Momen et al. [16] illustrated an experimental investigation of this kind of flow from the edge of a 2-D reservoir (rectangular geometry), coupled with a mathematical interpretation based on both direct Navier–Stokes simulations (DNS) and shallow-water (SW) theory, the latter relying on a thin-layer inertia–buoyancy approximation. The paper demonstrates that SW equations provide quite accurate predictions of the flow field as compared to DNS. Ungarish et al. [23] extended these results to the case of cylindrical reservoirs, that are more common in practice. In the latter paper, SW theory is applied and compared to DNS for two flow cases: (i) outward (diverging) drainage, when the collapsing boundary is the outer boundary of a full-radius reservoir, and (ii) inward (converging) drainage, which is the case of an inner collapsing boundary in an annular-shaped reservoir. The solution is provided in terms of an efficient finite difference approach, but also similarity solutions are derived for both cases; only for the outward drainage case does the similarity solution possess an analytic expression. The scales of velocity and time are found to be the same as those in Momen et al. [16], but the cylindrical geometry introduces significant differences.

Note that, for this kind of problems, the configuration of flow is such that the radial length of the current is defined a priori, being the distance between the internal radius of the annular-shaped reservoir (possibly zero) and the external radius of the tank. After the edge, the current drops as a jet and does not influence the flow of the current in the reservoir, because the regime is critical or supercrtitical at the edge section and perturbations cannot propagate inwards. One has also to consider differences between full-width gate lock-release (the entire cylindrical wall is removed) and partial width gate lock-release (partial lock-release, a sector of the cylindrical wall is removed): while the first case is symmetrical and allows self-similar solutions, the second case loses most of the symmetry and is strongly three-dimensional, and presently no self-similar solution is available nor expected. The partial width gate lock-release is actually more interesting from a practical point of view, since the collapse of the entire wall is a much less frequent case; in most cases, a local collapse of the wall of the reservoir induces fluid loss. Following Ungarish et al. [23], the modelling of the partial width gate lock-release can be effectively interpreted based on a box model.

Given that a precise analytic estimate for the error associated with the models developed by Ungarish et al. [23] is unavailable, our study extends the body of knowledge by providing a large series of laboratory experiments as a benchmark to test the interpretative capability of these models. The laboratory experiments are conducted investigating three cases representative of operational conditions for a drainage from the edge type of flow: (i) outward (diverging) drainage, (ii) inward (converging) drainage and (iii) outward partial width drainage. Specifically, we use: (a) SW equations to interpret the axisymmetric case of flow due to full-width gate lock-release from a cylindrical reservoir and (b) the box model to interpret the case of partial width gate lock-release. The SW approach is based on the one-layer assumption, for which effects induced by flow of the ambient fluid are negligible.

The paper is organized as follows. Section 2 provides the mathematical framework used to predict the shape of the interface, radial velocity and the decay of the volume in time. Section 3 presents the experimental set-up and approach, while Sect. 4 shows the experiments performed for both the outward and inward drainage flow cases. Section 5 includes a discussion of the results and provides a set of conclusions that closes the paper.

2 Theoretical models

In this section, we give a short overview of the problem; more detailed derivations are reported in Ungarish et al. [23]. The latter work indicates that the inertial–buoyancy flow in a cylinder reservoir is well captured by the simplified equations and methodology used for the investigation of inertial gravity currents (see Ungarish [21] and the references therein). For the axisymmetric case (in a full cylinder or wedge), it is convenient to apply the shallow-water (SW) formulation. When the flow field depends on the azimuthal angle $\theta$ (as in the case of a part dam-break situation), it is convenient to use a less accurate method usually referred to as “box model”. Here we present a brief summary of the main results which have been used in the comparisons with the experiments.

Fig. 2

Schematic of the theoretical model for a outward drainage, axial–radial plane section; b inward drainage, axial–radial plane section; overview for c outward drainage problem, d inward drainage problem and e outward drainage with partial width gate problem for the full circle ($\alpha =2\pi$). The dashed red lines delimit the volume of the dense fluid at rest at $t=0^-$ (color figure online)

The outer radius of the container is $r_o$, and the initial height of the dense fluid is $h_0$. We use a cylindrical system of coordinates $\{ r,\theta ,z \}$ with velocities $\{ u,v,w \}$, see Figs. 2a, c. We denote by t the time and by h the height of the dense fluid in the reservoir (in general, a function of $r, \theta , t$). The driving effect is the reduced gravity

$$\begin{aligned} g'= \left( 1 - \dfrac{\rho _a}{\rho _c} \right) g, \end{aligned}$$

(1)

where g is gravity acceleration. This suggests scaling the dimensional variables, denoted by an asterisk, to dimensionless variables as follows:

$$\begin{aligned} \{r^{*}, z^{*}, h^{*}, t^{*}, u^{*} \} = \{r_o r, h_0 z, h_0 h, T t, U u \}, \end{aligned}$$

(2)

where

$$\begin{aligned} U = (g' h_0)^{1/2}, \quad T = \dfrac{r_o}{U} \end{aligned}$$

(3)

are the velocity and timescale.

In the inward drainage process (see Fig. 2b, d), the radial gap is smaller, and hence, in this case it is useful to use the rescaled ${\tilde{t}}$ based on the reference time ${\tilde{T}} = (r_o - r^*_i)/U$. The conversion is ${\tilde{t}} = t/(1 - r_i)$, where $r_i = r^*_i/r_o$.

In the following, we use dimensionless variables unless stated otherwise.

2.1 Shallow-water (SW) axisymmetric model

Briefly, the model is derived as follows, using a cylindrical coordinate system as mentioned above. Assuming that the dense fluid is a thin layer (i.e. $h_0/r_o \ll 1$) while the ambient is much deeper, and the flow is axisymmetric, it is convenient to describe the flow in terms of the thickness (height of interface) h and the height-averaged radial speed u, as functions of r and t. The volume continuity provides the equation of motion of the interface

$$\begin{aligned} \dfrac{\partial h}{\partial t} + \dfrac{1}{r} \dfrac{ \partial (r h u ) }{\partial r} = 0. \end{aligned}$$

(4)

Since the layer is thin, the inertial z acceleration terms are small and the z momentum balance is well approximated by the hydrostatic pressure distribution $\partial p_i / \partial z = - \rho _i g$ (dimensional, with $i\equiv a, c$), supplemented by pressure continuity at $z = h$. We conclude that the driving pressure term in the dense fluid layer is $\partial p_c/ \partial r = (\rho _c - \rho _a) g \partial h/ \partial r$, which is also referred to as the radial buoyancy term. Finally, we use the radial momentum equation, with $\partial p_c/ \partial r$ replaced by the buoyancy term and neglecting the viscous terms, which are of the order of $1/\mathrm{Re}$, where $\mathrm{Re}$ is the Reynolds number defined below. By z-averaging over the thickness h, we obtain the equation of motion for u,

$$\begin{aligned} \dfrac{\partial u }{\partial t} + u \dfrac{\partial u }{\partial r}= - \dfrac{\partial h }{\partial r}. \end{aligned}$$

(5)

The Reynolds number is defined as $\mathrm{Re} = U h_0/\nu$, where $\nu$ is the kinematic viscosity of the dense fluid. This is a formal parameter; a more precise estimate of the ratio of inertial to viscosity effects will be presented later in Sect. 2.3.

The coupled equations of continuity and r-momentum, (4)–(5), for the variables h(r, t), u(r, t), form a hyperbolic system of PDEs. The characteristics are

$$\begin{aligned} \text {d}h \pm h^{{1/2}} \text {d}u = -\dfrac{u h}{r} \text {d}t \quad {\text {on}} \quad \dfrac{\text {d}r}{\text {d}t} =c_\pm = u \pm h ^{1/2}. \end{aligned}$$

(6)

An important associated variable is the volume of dense fluid (per radian)

$$\begin{aligned} {\mathcal {V}}(t) = \int _{r_i}^1 h(r,t) r \,\text {d}r. \end{aligned}$$

(7)

With the appropriate initial and boundary conditions (stated below), this system provides the drainage flow field in the reservoir and in particular the volume ratio ${\mathcal {V}}(t)/{\mathcal {V}}(0)$.

Formally, this is an asymptotic one-layer model for $h_0/r_o \rightarrow 0$ and $\mathrm{Re} \rightarrow \infty$. The one-layer name emphasizes the assumption that the effect of the flow of the ambient fluid in the domain $z>h$, called the “return flow”, is negligible. Suppose that the ambient fluid extends to $z = H$. The flow of the current with speed u is accompanied by a return flow in the ambient fluid of speed $u_a = u h /(H-h)$ evaluated by continuity of volume. The ratio of the inertial terms of ambient to current in the reservoir is of the order of $(\rho _a/\rho _c)(u_a / u)^2$. This ratio is an estimate of the hindrance effected by the flow of the less dense ambient fluid on the flow of the denser current. We conclude that the present one-layer model is a good approximation for $(\rho _a/\rho _c)(h_0/H)^2 \ll 1$. A more rigorous two-layer SW formulation is feasible (see Ungarish [20]), but this is not pursued here because it complicates the analysis and obscures the insights. Note that the accuracy of the one-layer assumption improves during the drainage process because h/H decreases.

A precise analytical estimate for the error, due to the simplifications of the model, is unavailable. Instead, the assessment of the accuracy of the predictions is performed by comparisons of the model prediction with realistic data. The need for this corroboration was a major motivation for the experimental study reported in this paper. There is a large body of evidence from the realm of gravity currents that these models provide correct qualitative insights and fairly accurate quantitative results for many problems of interest with practical moderately small $h_0/r_o$ and moderately large $\mathrm{Re}$. The typical quantitative benchmark for gravity currents is the speed of propagation. SW models overpredict this variable by about 5–15% compared to experimental data (see Ungarish [20] and the references therein). The discrepancy is attributed mainly to viscous effects. In the present case the speed of propagation (or the position of the nose) is irrelevant, and the main focus now is the volume drainage, conveniently expressed as ${\mathcal {V}}(t)/{\mathcal {V}}(0)$. This suggests that the present SW solution will overpredict the rate of the drainage by 5–15% (i.e. the predicted ${\mathcal {V}}(t)/{\mathcal {V}}(0)$ will be in general slightly smaller than the measurement). Again, this expectation needs experimental verification.

For progress, we must specify the initial and boundary conditions. We distinguish between two configurations.

2.1.1 Outward drainage

We consider a full-radius reservoir, $r_i=0$, see Figs. 2a, c. The initial conditions at $t = 0$ are $h=1, u=0$ for $0 \le r <1$. The dam-break condition is applied at $r=1$. We argue that when the motion starts the curvature terms are negligible. Therefore, as in the classical Cartesian inertial dam-break problem, the height at the removed gate drops instantaneously to $h(r=1, t=0^+) = 4/9$ (see Ungarish [21, §3.3]).

The boundary condition at the centre is simply $u(r=0, t) = 0$. We next consider the outflow boundary condition at $r=1$. There is a significant difference between the classical gravity current and the present flow. For the classical inertial current, a jump condition of the type $u= \mathrm {Fr} \, h^{1/2}$ is applied at the moving nose $r=r_N(t) > 1$, where $\mathrm {Fr}$ is a Froude number whose value is obtained from volume and momentum balances in an attached control volume, as indicated in Benjamin [3]. In the present problem, the dense fluid released from the lock plunges beyond the edge and does not form a gravity current, and hence, the aforementioned front condition cannot be applied. We are not interested in the flow of this outflowing fluid, but only in the behaviour of the fluid inside the reservoir. We apply the boundary condition at the fixed $r=1$, the position of the gate. Following the justification presented in Ungarish et al. [23], the lifted gate is replaced by the stationary characteristic with speed $c_- = 0$. In view of Eq. (6b), this can be expressed as the critical outflow condition

$$\begin{aligned} u = h^{1/2}\quad (r = 1, t > 0). \end{aligned}$$

(8)

This completes the formulation. A very recent study [19] pointed out that at some advanced time the outflow may become supercritical, and hence, a more accurate condition is $u \ge h^{1/2}$. The supercritical condition is applied when justified by the extrapolation of $u(r=1-\varDelta , t)$ to the position $r=1$, where $\varDelta$ is a small interval. Various tests indicate that this improved boundary condition has negligible influence on drainage process. In general, the solution of the SW model in the cylinder is obtained by a numerical method. Here we used a standard discretization of the h, u variables with fixed $\delta r$ intervals and $\delta t$ time steps. The time marching is performed with an explicit MacCormack method [2]. Artificial diffusion terms $s \delta r ^2 h_{rr}$ and $s \delta r ^2 u_{rr}$, with s of the order 1, were added to the continuity and momentum equation, respectively. The results presented for comparison with the experiments use $\delta r$ of 1/400–1/200, and $\delta t \approx 0.8 \delta r$. The numerical run is stopped when the calculated volume ratio ${\mathcal {V}}(t)/{\mathcal {V}}(0)$ gets below some prescribed value, typically 0.01. The results are referred to as “theoretical” for easy contrast with the experimental results of our investigation.

We wish to emphasize that the SW model is not intended as a substitute, nor a competitor, to the DNS simulation of the flow field; in our opinion, these are complementary tools. The SW model points out the scaling, major dimensionless parameters, connection with the general gravity currents theory and global (depth-averaged) behaviour of the drainage flow.

2.1.2 Inward drainage

In this case, the reservoir is an annulus $r \in [r_i, 1]$ (scaled with the outer radius $r_o$), see Fig. 2b, d. At $t=0$ the initial height is 1, and $u=0$. The dam-break occurs at the inner wall. The boundary conditions are now: $u(r = 1,t) =0$ and $u(r_i,t) = - [h(r_i,t)]^{1/2}$ (counterpart of 8). The flow is converging, from the periphery to the centre, and we expect a negative u.

The solution is obtained numerically, as in the previous case. The typical horizontal length of propagation of information by the characteristics is $1-r_i$, and hence, it is convenient to consider the process on the rescaled time variable ${\tilde{t}} = t/(1 - r_i)$. It is not necessary to change the equations, and the rescaling can be performed on the results of the finite difference solution. It is remarkable that this model predicts that the inward drainage (in scaled form) is governed by only one dimensionless input parameter, $r_i$.

2.2 Box model

We consider the outward flow case. The reservoir is a wedge of angle $\alpha$, and dam-break occurs for only a part of the outer boundary represented by the sector $\varTheta (< \alpha )$, see Figs. 2a, e. Since the flow field cannot be axisymmetric (independent of $\theta$), the SW equations presented above become invalid. However, this is a thin-layer inertial flow, and hence, the underlying components of the SW model are still relevant. These considerations suggest: (1) the outflow velocity is critical, which imposes the condition $u = h^{1/2}$ at the open sector; and (2) the spatial variations of the height of the interface are relatively small. With these simplifications, we can formulate a simple model for estimating ${\mathcal {V}}(t)/{\mathcal {V}}(0)$.

The major assumption is that the interface between the dense and ambient fluid is the horizontal $h=h(t)$. The current of dense fluid is now in a simple box, a slice of angle $\alpha$ and thickness h(t), therefore the name “box model”.

In the spirit of that method, we proceed as follows. The volume of the fluid in the box scaled with $h_0 r_o^2$ is given by ${\mathcal {V}}(t) = \frac{1}{2}\alpha h(t)$, and initially $h(0) = 1$.

Next, we claim that the outflux is governed by the local behaviour of the characteristics, and hence, the condition $u = h^{1/2}$, with the initial condition $h_I = 4/9$, can be applied over the broken boundary $r=1, 0< \theta < \varTheta$. Therefore, the rate of drainage of volume is given by

$$\begin{aligned} q \varTheta = u h \varTheta = \left\{ \begin{array}{ll} (4/9)^ {3/2} \varTheta &{}\;( t \le t_I), \\ \left[ h(t) \right] ^{3/2} \varTheta &{}\;( t > t_I), \end{array} \right. \end{aligned}$$

(9)

where $t_I$ is the time at which h(t) attains $h_I = 4/9$.

Finally, we apply the volume conservation $\alpha (\text {d}h/\text {d}t) = - q \varTheta$ and integrate. After some algebra, we obtain

$$\begin{aligned} h(t) = \dfrac{{\mathcal {V}}(t)}{{\mathcal {V}}(0)} = \left\{ \begin{array}{ll} 1 - \dfrac{\varTheta }{\alpha }\dfrac{8}{27} t &{}\; ( t \le t_I), \\ \dfrac{4}{9} \left[ 1 + \dfrac{1}{3} \dfrac{\varTheta }{\alpha }( t - t_I) \right] ^{-2} &{}\; ( t > t_I), \end{array} \right. \end{aligned}$$

(10)

and the relationship $h(t_I) = h_I = 4/9$ yields

$$\begin{aligned} t_I = \dfrac{15}{8} \dfrac{\alpha }{\varTheta }. \end{aligned}$$

(11)

It is remarkable that this model predicts that the inward drainage (in scaled form) is governed by only one dimensionless input parameter, $\varTheta /\alpha$.

2.3 Transition to the viscous regime

The formal criterion for the validity of the theoretical models is $\mathrm{Re} = (g' h_0)^{1/2}h_0/\nu \gg 1$. This is based on the conditions of the initial flow. However, during the process the speed and thickness decrease, and hence, the ratio of inertia to viscous forces decreases. A more stringent criterion is needed, the time-dependent effective Reynolds number, $\mathrm{Re}_e = \mathrm{Re}_e(t)$.

We make the following estimate. Let $u^*(r_o,t)$ and $h^*(r_o,t)$ be the dimensional values at the edge. The inertia per unit volume is $\rho _c [u^*(r_o,t)]^2/r_o$, while the viscous force per unit bottom area is $\rho _c \nu [u^*(r_o,t)] /h^*(r_o,t)$. The integral over the dense fluid then gives the ratio of inertial to viscous effects as

$$\begin{aligned} \mathrm{Re}_e = \dfrac{u^*(r_o,t) [h^*(r_o,t)]^2}{\nu r_o}. \end{aligned}$$

(12)

Switching to the dimensionless variables u and h yields

$$\begin{aligned} \mathrm{Re}_e = \left[ \mathrm{Re} \dfrac{h_0}{r_o}\right] u(r=1,t) [h(r = 1,t)]^2 = \left[ \mathrm{Re} \dfrac{h_0}{r_o}\right] \varGamma (t). \end{aligned}$$

(13)

The value of $\varGamma$ is of the order of unity at the beginning of the process, but decreases with time. Eventually, the simplified inertial–buoyancy flow is expected to undergo transition to a viscous–buoyancy regime when $\mathrm{Re}_e \approx 1$., i.e. when $\varGamma (t)$ becomes sufficiently small.

The function $\varGamma = u(r=1,t) [h (r=1,t)]^2$ can be simplified. First, we recall that $u = h^{1/2}$ at the outlet. Second, we employ the box model approximation $h(t)/h(0) \approx {\mathcal {V}}(t)/{\mathcal {V}}(0)$. We obtain

$$\begin{aligned} \mathrm{Re}_e \approx \left[ \mathrm{Re} \dfrac{h_0}{r_o}\right] [{\mathcal {V}}(t)/{\mathcal {V}}(0)] ^{5/2}. \end{aligned}$$

(14)

This indicates that even for moderately large $\mathrm{Re}\, {h_0}/{r_o}$ a very significant drainage occurs in the inertial regime. For example, if $\mathrm{Re}\, {h_0}/{r_o} = 10^3$ the regime $\mathrm{Re}_e > 1$ corresponds to ${\mathcal {V}}(t)/{\mathcal {V}}(0) > 0.065$.

This estimate can be applied to inward drainage, by using the gap $r_o (1-r_i)$ instead of $r_o$ in (13) and the subsequent uses of $\mathrm{Re}_e$.

3 The experimental layout and procedures

In order to validate the theoretical model and gain realistic visualizations of the flow, we conducted a series of experiments at the Hydraulic Laboratory of the University of Parma. The apparatus was a 53-cm-high poly-methyl-methacrylate circular sector, with a $30^\circ$ angle at the centre and an outer radius of $180\,\text {cm}$, see Fig. 3a. A horizontal circular sector plate of outer radius $r_o = 117.5\,\text {cm}$ and inner radius $r^*_i = 39\,\text {cm}$ was sealed to the lateral walls of the apparatus, at 15 cm from the bottom, and separated the denser fluid above from the ambient fluid below.

For the outward drainage of the fluid contained in the lock, a removable circular sector plate of radius $r^*_i = 39\,\text {cm}$ was inserted between the lock and the ambient fluid to prevent any flow between the two chambers, with sealing due to an O-ring. A gate at $r_o = 117.5\,\text {cm}$, as shown in Fig. 3b, was manually lifted.

For the inward drainage, sketched in Fig. 3c, two different configurations were adopted, with $r^*_i = 39\,\text {cm}$ and $r^*_i = 29\,\text {cm}$. In these configurations, a 12-cm-tall plastic fence was plugged onto the circular sector bottom plate at $r_o = 117.5\,\text {cm}$, as a back wall for the denser fluid. The plastic fence was slightly higher than the height of the denser fluid in the lock but still lower than the height of the ambient fluid to facilitate the recirculation of the ambient fluid during the inward draining flow, in order to reduce the ambient fluid disturbances. The gate at $r^*_i$ was manually lifted.

Fig. 3

Experimental apparatus for full gate experiments: a top view; b side view for outward radial drainage; c side view for inward radial drainage; d arrangement of the three UVP probes, side view and top view. Distances are expressed in centimetres. Below, the camera used for the side shot is shown

A third series of experiments were performed with three different partial width gates, 8.8, 14.0 and $19.2\,\text {cm}$ wide, in an outward radial drainage configuration, see Fig. 4. The gates were always in a guillotine arrangement, with one lateral side of the gates able to slide along a rail attached to the lateral wall of the tank. For these experiments, the dense fluid was fresh water and the ambient fluid was air.

Fig. 4

Layout of the experimental device for partial width gate experiments. a Top view; b side view. US1-4 are the ultrasonic distance meters. The fence is the fixed part of the side walls of the cylindrical container, the gate is the sliding part, which can be lifted to start the efflux process

The gates were stainless steel plates $0.1-0.2\,\text {cm}$ thick, and their opening took approximately $0.2\,\text {s}$, a negligible time if compared with the timescale of most experiments (in most cases $T\approx 4-6\,\text {s}$, with a minimum of 0.8 s for the high $\mathrm{Re}$ experiments). A criterion for establishing the maximum gate opening time can mimic that formulated by [9] for dam breaks on a dry horizontal bottom with a vertical lift gate: if the opening occurs in a time greater than $t_{\min }=\sqrt{2h_0/g}$, the initial flow field is distorted by the presence of the flat gate surface, increasing the discrepancy between theory and experiment. Applying this criterion, the critical condition for this experimental activity corresponds to $h_0= 0.10\,\text {m}$ with a water–air system, for which it results $t_{\min }=0.14\,\text {s}$, less than the opening time of 0.2 s for the present experiments. In all other conditions, in particular for saline water experiments where a reduced gravity is acting, the opening time is significantly less than the minimum time. We also point out that the conditions of these experiments have something in common with the scheme by [9] but do not coincide completely, in particular because downstream of the lift gate we have a free fall of the current, while in the scheme by [9] there is a flat horizontal bottom.

The experiments were recorded by a full HD video camera (Canon Legria HF 20, 1920 pixels $\times$ 1080 pixels) working at 25 frames per second, with a field of view (FOV) extended to the entire side of the lock. A grid with 5 cm horizontally and vertically spaced lines was stuck to the inner side of the lateral wall, in order to track the position of the density interface with time, by converting the pixel position of the images extracted from the video into metric coordinates. Completely stable and homogeneous illumination was provided by high-frequency neon lamps at the back wall of the tank. The resolution was approximately $0.1\,\mathrm {cm\,pixel}^{-1}$, and the overall uncertainty due to parallax errors or grid defects was approximately 0.2 cm. For the partial width gate experiments the height of the current was measured by the image analysis and also by four ultrasound distance meters (US1, US2, US3, US4) (TurkBanner Q45UR), with a data rate of 100 Hz and a nominal accuracy of 0.03 cm, positioned on the top of the tank (see Longo et al. [13], for details on these sensors). US1 was positioned 6.8 cm behind the gate, at $r = 0.91$ ($r*=110.7\,\text {cm},\theta =26^\circ$ positive counterclockwise, see Fig. 4a), while US2, US3 and US4 were aligned along the bisector of the tank at $r =0.71, 0.47, 0.23$, respectively. Figure 5 shows the comparison between the two techniques, with a fairly good agreement; the small discrepancies are due to heterogeneity on the level of the current in the azimuthal direction, especially close to the angle at the centre. For an easy visualization, US2, US3 and US4 data are shifted 5, 10 and 15 s, respectively.

Fig. 5

Free surface levels measured during exp 38 (outward drainage, partial width gate $b^*=8.8\,\text {cm}$, $r^*_i = 0$, $h_0 = 10.1\,\text {cm}$, $\rho _c = 0.998 \,\text {g}\,\text {cm}^{-3}$) by the four US distance meters (solid lines) and by means of the image analysis (symbols). Data series are shifted 5, 10 and 15 s, respectively, for an easy visualization

The fluid for the denser current was prepared by adding sodium chloride (NaCl) to softened tap water and aniline dye for an easy visualization of the density interface during the flow of the current. The ambient fluid was softened tap water ($\rho _a = 0.998\,\text {g}\,\text {cm}^{-3}$), sometimes slightly denser ($\rho _a = 1.001$–$1.002\,\text {g}\,\text {cm}^{-3}$) because of salt traces left from the previous experiment. According to the protocol of the experiments, the lock was first filled with a layer of the ambient fluid; then, the downstream portion of the tank was filled with ambient fluid in order to balance the force on the gate. At last, when the downstream ambient fluid attained approximately the same level of the fluid in the lock, both the lock and downstream were filled with water until the desired final level for the ambient fluid was reached. At the end, the denser fluid was gently pumped at the bottom of the lock, in order to minimize any mixing with the ambient fluid. A subset of experiments is performed with fresh water flowing in air in both the outward drainage configuration and inward drainage (only $r^*_i = 39 \,\text {cm}$), in order to compare the effects of the ambient fluid and of Reynolds number on the velocity and drainage of the current.

Fluid velocity data, at different radial positions, were recorded by three ultrasound velocity profilers (UVP, model DOP 2000 Signal-Processing, S.A., Switzerland, 2005) with a carrier frequency of 8 MHz, positioned at the base of the lock. The UVPs are aligned at 15$^{\circ }$ with respect to the vertical direction and were arranged as shown in Fig. 3d, with the axis of the probes along the edges of a tetrahedron. The dense current in the lock was seeded with TiO$_2$ parcels so that the three UVP probes could measure their axial velocity $u_1$, $u_2$ and $u_3$, at different space intervals (gates) along the respective 1, 2 and 3 axes of the probes. The velocity measurements are based on the Doppler shift of the echoes generated by the reflection of particles and turbulent eddies, and depend on the value of the celerity of ultrasounds in the fluid. The celerity depends on temperature and density of the fluid, and we corrected the data with the formula suggested by Mackenzie [15]. The three velocity components can then be transformed into a local Cartesian coordinate system $x - y - z$ (corresponding to $r-\theta -z$) by means of the relation $\{u,v,w\}^T=\mathbf{A} \cdot \{u_1,u_2,u_3\}^T$, where A is the matrix of transformation, u, v and w are the velocity components in the x (radial, positive in the outward direction), y (tangential, positive clockwise from the top of the tank) and z (vertical, positive upward) directions, respectively (see Longo [10], for details). Each probe has an axial space resolution of $\approx 1\,\text {mm}$ and a data rate of approximately 6 Hz (number of velocity profiles per second), considered sufficient to capture also the peaks of velocity. Part of the uncertainty of measurements taken with the UVP is related (i) to the geometry of the sonic field and (ii) to the sequential data acquisition.

The sonic field is conical with an aperture half-angle of $1.20^\circ$, which at 100 mm distance has a diameter of about 5 mm. Therefore, the spatial variability of the flow field intervenes in the velocity estimation, since measurements are taken as the average of the scattered signal by all tracers contained in the sonified volume of measurements, increasing with distance from the piezo-emitter. In addition, the three sonic cones overlap in a limited measurement volume. As a consequence, the transformation of the axial velocity components into components referred to a Cartesian coordinate system is characterized by an uncertainty that is minimal in the volume of overlap and is increasing away. In the configuration of the present experiments, the intersection of the axes of the probes is at approximately 100 mm in the vertical from the bottom of the tank, corresponding to almost 80 mm along the axis of the probes and where the cross section of the sonic cone is a circle with a diameter of about 4 mm, with an overlap of almost 10 mm.

The effect of sequential data sampling results in an uncertainty proportional to the degree of unsteadiness of the flow field. The first-order correction is documented in [14].

A switch triggered the start of the velocity measurements and simultaneously turned on an LED positioned inside the FOV of the camera. In this way, it was possible to synchronize the frames of the video with the velocity profiles.

Figure 6 shows a typical example of the radial, tangential and vertical velocity profiles at four different non-dimensional times for exp 26 (panels a–d), and for exp 29 (panels e–h), at $r = 0.62$ and 0.74, respectively. The horizontal dashed line represents the height of the current, measured by the image analysis. We can observe that the tangential and vertical components, v and w, are small compared to the radial one, u, confirming the correctness of the shallow-water approximation (the tangential velocity should be null). The vertical velocity is slightly negative only near the interface which is lowering.

Fig. 6

Velocity profiles measured a–d for exp 26 (inward drainage, $r^*_i = 39 \, \mathrm {cm}$, $h_0 = 10.0 \, \mathrm {cm}$, $\rho _c = 1.032\,\text {g}\,\text {cm}^{-3}$, $\rho _a = 1.002\,\text {g}\,\text {cm}^{-3}$), and e–f–g–h for exp 29 (inward drainage, $r^*_i = 29 \,\mathrm {cm}$, $h_0 = 10.0 \,\mathrm {cm}$, $\rho _c = 1.035\,\text {g}\,\text {cm}^{-3}$, $\rho _a = 1.000\,\text {g}\,\text {cm}^{-3}$) at different times shown at the top. The horizontal dashed line represents the instantaneous level of the interface between the dense current and the ambient fluid

3.1 The uncertainty in variables and parameters

The uncertainty of the variables and parameters was estimated on the basis of the instrument characteristics and of the process of measurement. Mass density was measured by a hydrometer with an accuracy of $10^{-3}\,\,\mathrm {g}\,\mathrm {cm}^{-3}$, hence the corresponding uncertainty for the reduced gravity $g' = (1-\rho _a/\rho _c)g$ is $\varDelta g'/g' \le 0.2$%. The level of the dense fluid in the lock was fixed with an accuracy of 0.2 cm and the relative uncertainty is $\varDelta h_0/h_0 \le 2$%. The velocity and timescales have both an uncertainty $\varDelta U/U, \, \varDelta T/T \le 2.5$%. The Reynolds number has an uncertainty $\varDelta \mathrm{Re}/\mathrm{Re} \le 4.5$%, also based on the assumption of an uncertainty of 1% in estimating the kinematic viscosity of brine.

The instantaneous velocities measured by the UVP, used to reconstruct the velocity field, have an uncertainty always $\varDelta u/u \le 7.5$%, with a minimum value of 0.3 $\mathrm {cm\,s^{-1}}$ (see Longo et al. [13], for more details). The uncertainty of the vertical position to which the velocity measurements refer is 0.01 cm.

The uncertainty of the volume of the dense fluid inside the lock increases in time as a consequence of the reduction of the depth, and it results $\varDelta {\mathcal {V}}/{\mathcal {V}} \le 5$% (for $t \le 2$ for outward drainage, and for $t \le 7$ for inward drainage), $\varDelta {\mathcal {V}}/{\mathcal {V}} \approx 12.5$% for $7<t \le 25$ in the case of inward drainage.

The nominal uncertainty in the measure of the free surface by ultrasonic distance meters is 0.03 cm, the real one is 0.05 cm.

4 The experiments

A number of 48 experiments were performed, with main parameters listed in Table 1: 26 experiments in an outward drainage configuration with $r^*_i = 0 \, \mathrm {cm}$, 9 experiments in an inward drainage configuration with $r^*_i = 39 \, \mathrm {cm}$ plus 5 experiments with $r^*_i = 29 \, \mathrm {cm}$, 8 experiments with a partial width gate of 19.2, 14.0 or 8.8 cm. For all the experiments, the external radius is $r_o = 117.5 \, \mathrm {cm}$; 16 of the 48 experiments were conducted with fresh water as dense fluid and air as ambient fluid, in order to check the effects of the Reynolds number and of the ambient fluid dynamics.

In order to check the effects of the viscous corner near the centre, and of the free surface perturbations of the ambient fluid, some experiments were conducted with a 5-cm-wide plastic corner with a triangle cross section inserted near the origin of the sector radial tank. In a couple of experiments, a vertical radial fence was inserted to reduce the angle to the centre to $\alpha =10^{\circ }$, with the aim of quantifying the boundary radial vertical walls effects. In most experiments, an absorptive panel made of sponge and polystyrene chips embedded in a wire mesh cylinder was installed at the vertical wall facing the gate, in order to reduce the free surface fluctuations of the ambient fluid.

Table 1 Parameters of the experiments, with the letter preceding the number indicating an outward radial (o), inward radial (i), and a partial width gate (p) experiment. $h_0$ is the initial depth of the denser fluid in the lock, $r^*_i$ and $r_o$ are the internal/external radii, $\rho _{a,c}$ is the mass density of the ambient/current fluid, $g'$ is the reduced gravity, U is the velocity scale, T is the timescale, $\mathrm{Re}$ is the initial Reynolds number

The results will be presented in three separate subsections for outward, inward and outward partial width gate drainage configuration.

4.1 Outward drainage

Figures 7 show a series of snapshots for exp 13 in order to give an overview of the general behaviour of an outward drainage. The time of each snapshot after the lift of the gate is visible at the top.

Fig. 7

Sequence of snapshots for experiment 13, outward drainage, $r^*_i = 0\,\mathrm {cm}$, $h_0 = 10.0\,\mathrm {cm}$, $\rho _c = 1.050\,\text {g}\,\text {cm}^{-3}$, $\rho _a = 1.050\,\text {g}\,\text {cm}^{-3}$. The enlarged domain shows some instability at the interface (color figure online)

The red fluid is the dense fluid current in the lock, while the ambient fluid is transparent fresh water. The black bar on the left-hand side is the corner with a triangle cross section, and its left side is set at $r=0$. The red colour is not uniform since the width of the coloured fluid in the tank increases from the corner towards the gate; hence, the light absorption increases as well. The tight black vertical line on the right is the gate, set at $r=1$. At $t^*=0$ (e.g. the first snapshot, in the top left corner), the fluid is still at rest, and at $t^*=1 \,\mathrm {s}$ after lifting the gate, we can observe some dye dispersed above the height of the current, transported by adhesion to the gate. This plume tends to move to the left as it is carried by the return flow of the ambient fluid. Some billows also develop (see the enlarged domain in the inset), favouring entrainment and mixing. It is also evident that near the edge the SW model assumptions fail, since strong curvature of the interface favours a finite value vertical velocity and a non-hydrostatic pressure distribution in the vertical. However, this effect is limited in space and also in time, as shown in the velocity profiles reported in Fig. 6. During the drainage, after an early stage where a dominant expansion wave propagates from the gate towards the axis of the tank, the current attains a fairly horizontal profile. Red dye in the ambient fluid is visible, as an effect of the mixing at the interface. A secondary gravity current (which is out of the present analysis) fed by the drained fluid develops at the bottom of the tank and propagates towards the axis of the tank, with a dynamics independent of the upper gravity current. We notice that the recirculation of the ambient fluid in front of the edge has minor effects on the current; only in the last stage of the drainage process ($t^*=12\,\text {s}$), the recirculation and mixing (mainly due to the finite size of the tank) may affect the outflow of the main upper current. In fact, at the initial stage the secondary gravity current advancing in the lower tank drains most of the dropped fluid; subsequently, fluid dropped from the edge accumulates until it reaches the threshold elevation, altering the ambient fluid density.

A comparison between the theoretical and experimental non-dimensional height of the current as a function of the radial position is shown in Fig. 8 for exp 21. The experimental error bars are smaller than the size of the symbols, and the agreement is fairly good. Some density interface oscillations can be observed, propagating inward from the gate. The experimental profiles are generally delayed with respect to the theory, which does not include mixing and entrainment at the interface and also neglects the ambient fluid dynamics (the model is a single-layer SW model). Secondary small oscillations of the density interface are reduced by the presence of the lid at the top of the ambient fluid, except for some billows of the intruding current at $r=1$ developing at early times after the gate lifting. The experimental profiles for the other experiments (not visualized) show a similar agreement with the theory.

Fig. 8

Non-dimensional theoretical (red solid line) and experimental profiles (blue solid line and blue dots) of the current for exp 21, outward drainage, $r^*_i = 0 \, \mathrm {cm}$, $h_0 = 10.0 \, \mathrm {cm}$, $\rho _c = 1.031\,\text {g}\,\text {cm}^{-3}$, $\rho _a = 0.998\,\text {g}\,\text {cm}^{-3}$. The vertical dashed line at $r=1$ marks the position of the gate (color figure online)

In order to check the effects of some elements of the experimental configurations, a set of experiments were performed with an almost constant value of $g'$ and a constant H (the level of the ambient fluid with respect to the bottom), assuming as a reference exp 6, and (i) changing the initial thickness of the fluid in the lock, $h_0$, in exp 2; (ii) inserting a top lid on the ambient fluid surface in exp 7; (iii) reducing the angle of the circular sector tank to $\alpha =10^{\circ }$ in exp 12; (iv) introducing a plastic corner near the origin in expts 13–14; and (v) adding a passive absorber in front of the gate in exp 19. The volume decay in time for the different experiments is shown in Fig. 9a, including also the theoretical estimate. The different configurations have a minor effect on the results, with data collapsing reasonably well and confirm fairly well the predictions of the theory, in particular in the early stage of the drainage. The experimental presence of the waves is one of the sources of discrepancies with the SW model, unable to consider vertical velocity effects always associated to waves. It is also a possible source of the peak delay of horizontal fluid velocity, since there is a superposition between the main flow field and the fluctuating flow field associated to the waves.

Figure 9b shows the volume decay of the current versus time for different values of $g'$. The agreement with theory is again fairly good and generally within the experimental error bars. We notice that the experimental results for exp 46–47–48, which were conducted with fresh water flowing in the air and with $\mathrm{Re}\sim O(10^5)$, appear much closer to the theoretical results, even at late times. This means that, for high $\mathrm{Re}$ and with a negligible interacting dynamics of the ambient fluid, the model gives excellent predictions. We bear in mind that these three experiments are the most susceptible to disturbances induced by the opening of the gate.

Fig. 9

a Volume decay as a function of time in outward drainage, with a constant $g'$ but different conditions: different height of the current $h_0$, with the presence of the top lid, with a reduced $\alpha =10^{\circ }$, with a triangle-shaped corner inserted along the angle at the centre, with the presence of an absorptive panel at the vertical wall of the tank; b volume decay as a function of time for different values of $g'$ in outward drainage condition. Expts 46–47–48 are high $\mathrm{Re}$ experiments, with air as ambient fluid. Error bars refer to the estimated uncertainty

Figures 10a, b show the comparison between the experimental and theoretical results for the radial velocity component at $r=0.87$ and $r=0.62$, respectively, with symbols representing the vertical average of the measured velocity profiles. The pattern of u as a function of t could be expected: the flow at a fixed r starts from rest, and develops because it is sucked from the open outlet. However, the outflux eventually decays, and this will also tend to reduce the radial flow inside the cylinder. The result is acceleration to a maximum, then deceleration, of u. Data are dispersed across theoretical predictions, and for some experiments (e.g. exp 46), some fluctuations are observed with a delay, in particular for measurements at $r=0.62$. The delay is also accompanied by a lower initial velocity, during acceleration, and a more pronounced peak, overestimating theory by $\approx 30$%. The high Reynolds number experiments (exp 46–47–48) do not show a better agreement of experimental and theoretical velocity than the low Reynolds number experiments. We therefore think that these discrepancies should be attributed to local instabilities and mixing. Our data are not sufficiently accurate for a more precise interpretation.

Fig. 10

Non-dimensional radial vertically averaged velocity as a function of time in outward drainage, a at $r=0.87$ and b at $r=0.62$

4.2 Inward drainage

All the experiments with an inward drainage were performed with the lid covering the top surface of the ambient fluid. Figure 11 shows a series of snapshots for exp 22.

Fig. 11

Sequence of snapshots for exp 22, inward drainage, $r^*_i = 39\, \mathrm {cm}$, $h_0 = 10.0 \,\mathrm {cm}$, $\rho _c = 1.056\,\text {g}\,\text {cm}^{-3}$, $\rho _a = 1.002\,\text {g}\,\text {cm}^{-3}$

The pattern is similar to the outward drainage experiments, with a dominant expansion wave propagating from the gate towards the fence at $r=1$, although the convergent geometry of the flux modifies its evolution with respect to the outward radial configuration; the amplitude of the wave is reduced with respect to the wave in the outward drainage configuration.

Figure 12 illustrates the comparison between the theoretical and experimental non-dimensional height of the current as a function of the radial position, for exp 31. The experimental error bars are smaller than the size of the symbols. Similarly to the outward drainage, a dominant density interface oscillation develops immediately after the opening of the gate, at $r=0.25$, and propagates outward, reaching the back wall of the tank, at $r=1$, at around ${\tilde{t}}=1.20$. In the early stage of propagation, the reduction of the depth of the dense fluid is delayed with respect to the theoretical one. We can attribute the delay to the effects of the return current, which is null in the theoretical model, whereas it assumes a finite value in the experiments.

Fig. 12

Theoretical (red solid line) and experimental profiles (blue solid line and blue dots) of the current for exp 31, inward drainage, $r^*_i = 29 \, \mathrm {cm}$, $h_0 = 10.0 \, \mathrm {cm}$, $\rho _c = 1.031\,\text {g}\,\text {cm}^{-3}$, $\rho _a = 1.00\,\text {g}\,\text {cm}^{-3}$. The vertical dashed line at $r=0.25$ marks the position of the gate, and the vertical bold line at $r=1$ marks the back wall of the tank (color figure online)

Figure 13a, b shows the volume decay of the current versus time for $r_i=0.33$ and for $r_i=0.25$, respectively, for different values of $g'$. Experiments 31–32 were conducted with fresh water flowing in the air. In the case of an inward drainage, an increase in $\mathrm{Re}$ or the thickness of the ambient fluid does not produce a substantially different draining rate of the volume of the current, as it happened for the outward drainage experiments. We suggest the following explanation: the curvature terms (convergence of the streamlines) in the inward flow enhance the inertia of the heavy fluid. Therefore, the viscous effects and the inertia of the ambient are less effective in the inward drainage. The discrepancy between the experimental and theoretical results increases with decreasing $r_i$, which is attributed to the wall boundary layers, which are more invasive for small $r_i$ than for large $r_i$.

Fig. 13

Volume decay as a function of time, inward drainage, a for $r_i=0.33$, and b for $r_i=0.25$

Figure 14a, b shows the comparison between the experimental and theoretical results for the vertically averaged radial velocity component at $r=0.62$ and $r=0.74$, respectively, for $r_i=0.33$, while Fig. 14c, d shows a similar comparison but for $r_i=0.25$. The experimental velocity of the current seems lower than the theoretical one, but increasing $\mathrm{Re}$ and increasing thickness of the ambient fluid, this difference is quite reduced (see exp 41–42–43 in Fig. 14a). Nevertheless, the peak velocity is quite well reproduced by theory for $r_i=0.33$, whereas for $r_i=0.25$ theory overestimates the experimental peak velocity. The interpretation of the major increase–decrease pattern of |u| is like for Fig. 10 presented earlier. The smaller-amplitude oscillations are a by-product of the motion of the characteristics $c_\pm$ between the outer wall and the outlet. The travel time of the wave between these positions is of the order of 1, in accord with the period observed in the figure; however, a precise calculation is difficult because $c_\pm$ depend implicitly on r and t.

Fig. 14

Non-dimensional radial velocity as a function of time, inward drainage. a Measurements at $r=0.62$ for experiments with $r_i=0.33$, with ${\tilde{t}}_{\mathrm{max}-\mathrm{theory}}=1.2$ and ${\tilde{t}}_{\mathrm{max}-\mathrm{exp}}\approx 1.6-1.8$ for low $\mathrm{Re}$ experiments, ${\tilde{t}}_{\mathrm{max}-\mathrm{exp}}\approx 1.4-1.5$ for high $\mathrm{Re}$ experiments; b Measurements at $r=0.74$ for experiments with $r_i=0.33$, with ${\tilde{t}}_{\mathrm{max}-\mathrm{theory}}=1.3$ and ${\tilde{t}}_{\mathrm{max}-\mathrm{exp}}\approx 1.7$; c-d) measurements at $r=0.62$ and $r=0.74$, respectively, for experiments with $r_i=0.25$, with ${\tilde{t}}_{\mathrm{max}-\mathrm{theory}}=1.2$ and ${\tilde{t}}_{\mathrm{max}-\mathrm{exp}}\approx 1.6-1.7$. Exp 41–42–43 are high $\mathrm{Re}$ experiments with air as ambient fluid

4.3 Outward partial width gate drainage

In experiments 33–40, the outward drainage occurred through a partial gate of $\varTheta / \alpha = 0.312, 0.228, 0.143$. The experimental volume of the current in the lock has been computed as a weighted average of the data measured by the US probes, assuming that each probe has its own area of influence, and the theoretical volume decay has been evaluated through Eq. (10), with $\alpha =\pi /6$. The volume decreases linearly in time in the early stage, until the height of the current attains $h = 4/9$, whereas the volume decreases with $t^{-2}$ in the late times, when $h < 4/9$. Moreover, the volume decay is faster for larger $\varTheta$, where $\varTheta$ is the angle at the centre of the sector defined by the partial width gate. In our experiments, $\varTheta = \left( 0.024, 0.038, 0.052\right) \pi$ for $b^* = 8.8, 14.0, 19.2\; \mathrm {cm}$, respectively. Figure 15 shows the volume of decay of all the experiments in partial width gate configuration as a function of time. Again, although theory overestimates the outflow rate, the trend is correctly reproduced, with small discrepancy in the initial phase, and more evident discrepancies in the late stage of the process. The agreement between theory and experiments seems not related to the width of the gate. Overall, the performance of the theory is satisfactory (and even remarkable) in view of the fact that the prediction is based on a very simple box model. The box model reduces the flow to a ODE; however, the boundary condition has been deduced from the SW PDEs, and this apparently gives physical reliability to the results.

Fig. 15

Volume decay as a function of time, outward drainage through a partial width gate

5 Discussions and conclusions

Radial gravity currents generated by the collapse of a cylindrical boundary (or a part of it) in a cylindrical reservoir (full circle or wedge) belong to the lock-release theory. For academic understating and practical use, it is important to consider the questions: (i) Is it possible to obtain a reliable conceptual picture of the flow processes without resorting necessarily to the more accurate and effort-consuming DNS? (ii) For different drainage configurations, what is the accuracy associated with predictions provided by simplified models based on SW equations? (iii) In particular, what is the behaviour of the volume decay in the reservoir as a function of time? To address these questions, we have provided a large set of laboratory experiments involving (i) outward diverging drainage, (ii) inward converging drainage and (iii) outward partial width gate drainage. The measurements were used to demonstrate the interpretative capacity of the model developed by Ungarish et al. [23] consisting of SW equations for outward/inward drainage, and a box model for outward partial width gate drainage.

Measurements of volume decay based on 26 experiments taken for the case of outward diverging drainage show a very good agreement with theory in the range of $t<0.7$; for the first subset of experiments (Fig. 9a), the error associated with model predictions increases with time and reaches a maximum of about 20% at $t \approx 2$. On the contrary, the second subset of experiments (Fig. 9b), for which different values of $g'$ are considered, returns a different picture: experiments associated with high $\mathrm{Re}$ numbers ($\mathrm{Re}\sim O(10^5)$) present measurements which deviate for increasing time from those of experiments with $\mathrm{Re} \sim O(10^4)$. For high $\mathrm{Re}$, the fluid volume decays faster, as the interaction with the ambient fluid becomes negligible, and the agreement with theory increases especially for late times. When comparing experimental and theoretical current heights (see Fig. 8) and experimental (vertically averaged) and theoretical velocities at $r=0.74$ (see Fig. 10a), a very good agreement is observed for $t=0.4 - 1$, while the worst model performance is mainly detected at early time, i.e. for $t<0.3$. Conversely, at $r=0.62$ (Fig. 10b), the best agreement with theory is observed at $t<0.4$; afterwards, the model prediction is shifted backwards with respect to measurements and the peak velocities are underestimated. Differences in model accuracy at different space–time locations are probably due to density interface oscillations that propagate inward from the gate, as shown in Fig. 8. The experimental profiles, after an initial adjustment time, are generally delayed with respect to the theoretical model as a consequence of the single-layer approximation: while the return velocity is zero in the model, it is finite in the experiments and counteracts the flow of the dense current.

Measurements of volume decay based on 14 experiments taken for the case of inward converging drainage show a very good agreement with theory in the range of ${\tilde{t}}<4$ at $r_i=0.33$ (Fig. 13a), and ${\tilde{t}}<2$ at $r_i=0.25$ (Fig. 13b). The error associated with model predictions at $r_i=0.33$ increases with time to reach a maximum of about 30% at ${\tilde{t}} \sim 25$; however, the theoretical value falls generally within the error bar associated with measurements. On the contrary, at $r_i=0.25$, model predictions deviate earlier and more significantly from measurements and the discrepancy is greater than the error bar. When comparing experimental and theoretical (vertically averaged) velocities at $r=0.62$ and $r=0.74$, for $r_i=0.33$ (Figs. 14a, b), we may observe that for high $\mathrm{Re}$ numbers ($\mathrm{Re}\sim O(10^5)$) measurements approximate theory much better, while model prediction is shifted backwards with respect to measurements and the peak velocities are underestimated in case of low $\mathrm{Re}$. The same effect is enhanced for $r_i=0.25$ (Figs. 14c, d). Also in this case, differences in model accuracy at different space–time locations can be attributed to density interface oscillations that propagate outward as shown in Fig. 12. The experimental drainage is generally delayed with respect to the theoretical model, also as a consequence of neglecting the return flow in the single-layer approximation.

Measurements of volume decay based on 8 experiments taken for the case of outward diverging drainage through a partial width gate show that theory is again able to capture the trend in time (Fig. 15), in spite of the simplicity of model equations (the box model estimates are employed in this case). The theoretical trend, which is linear in time until $h \ge 4/9$, overestimates measurements for $\varTheta / \alpha = 0.143$; when $h < 4/9$, the volume decreases with $t^{-2}$, and theory underestimates measurements similarly for the different values of $\varTheta / \alpha$.

Some experiments were conducted varying one or more conditions (adding or removing the top lid, suppressing the central viscous corner, reducing disturbances via an absorptive panel, varying the wedge angle); results of these tests demonstrated that inconsistencies between experimental set-up and model assumptions do not produce a significant increase in the discrepancy between theory and experiments. This discrepancy is at least partially associated with viscous effects, small but not entirely negligible, interfacial waves, instability and mixing.

As a conclusion of this experimental study, we observe that theoretical analysis based on SW equations provides a quite accurate prediction of the major behaviour of the system (interface, radial speed, volume). This confirms that the physical underlying balances are these of a classical buoyancy–inertial gravity current, discussed in detail in [21]: the driving force is the buoyancy due to the density difference and inclination of the interface; upon the removal of the gate this driving induces local horizontal accelerations (the inertial reaction) that vary with location and time. In spite of its simplicity, this mechanism generate various non-trivial patterns, depending on the geometry of the container (reservoir) and position of the outflux boundary. When the residual fluid in the container becomes very thin, a different buoyancy–viscous balance develops, which is outside the scope of the present investigation. The experiments confirm that the theory identifies correctly the scaling and the free dimensionless input parameters that govern the drainage. The time decay of the volume $\mathcal {V}(t)/\mathcal {V}(0)$ in the reservoir after the boundary collapse is well predicted in all the drainage configurations tested in this work. The height h(r, t) is well predicted. The radial speed (height-averaged) u(r, t) is also fairly well predicted; in particular, we note that this variable displays a non-monotonic time dependency, which appears in both experiments and theory. On account of these comparisons, the simple SW models considered here can be recommended as a reliable solution to obtain an accurate insight on the drainage process and the reduced computational cost associated with SW equations, makes this method suitable for a screening evaluation within a risk analysis framework. In this practical context, we wish to emphasize the generality of the results: upon scaling, what we analysed with a tank of 2 m is expected to apply to much larger reservoirs, with the same accuracy. This also elucidates some significant differences between the cylinder and rectangular (2D) reservoirs: in the cylinder (outflow) ${{\mathcal {V}}/{\mathcal {V}}(0)}$ decays faster than in 2D; in a cylinder (annulus) the drainage from the outer radius is different from that from the inner radius, while in 2D there is complete symmetry between the side boundaries. In scaled form, the dominant drainage flows in full cylinder and 2D are universal, i.e. independent of any input parameter; the inward drainage depends only on the parameter $r_i$. We think that it is remarkable that such simple models are able to provide so much information about such fairly complex flow fields. Improvement and extensions are possible, such as a two-layer SW model, and a non-axisymmetric SW model (to replace the box model). This, however, requires a significant amount of work and must be left for the future. We wish to emphasize that the SW models are not a substitute, nor a competitor, to the DNS solution of the flow field; in our opinion these are complementary tools.