1 Introduction

Compatible growth in soft structures is challenging as it may drive large changes of shape, maintaining the structure stress-free; nevertheless, growth-induced morphings which allow to store elastic energy are noteworthy, too. Nematic elastomers are a nice example of how to design the hybrid alignment of the nematic units in an elastomeric strip so to produce, under thermal stimuli, stress-free bending without any storage of elastic energy [1, 2]. On the other hand, heart mechanics delivers an amazing example of a pumping device which stores elastic energy during contraction and releases it during relaxation. Therein, anisotropic growth produces a spring-like effect which extends, dilates, and rotates the ventricle while storing elastic energy; release of elastic energy determines recovery of the initial configuration [3,4,5].

In both the situations, key issue is the control of the anisotropic growth process, of the induced morphing and of the elastic energy storage. This latter is strictly related to growth: whereas compatible growth determines stress-free morphings, a defect of compatibility produces deformations which are accompanied with elastic energy storage.

The research question we set here is about the control of the defect of compatibility of an anisotropic growth process and its effects on the storage of elastic energy occurring in the body along the growth-driven morphing. In our opinion, this is an interesting question when a layer-by-layer manufacture of a soft device is produced with each layer equipped by active fibers which can remodel under appropriate stimuli to produce a change of shape which depends on the fiber structure. On the other hand, remodeling of fibers and energy storage are two mechanisms which are strongly coupled in biological structures like human heart and chameleon tongue, just to cite some more biological structures where the active mechanism of elastic energy build-up is driven by muscular contraction corresponding to spiral fibers [6,7,8]. Actually, heart mechanics has driven our work. Indeed, it initiates from [9]. Therein, to highlight the relationships between compatibility issues and elastic energy storage, we investigated the general structure of compatible anisotropic growth fields in cylindrical tubes [9]. Successively, during our studies on heart mechanics [4, 10, 11], we discussed the role of compatibility of the growth processes which determine muscle contraction in the epicardium and endocardium layers of the human left ventricle. We conjectured that the defect of compatibility between the two layers, due to the different fiber orientations, is determinant in the storing of the elastic energy occurring during the contraction phase of the cardiac cycle when the left ventricle largely twists.

On the other end, incompatibility is likewise important during the successive release of the stored energy occurring along the relaxation phase which produces the back torsion of the left ventricle. In the present paper, we start studying layered tubes with differently fibered tube-like layers, as it holds for epicardium and endocardium layers in the heart and for the chameleon tongue. Firstly, we discuss the form of the compatible growth fields which would compete to each layer if it were free from the surroundings and of the corresponding morphings. We show how, fixed the fibers orientation, compatible growth fields can be fully explicitly characterized by two scalar parameters which are the values of the surface components of the growth fields at the inner radius of the tube. We also show how these parameters can be chosen to produce morphings with specific characteristics.

Secondly, we introduce a controlled defect of compatibility in the layered tube by gluing together tube-like layers, possibly with different fibers orientations, each of them suffering an anisotropic growth having the same structure of the compatible growth fields above explicitly characterized. The solution of the elastic problem evidences how the storage of elastic energy in the tube is localized at the interface of the tubes where also the defect of compatibility is concentrated. We present and discuss a few numerical experiments based on differently fibered tubes to highlight our results.

2 Background

Within the theory of elasticity, growth is introduced to model a change of the zero-stress state, or ground state, of any volume elements of a body \({\mathcal {B}}\), identified with its reference configuration in the 3D Euclidean ambient space \({\mathcal {E}}\). The mechanical state of that body is described by two smooth fields, the placement \(\chi \) and the growth tensor \({\mathbf {G}}\):

$$\begin{aligned} \begin{array}{clccll} \chi : &{} {\mathcal {B}}\rightarrow {\mathcal {E}}, &{} \quad \quad &{} {\mathbf {G}}: &{} {\mathcal {B}}\rightarrow {\mathbb {L}}\mathtt {in},\\ &{} p \mapsto x=\chi (p) &{} &{} &{} p \mapsto {\mathbf {G}}(X). \end{array} \end{aligned}$$
(2.1)
Fig. 1
figure 1

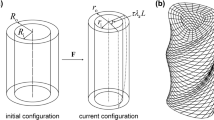
(Left) A volume element of the body (Right). The three-states map evidencing the reference volume element (light violet), the corresponding ground volume element under growth \({\mathbf {G}}\) (violet), and the current volume element (pink). Note that the reference and the ground volume elements are both attached at the same point p; for the sake of clarity, they are depicted in two different places (color figure online)

Full size image

The placement \(\chi \) associates to any material point \(p\in {\mathcal {B}}\) its position in space \(x=\chi (p)\in {\mathcal {E}}\) and determines the actual configuration \(\chi ({\mathcal {B}})\) of the body. Key geometrical functions are performed by its gradient \({\mathbf {F}}\), its adjugate \({\mathbf {F}}^*\), and its Jacobian determinant J:

$$\begin{aligned} {\mathbf {F}}= \nabla \chi = {\mathbf {I}}+ \nabla {{\mathbf {u}}},\quad {\mathbf {F}}^* = J\,{\mathbf {F}}^{-\!\top },\quad J = \det {\mathbf {F}}. \end{aligned}$$
(2.2)

Let a line element \({\mathbf {a}}\), a face \({\mathbf {a}}\times {\mathbf {b}}\) and a volume element \({\mathbf {a}}\times {\mathbf {b}}\cdot {\mathbf {c}}\), built out of the vectors \({\mathbf {a}},{\mathbf {b}},{\mathbf {c}}\in {\mathcal {V}}={\mathrm V}\!{\mathcal {E}}\,\), be attached to a place \(p\in {\mathcal {B}}\,\), as Fig. 1 (left panel) shows, then their images under the action of \(\chi \), attached to \(x=\chi (p)\,\), are gauged, respectively, by:

  1. (i)

    \({\mathbf {F}}(p)\,{\mathbf {a}}\,\);

  2. (ii)

    \({\mathbf {F}}^*(p)({\mathbf {a}}\!\times \!{\mathbf {b}})=({\mathbf {F}}(p)\,{\mathbf {a}})\!\times \!({\mathbf {F}}(p)\,{\mathbf {b}})\,\);

  3. (iii)

    \(J(p)({\mathbf {a}}\!\times \!{\mathbf {b}}\cdot {\mathbf {c}})= ({\mathbf {F}}(p)\,{\mathbf {a}})\!\times \!({\mathbf {F}}(p)\,{\mathbf {b}})\!\cdot \!({\mathbf {F}}(p)\,{\mathbf {c}})\,\).

On the other hand, the growth tensor \({\mathbf {G}}(p)\) associates to the line, face, and volume elements at \(p\in {\mathcal {B}}\) their ground states (see Fig. 1):

  1. (i)

    \({\mathbf {G}}(p)\,{\mathbf {a}}\,\);

  2. (ii)

    \({\mathbf {G}}^*(p)({\mathbf {a}}\!\times \!{\mathbf {b}})=({\mathbf {G}}(p)\,{\mathbf {a}})\!\times \!({\mathbf {G}}(p)\,{\mathbf {b}})\,\);

  3. (iii)

    \(J_g(p)({\mathbf {a}}\!\times \!{\mathbf {b}}\cdot {\mathbf {c}})= ({\mathbf {G}}(p)\,{\mathbf {a}})\!\times \!({\mathbf {G}}(p)\,{\mathbf {b}})\!\cdot \!({\mathbf {G}}(p)\,{\mathbf {c}})\,\),

with \(J_g = \det {\mathbf {G}}\). It is worth noting that these geometric elements belong to the tangent space of \({\mathcal {B}}\) at p. These two instances of 1D, 2D, and 3D body elements are in turn related by a tensor field \({\mathbf {F}}_\mathrm{e}\) such that:

$$\begin{aligned} {\mathbf {F}}={\mathbf {F}}_\mathrm{e}\,{\mathbf {G}}. \end{aligned}$$
(2.3)

Equation (2.3) represents the multiplicative decomposition of the deformation gradient \({\mathbf {F}}\) into the elastic deformation \({\mathbf {F}}_\mathrm{e}\) and the growth tensor \({\mathbf {G}}\).Footnote 1 It holds:

$$\begin{aligned} \mathrm{d}v=J\mathrm{d}V\quad \text {and}\quad \mathrm{d}V_g=J_g\mathrm{d}V\quad \Rightarrow \quad \mathrm{d}v=J_\mathrm{e}\mathrm{d}V_g, \end{aligned}$$
(2.4)

with \(J_\mathrm{e} = \det {\mathbf {F}}_\mathrm{e}\).

In general, a relaxed configuration cannot be realized, not even locally, and thus, it cannot be described by a placement: precisely, the symmetric tensor \({\mathbf {C}}_o={\mathbf {G}}^T\,{\mathbf {G}}\) may not be the metric tensor of any possible configuration. Each neighborhood of a material point p is allowed to grow (i.e., to change its relaxed state) as the growth tensor \({\mathbf {G}}\) at p prescribes; hence, the integrity of the body may not be preserved, unless an elastic deformation \({\mathbf {F}}_\mathrm{e}\) takes place to accommodate the growth \({\mathbf {G}}\), and realizes the final visible deformation \({\mathbf {F}}\). Thus, the (right Cauchy–Green) strain tensor \({\mathbf {C}}={\mathbf {F}}^T\,{\mathbf {F}}\) is the metric tensor of the realized configuration \(\chi ({\mathcal {B}})\).

2.1 Compatible growth fields

A special class of growth fields are the compatible growth fields which realize relaxed configurations which are different from the trivial reference configuration identified by \({\mathbf {G}}={\mathbf {I}}\), with \({\mathbf {I}}\) the identity tensor. They are distinguished solutions of the elastic problem characterized by a minimum of energy and zero stress and are the gradient of a placement \(\chi _c\).

Precisely, let us assume that the elastic strain energy density \(\varphi _o\) per unit ground volume associated with the mechanical state \((\chi , {\mathbf {G}})\) be a convex function \({\hat{\varphi _o}}\) of the elastic strain measure \({\mathbf {C}}_\mathrm{e} = {\mathbf {F}}_\mathrm{e}^T{\mathbf {F}}_\mathrm{e}\) (right Cauchy–Green strain):

$$\begin{aligned} \varphi _o= {\hat{\varphi _o}}({\mathbf {C}}_\mathrm{e}), \quad {\hat{\varphi _o}}({\mathbf {I}})=\text {min}. \end{aligned}$$
(2.5)

The corresponding Cauchy stress tensor \({\mathbf {T}}\) is

$$\begin{aligned} {\mathbf {T}}= {\hat{{\mathbf {T}}}}({\mathbf {F}}_\mathrm{e})= 2(\text {det}{\mathbf {F}}_\mathrm{e})^{-1}{\mathbf {F}}_\mathrm{e}\frac{\partial {\hat{\varphi _o}}}{\partial {\mathbf {C}}_\mathrm{e}}{\mathbf {F}}_\mathrm{e}^T, \quad {\hat{{\mathbf {T}}}}({\mathbf {I}})=\mathbf{0 }. \end{aligned}$$
(2.6)

Based on previous results [9, 15], we define a smooth growth field \({\mathbf {G}}\) as compatible, if there exists a placement \(\chi _c\) such that:

$$\begin{aligned} \nabla \chi _c^T\,\nabla \chi _c = {\mathbf {G}}^T\,{\mathbf {G}}= {\mathbf {C}}_o . \end{aligned}$$
(2.7)

If this is the case, \({\mathbf {C}}_o\) is an Euclidean metric tensor, and the relaxed configuration is realizable, provided \(\chi _c\) satisfies any possible boundary conditions. Straightforward consequences of (2.7) are that: (i) compatible growth fields realize zero elastic strains:

$$\begin{aligned} \nabla \chi _c^T\,\nabla \chi _c = {\mathbf {G}}^T\,{\mathbf {G}}\quad \Leftrightarrow \quad {\mathbf {G}}^{-T}\,\nabla \chi _c^T\,\nabla \chi _c\,{\mathbf {G}}^{-1} = {\mathbf {F}}_\mathrm{e}^T\,{\mathbf {F}}_\mathrm{e} = {\mathbf {C}}_\mathrm{e} = {\mathbf {I}}\,; \end{aligned}$$
(2.8)

(ii) compatible growth fields yield a global relaxed configuration \(\chi _c({\mathcal {B}})\):

$$\begin{aligned} \nabla \chi _c^T\,\nabla \chi _c = {\mathbf {G}}^T\,{\mathbf {G}}\quad \Leftrightarrow \quad {\mathbf {C}}_\mathrm{e} = {\mathbf {I}}\quad \Rightarrow \quad {\hat{\varphi }}({\mathbf {I}})=\text {min},\text { and }\, {\hat{{\mathbf {T}}}}({\mathbf {I}})=\mathbf{0}. \end{aligned}$$
(2.9)

A compatible growth field \({\mathbf {G}}\) yields a global relaxed configuration \(\chi _c({\mathcal {B}})\) of the body, and we say that the body suffers a stress-free morphing, which can be controlled by an accurate choice of the growth field \({\mathbf {G}}\) which must be compatible.

3 Anisotropic growth fields

We study compatible growth of incompressible cylindrical fibered tubes which twist, extend (shorten), and inflate without storing any elastic energy. Introducing a Cartesian frame \(\{o;\,{\mathbf {i}}_1,{\mathbf {i}}_2,{\mathbf {i}}_3\}\) with \({\mathbf {i}}_\mathrm{i}\in {\mathcal {V}}\) and origin \(o\in {\mathcal {E}}\), the map

$$\begin{aligned} (R,\theta ,Z)\mapsto p = o + R\,{\mathbf {e}}_R(\theta ) + Z\,{\mathbf {e}}_Z,\quad 0<\theta<2\pi ,\,\,Z\in [0,L],\,R_\mathrm{i}<R<R_\mathrm{e}, \end{aligned}$$
(3.10)

with \({\mathbf {e}}_R(\theta ) = \mathrm {cos}\,\theta \,{\mathbf {i}}_1 + \mathrm {sin}\,\theta \,{\mathbf {i}}_2\) the unit normal to the cylindrical surface, and \({\mathbf {e}}_Z={\mathbf {i}}_3\) the longitudinal axis of the tube, describes a tube \({\mathcal {T}}\subset {\mathcal {E}}\) of inner radius \(R_\mathrm{i}\), external radius \(R_\mathrm{e}\), and axis \({\mathbf {i}}_3\) in terms of cylindrical coordinates \((R,\theta ,Z)\) and the corresponding orthonormal polar basis \(({\mathbf {e}}_R(\theta ), {\mathbf {e}}'_R(\theta ), {\mathbf {e}}_Z)\). To each R, it corresponds a tube-like surface \({\mathcal {S}}_R\): the inner \({\mathcal {M}}_\mathrm{i}\) and outer \({\mathcal {M}}_\mathrm{e}\) boundaries of the tube correspond to the surfaces \({\mathcal {S}}_{R_\mathrm{i}}\) and \({\mathcal {S}}_{R_\mathrm{e}}\), respectively.

A helicoidal fiber field in \({\mathcal {T}}\) is identified by its tangent vector field

$$\begin{aligned} {\mathbf {e}}(\theta ,R)=\mathrm {cos}\,\alpha (R)\,{\mathbf {e}}_R'(\theta )+\mathrm {sin}\,\alpha (R)\,{\mathbf {e}}_Z,\quad \end{aligned}$$
(3.11)

with \(\alpha (R)\) the possibly radially varying angle measured with respect to the circumferential direction. We assume that the tube is fibered with radially uniform helicoidal fibers \((\alpha (R)=\alpha \)) and introduce the anisotropic growth tensor field \({\mathbf {G}}\) as:

$$\begin{aligned} {\mathbf {G}}(R,\theta )= \gamma _\parallel (R)\,{\mathbf {E}}(\theta ) + \gamma _\perp (R)\,{\mathbf {E}}^*(\theta ) + \gamma (R)\,{\mathbf {E}}_R(\theta ), \end{aligned}$$
(3.12)

with \({\mathbf {E}}={\mathbf {e}}\otimes {\mathbf {e}}, {\mathbf {E}}^\star ={\mathbf {e}}^*\otimes {\mathbf {e}}^*\), and \({\mathbf {E}}_R={\mathbf {e}}_R\otimes {\mathbf {e}}_R\) the orientation tensors corresponding to the fields \({\mathbf {e}}\), \({\mathbf {e}}^*={\mathbf {e}}_R\times {\mathbf {e}}\), and \({\mathbf {e}}_R\), respectively. The anisotropic growth tensor \({\mathbf {G}}\) is completely parameterized by the eigenvectors \(({\mathbf {e}}(\theta ), {\mathbf {e}}^*(\theta )\), and \({\mathbf {e}}_R(\theta ))\) and the corresponding eigenvalues \((\gamma _\parallel (R), \gamma _\perp (R)\), and \(\gamma (R))\). It is worth noting that for \(\alpha =\pi /2\) (as well as for \(\alpha =0\)), \({\mathbf {G}}\) describes the growth occurring along the longitudinal, circumferential, and radial direction by the fields \(\gamma _\parallel \) (\(\gamma _\perp \)), \(\gamma _\perp \) (\(\gamma _\parallel \)), and \(\gamma \), respectively.

3.1 Anisotropic compatible growth fields

We look for stress-free morphing of the tube which admits a description in terms of extension, torsion, and inflation of the tube. In [9], we solved and discussed the general representation problem of some classes of anisotropic growth fields and characterized the placement \(\chi _c\) which realizes the anisotropic growth \({\mathbf {G}}\). Before studying growth and remodeling paths, we shortly sum up the solution.

We considered placements \(\chi _c\) describing inflation, torsion, and extension of the tubes, with radially symmetric and longitudinally uniform gradients, keeping fixed the center of the end \(Z=0\) of the tube as well as hampering longitudinal displacements and rotation of that end around the vertical axis. We represent these placements as

$$\begin{aligned} \chi _c(R,\theta ,Z)=o+r(R)\,{\mathbf {a}}_r(\vartheta ) + \varepsilon Z{\mathbf {a}}_Z,\quad \vartheta = \theta +\tau \,z, \end{aligned}$$
(3.13)

with r(R) the radial-symmetric inflation, \(\tau \) the torsion, \(\varepsilon \) the axial strain of the tube, and the current cylindrical basis \(({\mathbf {a}}_r(\vartheta ),{\mathbf {a}}'_r(\vartheta ),{\mathbf {a}}_z)\) defined by \({\mathbf {a}}_r(\vartheta ) = \mathrm {cos}\,\vartheta \,{\mathbf {i}}_1 + \mathrm {sin}\,\vartheta \,{\mathbf {i}}_2\) and \({\mathbf {a}}_z={\mathbf {e}}_Z={\mathbf {i}}_3\). With this, in order that an anisotropic growth \({\mathbf {G}}\) be realized by a placement \(\chi _c\), the following equation must hold:

$$\begin{aligned} \nabla \chi _c^T\,\nabla \chi _c = {\mathbf {C}}_o={\mathbf {G}}^2 = \gamma _\parallel ^2(R)\,{\mathbf {E}}(\theta ) + \gamma _\perp ^2(R)\,{\mathbf {E}}^*(\theta ) + \gamma ^2(R)\,{\mathbf {E}}_R(\theta ). \end{aligned}$$
(3.14)

It corresponds to a system of six nonlinear differential-trigonometric equations in the six unknowns: the field r(R), and the constants \(\tau \) and \(\varepsilon \) characterizing \(\chi _c\), and the fields \(\gamma _\parallel (R), \gamma _\perp (R)\), and \(\gamma _R(R)\) characterizing \({\mathbf {G}}\). From Eq. (3.14), with some manipulations, we firstly obtained [9]:

$$\begin{aligned} \tau = \frac{1}{R_\mathrm{i}}\;\frac{a^2-1}{(a^2\cot \alpha +\tan \alpha )}\quad \text {and}\quad \varepsilon = \frac{{\bar{\gamma }}_\parallel }{(a^2\cos ^2 \alpha +\sin ^2\alpha )^{1/2}}, \end{aligned}$$
(3.15.1,2)

with \({\bar{\gamma }}_\parallel =\gamma _\parallel (R_\mathrm{i})\), \({\bar{\gamma }}_\perp =\gamma _\perp (R_\mathrm{i})\) and the anisotropic growth factor \(a={\bar{\gamma }}_\parallel /{\bar{\gamma }}_\perp \). With this, we obtained the representation forms of the surface growth fields \(\gamma _\parallel \) and \(\gamma _\perp \) as

$$\begin{aligned} \gamma _\parallel (R)= & {} {\bar{\gamma }}_\parallel \;(1+(1-a^2)(R/R_\mathrm{i}-1)\cos ^2\alpha )^{-1/2},\end{aligned}$$
(3.16)
$$\begin{aligned} \gamma _\perp (R)= & {} {\bar{\gamma }}_\perp \;(1+(1-a^{-2})(R/R_\mathrm{i}-1)\sin ^2\alpha )^{-1/2}, \end{aligned}$$
(3.17)

and of the inflation r as

$$\begin{aligned} r(R) = R(\gamma _\parallel ^2(R)\cos ^2\alpha + \gamma _\perp ^2(R)\sin ^2\alpha )^{1/2}, \end{aligned}$$
(3.18)

in terms of three parameters: \({\bar{\gamma }}_\parallel \), \({\bar{\gamma }}_\perp \), and \(\alpha \). From (3.14), we also obtained the equation \(\gamma ^2(R) =(\partial r(R)/\partial R)^2\) which delivers the growth along the thickness from the inflation r(R).

The requests that \(\gamma _\parallel ^2(R)\) and \(\gamma _\perp ^2(R)\) be positive determine an admissibility range for \(a^2\): for any \(R_\mathrm{i}<R<R_\mathrm{e}, (\gamma ^-(R))^2<a^2< (\gamma ^+(R))^2\) with \((\gamma ^-(R))^2=(R/R_\mathrm{i}-1)\;(R/R_\mathrm{i} +\text {cotg}^2\alpha )^{-1}\) and \((\gamma ^+(R))^2=(R/R_\mathrm{i} +\text {tg}^2\alpha )\;(R/R_\mathrm{i}-1)^{-1}\). As both \(\gamma ^-(R)\) and \(\gamma ^+(R)\) are monotone, the limit conditions are satisfied for any R if they are and only if are satisfied for \(R=R_\mathrm{e}\). With this, we can identify an admissible range \({\mathcal {R}}_a\) of the parameters \({\bar{\gamma }}_\parallel \) and \({\bar{\gamma }}_\perp \) defined by the following inequalities

$$\begin{aligned} {\bar{\gamma }}_\parallel >\gamma ^-(R_\mathrm{e}){\bar{\gamma }}_\perp \quad \text {and}\quad {\bar{\gamma }}_\parallel <\gamma ^+(R_\mathrm{e}){\bar{\gamma }}_\perp , \end{aligned}$$
(3.19)

for any \(0<({\bar{\gamma }}_\parallel ,{\bar{\gamma }}_\perp )<\infty \). For thin tubes, that is for \({\tilde{t}}=(R_\mathrm{e}-R_\mathrm{i})/R_\mathrm{i}<<1\), we get

$$\begin{aligned} \gamma ^-(R_\mathrm{e}) = \left( \frac{{\tilde{t}}}{1+{\tilde{t}}\sin \alpha ^2}\right) ^{1/2} \sin \alpha \quad \text {and}\quad \gamma ^+(R_\mathrm{e}) = \left( \frac{1+{\tilde{t}}\cos \alpha ^2}{{\tilde{t}}}\right) ^{1/2} \frac{1}{\cos \alpha }. \end{aligned}$$
(3.20)

For \({\tilde{t}}\rightarrow 0, \lim \gamma ^-=0\) and \(\lim \gamma ^+=\infty \), that is, \({\mathcal {R}}_a\) covers the full parameters plane.Footnote 2 Moreover, for thin tubes, once introduced the radial dimensionless coordinate \(\zeta \) such that \(R=R_\mathrm{i}(1+\zeta )\), we can identify the fields \(\gamma _\parallel \) and \(\gamma _\perp \) with their values at \(\zeta =0\), that is, \(R=R_\mathrm{i}\), and write:

$$\begin{aligned} \gamma _\parallel (R)= & {} \gamma _\parallel (R_\mathrm{i}(1+\zeta ))={\tilde{\gamma }}_\parallel (\zeta )\simeq {\tilde{\gamma }}_\parallel (0)={\bar{\gamma }}_\parallel , \end{aligned}$$
(3.21)
$$\begin{aligned} \gamma _\perp (R)= & {} \gamma _\perp (R_\mathrm{i}(1+\zeta ))={\tilde{\gamma }}_\perp (\zeta ) \simeq {\tilde{\gamma }}_\perp (0)={\bar{\gamma }}_\perp . \end{aligned}$$
(3.22)

So, inflation \({\bar{\varrho }}=r(R_\mathrm{i})/R_\mathrm{i}\) is determined as

$$\begin{aligned} {\bar{\varrho }} = ({\bar{\gamma }}_\parallel ^2\cos ^2\alpha + {\bar{\gamma }}_\perp ^2\sin ^2\alpha )^{1/2}, \end{aligned}$$
(3.23)

and growth-induced thickening \({\bar{\gamma }}\) as

$$\begin{aligned} {\bar{\gamma }} = \frac{1}{2}(\frac{1}{{\bar{\gamma }}_\perp ^2}+\frac{1}{{\bar{\gamma }}_\parallel ^2}) ({\bar{\gamma }}_\parallel ^2\cos ^2\alpha + {\bar{\gamma }}_\perp ^2\sin ^2\alpha )^{3/2}. \end{aligned}$$
(3.24)

In thin tubes, once chosen a pair \(({\bar{\gamma }}_\parallel ,{\bar{\gamma }}_\perp )\) and the fiber orientation \(\alpha \), we get the thickening growth \({\bar{\gamma }}\) as well as the inflation \({\bar{\varrho }}\) of the tube by Eqs. (3.23)–(3.24).

4 Growth and remodeling paths

Given \(({\bar{\gamma }}_\parallel ,{\bar{\gamma }}_\perp )\in {\mathcal {R}}_a\), we can evaluate the extension \(\varepsilon \) and the torsion \(\tau \) of the tube, the growths \(\gamma _\parallel (R)\) and \(\gamma _\perp (R)\) along the directions \({\mathbf {E}}\) and \({\mathbf {E}}^\star \) spanning the surface \({\mathcal {S}}_R\) of the tube, the inflation r(R),  and the growth-induced thickening \(\gamma (R)\) of the tube such that the deformation process \(\chi _c\) is realizable. So, the pair \(({\bar{\gamma }}_\parallel ,{\bar{\gamma }}_\perp )\) is the control parameter of the morphing process. We’ll follow the stress-free morphing under a continuous change of the pair \(({\bar{\gamma }}_\parallel ,{\bar{\gamma }}_\perp )\) for fixed \(\alpha \); and we say that we are following a growth path. Alternatively, we’ll do the same under a continuous change of the fiber orientation for a fixed pair \(({\bar{\gamma }}_\parallel ,{\bar{\gamma }}_\perp \)), and we say that we are following a remodeling path [16].

4.1 Extension and torsion under growth paths

Let us start with growth paths realizing a prescribed torsion \(\tau \) and axial extension \(\varepsilon \). Equation (3.15.1,2) allows to evaluate the isolines \(\tau =\)const and \(\varepsilon =\)const in the parameters plane \(({\bar{\gamma }}_\perp -{\bar{\gamma }}_\parallel )\). It is easy to verify from the explicit formula (3.15.1) that:

  • \(\tau =0\) for any values of \(\alpha \) if \({\bar{\gamma }}_\perp ={\bar{\gamma }}_\parallel \);

  • \(\tau =0\) for any pairs \(({\bar{\gamma }}_\perp ,{\bar{\gamma }}_\parallel )\) if \(\alpha =0,\pi /2\).

So, the bisectrix \({\bar{\gamma }}_\parallel ={\bar{\gamma }}_\perp \) divides the parameters plane into two portions: for any \({\bar{\gamma }}_\parallel <{\bar{\gamma }}_\perp \) (bottom portion) we get a negative (clockwise) torsion; for any \({\bar{\gamma }}_\parallel >{\bar{\gamma }}_\perp \) (top portion) we get a positive (counterclockwise) torsion, if \(\alpha \not = 0,\pi /2\). Following [16], we say that the bisectrix is a discriminant of perversion as torsion \(\tau \) changes sign across it.

Figure 2 shows tubes corresponding to different pairs \((\gamma _\bot ,\gamma _\Vert )\) along the \(\tau \) isolines, for \(\alpha =\pi /4\) and \(R_\mathrm{i}=1\). To each dot on the isotorsion lines, there corresponds a different morphing, depicted in the inset. In particular, the reference tube, gray dot on the dashed line, is stress-free morphed onto different configurations exhibiting thickening, inflation, and extension. Finally, the light pink-colored part of the parameters plane identifies the admissibility range \({\mathcal {R}}_a\) corresponding to \({\tilde{t}}=0.1\).

Fig. 2
figure 2

Isolines of \(\tau \) corresponding to \(\tau =-0.5\) (blue), \(\tau =-0.2\) (purple), \(\tau =0\) (black dashed), \(\tau =0.2\) (red), \(\tau =0.5\) (orange). The insets correspond to the following choice of parameters: from left-top moving counterclockwise we have \((\gamma _\perp ,\gamma _\parallel )\)= (1.73, 3), (1.15, 2), (1, 1), (1.73, 1), and (3.47, 2). We fixed \(R_\mathrm{i}=1\); the admissibility range \({\mathcal {R}}_a\) for \({\tilde{t}}=0.1\) is light pink-colored (color figure online)

Full size image

On the other side, the isolines corresponding to the axial strain \(\varepsilon =\,\)cost satisfy the equation

$$\begin{aligned} {\bar{\gamma }}_\perp ^2\;{\bar{\gamma }}_\parallel ^2=\varepsilon \, ({\bar{\gamma }}_\parallel ^2\cos \alpha ^2 +{\bar{\gamma }}_\perp ^2\sin \alpha ^2), \end{aligned}$$
(4.25)

arranged from (3.15.2). It is easy to verify that: for \(\alpha =0\), isolines correspond to straight lines \({\bar{\gamma }}_\perp =\)cost; for \(\alpha =\pi /2\), isolines correspond to straight lines \({\bar{\gamma }}_\parallel =\)cost; and for \(\alpha =\pi /4\), isolines correspond to a family of hyperboles parameterized by \(\varepsilon \) (see Fig. 3). We can identify both the straight lines and the hyperboles corresponding to \(\varepsilon =\)const\(=1\); they always divide the plane in two portions corresponding to axial shortening and extension, and, due to it, their points are perversion points. In Fig. 3, the black dashed line corresponds to \(\varepsilon =1\) for \(\alpha =\pi /4\). The black dots on the isoextension lines identify the values of the parameters \({\bar{\gamma }}_\perp \) and \({\bar{\gamma }}_\parallel \) which determine the shapes represented as insets in the Figure. Each shape is fully determined by a pair (\({\bar{\gamma }}_\perp , {\bar{\gamma }}_\parallel \)) which delivers the extension \(\varepsilon \) corresponding to the isoextension line other than torsion, inflation, surface growth, and thickening. It is worth noting that to all the shapes corresponding to dots on the bisectrix it does not correspond to any torsion as for \({\bar{\gamma }}_\perp ={\bar{\gamma }}_\parallel , \tau =0\). Comparing the shapes corresponding to the isoextension lines above and below the dashed black line allows to appreciate the lengthening opposed to the shortening of the tube. Finally, the light pink-colored part of the parameters plane identifies the admissibility range \({\mathcal {R}}_a\) corresponding to \({\tilde{t}}=.1\).

Fig. 3
figure 3

Isolines for the extension \(\varepsilon \) corresponding to \(\alpha =\pi /4\) and \(R_\mathrm{i}=1\): isolines \(\varepsilon =0.75\) (blue), \(\varepsilon =1\) (black dashed), \(\varepsilon =1.2\) (pink), \(\varepsilon =1.45\) (orange), \(\varepsilon =3\) (brown). We fixed \(R_\mathrm{i}=1\); the admissibility range \({\mathcal {R}}_a\) for \({\tilde{t}}=0.1\) is light pink-colored. The insets correspond to the following choice of parameters: from left-top moving counterclockwise we have \((\gamma _\perp ,\gamma _\parallel )\)= (1.6, 3), (1, 1), (0.8, 0.8), (1.5, 1.5), (2, 2), and (3, 3) (color figure online)

Full size image

4.2 Isochoric growth paths

In general, growth induces a change in volume. Producing a stress-free morphing by a compatible anisotropic growth field \({\mathbf {G}}\) which is also globally isochoric means keeping unchanged the volume of the tube:

$$\begin{aligned} V(\chi _c({\mathcal {T}}))=\pi (r(R_\mathrm{e})^2-r(R_\mathrm{i})^2)\varepsilon \,L = V({\mathcal {T}})=\pi (R_\mathrm{e}^2-R_\mathrm{i}^2)L. \end{aligned}$$
(4.26)

Using Eqs. (3.16)–(3.18), the isochoric condition (4.26) can be written in the form \(F({\bar{\gamma }}_\parallel ,{\bar{\gamma }}_\perp ,\alpha )=0\): it identifies, for any \(\alpha \), a constraint between the control parameters \({\bar{\gamma }}_\parallel \) and \({\bar{\gamma }}_\perp \). Figure 4 shows the globally compatible and isochoric paths in the plane \(({\bar{\gamma }}_\perp ,{\bar{\gamma }}_\parallel )\) for thick tubes (left panel) and thin tubes (right panel). For thick tubes (\({\tilde{t}}=.1\)), we show paths for \(\alpha =0\) (blue), \(\alpha =\pi /4\) (red), and \(\alpha =\pi /2\) (purple). All these paths lie within the admissibility domain (pink shaded) in the parameters plane.

Fig. 4
figure 4

(Left) Globally isochoric and compatible growth paths for thick tubes with \({\tilde{t}}=0.1\) corresponding to a fiber angle \(\alpha =0\), (blue), \(\pi /4\) (red), and \(\pi /2\) (purple). (Right) The same paths are represented for thin tubes with \({\tilde{t}}\rightarrow 0\); dashed green lines corresponding to a locally isochoric path are also shown (color figure online)

Full size image

When tubes are thin, it makes sense to identify a growth path which is also locally isochoric, that is, using Eqs. (3.21)–(3.24), pairs \(({\bar{\gamma }}_\parallel ,{\bar{\gamma }}_\perp )\) such that

$$\begin{aligned} {\bar{\gamma }} = \frac{1}{{\bar{\gamma }}_\parallel {\bar{\gamma }}_\perp }, \end{aligned}$$
(4.27)

or equivalently

$$\begin{aligned} ({\bar{\gamma }}_\parallel ^2+{\bar{\gamma }}_\perp ^2) ({\bar{\gamma }}_\parallel ^2\cos ^2\alpha + {\bar{\gamma }}_\perp ^2\sin ^2\alpha )^{3/2}=2{\bar{\gamma }}_\perp {\bar{\gamma }}_\parallel . \end{aligned}$$
(4.28)

Equation (4.28) says that: isochoric growth paths are driven by the pairs \(({\bar{\gamma }}_\parallel ,{\bar{\gamma }}_\perp )\) such that it holds

$$\begin{aligned} ({\bar{\gamma }}_\parallel ^2+{\bar{\gamma }}_\perp ^2)\, {\bar{\gamma }}_\parallel ^2=2\,{\bar{\gamma }}_\perp , \quad ({\bar{\gamma }}_\parallel ^2+{\bar{\gamma }}_\perp ^2)\, {\bar{\gamma }}_\perp ^2=2\,{\bar{\gamma }}_\parallel , \quad \frac{\sqrt{2}}{4}\,({\bar{\gamma }}_\parallel ^2 + {\bar{\gamma }}_\perp ^2)^{5/2}=2\,{\bar{\gamma }}_\perp \, {\bar{\gamma }}_\parallel , \end{aligned}$$
(4.29)

for \(\alpha =0,\pi /2,\pi /4\), respectively. These latter are represented in Fig. 4 (right panel) by dashed green lines which are superposed to the corresponding globally isochoric paths evaluated for \({{\tilde{t}}}\rightarrow 0\), according to the color code of the left panel. It is worth noting that for a thin tube the range of admissibility \({\mathcal {R}}_a\) of the parameters covers all the plane.

4.3 Extension and torsion under remodeling paths

We can study remodeling paths corresponding to fixed values of the pair \(({\bar{\gamma }}_\parallel ,{\bar{\gamma }}_\perp )\) for different values of the fiber angle \(\alpha \). Figure 5 represents torsion (left panel) and extension (right panel) under remodeling paths corresponding to different choices of the parameters. We note that

$$\begin{aligned} \alpha =0\quad \quad \,\Rightarrow \quad \tau =0\quad \text {and}\quad \varepsilon ={\bar{\gamma }}_\perp , \end{aligned}$$
(4.30)

and

$$\begin{aligned} \alpha =\pi /2\quad \Rightarrow \quad \tau =0\quad \text {and} \quad \varepsilon ={\bar{\gamma }}_\parallel . \end{aligned}$$
(4.31)

As observed in the previous Section, for \({\bar{\gamma }}_\parallel ={\bar{\gamma }}_\perp \), the torsion \(\tau =0\) (see the red line in Fig. 5, left panel). Moreover, we can enhance torsion at different values of the fiber angle \(\alpha \) switching \({\bar{\gamma }}_\parallel \) and \({\bar{\gamma }}_\perp \): for \(({\bar{\gamma }}_\parallel ,{\bar{\gamma }}_\perp )=(1,2)\) we get the maximum value of \(\tau \) at \(\alpha <\pi /4\) (solid purple line), whereas the same value can be attained for \(({\bar{\gamma }}_\parallel ,{\bar{\gamma }}_\perp )=(2,1)\) at \(\alpha >\pi /4\) (dashed purple line). Likewise, switching from the first to the second pair, we switch from an extension \(\varepsilon \) which is maximum at \(\alpha =0\) (solid purple line) to an extension \(\varepsilon \) which is maximum at \(\alpha =\pi /2\) (dashed purple line).

Fig. 5
figure 5

Remodeling paths: torsion (left panel) and extension (right panel) corresponding to different pairs \(({\bar{\gamma }}_\parallel ,{\bar{\gamma }}_\perp )\) for \(\alpha \) varying between 0 and \(\pi /2\)

Full size image

5 Finite elasticity with growth

As evidenced by the previous results, morphings driven by compatible growth fields are a sort of trivial universal solution of the three-dimensional elastic problem as they do not depend on the material response of the body. However, when a defect of compatibility is introduced in the modeling, material response is relevant and affects the solution of the problem.

We assumed that the elastic strain energy density \(\varphi _o\) associated with the mechanical state \((\chi , {\mathbf {G}})\) be a convex function \({\hat{\varphi _o}}\) of the elastic strain measure \({\mathbf {C}}_\mathrm{e}\), and the corresponding Cauchy stress tensor is \({\mathbf {T}}= 2\,(\text {det}{\mathbf {F}}_\mathrm{e})^{-1}\,{\mathbf {F}}_\mathrm{e}\,\partial {\hat{\varphi _o}}/\partial {\mathbf {C}}_\mathrm{e}\,{\mathbf {F}}_\mathrm{e}^T\). Other stress measures, which are useful in discussing the elastic problem, are the reference stress \({\mathbf {S}}\) and the ground stress \({\mathbf {S}}_o\); the relationships between them are

$$\begin{aligned} {\mathbf {S}}={\mathbf {T}}\,{\mathbf {F}}^*={\mathbf {S}}_o\,{\mathbf {G}}^*, \end{aligned}$$
(5.32)

that is, the reference stress \({\mathbf {S}}\) is the pull-back of the Cauchy stress by \({\mathbf {F}}^\star \) as well as the pull-back of the ground stress by \({\mathbf {G}}^\star \). Typically, in finite elasticity, it is convenient to write down the balance equations of forces in terms of the reference stress \({\mathbf {S}}\), to derive the constitutive representation of the stress from the elastic strain energy density in terms of the ground stress \({\mathbf {S}}_o\) and to discuss the solution of the elastic problem in terms of the actual Cauchy stress \({\mathbf {T}}\).

Assuming no bulk and boundary forces, the balance equations have the form

$$\begin{aligned} \texttt {div}\,{\mathbf {S}}=\mathbf{0 }\quad \text {in}\quad {\mathcal {B}}\quad \text {and}\quad {\mathbf {S}}{\mathbf {m}}=\mathbf{0 }\quad \text {on}\quad \partial {\mathcal {B}}. \end{aligned}$$
(5.33)

The material response of the body is described by the function \(\varphi _o\) which depends only on the present value of the elastic deformation \({\mathbf {C}}_\mathrm{e}\). As is quite common for soft materials, we also assume that the elastic deformation is isochoric, that is, \(J_\mathrm{e}=1\). As a consequence , the elastic strain energy determines the stress response but a constitutively indeterminate pressure term p which represents the reaction to the isochoric constraint. It holds

$$\begin{aligned} {{\dot{\varphi }}}_o=\frac{\partial {\hat{\varphi _o}}}{\partial {\mathbf {C}}_\mathrm{e}}\cdot {{\dot{{\mathbf {C}}}}}_\mathrm{e} =2\,{\mathbf {F}}_\mathrm{e}\,\frac{\partial {\hat{\varphi _o}}}{\partial {\mathbf {C}}_\mathrm{e}}\cdot {{\dot{{\mathbf {F}}}}}_\mathrm{e} =\frac{\partial {\hat{\varphi _o}}}{\partial {\mathbf {F}}_\mathrm{e}}\cdot {{\dot{{\mathbf {F}}}}}_\mathrm{e}, \end{aligned}$$
(5.34)

and Eq. (5.34) allows to identify the relationship between the symmetric ground stress \(\hat{{\mathbf {S}}}_{oc}=\partial {\hat{\varphi _o}}/\partial {\mathbf {C}}_\mathrm{e}\) and the ground stress \(\hat{{\mathbf {S}}}_o=\partial {\hat{\varphi _o}}/\partial {\mathbf {F}}_\mathrm{e}\) as \(\hat{{\mathbf {S}}}_o=2{\mathbf {F}}_\mathrm{e}\hat{{\mathbf {S}}}_{oc}\), where we denoted with a hat the elastic stress components. From that, we can derive the constitutively determined part \({\hat{{\mathbf {S}}}}\) and \({\hat{{\mathbf {T}}}}\) of the reference and Cauchy stress asFootnote 3

$$\begin{aligned} {\hat{{\mathbf {S}}}}= 2{\mathbf {F}}_\mathrm{e}\frac{\partial {\hat{\varphi _o}}}{\partial {\mathbf {C}}_\mathrm{e}}{\mathbf {G}}^\star \quad \text {and}\quad {\hat{{\mathbf {T}}}}=J^{-1}\left( 2{\mathbf {F}}_\mathrm{e}\frac{\partial {\hat{\varphi _o}}}{\partial {\mathbf {C}}_\mathrm{e}}{\mathbf {G}}^\star \right) {\mathbf {F}}^T, \end{aligned}$$
(5.35)

and the total stresses as

$$\begin{aligned} {\mathbf {S}}={\hat{{\mathbf {S}}}} -p\,{\mathbf {F}}^*\quad \text {and}\quad {\mathbf {T}}= {\hat{{\mathbf {T}}}} -p{\mathbf {I}}. \end{aligned}$$
(5.36)

Finally, we assume the neo-Hookean representation form for \({\hat{\varphi _o}}\) and write

$$\begin{aligned} {\hat{\varphi _o}}({\mathbf {C}}_\mathrm{e})=\frac{1}{2}\mu ({\mathbf {I}}\cdot {\mathbf {C}}_\mathrm{e}-3), \quad \text {det}{\mathbf {C}}_\mathrm{e}=1. \end{aligned}$$
(5.37)

Our isotropic choice implies that we are considering the active contribution of the fibers, whereas we neglect any reinforcing contributions of the fibers to the passive material response of the tube.

6 Growing bilayer tubes

From the solution of the compatibility equations, we know how to produce compatible growth/deformation fields within a tube, once the fiber main direction \(\alpha \) and the two parameters \({\bar{\gamma }}_\parallel \) and \({\bar{\gamma }}_\perp \) have been chosen. When two of these tubes are glued and within each tube a growth pattern, corresponding to a compatible growth pattern for the tube, is assigned, we expect that the defect of compatibility between the different growth patterns allows to produce a morphing with elastic energy storage and that such storing is concentrated at the interface between the two tubes. We set up the problem within the framework above shortly reviewed of finite elasticity with growth and numerically solve a few characteristic problems to investigate our expectations.

Let \({\mathcal {T}}_a\) and \({\mathcal {T}}_b\) be two fibered tubes which, glued together, produce a composite structure with an inner radius \(R_\mathrm{i}=R_a\) equal to the inner radius of \({\mathcal {T}}_a\) and an outer radius \(R_\mathrm{e}=R_b\) equal to the outer radius of \({\mathcal {T}}_b\). Moreover, the outer radius of \({\mathcal {T}}_a\) is equal to the inner radius of \({\mathcal {T}}_b\) and denoted as \(R_m\) (\(R_\mathrm{i}<R_m<R_\mathrm{e}\)). The passive material response of the two tubes is neo-Hookean, and \(\mu _a\) and \(\mu _b\) are the shear moduli in \({\mathcal {T}}_a\) and \({\mathcal {T}}_b\), respectively. Both the tubes are uniformly fibered, and the helicoidal unit-vector fields \({\mathbf {e}}_a(\theta )\) and \({\mathbf {e}}_b(\theta )\) define the tangent fields to the fibers:

$$\begin{aligned} {\mathbf {e}}_\text {j}(\theta )=\mathrm {cos}\,\alpha _j\,{\mathbf {e}}'_R(\theta )+\mathrm {sin}\,\alpha _j\,{\mathbf {e}}_Z,\quad j=a,b, \end{aligned}$$
(6.38)

with \(\alpha _j\) the angle between \({\mathbf {e}}_j(\theta )\) and the circumferential direction. Finally, we assume that the growth fields

$$\begin{aligned} {\mathbf {G}}_a(R,\theta )= \gamma _{\parallel a}(R)\,{\mathbf {E}}_a(\theta ) + \gamma _{\perp a}(R)\,{\mathbf {E}}_a^*(\theta ) + \gamma _a(R)\,{\mathbf {E}}_R(\theta ) \end{aligned}$$
(6.39)

and

$$\begin{aligned} {\mathbf {G}}_b(R,\theta )= \gamma _{\parallel b}(R)\,{\mathbf {E}}_b(\theta ) + \gamma _{\perp b}(R)\,{\mathbf {E}}_b^*(\theta ) + \gamma _b(R)\,{\mathbf {E}}_R(\theta ), \end{aligned}$$
(6.40)

where \({\mathbf {E}}_j={\mathbf {e}}_j\otimes {\mathbf {e}}_j, {\mathbf {E}}_j^\star ={\mathbf {e}}_j^*\otimes {\mathbf {e}}_j^*\) (\(j=a,b\)) are compatible in the tubes \({\mathcal {T}}_a\) and \({\mathcal {T}}_b\), respectively, that is, the fields \((\gamma _{\parallel j},\gamma _{\perp j},\gamma _j) (j=a,b)\) have the representation form discussed in Sect. 3 and are fully represented in terms of the parameters \({\bar{\gamma }}_\parallel \) and \({\bar{\gamma }}_\perp \) which take the values \({\bar{\gamma }}_{\parallel a}\) and \({\bar{\gamma }}_{\perp a}\) for the tube \({\mathcal {T}}_a\) and the values \({\bar{\gamma }}_{\parallel b}\) and \({\bar{\gamma }}_{\perp b}\) for the tube \({\mathcal {T}}_b\).

In general, a free choice of the six parameters \(({\bar{\gamma }}_{\parallel j},{\bar{\gamma }}_{\perp j},\alpha _j)\) for \(j=a,b\) would produce a compatible growth if the two tubes were not glued to, each other. In a composite structure, compatibility would be guaranteed by the choice

$$\begin{aligned} \alpha _a=\alpha _b,\quad \quad {\bar{\gamma }}_{\parallel b}=\gamma _{\parallel a}(R_m),\quad \quad {\bar{\gamma }}_{\perp b}=\gamma _{\perp a}(R_m), \end{aligned}$$
(6.41)

which leaves free only three parameters over six. When fibers orientation and growth fields are not continuous at the interface between \({\mathcal {T}}_a\) and \({\mathcal {T}}_b\), morphing is accompanied by elastic energy storage. The deprivation of compatibility can be controlled by releasing one by one the above conditions, as we’ll show in the next Sections by a few case studies.

In all the studies, we fixed the geometrical and material parameters as indicated in Table 1.

The balance equation (5.33) has been solved with the finite element method, by implementing the model equations of Sect. 5 into the software COMSOL Multiphysics. We used a tetrahedral mesh with \(\sim \,200\) k elements, having an average mesh size h=0.08 of the tube thickness, for a total of \(\sim 1.1\) M degrees of freedom; we adopted a mixed L2-P1 formulation, using second-order Lagrange shape functions for the displacement and linear ones for the pressure; the problem has been solved by the MUMPS direct method.

Table 1 Geometrical and material parameters of the layered tubes
Full size table

6.1 The compatible growth patterns

The first case studies correspond to a compatible growth pattern produced by an appropriate choice of the parameters \(({\bar{\gamma }}_{\parallel a},{\bar{\gamma }}_{\perp a},\alpha _a)\) and \(({\bar{\gamma }}_{\parallel b},{\bar{\gamma }}_{\perp b},\alpha _b)\) which satisfy all the three conditions (6.41). In this case, the bilayer tube behaves as a single tube: it twists, elongates, and inflates without any elastic energy expenditure with the torsion \(\tau \) and the elongation \(\varepsilon \) taking the values (3.15.1,2) with \({\bar{\gamma }}_\parallel ={\bar{\gamma }}_{\parallel a}\) and \({\bar{\gamma }}_\perp ={\bar{\gamma }}_{\perp a}\).

Fig. 6
figure 6

Elastic solutions corresponding to compatible growth patterns with \(\alpha =0\) and \({\bar{\gamma }}_{\parallel a}=1.2\) (left) and \(\alpha =\pi /2\) and \({\bar{\gamma }}_{\perp a}=1.6\) (right). The grey cartoon represents the reference tube. Fibers have been red-highlighted in \({\mathcal {T}}_a\) and blue-highlighted in \({\mathcal {T}}_b\). The elastic energy is everywhere null (green corresponds to 0 elastic energy); for \(\alpha =0\), growth produces a pure dilation, whereas for \(\alpha =\pi /2\) both the extension and the radial contraction are visible by the red arrows which correspond to the displacements at the top of the tube (color figure online)

Full size image

Firstly, we set \(\alpha _a=\alpha _b=0\), that is, fibers are circumferential, longitudinal, and radial, and \({\bar{\gamma }}_{\parallel j}\) and \({\bar{\gamma }}_{\perp j}\) (\(j=a,b\)) represent the circumferential and the longitudinal growth at \(R=R_\mathrm{i}\) (\(j=a\)) and at \(R=R_m\) (\(j=b\)). In this case, a compatible growth pattern for the two tubes has the following representation form [see Eqs. (3.15.1,2)–(3.18)]:

$$\begin{aligned} \gamma _{\parallel }(R)={\bar{\gamma }}_{\parallel }\;(1+(1-a^2)(R/R_\mathrm{i}-1))^{-1/2}, \end{aligned}$$
(6.42)

whereas

$$\begin{aligned} r(R)=R\gamma _{\parallel }(R)\quad \text {and}\quad \gamma (R)=r'(R). \end{aligned}$$
(6.43)

Moreover, it also holds \(\gamma _{\perp }(R)={\bar{\gamma }}_{\perp }\), \(\varepsilon ={\bar{\gamma }}_{\perp }\) and \(\tau =0\).

We numerically solve the elastic problem corresponding to

$$\begin{aligned} {\bar{\gamma }}_{\perp a}={\bar{\gamma }}_{\perp b}=1,\quad {\bar{\gamma }}_{\parallel a}\ge 1,\quad {\bar{\gamma }}_{\parallel b} = \gamma _{\parallel a}(R_m), \end{aligned}$$
(6.44)

by the numerical implementation in the finite element code. As expected, the morphing corresponds to a pure dilation under zero torsion and extension, whereas we found zero stresses and zero elastic energy everywhere. Figure  6 (left panel) shows the deformed (green) tube corresponding to \({\bar{\gamma }}_{\parallel a}=1.2\). The proximity between the reference (gray) tube and the green one allows to appreciate the large deformations induced by growth. Red arrows correspond to the radial displacement at the top end of the tube under the chosen compatible growth pattern, and the color code corresponds to the elastic energy which is everywhere null.

Figure  6 (right panel) shows the solution corresponding to the choice \(\alpha _a=\alpha _b=\pi /2\); in this case, growth produces extension combined with radial contraction of the tube which are both visible from the comparison between the gray and the green tube.

One more interesting case study corresponds to the choice \(\alpha _a=\alpha _b= \pm \pi /4\). The compatible surface growth pattern does not depend on the sign of the fiber angle \(\alpha \) as Eqs. (3.15.1,2)–(3.18) show, and is the same in the two cases. Also the extension \(\varepsilon \), which is an even function of \(\alpha \), is the same, whereas the torsion \(\tau \) takes opposite signs in the two cases. We numerically solve the elastic problem corresponding to

$$\begin{aligned} {\bar{\gamma }}_{\perp a}={\bar{\gamma }}_{\perp b}=1,\quad {\bar{\gamma }}_{\parallel a}\ge 1,\quad {\bar{\gamma }}_{\parallel b} = \gamma _{\parallel a}(R_m). \end{aligned}$$
(6.45)

The deformed configuration of the tube for \({\bar{\gamma }}_{\parallel a}=1.6\) is shown in Fig. 7 (left) for \(\alpha _a=\alpha _b= -\pi /4\). The right panel of the same figure shows how torsion \(\tau \) and extension/shortening change for \({\bar{\gamma }}_{\parallel a}\) taking values from 1 to 1.6. The blue line represents \(\varepsilon -1\) and shows the extension of the tube for growing values of \({\bar{\gamma }}_{\parallel a}\) (blue squares); the red line represents the torsion \(\tau \) (red circles) which is negative, that is, clockwise. At \({\bar{\gamma }}_{\parallel a}=1.6\), we read on the vertical axis that \(\varepsilon -1=0.2\), that is, the final length of the tube is 1.2 times the original length. Likewise, we read \(\tau =-0.45\) which corresponds to a clockwise rotation which changes along the length of the tube and is equal to \(-0.45 z=-0.45\varepsilon Z\). Putting together the data, we conclude that the end of a tube of length L rotates of an angle equal to \(-0.45\cdot 1.2\cdot L\).

Fig. 7
figure 7

Elastic solution corresponding to compatible growth patterns with \({\bar{\gamma }}_\parallel = 1.6\) and \(\alpha _a=\alpha _b=-\pi /4\); the elastic energy is everywhere null, and torsion \({\bar{\gamma }}_{\parallel a}=1.6\) is clockwise (left). Corresponding axial elongation (blue square line) and torsion (red circle line) for \({\bar{\gamma }}_{\parallel a}\in (1,1.6)\) (right) (color figure online)

Full size image

The specular situation corresponding to \(\alpha _a=\alpha _b= \pi /4\) shows analogous patterns even if, in that case, torsion is positive and rotation counterclockwise.

6.2 A localized deprivation of compatibility

Our challenge is controlling the deprivation of compatibility and localizing the elastic energy storage by introducing a small perturbation in the compatible growth field above studied, that is, by relaxing just one of the three conditions (6.41). The choice we do and whose outcome we show in the following correspond to assuming \(\alpha _a\not =\alpha _b\).

Actually, our choice as well as our studies on compatibility issues have been inspired by heart mechanics. Specifically, looking at the mechanics of the left ventricle, which we have been studying for ten years [4, 10, 11], it is well known that it is driven by blood pressure and the contraction of obliquely oriented myocardial fibers which induce a torsion of the organ about its long axis. Muscle contraction produces a sort of spring-like effect which extends, dilates, and rotates the ventricle while storing elastic energy, whereas the release of that elastic energy determines the recovery of the initial state [3, 4].

So, let us choose

$$\begin{aligned} \alpha _a=\frac{\pi }{4}\quad \text {and}\quad \alpha _b=-\frac{\pi }{4}, \end{aligned}$$
(6.46)

and, to confirm our heart-inspiration, denote \({\mathcal {T}}_a\) as the endotube and \({\mathcal {T}}_b\) as the epitube. The different orientation of the fibers can be appreciated by looking at the red (endo) and blue (epi) highlighted fibers in the left panel of Fig. 8.

Fig. 8
figure 8

Elastic solution corresponding to incompatible growth patterns with \({\bar{\gamma }}_\parallel = 1.5\) and \(\alpha _a=-\alpha _b=\pi /4\); the elastic energy is almost everywhere null but a small area around the interface; torsion is dominated by epifibers (left). Dimensionless elastic energy density along the dimensionless radius; dashed vertical line shows the interface position (right)

Full size image

Figure 8 shows different aspects of the solution, corresponding at \({\bar{\gamma }}_\parallel = 1.5\). Firstly, the left panel shows that torsion is clockwise, as in the left heart, due to the dominant effect of epifibers. However, the contrast offered by the endotube which would like to rotate counterclockwise determines an energy concentration around the interface between the two tubes which has been highlighted in the Figure. This energy storage aspect has been highlighted in the right panel of Fig. 8 where the dimensionless elastic energy density \(\varphi _o/\mu \) along the dimensionless radius has been represented; the red and blue lines correspond to the energy storage in the endotube and in the epitube, respectively. Interestingly, other than showing the peak of energy storage around the interface, it also shows an energy jump at the interface which holds even if we neglected any reinforcing contributions of the fibers to the passive material response of the tube. Indeed, the elastic energy depends also on the active material response by the elastic strain \({\mathbf {C}}_\mathrm{e}\) which is different in the two tubes, as fibers orientation is different. In this sense, the energy jump reveals the discontinuity in the active material response.

It sets also further issues, whose consideration is beyond the scope of the present work, which concern the possibility to reduce the energy peak and the energy jump by introducing different passive material response for the two tubes and/or further pills of compatibility deprivation.

7 Conclusions and future directions

The research question we set in the paper concerned the relationships between anisotropic growth, morphings, and storage of elastic energy in fibered soft tubes. We discussed the topic for compatible growth fields whose representation form in anisotropic fibered tubes has been explicitly characterized in [9]. Then, we investigated the effects of a deprivation of compatibility and the chances to control it to produce morphings with localized energy storage.

To do it, we glued together two tubes suffering a compatible growth to produce a composite tube which can admit a defect of compatibility at the interface between the two layers. The solution of the corresponding elastic problem showed that we produce a concentration of elastic energy at the interface between the two tubes.

The study has multiple scopes. On the one hand, it may drive the characterization of concentrated deprivation of compatibility due to growth patterns and explain morphing behaviors which can be found in Nature [8] and reproduced in synthetic structures. On the other hand, it may offer food for thought in additive manufacturing, whereas soft structures can be built layer after layer: an appropriate fiber structure of the layers can drive a controlled morphing of the structure under surface growth and small energy storage.

Moreover, after the identification of the compatible growth paths for a layered tube which allow to localize the major part of the energy stored during the growth at the interface between layers, we are asking how to drive growth in that way and to answer the question the modeling has to be set up within a dynamical context which includes the balance equations of forces and the balance equations of growth, as in [17,18,19,20].