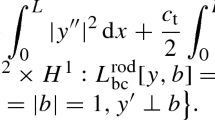Abstract
In this work, we present the mathematical formulation and the numerical implementation of a new model for initially straight, transversely isotropic rods. By adopting a configuration space that intrinsically avoids shear deformations and by systemically neglecting the energetic contribution due to torsion, the proposed model admits an unconstrained variational statement. Moreover, as the natural state of the rod is the trivial one and the mechanical properties are homogeneous on the cross section, the need for pull-back and push-forward operations in the formulation is totally circumvented. These features impose, however, some smoothness requirements on the stored energy function that need to be carefully considered when adopting general constitutive models. In addition to introducing the rod model, we propose a spatial discretization with the finite element method, and a time integration with a hybrid, implicit scheme. To illustrate the favorable features of the new model, we provide results corresponding to numerical simulations for plane and three-dimensional problems that are investigated in the static and dynamic settings. Finally, and to put the presented ideas in a suitable context, we compare solutions obtained with the new model against a rod model that allows for torsion and shear.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Rods undergoing stretching, shearing, bending and torsion have been subject of a very active research starting from the seminal contributions by Kirchhoff [25], Clebsch [10], Cosserat and Cosserat [11] and Love [30]. As the topic has a long tradition in applied mathematics and mechanics, there is already a plethora of excellent references dealing with this subject that certainly is very rich (see for instance the works by Antman [1,2,3], Simó [45], Singer and colleagues [24, 28, 46], Gorely and coworkers [20, 27, 31] and Audoly and collaborators [4, 6, 7], inter alia). Among all the models available in the literature, those rods that deform without shearing play a special role (see for instance O’Reilly [39] and/or Giusteri and Fried [18] for a deep exposure of the subject). As a consequence of this particular deformation behavior, the cross section, which is assumed to remain flat, is perpendicular to the tangent vector associated with the curve that describes the rod axis. Employing this hypothesis, we have, in the linear context, two classical models that are well known: the one by Euler and Bernoulli and the one by Rayleigh [23], where the latter does consider the inertial contribution due to the rotation of the cross section. Going further to the nonlinear realm, we have the generalization of the Rayleigh model, the so-called Kirchhoff rod that represents a point of departure for this work.
Non-sheareable rods have been deeply investigated from a theoretical point of view. However, there is a renewed interest with respect to their application in very dissimilar research areas such as the analysis of DNA molecules [5, 43, 44], motion prediction of human hair [7, 26], dynamics of cables [8, 12], mechanical analysis of Möbius bands [36], dynamics of drill strings [47], interactive simulations [40], bifurcation analysis of tethers [48], motion prediction of vortical filaments [13], stability of elastic knots [4, 24], clambering plants [32], morphoelastic rods [29, 37], stents and catheters [49], cooking-induced deformation of spaghetti [19] and others. Obtaining closed analytical solutions is in general not possible, mainly due to the complex nature of the governing equations. Therefore, in most of the cases the only way to obtain approximate solutions is through numerical methods. This fact has motivated the development of new computational approaches for elastic rods exhibiting no shear deformation [9, 21, 22, 34, 50,51,52].
Due to the non-integrable nature of vanishing shear deformations, it is well known that formulating the governing equation of this class of rods through a truly unconstrained variational statements is not possible, especially for dynamic problems. Moreover, we showed in a recent work [41] that the formulation of a nonlinear rod model relying on a unconstrained variational statement is in principle affordable, but some further simplifying hypotheses are still necessary. However, neither such a mathematical formulation nor its numerical implementation is available in the literature to the best of our knowledge. In connection with this, we describe as follows the main novelties of this work.
In the first place, we present a new structural model for initially straight, transversely isotropic rods, which disregards the energetic contribution of torsion and exhibits no shear deformation. Such a model relies on a configuration space which, by construction, completely prevents shearing and thus results in an unconstrained approach. As the natural state of the rod is the trivial one, the pull-back and push-forward operations are completely circumvented, and thus, no introduction of an exogenous triad, which would require a non-local constrained approach, is necessary. Discarding the torsional contribution to the potential and kinetic energies avoids the inclusion of further non-integrable constraints such as the one required to enforce the non-twisting condition [15]. Moreover, as a direct consequence of the adopted kinematic and energetic settings, this new model fully admits a variational statement, keeps the problem in its minimal irreducible representation, and is in fact an specialization of the static and dynamic variational principles for nonlinear Kirchhoff rods previously developed by the authors [41]. The proposed model can be also considered as the non-shearable counterpart of the torsion-free beam model presented in [42]. This contribution turns to be a main innovation of the current work.
In the second place, we present an strategy for the numerical implementation of the new model proposed. To this end, we consider for the spacial discretization a finite element approach that relies on a \(C^1\)-class approximation. It is worthwhile to mention that through this approximation, the frame-invariance and path-independence of the discrete model are identically retained. For the time discretization, we consider a hybrid combination of the midpoint and trapezoidal rules. Such an implicit hybrid combination, while being very simple, exhibits exact preservation of the linear and angular momenta as well as an excellent energy behavior and thus is good and robust enough for the purposes of the current work. The resulting discrete model can then be completely described by primal variables (there is no necessity of dual variables such as Lagrange multipliers) and thus results to be very robust with respect to conditioning issues typically exhibited by mixed primal-dual formulations. We use then the proposed numerical implementation of the new model to investigate static and dynamic, planar and three-dimensional cases with which we show its very promising features. This means that the proposed model has low computational cost, is robust and turns out to be suitable for real-time applications. In addition, and to put our ideas into a adequate context, we include results obtained with a nonlinear beam model that allows for shear and torsion. These examples will show numerically that the solution of that nonlinear beam model converges to the one of the newly proposed model for increasing shear stiffness. This contribution represents another contribution of the current work.
The remainder of this manuscript is as follows. Section 2 presents the mathematical formulation of the new model. This includes the kinematic description and the derivation of suitable deformation measures. Then, it introduces the potential and kinetic energies and, after applying a variational argument, concludes with the weak and strong forms of the governing equations. Section 3 deals with the discretization of the model in space and time. Section 4 presents numerical investigations of increasing complexity that show the promising features of the proposed model. To close the work, Sect. 5 presents concluding remarks.
2 Model description and formulation
2.1 Admissible motions
To derive the model’s governing equations of a rod that is transversely isotropic, disregards the energetic contributions of torsion, and does not exhibit shear deformation, we first need to introduce a suitable geometric setting. Instead of using a constrained theory, we select a configuration space that intrinsically disables shear deformation. In this way, and in contrast to other Kirchhoff rod theories, we will completely avoid the formulation of a primal-dual problem that requires Lagrange multipliers.
Let \(\{\varvec{E}_i\}_{i=1}^3\) denote the canonical Cartesian basis of \(\mathbb {R}^3\) and define \(\varvec{N}\equiv \varvec{E}_1\), \(\varvec{B}\equiv \varvec{E}_2\), \(\varvec{D}\equiv \varvec{E}_3\). With this notation, we define the configuration manifold of torsion-free, transversely isotropic Kirchhoff rods to be the set
where S is the length of the rod and we have selected clamped boundary conditions at \(s = 0\) for concreteness. A motion of the rod is a curve of configurations parameterized by time and we write \(\varvec{\varphi }_t(s)=\varvec{\varphi }(s,t)\) for \(s\in [0,S]\) and \(t\in [0,T]\). Moreover, we reduce the class of admissible motions to the ones that have as initial configuration
The constant vector \(\varvec{D}\) belongs to the unit sphere \(S^2:=\left\{ \varvec{d}\in \mathbb {R}^3\; |\; \varvec{d}\cdot \varvec{d}= 1\right\} \), and thus, it is referred to as a director. In addition, any configuration \(\varvec{\varphi }\in {\mathscr {Q}}\) defines a curve \(s\mapsto \varvec{\varphi }(s)\) in \({\mathbb {R}}^3\) with Frenet–Serret triad
that satisfy \(\varvec{b}= \varvec{d}\times \varvec{n}\). We note that the triad is ill-defined in those points where \(|\varvec{\varphi }''|=0\).
Remark 1
In all the regular points of a configuration, we can define the map
with \(\varvec{\chi }:\mathbb {R}^3\rightarrow \mathbb {R}^3\) and inverse
that satisfies \(\det (\varvec{\chi })=1\) and thus being an element of the Lie group SO(3). This rotation can be employed to pull-back and push-forward vectors and tensors defined at regular points of the current configuration to the reference one, and vice versa. Existing rod models in the literature employ instead a rotation without drill [8, 9, 21, 22, 33,34,35]. However, such an approach introduces a fictitious torsion and can only be applied in an incremental form; for more details see [41]. To avoid all the aforementioned problems, we argue that a rod model based on the configuration space (1) must completely circumvent the use of this kind of mappings between frames, showing in the remainder of this work that this is indeed possible.
2.2 Strain measures, their variations and the linearized strain operator
Next, we investigate all possible ways in which a rod of the type considered before can deform. The deformation modes that need to be properly captured are those related to the elongation and curvature’s change of the rod. An important fact to be noted is that due to the transversal isotropy, the strain measures are required to be independent of the orientation of the rod’s cross section. This suggests indeed that it is possible to find scalar measures for the axial and bending deformations of the rod.
Two spatial strain measures are introduced first. They are defined as
and gauge the axial and bending deformations, respectively. For future reference, let us note that the derivative of the director can also be related to the covariant derivative on the sphere
The bending deformation can be given the following geometric interpretation: given the curve \(s\mapsto \varvec{d}(s)\) on an oriented surface, here \(S^2\), the curvature can be split into a normal component and a tangent one. Since \(\varvec{d}(s)\) lives in \(S^2\), the normal component has always unit modulus, i.e., the intrinsic curvature of the sphere. The tangent component is precisely \(\varvec{\kappa }\), as defined in Eq. (6), and measures how \(\varvec{d}\) fails to be geodesic [38].
Next, we strive to obtain the equations of motion of the rod through a variational argument. Prior to this calculation, we need the expressions for the strain measure variations. These are summarized in the following lemma.
Lemma 1
Let \(\delta \varvec{\varphi }\) be an admissible variation of the rod configuration. Then, the variations of the two strain measures are:
with
being the symmetrized outer product of two vectors \(\varvec{a},\varvec{b}\in {\mathbb {R}}^3\).
Proof
The proof is based on a systematic application of the rules of differentiation. Details are hence omitted.
\(\square \)
It is convenient at this stage to introduce the linearized strain operator \(\mathscr {B}(\varvec{\varphi }',\varvec{\varphi }'')\) such that
and defined as
where we introduced the differential operators
2.3 Stored energy and stress measures
Next, we investigate the hyperelastic models for initially straight, torsion-free, non-shearable, transversely isotropic rods and identify the stress measures that are work-conjugate to the strain measures previously introduced.
To this end, we assume the existence of an objective stored energy density function, \({\tilde{\mathscr {U}}}:{\mathbb {R}}^3\times {\mathbb {R}}^3\rightarrow {\mathbb {R}}\) that is taken to be identical for all cross sections, for simplicity. The objectivity conditions requires that for every pair of strains \(\varvec{\epsilon },\varvec{\kappa }\) and every \(\varvec{Q}\in SO(3)\)
A standard argument employed to guarantee the objectivity of this energy function is to introduce two other stored energy functions \(\bar{{\mathscr {U}}}_a,\bar{{\mathscr {U}}}_b:{\mathbb {R}}^+\cup \{0\}\rightarrow {\mathbb {R}}\) and postulate
These considerations facilitate the formulation of stored energy functions because all that is required is to postulate two scalar functions defined in the non-negative real numbers. These potentials cannot be arbitrary either. In order to guarantee the existence of solutions, elastic problems impose certain coerciveness conditions on their stored energy functions. Without claiming that it is enough to ensure existence in the finite strain range, we adopt the following quadratic stored energy functions borrowed from the small-strain rod theories
where E is the Young modulus of the rod material, A is cross section area and I the inertia with respect to an axis contained in the cross section.
With these definitions at hand, we can define the potential energy functional of the rod as
Hence, its variation follows systematically as
where the stress measures, energy-conjugate to \(\varvec{\epsilon }\) and \(\varvec{\kappa }\),
naturally arise. The stress measure \(\varvec{n}\) can be identified with the axial force, parallel to \(\varvec{d}\) by definition, whereas the bending moment \(\varvec{m}\) is contained in the cross section of the rod and has the direction of the bending strain. In fact, for the stored energy function (14) it follows that the stress measures are
extending the classical results for the axial force and bending moment in a rod. In general, we emphasize that the stored energy functions \(\bar{{\mathscr {U}}}_a\) and \(\bar{{\mathscr {U}}}_b\) must be such that
In fact, this condition can be used to define the axial and bending stress measures to be always identically zero when the strains \(\varvec{\epsilon }\) and \(\varvec{\kappa }\) vanish, respectively, as automatically done by the definitions in Eq. (19).
2.4 Kinetic energy and its variation
Next, we define a kinetic energy density of the form
where \(A_{\varrho }\) is the mass per unit length and \(I_{\varrho }\) is the inertia density around any axis contained in the rod section (by the assumption of isotropy, all rotational inertias are identical). Based on the previous relation, the mass operator \(\mathscr {M}(\varvec{\varphi }')\) must be
On this basis, we can define the kinetic energy functional as
and its systematic variation is as follows:
where \({\hat{\nabla }}_{{\dot{\varvec{\varphi }}}}{\dot{\varvec{\varphi }}}\) denotes the field covariant derivative and a, b, and c are indices taking the values 1,2, and 3, for which the convention of repeated indices applies. The term \(\mathscr {M}(\varvec{\varphi }'){\hat{\nabla }}_{{\dot{\varvec{\varphi }}}}{\dot{\varvec{\varphi }}}\) contains not only the contribution \(\mathscr {M}(\varvec{\varphi }')\ddot{\varvec{\varphi }}\), but also the contribution \({\hat{\Gamma }}(\mathscr {M}(\varvec{\varphi }'))({\dot{\varvec{\varphi }}},{\dot{\varvec{\varphi }}})\). The corresponding connection coefficients are uniquely defined by
such that \({\hat{\nabla }}_{{\dot{\varvec{\varphi }}}} \mathscr {M}(\varvec{\varphi }')= \varvec{0 }\).
Equation (24) follows from the fact that
for vanishing \(\delta \varvec{\varphi }\) at \(t=0\) and \(t=T\). In addition, we have that
and
which are required to compute \({\hat{\Gamma }}(\mathscr {M}(\varvec{\varphi }'))({\dot{\varvec{\varphi }}},{\dot{\varvec{\varphi }}})\).
3 Variational derivation of the equations of motion
Hamilton’s principle of least action states that the governing equations of a mechanical system are the Euler–Lagrange equations of the action functional
whose solutions \(\varvec{\varphi }\in {\mathscr {Q}}\) render the action stationarity. The main result is summarized next:
Theorem 1
The (weak) Euler–Lagrange equations corresponding to the functional (29) are:
Proof
The proof of the theorem follows from the systematic calculation of \(\delta \mathscr {S}\), namely,
with
for \(\delta \varvec{\varphi }\) satisfying \(\delta \varvec{\varphi }(s,0)=\delta \varvec{\varphi }(s,T)=\varvec{0 }\). \(\square \)
From the variational equation (30), we can recover the strong form of the equations of motion of the Kirchhoff rod as presented next.
Theorem 2
The strong form of the equations of motion is
with the stress measures \(\varvec{n}\) and \(\varvec{m}\) introduced above and the momenta \(\varvec{p}\) and \(\varvec{\pi }\) defined as \(A_{\varrho }{\dot{\varvec{\varphi }}}\) and \(I_{\varrho }{\dot{\varvec{d}}}\), respectively. Moreover, for the clamped-free case, we have the concomitant boundary conditions
and the initial conditions
Proof
The proof of the theorem can be found in Romero and Gebhardt [41], and thus, we omit further details. \(\square \)
4 Discretization
The initial boundary value problem defined by Eqs. (33)–(35) is difficult to solve in general and often one has to resort to numerical methods to obtain approximations to the solution. In order to obtain the latter, the governing equations of the rod have to be discretized both in space and time. In this section, we provide the details of both discretizations, starting from a finite element spatial projection and completing the process with a mixed midpoint/trapezoidal time integration.
4.1 Spatial discretization
We start by defining a finite element spatial semi-discretization. For that, consider an approximation of the rod configuration to be of the form
where \(\nu \) is the number of nodes, \(N_a^x,N_a^d,{N}_a:[0,S]\rightarrow {\mathbb {R}}\) are \(C^1\) shape functions, \(\varvec{x}_a,\varvec{d}_a,\varvec{q}_a:[0,T]\rightarrow {\mathbb {R}}^3,S^2, \mathbb {R}^3\times S^2\) are the nodal positions, directors, and generalized coordinates, functions that must be twice differentiable in time. For convenience, we introduce the matrix \(\varvec{N}\) of shape functions and the global nodal vector \(\varvec{q}(t)\) such that
The nodal values of the director determine the discrete director field at these points. At interior points of the elements, this field can be calculated with the expression
Using the interpolations (37) and (38), the weak form (30) can be approximated as indicated next:
Lemma 2
The governing equations of motion, semi-discretized in space, are:
with the concomitant initial conditions \(\varvec{q}(0)=\varvec{q}_0\) and \({\dot{\varvec{q}}}(0)={\dot{\varvec{q}}}_0\).
Proof
Using the Galerkin approximation (36) of the configuration, the inertial contribution of Eq. (30) can be rewritten as
with
The right-hand side of (40) includes not only the contribution \(\varvec{M}(\varvec{q})\ddot{\varvec{q}}\) that corresponds to the first term of (41), but also the contribution \(\varvec{\Gamma }(\varvec{q})({\dot{\varvec{q}}},{\dot{\varvec{q}}})\) that corresponds to the second and third term. The corresponding connection coefficients are uniquely defined by
such that \(\nabla _{a}(M_{bc}) = \varvec{0 }\). For the term coming from the potential energy, we have, using again Galerkin’s approximation (36), that
with
Collecting the last two results, we obtain
Since, according to Eq. (30), this expression must vanish for arbitrary configurations, the integral on the right-hand side must itself be zero and the proof follows. \(\square \)
To complete the spatial semidiscretization, it remains to select an appropriate shape function so as to define the finite element space. A standard choice for \(C^1\) approximation functions is based on Hermite polynomials defined on a reference domain \([-1,+1]\) that are later pushed to each point of the rod. To do that, we consider the \(\nu -1\) line elements defined by the \(\nu \) nodes. Element e has two nodes with labels \(I=e\) and \(J=e+1\). A matrix of element shape functions can be defined as follows:
where \(\xi \in [-1,+1]\), \(S_e\) is the length of element e and we have used the standard Hermite polynomials
With these interpolation functions, a map \(\varvec{\Phi }_e:[-1,+1]\rightarrow {\mathbb {R}}^3\) can be defined with the expression
with \(\varvec{x}_{0,I},\varvec{x}_{0,J}, \varvec{d}_{0,I}, \varvec{d}_{0,J}\) being the position and directors of the element nodes in the reference configuration, respectively. The map \(\varvec{\Phi }_e\) can be used to evaluate the global shape function matrix \(\varvec{N}\) or any other function defined on the reference arc-length interval [0, S]. To see that, note that the mapping \(\xi \mapsto \varvec{\Phi }_e(\xi )\) defines the reference placement of the rod and a bijective application \(\Sigma _e:[-1,+1]\rightarrow [s_{e},s_{e+1}]\), with \(s_e\) corresponding to the s coordinate of node e, as
Then, the restriction of \(\varvec{N}\) to element e can be evaluated as
Moreover, the integral of any function \(f\circ \varvec{\varphi }\) defined on [0, S] can be approximated with the integral of \(f\circ \varvec{\varphi }_h\) and then evaluated as
This kind of integrals, or rather their numerical quadrature, will be employed in Sect. 5 to evaluate the balance equation (30) once it is discretized in time.
4.2 Time integration
Next, we describe the integration algorithm adopted to compute the dynamic simulations presented in this paper. To such an end, let us consider the governing equations, which are semi-discretized in space, evaluated at time instant \(t_{n+\frac{1}{2}}\in [t_n, t_{n+1}]\), i.e.,
where for sake of completeness, we include external generalized forces, namely \(\varvec{Q}^{\text {ext}}_{n+\frac{1}{2}}\).
In a recent publication [16], we showed that the hybrid combination of the midpoint and trapezoidal rules can render robust second-order, implicit integration methods that at least exactly preserve the linear and angular momenta. Therefore, this is the approach that we are going to pursue in the following. To approximate the inertial term \(\left( \varvec{M}(\varvec{q})\nabla _{{\dot{\varvec{q}}}}{\dot{\varvec{q}}}\right) _{n+\frac{1}{2}}\), we employ an extended version of the midpoint rule, i.e.,
where the first term approximates \(\varvec{M}(\varvec{q})\ddot{\varvec{q}}+{\dot{\varvec{M}}}(\varvec{q}){\dot{\varvec{q}}}\), i.e., the time derivative of the momentum \(\varvec{M}(\varvec{q}){\dot{\varvec{q}}}\), and the second term approximates the term arising from the derivative of the kinetic energy with respect to the vector of generalized coordinates. In addition, we consider the classical approximation formulas
Meanwhile, to approximate the internal term \(\left( \varvec{B}(\varvec{q})^T\varvec{\sigma }\right) _{n+\frac{1}{2}}\), we employ the trapezoidal rule, i.e.,
Finally, collecting all pieces together, we can solve the fully discretized governing equations at time instant \(t_{n+\frac{1}{2}}\) to find the discrete state of the system at time instant \(t_{n+1}\), i.e., \(\varvec{q}_{n+1}\) and \({\dot{\varvec{q}}}_{n+1}\). The discrete state of the system at time instant \(t_n\) is known, namely \(\varvec{q}_n\) and \({\dot{\varvec{q}}}_n\) are data of the problem. Moreover, \({\dot{\varvec{q}}}_{n+1}\) is computed as \(\frac{2}{h}(\varvec{q}_{n+1}-\varvec{q}_{n})-{\dot{\varvec{q}}}_{n}\) once \(\varvec{q}_{n+1}\) has been determined through an iterative method, for instance, the exact Newton–Raphson method.
Remark 2
The extension of the integration method to include holonomic constraints, e.g., for the length preservation of nodal directors or for setting a bundle of rods in hairlock modeling among others, requires to include the constraint equation at time instant \(t_{n+1}\), \(\varvec{g}(\varvec{q}_{n+1})=\varvec{0 }\), and to add the discrete restrictions forces at time instant \(t_{n+\frac{1}{2}}\), \(\partial _{\varvec{\xi }}(\varvec{g}(\varvec{\xi }))^T\mid _{\varvec{\xi }=\varvec{q}_{n+\frac{1}{2}}}\varvec{\lambda }_{n+\frac{1}{2}}\) to the fully discretized balance equations, which completes the discrete problem statement. Specifically, in the current numerical implementation, we consider an additive update of the nodal directors as elements of \(\mathbb {R}^3\) that are constrained to preserve their unit length. Nevertheless, a multiplicative actualization in \(S^2\), without constraints, is also possible for the current work as done in [42]. The latter are two alternative implementations of the time integration, with and without constraints. We stress, however, that the model itself is formulated without any constraint.
5 Results
In this section, we present four numerical examples chosen to show the performance of the discretized rod models previously proposed. The first two examples belong to the realm of statics, whereas that the two remaining ones are dynamic simulations. In addition, and as a further reference, we also present the results obtained with a model for geometrically exact beams that includes both torsion and shear deformations, which we refer to as the TS rod. Details on this particular formulation are to be found in [14, 17]. Such a model asymptotically converges, for the case of slender beams, i.e., \(L/\sqrt{I/A} \gg 1\), with vanishing shear deformations to the Kirchhoff rod model. We note that the aim of this section is not to provide a detailed comparison between models; however, this helps to put the proposed ideas into a suitable context and to provide further insights on the properties of the new formulation developed. Such a detailed comparative analysis falls outside the present scope and thus, is not carried out.
5.1 Statics
Here, we consider an initially straight, transversely isotropic rod with a length of \(40~\mathrm {m}\) that initially lies along the direction \(\varvec{D}= (1, 0, 0)\). The cross-sectional properties are \(EA = 100~\mathrm {N}\) and \(EI = 200~\mathrm {Nm^2}\). As boundary conditions, we consider that one end is fully fixed and the other one is free to move. For estimating the shear stiffness of the TS rod, we assume \(\nu = 0.3\) and thus, \(GA = 38.5~\mathrm {N}\). The rod is uniformly discretized into 40 two-node finite elements. The node corresponding to the fully fixed end is labeled 1 and the one corresponding to the free end has label 41. Finally, for all numerical examples the loading was applied, for plotting purposes, in 55 uniformly distributed load levels and a relative error-based tolerance of \(10^{-10}\) has been set for the Newton iterations, which also applies to the examples dealing with dynamic problems.
5.1.1 Cantilever beam subject to an in-plane loading
This first example investigates the rod’s response to a single load given by \((-1.5, 0.5, 0)~\mathrm {N}\), which is applied to the node corresponding to the free end. Figure 1 shows a sequence of twelve successive deformed configurations. The results obtained with the model proposed are drawn in blue, whereas the results obtained with the TS model are plotted in red. The fully fixed end representing the clamped boundary conditions is indicated in green. The results reveal that the two-dimensional mechanical behavior of both models is, as expected, similar, but not identical. To gain further insight regarding how the solution of the TS rod model converges to the solution obtained with the proposed model as GA increases, we present Fig. 2. For higher values of GA, the deformed configuration approaches the deformed configuration computed with the new formulation. As we are already dealing with a very slender rod, the values of GA do not need to take high values to clearly demonstrate the convergent behavior. We can observe, moreover, that for small values of GA, the normal directors are not tangent to the deformed rod axis. These normal directors tend to become tangent to the deformed rod axis as GA increases. In our formulation, the directors are always unitary and tangent to the rod axis, even in the fully discrete setting. In addition, Fig. 3 shows the convergence behavior of the solution as a function of GA, which is consistent with the linear theory; see Sect. 5.1.3. To further reduce the relative error, it is necessary to employ finer meshes, but the trend is always the same and thus, this is omitted. For practical reasons nevertheless, it is also important to highlight that for a fixed mesh as GA increases, the condition number of the tangent stiffness matrix in the TS model increases, complicating the Newton–Raphson convergence.
5.1.2 Cantilever rod subject to a out-of-plane loading
This second example considers two loads given by \((-1.5, 0.5, 0)~\mathrm {N}\) and \((1.5, -0.5, 0.5)~\mathrm {N}\), applied to the node corresponding to the free end and to the central node (located at the mid span of the rod), respectively. Figure 4 shows a sequence of twelve successive deformed configurations. For sake of consistency, we follow the same color convention as in the previous example, and it will be retained in the remainder of this work. Once again, the results reveal that the convergence behavior in the three-dimensional case is as well consistent with the linear theory; see Sect. 5.1.3. As done in the previous example, we present Fig. 5 that shows how the deformed configuration obtained with the TS rod model approaches the deformed configuration computed with the proposed model for increasing values of GA. Figure 6 shows, moreover, the convergence behavior of the solution as a function of GA. These results confirm the observations made in the previous example.
5.1.3 Discussion on some key properties of the model proposed
The static setting represents a suitable framework to investigate some key properties of the model proposed and its spatial discretization with the finite element method. These include the convergence of the solution with the mesh refinement as well as the convergence of the solution of the TS rod to the solution obtained with new model. Figure 7 shows the relative energy norm for a cantilever rod subject to an out-of-plane tip moment, i.e., a pure bending case. The tip moment applied is equal to \(EI \pi / 2 L\) and in the exact solution the rod bends to a quarter of circle. To investigate the convergence behavior, we consider meshes consisting of 5, 10, 20, 40, 80 and 160 finite elements. As expected, the convergence behavior exhibited is optimal and consistent with those results reported in [34] for such a standard benchmark case.
Figures 3 and 6 show a saturation in the relative difference between the solution obtained with the current model and the one resulting from the TS rod. To elucidate this behavior, we perform a comparison in the linear setting of the Euler–Bernoulli and the Timoshenko beam models referred to as E–B and T models, correspondingly. To this end, let us consider a straight beam with geometrical and material properties \(L = 40~\mathrm {m}\) and \(EI = 200~\mathrm {Nm^2}\) to which a tip load \(p = 0.05~\mathrm {N}\) is applied. Again, the meshes considered consist of 5, 10, 20, 40, 80 and 160 finite elements. Moreover, for the T model, GA is varied in the range from \(10^{-2}\) to \(10^6~\mathrm {N}\). Figure 8 presents the results, and from it we can draw interesting observations. The first one, that is precisely what we wanted to investigate, is the saturation for moderate to large GA that is observed in the nonlinear setting. The second and expected one is that the saturation value reduces as the number of elements increases. The third one is that the curves corresponding to all discretizations are indistinguishably in the range of relatively small GA. In the log–log plot, these are proportional to \((\text {number of elements})^{-1}\) and lie practically on the same curve. The four and last observation is that the relative error shows an abruptly downwards jump for a critical value of GA, when approached from both sides. Such a critical value of GA is mesh dependent and is higher for finer discretizations. This behavior has not been observed for the nonlinear case. We have to stress, however, that the nonlinear case considers axial and bending deformations simultaneously. Thus, it could happen that the presence of the axial deformation mitigates such a phenomenon due to stress stiffening of the rod, or simply that high-order effects mask this behavior.
The first, third and fourth observations can be explained by considered the same structure modeled, this time, with a single finite element. For the E–B model, we have the following stiffness matrix, load vector and displacement solution.
Similarly, for the T model, we have the following stiffness, load vector and displacement solution:
Now, we can define the relative difference for the bending deflection in terms of the first components of both solutions as
The relative difference saturates up from moderate values of GA and whose asymptotic value is \(\frac{1}{4}\). For GA equal to \(\frac{12EI}{L^2}\), the relative difference reaches the minimum, i.e., the zero value. A log–log plot of this function for \(GA\in {\mathbb {R}}_{>0}\) shows qualitatively the same behavior observed in Fig. 8 for the multi-element cases. Therefore, we can conclude that the saturation behavior observed in the nonlinear case is fully consistent with the linear theory.
5.2 Dynamics
Here, we consider two initially straight, transversely isotropic rods of length \(10~\mathrm {m}\), initially aligned with \(\varvec{D}= (1, 0, 0)\). The chosen material properties are \(E = 2.0\!\times \!10^{11}~\mathrm {Pa}\) and \(\rho = 7900~\mathrm {kg/m}^3\). Again, we assume \(\nu = 0.3\) for the TS rod. The rod is uniformly discretized into 20 two-node finite elements. The loads that will be specified later are scaled with a load intensity function that starting at \(t = 0~\mathrm {s}\) increases linearly from zero to one, reaching the maximum at \(t = 0.5 t_\mathrm {c}~\mathrm {s}\). After that instant, it decreases linearly from one to zero, reaching zero at \(t = t_\mathrm {c}~\mathrm {s}\). For \(t > t_\mathrm {c}~\mathrm {s}\), the load intensity function is identically zero. For both examples considered, we assume \(t_\mathrm {c} = 0.5~\mathrm {s}\). To integrate the equation of motion, we employ a hybrid combination of the midpoint and trapezoidal rules. To integrate the equations of motion corresponding to the TS rod model, we employ the energy-momentum integration described in [14, 17].
5.2.1 Clamped-free rod subject to a vanishing in-plane loading
This third example investigates a rod with diameter \(0.01~\mathrm {m}\). The node corresponding to the clamped end is the first one, and the one corresponding to the free end is the last one. A single load given by \((0, 30, 0)~\mathrm {N}\) is multiplied by the load intensity function and applied to node 21. Finally, the time step considered for the simulation is \(\Delta t = 0.005~\mathrm {s}\). Figure 9 shows a motion sequence. We observe that the rod moves upward reaching a configuration with the seemly maximum deformation on the upper half plane and then returns from that first apparent extreme configuration. Then the rod moves downward reaching a configuration with the seemly maximum deformation on the lower half plane and then returns from that second apparent extreme configuration. Finally, the rod moves upward snapping from the lower to the upper half plane. At the beginning, the solutions obtained with both models are practically indistinguishable, but after some time some subtle differences become noticeable. Although the responses are not identical, they remain very close and the agreement is indeed very good. For a long-time simulation, the observed differences will become larger, and then, the responses will not match any longer.
Such a behavior is to be attributable not only to the different features of the formulations, but to the different features of the time integration schemes adopted as well. Figure 10 presents the time evolution of the potential, kinetic and total energies. In addition, we include the energies computed with the TS rod model. The latter ones are indicated in black with thinner lines, following the same styling to ensure an immediate identification. The integration method adopted for the current model is not able to identically preserve energy for the load-free system. Nevertheless, the total energy shows an acceptable behavior even provided that for \(t>10~\mathrm {s}\), some subtle differences are observed for both the potential and kinetic energies. Such differences are consistent with the observations made on the corresponding motion sequence. Finally, the kinetic and potential energies show some moderate-frequency content that is not present in the reference solution. This can be presumably attributed to the simple integration method, which is well known for lacking robustness when compared to more reliable structure-preserving integration methods. However, a detailed explanation of such a behavior requires further investigations that are outside the scope of this work.
5.2.2 Flying rod subject to vanishing out-of-plane loading
The last example considers a rod with diameter \(0.005~\mathrm {m}\). Due to the absence of any kind of support, the rod is then free to move in space. A first pair of loads given by \((-30, -30, 0)~\mathrm {N}\) and \((30, 30, 0)~\mathrm {N}\) is applied to the nodes 1 and 21, whereas a second pair given by \((0, 0, -24)~\mathrm {N}\) and \((0, 0, 24)~\mathrm {N}\) is applied to the nodes 2 and 20, respectively. As before, the loads are multiplied by the load intensity function and the time step chosen for the simulation is \(\Delta t = 0.001~\mathrm {s}\). Figure 11 shows a motion sequence. We observe that the rod deforms and rotates in space, but the central node remains always located at the position \((0, 0, 0)~\mathrm {m}\). Since the applied forces have a vanishing resultant the linear momentum is zero at all times and it is not plotted. The results of both models are in a good agreement. As in the previous case, for a long-term simulation, the observed differences will become larger and then, the responses will not match any longer. Nevertheless, this is not an unexpected behavior. Figures 12 and 13 present the time evolution of the three components of the angular momentum and the time evolution of the potential, kinetic and total energies, respectively. As before, the same quantities computed with the TS rod are presented in black with thinner lines, following the same styling. We observe, as expected, that the components of the angular momentum are exactly preserved after the loads vanish. The energy behavior is, as in the previous case, reasonably good and its value is almost constant. Although some small differences can be observed, the quality of the results is good and are, to a good extend, similar to the reference. This suggests that the proposed model is working correctly.
6 Conclusion
This article presents the mathematical formulation and the numerical implementation of a new model for initially straight, transversely isotropic rods, that disregards the energetic contribution of torsion and exhibits no shear deformation.
Since the model disregards torsion and relies on a configuration space that precludes shearing, it is an unconstrained formulation. Let us recall that, in standard rod models, the elimination of the torsional and shear deformations can only be imposed by means of non-integrable restrictions that cannot be encompassed by a standard variational framework. In contrast, the model proposed admits a variational statement, as seen in its derivation from Hamilton’s principle, and is kept in its minimal irreducible representation. This is the first novelty of the present work.
We also present an strategy for the numerical discretization of the proposed model. It relies on finite elements for the spatial discretization, and a hybrid combination of the midpoint and trapezoidal rules for the time discretization. Through several examples, including static and dynamic cases, we show that the model has promising features due to its simplicity, low computational cost, and robustness. This is the second novelty of this work.
In a few words, the article combines theoretical modeling and numerical discretization for a model that, to the authors’ knowledge, has never been discussed in the literature. The robustness and low computational cost of the numerical solution presented makes it ideally suited for real-time applications of rods, for example, in multibody dynamics, polymer simulations, hair dynamics, etc. Specific applications such as these will be tackled in future works.
References
Antman, S.S.: The theory of rods. In: Handbuch der Physik, pp. 641–703. Springer, Berlin (1972)
Antman, S.S.: Kirchhoff’s problem for nonlinearly elastic rods. Q. Appl. Math. 32, 221–240 (1974)
Antman, S.S.: Nonlinear Problems of Elasticity. Springer, New York (1995)
Audoly, B., Clauvelin, N., Neukirch, S.: Elastic knots. Phys. Rev. Lett. 99, 137 (2007)
Benham, C.J.: An elastic model of the large-scale structure of duplex DNA. Biopolymers 18, 609–623 (1979)
Bergou, M., Wardetzky, M., Robinson, S., Audoly, B., Grinspun, E.: Discrete elastic rods. ACM Trans. Graph. 27, 1–12 (2008)
Bertails, F., Audoly, B., Cani, M.P., Querleux, B., Leroy, F., Lévêque, J.L.: Super-helices for predicting the dynamics of natural hair. ACM Trans. Graph. (TOG) 25, 1180–1187 (2006)
Boyer, F., De Nayer, G., Leroyer, A., Visonneau, M.: Geometrically exact Kirchhoff beam theory: application to cable dynamics. J. Comput. Nonlinear Dyn. 6, 041004–14 (2011)
Boyer, F., Primault, D.: Finite element of slender beams in finite transformations: a geometrically exact approach. Int. J. Numer. Methods Eng. 55, 669–702 (2004)
Clebsch, A.: Theorie der Elastizität fester Körper. B.G. Teubner, Leipzig (1862)
Cosserat, E., Cosserat, F.: Théorie des corps déformables. A. Hermann et fils, Paris (1909)
Coyne, J.: Analysis of the formation and elimination of loops in twisted cable. IEEE J. Ocean. Eng. 15, 72–83 (1990)
Fukumoto, Y.: Analogy between a vortex-jet filament and the Kirchhoff elastic rod. Fluid Dyn. Res. 39, 511–520 (2007)
Gebhardt, C.G., Hofmeister, B., Hente, C., Rolfes, R.: Nonlinear dynamics of slender structures: a new object-oriented framework. Comput. Mech. 63, 219–252 (2019)
Gebhardt, C.G., Romero, I.: The rotating rigid body model based on a non-twisting frame. J. Nonlinear Sci. 30, 3199–3233 (2020)
Gebhardt, C.G., Romero, I., Rolfes, R.: A new conservative/dissipative time integration scheme for nonlinear mechanical systems. Comput. Mech. 65, 405–427 (2020)
Gebhardt, C.G., Steinbach, M.C., Rolfes, R.: Understanding the nonlinear dynamics of beam structures: a principal geodesic analysis approach. Thin-Walled Struct. 140, 357–372 (2019)
Giusteri, G.G., Fried, E.: Importance and effectiveness of representing the shapes of cosserat rods and framed curves as paths in the special euclidean algebra. J. Elast. 132, 43–65 (2018)
Goldberg, N.N., O’Reilly, O.M.: Mechanics-based model for the cooking-induced deformation of spaghetti. Phys. Rev. E 101, 013001 (2020)
Goriely, A., Nizette, M., Tabor, M.: On the dynamics of elastic strips. J. Nonlinear Sci. 11, 3–45 (2001)
Greco, L., Cuomo, M.: B-Spline interpolation of Kirchhoff–Love space rods. Comput. Methods Appl. Mech. Eng. 256, 251–269 (2013)
Greco, L., Cuomo, M.: An implicit G\(^{1 }\)multi patch B-spline interpolation for Kirchhoff–Love space rod. Comput. Methods Appl. Mech. Eng. 269, 173–197 (2014)
Han, S.M., Benaroya, H., Wei, T.: Dynamics of transversely vibrating beams using four engineering theories. J. Sound Vib. 225, 935–988 (1999)
Ivey, T.A., Singer, D.A.: Knot types, homotopies and stability of closed elastic rods. Proc. Lond. Math. Soc. 79, 429–450 (1999)
Kirchhoff, G.: Ueber das Gleichgewicht und die Bewegung eines unendlich dünnen elastischen Stabes. Journal für die reine und angewandte Mathematik 56, 285–313 (1859)
Kmoch, P., Bonanni, U., Magnenat-Thalmann, N.: Hair simulation model for real-time environments. In: Computer Graphics International Conference, pp. 5–12. ACM, Victoria, British Columbia, Canada (2009)
Lafortune, S., Goriely, A., Tabor, M.: The dynamics of stretchable rods in the inertial case. Nonlinear Dyn. 43, 173–195 (2006)
Langer, J., Singer, D.A.: Lagrangian aspects of the Kirchhoff elastic rod. SIAM Rev. 38, 605–618 (1996)
Lessinnes, T., Moulton, D.E., Goriely, A.: Morphoelastic rods part II: growing birods. J. Mech. Phys. Solids 100, 147–196 (2017)
Love, A.E.H.: A Treatise on the Mathematical Theory of Elasticity, 4th edn. Cambridge University Press, Cambridge (1927)
Majumdar, A., Goriely, A.: Static and dynamic stability results for a class of three-dimensional configurations of kirchhoff elastic rods. Phys. D Nonlinear Phenom. 253, 91–101 (2013)
McMillen, T., Goriely, A.: Tendril perversion in intrinsically curved rods. J. Nonlinear Sci. 12, 241–281 (2002)
Meier, C., Popp, A., Wall, W.A.: An objective 3D large deformation finite element formulation for geometrically exact curved Kirchhoff rods. Comput. Methods Appl. Mech. Eng. 278, 445–478 (2014)
Meier, C., Popp, A., Wall, W.A.: Geometrically exact finite element formulations for slender beams: Kirchhoff–Love theory versus Simo–Reissner theory. Arch. Comput. Methods Eng. 26, 163–243 (2017)
Meier, C., Wall, W.A., Popp, A.: A unified approach for beam-to-beam contact. Comput. Methods Appl. Mech. Eng. 315, 972–1010 (2017)
Moore, A., Healey, T.: Computation of elastic equilibria of complete Möbius bands and their stability. Math. Mech. Solids 1–29 (2018) (in press)
Moulton, D., Lessinnes, T., Goriely, A.: Morphoelastic rods. Part I: a single growing elastic rod. J. Mech. Phys. Solids 61, 398–427 (2013)
O’Neil, B.: Elementary Differential Geometry, 2nd edn. Academic Press, New York (2006)
O’Reilly, O.M.: Kirchhoff’s rod theory. In: Modeling Nonlinear Problems in the Mechanics of Strings and Rods, pp. 187–268. Springer (2017)
Pai, D.K.: STRANDS: interactive simulation of thin solids using Cosserat models. Comput. Graph. Forum 21, 347–352 (2002)
Romero, I., Gebhardt, C.G.: Variational principles for nonlinear kirchhoff rods. Acta Mech. 231, 625–647 (2020)
Romero, I., Urrecha, M., Cyron, C.: A torsion-free non-linear beam model. Int. J. Non-Linear Mech. 58, 1–10 (2014)
Schlick, T.: Modeling superhelical DNA: recent analytical and dynamic approaches. Curr. Opin. Struct. Biol. 5, 245–262 (1995)
Shi, Y., Hearst, J.E.: The Kirchhoff elastic rod, the nonlinear Schrödinger equation, and DNA supercoiling. J. Chem. Phys. 101, 5186–5200 (1994)
Simo, J.C.: A finite strain beam formulation. Part I. The three-dimensional dynamic problem. Comput. Methods Appl. Mech. Eng. 49, 55–70 (1985)
Singer, D.A.: Lectures on elastic curves and rods. AIP Conf. Proc. 1002, 3–32 (2008)
Tucker, W.R., Wang, C.: An integrated model for drill-string dynamics. J. Sound Vib. 224, 123–165 (1999)
Valverde, J., Escalona, J.L., Domínguez, J., Champneys, A.R.: Stability and bifurcation analysis of a spinning space tether. J. Nonlinear Sci. 16, 507–542 (2006)
Wang, Z., Fratarcangeli, M., Ruimi, A., Srinivasa, A.R.: Real time simulation of inextensible surgical thread using a Kirchhoff rod model with force output for haptic feedback applications. Int. J. Solids Struct. 113–114, 192–208 (2017)
Weiss, H.: Dynamics of geometrically nonlinear rods: I. Nonlinear Dyn. 30, 357–381 (2002)
Weiss, H.: Dynamics of geometrically nonlinear rods: II. Numerical methods and computational examples. Nonlinear Dyn. 30, 383–415 (2002)
Zhao, Z., Ren, G.: A quaternion-based formulation of Euler–Bernoulli beam without singularity. Nonlinear Dyn. 67, 1825–1835 (2012)
Funding
Open access funding provided by University of Bergen (incl Haukeland University Hospital).
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
We declare that we have no conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Gebhardt, C.G., Romero, I. On a nonlinear rod exhibiting only axial and bending deformations: mathematical modeling and numerical implementation. Acta Mech 232, 3825–3847 (2021). https://doi.org/10.1007/s00707-021-03038-w
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00707-021-03038-w