Abstract
We derive the balance equations for a double poroelastic material which comprises a matrix with embedded subphases. We assume that the distance between the subphases (the local scale) is much smaller than the size of the domain (the global scale). We assume that at the local scale both the matrix and subphases can be described by Biot’s anisotropic, heterogeneous, compressible poroelasticity (i.e. the porescale is already smoothed out). We then decompose the spatial variations by means of the two-scale homogenization method to upscale the interaction between the poroelastic phases at the local scale. This way, we derive the novel global scale model which is formally of poroelastic-type. The global scale coefficients account for the complexity of the given microstructure and heterogeneities. These effective poroelastic moduli are to be computed by solving appropriate differential periodic cell problems. The model coefficients possess properties that, once proved, allow us to determine that the model is both formally and substantially of poroelastic-type. The properties we prove are a) the existence of a tensor which plays the role of the classical Biot’s tensor of coefficients via a suitable analytical identity and b) the global scale scalar coefficient \(\bar{\mathcal {M}}\) is positive which then qualifies as the global Biot’s modulus for the double poroelastic material.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The effective mechanical behaviour of a porous elastic material with fluid filled pores can be described by the Theory of Poroelasticity, which was developed in [5,6,7,8]. The formulation is applicable to a wide range of physical scenarios where interactions take place between the deformable solid and the fluid on the porescale. Some important applications where this modelling approach has been used include the bones (see [15] and [48]), artificial constructs that are used for regenerative therapies and biomaterials (see [11, 24]), the interstitial matrix of biological tissues (both healthy and tumorous, see [9, 19]) and soil and porous rocks [25, 47].
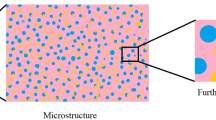
The physical systems that we model here are generally multiscale in nature. Multiscale modelling has been explored in a variety of physical settings, for example, it has been applied to investigate the elastic properties of bones by [21]. A hierarchical multiscale approach has also been taken to investigate the poroelastic role of water in the cell walls of softwood [3]. Within this work we will focus specifically on multiscale deformable porous media, in particular we consider materials which have three different length scales. These materials have a porous structure and the interactions that occur between the fluid and the solid take place on a scale (the porescale), which is much smaller than the size of the whole material (the global scale). However, a hierarchical porous medium is in general also characterized by intermediate length scales. For example, it is possible to identify a local scale related to poroelastic heterogeneities (see Fig. 1) and it is this scale and the global scale that are focused on here. In this work, we are not addressing a full three-scale modelling approach, see, e.g. [41] for an example related to elastic composites. We refer to the underlying porescale microstructure as the equations used here are those that would arise from upscaling of the porescale fluid–structure interaction between the fluid and solid phases, see [10, 38]. These equations are Biot’s anisotropic, heterogeneous, compressible equations for poroelasticity. This is the most general formulation and is not usually taken into account, as most of the works in the literature typically refer to isotropic, and also incompressible poroelasticity.
The governing equations for materials at the global scale can be obtained by upscaling the balance equations that describe the material on the local scale.
This process can be carried out by a variety of homogenization techniques, which are summarized for example in [17, 23].
Here, we focus on a specific upscaling method, namely the asymptotic homogenization technique [2, 22, 28, 36]. This technique exploits the pronounced difference between the local and global scales to enable spatial variations decoupling. It is a key feature of this technique that the relevant fields from the local scale problem are to be expressed as power series of the ratio between the two different scales. The resulting balance equations represent the poro-mechanics of the whole material on the global length scale. As a result of using this technique the coefficients of the global scale model encode information about the microstructure of the material and they are to be computed by solving differential problems on the local scale. The asymptotic homogenization technique has been also applied to various poroelastic physical systems (see for example [10, 27]) where Biot’s equations of poroelasticity are obtained. The theory has been extended to consider appositional growth between the fluid and solid phases [33], vascularized poroelastic materials [37] and poroelastic composites [29].
In this work we aim to determine the effective behaviour of a material which has the underlying microstructure comprising both a poroelastic matrix and a number of embedded poroelastic subphases (i.e. fibres, inclusions and strata) which are interacting with each other. We assume that the various phases are, in general, anisotropic and heterogeneous. The main motivation behind this work is to study the behaviour of materials which comprise multiple poroelastic phases which are interacting on the local scale. This structure has been considered by [31] where the authors study a poroelastic extracellular matrix in which poroelastic cells are embedded. They develop a set of equations describing such a material and use these equations to study the consolidation of a one-dimensional sample of tissue. The interstitial matrix of biological tissues, which comprises many poroelastic subphases such as cells and different types of collagen fibres embedded in the matrix [26], is an example of this type of structure. In [12, 43], the authors use the asymptotic homogenization technique to provide an analysis of a system comprising a poroelastic matrix with an embedded subphase. In these cases the simplification that the subphase is purely elastic is made, which provides a model with different applications to which we wish to consider here.
In the present work we generalize [12, 43] by using the asymptotic homogenization technique to upscale the interaction between the matrix and the subphases, where each phase is described by Biot’s anisotropic, heterogeneous, compressible poroelasticity. We assume the scale at which the various subphases are clearly resolved, denoted by the local scale, is much smaller than the size of the whole domain, denoted global scale. The upscaling can then be carried out, accounting for continuity of stresses, displacements, pressures and fluxes across the interface between the phases. The resulting global scale model is of Biot-type. The coefficients of the model encode the properties of the microstructure and are to be computed by solving differential problems on a finite subset of the domain. The model recovers the works [43] and [12] under a set of consistent simplifying assumptions.
The paper is organized as follows. In Sect. 2 we consider the quasi-static, multiphase problem consisting of the governing equations for both the poroelastic matrix and the poroelastic subphases and the appropriate interface conditions. The governing equations for the matrix and the subphases are the equations of Biot’s anisotropic, heterogeneous, compressible poroelasticity. In Sect. 3 we introduce the two-scale asymptotic homogenization method. In Sect. 4 we enforce the length scale separation that occurs between, the inter-subphase distance (the local scale) and the overall size of the domain (the global scale) to apply the asymptotic homogenization technique to upscale the problem to a system of global scale PDEs. In Sect. 5 we provide a detailed description of the effective coefficients of our novel global scale model. We then prove that our novel global scale model is both formally and substantially of poroelastic type by proving a) the existence of a global scale Biot’s tensor of coefficients and b) that the effective Biot’s Modulus of the system is positive. Section 6 concludes our work by discussing limitations of the model and by providing further perspectives. We also provide an appendix in which we recover previously known models by taking appropriate limiting cases of our global scale model and provide an explicit computational scheme for solving the global scale model.
2 Formulation of the problem
We have a set \(\varOmega \in {\mathbb {R}}^3\), where \(\varOmega \) is the union of a poroelastic matrix \(\varOmega _{\mathrm {M}}\) and a collection of K disjoint embedded poroelastic subphases \(\varOmega _{\mathrm {S}}\), where we can write
We have that \({\bar{\varOmega }}={\bar{\varOmega }}_{\mathrm {M}}\cup {\bar{\varOmega }}_{\mathrm {S}}\) and \(\varOmega _{\mathrm {M}}\cap \varOmega _{\mathrm {S}}=\emptyset \). A sketch of a cross section of the domain \(\varOmega \) is shown in Fig. 1, where we highlight the hierarchical structure of the material we are considering. At the local scale, Fig. 1b), we have the various subdomains \(\varOmega _{\mathrm {M}}\) and \(\varOmega _{\eta }\) for \(\eta =1,\dots , K.\) When zooming in on each of these subdomains separately, Fig. 1c), we find that \(\varOmega _{\mathrm {M}}\) and \(\varOmega _{\eta }\) have a standard poroelastic structure (see [10, 38]).
A schematic representing a cross section of the domain \(\varOmega \) showing the poroelastic matrix \(\varOmega _{\mathrm {M}}\) in red and the various subphases \(\varOmega _{\eta }\) in blue at the local scale. We highlight the local scale periodic cell with embedded subphases and highlight the hierarchical structure of the materials we are considering here by also showing their porescale structures
To set up an appropriate problem we require the governing equations for each of the subdomains and interface conditions. The balance equations in the matrix and each of the subphases are given by
respectively. We have \({\varvec{\sigma }}_{\mathrm {M}}\) and \({\varvec{\sigma }}_{\eta }\) appearing in (2–3), these are the effective stress tensors in the matrix and subphases, respectively. These are given by
where
is the symmetric part of the gradient operator. We have that \(\mathbf{u}_{\mathrm {M}}\) and \(\mathbf{u}_{\eta }\) are the elastic displacements in the matrix and each of the subphases, respectively, and \(\vartheta _{\mathrm {M}}\) and \(\vartheta _{\eta }\) are the pressures in the matrix and the subphases, respectively. The \({\mathbb {C}}_{\mathrm {M}}\) and \({\mathbb {C}}_{\eta }\) are the effective elasticity tensors which would be obtained from the homogenization at the finer hierarchical level. \({\mathbb {C}}_{\mathrm {M}}\) and \({\mathbb {C}}_{\eta }\) are the effective elasticity tensors obtained in [10, 38] for a standard poroelastic material. These effective elasticity tensors also possess major and minor symmetries as proved in [28]. We can therefore write the fourth rank effective elasticity tensors in components as \({\mathcal {C}}_{ijkl}^{\mathrm {M}}\) and \({\mathcal {C}}_{ijkl}^{\eta }\), for \(i, j, k, l =1, 2, 3\). Therefore, we have
The \({\varvec{\alpha }}_{\mathrm {M}}\) and \({\varvec{\alpha }}_{\eta }\) appearing in (4-5) are the effective Biot’s tensors of coefficients in the matrix and the subphases, respectively, which have been obtained from the homogenization at finer hierarchical scales. The second rank tensors \({\varvec{\alpha }}_{\mathrm {M}}\) and \({\varvec{\alpha }}_{\eta }\) are related to the ratio of fluid to solid volume changes at constant pressure in their respective poroelastic phases.
We also have Darcy’s law for both the matrix and the subphases. That is,
where \({\mathsf {K}}_{\mathrm {M}}\) and \({\mathsf {K}}_{\eta }\) are the hydraulic conductivities in the matrix and the subphases, respectively, and the \(\mathbf{w}_{\mathrm {M}}\) and \(\mathbf{w}_{\eta }\) are the relative fluid-solid velocities in the matrix and subphases, respectivelyFootnote 1.
The last governing equation of each compartment is the conservation of mass equations given by
for the matrix and subphases, respectively. The coefficients \({\mathcal {M}}_{\mathrm {M}}\) and \({\mathcal {M}}_{\eta }\) are the Biot’s moduli in each compartment, which can as well be obtained from the homogenization process at finer hierarchical scales. \({\mathcal {M}}_{\mathrm {M}}\) and \({\mathcal {M}}_{\eta }\) can be described physically as poroelastic coefficients that depend on the porescale geometry, porosity and the fluid bulk modulus. They also depend on the elastic properties of the matrix and subphases, respectively. We can interpret \({\mathcal {M}}_{\mathrm {M}}\) and \({\mathcal {M}}_{\eta }\) as the inverse of the variation of fluid volume in response to a variation in pore pressure. \({\mathcal {M}}_{\mathrm {M}}\) and \({\mathcal {M}}_{\eta }\) are positive definite (see [28], for proof of this property).
In order to close the problem in the whole domain \(\varOmega \) we require interface conditions between the matrix and each of the embedded subphases. We define the interfaces as \(\varUpsilon _{\eta }:=\partial \varOmega _{\mathrm {M}}\cap \partial \varOmega _{\eta }\) for \(\eta =1,..,K\). Then we impose continuity of stresses, displacements, pressures and fluxes. That is,
where the unit outward vectors (i.e. pointing into the subphase \(\varOmega _{\eta }\)) normal to the interfaces \(\varUpsilon _{\eta }\) are denoted by \(\mathbf{n}_{\eta }\) for \(\eta =1,\dots ,K\).
The problem is also to be closed by appropriate boundary conditions on the external boundary \(\partial \varOmega \). The latter could be, for example, of Dirichlet–Neumann type, as noted in [40]. The conditions on the external boundary typically do not play a role in the derivation of results carried out by formal asymptotic homogenization.
Within the next section we decouple spatial variations by introducing two distinct variables, we then introduce the two-scale asymptotic homogenization method and discuss the assumptions made to carry out the required analysis in the sections that follow.
3 The two-scale asymptotic homogenization method
Here we summarize the problem that we introduced in the previous section and now wish to perform a multiscale analysis of this system,
up to conditions on the external boundary \(\partial \varOmega \). We assume that the system can be characterized by two different length scales. The whole domain \(\varOmega \) has the average size denoted by L. This is the global scale. We assume the second length scale, l, to be the inter-subphase distance. This is the local scale.
We will now introduce the asymptotic homogenization technique which we will use to upscale (17–28) to a system of global scale PDEs. We make the assumption that the local length scale (this is where the individual subphases are distinctly visible from the surrounding matrix) denoted by l, is small compared to the average size of the global scale domain denoted by L. That is,
We also must introduce a spatial variable \(\mathbf{y}\). This variable captures local scale variations of the fields, that is
The global scale and local scale have corresponding spatial variables \(\mathbf{x}\) and \(\mathbf{y}\), respectively. These variables are formally independent. The gradient operator with the corresponding two-scales becomes
We assume that all fields in the system of equations (17–28) as well as \({\mathbb {C}}_{\mathrm {M}}\), \({\mathbb {C}}_{\eta }\), \({\mathsf {K}}_{\mathrm {M}}\), \({\mathsf {K}}_{\eta }\), \({\mathcal {M}}_{\mathrm {M}}\), \({\mathcal {M}}_{\eta }\), \({\varvec{\alpha }}_{\mathrm {M}}\) and \({\varvec{\alpha }}_{\eta }\) for \(\eta =1,\dots , K\) are functions of both the spatial variables \(\mathbf{x}\) and \(\mathbf{y}\). We also assume that each of the fields can be written as a power series in \(\epsilon \). That is,
where formally the series comprises an infinite number of terms and \(\psi \) represents a typical field in the current work.
Remark 1
(Local scale Periodicity) We assume that every field \(\psi ^{\epsilon }\) in (17–28), \({\mathbb {C}}_{\mathrm {M}}\), \({\mathbb {C}}_{\eta }\), \({\mathsf {K}}_{\mathrm {M}}\), \({\mathsf {K}}_{\eta }\), \({\mathcal {M}}_{\mathrm {M}}\), \({\mathcal {M}}_{\eta }\), \({\varvec{\alpha }}_{\mathrm {M}}\) and \({\varvec{\alpha }}_{\eta }\) are \(\mathbf{y}\)-periodic. This allows the analysis of the microstructure to be carried out on a single periodic cell. We make this assumption as it allows us to solve the local scale problems that we will obtain from the asymptotic homogenization technique on a finite subset of the domain. However, the analysis that follows could be carried out by assuming local boundedness of fields only (see, for example, [10, 36]).
Remark 2
(Uniformity on the global scale) It is clear that in principle the local scale geometry can vary with respect to the global scale (see [10, 16, 22, 32, 33]). This dependence is, however, in general neglected for the sake of simplicity. This means that the material can be described as macroscopically uniform, i.e. the local scale geometry does not depend on the global scale variable \(\mathbf{x}\). We make this assumption here. This means that we have the simple differentiation under the integral sign given by
where \((\bullet )\) denotes a tensor or a vector quantity.
Remark 3
(Local scale Geometry) Up to this point we have assumed that there are many different subphases in each periodic cell, this is highlighted in Fig. 1b. In general the microstructure of biological tissues is very heterogeneous and will have many local scale subphases. Therefore, by beginning the formulation with many subphases we are relating our problem to this type of microstructure. However, for the sake of simplicity and without loss of generality it is possible to restrict our analysis to the situation where there is only one subphase embedded within each periodic cell. This is shown in Fig. 2. It would be simple to extend the model to account for a number of subphases contained in the periodic cell if this was appropriate for a specific application (See [34] where this has been done for simple elastic composites). Therefore, the subscript \(\eta \) is no longer needed. Due to periodicity, we can identify the domain \(\varOmega \) with the periodic cell, which has matrix and subphase sections denoted by \(\varOmega _{\mathrm {M}}\) and \(\varOmega _{\mathrm {S}}\), respectively. The interface and corresponding normal can be defined by \(\varUpsilon :=\partial \varOmega _{\mathrm {M}}\cap \partial \varOmega _{\mathrm {S}}\) and \(\mathbf{n}\).
Remark 4
(Strain gradient effects) In this work we embrace the traditional, zeroth-order asymptotic homogenization method (also used for example in the derivation of the standard Biot’s equations in [10]), which means that we focus on obtaining a closed system of PDEs for the zeroth-order fields. We therefore formally derive the global scale model in the limit \(\epsilon \rightarrow 0\). The homogenized, zeroth-order solution, (provided that condition (29) is met) is supposed to be accurate assuming that strain gradient effects, which would be taken into account by fully considering further terms in the power series expansion (32), are negligible. In this work, this condition is deemed acceptable as we are assuming that there exists a sharp length scale separation in the system and we are considering a quasi-static scenario (i.e. inertia is neglected), so that rates are supposed to be small. However, it is possible not to enforce the strict limit as \(\epsilon \rightarrow 0\) (motivated by either the presence of non-negligible strain gradients triggered by fast rates and/or by \(\epsilon \) not being sufficiently small for higher order terms to be ignored) and to extend the macroscopic stress-strain relation to include strain gradients in the formulation. For a clear derivation of this extended macroscopic stress-strain relation for periodic elastic media see [20]. Additionally, for further details see [1, 45, 46], and the large number of references therein, where strain gradient effects are discussed in detail for a variety of physical scenarios of interest.
Next, we exploit the two-scale asymptotic homogenization method to obtain the global scale equations describing the behaviour of the double poroelastic material.
4 The global double poroelastic results
Assumptions (31) and (32) of the two-scale asymptotic homogenization technique can now be applied to the system of equations (17–28). This gives the following multiscale PDEs
where representation (32) is implied in relationships (34–45) and indicated by the superscript \(\epsilon \). We also have periodic conditions on the cell boundary \(\partial \varOmega \setminus \varUpsilon \). We then proceed by equating the same terms multiplying the various powers of \(\epsilon ^r\), \(r=0,1,\dots \). This way, we derive the global double poroelastic model in terms of the zeroth-order variables.
We can equate the coefficients of \(\epsilon ^0\) in equations (34-45), which gives,
From (48) and (49) we can see that \(\mathbf{u}_{\mathrm {M}}^{(0)}\) and \(\mathbf{u}_{\mathrm {S}}^{(0)}\) are rigid body motions in \(\mathbf{y}\) for each \(\mathbf{x}\) and so by \(\mathbf{y}\)-periodicity we deduce that
respectively. Since we also have the continuity of leading order displacements (55) then we can define
From (50) and (51) we have that
respectively. Again since we also have the continuity of leading order pressures (56) then we can define
We will use the new notations (59) and (61) in the remainder of this work.
Now equating the coefficients of \(\epsilon ^1\) in the system of PDEs (34–45) we obtain,
We also define the specific cell average operator as
Here, \(\psi _{\beta }\) is any of the components of the fields involved in our analysis in their respective subdomains, and \(|\varOmega |\) represents the volume of the periodic cell. As such we have
The cell average over the whole periodic cell is defined as
4.1 The global scale poroelastic constitutive relationship
Using Eqs. (46), (47), (54), (64), (65), and (71) we can write the problem for \(\mathbf{u}_{\mathrm {M}}^{(1)}\) and \(\mathbf{u}_{\mathrm {S}}^{(1)}\). That is,
Problem (77–80) admits a unique solution up to a \(\mathbf{y}\) constant function. The solution, exploiting linearity, is given as,
where \(c_1(\mathbf{x})\) and \(c_2(\mathbf{x})\) are \(\mathbf{y}\) constant functions. The third-order tensors \(\mathsf {B}_{\mathrm {M}}\) and \(\mathsf {B}_{\mathrm {S}}\) are the solutions of the local scale problems given below
The vectors \(\mathbf{b}_{\mathrm {M}}\) and \(\mathbf{b}_{\mathrm {S}}\) satisfy the elastic-type problem given by
Both problems (83–86) and (87–90) are to be solved on the cell and be equipped with periodic conditions on \(\partial \varOmega \setminus \varUpsilon \). We also require one further condition on the auxiliary variables \(\mathsf {B}_{\mathrm {M}}\), \(\mathsf {B}_{\mathrm {S}}\), \(\mathbf{b}_{\mathrm {M}}\) and \(\mathbf{b}_{\mathrm {S}}\) to ensure uniqueness, for example
For cell problems (83–86) and (87–90) in components see Appendix A.2.
We can use (81–82) to write the leading order effective stress tensors in both the matrix and the subphase, respectively, as
where we have the auxiliary tensors
and
where we have the auxiliary tensors
Summing up the integral averages of eq (62) and (63) gives
Application of the divergence theorem to the first two integrals and applying the assumption of macroscopic uniformity to the last two integrals gives
where \(\mathbf{n}\), \(\mathbf{n}^{\varOmega _{\mathrm {M}}\setminus {\varUpsilon }}\) and \(\mathbf{n}^{\varOmega _{\mathrm {S}}\setminus {\varUpsilon }}\) are the unit normals corresponding to \(\varUpsilon \), \(\partial \varOmega _{\mathrm {M}}\setminus \varUpsilon \) and \(\partial \varOmega _{\mathrm {S}}\setminus \varUpsilon \). The terms on the boundaries \(\partial \varOmega _{\mathrm {M}}\setminus \varUpsilon \) and \(\partial \varOmega _{\mathrm {S}}\setminus \varUpsilon \) cancel due to periodicity and the terms on \(\varUpsilon \) cancel due to (70). So we have
which can be written as
by exploiting notation (76). We therefore have
where
Relationship (101) represents the global scale constitutive equation for the double poroelastic material, where the effective drained elasticity tensor is defined as
Next, we derive the effective Darcy’s law and close the global scale system of PDEs.
4.2 The effective Darcy’s law
We can use (52), (53), (57) and (72) to write the following problem for \(\vartheta _{\mathrm {M}}^{(1)}\) and \(\vartheta _{\mathrm {S}}^{(1)}\)
Using expressions (66) and (67) for \(\mathbf{w}_{\mathrm {M}}^{(0)}\) and \(\mathbf{w}_{\mathrm {S}}^{(0)}\) we can rewrite problem (103–106) as
The problem given by (107–108) admits a unique solution up to a \(\mathbf{y}\) constant function (see [4, 13]). Exploiting linearity we have,
where \(c_3(\mathbf{x})\) and \(c_4(\mathbf{x})\) are \(\mathbf{y}\) constant functions and \({\hat{\varvec{\vartheta }}}_{\mathrm {M}}\) and \({\hat{\varvec{\vartheta }}}_{\mathrm {S}}\) are vectors which satisfy the following cell problem
The anisotropic Poisson’s-type cell problem (113–116) is to be supplemented by periodic conditions on the boundary \(\partial \varOmega \setminus \varUpsilon \) and a further condition has to be placed on \(\varvec{{\hat{\vartheta }}}_{\mathrm {M}}\) and \(\varvec{{\hat{\vartheta }}}_{\mathrm {S}}\) to ensure the solution is unique, for example
For cell problem (113-116) in components see Appendix A.2.
Using expressions (111) and (112) for \(\vartheta _{\mathrm {M}}^{(1)}\) and \(\vartheta _{\mathrm {S}}^{(1)}\) in (66) and (67) and taking the integral average (74) gives
where we have used the notation
and
where we have used the notation
Then we have the effective Darcy’s law
We can define the hydraulic conductivity tensor for this structure as
and rewrite Darcy’s Law as
We now wish to obtain the conservation of mass equation. We integrate expressions (68) and (69) in \(\varOmega _{\mathrm {M}}\) and \(\varOmega _{\mathrm {S}}\), respectively. That is
Applying the divergence theorem and using (73) cancels the final two integrals and we can rewrite the remaining terms as
We can use the expressions for \(\mathbf{u}_{\mathrm {M}}^{(1)}\) and \(\mathbf{u}_{\mathrm {S}}^{(1)}\) from (81) and (82) to obtain \({\dot{\mathbf{u}}}_{\mathrm {M}}^{(1)}\) and \({\dot{\mathbf{u}}}_{\mathrm {S}}^{(1)}\) and using these in (126) we obtain
Rearranging (127) to obtain an expression for \({\dot{\vartheta }}^{(0)}\) we obtain
where we define
which reminds of the Biot’s modulus for the system. We can also define the tensor
which has the form of an effective Biot’s tensor of coefficients.
Equations (100), (101), (122), (129), collectively represent, from a formal standpoint, a poroelastic-type system of PDEs in terms of the zeroth-order displacement, velocity, and pressure fields, i.e.
where we have that \({\vartheta }^{(0)}\) is the global scale pressure, \(\mathbf{w}_{\mathrm {eff}}\) comprises the average of \(\mathbf{w}_{\mathrm {M}}^{(0)}\) and \(\mathbf{w}_{\mathrm {S}}^{(0)}\) which are the leading order relative fluid velocities in the matrix and subphase, respectively, \(\mathbf{u}^{(0)}\) is the solid displacement and \(\dot{\mathbf{u}}^{(0)}\) is the solid velocity. Our model (132) is formally of poroelastic-type. We can conclude from our global scale model that the mechanical behaviour of a double poroelastic material can be fully described by the material’s effective elasticity tensor \({\widetilde{\mathbb {C}}}\), the hydraulic conductivity tensor \({\mathsf {W}}\), the tensor \({\bar{\varvec{\alpha }}}\) which is reminiscent of the classical Biot’s tensor of coefficients and the scalar quantity \({\bar{\mathcal {M}}}\) which can be identified with the Biot’s modulus. For a step-by-step guide to solving the global scale model (132) see Appendix A.2.
It is important to note that our global scale model (132) reduces to previously obtained results when we consider the following limit cases. The first case is in the limit of no fluid present in either our matrix or subphases. In this case the model reduces to that of elastic composites (see [35]). When we assume that the subphase is purely elastic and the matrix remains poroelastic we recover the works of [43] and [12]. We provide a more detailed description and recover these limits in appendix A.1.
Within the next section we will discuss each of the global scale coefficients in detail as well as discussing the key novelties of the new model. We will then prove that our model is both formally and substantially of poroelastic type by defining a global Biot’s tensor of coefficients and proving the resulting Biot’s modulus is positive.
5 Properties of the coefficients on the global scale
The coefficients of the global scale model (132) that fully characterize the mechanical behaviour of the double poroelastic material are the effective elasticity tensor \({\widetilde{\mathbb {C}}}\), the hydraulic conductivity tensor \({\mathsf {W}}\), the Biot’s tensor of coefficients \({\bar{\varvec{\alpha }}}\) and the scalar Biot’s modulus \({\bar{\mathcal {M}}}\). These can be interpreted physically as follows. The constitutive law, which is of poroelastic-type, has the drained effective elasticity tensor given by
We should note here that the \({\mathbb {C}}_{\mathrm {M}}\) and \({\mathbb {C}}_{\mathrm {S}}\) are actually the effective elasticity tensors from carrying out the homogenization process at the finer scale. These effective elasticity tensors are positive semi-definite and possess both major and minor symmetries. The hydraulic conductivity tensor is given by
This hydraulic conductivity tensor comprises the hydraulic conductivities \({\mathsf {K}}_{\mathrm {M}}\) and \({\mathsf {K}}_{\mathrm {S}}\) from the matrix and subphase, respectively, as well as two additional terms \({\mathsf {K}}_{\mathrm {M}}{\mathsf {R}}_{\mathrm {M}}\) and \({\mathsf {K}}_{\mathrm {S}}{\mathsf {R}}_{\mathrm {S}}\) which account for the differences in the hydraulic conductivities of the subphase and the matrix at different points on the local scale. This hydraulic conductivity tensor can be found by solving cell problem (113–116).
We can consider the effective Biot’s tensor of coefficients \({\bar{\varvec{\alpha }}}\).
Remark 5
(Effective Biot’s tensor of coefficients \({\bar{\varvec{\alpha }}}\)) We have the effective Biot’s tensor of coefficients given by
The first two terms are the Biot’s tensors from the matrix and subphase, respectively, and we should view the third and fourth terms of this expression as the contributions arising from considering the changing compressibility at different points on the microstructure. These final two terms can be thought of as a correction term to the typical cell average (see (74)). We should note however, that when \({\varvec{\alpha }}_{\mathrm {M}}={\varvec{\alpha }}_{\mathrm {S}}=\alpha \), where \(\alpha \) is a constant then we can write \({\bar{\varvec{\alpha }}}\) as
We have that \(\langle {\mathbb {L}}_{\mathrm {M}}+{\mathbb {L}}_{\mathrm {S}}\rangle _{\scriptscriptstyle \varOmega }=0\), as proved in [35], where the notation \({\mathbb {M}}\) has been used by [35] instead of \({\mathbb {L}}\) to denote the same auxiliary tensor. This holds here since cell problem (83)–(86) for \({\mathbb {L}}_{\mathrm {M}}\) and \({\mathbb {L}}_{\mathrm {S}}\) is the cell problem for composites found in [35]. Therefore, in this specific case \({\bar{\varvec{\alpha }}}\) is the proper cell average of the Biot’s tensor of coefficients from the individual phases given by
Finally, the resulting Biot’s modulus \({\bar{\mathcal {M}}}\) comprises the coefficients \({\mathcal {M}}_{\mathrm {M}}\) and \({\mathcal {M}}_{\mathrm {S}}\) as well as other terms involving \({\varvec{\alpha }}_{\mathrm {M}}\), \({\varvec{\alpha }}_{\mathrm {S}}\), \({\varvec{\tau }}_{\mathrm {M}}\) and \({\varvec{\tau }}_{\mathrm {S}}\). We can consider the physical interpretations of \({\bar{\mathcal {M}}}\) for two possible scenarios. When \({\varvec{\alpha }}_{\mathrm {M}}\) and \({\varvec{\alpha }}_{\mathrm {S}}\) are not equal or constants then \({\bar{\mathcal {M}}}\) comprises the average of \({\mathcal {M}}_{\mathrm {M}}\) and \({\mathcal {M}}_{\mathrm {S}}\) and two other terms that account for local changes in the compressibility occurring on the microstructure. When \({\varvec{\alpha }}_{\mathrm {M}}={\varvec{\alpha }}_{\mathrm {S}}=\alpha \), where \(\alpha \) is a constant then the effective Biot’s modulus \({\bar{\mathcal {M}}}\) is given by the harmonic mean. The effective Biot’s modulus \({\bar{\mathcal {M}}}\) is the inverse of a storage coefficient. Under constant volumetric strain, it can be defined as the increase in the amount of fluid as a result of a unit increase in pore pressure.
Our new model has key features that make it differ substantially from other models of poroelasticity, poroelastic composites or composite materials. That is, this model is able to account for the behaviour of two different poroelastic compartments and the interactions between them. We are therefore able to address the scenario where there exists a difference in the poroelastic properties of the material which could potentially be dictated by a difference in the elastic, fluid and geometrical properties at the local scale. This model is of particular benefit to physiological applications. For example, in the cardiac muscle the interstitial matrix with embedded fibroblast cells can be considered using this model (see [30]). The interstitial matrix is clearly poroelastic and so too are the fibroblast cells, so using our novel model in this situation would allow the poroelastic behaviour of each of these phases to be considered individually leading to a much more realistic description of the material. The key novelty between the current model and previous models in the literature is the fact that our model coefficients can encode the difference in a full set of poroelastic parameters. These coefficients are to be calculated by solving differential problems on a finite subset of the given microstructure. Cell problem (87–90), is novel and is the key feature that encodes the changes in compressibility, stiffness and geometry of the two phases in the model coefficients. This means that these local scale variations in compressibility, stiffness and geometry are encoded in the global scale coefficients such as the average Biot’s modulus and the Biot’s tensor of coefficients, which provides a precise description of the effective material behaviour. Overall our novel model reads as a comprehensive framework to describe materials that are composites comprising of two different poroelastic structures.
Within the next subsection we will prove properties of the effective coefficients of the model which allow us to conclude that our novel global scale model is truly of poroelastic type.
5.1 Biot’s tensor of coefficients and Biot’s modulus
In this Section we demonstrate a) the existence of a tensor which plays the role of the classical Biot’s tensor of coefficients via a suitable analytical identity and b) the global scale coefficient \({\bar{\mathcal {M}}}\) is positive, which then qualifies as the global Biot’s modulus for the double poroelastic material. Throughout the proofs of these properties we will use the cell problems in components which can be found in Appendix A.2. We will also make use of Gauss’ (divergence) theorem. The following two theorems involve the global scale model coefficients which we summarize here, for convenience, as
where \({\bar{\varvec{\alpha }}}\) and \({\bar{\mathcal {M}}}\) are from (130) and (131), respectively. The coefficient \({\varvec{\gamma }}\) multiplies the global scale pressure \({\vartheta }^{(0)}\) in the constitutive equation (101). We now state and prove the first theorem. We start by focusing on the Biot’s tensor of coefficients.
Theorem 1
(Biot’s tensor of coefficients) The global scale coefficients \({\varvec{\gamma }}\) and \({\bar{\varvec{\alpha }}}\) are related by the following relationship
The existence of this equality guarantees that the tensor \({\bar{\varvec{\alpha }}}\) can be regarded as the Biot’s tensor of coefficients for the double poroelastic material on the global scale.
Proof
We begin by writing \({\varvec{\gamma }}\) and \({\bar{\varvec{\alpha }}}\) in components as
We use (83) and (84) from the cell problems, in components, and multiply by \(b_{i}^{\mathrm {M}}\), \(b_{i}^{\mathrm {S}}\) (which are the cell problem solutions), respectively. Integrating over \(\varOmega _{\mathrm {M}}\) and \(\varOmega _{\mathrm {S}}\), respectively, yields
We perform integration by parts to obtain
Enforcing Gauss’ theorem and using minor symmetries of \({\mathbb {C}}_{\mathrm {M}}\) and \({\mathbb {C}}_{\mathrm {S}}\) we have
where \(\mathbf{n}\), \(\mathbf{n}^{\varOmega _{\mathrm {M}}\setminus {\varUpsilon }}\) and \(\mathbf{n}^{\varOmega _{\mathrm {S}}\setminus {\varUpsilon }}\) are the unit normals corresponding to \(\varUpsilon \), \(\partial \varOmega _{\mathrm {M}}\setminus \varUpsilon \) and \(\partial \varOmega _{\mathrm {S}}\setminus \varUpsilon \), and cancelling terms on the periodic boundaries due to \(\mathbf{y}\)-periodicity and accounting for the interface conditions (85) we obtain
Therefore, we have
We now wish to multiply (87) and (88), in components, by the cell problem solutions \(B_{ikl}^{\mathrm {M}}\), \(B_{ikl}^{\mathrm {S}}\), respectively, and then integrate over \(\varOmega _{\mathrm {M}}\) and \(\varOmega _{\mathrm {S}}\), respectively, to obtain
We perform integration by parts
We apply Gauss’ theorem and using both minor and major symmetries of \({\mathbb {C}}_{\mathrm {M}}\) and \({\mathbb {C}}_{\mathrm {S}}\) we have
where \(\mathbf{n}\), \(\mathbf{n}^{\varOmega _{\mathrm {M}}\setminus {\varUpsilon }}\) and \(\mathbf{n}^{\varOmega _{\mathrm {S}}\setminus {\varUpsilon }}\) are the unit normals corresponding to \(\varUpsilon \), \(\partial \varOmega _{\mathrm {M}}\setminus \varUpsilon \) and \(\partial \varOmega _{\mathrm {S}}\setminus \varUpsilon \). Cancelling terms on the periodic boundaries due to \(\mathbf{y}\)-periodicity and accounting for the interface conditions (89) and (86) the terms of \(\varUpsilon \) cancel. So we can write (151) as
Hence we have
From (153) and (148) we have that \(\langle {\mathbb {C}}_{\mathrm {M}}{\varvec{\tau }}_{\mathrm {M}}+ {\mathbb {C}}_{\mathrm {S}}{\varvec{\tau }}_{\mathrm {S}}\rangle _{\varOmega }=-\langle {\mathbb {L}}_{\mathrm {M}}^{\mathrm {T}}:{\varvec{\alpha }}_{\mathrm {M}}+{\mathbb {L}}_{\mathrm {S}}^{\mathrm {T}}:{\varvec{\alpha }}_{\mathrm {S}}\rangle _{\scriptscriptstyle \varOmega }\). Therefore, using this in the definitions of \({\varvec{\gamma }}\) and \({\bar{\varvec{\alpha }}}\), we have that \({\varvec{\gamma }}=-{\bar{\varvec{\alpha }}}\) as required. \(\square \)
Model (132) can be recast to show its genuine poroelastic character by means of the identity we proved, namely:
where we have
We can now state and prove our second theorem relating to our global scale coefficients
Theorem 2
(The Biot’s Modulus is positive) The Biot’s modulus that arises from our system, defined by
is positive i.e.
Proof
To show that \({\bar{\mathcal {M}}}>0\), we need to show that the denominator of (156) is positive. So we rearrange the denominator and we then need to show that
where \({\mathcal {M}}_{\mathrm {M}}\) and \({\mathcal {M}}_{\mathrm {S}}\) are positive definite from the homogenization process at the finer scale. We are able to show that
which means that (158) will be satisfied. To do this we begin by multiplying (87) and (88) by \(b_i^{\mathrm {M}}\) and \(b_i^{\mathrm {S}}\), respectively, and integrate over \(\varOmega _{\mathrm {M}}\) and \(\varOmega _{\mathrm {S}}\). That is
Performing integration by parts
By enforcing Gauss’ theorem and using minor symmetries of \({\mathbb {C}}_{\mathrm {M}}\) and \({\mathbb {C}}_{\mathrm {S}}\) we have
where \(\mathbf{n}\), \(\mathbf{n}^{\varOmega _{\mathrm {M}}\setminus {\varUpsilon }}\) and \(\mathbf{n}^{\varOmega _{\mathrm {S}}\setminus {\varUpsilon }}\) are the unit normals corresponding to \(\varUpsilon \), \(\partial \varOmega _{\mathrm {M}}\setminus \varUpsilon \) and \(\partial \varOmega _{\mathrm {S}}\setminus \varUpsilon \). Cancelling terms on the periodic boundaries due to \(\mathbf{y}\)-periodicity and using (89) and (90) the terms on \(\varUpsilon \) cancel and so we can write (162) as
The two terms on the RHS of (163) are positive, so we therefore have that
Equivalently,
In the case where \({\varvec{\alpha }}_{\mathrm {M}}={\varvec{\alpha }}_{\mathrm {S}}={\hbox {constant}}\) then
Therefore, we have that \({\bar{\mathcal {M}}}>0\) and the proof is complete. \(\square \)
We have now proved both these properties for our model coefficients. This means that our novel global scale model is both formally and substantially of poroelastic type.
6 Conclusion
We have presented a novel system of PDEs that describes the effective behaviour of double poroelastic materials, i.e. a poroelastic matrix with embedded poroelastic subphases. This type of structure represents many real-world scenarios including biological soft tissues (e.g. cardiac muscle, artery walls and tumours), soil and porous rocks. We have considered a quasi-static, multiphase problem, in the absence of body forces, consisting of the governing equations for both the poroelastic matrix and the poroelastic subphases (17–24). The governing equations for the matrix and the subphases are the equations of Biot’s poroelasticity assuming anisotropy. The problem is closed by the application of the appropriate interface conditions (25–28) that arise from the continuity of stresses, displacements, pressures and fluxes across the boundary between each of the subphases and the matrix. We have then enforced the length scale separation that occurs between, the inter-subphase distance (the local scale) and the overall size of the domain (the global scale) to apply the asymptotic homogenization technique to upscale the structure–structure interaction problem to the system of global scale PDEs (132). We prove that our novel global scale model (132) is both formally and substantially of poroelastic type by proving a) the existence of a global scale Biot’s tensor of coefficients and b) the effective Biot’s Modulus is positive.
The model obtained in this work generalizes [12, 43] and is also a next natural step in the modelling of hierarchical multiscale materials. The key novelty of this work resides in taking into account the difference in a full set of poroelastic parameters characterizing the matrix and the subphases. This is reflected in the new cell problem (87–90). This cell problem is driven by the changes in compressibility of the matrix and the subphase at different points in the microstructure. Solving this cell problem encodes this detail of the varying compressibility, stiffness and geometry of the microstructure in the quantities \({\varvec{\tau }}_{\mathrm {M}}\) and \({\varvec{\tau }}_{\mathrm {S}}\), which appear in the coefficients of the global scale model. This means that the local scale complexity is accounted for even at the global scale within the average Biot’s modulus and the Biot’s tensor of coefficients. We have therefore addressed the scenario where there exists a difference in the poroelastic properties of the material which could potentially be dictated by a difference in the elastic, fluid and geometrical properties of the material at the local scale. For these reasons our new formulation provides a robust framework for fully describing double poroelastic materials effectively.
The current model assumes two standard poroelastic phases at the local scale; however, it is possible to assume that one or both phases are a poroelastic composite [29]. This situation would not change the overall global scale model; however, different properties would be encoded in the model coefficients due to the different porescale microstructure. The problem detailed in Sect. 2 would instead use the global scale model derived in [29] as the governing equations for the matrix compartment and continue with the upscaling as carried out here. The effective elasticity tensor would encode the properties of the inhomogeneous porescale material in the contributions \({\mathbb {C}}_{\mathrm {M}}\) and \({\mathbb {C}}_{\mathrm {S}}\). A situation like this could provide a more realistic setup for biological applications.
Our current model has some limitations and there are possible extensions to this current work that would extend the applicability to a wider range of scenarios. At present the model has been formulated to provide the global scale model in a quasi-static, linearized setting.
It would be straight-forward to generalize our model to include linearized inertia and would result in additional terms in our global scale model. These changes would include the appearance of leading order linearized inertia in the effective balance equation for the effective stress (132a). The addition of these terms could help provide a more realistic poroelastic modelling framework for biological tissues such as organs. For example, in the lungs, this model with the addition of the inertia could lead to advances in the understanding of the acoustic properties of the lungs and be of use in non-invasive diagnosis of pulmonary diseases [44]. The extension of this work to a nonlinear elasticity setting is more challenging whilst using the two-scale asymptotic homogenization technique. There have however, been recent advances in the literature (see, for example [14, 40]).
The natural next step would be to obtain solutions to the model on the basis of a specific microstructure with parameters specified by real-world data. This data could relate to a wide variety of biological examples. In the literature there have been three-dimensional numerical simulations carried out on the cell problems obtained from asymptotic homogenization for elastic composites and poroelastic/porous materials [18, 34, 42]. The numerical simulations for the cell problems associated with this model would combine the strategies used within the literature. With experimental data that characterized our material on the porescale and the local scale then we would be able to produce numerical simulations for our model on three scales.
Notes
They should be in principle multiplied by the porosities, however, the latter can be incorporated in the definition of each hydraulic conductivity tensor.
References
Andrianov, I.V., Bolshakov, V.I., Danishevs’kyy, V.V., Weichert, D.: Higher order asymptotic homogenization and wave propagation in periodic composite materials. Proc. R. Soc. 464, 1181–1201 (2008)
Auriault, J.L., Boutin, C., Geindreau, C.: Homogenization of Coupled Phenomena in Heterogenous Media, vol. 149. Wiley, New York (2010)
Bader Thomas, K., Hofstetter, K., Hellmich, C., Eberhardsteiner, J.: The poroelastic role of water in cell walls of the hierarchical composite “softwood.” Acta Mechanica 217, 75–100 (2011)
Bakhvalov, N., Panasenko, G.: Homogenization: Averaging Processes in Periodic Media. Kluwer Academic Publishers, Cambridge (1989)
Biot, M.A.: Theory of elasticity and consolidation for a porous anisotropic solid. J. Appl. Phys. 26(2), 182–185 (1955)
Biot, M.A.: General solutions of the equations of elasticity and consolidation for a porous material. J. Appl. Mech 23(1), 91–96 (1956)
Biot, M.A.: Theory of propagation of elastic waves in a fluid-saturated porous solid II higher frequency range. J. Acoust. Soc. Am. 28(2), 179–191 (1956)
Biot, M.A.: Mechanics of deformation and acoustic propagation in porous media. J Appl Phys 33(4), 1482–1498 (1962)
Bottaro, A., Ansaldi, T.: On the infusion of a therapeutic agent into a solid tumor modeled as a poroelastic medium. J. Biomech. Eng. 134(8), 084501 (2012)
Burridge, R., Keller, J.B.: Poroelasticity equations derived from microstructure. J. Acoust. Soc. Am. 70(4), 1140–1146 (1981)
Chalasani, R., Poole-Warren, L., Conway, R.M., Ben-Nissan, B.: Porous orbital implants in enucleation: a systematic review. Surv Ophthalmol 52(2), 145–155 (2007)
Chen, M.J., Kimpton, L.S., Whitley, J.P., Castilho, M., Malda, J., Please, C.P., Waters, S.L., Byrne, H.M.: Multiscale modelling and homogensation of bre-reinforced hydrogels for tissue engineering. Eur. J. Appl. Math. 31(1), 143–171 (2018)
Cioranescu, D., Donato, P.: An Introduction to Homogenization. Oxford University Press, Oxford (1999)
Collis, J., Brown, D., Hubbard, M., O’Dea, R.: Effective equations governing an active poroelastic medium. In: Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences (2017)
Cowin, S.C.: Bone poroelasticity. J. Biomech. 32(3), 217–238 (1999)
Dalwadi, M.P., Griffiths, I.M., Bruna, M.: Understanding how porosity gradients can make a better filter using homogenization theory. Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences 471(2182) (2015)
Davit, Y., Bell, C.G., Byrne, H.M., Chapman, L.A., Kimpton, L.S., Lang, G.E., Leonard, K.H., Oliver, J.M., Pearson, N.C., Shipley, R.J.: Homogenization via formal multiscale asymptoticsand volume averaging:how do the two techniques compare? Adv. Water Resour. 62, 178–206 (2013)
Dehghani, H., Penta, R., Merodio, J.: The role of porosity and solid matrix compressibility on the mechanical behavior of poroelastic tissues. Mater. Res. Express 6(3), 035404 (2018)
Flessner, M.F.: The role of extracellular matrix in transperitoneal transport of water and solutes. Peritoneal Dial. Int. 21(Suppl 3), S24–S29 (2001)
Gambin, B., Kröner, E.: Higher-order terms in the homogenized stress-strain relation of periodic elastic media. Phys. Stat. Solidi B 151, 513–519 (1989)
Hamed, E., Lee, Y., Jasiuk, I.: Multiscale modeling of elastic properties of cortical bone. Acta Mechanica 213, 131–154 (2010)
Holmes, M.H.: Introduction to Perturbation Methods, vol. 20. Springer, Berlin (2012)
Hori, M., Nemat-Nasser, S.: On two micromechanics theories for determining micro-macro relations in heterogeneous solid. Mech. Mater. 31, 667–682 (1999)
Karageorgiou, V., Kaplan, D.: Porosity of 3d biomaterial scaffolds and osteogenesis. Biomaterials 26(27), 5474–5491 (2005)
Kümpel, H.J.: Poroelasticity: parameters reviewed. Geophys. J. Int. 105(3), 783–799 (1991)
Laurila, P., Leivo, I.: Basement membrane and interstitial matrix components form separate matrices in heterokaryons of pys-2 cells and fibroblasts. J. Cell Sci. 104(1), 59–68 (1993)
Lévy, T.: Propagation of waves in a fluid-saturated porous elastic solid. Int. J. Eng. Sci. 17(9), 1005–1014 (1979)
Mei, C.C., Vernescu, B.: Homogenization Methods for Multiscale Mechanics. World scientific, Singapore (2010)
Miller, L., Penta, R.: Effective balance equations for poroelastic composites. Continuum Mech. Thermodyn. (2020)
Moeendarbary, E., Valon, L., Fritzsche, M., Harris, A., Moulding, D., Thrasher, A., Stride, E., L., M., Charras, G.: The cytoplasm of living cells behaves as a poroelastic material. Nat. Mater. 12 (2013)
Pena, A., Bolton, M.D., Pickard, J.D.: Cellular poroelasticity: A theoretical model for soft tissue mechanics. In: Poromechanics, pp. 475–480 (1998)
Penta, R., Ambrosi, D., Quarteroni, A.: Multiscale homogenization for fluid and drug transport in vascularized malignant tissues. Math. Models Methods Appl. Sci. 25(1), 79–108 (2015)
Penta, R., Ambrosi, D., Shipley, R.: Effective governing equations for poroelastic growing media. Q. J. Mech. Appl. Math. 67(1), 69–91 (2014)
Penta, R., Gerisch, A.: Investigation of the potential of asymptotic homogenization for elastic composites via a three-dimensional computational study. Comput. Vis. Sci. 17(4), 185–201 (2015)
Penta, R., Gerisch, A.: The asymptotic homogenization elasticity tensor properties for composites with material discontinuities. Continuum Mech. Thermodyn. 29(1), 187–206 (2017)
Penta, R., Gerisch, A.: An introduction to asymptotic homogenization. In: Multiscale Models in Mechano and Tumor Biology, pp. 1–26. Springer (2017)
Penta, R., Merodio, J.: Homogenized modeling for vascularized poroelastic materials. Meccanica 52(14), 3321–3343 (2017)
Penta, R., Miller, L., Grillo, A., Ramírez-Torres, A., Mascheroni, P., Rodríguez-Ramos, R.: Porosity and diffusion in biological tissues. recent advances and further perspectives. In: Constitutive modelling of solid continua, pp. 311–356. Springer (2020)
Penta, R., Ramírez-Torres, A., Merodio, J., Rodríguez-Ramos, R.: Effective governing equations for heterogenous porous media subject to inhomogeneous body forces. Math. Eng. 3(4), 1–17 (2021)
Ramírez-Torres, A., Di Stefano, S., Grillo, A., Rodríguez-Ramos, R., Merodio, J., Penta, R.: An asymptotic homogenization approach to the microstructural evolution of heterogeneous media. Int. J. Non-Linear Mech. 106, 245–257 (2018)
Ramírez-Torres, A., Penta, R., Rodríguez-Ramos, R., Grillo, A.: Effective properties of hierarchical fiber-reinforced composites via a three-scale asymptotic homogenization approach. Math. Mech. Solids (2019)
Ramírez-Torres, A., Penta, R., Rodríguez-Ramos, R., Grillo, A., Preziosi, L., Merodio, J., Guinovart-Díaz, R., Bravo-Castillero, J.: Homogenized out-of-plane shear response of three-scale fiber-reinforced composites. Computing and Visualization in Science pp. 1–9 (2018)
Royer, P., Recho, P., Verdier, C.: On the quasi-static effective behaviour of poroelastic media containing elastic inclusions. Mech. Res. Commun. 96, 19–23 (2019)
Siklosi, M., Jensen, O.E., Tew, R.H., Logg, A.: Multiscale modeling of the acoustic properties of lung parenchyma. In: ESAIM: Proceedings, vol. 23, pp. 78–97. EDP Sciences (2008)
Smyshlyaev, V.P., Cherednichenko, K.D.: On rigorous derivation of strain gradient effects in the overall behaviour of periodic heterogeneous media. J. Mech. Phys. Solids 48, 1325–1357 (2000)
Tong, L.H., Ding, H.B., Yan, J.W., Xu, C., Lei, Z.: Strain gradient nonlocal biot poromechanics. Int. J. Eng. Sci. 156,(2020)
Wang, H.F.: Theory of Linear Poroelasticity with Applications to Geomechanics and Hydrogeology. Princeton University Press, Oxford (2017)
Weiner, S., Wagner, H.D.: The material bone: structure-mechanical function relations. Annu. Rev. Mater. Sci. 28(1), 271–298 (1998)
Acknowledgements
LM is funded by EPSRC with Project Number EP/N509668/1 and RP is partially funded by EPSRC Grant EP/S030875/1 and EP/T017899/1.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix
Appendix
1.1 Limit cases for the global scale model
It is important to note that our global scale model (132) reduces to previously obtained results when we consider the following limit cases. The first case is in the limit of no fluid present. This means that we are able to set \({\vartheta }^{(0)}\) to zero and therefore \({\dot{\vartheta }}^{(0)}\) is also zero and the relative fluid velocities \(\mathbf{w}_{\mathrm {M}}\) and \(\mathbf{w}_{\mathrm {S}}\) are both zero. In this case the mechanical behaviour of the material is described by only the balance equation with no pressure contribution in the effective stress, Therefore, the model reduces to only two equations and has the form
This is the model for a simple elastic composite material. We also note that the only cell problem that is relevant in this case is (83–86). This model coincides with the models for elastic composites found in the literature [35].
The second limit case we consider is where our subphase has no fluid (i.e. the subphase is purely elastic) and our matrix remains poroelastic. This is the setting considered by [43] and, assuming also incompressibility of the phases, [12]. To reduce our model to this case we assume that \({\varvec{\alpha }}_{\mathrm {S}}=\mathbf{0}\), \(\mathbf{w}_{\mathrm {S}}=0\) and that \(\vartheta _{\mathrm {S}}=0\). Under this assumption our model looks like
where
and \({\widetilde{\mathbb {C}}}\) is the same as in (133). The effective behaviour of our material under these assumptions is characterized by the coefficients \({\widetilde{\mathbb {C}}}\), \({\widetilde{\varvec{\alpha }}}\), \(\widetilde{{\mathsf {W}}}\), \({\widetilde{\varvec{\gamma }}}\) and \({\mathcal {M}}\). We can make the following identifications in our notation with the notation used in [43], where a weak formulation has also been used, which are
We have that our \({\widetilde{\varvec{\gamma }}}\) is identifiable with [43]’s \(A^{\mathrm {eff}}\) up to a change in sign due to the difference in sign used within the ansatz between their work and ours. As noted by [43] the effective elasticity tensor found here is that of elastic composites [35]. It is also possible to show that \(A^{\mathrm {eff}}=G^{\mathrm {eff}}\) and that \(B^{\mathrm {eff}}\) is positive as in [43]. We can also identify our coefficients with those used in [12]. We enforce the assumption that our material is incompressible in both phases to our coefficients in (169) and then we can make the following identifications
We can also find a correspondence the cell problems found in [12, 43] and those found here. The cell problem (83–86) which is the cell problem for elastic composites is the cell problem found in [12] when the assumptions of isotropy and incompressibility are applied and the cell problem found in [43] where a weak formulation has been used. The second cell problem (87–90) reduces in this limit case. We have that \({\varvec{\alpha }}_{\mathrm {S}}=0\) due to there being no fluid in the subphase. The reduced cell problem is
When the assumptions of isotropy and incompressibility are made we also have that \({\varvec{\alpha }}_{\mathrm {M}}=1\). This means that the right hand side of (172) and (173) are both zero. This again coincides with the cell problems found in [12] and [43]. The anisotropic Poisson problem (113–116) reduces in this limit also. Since there is no fluid in the subphase from the commencement then there is no requirement for the continuity of pressure interface condition or for a Darcy’s law equation in the subphase, that is \(\mathbf{w}_{\mathrm {S}}=0\). This means that the problem retains only two equations. The reduced cell problem is therefore
This corresponds to the cell problem in [43] and the cell problem in [12] when again in this latter case the assumptions of isotropy and incompressibility are made as well as assuming the hydraulic conductivity tensor \({\mathsf {K}}_{\mathrm {M}}=1\).
1.2 Computational scheme
We aim to provide a clear step-by-step guide to finding our effective coefficients and solving our global scale model (132) encoding structural details from three scales. We also provide, where available, particular references that would assist the reader with the type of numerical simulations that would need to be carried out. Since we have made the assumption of global scale uniformity of the material then we can propose the following steps to solve the model. The process is as follows:
-
1.
We begin by fixing the original material properties of the poroelastic matrix and the poroelastic subphases at the local scale. We require the effective elasticity tensors \({\mathbb {C}}_{\mathrm {M}}\) and \({\mathbb {C}}_{\mathrm {S}}\), the Biot’s tensors \({\varvec{\alpha }}_{\mathrm {M}}\) and \({\varvec{\alpha }}_{\mathrm {S}}\), the Biot’s moduli \({\mathcal {M}}_{\mathrm {M}}\) and \({\mathcal {M}}_{\mathrm {S}}\) and finally the hydraulic conductivities \({\mathsf {K}}_{\mathrm {M}}\) and \({\mathsf {K}}_{\mathrm {S}}\) from both the matrix and the subphases. Under the assumption of isotropy we are required to fix 5 parameters for the matrix and 5 parameters for the subphase. These parameters are two independent elastic constants e.g. the Poisson ratio and Young’s modulus (or alternatively the Lamé constants), hydraulic conductivity, Biot’s coefficient and Biot’s modulus.
-
2.
The local scale geometry then must be defined and we fix a single periodic cell at this stage.
-
3.
We would then be able to solve the elastic-type cell problems (83–86) and (87–90) to obtain the auxiliary tensors \({\mathbb {L}}_{\mathrm {M}}, {\mathbb {L}}_{\mathrm {S}}, {\varvec{\tau }}_{\mathrm {M}}\) and \({\varvec{\tau }}_{\mathrm {S}}\) which appear in the global scale model coefficients. The cell problems to be solved are, in components,
$$\begin{aligned} \frac{\partial }{\partial y_j}\left( {\mathcal {C}}^{\mathrm {M}}_{ijpq}\zeta _{pq}^{kl}(B^{\mathrm {M}})\right) +\frac{\partial {\mathcal {C}}_{ijkl}^{\mathrm {M}}}{\partial y_j}=0&\qquad \text{ in }\qquad \varOmega _{\mathrm {M}}, \end{aligned}$$(178)$$\begin{aligned} \frac{\partial }{\partial y_j}\left( {\mathcal {C}}^{\mathrm {S}}_{ijpq}\zeta _{pq}^{kl}(B^{\mathrm {S}})\right) +\frac{\partial {\mathcal {C}}_{ijkl}^{\mathrm {S}}}{\partial y_j}=0&\qquad \text{ in }\qquad \varOmega _{\mathrm {S}}, \end{aligned}$$(179)$$\begin{aligned} {\mathcal {C}}^{\mathrm {M}}_{ijpq}\zeta _{pq}^{kl}\left( B^{\mathrm {M}}\right) n_{j}-{\mathcal {C}}^{\mathrm {S}}_{ijpq}\zeta _{pq}^{kl}(B^{\mathrm {S}})n_j=\left( {\mathcal {C}}^{\mathrm {S}}-{\mathcal {C}}^{\mathrm {M}}\right) _{ijkl}n_j&\qquad \text{ on }\qquad \varUpsilon , \end{aligned}$$(180)$$\begin{aligned} B^{\mathrm {M}}_{ikl}=B^{\mathrm {S}}_{ikl}&\qquad \text{ on }\qquad \varUpsilon , \end{aligned}$$(181)as well as another elastic-type cell problem driven by variations in the constituents’ compressibility
$$\begin{aligned} \frac{\partial }{\partial y_j}\big ({\mathcal {C}}^{\mathrm {M}}_{ijpq}\zeta _{pq}({ b}^{\mathrm {M}})\big )=\frac{\partial \alpha _{ij}^{\mathrm {M}}}{\partial y_j}&\qquad \text{ in }\qquad \varOmega _{\mathrm {M}}, \end{aligned}$$(182)$$\begin{aligned} \frac{\partial }{\partial y_j}\big ({\mathcal {C}}^{\mathrm {S}}_{ijpq}\zeta _{pq}({b}^{\mathrm {S}})\big )=\frac{\partial \alpha _{ij}^{\mathrm {S}}}{\partial y_j}&\qquad \text{ in }\qquad \varOmega _{\mathrm {S}}, \end{aligned}$$(183)$$\begin{aligned} {\mathcal {C}}^{\mathrm {M}}_{ijpq}\zeta _{pq}\left( {b}^{\mathrm {M}}\right) n_{j}-{\mathcal {C}}^{\mathrm {S}}_{ijpq}\zeta _{pq}\left( {b}^{\mathrm {S}}\right) n_j=-\left( \alpha ^{\mathrm {S}}-\alpha ^{\mathrm {M}}\right) _{ij}n_j&\qquad \text{ on }\qquad \varUpsilon , \end{aligned}$$(184)$$\begin{aligned} b^{\mathrm {M}}_{i}=b^{\mathrm {S}}_{i}&\qquad \text{ on }\qquad \varUpsilon , \end{aligned}$$(185)where we have used the notation
$$\begin{aligned} \zeta _{pq}^{kl}\left( B^{\beta }\right) =\frac{1}{2}\bigg (\frac{\partial B_{pkl}^{\beta }}{\partial y_q}+\frac{\partial B_{qkl}^{\beta }}{\partial y_p}\bigg )\quad \text{ and } \quad \zeta _{pq}\left( \mathbf{b}^{\beta }\right) =\frac{1}{2}\bigg (\frac{\partial b_p^{\beta }}{\partial y_q}+\frac{\partial b_q^{\beta }}{\partial y_p}\bigg ), \end{aligned}$$(186)and the superscript \(\beta =\mathrm {M, S}\) refers to either the matrix or the subphase. The solution of the problem (178–181) can be obtained by solving six elastic-type cell problems by fixing the couple of indices \(k,l=1,2,3\). By doing this we can see that \(\zeta _{pq}^{kl}(B^{\beta })\) represents a strain and that for each fixed couple of indices k, l we have a linear elastic problem. For an example of where this cell problem has been solved computationally, see the recent works [34] and [35]. The solution of problem (182–185) is obtained by solving 3 cell problems for each \(i=1,2,3\).
The auxiliary second rank tensors \({\mathsf {R}}_{\mathrm {M}}\) and \({\mathsf {R}}_{\mathrm {S}}\) can be computed by solving the vector cell problem given by (113–116). The latter corresponds to three scalar anisotropic Poisson’s problems (for each \(j=1,2,3\)) equipped with continuity and transmission interface conditions, component-wise. The cell problem in components is
$$\begin{aligned} \frac{\partial }{\partial y_i}\bigg (K_{il}^{\mathrm {M}}\frac{\partial \hat{\vartheta }^{\mathrm {M}}_{j}}{\partial y_l}\bigg )=-\frac{\partial K_{ij}^{\mathrm {M}}}{\partial y_i}&\qquad \text{ in }\qquad \varOmega _{\mathrm {M}}, \end{aligned}$$(187)$$\begin{aligned} \frac{\partial }{\partial y_i}\bigg (K_{il}^{\mathrm {S}}\frac{\partial \hat{\vartheta }^{\mathrm {S}}_{j}}{\partial y_l}\bigg )=-\frac{\partial K_{ij}^{\mathrm {S}}}{\partial y_i}&\qquad \text{ in }\qquad \varOmega _{\mathrm {S}}, \end{aligned}$$(188)$$\begin{aligned} \hat{\vartheta }^{\mathrm {M}}_{j}= \hat{\vartheta }^{\mathrm {S}}_{j}&\qquad \text{ on }\qquad \varUpsilon ,\ \end{aligned}$$(189)$$\begin{aligned} \bigg ( K_{il}^{\mathrm {M}}\frac{\partial \hat{\vartheta }^{\mathrm {M}}_{j}}{\partial y_l}-K_{il}^{\mathrm {S}}\frac{\partial \hat{\vartheta }^{\mathrm {S}}_{j}}{\partial y_l}\bigg )n_i=\left( K^{\mathrm {S}}-K^{\mathrm {M}}\right) _{ij}n_i&\qquad \text{ on }\qquad \varUpsilon . \end{aligned}$$(190)This problem is the same as the classical problem that arises from applying the asymptotic homogenization technique to the diffusion problem and porous media problems, see [4, 13], and [39]
-
4.
We also require one more condition to ensure uniqueness of solution. We can enforce that the cell averages of the cell problem solutions are zero. That is, \(\langle \mathsf {B}_{\mathrm {M}}+ \mathsf {B}_{\mathrm {S}}\rangle _{\scriptscriptstyle \varOmega }=0\), \(\langle \mathbf{b}_{\mathrm {M}}+ \mathbf{b}_{\mathrm {S}}\rangle _{\scriptscriptstyle \varOmega }=0\) and \(\langle {\hat{\varvec{\vartheta }}}_{\mathrm {M}}+ {\hat{\varvec{\vartheta }}}_{\mathrm {S}}\rangle _{\scriptscriptstyle \varOmega }=0\)
-
5.
The auxiliary tensors arising form the cell problems (i.e. the quantities \({\mathbb {L}}_{\mathrm {M}}\), \({\mathbb {L}}_{\mathrm {S}}\), \({\varvec{\tau }}_{\mathrm {M}}\), \({\varvec{\tau }}_{\mathrm {S}}\), \({\mathsf {R}}_{\mathrm {M}}\) and \({\mathsf {R}}_{\mathrm {S}}\)) can then be used to determine the global scale model coefficients.
-
6.
The geometry at the global scale then must be prescribed. The boundary conditions for the homogenized cell boundary must also be given, and the system is to be supplemented with initial conditions for the global scale solid displacement and pressure.
-
7.
Finally, the global scale model (132) for a double poroelastic material can then be solved.
Remark 6
(Computational scheme on three scales) If porescale data was available for our material then we would be able to obtain a solution encoding structural detail on three scales. We would begin by fixing the original material properties on the porescale. This includes fixing the stiffness of the solid phase in both the matrix and subphase, defining the pore structures, and determining the fluid properties, which are, the viscosity and potentially the bulk moduli for compressible fluids. At this scale we are considering both these poroelastic materials separately. We then must define the porescale geometry for both the matrix and the subphases. This includes fixing a periodic cell in both the matrix and the subphases. We would then be able to solve the separate cell problems for the matrix and the subphase. These cell problems are the standard cell problems of poroelasticity found in [10] and with a step-by step computational scheme found in [38]. These cell problem solutions would then be used to determine the local scale coefficients such as the elasticity tensors \({\mathbb {C}}_{\mathrm {M}}\) and \({\mathbb {C}}_{\mathrm {S}}\), the Biot’s tensors of coefficients in the matrix and the subphases \({\varvec{\alpha }}_{\mathrm {M}}\) and \({\varvec{\alpha }}_{\mathrm {S}}\), the Biot’s moduli \({\mathcal {M}}_{\mathrm {M}}\) and \({\mathcal {M}}_{\mathrm {S}}\), and the hydraulic conductivities \({\mathsf {K}}_{\mathrm {M}}\) and \({\mathsf {K}}_{\mathrm {S}}\), which would then be used in Step 1 above. For an example of where these elastic and fluid cell problems have been solved numerically see the recent work [18].
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Miller, L., Penta, R. Double poroelasticity derived from the microstructure. Acta Mech 232, 3801–3823 (2021). https://doi.org/10.1007/s00707-021-03030-4
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00707-021-03030-4