Investigation on cross-scale indentation scaling relationships of elastic–plastic solids

Abstract

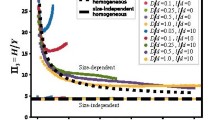
Indentation scaling relationships provide normalized guidance for measuring and predicting mechanical properties in indentation experiments. At the nano-scale, the material size-effect is significant, while conventional scaling relationships fail to depict this phenomenon in nanoindentation precisely. In the present research, cross-scale indentation scaling relationships are investigated using a strain gradient theory. The nanoindentation response is found to be sensitive to different material parameters, including the material intrinsic length, yield stress, and work-hardening exponent across size-scales. If the strain gradient effect is ignored, the nanoindentation scaling relationships approach the macroscopic conventional ones. The cross-scale indentation scaling relationships obtained in the form of dimensionless functions in this work provide quantitative references to instrumented indentation tests on multiple size-scales, coinciding well with experimental results. The understanding of nanoindentation hardness is enhanced by the present work.

Appendix A: Conventional theory of mechanism-based strain gradient

Multiple material models have been suggested by many researchers to overcome the limitation that the conventional theory failed to predict the size-effect of materials. A strain gradient term together with a length-dimension parameter were introduced into the continuum constitutive relation, which was suggested by many scholars [64, 65]. Wei and Hutchinson performed a strain gradient plasticity theory on the crack growth and fracture problem [66], and Nix and Gao applied it with the indentation of crystalline materials [42]. Gao et al. proposed a mechanism-based strain gradient plasticity (MSG) theory [67, 68] established from the Taylor dislocation model [69, 70]. This mechanism-based theory gave a reasonable explanation of the length parameter introduced by the strain gradient. Based on the MSG theory, Huang et al. introduced a conventional theory of mechanism-based strain gradient plasticity (CMSG) [43, 44, 71, 72], which avoids the higher-order boundary conditions and hence is more feasible than earlier theories.

The taylor dislocation model gives the relation between dislocation density and the shear flow stress $\tau$ as

$$\tau = \alpha \mu b\sqrt \rho = \alpha \mu b\sqrt {\rho_{{\text{S}}} + \rho_{{\text{G}}} }$$

(10)

where $b$ is the magnitude of the Burgers vector, and $\mu$ the shear modulus, $\alpha$ an empirical parameter taking a value in the range from 0.2 to 0.5 for most materials, and $\rho$ the total dislocation density, composed by the statistically stored dislocation (SSD) density $\rho_{{\text{S}}}$ and the geometrically necessary dislocation (GND) density $\rho_{{\text{G}}}$.

The flow stress $\sigma_{{{\text{flow}}}}$ is related to the shear flow stress by

$$\sigma_{{{\text{flow}}}} = M\tau = M\alpha \mu b\sqrt {\rho_{{\text{S}}} + \rho_{{\text{G}}} }$$

(11)

with the Taylor factor $M = 3.06$ for most face-centered-cubic (fcc) metals. In the uniaxial test, $\rho_{{\text{S}}}$ can be determined where $\rho_{{\text{G}}}$ equals zero,

$$\rho_{{\text{S}}} = \left( {\frac{{\sigma_{{{\text{flow}}}} }}{M\alpha \mu b}} \right)^{2} ,$$

(12)

and $\rho_{{\text{G}}}$ is related to the effective plastic strain gradient $\eta^{p}$ by

$$\rho_{{\text{G}}} = \overline{r}\frac{{\eta^{p} }}{b}$$

(13)

introduced by Nye with a factor of $\overline{r} = 1.90$ for fcc metals. Thus, in a microscopic view, the flow stress is

$$\sigma_{{{\text{flow}}}} = M\tau = M\alpha \mu b\sqrt {\rho_{{\text{S}}} + \overline{r}\frac{{\eta^{p} }}{b}} .$$

(14)

Meanwhile, in a macroscopic view, the flow stress is also

$$\sigma_{{{\text{flow}}}} = \sigma_{{\text{Y}}} f\left( {\varepsilon^{p} } \right)$$

(15)

where $\sigma_{{\text{Y}}}$ is the initial yield stress, $\varepsilon^{p}$ is the effective plastic strain, and the function $f$ between them can be determined by the uniaxial tension test. One of the most used models is the power-law work-hardening model,

$$f\left( {\varepsilon^{p} } \right) = \left( {1 + \frac{{E\varepsilon^{p} }}{{\sigma_{{\text{Y}}} }}} \right)^{n} ,$$

(16)

where $E$ is the elastic modulus and $n$ the work-hardening exponent. Linking the microscopic laws with the macroscopic ones, the SSD density $\rho_{{\text{S}}}$ is

$$\rho_{{\text{S}}} = \left( {\frac{{\sigma_{{\text{Y}}} f\left( {\varepsilon^{p} } \right)}}{M\alpha \mu b}} \right)^{2} , $$

(17)

and from Eq. (14),

$$\sigma_{{\text{flow }}} = \sqrt {\left[ {\sigma_{{\text{Y}}} f\left( {\varepsilon^{p} } \right)} \right]^{2} + (M\alpha \mu b)^{2} \overline{r}\frac{{\eta^{p} }}{b}} = \sigma_{{\text{Y}}} \sqrt {f^{2} \left( {\varepsilon^{p} } \right) + l\eta^{p} }$$

(18)

where $l$ is introduced as the material intrinsic length by Gao et al. [67], where

$$l = M^{2} \overline{r}\alpha^{2} \left( {\frac{\mu }{{\sigma_{{\text{Y}}} }}} \right)^{2} b \approx 18\alpha^{2} \left( {\frac{\mu }{{\sigma_{{\text{Y}}} }}} \right)^{2} b .$$

(19)

The calculation of the effective plastic strain gradient $\eta^{p}$ in Eq. (13) is proposed by Gao et al. as

$$\eta^{p} = \sqrt {\frac{1}{4}\eta_{ijk}^{p} \eta_{ijk}^{p} } ,$$

(20)

$$\eta_{ijk}^{p} = \varepsilon_{ik,j}^{p} + \varepsilon_{jk,i}^{p} - \varepsilon_{ij,k}^{p}$$

(21)

where $\varepsilon_{ij}^{p}$ is the plastic strain tensor. The numerical calculation of $\eta^{p}$ in an axisymmetric model could be referred to Swaddiwudhipong et al.’s work [45].

Huang et al. suggested a visco-plastic formula to relate the effective stress $\sigma_{{\text{e}}}$ directly to the plastic strain rate $\dot{\varepsilon }^{p}$ to avoid the involvement of the higher-order effective stress rate $\dot{\sigma }_{{\text{e}}}$ by setting a large value of the exponent $m,m \ge 20$. Together with Eq. (18), the effective strain gradient is introduced by the flow stress as

$$\dot{\varepsilon }^{p} = \dot{\varepsilon }\left( {\frac{{\sigma_{{\text{e}}} }}{{\sigma_{{\text{flow }}} }}} \right)^{m} = \dot{\varepsilon }\left( {\frac{{\sigma_{{\text{e}}} }}{{\sigma_{{\text{Y}}} \sqrt {f^{2} \left( {\varepsilon^{p} } \right) + l\eta^{p} } }}} \right)^{m}$$

(22)

where $\dot{\varepsilon } = \sqrt {\frac{2}{3}\dot{\varepsilon }_{ij}^{\prime } \dot{\varepsilon }_{ij}^{\prime } }$ is the effective strain rate.

Thus, similar to the conventional plasticity theory, the strain rate is composed of the elastic part and the plastic part as

$$\dot{\varepsilon }_{ij} = \dot{\varepsilon }_{ij}^{e} + \dot{\varepsilon }_{ij}^{p} = \frac{1}{2\mu }\dot{\sigma }_{ij}^{\prime } + \frac{{\dot{\sigma }_{kk} }}{9K}\delta_{ij} + \frac{{3\dot{\varepsilon }^{p} }}{{2\sigma_{{\text{e}}} }}\sigma_{ij}^{\prime } ,$$

(23)

and the elastic strain rate is

$$\dot{\varepsilon }_{ij}^{e} = \frac{1}{2\mu }\dot{\sigma }_{ij}^{\prime } + \frac{{\dot{\sigma }_{kk} }}{9K}\delta_{ij}$$

(24)

where $\dot{\sigma }_{ij}^{\prime }$ is the deviatoric stress rate, $K$ the bulk modulus, and $\delta_{ij}$ the Kronecker delta. Hence, with $\dot{\varepsilon }_{kk} = \frac{{\dot{\sigma }_{kk} }}{3K}$, the deviatoric strain rate is

$$\dot{\varepsilon }_{ij}^{\prime } = \dot{\varepsilon }_{ij} - \frac{1}{3}\dot{\varepsilon }_{kk} \delta_{ij} = \frac{1}{2\mu }\dot{\sigma }_{ij}^{\prime } + \frac{{3\dot{\varepsilon }^{p} }}{{2\sigma_{{\text{e}}} }}\sigma_{ij}^{\prime } ,$$

(25)

Substituting Eq. (22) into Eq. (25), the deviatoric strain rate is related to the effective strain gradient by

$$\dot{\varepsilon }_{ij}^{\prime } = \frac{1}{2\mu }\dot{\sigma }_{ij}^{\prime } + \frac{{3\dot{\varepsilon }}}{{2\sigma_{{\text{e}}} }}\left( {\frac{{\sigma_{{\text{e}}} }}{{\sigma_{{\text{Y}}} \sqrt {f^{2} \left( {\varepsilon^{p} } \right) + l\eta^{p} } }}} \right)^{m} \sigma_{ij}^{\prime }$$

(26)

which is commonly written as

$$\dot{\sigma }_{ij} = K\dot{\varepsilon }_{kk} \delta_{ij} + 2\mu \left[ {\dot{\varepsilon }_{ij}^{\prime } - \frac{{3\dot{\varepsilon }}}{{2\sigma_{{\text{e}}} }}\left( {\frac{{\sigma_{{\text{e}}} }}{{\sigma_{{\text{Y}}} \sqrt {f^{2} \left( {\varepsilon^{p} } \right) + l\eta^{p} } }}} \right)^{m} \sigma_{ij}^{\prime } } \right] .$$

(27)

Equation (27) suggested by Huang et al. is the constitutive relation with the consideration of the plastic strain gradient by introducing a material intrinsic length. With this length-dimension parameter, the difference between size-scales of the material can be hence depicted. When $l \to 0$ or correspondingly the length scale of deformation is much larger than the material intrinsic length, the CMSG theory degenerates into the conventional theory.