A co-rotational triangular finite element for large deformation analysis of smooth, folded and multi-shells

Abstract

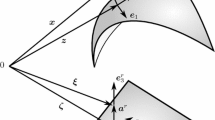
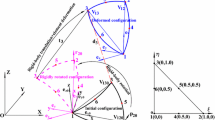
A six-node co-rotational curved triangular shell finite element with a novel rotation treatment for folded and multi-shell structures is presented. Different from other co-rotational triangular element formulations, rotations are not represented by axial (pseudo) vectors, but by components of polar (proper) vectors, of which additivity and commutativity lead to symmetry of the tangent stiffness matrices in both local and global coordinate systems. In the co-rotational local coordinate system, the two smallest components of the shell director are defined as the nodal rotational variables. Similarly, the two smallest components of each director in the global coordinate system are adopted as the global rotational variables for nodes located either on smooth shells or away from non-smooth shell intersections. At intersections of folded and multi-shells, global rotational variables are defined as three selected components of an orthogonal triad initially oriented along the global coordinate system axes. As such, the vectorial rotational variables enable simple additive update of all nodal variables in an incremental-iterative procedure, resulting in significant enhancement in computational efficiency for large deformation analysis. To alleviate membrane and shear locking phenomena, an assumed strain method is employed in obtaining the element tangent stiffness matrices and the internal force vector. The effectiveness of the presented co-rotational triangular shell element formulation is verified by analyzing several benchmark problems of smooth, folded and multi-shell structures undergoing large displacements and large rotations.

Appendices

Appendices

1.1 Appendix A: Various derivatives of strains with respect to local nodal variables

The first-order derivatives of membrane strains with respect to local nodal variables lead to the following gradient matrix:

$${\mathbf{B}}_{m} = \left[ {\begin{array}{*{20}c} {{\mathbf{B}}_{m1} } &\quad {\mathbf{0}} &\quad \ldots &\quad {{\mathbf{B}}_{m6} } &\quad {\mathbf{0}} \\ \end{array} } \right]$$

(47)

in which the sub-matrix is expressed as

$${\mathbf{B}}_{mi} = \left[ {\begin{array}{*{20}c} {N_{i,x} } &\quad 0 &\quad 0 \\ 0 &\quad {N_{i,y} } &\quad 0 \\ {N_{i,y} } &\quad {N_{i,x} } &\quad 0 \\ \end{array} } \right],\quad i = 1,2, \ldots ,6.$$

(48)

Following Eqs. (33a, b), the shape function derivatives can be expressed as follows:

$$N_{i,x} = J_{11}^{ - 1} N_{i,\xi } + J_{12}^{ - 1} N_{i,\eta },$$

(49)

$$N_{i,y} = J_{21}^{ - 1} N_{i,\xi } + J_{22}^{ - 1} N_{i,\eta },$$

(50)

where $J_{jk}^{ - 1} \;\left( {j,k = 1,2} \right)$ is the component of the inverse Jacobian matrix at the jth row and kth column; $N_{i,\xi }$ and $N_{i,\eta }$ are, respectively, the first-order derivative of the shape function N_i with respect to $\xi$ and $\eta$.

The first-order derivatives of shear strains with respect to local nodal variables lead to the following gradient matrix:

$$\varvec{B}_{\gamma } = \left[ {\begin{array}{*{20}c} {\varvec{B}_{\gamma 1} } & {\varvec{B}_{\gamma 2} } & \ldots & {\varvec{B}_{\gamma 11} } & {\varvec{B}_{\gamma 12} } \\ \end{array} } \right]$$

(51)

in which

$${\mathbf{B}}_{\gamma (2i - 1)} = \left[ {\begin{array}{*{20}c} 0 &\quad 0 &\quad {N_{i,x} } \\ 0 &\quad 0 &\quad {N_{i,y} } \\ \end{array} } \right]\quad i = 1,2, \ldots ,6,$$

(52)

$${\mathbf{B}}_{\gamma (2i)} = \left[ {\begin{array}{*{20}c} {N_{i} } &\quad 0 \\ 0 &\quad {N_{i} } \\ \end{array} } \right]\quad i = 1,2, \ldots ,6.$$

(53)

The first-order derivatives of bending strains with respect to local nodal variables lead to the following gradient matrix:

$${\mathbf{B}}_{b} = \left[ {\begin{array}{*{20}c} {\mathbf{0}} & {{\mathbf{B}}_{b1} } & \ldots & {\mathbf{0}} & {{\mathbf{B}}_{b6} } \\ \end{array} } \right]$$

(54)

in which

$${\mathbf{B}}_{bi} = \left[ {\begin{array}{*{20}c} {N_{i,x} } &\quad 0 \\ 0 &\quad {N_{i,y} } \\ {N_{i,y} } &\quad {N_{i,x} } \\ \end{array} } \right]\quad i = 1,2, \ldots ,6.$$

(55)

The first-order derivatives of assumed membrane strains with respect to local nodal variables lead to the following gradient matrix

$${\bar{\mathbf{B}}}_{m} = \left[ {\begin{array}{*{20}c} {{\bar{\mathbf{B}}}_{m1} } &\quad {\mathbf{0}} &\quad \ldots &\quad {{\bar{\mathbf{B}}}_{m6} } &\quad {\mathbf{0}} \\ \end{array} } \right]$$

(56)

in which the sub-matrix is expressed as

(57)

The first-order derivatives of assumed shear strains with respect to local nodal variables lead to the following gradient matrix:

$${\bar{\mathbf{B}}}_{\gamma } = \left[ {\begin{array}{*{20}c} {{\bar{\mathbf{B}}}_{\gamma 1} } & {{\bar{\mathbf{B}}}_{\gamma 2} } & \ldots & {{\bar{\mathbf{B}}}_{\gamma 11} } & {{\bar{\mathbf{B}}}_{\gamma 12} } \\ \end{array} } \right]$$

(58)

in which the sub-matrices are expressed as

(59)

$${\bar{\mathbf{B}}}_{\gamma (2i)} = \left[ {\begin{array}{*{20}c} {N_{j,x} \left( {\left. {\displaystyle\int_{{\xi_{1} }}^{{\xi_{j} }} {J_{1,1} N_{i} d\xi } } \right|\left. {_{{\eta = \eta_{j} }} + \displaystyle\int_{{\eta_{1} }}^{{\eta_{j} }} {J_{2,1} N_{i} d\eta } } \right|_{{\xi = \xi_{j} }} } \right)} & 0 \\ 0 & {N_{j,y} \left( {\left. {\displaystyle\int_{{\xi_{1} }}^{{\xi_{j} }} {J_{1,2} N_{i} d\xi } } \right|_{{\eta = \eta_{j} }} + \left. {\displaystyle\int_{{\eta_{1} }}^{{\eta_{j} }} {J_{2,2} N_{i} d\eta } } \right|_{{\xi = \xi_{j} }} } \right)} \\ \end{array} } \right],$$

(60)

1.2 Appendix B: Sub-matrices of transformation matrix T and its derivatives with respect to global nodal variables

The sub-matrices of the transformation matrix T can be expressed as

$$\frac{{\partial {\mathbf{t}}_{k} }}{{\partial {\mathbf{d}}_{l}^{T} }} = \frac{{\partial {\mathbf{R}}}}{{\partial {\mathbf{d}}_{l}^{T} }}({\mathbf{d}}_{k} + {\mathbf{v}}_{k0} ) + {\mathbf{R}}\delta_{kl} {\mathbf{I}} = \left( {\frac{\partial }{{\partial {\mathbf{d}}_{l}^{T} }}\left[ {\begin{array}{*{20}c} {{\mathbf{e}}_{x}^{T} } \\ {{\mathbf{e}}_{y}^{T} } \\ {{\mathbf{e}}_{z}^{T} } \\ \end{array} } \right]} \right)({\mathbf{d}}_{k} + {\mathbf{v}}_{k0} ) + {\mathbf{R}}\delta_{kl} {\mathbf{I}}.$$

(61)

If Node k is within a piece of smooth shell or away from intersections of non-smooth shells, two vectorial rotational variables are employed in the global coordinate system. Hence, the corresponding sub-matrices of ${\mathbf{T}}$ are evaluated as follows:

$$\frac{{\partial {\varvec{\uptheta}}_{k} }}{{\partial {\mathbf{d}}_{l}^{T} }} = \frac{{\partial {\mathbf{R}}_{h} }}{{\partial {\mathbf{d}}_{l}^{T} }}{\mathbf{p}}_{k} = \left( {\frac{\partial }{{\partial {\mathbf{d}}_{l}^{T} }}\left[ {\begin{array}{*{20}c} {{\mathbf{e}}_{x}^{T} } \\ {{\mathbf{e}}_{y}^{T} } \\ \end{array} } \right]} \right){\mathbf{p}}_{k},$$

(62)

$$\frac{{\partial {\varvec{\uptheta}}_{k} }}{{\partial {\mathbf{n}}_{gl}^{T} }} = {\mathbf{R}}_{h} \delta_{kl} \frac{{\partial {\mathbf{p}}_{k} }}{{\partial {\mathbf{n}}_{gl}^{T} }} = \left[ {\begin{array}{*{20}c} {{\mathbf{e}}_{x}^{T} } \\ {{\mathbf{e}}_{y}^{T} } \\ \end{array} } \right]\delta_{kl} \frac{{\partial {\mathbf{p}}_{k} }}{{\partial {\mathbf{n}}_{gl}^{T} }},$$

(63)

$$\frac{{\partial {\mathbf{e}}_{x} }}{{\partial {\mathbf{d}}_{l}^{T} }} = \left( {\frac{{\mathbf{I}}}{{\left| {{\mathbf{v}}_{12} } \right|}} - \frac{{{\mathbf{v}}_{12} \otimes {\mathbf{v}}_{12} }}{{\left| {{\mathbf{v}}_{12} } \right|^{3} }}} \right)\frac{{\partial {\mathbf{v}}_{12} }}{{\partial {\mathbf{d}}_{l}^{T} }},$$

(64)

$$\frac{{\partial {\mathbf{e}}_{z} }}{{\partial {\mathbf{d}}_{l}^{T} }} = \left[ {\frac{{\mathbf{I}}}{{\left| {{\mathbf{v}}_{12} \times {\mathbf{v}}_{13} } \right|}} - \frac{{\left( {{\mathbf{v}}_{12} \times {\mathbf{v}}_{13} } \right) \otimes \left( {{\mathbf{v}}_{12} \times {\mathbf{v}}_{13} } \right)}}{{\left| {{\mathbf{v}}_{12} \times {\mathbf{v}}_{13} } \right|^{3} }}} \right]\left( {\frac{{\partial {\mathbf{v}}_{12} }}{{\partial {\mathbf{d}}_{l}^{T} }} \times {\mathbf{v}}_{13} + {\mathbf{v}}_{12} \times \frac{{\partial {\mathbf{v}}_{13} }}{{\partial {\mathbf{d}}_{l}^{T} }}} \right),$$

(65)

$$\frac{{\partial {\mathbf{e}}_{y} }}{{\partial {\mathbf{d}}_{l}^{T} }} = \frac{{\partial {\mathbf{e}}_{z} }}{{\partial {\mathbf{d}}_{l}^{T} }} \times {\mathbf{e}}_{x} + {\mathbf{e}}_{z} \times \frac{{\partial {\mathbf{e}}_{x} }}{{\partial {\mathbf{d}}_{l}^{T} }}.$$

(66)

In Eqs. (64)–(65), $\frac{{\partial {\mathbf{v}}_{12} }}{{\partial {\mathbf{d}}_{l}^{T} }} = - {\mathbf{I}}$, $l = 1$; $\frac{{\partial {\mathbf{v}}_{12} }}{{\partial {\mathbf{d}}_{l} }} = {\mathbf{I}}$, $l = 2$; $\frac{{\partial {\mathbf{v}}_{12} }}{{\partial {\mathbf{d}}_{l}^{T} }} = 0$, $l =$ 3, 4, 5 or 6; $\frac{{\partial {\mathbf{v}}_{13} }}{{\partial {\mathbf{d}}_{l}^{T} }} = - {\mathbf{I}}$, $l = 1$; $\frac{{\partial {\mathbf{v}}_{13} }}{{\partial {\mathbf{d}}_{l}^{T} }} = {\mathbf{I}}$, $l = 2$; $\frac{{\partial {\mathbf{v}}_{13} }}{{\partial {\mathbf{d}}_{l} }} = 0$, $l =$ 2, 4, 5 or 6, and

$$\frac{{\partial {\mathbf{p}}_{k} }}{{\partial {\mathbf{n}}_{gk}^{T} }} = \left[ {\begin{array}{*{20}c} {\frac{{\partial p_{k,X} }}{{\partial p_{k,n} }}} & {\frac{{\partial p_{k,X} }}{{\partial p_{k,m} }}} \\ {\frac{{\partial p_{k,Y} }}{{\partial p_{k,n} }}} & {\frac{{\partial p_{k,Y} }}{{\partial p_{k,m} }}} \\ {\frac{{\partial p_{k,Z} }}{{\partial p_{k,n} }}} & {\frac{{\partial p_{k,Z} }}{{\partial p_{k,m} }}} \\ \end{array} } \right],$$

(67)

where $p_{k,X}$, $p_{k,Y}$, $p_{k,Z}$ are the three components of the shell director ${\mathbf{p}}_{i}$ along the directions of the global coordinate axes; $p_{k,n} ,p_{k,m}$ are the two vectorial rotational variables of Node $i$, which are the two smallest components among $p_{k,X}$, $p_{k,Y}$, $p_{k,Z}$; $\frac{{\partial p_{k,n} }}{{\partial p_{k,n} }} = \frac{{\partial p_{k,m} }}{{\partial p_{k,m} }} = 1$; $\frac{{\partial p_{k,n} }}{{\partial p_{k,m} }} = \frac{{\partial p_{k,m} }}{{\partial p_{k,n} }} = 0$; $\frac{{\partial p_{k,l} }}{{\partial p_{k,n} }} = - \frac{{p_{k,n} }}{{p_{k,l} }}$ and $\frac{{\partial p_{k,l} }}{{\partial p_{k,m} }} = - \frac{{p_{k,m} }}{{p_{k,l} }}$, $l \ne n \ne m,$ $l,n,m \in \left\{ {X,Y,Z} \right\}$.

If Node k is located at an intersection of non-smooth shells, three vectorial rotational variables are employed in the global coordinate system, which are the two smallest components of one vector and the smallest or second smallest component of another vector of an orthogonal triad oriented initially to three axes of the global coordinate system, and thus

$$\frac{{\partial {\varvec{\uptheta}}_{i} }}{{\partial {\mathbf{d}}_{j}^{T} }} = \frac{{\partial {\mathbf{R}}_{h} }}{{\partial {\mathbf{d}}_{j}^{T} }}{\mathbf{R}}_{i}^{T} {\mathbf{R}}_{i0} {\mathbf{p}}_{i0} = \frac{\partial }{{\partial {\mathbf{d}}_{j}^{T} }}\left[ {\begin{array}{*{20}c} {{\mathbf{e}}_{x}^{T} } \\ {{\mathbf{e}}_{y}^{T} } \\ \end{array} } \right]{\mathbf{R}}_{i}^{T} {\mathbf{R}}_{i0} {\mathbf{p}}_{i0},$$

(68)

$$\frac{{\partial {\varvec{\uptheta}}_{i} }}{{\partial {\mathbf{n}}_{gj}^{T} }} = \delta_{ij} {\mathbf{R}}_{h} \frac{{\partial {\mathbf{R}}_{i}^{T} }}{{\partial {\mathbf{n}}_{gj}^{T} }}{\mathbf{R}}_{i0} {\mathbf{p}}_{i0} = \delta_{ij} {\mathbf{R}}_{h} \frac{\partial }{{\partial {\mathbf{n}}_{gj}^{T} }}\left[ {\begin{array}{*{20}c} {{\mathbf{e}}_{ix} } & {{\mathbf{e}}_{iy} } & {{\mathbf{e}}_{iz} } \\ \end{array} } \right]{\mathbf{R}}_{i0} {\mathbf{p}}_{i0}.$$

(69)

The first-order derivative on the right side of Eq. (68) is the same as Eqs. (64)–(66), and the first-order derivatives on the right side of Eq. (69) are evaluated as follows:

$$\frac{{\partial {\mathbf{e}}_{ix} }}{{\partial {\mathbf{n}}_{gi}^{T} }} = \frac{{\partial {\mathbf{e}}_{iy} }}{{\partial {\mathbf{n}}_{gi}^{T} }} \times {\mathbf{e}}_{iz} + {\mathbf{e}}_{iy} \times \frac{{\partial {\mathbf{e}}_{iz} }}{{\partial {\mathbf{n}}_{gj}^{T} }},$$

(70)

$$\frac{{\partial {\mathbf{e}}_{iy} }}{{\partial {\mathbf{n}}_{gi}^{T} }} = \left[ {\begin{array}{*{20}c} {\frac{{\partial {\mathbf{e}}_{iy} }}{{\partial e_{iy,n} }}} & {\frac{{\partial {\mathbf{e}}_{iy} }}{{\partial e_{iy,m} }}} & {\mathbf{0}} \\ \end{array} } \right],$$

(71)

$$\frac{{\partial {\mathbf{e}}_{iz} }}{{\partial {\mathbf{n}}_{gi}^{T} }} = \left[ {\begin{array}{*{20}c} {\frac{{\partial {\mathbf{e}}_{iz} }}{{\partial e_{iy,n} }}} & {\frac{{\partial {\mathbf{e}}_{iz} }}{{\partial e_{iy,m} }}} & {\frac{{\partial {\mathbf{e}}_{iz} }}{{\partial e_{iz,n} }}} \\ \end{array} } \right].$$

(72)

The components in Eqs. (70)–(72) are calculated as follows:

$$\frac{{\partial e_{{iy,n_{i} }} }}{{\partial e_{{iy,n_{i} }} }} = 1;\quad \frac{{\partial e_{iy,m} }}{{\partial e_{iy,m} }} = 1;\quad \frac{{\partial e_{iy,l} }}{{\partial e_{iy,n} }} = - \frac{{e_{iy,n} }}{{e_{iy,l} }};$$

(73a, b, c)

$$\frac{{\partial e_{iy,l} }}{{\partial e_{iy,m} }} = - \frac{{e_{iy,m} }}{{e_{iy,l} }};\quad \frac{{\partial e_{iz,n} }}{{\partial e_{iz,n} }} = 1;$$

(73d,e)

$$\frac{{\partial e_{iz,l} }}{{\partial e_{iy,n} }} = \frac{1}{{1 - e_{iy,n}^{2} }}\left( { - \frac{{\partial e_{iy,l} }}{{\partial e_{iy,n} }}e_{iy,n} e_{iz,n} - e_{iy,l} e_{iz,n} - s_{1} s_{3} e_{iy,m} \frac{{\partial c_{0} }}{{\partial e_{iy,n} }} + 2e_{iz,l} e_{iy,n} } \right),$$

(73f)

$$\frac{{\partial e_{iz,l} }}{{\partial e_{iy,m} }} = \frac{1}{{1 - e_{iy,n}^{2} }}\left( { - \frac{{\partial e_{iy,l} }}{{\partial e_{iy,m} }}e_{iy,n} e_{iz,n} - s_{1} s_{3} c_{0} } \right);$$

(73g)

$$\frac{{\partial e_{iz,l} }}{{\partial e_{iz,n} }} = \frac{1}{{1 - e_{iy,n}^{2} }}\left( { - e_{iy,l} e_{iy,n} - s_{1} s_{3} e_{iy,m} \frac{{\partial c_{0} }}{{\partial e_{iz,n} }}} \right);$$

(73h)

$$\frac{{\partial e_{iz,m} }}{{\partial e_{iy,n} }} = - \frac{{e_{iz,l} }}{{e_{iz,m} }}\frac{{\partial e_{iz,l} }}{{\partial e_{iy,n} }};\quad \frac{{\partial e_{iz,m} }}{{\partial e_{iy,m} }} = - \frac{{e_{iz,l} }}{{e_{iz,m} }}\frac{{\partial e_{iz,l} }}{{\partial e_{iy,m} }};$$

(73i,j)

$$\frac{{\partial e_{iz,m} }}{{\partial e_{iz,n} }} = \frac{{ - e_{iz,n} }}{{e_{iz,m} }} - \frac{{e_{iz,l} }}{{e_{iz,m} }}\frac{{\partial e_{iz,l} }}{{\partial e_{iz,n} }}.$$

(73k)

In Eqs. (73f)–(73h),

$$c_{0} = \sqrt {1 - e_{iy,n}^{2} - e_{iz,n}^{2} },$$

(74a)

$$\frac{{\partial c_{0} }}{{\partial e_{iy,n} }} = \frac{{ - e_{iy,n} }}{{c_{0} }},\quad \frac{{\partial c_{0} }}{{\partial e_{iz,n} }} = \frac{{ - e_{iz,n} }}{{c_{0} }}.$$

(74b, c)

The first-order derivatives of the transformation matrix ${\mathbf{T}}$ with respect to the global nodal variables lead to the following sub-matrices:

$$\frac{{\partial^{2} {\mathbf{t}}_{i} }}{{\partial {\mathbf{d}}_{j}^{T} \partial {\mathbf{u}}_{g}^{T} }} = \left[ {\begin{array}{*{20}c} {\frac{{\partial^{2} {\mathbf{t}}_{i} }}{{\partial {\mathbf{d}}_{j}^{T} \partial {\mathbf{d}}_{1}^{T} }}} & 0 & \ldots & {\frac{{\partial^{2} {\mathbf{t}}_{i} }}{{\partial {\mathbf{d}}_{j}^{T} \partial {\mathbf{d}}_{6}^{T} }}} & 0 \\ \end{array} } \right],$$

(75)

$$\frac{{\partial^{2} {\varvec{\uptheta}}_{i} }}{{\partial {\mathbf{d}}_{j}^{T} \partial {\mathbf{u}}_{g}^{T} }} = \left[ {\begin{array}{*{20}c} {\frac{{\partial^{2} {\varvec{\uptheta}}_{i} }}{{\partial {\mathbf{d}}_{j}^{T} \partial {\mathbf{d}}_{1}^{T} }}} & {\frac{{\partial^{2} {\varvec{\uptheta}}_{i} }}{{\partial {\mathbf{d}}_{j}^{T} \partial {\mathbf{n}}_{g1}^{T} }}} & \ldots & {\frac{{\partial^{2} {\varvec{\uptheta}}_{i} }}{{\partial {\mathbf{d}}_{j}^{T} \partial {\mathbf{d}}_{6}^{T} }}} & {\frac{{\partial^{2} {\varvec{\uptheta}}_{i} }}{{\partial {\mathbf{d}}_{j}^{T} \partial {\mathbf{n}}_{g6}^{T} }}} \\ \end{array} } \right],$$

(76)

$$\frac{{\partial^{2} {\varvec{\uptheta}}_{i} }}{{\partial {\mathbf{n}}_{gj}^{T} \partial {\mathbf{u}}_{g}^{T} }} = \left[ {\begin{array}{*{20}c} {\frac{{\partial^{2} {\varvec{\uptheta}}_{i} }}{{\partial {\mathbf{n}}_{gj}^{T} \partial {\mathbf{d}}_{1}^{T} }}} & {\frac{{\partial^{2} {\varvec{\uptheta}}_{i} }}{{\partial {\mathbf{n}}_{gj}^{T} \partial {\mathbf{n}}_{gk}^{T} }}} & \ldots & {\frac{{\partial^{2} {\varvec{\uptheta}}_{i} }}{{\partial {\mathbf{n}}_{gj}^{T} \partial {\mathbf{d}}_{6}^{T} }}} & {\frac{{\partial^{2} {\varvec{\uptheta}}_{i} }}{{\partial {\mathbf{n}}_{gj}^{T} \partial {\mathbf{n}}_{g6}^{T} }}} \\ \end{array} } \right],$$

(77)

$$\frac{{\partial^{2} {\mathbf{t}}_{i} }}{{\partial {\mathbf{d}}_{j}^{T} \partial {\mathbf{d}}_{k}^{T} }} = \frac{{\partial^{2} {\mathbf{R}}}}{{\partial {\mathbf{d}}_{j}^{T} \partial {\mathbf{d}}_{k}^{T} }}\left( {{\mathbf{d}}_{i} + {\mathbf{v}}_{i0} } \right) + \frac{{\partial {\mathbf{R}}}}{{\partial {\mathbf{d}}_{j}^{T} }}\delta_{ik} {\mathbf{I}} + \frac{{\partial {\mathbf{R}}}}{{\partial {\mathbf{d}}_{k}^{T} }}\delta_{ij} {\mathbf{I}} = \left[ {\begin{array}{*{20}c} {\frac{{\partial^{2} {\mathbf{e}}_{x}^{T} }}{{\partial {\mathbf{d}}_{j}^{T} \partial {\mathbf{d}}_{k}^{T} }}} \\ {\frac{{\partial^{2} {\mathbf{e}}_{y}^{T} }}{{\partial {\mathbf{d}}_{j}^{T} \partial {\mathbf{d}}_{k}^{T} }}} \\ {\frac{{\partial^{2} {\mathbf{e}}_{z}^{T} }}{{\partial {\mathbf{d}}_{j}^{T} \partial {\mathbf{d}}_{k}^{T} }}} \\ \end{array} } \right]\left( {{\mathbf{d}}_{i} + {\mathbf{v}}_{i0} } \right) + \left[ {\begin{array}{*{20}c} {\frac{{\partial {\mathbf{e}}_{x}^{T} }}{{\partial {\mathbf{d}}_{j}^{T} }}} \\ {\frac{{\partial {\mathbf{e}}_{y}^{T} }}{{\partial {\mathbf{d}}_{j}^{T} }}} \\ {\frac{{\partial {\mathbf{e}}_{z}^{T} }}{{\partial {\mathbf{d}}_{j}^{T} }}} \\ \end{array} } \right]\delta_{ik} {\mathbf{I}} + \left[ {\begin{array}{*{20}c} {\frac{{\partial {\mathbf{e}}_{x}^{T} }}{{\partial {\mathbf{d}}_{k}^{T} }}} \\ {\frac{{\partial {\mathbf{e}}_{y}^{T} }}{{\partial {\mathbf{d}}_{k}^{T} }}} \\ {\frac{{\partial {\mathbf{e}}_{z}^{T} }}{{\partial {\mathbf{d}}_{k}^{T} }}} \\ \end{array} } \right]\delta_{ij} {\mathbf{I}}.$$

(78)

If Node k is away from intersections of non-smooth shells, or if it is on a smooth shell mid-surface,

$$\frac{{\partial^{2} {\varvec{\uptheta}}_{i} }}{{\partial {\mathbf{d}}_{j}^{T} \partial {\mathbf{d}}_{k}^{T} }} = \frac{{\partial^{2} {\mathbf{R}}_{h} }}{{\partial {\mathbf{d}}_{j}^{T} \partial {\mathbf{d}}_{k}^{T} }}{\mathbf{p}}_{i} = \left[ {\begin{array}{*{20}c} {\frac{{\partial^{2} {\mathbf{e}}_{x}^{T} }}{{\partial {\mathbf{d}}_{j}^{T} \partial {\mathbf{d}}_{k}^{T} }}} \\ {\frac{{\partial^{2} {\mathbf{e}}_{y}^{T} }}{{\partial {\mathbf{d}}_{j}^{T} \partial {\mathbf{d}}_{k}^{T} }}} \\ \end{array} } \right]{\mathbf{p}}_{i},$$

(79)

$$\frac{{\partial^{2} {\varvec{\uptheta}}_{i} }}{{\partial {\mathbf{d}}_{j}^{T} \partial {\mathbf{n}}_{gk}^{T} }} = \frac{{\partial {\mathbf{R}}_{h} }}{{\partial {\mathbf{d}}_{j}^{T} }}\delta_{ik} \frac{{\partial {\mathbf{p}}_{i} }}{{\partial {\mathbf{n}}_{gk}^{T} }} = \left[ {\begin{array}{*{20}c} {\frac{{\partial {\mathbf{e}}_{x}^{T} }}{{\partial {\mathbf{d}}_{j}^{T} }}} \\ {\frac{{\partial {\mathbf{e}}_{y}^{T} }}{{\partial {\mathbf{d}}_{j}^{T} }}} \\ \end{array} } \right]\delta_{ik} \frac{{\partial {\mathbf{p}}_{i} }}{{\partial {\mathbf{n}}_{gk}^{T} }},$$

(80)

$$\frac{{\partial^{2} {\varvec{\uptheta}}_{i} }}{{\partial {\mathbf{n}}_{gj}^{T} \partial {\mathbf{n}}_{gk}^{T} }} = {\mathbf{R}}_{h} \delta_{ij} \delta_{ik} \frac{{\partial^{2} {\mathbf{p}}_{i} }}{{\partial {\mathbf{n}}_{gj}^{T} \partial {\mathbf{n}}_{gk}^{T} }},$$

(81)

$$\frac{{\partial^{2} {\mathbf{e}}_{x} }}{{\partial {\mathbf{d}}_{j}^{T} \partial {\mathbf{d}}_{k}^{T} }} = - \frac{1}{{\left| {{\mathbf{v}}_{12} } \right|^{3} }}\left[ {\frac{{\partial {\mathbf{v}}_{12} }}{{\partial {\mathbf{d}}_{j}^{T} }} \otimes {\mathbf{v}}_{12} \frac{{\partial {\mathbf{v}}_{12} }}{{\partial {\mathbf{d}}_{k}^{T} }} + \frac{{\partial {\mathbf{v}}_{12} }}{{\partial {\mathbf{d}}_{k}^{T} }} \otimes {\mathbf{v}}_{12} \frac{{\partial {\mathbf{v}}_{12} }}{{\partial {\mathbf{d}}_{j}^{T} }} + {\mathbf{v}}_{12} \otimes \left( {\frac{{\partial {\mathbf{v}}_{12} }}{{\partial {\mathbf{d}}_{j}^{T} }}} \right)^{T} \frac{{\partial {\mathbf{v}}_{12} }}{{\partial {\mathbf{d}}_{k}^{T} }}} \right] + \frac{{3{\mathbf{v}}_{12} }}{{\left| {{\mathbf{v}}_{12} } \right|^{5} }} \otimes {\mathbf{v}}_{12} \frac{{\partial {\mathbf{v}}_{12} }}{{\partial {\mathbf{d}}_{j}^{T} }} \otimes {\mathbf{v}}_{12} \frac{{\partial {\mathbf{v}}_{12} }}{{\partial {\mathbf{d}}_{k}^{T} }},$$

(82)

$$\frac{{\partial^{2} {\mathbf{e}}_{z} }}{{\partial {\mathbf{d}}_{j}^{T} \partial {\mathbf{d}}_{k}^{T} }} = \left[ {\frac{{\mathbf{I}}}{{\left| {{\mathbf{v}}_{12} \times {\mathbf{v}}_{13} } \right|}} - \frac{{\left( {{\mathbf{v}}_{12} \times {\mathbf{v}}_{13} } \right) \otimes \left( {{\mathbf{v}}_{12} \times {\mathbf{v}}_{13} } \right)}}{{\left| {{\mathbf{v}}_{12} \times {\mathbf{v}}_{13} } \right|^{3} }}} \right]\left( {\frac{{\partial {\mathbf{v}}_{12} }}{{\partial {\mathbf{d}}_{j}^{T} }} \times \frac{{\partial {\mathbf{v}}_{13} }}{{\partial {\mathbf{d}}_{k}^{T} }} + \frac{{\partial {\mathbf{v}}_{12} }}{{\partial {\mathbf{d}}_{k}^{T} }} \times \frac{{\partial {\mathbf{v}}_{13} }}{{\partial {\mathbf{d}}_{j}^{T} }}} \right) - \left( {\frac{{\partial {\mathbf{v}}_{12} }}{{\partial {\mathbf{d}}_{j}^{T} }} \times {\mathbf{v}}_{13} + {\mathbf{v}}_{12} \times \frac{{\partial {\mathbf{v}}_{13} }}{{\partial {\mathbf{d}}_{j}^{T} }}} \right) \otimes \frac{{\left( {{\mathbf{v}}_{12} \times {\mathbf{v}}_{13} } \right)}}{{\left| {{\mathbf{v}}_{12} \times {\mathbf{v}}_{13} } \right|^{3} }}\left( {\frac{{\partial {\mathbf{v}}_{12} }}{{\partial {\mathbf{d}}_{k}^{T} }} \times {\mathbf{v}}_{13} + {\mathbf{v}}_{12} \times \frac{{\partial {\mathbf{v}}_{13} }}{{\partial {\mathbf{d}}_{k}^{T} }}} \right) - \frac{{\left( {{\mathbf{v}}_{12} \times {\mathbf{v}}_{13} } \right)}}{{\left| {{\mathbf{v}}_{12} \times {\mathbf{v}}_{13} } \right|^{3} }} \otimes \left( {\frac{{\partial {\mathbf{v}}_{12} }}{{\partial {\mathbf{d}}_{j}^{T} }} \times {\mathbf{v}}_{13} + {\mathbf{v}}_{12} \times \frac{{\partial {\mathbf{v}}_{13} }}{{\partial {\mathbf{d}}_{j}^{T} }}} \right)^{T} \left( {\frac{{\partial {\mathbf{v}}_{12} }}{{\partial {\mathbf{d}}_{k}^{T} }} \times {\mathbf{v}}_{13} + {\mathbf{v}}_{12} \times \frac{{\partial {\mathbf{v}}_{13} }}{{\partial {\mathbf{d}}_{k}^{T} }}} \right) - \left( {\frac{{\partial {\mathbf{v}}_{12} }}{{\partial {\mathbf{d}}_{k}^{T} }} \times {\mathbf{v}}_{13} + {\mathbf{v}}_{12} \times \frac{{\partial {\mathbf{v}}_{13} }}{{\partial {\mathbf{d}}_{k}^{T} }}} \right) \otimes \frac{{\left( {{\mathbf{v}}_{12} \times {\mathbf{v}}_{13} } \right)}}{{\left| {{\mathbf{v}}_{12} \times {\mathbf{v}}_{13} } \right|^{3} }}\left( {\frac{{\partial {\mathbf{v}}_{12} }}{{\partial {\mathbf{d}}_{j}^{T} }} \times {\mathbf{v}}_{13} + {\mathbf{v}}_{12} \times \frac{{\partial {\mathbf{v}}_{13} }}{{\partial {\mathbf{d}}_{j}^{T} }}} \right) + \frac{{3\left( {{\mathbf{v}}_{12} \times {\mathbf{v}}_{13} } \right) \otimes \left( {{\mathbf{v}}_{12} \times {\mathbf{v}}_{13} } \right)}}{{\left| {{\mathbf{v}}_{12} \times {\mathbf{v}}_{13} } \right|^{5} }}\left( {\frac{{\partial {\mathbf{v}}_{12} }}{{\partial {\mathbf{d}}_{j} }} \times {\mathbf{v}}_{13} + {\mathbf{v}}_{12} \times \frac{{\partial {\mathbf{v}}_{13} }}{{\partial {\mathbf{d}}_{j} }}} \right) \otimes \left( {{\mathbf{v}}_{12} \times {\mathbf{v}}_{13} } \right)\left( {\frac{{\partial {\mathbf{v}}_{12} }}{{\partial {\mathbf{d}}_{k} }} \times {\mathbf{v}}_{13} + {\mathbf{v}}_{12} \times \frac{{\partial {\mathbf{v}}_{13} }}{{\partial {\mathbf{d}}_{k} }}} \right),$$

(83)

$$\frac{{\partial^{2} {\mathbf{e}}_{y} }}{{\partial {\mathbf{d}}_{j}^{T} \partial {\mathbf{d}}_{k}^{T} }} = \frac{{\partial^{2} {\mathbf{e}}_{z} }}{{\partial {\mathbf{d}}_{j}^{T} \partial {\mathbf{d}}_{k}^{T} }} \times {\mathbf{e}}_{x} + {\mathbf{e}}_{z} \times \frac{{\partial^{2} {\mathbf{e}}_{x} }}{{\partial {\mathbf{d}}_{j}^{T} \partial {\mathbf{d}}_{k}^{T} }} + \frac{{\partial {\mathbf{e}}_{z} }}{{\partial {\mathbf{d}}_{j}^{T} }} \times \frac{{\partial {\mathbf{e}}_{x} }}{{\partial {\mathbf{d}}_{k}^{T} }} + \frac{{\partial {\mathbf{e}}_{z} }}{{\partial {\mathbf{d}}_{k}^{T} }} \times \frac{{\partial {\mathbf{e}}_{x} }}{{\partial {\mathbf{d}}_{j}^{T} }},$$

(84)

$$\frac{{\partial^{2} {\mathbf{p}}_{i} }}{{\partial {\mathbf{n}}_{gi}^{2} }} = \left[ {\begin{array}{*{20}c} {\frac{{\partial^{2} {\mathbf{p}}_{i} }}{{\partial p_{{i,n_{i} }}^{2} }}} & {\frac{{\partial^{2} {\mathbf{p}}_{i} }}{{\partial p_{{i,n_{i} }} \partial p_{{i,m_{i} }} }}} \\ {\frac{{\partial^{2} {\mathbf{p}}_{i} }}{{\partial p_{{i,m_{i} }} \partial p_{{i,n_{i} }} }}} & {\frac{{\partial^{2} {\mathbf{p}}_{i} }}{{\partial p_{{i,m_{i} }}^{2} }}} \\ \end{array} } \right],$$

(85)

$$\frac{{\partial^{2} {\mathbf{p}}_{i} }}{{\partial p_{{i,n_{i} }}^{2} }} = \left\{ {\begin{array}{*{20}c} {\frac{{\partial^{2} p_{i,X} }}{{\partial p_{{i,n_{i} }}^{2} }}} \\ {\frac{{\partial^{2} p_{i,Y} }}{{\partial p_{{i,n_{i} }}^{2} }}} \\ {\frac{{\partial^{2} p_{i,Z} }}{{\partial p_{{i,n_{i} }}^{2} }}} \\ \end{array} } \right\},\quad \frac{{\partial^{2} {\mathbf{p}}_{i} }}{{\partial p_{{i,m_{i} }}^{2} }} = \left\{ {\begin{array}{*{20}c} {\frac{{\partial^{2} p_{i,X} }}{{\partial p_{{i,m_{i} }}^{2} }}} \\ {\frac{{\partial^{2} p_{i,Y} }}{{\partial p_{{i,m_{i} }}^{2} }}} \\ {\frac{{\partial^{2} p_{i,Z} }}{{\partial p_{{i,m_{i} }}^{2} }}} \\ \end{array} } \right\},\quad \frac{{\partial^{2} {\mathbf{p}}_{i} }}{{\partial p_{{i,n_{i} }} \partial p_{{i,m_{i} }} }} = \left\{ {\begin{array}{*{20}c} {\frac{{\partial^{2} p_{i,X} }}{{\partial p_{{i,n_{i} }} \partial p_{{i,m_{i} }} }}} \\ {\frac{{\partial^{2} p_{i,Y} }}{{\partial p_{{i,n_{i} }} \partial p_{{i,m_{i} }} }}} \\ {\frac{{\partial^{2} p_{i,Z} }}{{\partial p_{{i,n_{i} }} \partial p_{{i,m_{i} }} }}} \\ \end{array} } \right\},$$

(86a, b, c)

$$\frac{{\partial^{2} p_{{i,l_{i} }} }}{{\partial p_{{i,n_{i} }}^{2} }} = - \frac{1}{{p_{{i,l_{i} }} }} - \frac{{p_{{i,n_{i} }}^{2} }}{{p_{{i,l_{i} }}^{3} }},\quad \frac{{\partial^{2} p_{{i,l_{i} }} }}{{\partial p_{{i,m_{i} }}^{2} }} = - \frac{1}{{p_{{i,l_{i} }} }} - \frac{{p_{{i,m_{i} }}^{2} }}{{p_{{i,l_{i} }}^{3} }},\quad \frac{{\partial^{2} p_{{i,l_{i} }} }}{{\partial p_{{i,n_{i} }} \partial p_{{i,m_{i} }} }} = - \frac{{p_{{i,n_{i} }} p_{{i,m_{i} }} }}{{p_{{i,l_{i} }}^{3} }}.$$

(87a, b, c)

where second-order derivatives of the other two components with respect to the vectorial rotational variables are equal to zero.

If Node k is located at an intersection of non-smooth shells,

$$\frac{{\partial^{2} {\varvec{\uptheta}}_{i} }}{{\partial {\mathbf{d}}_{j}^{T} \partial {\mathbf{d}}_{k}^{T} }} = \frac{{\partial^{2} {\mathbf{R}}_{h} }}{{\partial {\mathbf{d}}_{j}^{T} \partial {\mathbf{d}}_{k}^{T} }}{\mathbf{R}}_{i}^{T} {\mathbf{R}}_{i0} {\mathbf{p}}_{i0} = \left[ {\begin{array}{*{20}c} {\frac{{\partial^{2} {\mathbf{e}}_{x}^{T} }}{{\partial {\mathbf{d}}_{j}^{T} \partial {\mathbf{d}}_{k}^{T} }}} \\ {\frac{{\partial^{2} {\mathbf{e}}_{y}^{T} }}{{\partial {\mathbf{d}}_{j}^{T} \partial {\mathbf{d}}_{k}^{T} }}} \\ \end{array} } \right]{\mathbf{R}}_{i}^{T} {\mathbf{R}}_{i0} {\mathbf{p}}_{i0}.$$

(88)

The second-order derivatives on the right-hand side of Eq. (88) are the same as Eqs. (82)-(84):

$$\frac{{\partial^{2} {\varvec{\uptheta}}_{i} }}{{\partial {\mathbf{d}}_{j}^{T} \partial {\mathbf{n}}_{gk}^{T} }} = \frac{{\partial {\mathbf{R}}_{h} }}{{\partial {\mathbf{d}}_{j}^{T} }}\delta_{ik} \frac{{\partial {\mathbf{R}}_{i}^{T} }}{{\partial {\mathbf{n}}_{gk}^{T} }}{\mathbf{R}}_{i0} {\mathbf{p}}_{i0} = \left[ {\begin{array}{*{20}c} {\frac{{\partial {\mathbf{e}}_{x}^{T} }}{{\partial {\mathbf{d}}_{j}^{T} }}} \\ {\frac{{\partial {\mathbf{e}}_{y}^{T} }}{{\partial {\mathbf{d}}_{j}^{T} }}} \\ \end{array} } \right]\delta_{ik} \left[ {\begin{array}{*{20}c} {\frac{{\partial {\mathbf{e}}_{ix} }}{{\partial {\mathbf{n}}_{gk}^{T} }}} & {\frac{{\partial {\mathbf{e}}_{iy} }}{{\partial {\mathbf{n}}_{gk}^{T} }}} & {\frac{{\partial {\mathbf{e}}_{iz} }}{{\partial {\mathbf{n}}_{gk}^{T} }}} \\ \end{array} } \right]{\mathbf{R}}_{i0} {\mathbf{p}}_{i0},$$

(89)

$$\frac{{\partial^{2} {\varvec{\uptheta}}_{i} }}{{\partial {\mathbf{n}}_{gj}^{T} \partial {\mathbf{n}}_{gk}^{T} }} = {\mathbf{R}}_{h} \delta_{ij} \delta_{ik} \frac{{\partial^{2} {\mathbf{R}}_{i}^{T} }}{{\partial {\mathbf{n}}_{gj}^{T} \partial {\mathbf{n}}_{gk}^{T} }}{\mathbf{R}}_{i0} {\mathbf{p}}_{i0} = {\mathbf{R}}_{h} \delta_{ij} \delta_{ik} \left[ {\begin{array}{*{20}c} {\frac{{\partial^{2} {\mathbf{e}}_{ix} }}{{\partial {\mathbf{n}}_{gj}^{T} \partial {\mathbf{n}}_{gk}^{T} }}} & {\frac{{\partial^{2} {\mathbf{e}}_{iy} }}{{\partial {\mathbf{n}}_{gj}^{T} \partial {\mathbf{n}}_{gk}^{T} }}} & {\frac{{\partial^{2} {\mathbf{e}}_{iz} }}{{\partial {\mathbf{n}}_{gj}^{T} \partial {\mathbf{n}}_{gk}^{T} }}} \\ \end{array} } \right]{\mathbf{R}}_{i0} {\mathbf{p}}_{i0},$$

(90)

$$\frac{{\partial^{2} {\mathbf{e}}_{ix} }}{{\partial {\mathbf{n}}_{gj}^{T} \partial {\mathbf{n}}_{gk}^{T} }} = \frac{{\partial^{2} {\mathbf{e}}_{iy} }}{{\partial {\mathbf{n}}_{gj}^{T} \partial {\mathbf{n}}_{gk}^{T} }} \times {\mathbf{e}}_{iz} + {\mathbf{e}}_{iy} \times \frac{{\partial^{2} {\mathbf{e}}_{iz} }}{{\partial {\mathbf{n}}_{gj}^{T} \partial {\mathbf{n}}_{gk}^{T} }} + \frac{{\partial {\mathbf{e}}_{iy} }}{{\partial {\mathbf{n}}_{gj}^{T} }} \times \frac{{\partial {\mathbf{e}}_{iz} }}{{\partial {\mathbf{n}}_{gk}^{T} }} + \frac{{\partial {\mathbf{e}}_{iy} }}{{\partial {\mathbf{n}}_{gk}^{T} }} \times \frac{{\partial {\mathbf{e}}_{iz} }}{{\partial {\mathbf{n}}_{gi}^{T} }}.$$

(91)

The first-order derivatives in Eqs. (89) and (91) are calculated as Eqs. (64)–(66), and Eqs. (70)–(74). The second-order derivatives in Eqs. (90) and (91) are calculated as follows:

$$\frac{{\partial^{2} e_{iy,l} }}{{\partial^{2} e_{iy,n} }} = - \frac{{e_{iy,n}^{2} }}{{e_{iy,l}^{3} }} - \frac{1}{{e_{iy,l} }};\quad \frac{{\partial^{2} e_{iy,l} }}{{\partial e_{iy,n} \partial e_{iy,m} }} = - \frac{{e_{iy,n} e_{iy,m} }}{{e_{iy,l}^{3} }};\quad \frac{{\partial^{2} e_{iy,l} }}{{\partial^{2} e_{iy,m} }} = - \frac{{e_{iy,m}^{2} }}{{e_{iy,l}^{3} }} - \frac{1}{{e_{iy,l} }},$$

(92a, b, c)

$$\frac{{\partial^{2} c_{0} }}{{\partial^{2} e_{iy,n} }} = - \frac{{e_{iy,n}^{2} }}{{c_{0}^{3} }} - \frac{1}{{c_{0} }};\quad \frac{{\partial^{2} c_{0} }}{{\partial e_{iy,n} \partial e_{iz,n} }} = - \frac{{e_{iy,n} e_{iz,n} }}{{c_{0}^{3} }};\quad \frac{{\partial^{2} c_{0} }}{{\partial^{2} e_{iz,n} }} = - \frac{{e_{iz,n}^{2} }}{{c_{0}^{3} }} - \frac{1}{{c_{0} }},$$

(92d,e,f)

$$\frac{{\partial^{2} e_{iz,l} }}{{\partial e_{iy,n}^{2} }} = \frac{1}{{1 - e_{iy,n}^{2} }}\left\{ { - \left[ {\frac{{\partial^{2} e_{iy,l} }}{{\partial e_{iy,n}^{2} }}e_{iy,n} + 2\frac{{\partial e_{iy,l} }}{{\partial e_{iy,n} }}} \right]e_{iz,n} - s_{1} s_{3} e_{iy,m} \frac{{\partial^{2} c_{0} }}{{\partial e_{iy,n}^{2} }} + 2e_{iy,n} \frac{{\partial e_{iz,l} }}{{\partial e_{iy,n} }} + 2e_{iz,l} } \right\} + \frac{{2e_{iy,n} }}{{1 - e_{iy,n}^{2} }}\frac{{\partial e_{iz,l} }}{{\partial e_{iy,n} }},$$

(92g)

$$\frac{{\partial^{2} e_{iz,l} }}{{\partial e_{iy,n} \partial e_{iy,m} }} = \frac{ - 1}{{1 - e_{iy,n}^{2} }}\left[ {\left( {\frac{{\partial^{2} e_{iy,l} }}{{\partial e_{iy,n} \partial e_{iy,m} }}e_{iy,n} + \frac{{\partial e_{iy,l} }}{{\partial e_{iy,m} }}} \right)e_{iz,n} + s_{1} s_{3} \frac{{\partial c_{0} }}{{\partial e_{iy,n} }} - 2e_{iy,n} \frac{{\partial e_{iz,l} }}{{\partial e_{iy,m} }}} \right],$$

(92h)

$$\frac{{\partial^{2} e_{iz,l} }}{{\partial e_{iy,n} \partial e_{iz,n} }} = \frac{ - 1}{{1 - e_{iy,n}^{2} }}\left( {e_{iy,n} \frac{{\partial e_{iy,l} }}{{\partial e_{iy,n} }} + e_{iy,l} + s_{1} s_{3} e_{iy,m} \frac{{\partial^{2} c_{0} }}{{\partial e_{iy,n} \partial e_{iz,n} }} + 2e_{iy,n} \frac{{\partial e_{iz,l} }}{{\partial e_{iz,n} }}} \right),$$

(92i)

$$\frac{{\partial^{2} e_{iz,l} }}{{\partial e_{iy,m}^{2} }} = - \frac{{e_{iy,n} e_{iz,n} }}{{1 - e_{iy,n}^{2} }}\frac{{\partial^{2} e_{iy,l} }}{{\partial e_{iy,m}^{2} }},$$

(92j)

$$\frac{{\partial^{2} e_{iz,l} }}{{\partial e_{iy,m} \partial e_{iz,n} }} = \frac{1}{{1 - e_{iy,n}^{2} }}\left( { - \frac{{\partial e_{iy,l} }}{{\partial e_{iy,m} }}e_{iy,n} - s_{1} s_{3} \frac{{\partial c_{0} }}{{\partial e_{iz,n} }}} \right),$$

(92k)

$$\frac{{\partial^{2} e_{iz,l} }}{{\partial e_{iz,n}^{2} }} = \frac{{ - s_{1} s_{3} e_{iy,m} }}{{1 - e_{iy,n}^{2} }}\frac{{\partial^{2} c_{0} }}{{\partial e_{iz,n}^{2} }},$$

(92l)

$$\frac{{\partial^{2} e_{iz,m} }}{{\partial e_{iy,n}^{2} }} = - \left[ {\frac{1}{{e_{iz,m} }}\left( {\frac{{\partial e_{iz,l} }}{{\partial e_{iy,n} }}} \right)^{2} + \frac{{e_{iz,l} }}{{e_{iz,m} }}\frac{{\partial^{2} e_{iz,l} }}{{\partial e_{iy,n}^{2} }}} \right] - \frac{1}{{e_{iz,m} }}\left( {\frac{{\partial e_{iz,m} }}{{\partial e_{iy,n} }}} \right)^{2},$$

(92m)

$$\frac{{\partial^{2} e_{iz,m} }}{{\partial e_{iy,n} \partial e_{iy,m} }} = - \frac{1}{{e_{iz,m} }}\frac{{\partial e_{iz,l} }}{{\partial e_{iy,n} }}\frac{{\partial e_{iz,l} }}{{\partial e_{iy,m} }} - \frac{{e_{iz,l} }}{{e_{iz,m} }}\frac{{\partial^{2} e_{iz,l} }}{{\partial e_{iy,n} \partial e_{iy,m} }} - \frac{1}{{e_{iz,m} }}\frac{{\partial e_{iz,m} }}{{\partial e_{iy,n} }}\frac{{\partial e_{iz,m} }}{{\partial e_{iy,m} }},$$

(92n)

$$\frac{{\partial^{2} e_{iz,m} }}{{\partial e_{iy,n} \partial e_{iz,n} }} = - \frac{1}{{e_{iz,m} }}\frac{{\partial e_{iz,l} }}{{\partial e_{iy,n} }}\frac{{\partial e_{iz,l} }}{{\partial e_{iz,n} }} - \frac{{e_{iz,l} }}{{e_{iz,m} }}\frac{{\partial^{2} e_{iz,l} }}{{\partial e_{iy,n} \partial e_{iz,n} }} - \frac{1}{{e_{iz,m} }}\frac{{\partial e_{iz,m} }}{{\partial e_{iy,n} }}\frac{{\partial e_{iz,m} }}{{\partial e_{iz,n} }},$$

(92o)

$$\frac{{\partial^{2} e_{iz,m} }}{{\partial e_{iy,m}^{2} }} = - \frac{1}{{e_{iz,m} }}\left( {\frac{{\partial e_{iz,l} }}{{\partial e_{iy,m} }}} \right)^{2} - \frac{{e_{iz,l} }}{{e_{iz,m} }}\frac{{\partial^{2} e_{iz,l} }}{{\partial e_{iy,m}^{2} }} - \frac{1}{{e_{iz,m} }}\left( {\frac{{\partial e_{iz,m} }}{{\partial e_{iy,m} }}} \right)^{2},$$

(92p)

$$\frac{{\partial^{2} e_{iz,m} }}{{\partial e_{iy,m} \partial e_{iz,n} }} = - \frac{1}{{e_{iz,m} }}\frac{{\partial e_{iz,l} }}{{\partial e_{iy,m} }}\frac{{\partial e_{iz,l} }}{{\partial e_{iz,n} }} - \frac{{e_{iz,l} }}{{e_{iz,m} }}\frac{{\partial^{2} e_{iz,l} }}{{\partial e_{iy,m} \partial e_{iz,n} }} - \frac{1}{{e_{iz,m} }}\frac{{\partial e_{iz,m} }}{{\partial e_{iy,m} }}\frac{{\partial e_{iz,m} }}{{\partial e_{iz,n} }},$$

(92q)

$$\frac{{\partial^{2} e_{iz,m} }}{{\partial e_{iz,n}^{2} }} = - \frac{1}{{e_{iz,m} }} - \frac{{e_{iz,l} }}{{e_{iz,m} }}\frac{{\partial^{2} e_{iz,l} }}{{\partial e_{iz,n}^{2} }} - \frac{1}{{e_{iz,m} }}\left( {\frac{{\partial e_{iz,l} }}{{\partial e_{iz,n} }}} \right)^{2} - \frac{1}{{e_{iz,m} }}\left( {\frac{{\partial e_{iz,m} }}{{\partial e_{iz,n} }}} \right)^{2}.$$

(92r)