Numerical simulation of the mechanical behavior of a carbon nanotube bundle

Abstract

Due to their outstanding mechanical properties, carbon nanotubes (CNTs) are very promising materials for further applications in the field of lightweight construction. Carbon nanotube fibers, whose structure consists of a multitude of load-bearing carbon nanotube bundles interconnected by threads, are an excellent possibility to utilize these properties as engineering material. In the present research, a new method for the prediction of the mechanical properties of carbon nanotube bundles is presented. Within this, the complex structure is transformed into a simplified model based on suitable assumptions. Several parameters of the bundle are taken into account such as different types of nanotubes and various nanotube lengths. The model is applied to different configurations of carbon nanotube bundles by using a molecular mechanics approach. The interactions between the nanotubes are investigated by analyzing the Lennard–Jones potential in a virtual tensile loading test. For different configurations, the resulting forces and stresses are obtained. The results give a clear insight into the influencing parameters and demonstrate their effect on the mechanical behavior. In conclusion, the present approach is an excellent method to analyze the mechanical behavior of CNT bundles.

1 Introduction

The singular mechanical properties of carbon nanotubes (CNTs) have opened many areas of application. The ongoing interest for this outstanding material is based on the discoveries made by Iijima in 1991 [1]. Since then, carbon nanotubes have been the subject of numerous and manifold studies. This includes the investigation of their properties as well as the consideration of this material for versatile applications, e.g., from medicine and electronics to applications for lightweight construction [2]. In particular, the outstanding mechanical properties of carbon nanotubes are desirable for many technical applications, e.g., in composites [3] and for nanoscale reinforcements [4]. The fabrication of fibers from carbon nanotubes is one specific example of utilizing the characteristics for technical lightweight applications [5]. The structure of the carbon nanotube fibers consist of bundles formed by a multitude of carbon nanotubes as well as threads interconnecting those bundles mainly in the transversal direction. The major load is borne by the bundles which are oriented in the longitudinal direction of the fiber.

Lu et al. summarize in their work the state of the art and the challenges about the mechanical characteristics of carbon nanotube fibers [6]. The comparison of CNT fibers, produced with various methods, shows huge differences in their mechanical properties. As shown in experimental investigations, the specific load-carrying capacity of singular carbon nanotubes is higher than that of the whole fiber. Due to the influence of the weak van der Waals forces and the presence of lattice defects, synthetically manufactured CNT fibers can withstand consistently lower loads than what the theoretical calculated values predict [7]. Yang et al. [8] have performed extensive experimental investigations about the mechanical properties and the behavior of CNT fibers. The analysis of a carbon nanotube fiber in a tensile strength test has shown that the strength of the bundles contributes fundamentally to the mechanical characteristics of the fiber. The fiber begins to break when the nanotubes inside the bundles slip apart. Therefore, the mechanical analysis of carbon nanotube bundles plays an important role in improving the mechanical properties of the entire fiber.

Simulation approaches are a powerful and efficient tool for investigations of the mechanical behavior of complex structures like individual carbon nanotubes or CNT assemblies; see, e.g., Eberhardt and Wallmersperger [9, 10], and Talukdar et al. [11]. An overview of modeling approaches for carbon nanotubes is given in the review paper of Kosidlo et al. [12]. Some theoretical/numerical investigations utilize the approach of atomistic simulations of a small number of nanotubes or the detailed investigation of a singular nanotube. Li and Chou [13] started using a molecular structural mechanics (MSM) approach to describe the mechanical properties of single wall carbon nanotubes. Eberhardt and Wallmersperger [14] extended this approach and created a model which is energetically consistent with its underlying chemical force field. In the next step of their work, the second-generation reactive bond-order (REBO) potential was integrated into the MSM approach [15]. Talukdar et al. [11], Qian et al. [16] and Chowdhury et al. [17], on the other hand, took a molecular dynamic approach by applying interatomic potentials, e.g., the reactive empirical bond-order potential and the Tersoff–Brenner potential to simulate bundles with a various number of nanotubes. Other scientific works aim at simulating the whole fiber. For example, Beese et al. [18] simulated an entire fiber containing 340 bundles by the approach of calculating the fiber strength through tension transfer in the contact areas between the bundles. Vilatela et al. [19] simulate the mechanical properties of a yarn-like structure of carbon nanotubes by using a molecular dynamics approach. Fernandez-Toribo et al. [20] calculated the mechanical properties of an entire fiber using the approach of uniaxial composite materials. Korznikova et al. [21] used the approach of an atomistic chain model to simulate a carbon nanotube bundle under plane strain conditions. In contrast to the approaches just mentioned, Wang et al. [22] created a helical finite element model for the qualitative analysis of the ductile–brittle mechanisms of a helical CNT fiber structure by using experimentally determined material parameters.

In the present research, the mechanical behavior of a CNT bundle is investigated numerically in order to observe the parameters that influence the mechanical properties. The present modeling approach is situated between the detailed consideration of an atomistic model and the macroscopic modeling of an entire fiber. It uses a rigid structure model including all atoms of a single carbon nanotube and assembles several of these nanotubes together to form a bundle. The simulation is based on the calculation and evaluation of the Lennard–Jones potential between the atoms of the singular nanotubes. The paper is structured as follows. In Sect. 2 the model of the CNT bundle and the basic physical properties are presented. In Sect. 3, this model is used for numerical simulations to investigate the mechanical behavior and more specifically the occurring forces and displacements. Section 4 gives an overview about the results and the parameters influencing the mechanical behavior of the bundle model. Finally, Sect. 5 summarizes the presented work and gives an outlook toward further research, e.g., for a more detailed bundle model.

2 Modeling of the CNT bundle

In order to simplify the complex structure of a fiber made of carbon nanotubes, a series of modeling approaches feasible for theoretical investigations is chosen. As mentioned previously, bundles are the main load-bearing elements of a CNT fiber. Therefore, the present numerical investigation follows up on the model, focusing on one specific bundle containing a variable number of nanotubes. The calculations of this bundle are based on interactions between individual nanotubes. To depict these interactions, the model uses a total potential surface which consists of various partial potentials. Some of these are based on the interactions of covalently bonded atoms, i.e., the bond stretching potential $U_{r}$, the bond bending potential $U_{\theta }$ and the bond torsion potential $U_{\tau }$. Other partial potentials belong to unbonded atoms as for example the electrostatic potential $U_\mathrm{el}$ and the potential resulting from the van der Waals interactions $U_\mathrm{vdW}$ [23]:

$$\begin{aligned} U_\mathrm{tot} = \sum U_{r} + \sum U_{\theta } + \sum U_{\tau } + \sum U_\mathrm{el} + \sum U_\mathrm{vdW}. \end{aligned}$$

(1)

In contrast to the molecular structural mechanics approach, see, e.g., Li and Chou [13], the individual nanotubes are assumed to be rigid in the present bundle model. This can be justified with the strain transfer factor, which is the ratio of the strain of individual nanotubes to the total strain of the macroscopic fiber under tension. According to Ma et al. [24], the strain transfer factor for dry spun CNT fibers is 0.045. Hence, the strain of individual nanotubes in bundles or fibers is negligible. This assumption can be justified with the comparatively weak van der Waals forces of unbonded atoms in contrast to the strong forces of covalently bonded atoms. The analysis of load transfer mechanisms of CNT fibers shows the importance of van der Waals forces transmitting tension between carbon nanotubes [16]. Therefore, the partial potentials based on the interactions of bonded atoms can be omitted. Additionally, the electrostatic potential is also omitted, as no charges or ions are bonded to the nanotubes. In summary, the total potential consists only of the potential resulting from the van der Waals forces:

$$\begin{aligned} U_\mathrm{tot} \approx \sum U_\mathrm{vdW}. \end{aligned}$$

(2)

The Lennard–Jones potential is used to calculate the interactions between the atoms based on the van der Waal bonds:

$$\begin{aligned} U_\mathrm{vdW} = U_\mathrm{LJ} = 4 \epsilon \left( \left( \frac{\sigma }{r_{ij}}\right) ^{12}-\left( \frac{\sigma }{r_{ij}}\right) ^{6}\right) . \end{aligned}$$

(3)

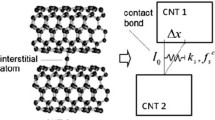
The alignment and distribution of the individual CNTs in the bundle are based on the course of the Lennard–Jones potential, using the Lennard–Jones parameters $\sigma$ and $\epsilon$. Here, $\sigma$ denotes the atomic distance where the potential is zero and $\epsilon$ is the interaction energy value of two atoms in equilibrium distance. The curve of the potential—using the Lennard–Jones parameter of $\sigma _\mathrm{graphene}=3.4$ Å and $\epsilon _\mathrm{graphene}=3.829 \cdot 10^{-22}$ J for carbon in graphene configuration—has a minimum at the atomic distance of approx. $a_\mathrm{c-c}=3.8\,$Å  [25]. Below this distance, the atoms repel each other; above this distance, they attract each other. Free-moving CNTs are therefore always arranged with an intertube distance of $a_\mathrm{c-c}=3.8\,$Å. This leads to a uniformly dense arrangement at the cross section of the x–y plane. The cross section of our bundle model consists of 19 or 37 nanotubes; see Fig. 1b. The distance of $a_\mathrm{CNT-CNT}=a_\mathrm{c-c}=3.8\,$Å is also used in the vertical direction where three CNTs are located one above the other; see Fig. 1b. As shown, this vertical arrangement of the nanotube leads to a bundle model consisting of three parts.

Fig. 1

a Cross section of the bundle model, b 3D model of the whole bundle

The model described above is implemented in MATLAB. It begins with the implementation of the exact structure of a carbon nanotube according to the work of Cox and Hill [26]. This implementation gives the coordinates of all atoms of the nanotube. In the next step, the nanotube is arranged according to the geometric assumptions and chosen parameters of our model; see Fig. 1.

Fig. 2

a Less dense arrangement of the bundle consisting of 19 nanotubes with different diameters in the cross section (configuration A), b dense arrangement of the bundle with constant nanotube diameters (configuration B)

In the following study, we investigate different types of nanotubes in order to create a realistic model of a CNT bundle. This bundle consists of armchair and zigzag CNTs. To vary the diameter of the individual CNTs, we use a Gaussian distribution with the expected nanotube diameter of $d_\mathrm{CNT}\approx 10\,$Å. In order to have CNTs with the required diameter, armchair nanotubes of (n, m) = (7,7) type and zigzag nanotubes of (n, m) = (13,0) type have to be chosen [14]. These values n, m are part of the chirality vector which describes the virtual direction in which a graphene layer is rolled up to a nanotube; for more details, see, e.g., Dresselhaus et al. [27]. Due to the variation of the nanotube diameters and to the huge repulsive force between carbon atoms below the desired atomic distance of $a_\mathrm{c-c}=3.8\,$Å, it is important to ensure that the mean distance between two nanotubes in the cross section of the bundle is higher than $a_\mathrm{c-c}=3.8\,$Å. Therefore, we arrange the nanotubes less densely in the cross section; see Fig. 2a.

In order to realize different CNT lengths, again a Gaussian distribution is used as mentioned previously for the CNT diameter. The expected nanotube length is $l_\mathrm{CNT}=50\,$Å. As already described, the model consists of three nanotubes vertically arranged above one another. Hence, the length of the whole bundle is $l_\mathrm{bundle}\approx 158$ Å. In our investigations, the nanotubes are much shorter than real CNTs. This restriction is necessary in order to limit the computational effort. To determine the impact of the nanotube length in one test case, the bundle is also simulated with a CNT length of $l_\mathrm{CNT}=100\,$Å. The last parameter in order to create a realistic model is to use an individual offset for every nanotube above the x–y plane. If we understand our model as a section of a real bundle, the starting points of the nanotubes in the lower part of the bundle are not all located in the x–y plane; see Fig. 3.

Fig. 3

a Illustration of the displacement variables of the parts of the bundle, b forces between the parts of the bundle and the maximal force $F_\mathrm{res}$

To verify the influence of the parameters discussed above on the mechanical properties of the bundle, the model is applied for the evaluation of the following test cases:

• Test case 0: reference test case with the default model parameters,

• Test case 1: change of the expected CNT diameter $d_\mathrm{CNT}$,

• Test case 2: change of the expected CNT length $l_\mathrm{CNT}$,

• Test case 3: change of the number of CNTs in the cross section,

• Test case 4: change of the offset above the x–y plane,

• Test case 5: change of the cross-sectional arrangement of the CNTs.

An overview of the different test cases is given in Table 1. In test case 0, the model is used in the default configuration with the parameters mentioned above. By default, a CNT length of $l_\mathrm{CNT}=50\,$Å  and a CNT diameter of $d_\mathrm{CNT}=10\,$Å  are used in the model consisting of 37 nanotubes in every part of the bundle. These nanotubes are less densely arranged due to the distribution of diameters, see Fig. 2a, and have an individual offset uniformly distributed between $d_\mathrm{offset}=0\ldots 20\,$Å. Based on this configuration, in the following test cases always one of the parameters was changed in order to get a result of the influence of each parameter, separately. In test case 1, the CNT diameter $d_\mathrm{CNT}$ is changed to investigate the influence of the CNT diameter on the mechanical properties simulatively. In test case 2, the CNT length $l_\mathrm{CNT}$ is changed. Test case 3 investigates the influence of the number of CNTs in the cross section. In test case 4, the offset for every nanotube above the x–y plane is changed. Finally, in test case 5, we arranged the nanotubes more densely in the cross section, to investigate the influence of the cross-sectional nanotube distance $a_\mathrm{c-c}$ on the mechanical properties. Here, arrangement A means less densely assembled CNTs, see Fig. 2a, in the cross section in contrast to arrangement B, see Fig. 2b, with densely assembled nanotubes.

Table 1 Overview over the model parameters for the different test cases

3 Numerical simulation of the mechanical model behavior

In the present research, the numerical simulation of the mechanical behavior of CNT bundles is performed. By applying the model presented in Sect. 2, the distances between the atoms of the rigid nanotubes are computed using MATLAB. The model of the bundle—investigated in various configurations—consists of three parts. These parts arise from the vertical arrangement of three nanotubes located one above another. The lower part of the bundle is fixed at the bottom; see Fig. 3. On the upper part of the bundle, a displacement $u_{z_{2}}$ in axial direction is prescribed. Hence, the nanotubes in this part of the bundle are considered to move simultaneously. The CNTs in the middle part of the bundle can move independently in the z-direction. Thus, a system with 37 or 19 DOFs is created. The entire model is fixed in the x- and y-directions. This simplification is justified with the chosen cross-sectional alignment of the CNTs where the intertube distance is due to the equilibrium distance of carbon atoms based on the Lennard–Jones potential. For the consideration of a load case for a yarn-like structure, this should correspond to a uniaxial stress case in which the displacement perpendicular to the direction of the load is negligible.

In order to limit the computational effort, a cutoff radius of $r_\mathrm{cut}=20\,$Å  is used for the calculation of the atomic distances. This value is chosen as a compromise between the computational effort and the quality of the calculated total potential. As each bundle consists of three parts, see Fig. 1b, the atomic coordinates of the nanotubes in each part are assigned in three matrices. These three matrices are used for the calculation of the atomic distances. From these distances, only the ones below the cutoff radius are taken. These n atomic distances are arranged in a corresponding vector. The total potential $U_\mathrm{tot}$ with respect to the positions of the nanotubes $u_{z_{1,i}}$ and $u_{z_{2}}$ is calculated by summing up the n partial Lennard–Jones potentials $U_{\mathrm{LJ}_k}$:

$$\begin{aligned} U_\mathrm{tot}(u_{z_{1,i}},u_{z_{2}}) = \sum _{k=1}^n U_{\mathrm{LJ}_{k}}. \end{aligned}$$

(4)

The numerical simulation is carried out by continuously calculating and evaluating this potential. In the simulation, the distances between the atoms of the nanotubes are recalculated in each step. Atomic distances are calculated only if the nanotubes can move independently. As mentioned above, the nanotubes in the upper part and the lower part of the bundle cannot move independently. Hence, no interaction between the nanotubes in these parts is taken into account and no atomic distances are calculated between these nanotubes. In the middle part of the bundle, however, all nanotubes can move freely in z-direction. In order to calculate the forces between the individual CNTs of the middle part and the CNT group of the lower part and the upper part of the bundle during the simulation, the Lennard–Jones potential and its derivatives are numerically calculated in each simulation step.

At the beginning of the simulation, the bundle is brought to the equilibrium state by using a conjugate gradient method [28] with 37 DOFs ($u_{z_{1,i}}$) in z-direction for the case of 37 nanotubes or 19 DOFs ($u_{z_{1,i}}$) in z-direction for the case of 19 nanotubes. For both cases, one DOF for $u_{z_{2}}$ in z-direction is used additionally. This method uses the numerical derivatives of the total potential $U_\mathrm{tot}$, see Eq. (4), with respect to the position of the individual nanotubes in the middle part of the bundle $u_{z_{1,i}}$ and the upper part of the bundle $u_{z_{2}}$ in order to obtain a minimum of the total potential. In the present work, this numerical method is implemented as iterative algorithm in MATLAB. The procedure is given in detail in the Appendix.

Before starting the simulation, a final displacement value for the upper part of the bundle and an increment is chosen. Subsequently, the upper part of the bundle is moved in each simulation step by the previously defined increment $\Delta u_{z_{2}}$ in the z-direction until the final displacement value is reached; see Fig. 3. This means that a path-controlled simulation is conducted. The equilibrium position of the CNTs in the middle part in z-direction of the bundle is obtained anew for each step of the simulation by applying the conjugate gradient method mentioned above. Additionally, with each simulation step, the changes in the position of the CNTs in the middle part of the bundle that are necessary for reaching the equilibrium position are recorded.

The total forces in the bundle are calculated and recorded by numerically deriving the total potential with respect to the displacement of the associated bundle part by using Eq. (5):

$$\begin{aligned} F_{1,2}(u_{z}) = \frac{\mathrm{d}U_\mathrm{tot}}{\mathrm{d}u_{z_{1,2}}}. \end{aligned}$$

(5)

The force–displacement curves can now be given for all the investigated test cases to get an overview of the influence of the model parameters on the mechanical properties. The chosen representation of the results as a force–displacement curve is due to the fact that the exact definition of the effective cross-sectional area of a CNT bundle is still ambiguous.

4 Results

In the present section, the results of the numerical simulation are given and compared for the different test cases. The important results are

• the total potential,

• the forces $F_{1,2}$ and the resulting force $F_\mathrm{res}$, and

• the displacements of the nanotubes in the middle part of the bundle $u_{z_{1,i}}$.

Fig. 4

Curve of a the total potential and b the forces $F_{1}$ and $F_{2}$ between the parts of the bundle

In Fig. 4, the total potential and the forces $F_{1}$ and $F_{2}$ are plotted versus the simulation step number. At the start of the curve of the Lennard–Jones potential, the equilibrium position of the bundle can be found. The forces start with $F=0$ representing the minimum of the potential; see Fig. 4a. Afterward, the forces increase as the bundle starts to be pulled apart and the potential has the highest positive increase. The potential reaches the point of inflection (here at 4 simulation steps) and gives a maximum of the forces. Afterward, the potential’s increase becomes less steep and the forces decrease. The equilibrium state of the model for each simulation step can be deduced from the evolution of the forces. Forces $F_{1}$ and $F_{2}$ both show a very similar course; see Fig. 4b. The slight deviations of $F_{1}$ and $F_{2}$ occur due to the tolerance criterion of the conjugate gradient algorithm and the simulation step size. For a reduction in the step size, the difference between $F_{1}$ and $F_{2}$ reduces. In order to handle the computational effort, a simulation step size of $s = 0.1$ Å is chosen in the complete research. The maximal force is the resulting force $F_\mathrm{res}$ that is necessary to pull the bundle apart virtually; see Table 2.

Table 2 Overview of the results

By using the resulting force $F_\mathrm{res}$ and the cross-sectional area A of the bundle, a maximum stress $\sigma _\mathrm{res}$ can be calculated by

$$\begin{aligned} \sigma _\mathrm{res} = \frac{F_\mathrm{res}}{A}. \end{aligned}$$

(6)

Here, A denotes the cross-sectional area of the bundle, assumed as a circle with the diameter of the bundle $d_\mathrm{bundle}$. The calculated stresses are given in order to enable comparability to other investigations available in the literature.

Fig. 5

Overview about the influence of different parameters to the mechanical behavior

The simulation using the default parameters shows a resulting force of $F_\mathrm{res}=11.2\,\hbox {nN}$ and a stress of $\sigma _\mathrm{res}=142\,\hbox {MPa}$. As shown in Table 2, for smaller nanotube diameters, the resulting force is decreased, while the stress remains at almost the same value. Using longer CNTs has nearly no effect on the resulting force and on the stress. It is also found that by decreasing the number of CNTs in the cross section, a much smaller resulting force is obtained, while the stress remains almost at the same value with respect to the reference test case 0. The small variations of the stresses may be explained by a limited intertube load transfer mechanism due to the weak van der Waals forces between the carbon nanotubes. Even if the contact area between the nanotubes varies, the resulting force changes with respect to the contact area. Further, there is possibly a maximal intertube stress transfer occurring between carbon nanotubes, which can be increased by adapting geometric parameters. Test case 5 shows that the change of the cross-sectional arrangement of the CNTs has a high impact on the mechanical properties. Arranging the nanotubes more densely leads to a much higher resulting force and a larger stress. The value of the intertube stress comes closer to its maximum, when the nanotubes are positioned in their preferred formation, i.e., according to the desired atomic distance. Figure 5 gives an overview of the different parameters that influence the mechanical properties of the bundle model. From the direction of the arrows, it is obtained how the examined parameters influence the resulting force and the stress.

Fig. 6

Course of the displacement $u_{z_{1,i}}$ of every nanotube in the middle part of the bundle versus the simulation step number for the reference test case

In Fig. 6, the displacement $u_{z_{1,i}}$ in z-direction of every singular CNT in the middle part of the bundle is plotted. These curves show that the entire bundle is evenly pulled apart in the first simulation steps. The individual nanotubes start to move up and are at first located in equilibrium positions in the center between the lower and the upper parts of the bundle. After approx. 5 simulation steps, the first of the displacement curves reaches its maximum and starts to decline. Subsequently, more and more curves reach the maximal value and their values decrease again. This marks the turning point for pulling apart the CNT bundle, and the bundle starts to divide. The experimental investigations of Yang et al. [8] have shown that the failure of an entire CNT fiber starts with the fracture of a bundle. The transition between the elastic and plastic part of the mechanical behavior is marked by the slipping apart of the individual carbon nanotubes within the bundles. In contrast to the plasticity of metallic materials, the plastic behavior of CNT fibers is not related to the occurrence of lattice defects or atomic misalignments. Furthermore, the intra-bundle slipping can be seen as misalignment of individual nanotubes in comparison with the previous CNT orientation. We assume the back relaxation of the nanotubes in the middle part of the bundle model as misalignment. This can be understood as starting point for the slipping apart of the entire bundle, similarly to intra-bundle slipping of real CNT bundles. Following the work of Yang et al. [8], this can be seen as the starting point of the plastic stage of the mechanical behavior of the model.

Table 3 Overview of selected experimental and simulative investigations of carbon nanotube bundles and fibers

The presented investigations are categorized between a detailed atomistic approach and the macroscopic modeling of an entire fiber. The nanotubes in the presented model consist of individual atoms, similar to atomistic approaches. Due to the consideration of strong interactions between covalent bonded atoms, atomistic approaches give mostly larger values of the mechanical properties. In this case, the computing effort limits the number of CNT and makes it difficult to realize a model consisting of free-moving nanotubes. Analogously to macroscopic modeling approaches, the presented bundle consists of many individual nanotubes, which can move independently. Therefore, the results of the investigated test cases are in very good agreement with other theoretical and experimental research. In comparison with the work of Beese et al. [18] which uses the approach of modeling an entire fiber consisting of many individual bundles, the results of the present numerical investigations give similar values for the failure stress of the bundle. Zhang et al. [29] and Li et al. [30] obtained comparable stress values by experimental investigations with CNT fibers under tension. However, it should be noted that the present numerical investigation considers a CNT bundle, which is only a small part of an entire CNT fiber. In Table 3, an overview of the results of different experimental and theoretical approaches is given.

5 Conclusion

In the present work, a model of a CNT bundle consisting of rigid structure models of carbon nanotubes is given. The mechanical behavior of this model is investigated numerically by calculating and analyzing the Lennard–Jones potential. In different test cases, several parameters of the bundle model were changed: The reference test case gives a resulting force of $F_\mathrm{res}=\,11.2$ nN and a resulting stress of $\sigma _\mathrm{res}=\,142$ MPa. A smaller nanotube diameter leads to a lower resulting force and a smaller resulting stress. Changing the nanotube length has no noticeable impact on the results. In addition, different offset values do not have a large impact on the mechanical behavior. On the other hand, changing the arrangement of the CNTs in the cross section of the bundle has a high impact on the results: A dense arrangement of the nanotubes with equal cross-sectional nanotube distances leads to both a higher resulting force and a higher stress. Furthermore, using a model configuration with a smaller number of CNTs per layer leads to a smaller resulting force and an almost constant stress, as the force and the diameter of the bundle decrease with respect to each other. An important fact of the presented work is the possibility of following the curve of the positions of every single nanotube in the bundle model. This gives the possibility to assign the behavior of the model to the phases of an experimental carbon nanotube fiber stress test.

In further research, the presented model will be extended regarding geometric aspects, e.g., with several bundles, interconnecting threads and a fiber twist angle. As shown in experimental and theoretical works, geometric fiber properties are important factors for the mechanical behavior of CNT fibers [8, 31]. Based on these considerations, optimized parameter sets for improved mechanical properties—compared to the present research—are expected. Additionally, the model can be used for investigating new test cases, for example to find an optimal combination of parameters which increase the mechanical properties. Furthermore, the presented model of a CNT bundle enables the opportunity to be extended using a molecular structural mechanics approach. This can be performed in order to verify the influence of the strong interactions of covalently bonded atoms in the nanotubes.

In conclusion, in the presented work a new model for the investigation of the behavior of carbon nanotube bundles is given. The obtained results indicate the influencing factors on the mechanical properties and therefore of the mechanical behavior. This offers a great possibility for further investigations on the way to a better understanding of the mechanical behavior of carbon nanotube fibers.

Appendix

In the present work, a conjugate gradient method is used in order to obtain a minimum of the total potential. The procedure is implemented as iterative algorithm in MATLAB. The displacement of the individual nanotubes in the middle part of the bundle $u_{z_{1,i}}$ and the upper part of the bundle $u_{z_{2}}$ for the next iteration step $k+1$ is given by the current displacement $u_{z_{1,i/2}}^{k}$, the step size $\alpha ^k$ and the search direction $s^k$:

$$\begin{aligned} u_{z_{1,i/2}}^{k+1} = u_{z_{1,i/2}}^{k} + \alpha ^k s^k. \end{aligned}$$

(7)

The search direction of the first iteration step $s^0$ is given by the negative gradient of the total potential,

$$\begin{aligned} s^0&= - \nabla U_\mathrm{tot}\left( u_{z_{1,i/2}}^{0}\right) , \end{aligned}$$

(8)

$$\begin{aligned} \text {where} \qquad \nabla U_\mathrm{tot}&= \left( \frac{\partial U_\mathrm{tot}}{\partial u_{z_{1,1}}}, \ldots , \frac{\partial U_\mathrm{tot}}{\partial u_{z_{2}}} \right) ^\mathrm{T}. \end{aligned}$$

(9)

For the following iteration steps, the search direction $s^k$ is extended by a correction term $\beta ^k$—based on the work of Fletscher and Reeves [28]—which includes the previous search direction and leads to a faster convergence,

$$\begin{aligned} s^k&= - \nabla U_\mathrm{tot}\left( u_{z_{1,i/2}}^{k}\right) + \beta ^k s^{k-1}~, \end{aligned}$$

(10)

$$\begin{aligned} \text {where} \qquad \beta ^k&= \frac{ \big |\big | \nabla U_\mathrm{tot}\left( u_{z_{1,i/2}}^{k}\right) \big |\big |^2 }{\big |\big |\nabla U_\mathrm{tot}\left( u_{z_{1,i/2}}^{k-1}\right) \big |\big |^2}. \end{aligned}$$

(11)