1 Introduction

Functionally graded materials (FGMs) are composite materials where the material properties vary throughout the body. The simplest way of designing a graded material is by taking isotropic homogenous layers with different material parameters, which are perfectly bonded together. This special case is a laminate, where the material properties vary discontinuously. The first FGMs were compositions of metallic and ceramic materials where the thermal expansion coefficients varied continuously. A prominent example of a previous FGM application was the space shuttle where a material made of ceramic and metal provided thermal protection and increased the load-carrying capability during re-entering the earth’s atmosphere. One of the most significant aspects of designing FGMs is to close the gap in the properties of different materials continuously. For an introduction the reader is referred to Mahamood [1] and Udupa [2] who give a compact overview of the topic. A mechanical advantage of FGMs is the stress continuity (where the stress distribution is nonlinear in general) and the lower stress gradient inside the material which reduce peak stresses, compared to rigidly bonded plies. The literature on FGMs, where the focus is laid on the derivation of a mechanical model which is valid for arbitrary material property variations, is limited. Here, beam types structures are investigated and a very general modeling strategy is presented to find accurate beam models for a large class of FGMs. Mian [3] focuses on a three-dimensional solution with transversal-dependent elasticity parameters by solving two-dimensional equations for an equivalent homogeneous plate with averaged elastic parameters. The work of Sankar [4] contains the study of a sinusoidally-loaded, simply supported beam with orthotropic material parameters that vary exponentially. The Bernoulli–Euler theory solution is obtained by starting with the assumed axial and transversal displacements. Strains and stresses are computed afterwards. The Airy stress function for an anisotropic FGM beam subjected to normal and axial loads is computed by Ding [5] who assumes the stress function as a sum of products of the independent variables. The suggested method of [5] is applied similarly by Zong [6], Hu [7] and Yang [8]. A cantilever subjected to a linearly distributed normal force is analyzed in [7], whereas in [8] the Airy stress function for a two-layer FGM cantilever with concentrated end loads is computed. A number of various different loading and boundary value problems is solved in [5], and a finite element analysis is performed to compare analytical and numerical results in [5] and [7]. Sakurai [9] developed the Airy stress function for exponentially graded orthotropic beams by an infinite series of products of independent variables. The stress distributions are presented for a simply supported beam subjected to a sinusoidally distributed normal force and a cantilever under uniform pressure. A two-dimensional solution for pure bending and tension is derived in an analogous way by [5,6,7,8] and by Chu [10] for transversal and axial isotropic exponentially graded material. The elastic buckling and bending of a functionally graded, Timoshenko theory-based porous beam, with transversal cosine-dependent material parameters is studied by Chen [11]. Hadji [12] analyzes the static bending and free vibrations of a shear-deformable FGM beam where the strains are assumed to be exponentially distributed in the transverse direction and the material parameters are power-law distributed. A similar analysis of a shear-deformable FGM beam is found in Guenfod [13]. In the work of Xia [14] a comparison of an FGM Reddy–Bickford beam versus a homogenous Bernoulli–Euler beam is presented: The investigation starts with strain assumptions where the transversal strain is disregarded, and as a result, the solutions of determinate and indeterminate beams are shown. A higher-order shear-deformable finite beam element for an FGM sandwich structure is derived by Li [15] where higher-order strain assumptions are taken into account, but the transversal strain is neglected as in [14]. Our motivation in this contribution is to provide an analytical method (under classical plane-stress assumption) to determine a beam model without any a priori assumptions on the displacement or the stress field. This strategy dates back to works of von Karman [16] and Sewald [17] who showed that the curvature of an isotropic beam does depend not only on the bending moment, but also on its even-numbered spatial derivatives. In our contribution, we adopt an iterative solution method for the bi-potential equation, which arises by evaluating the compatibility equations when an isotropic, homogeneous material is considered, see Boley and Tolins [18]. The method of Boley and Tolins [18] consists of a step-by-step procedure to compute the Airy stress function as the solution of the bi-potential equation. The result of the first iteration step yields the classical Bernoulli–Euler (BE) solution, whereas the higher-order iterations are correction terms which take into account the thickness-to-length ratio and become more relevant for thicker beams. Furthermore, one can derive more accurate distributions for the stress components, and cross-sectional warping effects are automatically accounted for. Boley’s method is extended up to the fourth iteration by Irschik [19], who calculates the bending moment for different thickness-to-length ratios to demonstrate the influence of different boundary conditions for a statically indeterminate beam. In a further contribution, the thermoelastic effect is considered in Boley [20], see also the book on thermal stresses by Boley and Weiner [21]. Krommer and Irschik [22] use this method to approximately solve the charge equation of electrostatics for the electric potential if a certain displacement field is assumed. For piezoelectric materials, Schoeftner and Benjeddou [23] give an iterative solution for the electric potential and the Airy stress function in case of piezoelectricity. It is found that the compatibility and the charge equation, which both depend on the stress and the electric potential, are coupled. For a simply supported piezoelectric bimorph with sinusoidal mechanical and electrical actuation, the result is compared to (2D) analytical results. Motivated by the latter contributions, the iterative method from Boley is extended to FGMs. Instead of the bi-potential equation, we derive a fourth-order partial differential equation for the Airy stress function from the compatibility equations. Hereby, no a priori assumptions are made, neither on the displacement field nor on the stress field. The Airy stress function is computed iteratively, and the external loads are replaced by the stress resultants such as normal force, shear force and bending moment. As previously mentioned the first iteration solution is denoted as an elementary solution, and the higher-order solutions can be interpreted as an extension of the Bernoulli–Euler result for a graded material. The results of the further iterations contain the thickness-to-length ratio and further components of the compliance matrix as well. Numerical results are given for an isotropic FGM cantilever with exponentially varying Young’s modulus subjected to a shear load. The results are presented to demonstrate the influence of the graded material on stresses and deformations. The beam model is verified by a two-dimensional (2D) finite element calculation performed with ABAQUS where analytical and numerical results are in excellent agreement.

2 Problem statement

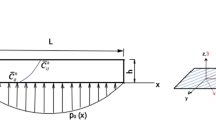
The following presented solution, based on Boley’s method [18], allows the determination of the Airy stress function of a functionally graded beam. The tractions acting on the upper and on the lower surface are polynomials in x. The cross section of the beam is rectangular and constant along the beam length L, the thickness is 2c, and the width is b is set to unit one. It is assumed that the thickness of the beam is sufficiently larger than b, i.e., that the rectangular beam is narrow, such that the state of plane stress can be taken into account. A global Cartesian (x,y)-coordinate system is attached to the mid-span axis, where the axial coordinate is denoted by x, and the transverse coordinate by y (Fig. 1).

Fig. 1
figure 1

Beam element with thickness 2c and width b subjected to normal and shear forces at the boundary surfaces at \(y= \pm c\)

Full size image

The traction vectors at the upper surface at \(y = c\) and at the lower one at \(y = -c\) read

$$\begin{aligned} {\varvec{t}}_u&= \left\{ \begin{array}{cc} n_u(x) \\ q_u(x) \\ \end{array}\right\} / b,&{\varvec{t}}_l&= \left\{ \begin{array}{cc} n_l (x) \\ q_l(x) \\ \end{array}\right\} / b. \end{aligned}$$
(1)

In Eq. (1), the subscripts u and l denote the upper and lower surface. The material characteristics of the beam are described by the compliance matrix \({\varvec{S}}\), where we restrict ourselves to transversal dependency only in this contribution:

$$\begin{aligned} {\varvec{S}} = \left[ \begin{array}{ccc} 1&{} -\nu &{}0 \\ -\nu &{}1&{} 0 \\ 0 &{}0 &{} 2(1+\nu ) \\ \end{array}\right] \frac{1}{E(y)} \end{aligned}$$
(2)

with Poisson’s ratio \(\nu \) and the y-dependent Young’s modulus E(y).

3 Method of solution

Under the prescribed constitutions, we have to find solutions of the plane linear theory of elasticity, which satisfies exactly the equilibrium equations,

$$\begin{aligned} \sigma _{x ,x} +\tau _{xy,y}&= 0,&\tau _{xy,x} +\sigma _{y, y}&= 0, \end{aligned}$$
(3)

the strain–displacement relations,

$$\begin{aligned} u_{,x}&= \varepsilon _x,&v_{,y}&= \varepsilon _y,&u_{,y} + v_{,x}&= \gamma _{xy}, \end{aligned}$$
(4)

the stress boundary conditions at the upper and lower surface of the beam at \(y = \pm c\) and the stress–strain relations, see Eq. (7). The normal stresses are \(\sigma _x\) and \(\sigma _y\), \(\tau _{xy}\) is the shear stress, \(\varepsilon _x\) and \(\varepsilon _y\) are normal strains, \(\gamma _{xy}\) is the shear angle, u is the axial, and v is the transversal displacement, respectively. Note that we take advantage of the following definitions for the partial derivatives with respect to x and y:

$$\begin{aligned} ()_{,x}&=\frac{\partial ()}{\partial x},&()_{,y}&=\frac{\partial ()}{\partial y}. \end{aligned}$$
(5)

If the stresses in Eq. (3) are expressed as derivatives of the introduced Airy stress function \(\psi (x,y)\), see Timoshenko and Goodier [24],

$$\begin{aligned} \sigma _{x}&= \psi _{,yy},&\sigma _{y}&= \psi _{,xx},&\tau _{xy}&= -\psi _{,xy}, \end{aligned}$$
(6)

the equilibrium equations in Eq. (3) are automatically satisfied. The stress–strain relation expressed in Voigt’s notation reads

$$\begin{aligned} \left\{ \begin{array}{ccc} \varepsilon _{x} &{}\varepsilon _{y}&{}\gamma _{xy}\\ \end{array}\right\} ^T = {\varvec{S}} \left\{ \begin{array}{ccc} \psi _{,yy} &{}\psi _{,xx} &{}-\psi _{,xy} \\ \end{array}\right\} ^T \end{aligned}$$
(7)

if Eq. (6) is substituted for the stresses. The so-called compatibility condition can be derived from Eq. (4) which leads to

$$\begin{aligned} \varepsilon _{x,yy} +\varepsilon _{y,xx} - \gamma _{xy,xy} = 0. \end{aligned}$$
(8)

Inserting Eq. (7) into Eq. (8) leads to a fourth-order partial differential equation (PDE)

$$\begin{aligned}&\psi _{,yyyy}-\frac{2 E_{,y}}{E}\psi _{,yyy}+\left( \frac{2 E_{,y}^2 }{E^2}-\frac{E_{,yy}}{E}\right) \psi _{,yy} \nonumber \\&\quad =\nu \frac{2E_{,y}^2 - E E_{,yy}}{E^2}\psi _{,xx}+ 2\frac{E_{,y}}{E}\psi _{,xxy}- 2 \psi _{,xxyy}- \psi _{,yyyy}. \end{aligned}$$
(9)

In the case of a constant Young’s modulus with \(E_{,y} = 0\), Eq. (9) simplifies to the bi-harmonic equation

$$\begin{aligned} \psi _{,yyyy} = - 2\psi _{,xxyy} - \psi _{,yyyy}. \end{aligned}$$
(10)

In order to find a solution of Eq. (9) we take advantage of a method which was originally developed by Boley [18] for isotropic beams. Boley’s methodology computes the Airy stress function in an iterative procedure, where the solution \(\psi \) can be written as a sum of iteration solutions,

$$\begin{aligned} \psi = \sum _{i=1}^n \psi _i \end{aligned}$$
(11)

with \(\psi _i\) as the solution of the \(i^{\text {th}}\) iteration. The total number of iterations is n. The solution of the first iteration can be interpreted as the Bernoulli–Euler (BE) result, (i.e., see \(u_1\) and \(v_1\) in Eqs. (47) and (48)), whereas the higher-order solutions \(\psi _2,\,\psi _3, \dots \) represent higher-order terms which include a thickness-to-length ratio \(\lambda = 2c/L\). We adapt here Boley’s method to an FGM configuration where the iteration rule reads

$$\begin{aligned}&\psi _{i,yyyy}-\frac{2 E_{,y}}{E}\psi _{i,yyy}+\left( \frac{2 E_{,y}^2 }{E^2}-\frac{E_{,yy}}{E}\right) \psi _{i,yy} \nonumber \\&\quad =\nu \frac{2E_{,y}^2 - E E_{,yy}}{E^2}\psi _{i-1,xx}+ 2\frac{E_{,y}}{E}\psi _{i-1,xxy}- 2 \psi _{i-1,xxyy}- \psi _{i-2,yyyy} \end{aligned}$$
(12)

and the convention that

$$\begin{aligned} \psi _i&= 0,&\text {for}&\;i < 1. \end{aligned}$$
(13)

holds. The stress boundary conditions at \(y = \pm c\) are satisfied by means of the first term \(\psi _1\) only. Inserting Eq. (6) into Eq. (1), the boundary conditions at the surfaces read

$$\begin{aligned} n_u(x)/b&= -\psi _{1,xy}(x,c),&n_l(x)/b&= -\psi _{1,xy}(x,-c), \nonumber \\ q_u(x)/b&= \psi _{1,xx}(x,c),&q_l(x)/b&= \psi _{1,xx}(x,-c). \end{aligned}$$
(14)

For all further iterations, (i.e., \(\psi _{i > 1} \)) the stress boundary conditions are trivial:

$$\begin{aligned} \psi _{i,xx}(x,c) =\psi _{i,xx}(x,-c) = \psi _{i,xy}(x,c) =\psi _{i,xy}(x,-c)&= 0 \end{aligned}$$
(15)

for \(i \ge 2\).

3.1 First iteration

For the computation of the first potential \(\psi _1\) we consider Eqs. (12) and (13), and we find for the first iteration

$$\begin{aligned} \psi _{1,yyyy}-\frac{2 E_{,y}}{E}\psi _{1,yyy}+\left( \frac{2 E_{,y}^2 }{E^2}-\frac{E_{,yy}}{E}\right) \psi _{1,yy} = 0. \end{aligned}$$
(16)

Equation (16) is a fourth-order ordinary differential equation (ODE) with variable coefficients. A solution of Eq. (16) is

$$\begin{aligned} \psi _1 = \sum _{j =1}^4 g_j(y) k_j, \end{aligned}$$
(17)

see Lang and Pucker [28], with four remaining constants \(k_j\) and functions \(g_j(y)\) which are results when solving Eq. (16). To ensure the x, y dependency of \(\psi _1\) the constants \(k_j\) are replaced by functions \(f_j(x)\) which leads to

$$\begin{aligned} \psi _1 = \sum _{j =1}^4 g_j(y) f_j(x). \end{aligned}$$
(18)

Integration of the first row of Eq. (14) once, and the second of Eq. (14) twice with respect to x leads to the following vector-matrix notation:

$$\begin{aligned} {\varvec{A}}{\varvec{f}} = {\varvec{q}} \end{aligned}$$
(19)

with

$$\begin{aligned} {\varvec{A}}= & {} \left\{ \begin{array}{cccc} {\varvec{g}}(y \!=\! c)&{}-{\varvec{g}}_{,y}(y \!=\! c)&{}{\varvec{g}}(y \!=\! -c)&{}-{\varvec{g}}_{,y}(y \!=\! -c) \\ \end{array} \right\} ^T, \end{aligned}$$
(20)
$$\begin{aligned} {\varvec{g}}= & {} \left\{ \begin{array}{cccc} g_1(y)&{}g_2(y)&{}g_3(y)&{}g_4(y) \\ \end{array} \right\} , \end{aligned}$$
(21)
$$\begin{aligned} {\varvec{f}}= & {} \left\{ \begin{array}{cccc} f_1(x)&{}f_2(x)&{}f_3(x)&{}f_4(x) \\ \end{array} \right\} ^T, \end{aligned}$$
(22)
$$\begin{aligned} {\varvec{q}}= & {} \left\{ \begin{array}{c} \iint q_u /b\,dx^2 + C_1 x + C_2 \\ \int n_u/b \,dx +C_3 \\ \iint q_l /b\,dx^2 + K_1 x + K_2 \\ \int n_l/b \,dx +K_3 \\ \end{array}\right\} . \end{aligned}$$
(23)

The vector \({\varvec{q}}\) contains the integrated surface loads, \({\varvec{A}}\) denotes a 4\(\times \)4 coefficient matrix, \({\varvec{f}}\) is the vector with the unknowns \(f_j(x)\), and \({\varvec{g}}\) denotes the vector of fundamental solutions \(g_j(y)\). Taking into account Eqs. (18)–(23) the solution of \(\psi _i\) in Eq. (18) reads

$$\begin{aligned} \psi _1 = {\varvec{g}}{\varvec{A}}^{-1}{\varvec{q}}. \end{aligned}$$
(24)

3.1.1 Stress function in terms of stress resultants

The remaining constants \(C_1,\;C_2,\;C_3\) and \(K_1,\;K_2,\;K_3\) in Eq. (23) are computed by introducing the stress resultants, such as bending moment M(x), shear force Q(x) and the normal force N(x),

$$\begin{aligned} M(x)&= b \int _{-c}^c \sigma _x y dy,&Q(x)&=b \int _{-c}^c \tau _{xy} dy,&N(x)&= b \int _{-c}^c \sigma _x dy. \end{aligned}$$
(25)

Substituting Eqs. (6) and (24) into Eq. (25), it follows that

$$\begin{aligned} M(x)&= \underbrace{- \iint q_udx^2-C_1 x - C_2}_{M_{q_u}} +\underbrace{ \iint q_ldx^2+K_1 x + K_2}_{M_{q_l}}\nonumber \\&\quad - c\left( \int n_u dx + C_3\right) -c \left( \int n_ldx + K_3\right) , \end{aligned}$$
(26)
$$\begin{aligned}&Q(x) =-\int q_u dx - C_1 +\int q_l dx + K1, \end{aligned}$$
(27)
$$\begin{aligned}&N(x) = \underbrace{-\left( \int n_u dx+ C_3\right) }_{N_{n_u}} + \underbrace{ \int n_l dx + K_3}_{N_{n_l}}, \end{aligned}$$
(28)

where \(M_{q_u}(x)\), \(M_{q_l}(x)\), \(N_{n_u}(x)\), \(N_{n_l}(x)\) are the bending moments and the normal forces caused by the tractions \(q_u(x)\), \(q_l(x)\), \(n_u(x)\), \(n_l(x)\), respectively, see Eq. (23). \(C_1\) and \(K_1\) are constant portions of the shear force Q(x), \(C_2\) and \(K_3\) belong to the bending moment M(x), and \(C_3\) and \(K_3\) are constant portions of the normal force N(x). Differentiation of Eqs. (26)–(28) gives the beam equilibrium equations:

$$\begin{aligned} M_{,x}&= Q - c(n_l+n_u),&Q_{,x}&= q_l - q_u,&N_{,x}&= n_l-n_u. \end{aligned}$$
(29)

The results in Eq. (29) correspond to the sign convention for a right-handed coordinate system xyz as that shown in Fig. 2 for a differential beam element (i.e., at \(x+dx\) the positive normal force N(x) and the positive shear force Q(x) are parallel to the x- and y-directions, respectively, but the positive bending moment M(x) is in opposite direction to the positive z-direction). It is noted that if the positive directions of the coordinates do not match with those in Fig. 2, one observes that the resulting equilibrium equations on beam level and those in Eq. (29) will differ in signs.

Fig. 2
figure 2

Stress resultants of a differential beam element

Full size image

3.2 Second iteration

To compute the second stress function \(\psi _2\), we set \(i=2\) in Eq. (12), and by considering Eq. (13) we find

$$\begin{aligned}&\psi _{2,yyyy}-\frac{2 E_{,y}}{E}\psi _{2,yyy}+\left( \frac{2 E_{,y}^2 }{E^2}-\frac{E_{,yy}}{E}\right) \psi _{2,yy} \nonumber \\&\qquad \qquad =\nu \frac{2E_{,y}^2 - E E_{,yy}}{E^2}\psi _{1,xx}+ 2\frac{E_{,y}}{E}\psi _{1,xxy}- 2 \psi _{1,xxyy} \end{aligned}$$
(30)

with the trivial boundary conditions from Eq. (15). The solution of \(\psi _2\) is a long expression in general, but can be determined by symbolic computation software.

3.3 Further iterations

We repeat the prescribed procedure and obtain for the third iteration step for \(i=3\) in Eq. (12)

$$\begin{aligned}&\psi _{3,yyyy}-\frac{2 E_{,y}}{E}\psi _{3,yyy}+\left( \frac{2 E_{,y}^2 }{E^2}-\frac{E_{,yy}}{E}\right) \psi _{3,yy} \nonumber \\&\qquad \qquad =\nu \frac{2E_{,y}^2 - E E_{,yy}}{E^2}\psi _{2,xx}+ 2\frac{E_{,y}}{E}\psi _{2,xxy}- 2 \psi _{2,xxyy}- \psi _{1,yyyy}. \end{aligned}$$
(31)

The solution of \(\psi _3\) depends on the previous solutions \(\psi _1\), \(\psi _2\). As for the second iteration, trivial boundary conditions are assumed, see Eq. (15).

4 Shear-loaded beam

The developed solution procedure is verified by the following example. An FGM beam is investigated which is subjected to a shear force at the upper surface at \(y= c\), see Fig. 3.

Fig. 3
figure 3

FGM beam subjected to a shear force \(n_u(x)\) on the upper boundary surface at \(y=c\)

Full size image

The boundary tractions are as follows:

$$\begin{aligned} {\varvec{t}}_u&= \left\{ \begin{array}{cc} n_u(x)/b \\ 0 \\ \end{array}\right\} ,&{\varvec{t}}_l = \left\{ \begin{array}{cc} 0 \\ 0 \\ \end{array}\right\} . \end{aligned}$$
(32)

We assume an isotropic graded material with an exponential variation of the Young’s modulus in transverse direction where the compliance matrix of Eq. (2) becomes

$$\begin{aligned} {\varvec{S}}&= \left[ \begin{array}{ccc} 1 &{}\quad -\nu &{}\quad 0 \\ -\nu &{} \quad 1 &{}\quad 0 \\ 0&{} \quad 0&{}\quad 2(1+\nu ) \\ \end{array}\right] \frac{1}{E(y)},&E(y)&= E_0 e^{\alpha y/c}, \end{aligned}$$
(33)

with an introduced nondimensional gradient \(\alpha \) and the Young’s modulus \(E_0\) at the midspan axis at \(y=0\). The stress–strain relations become

$$\begin{aligned} \varepsilon _x&= \frac{1}{E_0 e^{\alpha y/c}}\left( \sigma _x - \nu \sigma _y\right) ,&\varepsilon _y&= \frac{1}{E_0 e^{\alpha y/c}}\left( \sigma _y -\nu \sigma _x\right) ,&\gamma _{xy} = \frac{2(1+\nu )}{E_0 e^{\alpha y/c}}\tau _{xy}. \end{aligned}$$
(34)

Reinserting the relations of Eq. (34) into Eq. (8) leads to the iteration rule for computation of the stress function \(\psi \)

$$\begin{aligned}&\psi _{i,yyyy} - 2 \frac{\alpha }{c}\psi _{i,yyy} + \frac{\alpha ^2}{c^2}\psi _{i,yy} = -2 \psi _{i-1,xxyy} +\nu \frac{\alpha ^2 }{c^2}\psi _{i-1,xx} +2 \frac{\alpha }{c}\psi _{i-1,xxy} - \psi _{i-2,xxxx} \end{aligned}$$
(35)

with the conventions of Eq. (13) to be considered. If we set \(\alpha = 0\), which corresponds to isotropic material, we obtain the iteration rule as stated in the paper of Boley [18]:

$$\begin{aligned} \psi _{i,yyyy} = -2 \psi _{i-1,xxyy} - \psi _{i-2,xxxx}. \end{aligned}$$
(36)

4.1 First iteration

Setting \(i=1\) in Eq. (35) one finds for the computation of the first stress function

$$\begin{aligned} \psi _{1,yyyy} - 2 \frac{\alpha }{c}\psi _{1,yyy} + \frac{\alpha ^2}{c^2}\psi _{1,yy} =0. \end{aligned}$$
(37)

The solution of Eq. (37) follows as

$$\begin{aligned} \psi _1 = \frac{c^2}{\alpha ^2} e^{ \alpha \, y /c} \bigg [f_1(x)+ \left( y-\frac{2c}{\alpha } \right) f_2(x)\bigg ]+y f_3(x) +f_4(x). \end{aligned}$$
(38)

The unknown functions \(f_j(x)\) can be determined from the tractions at \(y=\pm c\), see Eq. (32); with the coefficient matrix \({\varvec{A}}\) and the load vector \({\varvec{q}}\) we can write:

$$\begin{aligned} \underbrace{\left[ \begin{array}{cccc} c^2\dfrac{e^{\alpha } }{\alpha ^2} &{}c^3\dfrac{e^{\alpha } (\alpha -2) }{\alpha ^3} &{}1&{} c \\ -c\dfrac{e^{\alpha }}{\alpha }&{}-c^2\dfrac{e^{\alpha } (\alpha -1) }{\alpha ^2} &{}0 &{} -1 \\ c^2\dfrac{e^{-\alpha } }{\alpha ^2}&{} -c^3\dfrac{e^{-\alpha } (\alpha +2)}{\alpha ^3} &{}1 &{} -c \\ -c\dfrac{e^{-\alpha } }{\alpha }&{}c^2\dfrac{e^{-\alpha } (\alpha +1) }{\alpha ^2} &{}0&{}-1\\ \end{array}\right] }_{{{\varvec{A}}}} \underbrace{\left\{ \begin{array}{c} f_1(x) \\ f_2(x) \\ f_3(x) \\ f_4(x)\\ \end{array}\right\} }_{{{\varvec{f}}}} = \underbrace{ \left\{ \begin{array}{c} C_1 x + C_2 \\ \! \displaystyle \int n_u \; dx + C_3 \\ K_1 x + K_2 \\ K_3 \\ \end{array}\right\} }_{{{\varvec{q}}}}. \end{aligned}$$
(39)

The result of \(\psi _1\) is lengthy, and to simplify the expression, we introduce entities corresponding to the elementary theory: the so-called effective axial rigidity \([EA]_{\text {eff}}\), the flexural rigidity \([EI]_{\text {eff}}\) and the location of the neutral axis \(c_0\). For computing these elementary entities see e.g. Ziegler [26]:

$$\begin{aligned}{}[EA]_{\text {eff}}&= b c\frac{e^{-\alpha } \left( e^{2 \alpha }-1\right) }{\alpha }E_0,&[EI]_{\text {eff}}&=b c^3\frac{e^{-\alpha } \left( -2 e^{2 \alpha } \left( 2 \alpha ^2+1\right) +e^{4 \alpha }+1\right) }{\left( e^{2 \alpha }-1\right) \alpha ^3}E_0, \end{aligned}$$
(40)
$$\begin{aligned} \zeta _0&= \frac{\left( e^{2 \alpha } (\alpha -1)+\alpha +1\right) }{\left( e^{2 \alpha }-1\right) \alpha },&c_0&= \zeta _0c. \end{aligned}$$
(41)

The normal stress \(\sigma _{1x} = \psi _{1,yy}\) as a result of the first iteration in terms of the introduced entities of Eqs. (40) and (41) reads

$$\begin{aligned} \sigma _{1x}&= c\, \frac{\eta -\zeta _0}{[EI]_{\text {eff}}} M(x)E_0 e^{\alpha y/c}+ \bigg [c^2\zeta _0 \frac{\zeta _0-\eta }{[EI]_{\text {eff}}}+ \frac{1}{[EA]_{\text {eff}}} \bigg ] N(x) E_0 e^{\alpha y/c}\nonumber \\ \end{aligned}$$
(42)

and the shear stress \(\tau _{1xy} = -\psi _{1,xy}\)

$$\begin{aligned} \tau _{1xy}&=-\frac{2 \alpha ^2 \left[ (\eta -1) e^{\alpha (\eta +3)}- (\eta +1) e^{\alpha (1+\eta )}\right] -2 e^{2 \alpha }+e^{4 \alpha }+1}{2 \left[ 1-2 e^{2 \alpha } \left( 2 \alpha ^2+1\right) +e^{4 \alpha }\right] } \frac{M_{,x}}{bc}\nonumber \\&\quad +\frac{2 e^{\alpha (3+\eta )} [\alpha (\alpha -1) (\eta -1)-1]+2 e^{\alpha (1+ \eta )} [\alpha (\alpha +1) (\eta +1)+1]-4 e^{2 \alpha } \alpha +e^{4 \alpha }-1}{2[1- e^{2 \alpha } \left( 4 \alpha ^2-e^{2 \alpha }+2\right) ]}\frac{N_{,x}}{b}\nonumber \\ \end{aligned}$$
(43)

with \(\eta = y/c\). The distribution of the normal stress depends on the variation of the Young’s modulus, where for the case of \(E_{,y}\approx 0\) the nonlinear distributions as well as the linear portion of the axial stress \(\sigma _{1xN}\) are negligible, see Eqs. (40)–(42). A special case is the isotropic homogeneous beam, i.e., \(\alpha \rightarrow 0\). Applying L’Hospital’s rule for Eqs. (40)–(42) one finds

$$\begin{aligned}{}[EA]_{\text {eff}}&= E_0 2 b c,&[EI]_{\text {eff}}&=E_0\frac{2bc^3}{3},&\zeta _0&= 0. \end{aligned}$$
(44)

For the normal stress \(\sigma _{1x}\) there remains a linear distribution due to the bending moment M(x) and a constant part due to the normal force N(x):

$$\begin{aligned} \sigma _{1x,\alpha \!=\!0}&= c\, \frac{M(x)}{I}\eta + \frac{N(x)}{A}. \end{aligned}$$
(45)

4.2 Second iteration

Inserting \(\psi _1\) into Eq. (35) leads to the computation rule for \(\psi _2\):

$$\begin{aligned}&\psi _{2,yyyy} - 2 \frac{\alpha }{c}\psi _{2,yyy} + \frac{\alpha ^2}{c^2}\psi _{2,yy} = - 2 \psi _{1,xxyy} +\nu \frac{\alpha ^2 }{c^2}\psi _{1,xx} + 2 \frac{\alpha }{c}\psi _{1,xxy}, \end{aligned}$$
(46)

following the boundary conditions (15). If a linear distribution of the shear force is assumed, the iteration procedure ends at \(i = 2\), which corresponds to the second-order polynomial of the load vector \({\varvec{q}}\), see Eq. (39).

4.3 Displacements

The displacements u(x, y) and v(x, y) are computed by integration of the normal strains \(\varepsilon _x\) and \(\varepsilon _y\) and then adjusting the arbitrary functions F(x) and G(y) so that \(u_{,y} + v_{,x}-\gamma _{xy} =0\) is satisfied. During this procedure, three constants preventing rigid body motion, \(u_0\), \(v_0\) and \(r_0\), remain, which have to be determined by setting up a boundary value problem, see Sect. 5. For more details of this standardized procedure see, e.g., Timoshenko and Goodier [24]. The expressions of the displacements are very lengthy, so we show the displacements of the first iteration \(u_1\) and \(v_1\) only:

$$\begin{aligned}&u(x,y)= \underbrace{\frac{y- c_0}{[EI]_{\text {eff}}} \int M dx + \left[ \frac{1}{[EA]_{\text {eff}}} + c_0\frac{c_0 - y }{[EI]_{\text {eff}}}\right] \int N dx}_{\text {elementary solution for }u_1} + \underbrace{\sum _{i =2}^n u_i(x,y)}_{\text {higher-order terms}} + r_0 \, y + u_0, \end{aligned}$$
(47)
$$\begin{aligned}&v(x,y)= \underbrace{\frac{1}{[EI]_{\text {eff}}}\bigg [c_0 \iint N \, dx^2- \iint M\, dx^2 \bigg ]}_{\text {elementary solution for }v_1} +\underbrace{ \sum _{i =2}^n v_i(x,y)}_{\text {higher-order terms }} - r_0x + v_0. \end{aligned}$$
(48)

It has to be noted that the coupling relations of M(x) and N(x) due to u and v vanish if an isotropic homogeneous material is assumed, i.e., u(x, y) depends on N(x) and v(x, y) depends on M(x) only because in this case \(c_0=0\). For the case \(\alpha \ne 0\) it follows that \(c_0 \ne 0\); hence, \(M(x){-}N(x)\) coupling occurs in both equations for the elementary solutions \(u_1\) and \(v_1\). The midspan axis displacements \(U(x)= u(x,0)\) and \(V(x) = v(x,0)\) corresponding to the example problem of Sect. 5 are presented in the Appendix, Table 2.

5 Numerical example

The previously determined results are applied to a cantilever beam with length L, thickness 2c and a thickness-to-length ratio \(\lambda = 2c/L = 1/10\), see the scaled sketch in Fig. 4. The beam is loaded by a linearly distributed shear force at the upper surface, and the stress distributions and the displacements are determined due to variations of the Young’s modulus in the y-direction.

Fig. 4
figure 4

FGM cantilever subjected to a linear distributed shear force acting on the upper surface of the beam, a. Boundary conditions at \(x=0\) and the definition of the cross-sectional rotation \(\phi (x)\) are shown in b, for equivalent boundary conditions see Szabo [27]

Full size image

The graded material is assumed for a constant Poisson’s ratio \(\nu \) and an exponentially distributed Young’s modulus \(E(y) = E_0e ^{\alpha y/c}\), see Eq. (33). The derived results are compared to a two-dimensional (2D) finite element analysis (FEA) performed with the commercial software ABAQUS. The example beam (length \(L=50\,\mathrm {mm}\) and thickness \(2c =5 \; \mathrm {mm}\)) is meshed with CPS8, an 8-node biquadratic plane stress quadrilateral element. To model the FGM characteristics of the beam, the cross section is separated into 50 isotropic linear elastic layers with constant Poisson’s ratio \(\nu \) and constant Young’s modulus \(E_n\). The layer-wise Young’s modulus \(E_n\) is computed from

$$\begin{aligned} E_n = E_0 e^{\alpha \beta _n} \end{aligned}$$
(49)

with \(\beta _n = (2n - 51)/ 50\), \(\; 1 \le n\le 50\). For the FEA model, we only investigate the case \(\alpha =1/2\) and one finds the parameters for the FEA collected in Table 1.

Table 1 Parameters for the (2D) ABAQUS finite element model
Full size table

The three kinematical constants \(u_0, v_0\) and \(r_0\) (see Eqs. (47) and (48)) are computed by three kinematical boundary conditions, in order to prevent two rigid body translations and one rigid body rotation. It holds that

$$\begin{aligned} u(0,0)&=0,&v(0,0)&=0, \end{aligned}$$
(50)

and

$$\begin{aligned} \phi (x)&= \frac{u(x,c)- u(x,-c)}{2c} \quad \longrightarrow \quad \phi (0) = 0 . \end{aligned}$$
(51)

The latter constraint for the cross-sectional rotation was suggested by Szabo [27] and applied in the work of Gahleitner and Schoeftner [25] in order to get similar results as for a rigid clamped end with \(u(0,y) = v(0,y)=0\).

In our simulation the FE model is subjected to the same tractions as the analytical model (see Fig. 3). The upper surface traction \({\varvec{t}}_u\) at \(y=c\) contains the imposed shear load \(n_u(x)\), while the lower layer traction \({\varvec{t}}_l\) at \(y=-c\) vanishes. It is important to note that at the clamped end at \(x=0\) the traction components of \({\varvec{t}}_0\) read \(\sigma _x(0) = \psi _{1,yy}(0,y) + \psi _{2,yy}(0,y)\) and \(\tau _{xy}(0) = - \psi _{1,xy}(0,y)\), see Eqs. (42) and (43) for the first iterations and the solution of (46) for the second iteration (lengthy expression). For the free end at \(x=L\) the x- and the y-components of the traction \({\varvec{t}}_L\) read \(\sigma _x(L) = \psi _{2,yy}(L,y)\) (see Eq. (46), and the bending moment vanishes, consequently \(\psi _{1,yy}(L,y)=0\) and \(-\psi _{1,xy}(L,y)=0\)) (Fig. 5).

Fig. 5
figure 5

Tractions at the boundary surfaces \({\varvec{t}}_0, {\varvec{t_L}} , {\varvec{t}}_u, {\varvec{t}}_l\) for the FE model

Full size image

The analytical results are presented for four different Young’s modulus distributions, see Eq. (33) with \(\alpha =\lbrace 0,1/10,1/5,1/2\rbrace \) and \(E_0\) and \(c=h/2\) according to Table 1. Here the nondimensional transverse coordinate \(\eta =y/c\) is introduced. If \(\alpha \ll 1\) holds, the Young modulus is almost linearly distributed, i.e., \(E(y)=E_0(1+ \alpha y /c)\) for \(\alpha \ll 1\) or \(E(\eta )=E_0(1+ \alpha \eta )\).

Fig. 6
figure 6

Young’s modulus distribution of the example beam with \(E = E_0 e ^{\alpha \eta }\) and stiffness relations in accordance with the material gradient \(\alpha \), for \([EA]_{\text {eff}}\), \([EI]_{\text {eff}}\) see Eq. (40) also

Full size image

In Fig. 6b the dependency of the stiffness entities is plotted for a gradient range of \(0 \le \alpha \le 1/2\) where EA, EI denote the homogenous stiffness entities for \(\alpha = 0\).

5.1 Stress field

The stress resultants can be determined by integrating the beam equilibrium relations, see Eq. (29):

$$\begin{aligned} N_{,x}&= -n_u,&Q_{,x}&= 0,&M_{,x}&=Q -c \, n_{u}. \end{aligned}$$
(52)

Considering 3 boundary conditions at \(x=L\),

$$\begin{aligned} M(L)&=0,&N(L)&=0,&Q(L)&=0, \end{aligned}$$
(53)

one finds for M, Q and N:

$$\begin{aligned} M&=-\frac{n_0}{2} c L (\xi -1)^2,&N&=-\frac{n_0}{2} L (\xi -1)^2,&Q&=0, \end{aligned}$$
(54)

where the nondimensional axial coordinate \(\xi = x/L\) is introduced. In Figs. 7a, b, normal stresses are plotted as functions of Young’s modulus \(E(\eta )=E_0e^{\alpha \eta }\) with \(\alpha =\lbrace 0,1/10,1/5,1/2\rbrace \). Figure 7a shows the stress as a function of the normal force N(x), and Fig. 7b shows the stress as a function of the bending moment M(x). It is noted that the normalized axial stress is plotted: the reference stress \(\sigma ^* = | M |c/I = 75 \, \mathrm {N/mm^2}\) denotes the absolute axial stress at the upper fiber at \(\eta =1\) and \(\xi =1/2\) due to the bending moment M(1/2) of a homogeneous configuration with \(\alpha = 0\) and the moment of inertia \(I = 2 bc^3/3\), see the linear portion of Eq. (45). It can be seen that the nonlinearity due to the normal force in Fig. 7a is negligible also for highly graded materials (i.e., even for \(\alpha \ge 1/2\) because the nonlinear part in Fig. 7a is relatively small compared to the mean value 0.33). On the other hand the nonlinearity due to the bending moment can be observed for \(\alpha > 1/5\).

Fig. 7
figure 7

Nondimensional axial stress distributions of a moderately thick beam with \(\lambda = 1/10\) for different Young’s modulus variations. The variable \(\sigma ^* = | M |c/I = 75 \, \mathrm {N/mm^2}\) denotes the axial stress of the upper fiber at \(\eta =1\) of an isotropic homogeneous beam (i.e., \(\alpha =0\)) due to pure bending. FEA calculations are performed for the configuration with the highest material gradient \(\alpha = 1/2\), see (c)

Full size image

In Fig. 7c the total normalized axial stress \(\sigma _x/\sigma ^* = (\sigma _{xN} + \sigma _{xM})/\sigma ^*\) is shown and compared to the FEA (black points for \(\alpha = 1/2\)) showing an excellent agreement of analytical and numerical results. It has to be noted that for \(\alpha = 1/2\), the maximum normal stress \(\sigma _{x \, \text {max}}\) is \(27 \%\) larger than \(\sigma ^*\). The axial stress of the higher iterations \(\sigma _x^0\) (derived from \(\psi _i\) with \(i>1\)) is plotted in Fig. 7d. It is noted that this is a self-equilibrated stress, which means that stress resultants vanish by integration over the cross-sectional area. One observes that the quantity of \(\sigma _{x}^0\) is very low (i.e., below \(0.75 \%\) of \(\sigma ^*\)) and the influence of the residual stress \(\sigma _x^0\) is practically negligible.

In Fig. 8a the normal stress \(\sigma _y\) is plotted. This stress is often denoted as compressive stress in the literature, and it vanishes at both surfaces, and also its derivative vanishes at \(\eta = -1\): This follows directly from the boundary conditions because \( \sigma _y \propto \psi = 0 \) at \(\eta = \pm 1\) and \( \sigma _{y,y} \propto \psi _{,y} \propto \tau _{xy} = 0 \) at \(\eta = -1\) hold. In relation to the stress \(\sigma _x^0\) presented in Fig. 7d, the quantity of \(\sigma _y\) is of very low influence: in general it holds that \({\mathcal {O}}(\sigma _y)={\mathcal {O}}(\sigma _x)\lambda ^2\), i.e., the order of magnitude of the compressive stress is lower by a factor \(\lambda ^2\) than the axial stress. The shear stress distribution is shown in Fig. 8b: It vanishes at the lower surface at \(\eta = -1\) and fulfils the normalized traction load \(n_0/\sigma _x^*\) at the upper surface at \(\eta = 1\). The FEA results for \(\sigma _y\) and \(\tau _{xy}\) are given for \(\alpha = 1/2\) and those match perfectly with our analytical solution.

Fig. 8
figure 8

Nondimensional compressive stress distribution (a) and shear stress distribution (b). FEA results are compared to the analytical solutions for \(\alpha = 1/2\)

Full size image

Some final remarks concerning the stresses are made: The nondimensional residual stress \(\sigma _x^0/\sigma ^*\), in Fig. 7d, and the compressive stress \(\sigma _y/\sigma ^*\) in Fig. 8a are lower-order terms (quadratic order with respect to thickness-to-length ratio \(\lambda \)) in comparison with the nondimensional axial stress \(\sigma _x/\sigma ^*\) (e.g., \(\sigma _{y \text {max}}/\sigma ^* = 0.0033\)). Independent of the thickness-to-length ratio self-equilibrated stresses are of low impact and the compressive stress is low. In addition to the beam considered in this study (\(\lambda =1/10\)) this influence remains negligible even for a thicker beam (\(\lambda = 1/5\): the maximum value is \(\sigma _y/{{\bar{\sigma }}}^*\approx 0.014\)).

5.2 Displacements

The displacements are presented for different Young’s moduli in Fig. 9. The axial and transverse deflection curves \(u(\xi ,0)\) and \(v(\xi ,0)\) are shown in Figs. 9a and b where the nondimensional axial coordinate \(\xi = x/L\) is introduced. The displacement \(v^* = v_{\alpha = 0}(\xi \!=\!1,0)=1.07 \, \mathrm {mm}\) denotes the vertical tip deflection of a homogeneous beam with \(\alpha =0\). Additionally, the deflection curves are plotted if only the results from the first iteration are used, see Eqs. (47) and (48) for \(u_1\) and \(v_1\) (red curve for \(\alpha =1/2\)). It has to be noted that for our example beam, where a thickness-to-length ratio of \(\lambda = 1/10\) is considered which refers to a moderate thick beam, the higher-order solution is almost equal to the first-order solution. The obtained analytical results are in a very good accordance with the FEA solution. One observes that the higher the material is graded, the lower is the horizontal deflection at \(\eta = 0\) (Fig. 9a). This also holds for the vertical deflection (Fig. 9b). Furthermore, considering only the first iterations (red curves for \(\alpha = 1/2\)), one finds a very good agreement with FEA results (black dots): The difference is less than \(< 1 \%\). Taking into account also the higher-order terms (black), the analytical solutions (black) practically coincide with FE results.

Fig. 9
figure 9

Nondimensional deflections of the midspan axis for a beam with \(\lambda = 1/10 \) and the Young’s modulus \(E(\eta ) = E_0e^{\alpha \eta }\). FEA results are compared to the analytical solutions for \(\alpha = 1/2\). The vertical tip deflection \(v^* = 1.07\,\mathrm {mm}\) due to an isotropic homogeneous beam is used for normalization

Full size image

In Figs. 10a and b the normalized horizontal and vertical deflections are shown over the cross section at \(\xi =1/2\). Again, the vertical tip deflection of an isotropic homogeneous beam \(v^* = 1.07\,\mathrm {mm}\) is used for normalization. The FEA results are performed for the material gradient \(\alpha = 1/2\).

Fig. 10
figure 10

Nondimensional displacement over the cross section at \(\xi = 1/2\) for a beam with \(\lambda = 1/10\) and Young’s modulus \(E(y) = E_0e^{\alpha y/c}\). The FEA results are compared to the analytical solutions for \(\alpha = 1/2\)

Full size image

The influence of the higher-order terms, besides the fundamental solution from Eqs. (47) and (48), is marginal. At the lower fiber at \(\eta = - 1\), the normalized axial deflection is 0.038 for all material configurations, see Fig. 10a. The distribution remains almost linearly, but it decreases for higher graded materials. Again, the FEA results agree with the analytical results, regardless of whether the higher-order terms are considered or not (c.f. red, black and pointed curves). The vertical cross-sectional deflection is almost constant with respect to the thickness (Fig. 10b). The first-order solution only differs slightly from the higher order and the FEA result (error \(<0.1 \%\)).

As a final statement the authors suggest that for thin beams (\(\lambda < 1/20\)) the first-order results yield accurate solutions for industrial use, see Eqs. (44) and (45) for the normal stress distributions and column 1 of Table 2 in the Appendix for the displacements.

6 Comparison to literature

An additional verification of our theory is performed in this section, where we compare our results to an example given in Chu [10]. In order to obtain a stress function in the case of vanishing tractions with \({\varvec{t}}_u = {\varvec{t}}_l = \{ 0 , 0\}^T\), see Eq. (1), the computation procedure for the stress function is similar to Sect. 4, but the load vector is adjusted to \({\varvec{q}} = \{ C_1 x + C_2, \, C_3, \,K_1 x + K_2, \, K_3\}^T\).

A cantilever beam is investigated which is loaded by the end moment B, the shear force V and the normal force H at \(x=L\) (see Fig. 11).

Fig. 11
figure 11

FGM cantilever with length L and thickness 2c subjected to a shear force V, a normal force H and a end moment B at the free end at \(x=L\)

Full size image

The constants \(C_1,\;C_2,\;C_3\) and \(K_1,\;K_2,\;K_3\) are related to three constants \(N_0=K_3-C_3\), \(Q_0 = K_1-C_1\) and \(M_0= K_2-C_2-c(C_3+K_3)\), see Eqs. (26)–(28) and determined by setting up three boundary conditions at the free end at \(x=L\):

$$\begin{aligned} M(L)&= -B,&Q(L)&= V,&N(L),&= H. \end{aligned}$$
(55)

It follows for the stress resultants and the stresses:

$$\begin{aligned} M(x)&= -B - V(L-x),&Q(x)&= V,&N(x)&= H, \end{aligned}$$
(56)
$$\begin{aligned} \sigma _{x1M}&= -\alpha ^2e^{\frac{\alpha y}{c}}\frac{ \alpha c \cosh (\alpha )-\sinh (\alpha ) (c+\alpha y)}{c^3 \left( 2 \alpha ^2-\cosh (2 \alpha )+1\right) }\bigg [B +V(L-x) \bigg ], \nonumber \\ \sigma _{x1N}&= \alpha e^{\frac{\alpha y}{c}} \frac{\alpha \cosh (\alpha ) (2 c+\alpha y)-\sinh (\alpha ) \left[ \left( \alpha ^2+2\right) c+\alpha y\right] }{c^2 \left( 2 \alpha ^2-\cosh (2 \alpha )+1\right) } H, \nonumber \\ \tau _{xy}&= \alpha ^2e^{-\alpha }\frac{ -2 e^{\alpha } c+c e^{\frac{\alpha y}{c}}+(c-y) e^{\alpha \left( \frac{y}{c}+2\right) }+y e^{\frac{\alpha y}{c}}}{2 c^2 \left( \cosh (2 \alpha )-2 \alpha ^2-1\right) } V,&\sigma _y&= 0. \end{aligned}$$
(57)

Chu [10] gives in his contribution the solution for the case where the bending moment \(M(x) = -B\). The solution of Eq. (57) in Chu [10] and our solution are identical if one sets \(\alpha = \lambda _2c\), \(c = h/2\), \(V=0\) and \(H=0\) in Eq. (57).

7 Conclusion

In the present contribution, an iterative solution procedure has been derived for the computation of the Airy stress function of a functionally graded beam with rectangular cross section and transversely varying material parameters. For this purpose, Boley’s method, which was initially developed for deriving analytical beam solutions for isotropic thick beams, is here extended. We assume a functionally graded material (FGM) and do not take advantage of a priori axiomatic assumptions, neither for the stress field nor for the displacement field. Explicit results are given for a cantilever beam subjected to a linearly distributed shear load. For other kinematic (no matter if statically determinate or indeterminate beams) and load boundary conditions the proposed method can be easily adjusted. The analytical solution is obtained by solving algebraic equations for the first iteration and simple ordinary differential equations for the higher iteration. Finally, a numerical verification of our functionally graded beam model is presented. The solution is compared to two-dimensional (2D) finite element results performed in ABAQUS, showing that the analytical results are in excellent agreement with the ABAQUS outcome. The obtained solution is an extension of the Bernoulli–Euler (BE) theory for FGM which takes into account the thickness-to-length ratio of the structure; hence, it is valid for thicker structures.