Modeling and design of tuned mass dampers using sliding variable friction pendulum bearings

Abstract

An effective vibration control device, the pendulum tuned mass damper (P-TMD), can be easily realized as a mass supported on rolling or sliding pendulum bearings. While the bearings’ concavity provides the desired gravitational restoring force, the necessary dissipative force can be obtained either from additional dampers installed in parallel with the bearings or from the same friction resistance developing within each bearing between the roller/slider and the rolling/sliding surface. The latter solution may prove cheaper and more compact but implies that the P-TMD effectiveness will be amplitude dependent if the friction coefficient is kept uniform along the rolling/sliding surface, as in conventional friction bearings. In this case, the friction P-TMD will be as efficient as a viscous P-TMD only at a given vibration level, with large performance reductions at other levels. To avoid this inconvenience, this paper proposes a new type of sliding variable friction pendulum (VFP) TMD, called the VFP-TMD, in which the sliding surface is divided into two concentric regions: a circular inner region, having the lowest possible friction coefficient and the same dimensions of the slider, and an annular outer region, having a friction coefficient set to an optimal value. A similar arrangement has been recently proposed to realize adaptive seismic isolation devices, but no specific application to TMDs is reported. To assess the VFP-TMD performance, first its analytical model is derived, rigorously accounting for geometric nonlinearities as well as for the variable (in time and space) pressure distribution along the contact area, and then, an optimal design methodology is presented. Finally, numerical simulations show the influence of the main design parameters on the device behavior and demonstrate that the VFP-TMD can achieve nearly the same effectiveness of viscous P-TMDs, while considerably outperforming conventional uniform-friction P-TMDs. The proposed analytical model can be used to enhance or validate existing models of VFP isolators that assume a constant and uniform contact pressure distribution.

1 Introduction

Tuned mass dampers (TMDs) are well-known passive control devices, extensively studied and widely applied for the vibration mitigation of low-damped structures under natural and anthropic loads [1,2,3,4,5,6]. A TMD is essentially a single-degree-of-freedom (SDOF) oscillator attached to the main structure, dynamically interacting with a selected target structural mode by frequency tuning and damping optimization, and consequently absorbing and dissipating part of its vibrational energy [7]. To control horizontal vibrations, pendulum TMDs (P-TMDs) are commonly employed, using gravity to produce the required restoring force, and consisting of damped masses constrained to move along curved profiles or surfaces, whose curvature determines the P-TMD natural frequency. While hanging-type P-TMDs are suspended by ropes or bars [8], supported-type P-TMDs roll or slide on concave tracks or bearings [9]. Increasing interest for supported P-TMDs has been recently observed, because of their greater compactness, durability, and versatility in shape. This has resulted in the availability of various supported P-TMDs configurations, including rolling and sliding P-TMDs [10], ball-type P-TMDs [11], unbalanced rolling P-TMDs [12], and track nonlinear energy sinks [13]. Each configuration can be realized as a unidirectional or a bidirectional arrangement, in this latter case recurring either to a pair of orthogonal tracks mounted in series, or to one three-dimensional (3D) optimal surface, non-axial–symmetrical when the two principal frequencies of the main structure are different [14].

Whatever the configuration, two main solutions exist to provide a supported P-TMD with the required energy dissipation capability. The first consists in connecting its mass to the structure by an additional dissipative link, e.g., a linear viscous damper [14]. The second consists in exploiting the rolling or sliding friction resistance developing along the pendulum surface during P-TMD motion [15]. Avoiding the additional damping devices, this second solution is simpler, more compact, and potentially cheaper than the first one, and always adopted in ball-type P-TMDs [16,17,18]. However, as long as the friction coefficient is uniform along the surface, the friction force is virtually constant [19], which makes the P-TMD equivalent damping ratio inversely proportional to the P-TMD displacement amplitude, and the P-TMD effectiveness amplitude dependent [15, 20]. To avoid this inconvenience, inspired by the homogeneous friction concept proposed by Inaudi and Kelly [21] and developed by Almazan et al. [8], Matta [22] proposed a new type of supported P-TMD, characterized by a friction coefficient that varies along the pendulum surface proportionally to the modulus of the surface gradient. In the first-order approximation, such friction model is nonlinear but homogeneous: the friction force increases proportionally to the radial displacement, and the P-TMD effectiveness results amplitude independent. By an appropriate choice of the proportionality coefficient, the optimal friction pattern is determined, and the same performance of an optimal viscous P-TMD is obtained, for any vibration level. Theoretically applicable to both rolling and sliding P-TMDs, the concept has been experimentally validated on small-scale prototypes of rolling P-TMDs [22] and ball-type P-TMDs [23], where the continuous optimal friction pattern is approximated by coating the rolling surface with a series of concentric rubber layers of increasingly larger friction properties.

Fig. 1

Some possible arrangements of a VFP-TMD: a the absorber on two double pendulum bearings (lateral and planar views); b single pendulum bearing; c flat bearing; d rocking pendulum TMD

Fig. 2

Planar view of a flat slider moving along x on a two-region flat sliding surface, the inner region having the same dimensions of the slider: a rectangular slider; b circular slider. $A^{a}$ and $A^{b}$ are the contact areas between the slider and, respectively, the inner region “a” and the outer region “b,” while $\mu ^{a}$ and $\mu ^{b}$ are their respective friction coefficients

Focusing on spherical sliding P-TMDs, this paper proposes a new type of variable friction pendulum (VFP) TMD, called the VFP-TMD, in which each sliding surface is divided into two concentric regions: an inner circular region, having the lowest possible friction coefficient and the same dimensions of the slider, and an outer annular region, having a friction coefficient set to an optimal value (Fig. 1). In this way, as the slider moves across the two regions, the effective friction coefficient changes as a monotonic increasing function of its radial displacement. A similar arrangement has been recently adopted to realize “adaptive” seismic isolators, although several concentric regions are in that case generally admitted. VFP isolators have been postulated in [24], proposed in [25,26,27], and later analyzed by several authors (e.g., [28, 29]). They are meant to outperform conventional friction pendulum bearings [30] by undergoing desired stiffness and damping modifications at specified displacement amplitudes, so that the isolation system can be optimized for multiple performance objectives [31]. With respect to multiple friction pendulums [32, 33], VFP isolators can achieve this without increasing the number of sliding surfaces. Although a research program involving experimental activities is reportedly ongoing [28], no experimental results have been published to date. On the other hand, the literature reports extensive simulations of VFP isolators, showing them a viable alternative to traditional systems. These simulations are generally performed on simplified analytical models, neglecting second-order effects and assuming a uniform pressure on the contact area. To the authors’ knowledge, no specific application of VFPs to TMDs is reported.

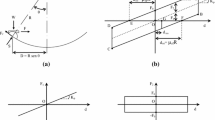
The VFP-TMD proposed in this paper consists of a mass (upper mass) supported on one or more VFP bearings. Figure 1a shows one possible arrangement, comprising two identical VFP bearings, each consisting of a double friction pendulum. According to this (planar) scheme, each bearing is made of two concave plates and a slider in between. For each VFP, the lower and upper sliding surfaces may differ from each other in shape and material properties. Figure 1b, c shows two alternative arrangements, in which the double pendulum is replaced with, respectively, a single pendulum bearing (Fig. 1b) and a flat bearing (Fig. 1c). In this latter case, horizontal springs should be added in parallel, not shown for brevity. A rocking pendulum arrangement is shown in Fig. 1d, in which the slider and the upper mass coincide and a single sliding surface exists. Clearly, arrangements 1b to 1d are special cases of the general arrangement 1a. Figure 1a also identifies the low-friction inner region “a” (white color), as large as the slider, and the high-friction region “b” (gray color), thick enough to contain the slider. The edge of the sliding surface is raised to prevent excessive strokes.

In the remaining of this paper, the working principles of the VFP-TMD are demonstrated, and its effectiveness is compared to that of existing P-TMD types. To this aim, first its fully nonlinear analytical model is derived, then an optimal design method is proposed, and finally, numerical simulations are performed.

2 Analytical modeling of a VFP-TMD

This Section derives the fully nonlinear model of a VFP-TMD, based on the double pendulum arrangement shown in Fig. 1a. The model is first obtained for the device alone and then augmented to include the main structure. For simplicity, the motion is supposed to occur in a vertical plane, and the model is planar.

2.1 The variable friction concept

The variable friction concept is explained in Fig. 2, referring for simplicity to a single flat sliding surface. Denoting with x the axis of the relative sliding motion u, Fig. 2a, b, respectively, describes a rectangular slider of side length D (measured along x) and a circular slider of diameter D, sliding on a two-region flat surface, the inner region having the same shape and dimensions of the slider. In both figures, $A^{a}$ and $A^{b}$ are the contact areas between the slider and, respectively, the inner region “a” and the outer region “b,” while $\mu ^{a}$ and $\mu ^{b}$ are their respective friction coefficients. Let $A = A^{a} + A^{b}$ be the area of the slider surface, $\sigma = \sigma (x,y)$ be the contact pressure distribution along A, and N be the normal contact force. Assuming a Coulomb friction model, the infinitesimal friction force dV exchanged through the generic infinitesimal area dA is

$$\begin{aligned} \mathrm{d}V=\mu \sigma \mathrm{d}A \end{aligned}$$

(1)

where $\mu = \mu (x,y)$ is the friction coefficient distribution along A. Supposing the contact pressure uniform along A and therefore equal to $\sigma = N/A$ and denoting with V the tangential contact force, i.e., the friction force, the effective friction coefficient can be computed as the following function of u:

$$\begin{aligned} \mu _{\mathrm{eff}} =\frac{V}{N}=\frac{1}{N}\int \limits _A {\mathrm{d}V} =\frac{1}{A}\int \limits _A {\mu (x,y)} \mathrm{d}A=\frac{1}{A}(\mu ^{a}A^{a}+\mu ^{b}A^{b})=\mu ^{a}+\left( {\mu ^{b}-\mu ^{a}} \right) \frac{A^{b}}{A} \end{aligned}$$

(2)

where

$$\begin{aligned} \frac{A^{b}}{A}=\frac{\left| u \right| }{D}\le 1 \end{aligned}$$

(3)

for the rectangular case and

$$\begin{aligned} \frac{A^{b}}{A}=1-\frac{2}{\pi }\left( {\alpha -\frac{\left| u \right| }{D}\sin \alpha } \right) \le 1 \end{aligned}$$

(4)

for the circular case, with $\alpha = \hbox {arccos}(| u| /D)$.

Equation (2) clearly shows that $\mu _{\mathrm{eff}}$ is the average of the two friction coefficients, weighted by their respective contact areas. Equations (3) and (4) provide the relative weight of the outer region “b,” which is a linear function of |u| in the rectangular case and a nonlinear function of |u| in the circular case.

Fig. 3

Effective friction coefficient as a function of the normalized relative displacement, for the flat configurations depicted in Fig. 2, assuming $\mu ^{a} = 0.02$ and $\mu ^{b} = 0.20$

Fig. 4

Mechanical model of the VFP-TMD system. Geometry (a) and free-body diagram (b) of the individual VFP bearing. Geometry and free-body diagram of the TMD upper mass (c). Blue color: dimensions; red color: forces (color figure online)

Assuming, for example, $\mu ^{a} = 0.02$ and $\mu ^{b} = 0.20$, Fig. 3 shows $\mu _{\mathrm{eff}}$ as a function of the slider normalized displacement, u/D. In the ideal case where the inner region was frictionless ($\mu ^{a} = 0$), the rectangular configuration would ensure an exact proportionality between V and u, i.e., a homogeneous dissipative model, and the circular configuration a rough approximation of it, i.e., a nearly homogeneous dissipative model. On the other hand, the circular configuration has the advantage of being axial–symmetrical and therefore equally effective in every direction. Not shown in Fig. 3, if u exceeds D, then $\mu _{\mathrm{eff}}$ will remain equal to $\mu ^{b}$ in both cases, unless a third region is introduced with $\mu ^{c} > \mu ^{b}$, so that further increments are possible.

2.2 The general VFP-TMD model

2.2.1 Kinematic relations

The planar model of the double VFP-TMD shown in Fig. 1a is schematized in Fig. 4. Figure 4a, b depicts the geometry and the free-body diagram of each individual VFP bearing, while Fig. 4c shows the geometry and the free body diagram of the upper mass, supported on two identical VFP bearings. All bodies are assumed rigid. The motion is supposed to occur in the xz vertical plane, but the model accounts for the three dimensionalities of the spherical shape. Dimensions are in blue, and forces in red. For brevity, the subscripts “L” and “R,” denoting in Fig. 4c the left and right bearings, are omitted in Fig. 4a, b, referring to the generic bearing, and will be avoided in the sequel unless necessary.

Each VFP bearing comprises a lower plate, integral with the main structure, an upper plate, integral with the upper mass, and a slider. The lower sliding and slider surfaces are spherical caps of radius $R_{\mathrm {1}}$ and center $\hbox {O}_{\mathrm {1}}$. The upper sliding and slider surfaces are spherical caps of radius $R_{\mathrm {2}}$ and center $\hbox {O}_{\mathrm {2}}$. $\hbox {C}_{\mathrm {1}}$ and $\hbox {C}_{\mathrm {2}}$ are the central points of the lower and upper slider surfaces. The slider has mass $m_{\mathrm {1}}$, center of mass $\hbox {G}_{\mathrm {1}}$, and central moment of inertia $J_{\mathrm {1}}$. The upper plate has mass $m_{\mathrm {2}}$ and center of mass $\hbox {G}_{\mathrm {2}}$. The upper mass has mass $m_{\mathrm {3}}$ and center of mass $\hbox {G}_{\mathrm {3}}$. $h_{\mathrm {1}}$ and $h_{\mathrm {2}}$ are the distances of $\hbox {G}_{\mathrm {1}}$ from $\hbox {C}_{\mathrm {1}}$ and $\hbox {C}_{\mathrm {2}}$; $h_{\mathrm {3}}$ and $h_{\mathrm {4}}$ are the distances of $\hbox {G}_{\mathrm {2}}$ from the upper sliding surface and from the upper mass; $h_{\mathrm {5}}$ is the height of $\hbox {G}_{\mathrm {3}}$ above the upper plates; b is the relative distance between the two VFP bearings, symmetrical w.r.t. $\hbox {G}_{\mathrm {3}}$.

For convenience, two local Cartesian coordinate systems are associated with each sliding interface. Referring to the lower interface, they are both centered in $\hbox {O}_{\mathrm {1}}$: the system $x_{\mathrm {1}}y_{\mathrm {1}}z_{\mathrm {1}}$ is integral with the lower plate (i.e., with the structure); the system $x_{\mathrm {10}}y_{\mathrm {10}}z_{\mathrm {10}}$ is integral with the slider. Referring to the upper interface, they are both centered in $\hbox {O}_{\mathrm {2}}$: the system $x_{\mathrm {2}}y_{\mathrm {2}}z_{\mathrm {2}}$ is integral with the upper plate (i.e., with the TMD upper mass), and the system $x_{\mathrm {20}}y_{\mathrm {20}}z_{\mathrm {20}}$ is integral with the slider.

The overall system has one degree of freedom, because the three rigid bodies are constrained by four double constraints (i.e., the sliding interfaces). No detachment is assumed possible at the sliding interfaces. Because the two VFP bearings are identical, the upper mass cannot rotate, and the coordinate systems $x_{\mathrm {1}}y_{\mathrm {1}}z_{\mathrm {1}}$ and $x_{\mathrm {2}}y_{\mathrm {2}}z_{\mathrm {2}}$ are parallel to each other and to the xyz system of the main structure, while the systems $x_{\mathrm {10}}y_{\mathrm {10}}z_{\mathrm {10}}$ and $x_{\mathrm {20}}y_{\mathrm {20}}z_{\mathrm {20}}$ are parallel to each other and rotated by a certain $\theta$ angle w.r.t. xyz. $\theta$, being the counterclockwise rotation of the slider in the xz plane, is unique for the two VFP bearings and the only Lagrangian of the system.

Fig. 5

Position of the generic point P of the slider according to the three local reference systems associated with the lower interface: $x_{\mathrm {1}}y_{\mathrm {1}}z_{\mathrm {1}}$, $x_{\mathrm {10}}y_{\mathrm {10}}z_{\mathrm {10}}$ and $\rho _{\mathrm {1}}\varphi _{\mathrm {1}}\psi _{\mathrm {1}}$

Partially shown in Fig. 4 and better explained in Fig. 5, one further local coordinate system is associated with each sliding interface. Referring to the lower interface (the only one shown in Fig. 5, for brevity), this system, denoted as $\rho _{\mathrm {1}}\varphi _{\mathrm {1}}\psi _{\mathrm {1}}$, is a polar system centered in $\hbox {O}_{\mathrm {1}}$ and integral with the slider. According to this system, the position of any point P of the slider is expressed by $\rho _{\mathrm {1}}$, i.e., the modulus of the vector $\hbox {O}_{\mathrm {1}}$P, by $\varphi _{\mathrm {1}}$, i.e., the inclination of the plane containing $\hbox {O}_{\mathrm {1}}$P and $y_{\mathrm {10}}$ w.r.t. the $y_{\mathrm {10}}z_{\mathrm {10}}$ plane, and by $\psi _{\mathrm {1}}$, i.e., the inclination of $\hbox {O}_{\mathrm {1}}$P w.r.t. the vertical plane $x_{\mathrm {10}}z_{\mathrm {10}}$. In this $\rho _{\mathrm {1}}\varphi _{\mathrm {1}}\psi _{\mathrm {1}}$ system, all points on the slider surface have $\rho _{\mathrm {1}} = R_{\mathrm {1}}$, and particularly $\hbox {C}_{\mathrm {1}}$ has $\varphi _{\mathrm {1}} = \psi _{\mathrm {1}} = 0$, while the two points where the edge of the slider intersects the $x_{\mathrm {1}}z_{\mathrm {1}}$ plane have $\psi _{\mathrm {1}} = 0$ and $\varphi _{\mathrm {1}} = \pm {\bar{\varphi }}_{1}$, where ${\bar{\varphi }}_{1} > 0$ is the angular semi-width of the slider. In the same way, a polar system $\rho _{\mathrm {2}}\varphi _{\mathrm {2}}\psi _{\mathrm {2}}$ is associated with the upper interface, centered in $\hbox {O}_{\mathrm {2}}$ and integral with the slider.

The relations between the two Cartesian systems and the polar system are

$$\begin{aligned} x_{i}= & {} \rho _{i} \cos \psi _{i} \sin (\varphi _{i} +\theta ), \end{aligned}$$

(5.1)

$$\begin{aligned} y_{i}= & {} \rho _{i} \sin \psi _{i}, \end{aligned}$$

(5.2)

$$\begin{aligned} z_{i}= & {} \rho _{i} \cos \psi _{i} \cos (\varphi _{i} +\theta ), \end{aligned}$$

(5.3)

$$\begin{aligned} x_{i0}= & {} x_{i} (\theta =0)=\rho _{i} \cos \psi _{i} \sin \varphi _{i}, \end{aligned}$$

(6.1)

$$\begin{aligned} y_{i0}= & {} y_{i} (\theta =0)=\rho _{i} \sin \psi _{i} =y_{i}, \end{aligned}$$

(6.2)

$$\begin{aligned} z_{i0}= & {} z_{i} (\theta =0)=\rho _{i} \cos \psi _{i} \cos \varphi _{i} \end{aligned}$$

(6.3)

where the subscript i stands for either 1 or 2, depending on which interface is referred to.

Equations (5.1), (5.2), (5.3), (6.1), (6.2), and (6.3) show that, during motion, any point of the slider undergoes a circular motion around each $y_{i}$ axis, described by the radius $\rho _{i\, }\text {cos}\psi _{i}$ and the angle $\varphi _{i} + \theta$. Considering in particular the point $\hbox {G}_{\mathrm {1}}$ (characterized by $\rho _{i} = \rho _{i\mathrm{G1}}$ and $\varphi _{i} = \psi _{i} = y_{i} = 0$), its motion w.r.t. $\hbox {O}_{{i}}$ is given by $x_{i\mathrm {G1}} = \rho _{i\mathrm {G1\, }}\hbox {sin}\theta$ and $z_{i{\mathrm {G1}}} = \rho _{i\mathrm {G1\, }}\text {cos}\theta$. This implies that the motion of $\hbox {O}_{\mathrm {2}}$ w.r.t. $\hbox {O}_{\mathrm {1}}$ is given by $x_{\mathrm {1O2}} = \rho _{\mathrm {1O2\, }}\hbox {sin}(\theta )$ and $z_{\mathrm {1O2}} = \rho _{\mathrm {1O2\, }}\text {cos}\theta$, with $\rho _{\mathrm {1O2\, }}= \rho _{\mathrm {1G1\, }}+_{\mathrm {\, }}\rho _{\mathrm {2G1}} = R_{\mathrm {1}} + R_{\mathrm {2}}$ – ($h_{\mathrm {1}}+h_{\mathrm {2}})$, as evident in Fig. 4a. Because the upper mass translates like $\hbox {O}_{\mathrm {2}}$, $\rho _{\mathrm {1O2}}$ represents the equivalent radius of the upper mass and indeed the equivalent radius of the entire TMD system if the slider mass is negligible.

2.2.2 Dynamic equations

Figure 4b and 4c shows the free-body diagrams of the VFP-TMD components. Denoting as $a_{x}$ and $a_{z}$ the horizontal and vertical components of the structural acceleration imparted to the lower plate, the actions on the various system components include weights, inertia forces and moments, contact forces, restrainer forces, and connection forces. In particular, the contact forces $N_{i}$ and $V_{i}$ are the resultants of, respectively, the pressures and the friction forces at the $i^{\mathrm {th}}$ interface, while the restrainer force $F_{i}$ is the force between the slider and the raised edge of the $i^{\mathrm {th}}$ sliding surface. Because pressures are oriented toward $\hbox {O}_{{i}}$ but generally not evenly distributed around $C_{i}$, $N_{i}$ is directed toward $\hbox {O}_{i}$ but inclined w.r.t. $z_{i\mathrm {0}}$ by an offset angle $\varphi _{iN}$. Because friction forces are tangential but generally not evenly distributed, and set at a variable distance $R_{i\, }\text {cos}\psi _{i} \le R_{i}$ from $\hbox {O}_{{i}}$, $V_{i}$ is inclined by an angle $\varphi _{iV}$ w.r.t. $x_{i\mathrm {0}}$ and set at a generic distance $\rho _{iV}$ $\le R_{i}$ from $\hbox {O}_{{i}}$. Because the restrainer force $F_{i}$ arises at the contact point between the edge of the slider and the edge of the sliding surface, having coordinates $\rho _{i} = R_{i}, \varphi _{i} = \varphi _{iF} =\hbox { sgn }\theta {\bar{\varphi }}_{i} , \psi _{i} = 0$, it follows that $F_{i}$ is tangentially applied at this point, i.e., inclined by an angle $\varphi _{iF}$ w.r.t. $x_{i\mathrm {0}}$, and set at a distance $R_{i}$ from $\hbox {O}_{i}$. Finally, $N_{\mathrm {3,L}}$, $V_{\mathrm {3,L}}$, $M_{\mathrm {3,L}}$ and $N_{\mathrm {3,R}}$, $V_{\mathrm {3,R}}$, $M_{\mathrm {3,R}}$ are the connection forces and moments between the TMD upper mass and the upper plate of, respectively, the left and right bearings.

Fig. 6

Vertical section in the xz plane of motion of the pendulum TMD in its generic deformed position. Determination of the pressure distribution for an assigned $N_{i\, }$–$_{\mathrm {\, }}\varphi _{iN}$ pair

Based on the free-body diagrams of Fig. 4, the following 9 equations of motion are obtained:

$$\begin{aligned}&m_{1} (g+a_{z} )\sin \theta +m_{1} a_{x} \cos \theta +m_{1} \rho _{1G1} {\ddot{\theta }}+N_{1} \sin \varphi _{1N} +V_{1} \cos \varphi _{1V} ,\nonumber \\&\quad +F_{1} \cos {\bar{\varphi }}_{1} -N_{2} \sin \varphi _{2N} -V_{2} \cos \varphi _{2V} -F_{2} \cos {\bar{\varphi }}_{2} =0, \end{aligned}$$

(7.1)

$$\begin{aligned}&m_{1} (g+a_{z} )\cos \theta -m_{1} a_{x} \sin \theta +m_{1} \rho _{1G1} {\dot{\theta }}^{2}-N_{1} \cos \varphi _{1N} +V_{1} \sin \varphi _{1V}\nonumber \\&\quad +\mathrm{sgn}\,\,\theta \cdot F_{1} \sin {\bar{\varphi }}_{1} +N_{2} \cos \varphi _{2N} -V_{2} \sin \varphi _{2V} -\mathrm{sgn}\,\,\theta \cdot F_{2} \sin {\bar{\varphi }}_{2} =0, \end{aligned}$$

(7.2)

$$\begin{aligned}&J_{1} {\ddot{\theta }}-N_{1} \rho _{1G1} \sin \varphi _{1N} +V_{1} (\rho _{1V} -\rho _{1G1} \cos \varphi _{1V} )+F_{1} (R_{1} -\rho _{1G1} \cos {\bar{\varphi }}_{1} )\nonumber \\&\quad -N_{2} \rho _{2G1} \sin \varphi _{2N} +V_{2} (\rho _{2V} -\rho _{2G1} \cos \varphi _{2V} )+F_{2} (R_{2} -\rho _{2G1} \cos {\bar{\varphi }}_{2} )=0, \end{aligned}$$

(7.3)

$$\begin{aligned}&[m_{2} (g+a_{z} )+N_{3} ]\sin \theta +(m_{2} a_{x} -V_{3} )\cos \theta +m_{2} \rho _{1O2} {\ddot{\theta }}+N_{2} \sin \varphi _{2N}\nonumber \\&\quad +V_{2} \cos \varphi _{2V} +F_{2} \cos {\bar{\varphi }}_{2} =0, \end{aligned}$$

(7.4)

$$\begin{aligned}&[m_{2} (g+a_{z} )+N_{3} ]\cos \theta -(m_{2} a_{x} -V_{3} )\sin \theta +m_{2} \rho _{1O2} {\dot{\theta }}^{2}-N_{2} \cos \varphi _{2N}\nonumber \\&\quad +V_{2} \sin \varphi _{2V} +\mathrm{sgn}\,\,\theta \cdot F_{2} \sin {\bar{\varphi }}_{2} =0, \end{aligned}$$

(7.5)

$$\begin{aligned}&M_{3} +V_{3} h_{4} +N_{2} \rho _{2G2} \sin (\theta +\varphi _{2N} )+V_{2} [\rho _{2V} -\rho _{2G2} \cos (\theta +\varphi _{2V} )]\nonumber \\&\quad +F_{2} [R_{2} -\rho _{2G2} \cos (\theta +{\bar{\varphi }}_{2} )]=0, \end{aligned}$$

(7.6)

$$\begin{aligned}&V_{3,L} +V_{3,R} +m_{3} a_{x} +m_{3} \rho _{1O2} ({\ddot{\theta }}\cos \theta -{\dot{\theta }}^{2}\sin \theta )=0, \end{aligned}$$

(7.7)

$$\begin{aligned}&N_{3,L} +N_{3,R} -m_{3} (g+a_{z} )-m_{3} \rho _{1O2} ({\ddot{\theta }}\sin \theta +{\dot{\theta }}^{2}\cos \theta )=0, \end{aligned}$$

(7.8)

$$\begin{aligned}&M_{3,L} +M_{3,R} -(N_{3,L} -N_{3,R} )b/2-(V_{3,L} +V_{3,R} )h_{5} =0. \end{aligned}$$

(7.9)

Equations (7.1)–(7.3) refer to the slider and are, respectively, written along $x_{\mathrm {10}}$, along $z_{\mathrm {10}}$, and around $\hbox {G}_{\mathrm {1}}$. Equations (7.4)–(7.6) refer to the upper plate, respectively, along $x_{\mathrm {20}}$, along $z_{\mathrm {20}}$, and around $\hbox {G}_{\mathrm {2}}$. Equations (7.7)–(7.9) refer to the upper mass, respectively, along $x_{\mathrm {2}}$, along $z_{\mathrm {2}}$, and around $\hbox {G}_{\mathrm {3}}$. To completely describe the VFP-TMD system, Eqs. (7.1)–(7.6), referring to the individual VFP bearing, are to be written twice, i.e., once for the left bearing and once for the right, providing a total of 15 equations; 31 variables appear in these 15 equations. They include the Lagrangian $\theta$ (the only time-differentiated variable) plus 15 variables for each bearing, i.e., 6 contact/restrainer forces at each interface ($N_{i}$, $\varphi _{iN}$, $V_{i}$, $\varphi _{iV}$, $\rho _{iV}$, $F_{i})$ plus 3 connection forces and moments ($N_{\mathrm {3}}$, $V_{\mathrm {3}}$, $M_{\mathrm {3}}$). The 16 missing equations required to solve the system are four constitutive equations at each of the four interfaces, including: (i) three contact equations, providing $V_{i}$, $\varphi _{iV}$ and $\rho _{iV}$ as functions of $N_{i}$, $\varphi _{iN}$, $\theta$ and ${\dot{\theta }}$, and (ii) one restrainer equation, providing $F_{i}$ as a function of $\theta$ and ${\dot{\theta }}$.

2.2.3 Constitutive equations

The three contact equations at each interface are obtained by the two-step procedure explained below.

As the first step, $N_{i}$ and $\varphi _{iN}$ are used to derive the distribution of pressures $\sigma _{i}$ over the interface $A_{i}$. The problem is statically indeterminate, so the arbitrary assumption is made that

$$\begin{aligned} \sigma _{i} =\sigma _{\mathrm{im}} \cos \psi _{i} \cos (\varphi _{i} -\varphi _{\mathrm{im}} )\ge 0 \end{aligned}$$

(8)

where $\sigma _{\mathrm{im}}$ is the maximum (real or virtual, depending if it falls within $A_{i}$ or not) of the distribution, and $\varphi _{\mathrm{im}}$ is the offset angle of the plane containing $\sigma _{\mathrm{im}}$. Figure 6, referring to the lower interface, exemplifies Eq. (8) when $\sigma _{\mathrm{im}}$ is virtual ($| \varphi _{\mathrm{im}}| > {\bar{\varphi }}_{i} )$ and the neutral axis (located at $\varphi _{i} = \varphi _{\mathrm{im}} -\hbox { sgn }(\varphi _{\mathrm{im}})\cdot \pi /2$) intersects the interface $A_{i}$. Denoting with $x_{\mathrm{im}}y_{\mathrm{im}}z_{\mathrm{im}}$ the local reference system obtained rotating $x_{i\mathrm {0}}y_{i\mathrm {0}}z_{i\mathrm {0}}$ around $y_{i\mathrm {0}}$ by the angle $\varphi _{\mathrm{im}}$, Eq. (8) states that $\sigma _{i}$ is proportional to the distance from the $x_{\mathrm{im}}y_{\mathrm{im}}$ plane according to $\sigma _{i} = \sigma _{\mathrm{im}}\cdot z_{\mathrm{im}}/R_{i}$ and becomes null in the half-space where $z_{\mathrm{im}} < 0$, as negative pressures are impossible. If the spherical surface tends to become flat (i.e., ${\bar{\varphi }}_{i}$, $\varphi _{i}$, and $\psi _{i}$ tend to 0), Eq. (8) converges to $\sigma _{i} =\sigma _{\mathrm{im}} (\cos \varphi _{\mathrm{im}} +\varphi _{i} \sin \varphi _{\mathrm{im}} )\ge 0$, corresponding to the Navier–Bernoulli planar beam section theory.

According to Eq. (8), the pressure distribution depends entirely on $\sigma _{\mathrm{im}}$ and $\varphi _{\mathrm{im}}$, which on their turn can be determined by expressing the contact force $N_{i}$ as the resultant of $\sigma _{i}$ over $A_{i}$. Written along $z_{i\mathrm {0}}$ and around $\hbox {C}_{{i}}$, this equivalence, respectively, provides

$$\begin{aligned} N_{i} \cos \varphi _{iN}= & {} \int \limits _{A_{i} } {\sigma _{i} dA_{i} \cos \psi _{i} \cos \varphi _{i} } \nonumber \\&\quad =\sigma _{\mathrm{im}} \int \limits _{A_{ci} } {\cos (\varphi _{i} -\varphi _{\mathrm{im}} )dA_{i} \cos ^{2}\psi _{i} \cos \varphi _{i} } =\sigma _{\mathrm{im}} R_{i}^{2} B_{1} ({\bar{\varphi }}_{i} ,\varphi _{\mathrm{im}}) \end{aligned}$$

(9)

and

$$\begin{aligned} N_{i} \sin \varphi _{iN} R_{i}= & {} \int \limits _{A_{i} } {\sigma _{i} dA_{i} \cos \psi _{i} R_{i} \sin \varphi _{i} } \nonumber \\= & {} \sigma _{\mathrm{im}} R_{i} \int \limits _{A_{ci} } {\cos (\varphi _{i} -\varphi _{\mathrm{im}} )dA_{i} \cos ^{2}\psi _{i} \sin \varphi _{i} } =\sigma _{\mathrm{im}} R_{i}^{3} B_{2} ({\bar{\varphi }}_{i}, \varphi _{\mathrm{im}}) \end{aligned}$$

(10)

where $A_{ci}$ is the compressed part of $A_{i}$ and functions $B_{\mathrm {1}}$ and $B_{2}$ are detailed in Appendix A.

Dividing Eq. (10) by Eq. (9), the following relation is finally obtained:

$$\begin{aligned} \tan \varphi _{iN} =\frac{B_{2} ({\bar{\varphi }}_{i} ,\varphi _{\mathrm{im}} )}{B_{1} ({\bar{\varphi }}_{i} ,\varphi _{\mathrm{im}} )}=B_{3} ({\bar{\varphi }}_{i} ,\varphi _{\mathrm{im}} ). \end{aligned}$$

(11)

Remarkably, $B_{\mathrm {1}}$, $B_{\mathrm {2}}$ and therefore $B_{\mathrm {3}}$ are functions of only ${\bar{\varphi }}_{i}$ and $\varphi _{\mathrm{im}}$. Because ${\bar{\varphi }}_{i}$ is a constant parameter depending only on the slider’s shape and $B_{\mathrm {3}}$ is an odd monotonically increasing function of $\varphi _{\mathrm{im}}$, then Eq. (11) univocally relates $\varphi _{\mathrm{im}}$ with $\varphi _{iN}$. Once $\varphi _{\mathrm{im}}$ is derived from $\varphi _{iN}$ by inverting Eq. (11), $\sigma _{\mathrm{im}}$ is subsequently obtained from Eq. (9) as $\sigma _{\mathrm{im}} =N_{i} \cos \varphi _{iN} /[R_{i}^{2} B_{1} ({\bar{\varphi }}_{i} ,\varphi _{\mathrm{im}} )]$.

Fig. 7

Dependence of $\varphi _{\mathrm{im}}$ on $\varphi _{iN}$ obtained by inverting Eq. (16), for 4 different values of ${\bar{\varphi }}_{i}$. Functions are plotted only for $\varphi _{iN}$ $\ge 0$ because they are symmetrical with respect to $\varphi _{\mathrm{im}} = \varphi _{iN} = 0$

Fig. 8

Steady-state response of an SDOF structure under a harmonic force input, controlled with a linear viscous TMD or with a homogeneous friction TMD ($\zeta _{s} = 1{\%}, m_{R} = 1{\%}$): a TFs for the two optimal TMDs; b dissipative force–displacement loops for the two optimal TMDs (at $\omega _{f} = \omega _{s})$

So, the pressure distribution along each interface can be determined at every instant. Noticeably, inverting Eq. (11) can be performed numerically offline, rather than during the integration of the dynamic equations, drastically reducing the computational effort. For example, Fig. 7 shows $\varphi _{\mathrm{im}}$ as a function of $\varphi _{iN}$, for four different values of ${\bar{\varphi }}_{i}$, i.e., for four different shapes of the slider. This is obtained by directly computing Eq. (11) for discrete values of $\varphi _{\mathrm{im}}$ ranging from — $\uppi /2$ — ${\bar{\varphi }}_{i}$ to $\uppi /2 + {\bar{\varphi }}_{i}$. A linear interpolation of this function ensures a rapid and sufficiently accurate evaluation of the pressure distribution during simulation.

As the second step of the procedure, Eq. (1) is recalled to obtain the distribution of the infinitesimal friction forces dV$_{i}$ on the $i^{\mathrm {th}}$ interface, and the equivalence is then imposed between such distribution and the resultant force $V_{i}$ (Fig. 4). By imposing the equivalence along $x_{i\mathrm {0}}$, along $z_{i\mathrm {0}}$, and around $\hbox {O}_{{i}}$, the following equations are, respectively, obtained:

$$\begin{aligned} V_{i} \cos \varphi _{iV}= & {} \mathrm{sgn}\,\,{\dot{\theta }}\int \limits _{A_{i} } {\cos \varphi _{i} dV_{i} }, \end{aligned}$$

(12)

$$\begin{aligned} V_{i} \sin \varphi _{iV}= & {} \mathrm{sgn}\,\,{\dot{\theta }}\int \limits _{A_{i} } {\sin \varphi _{i} dV_{i} }, \end{aligned}$$

(13)

$$\begin{aligned} V_{i} \rho _{iV}= & {} \mathrm{sgn}\,\,{\dot{\theta }}R_{i} \int \limits _{A_{i} } {\cos \psi _{i} dV_{i} }. \end{aligned}$$

(14)

Equations (12)–(14), with dV$_{i}$ determined by Eqs. (1), (8), (9), and (11), represent the three constitutive contact equations, providing $V_{i}$, $\varphi _{iV}$, and $\rho _{iV}$ as functions of $N_{i}$, $\varphi _{iN}$, $\theta$, and ${\dot{\theta }}$, and directly usable in Eqs. (7.1)–(7.9). The evaluation of the integrals in their right-hand side must be performed numerically on each interface, accounting for a friction coefficient distribution that varies along the interface with time, as the slider moves across the two regions. Denoting with $\mu _{i}^{a}$ and $\mu _{i}^{b}$ the friction coefficients of the inner and outer regions (as shown in Figs. 1 and 2), and assuming that the inner region has the same dimensions of the slider, the distribution of the friction coefficient $\mu _{i}$ along the $i^{\mathrm {th}}$ interface is expressed by the following step-wise function of ${\bar{\varphi }}_{i}$, $\theta$, $\varphi _{i}$, and $\psi _{i}$:

$$\begin{aligned} \mu _{i} =\mu _{i} ({\bar{\varphi }}_{i} ,\theta ,\varphi _{i} ,\psi _{i} )=\left\{ {{\begin{array}{*{20}c} {\mu _{i}^{a}, \quad \hbox {if} \quad \cos \psi _{i} \cos (\varphi _{i} +\theta )\ge \cos {\bar{\varphi }}_{i}} \\ {\mu _{i}^{b}, \quad \hbox {if} \quad \cos \psi _{i} \cos (\varphi _{i} +\theta )<\cos {\bar{\varphi }}_{i} } \\ \end{array} }} \right. . \end{aligned}$$

(15)

With the friction coefficient distribution expressed by Eq. (15), a partially analytic solution of the integrals in Eqs. (12) to (14) becomes possible, which considerably reduces the computational effort. The procedure is reported in Appendix B and ultimately provides the values of $\int \limits _{A_{i} } {\cos \varphi _{i} dV_{i} }$, $\int \limits _{A_{i} } {\sin \varphi _{i} dV_{i} }$, and $\int \limits _{A_{i} } {\cos \psi _{i} dV_{i} }$ as functions of the constant parameters $R_{i}$, ${\bar{\varphi }}_{i}$, $\mu _{i}^{a}$, $\mu _{i}^{b}$, and of the variables $\theta$, $\sigma _{\mathrm{im}}$, and $\varphi _{\mathrm{im}}$.

On the other hand, the restrainer constitutive equation, providing $F_{i}$ as a function of $\theta$ and ${\dot{\theta }}$, is defined as

$$\begin{aligned} F_{i} =[\mathrm{sgn}\,\,\theta \cdot k_{Fi} (\vert \theta \vert -\theta _{Fi} )+c_{Fi} {\dot{\theta }}]R_{i} \cdot \text{ step }(\vert \theta \vert -\theta _{Fi} ). \end{aligned}$$

(16)

Equation (16) represents a dissipative viscoelastic impact, occurring whenever $\vert \theta \vert$ exceeds an activation angle $\theta _{Fi} > 0$, and is governed by the stiffness $k_{Fi}$ and the damping coefficient $c_{Fi}$ of a Kelvin–Voigt spring–dashpot system placed along the sliding surface, i.e., at a distance $R_{i}$ from $\hbox {O}_{{i}}$. Remarkably, if $\theta _{Fi} = 2{\bar{\varphi }}_{i}$, the restrainer is activated exactly when the slider entirely exits the inner region.

Equations (12)–(14) and Eq. (16) are the four constitutive equations at each sliding interface making the problem statically determined.

2.2.4 Integration of the equations of motion

The VFP-TMD response to an assigned acceleration input is obtained by solving Eq. (7.1), (7.2), (7.3), (7.4), (7.5), (7.6), (7.7), (7.8), and (7.9), supplemented with Eqs. (12)–(14), and (16). The integration is performed numerically using a MATLAB ODE solver, working in the state space according to the following incremental procedure, applied at every time step:

• The integrals in Eqs. (12)–(14) are computed according to Appendix B, based on the values of $\theta$, $\sigma _{\mathrm{im}}$, and $\varphi _{\mathrm{im}}$ obtained at the previous step.

• Equations (12)–(14) and (16) then provide $V_{i\, }\text {cos}\varphi _{iV}$, $V_{i}\,\hbox {sin}\varphi _{iV}$, $V_{i\, }\rho _{iV}$, and $F_{i}$ as known functions of $\theta$, and ${\dot{\theta }}$, making the TMD system completely described by Eqs. (7.1), (7.2), (7.3), (7.4), (7.5), (7.6), (7.7), (7.8), and (7.9).

• Denoting the state variables as $q_{\mathrm {1}} = \theta$ and $q_{\mathrm {2}} = {\dot{\theta }}$ and adding the further equation ${\dot{q}}_{1} =q_{2}$, a system of 16 equations in 16 variables is obtained. The 16 equations are nonlinear w.r.t. the states, $q_{\mathrm {1}}$ and $q_{\mathrm {2}}$, but linear w.r.t. the state derivatives, ${\dot{q}}_{1}$ and ${\dot{q}}_{2}$, as well as w.r.t. the remaining following 14 variables: $N_{i\, }\text {cos}\varphi _{iN}$ and $N_{i\, }$sin$\varphi _{iN}$ (repeated 4 times, once for each interface), and $N_{\mathrm {3}}$, $V_{\mathrm {3}}$, $M_{\mathrm {3}}$ (repeated twice, once for each bearing).

• Algebraically solving the linear system provides ${\dot{q}}_{1}$, ${\dot{q}}_{2}$ and the 14 variables as nonlinear functions of $q_{\mathrm {1}}$ and $q_{\mathrm {2}}$ and as linear functions of the acceleration input. The knowledge of ${\dot{q}}_{1}$ and ${\dot{q}}_{2}$ feeds the dynamic integration algorithm. The knowledge of the 14 variables provides $N_{i}$ $\hbox {and}_{\mathrm {\, }}\varphi _{iN}$ and ultimately $\sigma _{\mathrm{im}}$ and $\varphi _{\mathrm{im}}$ for the next step.

2.3 Reduced VFP-TMD models

The VFP-TMD model derived in Sect. 2.2 can represent any arrangement in Fig. 1, but gets simpler if some additional assumptions are made. Four possible reduced models are described below.

2.3.1 Reduced model $\texttt {M}_{1}$: infinitely distant bearings

If the two bearings are infinitely distant from each other ($b \rightarrow \infty )$, then they are subjected to the same values of $N_{\mathrm {3}}$, $V_{\mathrm {3}}$, $M_{\mathrm {3}}$ and can be jointly modeled as a single bearing. The dynamic model reduces to Eq. (7.1)–(7.5) in the 5 variables $\theta$, $N_{\mathrm {1}}$, $\varphi _{\mathrm {1}N}$, $N_{\mathrm {2}}$, $\varphi _{\mathrm {2}N}$, with $V_{\mathrm {3}}$ and $N_{\mathrm {3}}$ derived from Eq. (7.7) and (7.8) as follows:

$$\begin{aligned} V_{3}= & {} -[m_{3} a_{x} +m_{3} \rho _{1O2} ({\ddot{\theta }}\cos \theta -{\dot{\theta }}^{2}\sin \theta )]/2 , \end{aligned}$$

(17.1)

$$\begin{aligned} N_{3}= & {} [m_{3} (g+a_{z} )+m_{3} \rho _{1O2} ({\ddot{\theta }}\sin \theta +{\dot{\theta }}^{2}\cos \theta )]/2. \end{aligned}$$

(17.2)

$M_{\mathrm {3}}$ is irrelevant for the integration and, if of interest, can be computed using Eq. (7.6).

2.3.2 Reduced model $\texttt {M}_{2}$: infinitely distant symmetrical bearings with massless slider

If not only are the two bearings infinitely distant (as in model $\texttt {M}_{\mathrm {1}})$, but also their lower and upper surfaces are identical (symmetrical double VFP bearing) and the slider mass is negligible ($m_{\mathrm {1}} = 0$), then the two interfaces are symmetrically excited, i.e., $N_{\mathrm {1}} = N_{\mathrm {2}}, \varphi _{\mathrm {1}N} = \varphi _{\mathrm {2}N}, V_{\mathrm {1}} = V_{\mathrm {2}}$, $\varphi _{\mathrm {1}V} = \varphi _{\mathrm {2}V}$, $\rho _{\mathrm {1}V} = \rho _{\mathrm {2}V}$, $F_{\mathrm {1}} = F_{\mathrm {2}}$. The dynamic model reduces to the following three equations in $\theta$, $N_{\mathrm {1}}$, and $\varphi _{\mathrm {1}N}$:

$$\begin{aligned}&m^{*}[L{\ddot{\theta }}+(g+a_{z} )\sin \theta +a_{x} \cos \theta ]+N_{1} \sin \varphi _{1N} +V_{1} \cos \varphi _{1V} +F_{1} \cos {\bar{\varphi }}_{1} =0, \end{aligned}$$

(18.1)

$$\begin{aligned}&m^{*}[(g+a_{z} )\cos \theta -a_{x} \sin \theta +L{\dot{\theta }}^{2}]-N_{1} \cos \varphi _{1N} +V_{1} \sin \varphi _{1V} +\mathrm{sgn}\,\theta \cdot F_{1} \sin {\bar{\varphi }}_{1} =0, \end{aligned}$$

(18.2)

$$\begin{aligned}&J_{1} {\ddot{\theta }}-N_{1} L\sin \varphi _{1N} +V_{1} (\kappa \rho _{1V} -L\cos \varphi _{1V} )+F_{1} (\kappa R_{1} -L\cos {\bar{\varphi }}_{1} )=0 \end{aligned}$$

(18.3)

where $m^{{*}} = m_{\mathrm {2}} + m_{\mathrm {3}}/2$ is the amount of TMD mass pertaining to the individual bearing, L is the equivalent pendulum length, here coinciding with $\rho _{\mathrm {1O2}}$, and $\kappa$ is the multiplicative factor, here equal to 2.

2.3.3 Reduced model $M_3$: rocking P-TMD

If instead of a supported TMD a rocking TMD is considered (Fig. 1d), the upper TMD mass and the upper plate disappear. Equations (18.1), (18.2), and (18.3) are still valid, with $m^{{*}} = m_{\mathrm {1}}, L = \rho _{\mathrm {1G1}}$, and $\kappa = 1$.

2.3.4 Integration of the equations of motion for the reduced models $\texttt {M}_2$ and $\texttt {M}_3$

The integration procedure presented above for the general VFP-TMD model gets simpler for the reduced models $\texttt {M}_{\mathrm {2}}$ and $\texttt {M}_{\mathrm {3}}$, described by Eqs. (18.1), (18.2), and (18.3). Combining Eqs. (18.1) and (18.3) and rearranging Eq. (18.2) give

$$\begin{aligned} {\ddot{\theta }}= & {} -\{Lm^{*}[(g+a_{z} )\sin \theta +a_{x} \cos \theta ]+\kappa (V_{1} \rho _{1V} +F_{1} R_{1} )\}/J^{*}, \end{aligned}$$

(19.1)

$$\begin{aligned} N_{1} \cos \varphi _{1N}= & {} m^{*}[(g+a_{z} )\cos \theta -a_{x} \sin \theta +L{\dot{\theta }}^{2}]+V_{1} \sin \varphi _{1V} +\mathrm{sgn}\,\theta \cdot F_{1} \sin {\bar{\varphi }}_{1}, \end{aligned}$$

(19.2)

$$\begin{aligned} N_{1} \sin \varphi _{1N}= & {} -\frac{J_{1} }{J^{*}}m^{*}[(g+a_{z} )\sin \theta +a_{x} \cos \theta ]+V_{1} \left( {\kappa \frac{m^{*}L\rho _{1V} }{J^{*}}-\cos \varphi _{1V} } \right) \nonumber \\&+F_{1} \left( {\kappa \frac{m^{*}LR_{1} }{J^{*}}-\cos {\bar{\varphi }}_{1} } \right) \end{aligned}$$

(19.3)

where $J^{*}=J_{1} +m^{*}L^{2}$ is the rotational inertia around $\hbox {O}_{\mathrm {1}}$ of the slider plus that of $m^{{*}}$ supposed hinged in $\hbox {O}_{\mathrm {2}}$. Introducing the state variables $q_{\mathrm {1}} = \theta$ and $q_{\mathrm {2}} = {\dot{\theta }}$, the following state space system is obtained:

$$\begin{aligned} {\dot{q}}_{1}= & {} q_{2}, \end{aligned}$$

(20.1)

$$\begin{aligned} {\dot{q}}_{2}= & {} f_{1} (q_{1} ,q_{2} ,a_{x} ,a_{z} ), \end{aligned}$$

(20.2)

$$\begin{aligned} N_{1} \cos \varphi _{1N}= & {} f_{2} (q_{1} ,q_{2} ,a_{x} ,a_{z} ), \end{aligned}$$

(20.3)

$$\begin{aligned} N_{1} \sin \varphi _{1N}= & {} f_{3} (q_{1} ,q_{2} ,a_{x} ,a_{z} ) \end{aligned}$$

(20.4)

where Eqs. (20.1) and (20.2) are the two first-order ODEs (respectively, linear and nonlinear) describing the evolution of the dynamic system, while Eqs. (20.3) and (20.4) are two algebraic equations updating $N_{\mathrm {1}}$ and $\varphi _{\mathrm {1}N}$.

2.4 The mechanical model of the VFP-TMD on an MDOF structure

Let us consider a linear multi-degree-of-freedom (MDOF) planar structure, modeled as an $n_{s}$-storey building having one lateral DOF per storey, with the VFP-TMD attached to the $j^{\mathrm {th}}$ storey. Denoting by u$_{s}$ the structural displacement vector, by M$_{s}$, C$_{s}$, and K$_{s}$ the structural mass, damping, and stiffness matrices, by f$_{s}$ the external force vector, and by ${\ddot{u}}_{g}$ and ${\ddot{w}}_{g}$ the horizontal and vertical ground acceleration components, the equation of motion of the $i^{\mathrm {th}}$ storey is

$$\begin{aligned} m_{si} ({\ddot{u}}_{g} +{\ddot{u}}_{si} )+\mathbf{C }_{si} {{\dot{\mathbf{u }}}_s} +\mathbf{K }_{si} \mathbf{u }_{s} =f_{si} +\delta _{ij} \lambda _{d} , i = 1, 2, ... , n_{s} \end{aligned}$$

(21)

where (i) the subscript i denotes the $i^{\mathrm {th}}$ row of a vector/matrix, (ii) the topological operator $\delta _{ij}$ is 1 if $i = j$ and 0 otherwise, and (iii) $\lambda _{d}$ is the horizontal component of the TMD reaction force, given by

$$\begin{aligned} \lambda _{d} =-\sum \limits _k {m_{k} [a_{x} +{\ddot{x}}_{1k} } ]=-\sum \limits _k {m_{k} [a_{x} +\rho _{1k} (\cos \theta {\ddot{\theta }}-\sin \theta {\dot{\theta }}^{2})]} \end{aligned}$$

(22)

where the index k denotes the $k^{\mathrm {th}}$ component of the TMD.

Equations (21) and (22), complemented with the equations of the VFP-TMD, are the equations of motion of the structure-TMD coupled system, with $a_{x} ={\ddot{u}}_{g} +{\ddot{u}}_{sj}$ and $a_{z} = {\ddot{w}}_{g}$ being the acceleration of the TMD support.

2.5 The simplified TMD model on a generalized SDOF structure

To better understand the VFP-TMD properties and to establish an optimal design method, some simplifications of the fully nonlinear models presented above are appropriate.

Regarding the structure, this is approximated as a generalized SDOF system.

Regarding the absorber, the following assumptions are made:

• The reduced model $\texttt {M}_{\mathrm {2}}$ is adopted, expressed by Eqs. (19.1), (19.2) and (19.3) with $m^{{*}} = m_{\mathrm {2}} + m_{\mathrm {3}}/2$, $L = \rho _{\mathrm {1O2}}$ and $\kappa = 2$.

• The slider angular amplitude ${\bar{\varphi }}_{1}$ and the rotation $\theta$ are assumed very small, so only first-order terms are retained in their nonlinear expansions. Accordingly, any spherical region degenerates in its horizontal projection, so that $\rho _{\mathrm {1}V} = R_{\mathrm {1}}$.

• The normal contact force $N_{\mathrm {1}}$ is supposed to be centered on $A_{\mathrm {1}}$ (i.e., $\varphi _{\mathrm {1}N} = \varphi _{\mathrm {1}m} = 0$), as if the slider height were null ($h_{\mathrm {1}} = 0$).

• The vertical acceleration input is neglected ($a_{z} = 0$), as well as the slider inertia ($J_{\mathrm {1}} = 0$).

Under these assumptions, the pressure gets uniform on $A_{\mathrm {1}}$ and equal to

$$\begin{aligned} \sigma _{1} =\sigma _{1m} =\frac{N_{1} }{A_{1} }=\frac{m^{*}g}{A_{1} }, \end{aligned}$$

(23)

the friction force consequently becomes

$$\begin{aligned} V_{1} =\mathrm{sgn}\,\,{\dot{\theta }}\int \limits _{A_{1} } {dV_{1} } =\mathrm{sgn}\,\,{\dot{\theta }}\sigma _{1} \int \limits _{A_{1} } {\mu _{1} dA_{1} } =\mathrm{sgn}\,\,{\dot{\theta }}m^{*}g\mu _{\mathrm{eff}1} \end{aligned}$$

(24)

where

$$\begin{aligned} \mu _{\mathrm{eff}1} =\frac{1}{A_{1} }\int \limits _{A_{1} } {\mu _{1} dA_{1} } =\frac{1}{A_{1} }\left( {\mu _{1}^{a} A_{1}^{a} +\mu _{1}^{b} A_{1}^{b} } \right) =\mu _{1}^{a} +(\mu _{1}^{b} -\mu _{1}^{a} )\frac{A_{1}^{b} }{A_{1} }, \end{aligned}$$

(25)

the VFP-TMD equation of motion becomes

$$\begin{aligned} L{\ddot{\theta }}+\mathrm{sgn}\,\,{\dot{\theta }}\eta g\mu _{\mathrm{eff}1} +\eta F_{1} /m^{*}+g\theta +a_{x} =0, \end{aligned}$$

(26)

and the overall TMD reaction force becomes:

$$\begin{aligned} \lambda _{d} =-m(a_{x} +L{\ddot{\theta }}) \end{aligned}$$

(27)

where $\eta = 2R_{\mathrm {1}}/L \ge 1$ and $m = 2m^{{*}}$ is the total TMD mass.

As a result of these simplifications, the coupled system is eventually described by

$$\begin{aligned} {\ddot{u}}_{s} +2\zeta _{s} \omega _{s} {\dot{u}}_{s} +\omega _{s}^{2} u_{s}= & {} f_{s} /m_{s} -{\ddot{u}}_{g} -m_{R} ({\ddot{u}}_{g} +{\ddot{u}}_{s} +L{\ddot{\theta }}), \end{aligned}$$

(28.1)

$$\begin{aligned} L{\ddot{\theta }}+\omega ^{2}L({\bar{f}}_{\mu } +{\bar{f}}_{F} +\theta )= & {} -({\ddot{u}}_{g} +{\ddot{u}}_{s} ) \end{aligned}$$

(28.2)

where $\omega _{s} =\sqrt{k_{s} /m_{s} }$ is the structural circular frequency, $\zeta _{s} =c_{s} /(2\omega _{s} m_{s} )$ is the structural damping ratio, $m_{R} =m/m_{s}$ is the TMD mass ratio, $\omega =\sqrt{g/L}$ is the TMD circular frequency, ${\bar{f}}_{F} =\eta F_{1} /(m^{*}g)$ is the TMD normalized restrainer force, and

$$\begin{aligned} {\bar{f}}_{\mu } ={\bar{f}}_{\mu } (\theta ,{\dot{\theta }})=\eta V_{1} /(m^{*}g)=\mathrm{sgn}\,\,{\dot{\theta }}\eta \mu _{\mathrm{eff}1} \end{aligned}$$

(29)

is the TMD normalized equivalent friction force.

Equations (28.1) and (28.2) represents a linear system except for ${\bar{f}}_{\mu }$ and ${\bar{f}}_{F}$, intrinsically nonlinear. However, in the ideal case where $\mu _{1}^{a} = 0$, and for any $|\theta |$ not significantly larger than $2{\bar{\varphi }}_{1}$, $\mu _{\mathrm{eff}1}$ can be approximated as a linear function of $|\theta |$, i.e., as $\mu _{\mathrm{eff}1} = {\tilde{\mu }}_{\mathrm{eff}1} \left| \theta \right|$. In fact, for $|\theta |\rightarrow 0$ the (tangential) linearized expression for $\mu _{\mathrm{eff}1}$ can be derived as

$$\begin{aligned} \mu _{\mathrm{eff}1} =\mu _{\mathrm{eff}1}^{+} =\frac{4}{\pi }\mu _{1}^{b} \frac{\left| \theta \right| }{2{\bar{\varphi }}_{1} }={\tilde{\mu }}_{\mathrm{eff}1}^{+} \left| \theta \right| \end{aligned}$$

(30)

while for $|\theta |= 2{\bar{\varphi }}_{1}$ the (secant) linearized expression for $\mu _{\mathrm{eff}1}$ is

$$\begin{aligned} \mu _{\mathrm{eff}1} =\mu _{\mathrm{eff}1}^{-} =\mu _{1}^{b} \frac{\left| \theta \right| }{2{\bar{\varphi }}_{1} }={\tilde{\mu }}_{\mathrm{eff}1}^{-} \left| \theta \right| \end{aligned}$$

(31)

where $\mu _{\mathrm{eff}1}^{-} \le \mu _{\mathrm{eff}1} (\theta ) \le \mu _{\mathrm{eff}1}^{+}$ for any $|\theta | \le 2{\bar{\varphi }}_{1}$.

With this linearization, Eq. (29) becomes

$$\begin{aligned} {\bar{f}}_{\mu } ={\bar{f}}_{\mu } (\theta ,{\dot{\theta }})=\mathrm{sgn}\,({\dot{\theta }})\eta {\tilde{\mu }}_{\mathrm{eff}1} \left| \theta \right| \end{aligned}$$

(32)

where ${\tilde{\mu }}_{\mathrm{eff}1}$ denotes either ${\tilde{\mu }}_{\mathrm{eff}1}^{-}$ or ${\tilde{\mu }}_{\mathrm{eff}1}^{+}$ depending on the expected range of $\theta$, and the constant factor $\chi = \eta {\tilde{\mu }}_{\mathrm{eff}1}$ is the friction ratio of the absorber, as defined in [22].

With all the previous assumptions, and as long as the collision with the restrainer is avoided, the VFP-TMD and hence the coupled system are nonlinear but homogeneous systems, and their response is proportional to the excitation amplitude. Because those assumptions and this result hold only to an approximate extent, Sect. 3 tests their validity by numerical simulations.

3 Design and simulation of the device

In this Section, a nearly optimal design procedure is first presented for VFP-TMDs, and then, the optimized absorber is simulated on SDOF and MDOF structures. For brevity, only the reduced model $\texttt {M}_{\mathrm {2}}$ is addressed. The restrainer stiffness and damping parameters, $k_{F\mathrm {1}}$ and $c_{F\mathrm {1}}$, excluded from optimization, are assigned to represent a relatively rigid inelastic impact. Recalling that in the $\texttt {M}_{\mathrm {2}}$ model the lower and upper plates are connected by two identical restrainers placed in series, and denoting by $k_{Feq} = k_{F\mathrm {1}}/2$ and $c_{Feq} = c_{F\mathrm {1}}/2$ their equivalent coefficients, it is assumed that:

• $k_{F1} =2k_{Feq} =2\omega _{Feq}^{2} m^{*}$, with $\omega _{Feq} =10\omega$ [34];

• $c_{F1} =2c_{Feq} =4\zeta _{Feq} \omega _{Feq} m^{*}$, with $\zeta _{Feq} =-\frac{\ln e_{Feq} }{\sqrt{\pi ^{2}+\ln ^{2}e_{Feq} } }$, where $e_{Feq}$ is the elastic restitution coefficient [35], here taken as 0.5.

3.1 Design methodology

Several TMD design approaches exist in the literature [36, 37]. A nearly optimal criterion is here proposed for VFP-TMDs, based on the simplified model obtained in Sect. 2.5. Because that model is approximately homogeneous, the criterion is inspired by the optimal design method proposed for homogeneous P-TMDs in [22] and improved in [38]. Such method consists in a first-order $H_{{\infty }}$ or $H_{\mathrm {2}}$ optimum synthesis, minimizing the corresponding norm of an appropriate input–output transfer function (TF) of the structure-TMD system. A similar approach is adopted here, with due modifications accounting for VFP bearings features.

In detail, referring to the ideal case where $\mu _{1}^{a} =$ 0, the design criterion comprises the following steps:

• 1. Identification of the structural damping ratio $\zeta _{s}$ and choice of the TMD mass ratio $m_{R}$.

• 2. Determination of the optimal values of the TMD frequency ratio, $\omega _{R} = \omega /\omega _{s}$, and the TMD friction ratio, $\chi =\eta {\tilde{\mu }}_{\mathrm{eff}1}$, by minimizing the $H_{{\infty }}$ or $H_{\mathrm {2}}$ norm of a selected TF.

• 3. Derivation of the optimal equivalent pendulum length $L=\rho _{1O2} =g/\omega ^{2}=g/(\omega _{R} \omega _{s} )^{2}$.

• 4. Assumption of a value for the slider angular semi-width ${\bar{\varphi }}_{1}$.

• 5. Assumption of a value for the restrainer activation angle $\theta _{F\mathrm {1}} \ge 2{\bar{\varphi }}_{1}$.

• 6. Assumption of a value for the height $s_{\mathrm {1}}$ of the surface raised edge and derivation of (i) the sliding surface radius $R_{1} =(L/2+s_{1} )/\cos (\theta _{F1} +{\bar{\varphi }}_{1} )$, (ii) the ratio $\eta = 2R_{\mathrm {1}}/L$; (iii) the slider semi-height $h_{1} =R_{1} -L/2=R_{1} (1-1/\eta )$; and (iv) the slider aspect ratio $a_{R} =h_{1} /(R_{1} \sin {\bar{\varphi }}_{1} )=(1-1/\eta )/\sin {\bar{\varphi }}_{1}$.

• 7. Determination of the optimal friction coefficient $\mu _{1}^{b}$ for the $A_{1}^{b}$ region, computed as $\mu _{1}^{b} =\frac{\pi }{2}{\tilde{\mu }}_{\mathrm{eff}1} {\bar{\varphi }}_{1}$ or as $\mu _{1}^{b} =2{\tilde{\mu }}_{\mathrm{eff}1} {\bar{\varphi }}_{1}$ depending if small or large displacements are expected; in these expressions, ${\tilde{\mu }}_{\mathrm{eff}1}$ is computed as ${\tilde{\mu }}_{\mathrm{eff}1} = \chi /\eta$ from the results of previous steps.

• 8. After simulations under the design loads, iterative improvement of ${\bar{\varphi }}_{1}$ and $\theta _{F\mathrm {1}}$ in steps 4 and 5.

The above design criterion has two limitations: First, it is based on a simplified model that assumes small displacements and a flat surface. Second, it presumes a frictionless inner region ($\mu _{1}^{a} = 0$). These limitations are discussed in the sequel.

3.2 Simulations of the simplified VFP-TMD model on an SDOF structure

In this Section, the simplified TMD model presented in Sect. 2.5 is used to simulate the response of a VFP-TMD on an SDOF structure under a sinusoidal force input. That model, representing the nearly flat case, seems appropriate for a preliminary performance assessment, being simple enough to neglect the effects of geometrical nonlinearities and uneven contact pressure distributions, but also advanced enough to catch the nonlinear dependence of the friction force and the restrainer force on $\theta$, and the consequent control losses w.r.t. a perfectly homogeneous device. To highlight these losses, first a homogeneous TMD is considered in Sect. 3.2.1, and then, the actual VFP-TMD is analyzed in Sect. 3.2.2.

3.2.1 Perfectly homogeneous TMD

An SDOF structure having frequency $\omega _{s}$ and damping ratio $\zeta _{s} = 0.01$ is analyzed under a sinusoidal force having amplitude $f_{s0}$, circular frequency $\omega _{f}$ and duration sufficient to approximately induce a steady-state response. A TMD is considered, having mass ratio $m_{R} = 0.01$ and being either a perfectly linear viscous TMD or a perfectly homogeneous friction TMD. The viscous TMD is classically defined [7]. The friction TMD is defined by Eqs. (28.2) and (29), assuming ${\bar{f}}_{F} = 0$ (no restrainer) and $\mu _{\mathrm{eff}1} = {\tilde{\mu }}_{\mathrm{eff}1} \left| \theta \right|$, as per Eq. (30) or (31). For simplicity, admittedly, $s_{\mathrm {1}} = 0$, so that $\eta = 1$ and ${\tilde{\mu }}_{\mathrm{eff}1} = \chi$. Both TMD types are designed to minimize the $H_{{\infty }}$ norm of the TF from the force to the structural displacement [38]. Because both models are homogeneous (linearly or nonlinearly), the design solution is amplitude independent. The optimal parameters of the linear TMD are $\omega _{R} = 0.9886$ and $\zeta = 0.0625$ ($\zeta$ being the TMD viscous damping ratio); those of the homogeneous TMD are $\omega _{R} = 0.9971$ and ${\tilde{\mu }}_{\mathrm{eff}1} = 0.1945$. Figure 8a compares the corresponding TFs, normalized to the uncontrolled TF peak $u_{s,peak}^{unc}$, which appear nearly identical. Figure 8b shows the corresponding steady-state dissipative force–displacement loops under a harmonic force having $\omega _{f} = \omega _{s}$. The two loops have different shapes but similar area, i.e., similar cyclic energy dissipation. The homogeneous friction TMD is concluded to be as effective as a linear TMD.

3.2.2 Actual VFP-TMD

In fact, even the VFP-TMD simplified model is homogeneous only in approximate terms and for limited values of $\theta$. Its actual performance degrades for three reasons: (i) the dependence of $\mu _{\mathrm{eff}1}$ on $| \theta |$ is nonlinear even if $\mu _{1}^{a} = 0$ and if $|\theta |\le \theta _{F\mathrm {1}}$; (ii) it may be that $\mu _{1}^{a} > 0$; (iii) it may be that $| \theta | > \theta _{F\mathrm {1}}$ (restrainer activated). To examine this degradation, but also the advantages of the VFP-TMD over uniform-friction devices, four cases are considered:

• Case I: $\mu _{1}^{a} = 0$ & $\theta _{F\mathrm {1}} \rightarrow \infty$

• Case II: $\mu _{1}^{a} = 0$ & $\theta _{F\mathrm {1}} = 2{\bar{\varphi }}_{1}$

• Case III: $\mu _{1}^{a} = \mu _{1}^{b}$& $\theta _{F\mathrm {1}} \rightarrow \infty$

• Case IV: $\mu _{1}^{a} = \mu _{1}^{b}$/10 & $\theta _{F\mathrm {1}} \rightarrow \infty$

Cases I and II represent the ideal condition of a frictionless inner region. In case I, the restrainer is inactive, while in case II it activates as the slider exits the inner region. Cases III and IV, both unrestrained, admit friction in the inner region. In particular, case III represents a uniform-friction P-TMD, while case IV represents a VFP-TMD in which $\mu _{1}^{a}$ is 10% of $\mu _{1}^{b}$.

The structure is the same SDOF system assumed above ($\zeta _{s} = 0.01$), and the VFP-TMD is derived from the same optimal homogeneous TMD ($m_{R} = 0.01, \omega _{R} = 0.9971$, ${\tilde{\mu }}_{\mathrm{eff}1} = \chi = 0.1945$), by further applying Eq. (30) to obtain $\mu _{1}^{b}$ from the assigned ${\bar{\varphi }}_{1}$. The system is still excited by a sinusoidal force of varying frequency and sufficient duration, but its amplitude $f_{s0}$ is now varied, to highlight the amplitude dependence of the response. For the results to be independent from the assigned ${\bar{\varphi }}_{1}$, $f_{s0}$ is normalized to $2\text {mg}{\bar{\varphi }}_{1}$, i.e., to the force which, statically applied to the TMD, would make the slider exit the inner region.

Fig. 9

Amplitude dependence of the input–output transfer functions (TFs) in the assumption of the simplified model. Top subfigures: force-to-structural displacement TFs. Bottom subfigures: force-to-TMD displacement TFs. a and e: Case I. b and f: Case II. c and g: Case III. d and h: Case IV. In each subfigure, TFs are drawn for 10 different values of the normalized force amplitude $f_{s0} /(2\hbox {mg}{\bar{\varphi }}_{1} )$, ranging from 0.01 to 10.0 (as per the legend)

Fig. 10

Amplitude dependence of the peak value of the input–output TFs in the assumption of the simplified model. a: structural displacement. b: TMD displacement. Cases I to IV described in the legend. Black dashed line in subfigure b: $\theta = 2{\bar{\varphi }}_{1}$

Results are reported in Figs. 9 and 10.

Figure 9 shows the TFs obtained in the four cases for 10 values of $f_{s0} /(2\mathrm{mg}{\bar{\varphi }}_{1} )$ (from 0.01 to 10). Figure 9a–d shows the structural displacement, Fig. 9e–h the TMD displacement. The 8 subfigures are arranged in four columns, orderly referred to cases I to IV.

Figure 10 shows the peak of the same TFs as a function of $f_{s0} /(2\mathrm{mg}{\bar{\varphi }}_{1} )$, for the four cases. Figure 10a shows the structural displacement and Fig. 10b the TMD displacement. The black dashed line in Fig. 10b represents the TMD displacement at which the TMD exits the inner region.

Figures 9 and 10 show that:

• Cases I and II substantially ensure the same performance of a homogeneous TMD as long as $f_{s0} /(2\mathrm{mg}{\bar{\varphi }}_{1} ) \le$ 1.15, i.e., as long as $| \theta |\le 2{\bar{\varphi }}_{1}$. In this range, the nonlinear dependence of $\mu _{\mathrm{eff}1}$ on $| \theta |$ does not practically affect effectiveness.

• As $| \theta |$ exceeds $2{\bar{\varphi }}_{1}$, case I undergoes a gradual performance degradation, as $\mu _{\mathrm{eff}1}$ can no longer increase beyond $\mu _{1}^{b}$ and the TMD equivalent damping ratio decreases. Case II, instead, undergoes a sudden degradation as the slider collides against the restrainer, worsening with increasing excitation. Softening the restrainer and/or increasing its activation angle will reduce and/or delay this degradation, but will also increase the bearing dimensions and the slider aspect ratio. This trade-off should be carefully considered in design.

• Case III shows the limitations of a uniform-friction TMD. Unrestrained as case I, case III achieves a similar performance only at a specific input amplitude (i.e., at $f_{s0} /(2\;\mathrm{mg}{\bar{\varphi }}_{1} )\approx 1$), proving otherwise less effective, either because insufficiently damped (at larger amplitudes) or excessively damped (at smaller amplitudes). Under a certain input threshold, the friction force exceeds the inertial force on the TMD, which remains stuck to the structure.

• Case IV shows pros and cons of a plausible realization of VFP-TMD. It is nearly as effective as case I over a wide range of force amplitudes and still quite effective under amplitudes at which case III is totally useless. The complete inefficiency of the device occurs only at a very small input amplitude, 100 times smaller than that which activates the restrainer.

3.3 Simulations of the rigorous VFP-TMD model on an SDOF structure

If the rigorous VFP-TMD model is used instead of the simplified one, other interesting nonlinear phenomena are visible. The same SDOF structure examined before is reconsidered under a long-duration sinusoidal force having $\omega _{f} = \omega _{s}$. TMD parameters $m_{R}$, $\omega _{R}$, and $\chi$ are also the same. Five VFP-TMDs are considered, with ${\bar{\varphi }}_{1}$ varying from $1^\circ$ to $20^\circ$ following Table 1. In all cases, $\theta _{F\mathrm {1}} = 2{\bar{\varphi }}_{1}$, $\mu _{1}^{a} = 0$, and Eq. (30) holds, as in previous case II. Assuming $s_{\mathrm {1}} = 0$, the slider aspect ratio significantly increases with ${\bar{\varphi }}_{1}$, augmenting the slider’s susceptibility to overturning under the couple of friction forces acting at its lower and upper surfaces. Also $\eta$ increases with ${\bar{\varphi }}_{1}$, and ${\tilde{\mu }}_{\mathrm{eff}1} =\chi _{1} /\eta$ and $\mu _{1}^{b} =\pi {\tilde{\mu }}_{\mathrm{eff}1} {\bar{\varphi }}_{1} /2$ vary accordingly (Table 1).

Table 1 Simulations of the rigorous VFP-TMD model on an SDOF structure—the 5 examined cases

In all cases, the normalized force amplitude $f_{s0} /(2\mathrm{mg}{\bar{\varphi }}_{1} )$ is progressively increased (from 0.01 to 10) and the amplitude dependence of the response is observed.

Fig. 11

Amplitude dependence of the VFP-TMD response in the assumption of the rigorous model, for 5 values of ${\bar{\varphi }}_{1}$ (in the legend). Appropriately normalized, the following response quantities are reported: a structural displacement; b TMD displacement; c restrainer force; d offset angle; e normal contact force; f friction force

Fig. 12

Normalized friction force (a) and the normal contact force (b) versus the TMD displacement for 5 values of ${\bar{\varphi }}_{1}$ (in the legend), under the largest input amplitude with no restrainer activation

Results are presented in Figs. 11 and 12.

In Fig. 11, $f_{s0} /(2\mathrm{mg}{\bar{\varphi }}_{1} )$ is reported in the abscissae and various response quantities in the ordinates, namely the steady-state structural displacement $u_{s}$, normalized to $u_{s,\mathrm{peak}}^{unc}$; the steady-state TMD displacement u, normalized to $u_{s,\mathrm{peak}}^{unc}$; the maximum (over time) transient total restrainer force $2F_{1,\max }$, normalized to $f_{s0}$; the maximum (over time) transient offset angle $\varphi _{1N,\max }$, normalized to ${\bar{\varphi }}_{1}$; the steady-state minimum and maximum normal contact force $N_{1}$, normalized to $m^{*}g$; the steady-state total friction force $2V_{1}$, scaled times $\eta$ and normalized to $f_{s0}$.

Figures 11a and 11b are similar to Figs. 10a and 10b. At a first glance, they show a similar performance of the 5 cases, with a nearly optimal effectiveness until restrainer activation, which approximately occurs at the same force amplitude for the 5 cases (Fig. 11c). After that, the structural displacement increases, and the TMD displacement decreases. A major difference, however, exists with respect to Fig. 10, because, except for ${\bar{\varphi }}_{1} = 1^\circ$ , the curves are defined only until a certain threshold input amplitude, beyond which a steady-state response is no longer possible. At some instant during the transient response, in fact, $\varphi _{1N,\max }$ exceeds ${\bar{\varphi }}_{1}$ (Fig. 11d), i.e., $N_{\mathrm {1}}$ exits the slider contour, and equilibrium is violated. Although a more comprehensive model, accounting for the slider detachment, might track the actual TMD behavior after that instant, the condition $\varphi _{1N,\max } = {\bar{\varphi }}_{1}$ reasonably defines a failure state. From Fig. 11c, such failure always follows the restrainer activation. The smaller ${\bar{\varphi }}_{1}$, the larger the margin from restrainer activation to failure. While for ${\bar{\varphi }}_{1} = 1^\circ$ this margin is conspicuous, for cases 4 and 5 failure immediately follows. Obviously, the susceptibility to overturning is related to the slider aspect ratio and therefore increasing with ${\bar{\varphi }}_{1}$ (Table 1). Another obvious effect of increasing ${\bar{\varphi }}_{1}$ is that geometric nonlinearities increase. This is evident in Fig. 11e, where the minimum and maximum normalized normal contact force (respectively, reached when |u| is maximum and when u is zero) increasing diverge from 1 as $f_{s0} /(2\mathrm{mg}{\bar{\varphi }}_{1} )$ increases and/or as ${\bar{\varphi }}_{1}$ increases. Less significant is, instead, the influence of ${\bar{\varphi }}_{1}$ on the friction force (Fig. 11f), nearly constant before the restrainer activation, and decreasing after it.

Finally, in Figs. 12a and 12b, the normalized friction force $2\eta V_{1} /f_{s0}$ and the normalized normal contact force $N_{1} /(m^{*}g)$ are plotted versus the normalized TMD displacement $u/u_{s,\mathrm{peak}}^{unc}$. They are obtained, for each value of ${\bar{\varphi }}_{1}$, under the largest input force that does not activate the restrainer. The friction loops in Fig. 12a correspond to the triangular loops of a homogeneous model. For small ${\bar{\varphi }}_{1}$, the loops follow Eq. (25). For large ${\bar{\varphi }}_{1}$, the loops change with the instantaneous amplitude of the TMD strokes: for small amplitudes (in the first instants of the transient), the loops follow Eq. (25), while for large amplitudes (as the response becomes steady) they appear increasingly curved. As visible in Fig. 12b, this is because $N_{\mathrm {1}}$ increasingly deviates from its static value as the TMD amplitude of motion increases. Because $N_{\mathrm {1}}$ is maximum when $u =$ 0 and minimum when |u| is maximum, the ordinates of the friction loops increase with the motion amplitude for small values of |u| and decrease with the motion amplitude for large values of |u|. Furthermore, the friction loops in Fig. 12a are asymmetric w.r.t. the horizontal axis because $N_{\mathrm {1}}$ in Fig. 12b depends, for any value of u, on the direction of motion.

3.4 Simulation of the device on an MDOF structure

In this Section, the VFP-TMD is simulated on an MDOF high-rise building under wind excitation. The VFP-TMD design follows Sect. 3.1, and analyses adopt the fully nonlinear reduced model $\texttt {M}_{\mathrm {2}}$. The VFP-TMD is compared with classical TMD types and observed under deviations of $\mu _{1}^{a}$ and $\mu _{1}^{b}$ from optimum.

3.4.1 The structure

The structure is the 42-storey high-rise building studied in [38], having a 168 m height and a $25\times 25$ $\hbox {m}^{\mathrm {2}}$ square section. The model is a planar 10-elements tapered cantilever beam, with a total mass of $22.69\cdot 10^{\mathrm {6}}$ kg. The first three modes have periods of 4.00 s, 1.23 s, and 0.52 s, and participating modal masses of 45.3%, 21.8%, and 11.1%. A 2% damping ratio $\zeta _{s}$ is assumed in every mode.

3.4.2 The wind load

The planar model is separately simulated under the along-wind or the across-wind components of a moderate-to-high wind flow, blowing for 60 min. Both components are applied to the structural nodes as deterministic wind load time histories, obtained as the realization of a stationary nonhomogeneous stochastic process, exactly defined as described in [38].

3.4.3 The VFP-TMD

The VFP-TMD is tuned to the structural fundamental mode ($\omega _{s} = 1.571$ rad/s), and its mass m is chosen as 1% the building mass ($m = 226900$ kg), corresponding to an ‘effective’ mass ratio $m_{R} = 6.45{\%}$. This assumption is the same as made in [38]. Because the structure and the wind loads are also the same, the results obtained here for the VFP-TMD can be compared with those obtained in [38] for other devices and for the uncontrolled building. Solving the $\hbox {H}_{{\infty }}$ SDOF design problem for $\zeta _{s} = 2{\%}$ and $m_{R} = 6.45{\%}$ provides the VFP-TMD optimal dimensionless parameters, $\omega _{R} = 0.982$ and $\chi = 0.4524$, resulting in $\omega = \omega _{R}\cdot \omega _{s} =1.542$ rad/s and $L = \rho _{\mathrm {1O2}} = g/\omega ^{\mathrm {2}} = 4122$ mm. Adopting $\theta _{F\mathrm {1}} = 2{\bar{\varphi }}_{1}$, ${\bar{\varphi }}_{1}$ is tentatively assumed as $6^\circ$, resulting in $\theta _{F\mathrm {1}} = 12^\circ$. With $s_{1} = 10$ mm, this implies $R_{\mathrm {1}} = 2177$ mm and $h_{\mathrm {1}} = 117$ mm, eventually producing a slider having height 233 mm and width 455 mm ($a_{R} = 0.512$) and a sliding surface having width 1346 mm. This also gives ${\tilde{\mu }}_{\mathrm{eff}1} = \chi /(2R_{1} /L) = 0.4282$. Once ${\tilde{\mu }}_{\mathrm{eff}}$ and ${\bar{\varphi }}_{1}$ are established, the optimal friction coefficient $\mu _{1}^{b}$ is to be determined, and an assumption is to be made about $\mu _{1}^{a}$. To this regard, the following four cases are considered:

• Case 1: $\mu _{1}^{b} =\frac{\pi }{2}{\tilde{\mu }}_{\mathrm{eff}1} {\bar{\varphi }}_{1} = 7.04{\%}$ & $\mu _{1}^{a} =$ 0,

• Case 2: $\mu _{1}^{b} =2{\tilde{\mu }}_{\mathrm{eff}1} {\bar{\varphi }}_{1} =$ 8.97% & $\mu _{1}^{a} =$ 0,

• Case 3: $\mu _{1}^{b} =4{\tilde{\mu }}_{\mathrm{eff}1} {\bar{\varphi }}_{1} =$ 17.94% & $\mu _{1}^{a} =$ 0,

• Case 4: $\mu _{1}^{b} =\frac{10}{11}2{\tilde{\mu }}_{\mathrm{eff}1} {\bar{\varphi }}_{1} =$ 8.15% & $\mu _{1}^{a} =\frac{1}{10}\mu _{1}^{b} =$ 0.815%.

Cases 1 to 3 assume $\mu _{1}^{a} = 0$ (ideal case) and $\mu _{1}^{b}$, respectively, given by Eq. (30), by Eq. (31), and by twice this latter value. Case 4 approximates case 2, assuming, more realistically, $\mu _{1}^{a} = \mu _{1}^{b} /10$ and $\mu _{1}^{b} =\frac{10}{11}2{\tilde{\mu }}_{\mathrm{eff}1} {\bar{\varphi }}_{1}$.

3.4.4 Results

Results of wind analyses are reported in Tables 2 and 3, respectively, for the along-wind and across-wind components; 6 configurations are compared in each Table. The first two configurations correspond to the uncontrolled structure and to the structure controlled via a linear TMD. The remaining four configurations correspond to the four VFP-TMD cases. Various response quantities are used to measure the absorber performance. Denoting by $u_{sN}$ the top storey displacement, by $a_{x}$ the top storey acceleration and by u the TMD horizontal stroke, those quantities include: maximum and rms structural displacement ($u_{sN,\mathrm{max}}$ and $u_{sN,rms})$, maximum and rms structural acceleration ($a_{x,\mathrm{max}}$ and $a_{x,rms})$, maximum and rms TMD stroke ($u_{\mathrm{max}}$, and $u_{rms})$, maximum normalized friction and restrainer forces ($V_{\mathrm {1,max}}/(m^{{*}}g)$ and $F_{\mathrm {1,max}}/(m^{{*}}g))$, and maximum normalized offset angle ($\varphi _{\mathrm {1}N\, }/{\bar{\varphi }}_{1} )$.

Furthermore, for the four VFP-TMD cases, the dissipative loops described by the normalized friction force $V_{\mathrm {1}}/(m^{{*}}g)$ vs the TMD angular displacement $\theta$ are presented in Fig. 13a and 13b, respectively, for the along-wind and the across-wind components.

Table 2 Case study: maximum and rms responses to the along-wind component

Table 3 Case study: maximum and rms responses to the across-wind component

Fig. 13

Case study: friction force vs angular stroke dissipative loops for the four examined VFP-TMD cases, respectively, under: a the along-wind component; b the across-wind component

Fig. 14

Assignment of the integration boundaries in Eqs. (A.11) and (A.12) in the 7 possible cases when $\theta \ge 0$. Left column: conditions on $\theta$ and $\varphi _{\mathrm{im}}$ for each case. Middle column: graphical representation of the 4 (or less) portions of the interface surface. Right column: identification the integration boundaries for $A_{ci}^{a}$ and $A_{ci}^{b}$ ($\psi _{i}^{s}$ and $\psi _{i}^{r}$ defined according to Eqs. (A.13) and (A.14))

3.4.5 Discussion

Previous results can be commented as follows:

• (i) For the uncontrolled structure, the response to the along-wind component is 4$\div$ 5 times smaller than the response to the across-wind component, with the maximum displacement being, respectively, 16 cm (along wind) and 74 cm (across wind). These two load scenarios allow investigating the VFP-TMD performance under two significantly different input levels.

• (ii) The linear TMD appears quite effective, particularly for the across-wind component (which induces larger dynamic amplifications). The max and rms structural response (in both displacement and acceleration) drops to 70% and 63% under the along-wind load and to 48% and 44% under the across-wind load. The maximum TMD displacement is 19 cm under the along-wind component and 99 cm under the across-wind component.

• (iii) The VFP-TMD designed according to cases 1 and 2 achieves nearly the same performance as the linear TMD, under both wind components, with even a reduction in the TMD displacement. In case 1, such good performance occurs despite the activation of the restrainer under the across-wind load. In case 2, the larger friction ratio naturally reduces the TMD strokes and avoids bumping, slightly outperforming case 1. The similarity of cases 1 and 2 shows the VFP-TMD robustness to variations in its friction ratio.

• (iv) The VFP-TMD designed according to case 3 proves less effective, with a significant increase in structural displacements and, even more, accelerations. This is the drawback of doubling the friction ratio. The advantage is the reduction in the TMD stroke, which decreases by 44% with respect to the linear TMD.

• (v) The VFP-TMD described by case 4 resents the presence of friction in the inner region ($\mu _{1}^{a} > 0$), which diminishes control under low excitation levels. Compared to case 2, the TMD effectiveness diminishes against the less severe along-wind load, but keeps substantially unchanged against the across-wind load, also showing similar strokes. This proves that, even removing the zero friction assumption, still the VFP-TMD can achieve a satisfactory performance provided that $\mu _{1}^{a}$ is sufficiently smaller than $\mu _{1}^{b}$.

• (vi) The last three columns of Tables 2 and 3 indicate that only in one case the restrainer is activated and that relatively small friction forces are applied on the sliding surfaces. The normal contact force is generally quite centered on the sliding interface, except for case 1 under the across-wind load, when the maximum offset angle $\varphi _{1N}$ equals 0.4${\bar{\varphi }}_{1}$, in which case $\varphi _{\mathrm{im}} = 87.0^\circ$ (partial decompression of the sliding interface).

• (vii) Figures 13a and 13b compare the dissipative loops of the four VFP-TMD cases. Figure 13a shows a nearly linear increase of $V_{\mathrm {1}}$ with $\theta$, because of the small angular displacements occurring during along-wind load. In cases 1 to 3, the linear trend is also proportional (in fact homogeneous), and the loops pass through the origin with a slope dictated by $\mu _{1}^{b}$. In case 4, the linear trend is no longer proportional, and the loops intersect the vertical axis at $V_{\mathrm {1,}max}/(m^{{*}}g) = \pm \mu _{1}^{a}$. Figure 13b shows the curved loops typical of large angular displacements, with the vertical intersect of case 4 appearing less significant.

4 Conclusions

The VFP-TMD is presented in this paper, consisting of a mass supported on sliding pendulum bearings, in which each sliding surface is divided into two concentric regions: an inner circular region, having the lowest possible friction coefficient and the dimensions of the slider, and an outer annular region, with a friction coefficient set to an optimal value. To assess the VFP-TMD performance, its model is derived, a design methodology is established, and simulations are performed, comparing it with classical TMD types.

The main conclusions can be summarized as follows:

• 1. The proposed analytical model improves conventional models of sliding friction pendulums, and particularly existing models of VFP isolators, by considering (i) the spherical geometry of the problem, (ii) the effects of geometric nonlinearities, and (iii) the dependence of the friction force vector on the distributions of contact pressures along the sliding interface. From the rigorous general model, several simplified models are derived which can be useful in specific situations.

• 2. The proposed design methodology proves simple and effective. Fundamental design parameters are the slider angular width, ${\bar{\varphi }}_{1}$, and the restrainer activation angle, $\theta _{F\mathrm {1}}$, which governs: (i) bearing dimensions (i.e., cost); (ii) TMD displacement capacity (i.e., efficiency); (iii) slider aspect ratio (i.e., susceptibility to overturning). Other main design parameters are obviously the friction coefficients of the two regions, which should be kept as different as possible.

• 3. Numerical simulations have shown the influence of design parameters on VFP-TMD behavior in different design scenarios. In the ideal case of a frictionless inner region ($\mu _{1}^{a} = 0$), the VFP-TMD is substantially equivalent to a linear TMD, provided that no collision with the restrainer occurs; otherwise, a control loss is observed, whose mode and extent depend on ${\bar{\varphi }}_{1}$ (gradual loss with fully compressed interface at low ${\bar{\varphi }}_{1}$, sudden loss with incipient slider upheaval at large ${\bar{\varphi }}_{1} )$. In the realistic case that $0< \mu _{1}^{a}<< \mu _{1}^{b}$, the effectiveness slightly decreases at small excitation levels but remains nearly optimal at large levels.

• 4. In all examined cases, the VFP-TMD achieves nearly the same effectiveness of viscous P-TMDs, while considerably outperforming conventional uniform-friction P-TMDs.

Appendices

Appendix A—Evaluation of the $B_i$ functions in Eqs. (9) and (10)

The functions $B_{\mathrm {1}}$ and $B_{\mathrm {2}}$ introduced in Eqs. (9) and (10) are defined, respectively, as

$$\begin{aligned} B_{1} ({\bar{\varphi }}_{i} ,\varphi _{\mathrm{im}} )= & {} \frac{1}{R_{i}^{2} }\left[ {\cos \varphi _{\mathrm{im}} \int \limits _{A_{ci} } {\cos ^{2}\varphi _{i} \cos ^{2}\psi _{i} dA_{i} +\sin \varphi _{\mathrm{im}} \int \limits _{A_{ci} } {\sin \varphi _{i} \cos \varphi _{i} \cos ^{2}\psi _{i} dA_{i} } } } \right] \nonumber \\= & {} \cos \varphi _{\mathrm{im}} \int \limits _{A_{ci} } {\cos ^{2}\varphi _{i} \cos ^{2}\psi _{i} d\varphi _{i} d\psi _{i} +\sin \varphi _{\mathrm{im}} \int \limits _{A_{ci} } {\sin \varphi _{i} \cos \varphi _{i} \cos ^{2}\psi _{i} d\varphi _{i} d\psi _{i} } } \nonumber \\= & {} \cos \varphi _{\mathrm{im}} B_{11} ({\bar{\varphi }}_{i} ,\varphi _{\mathrm{im}} )+\sin \varphi _{\mathrm{im}} B_{12} ({\bar{\varphi }}_{i} ,\varphi _{\mathrm{im}} ) \end{aligned}$$

(A.1)

and as

$$\begin{aligned} \begin{aligned}{l} B_{2} ({\bar{\varphi }}_{i} ,\varphi _{\mathrm{im}} )&=\frac{1}{R_{i}^{2} }\left[ {\cos \varphi _{\mathrm{im}} \int \limits _{A_{ci} } {\sin \varphi _{i} \cos \varphi _{i} \cos ^{2}\psi _{i} dA_{i} +\sin \varphi _{\mathrm{im}} \int \limits _{A_{ci} } {\sin ^{2}\varphi _{i} \cos ^{2}\psi _{i} dA_{i} } } } \right] \\&=\cos \varphi _{\mathrm{im}} \int \limits _{A_{ci} } {\sin \varphi _{i} \cos \varphi _{i} \cos ^{2}\psi _{i} d\varphi _{i} d\psi _{i} +\sin \varphi _{\mathrm{im}} \int \limits _{A_{ci} } {\sin ^{2}\varphi _{i} \cos ^{2}\psi _{i} d\varphi _{i} d\psi _{i} } } \\&=\cos \varphi _{\mathrm{im}} B_{12} ({\bar{\varphi }}_{i} ,\varphi _{\mathrm{im}} )+\sin \varphi _{\mathrm{im}} B_{22} ({\bar{\varphi }}_{i} ,\varphi _{\mathrm{im}} ) \\ \end{aligned} \end{aligned}$$

(A.2)

where $B_{\mathrm {11}}$, $B_{\mathrm {12}}$ and $B_{\mathrm {22}}$ are given as follows:

$$\begin{aligned} B_{11} ({\bar{\varphi }}_{i} ,\varphi _{\mathrm{im}} )= & {} \int \limits _{A_{ci} } {\cos ^{2}\varphi _{i} \cos ^{2}\psi _{i} d\varphi _{i} d\psi _{i} } =\int \limits _{\max (-{\bar{\varphi }}_{i} ;\varphi _{\mathrm{im}} -\pi /2)}^{\min ({\bar{\varphi }}_{i} ;\varphi _{\mathrm{im}} +\pi /2)} {\cos ^{2}\varphi _{i} \left( {2\int \limits _0^{\psi _{i}^{s} } {\cos ^{2}\psi _{i} d\psi _{i} } } \right) d\varphi _{i} } \nonumber \\= & {} \int \limits _{\max (-{\bar{\varphi }}_{i} ;\varphi _{\mathrm{im}} -\pi /2)}^{\min ({\bar{\varphi }}_{i} ;\varphi _{\mathrm{im}} +\pi /2)} {\cos ^{2}\varphi _{i} \left[ {\cos \psi _{i} \sin \psi _{i} +\psi _{i} } \right] _{0}^{\psi _{i}^{s} } d\varphi _{i} } \nonumber \\= & {} \int \limits _{\max (-{\bar{\varphi }}_{i} ;\varphi _{\mathrm{im}} -\pi /2)}^{\min ({\bar{\varphi }}_{i} ;\varphi _{\mathrm{im}} +\pi /2)} {\cos ^{2}\varphi _{i} (\cos \psi _{i}^{s} \sin \psi _{i}^{s} +\psi _{i}^{s} )d\varphi _{i} }, \end{aligned}$$

(A.3)

$$\begin{aligned} B_{12} ({\bar{\varphi }}_{i} ,\varphi _{\mathrm{im}} )= & {} \int \limits _{A_{ci} } {\sin \varphi _{i} \cos \varphi _{i} \cos ^{2}\psi _{i} d\varphi _{i} d\psi _{i} }\nonumber \\= & {} \int \limits _{\max (-{\bar{\varphi }}_{i} ;\varphi _{\mathrm{im}} -\pi /2)}^{\min ({\bar{\varphi }}_{i} ;\varphi _{\mathrm{im}} +\pi /2)} {\sin \varphi _{i} \cos \varphi _{i} (\cos \psi _{i}^{s} \sin \psi _{i}^{s} +\psi _{i}^{s} )d\varphi _{i} }, \end{aligned}$$

(A.4)

$$\begin{aligned} B_{22} ({\bar{\varphi }}_{i} ,\varphi _{\mathrm{im}} )= & {} \int \limits _{A_{ci} } {\sin ^{2}\varphi _{i} \cos ^{2}\psi _{i} d\varphi _{i} d\psi _{i} } =\int \limits _{\max (-{\bar{\varphi }}_{i} ;\varphi _{\mathrm{im}} -\pi /2)}^{\min ({\bar{\varphi }}_{i} ;\varphi _{\mathrm{im}} +\pi /2)} {\sin ^{2}\varphi _{i} (\cos \psi _{i}^{s} \sin \psi _{i}^{s} +\psi _{i}^{s} )d\varphi _{i} }. \end{aligned}$$

(A.5)

In Eqs. (A.3) to (A.5), the integration boundaries are chosen to delimit the compressed interface $A_{ci}$. The relation $\psi _{i}^{s} =\arccos \left( {\cos {\bar{\varphi }}_{i} /\cos \varphi _{i} } \right)$ expresses the $\psi _{i}$ coordinate of the contour of $A_{ci}$ as a function of its $\varphi _{i}$ coordinate and of the geometric parameter ${\bar{\varphi }}_{i}$.

Appendix B—Evaluation of the integrals in Eqs. (17.1), (17.2) to (19.1), (19.2), (19.3)

This Appendix presents a procedure for evaluating the integrals in Eqs. (12) to (14) as functions of the constant parameters $R_{i}$, $\bar{\varphi }_i$, $\mu ^a_i$, $\mu ^b_i$ and of the variables $\theta$, $\sigma _{\mathrm{im}}$, and $\varphi _{\mathrm{im}}$. The procedure is partly analytical and partly numerical. Using Eqs. (1) and (8), the three said integrals can be expressed as follows:

$$\begin{aligned} \int \limits _{A_{i} } {\cos \varphi _{i} dV_{i} }= & {} \sigma _{\mathrm{im}} \int \limits _{A_{ic} } {\mu _{i} \cos \varphi _{i} } \cos \psi _{i} \cos (\varphi _{i} -\varphi _{\mathrm{im}} )dA_{i} =\sigma _{\mathrm{im}} R_{i}^{2} \left[ {\cos \varphi _{\mathrm{im}} E_{11} +\sin \varphi _{\mathrm{im}} E_{12} } \right] , \end{aligned}$$

(B.1)

$$\begin{aligned} \int \limits _{A_{i} } {\sin \varphi _{i} dV_{i} }= & {} \sigma _{\mathrm{im}} \int \limits _{A_{ic} } {\mu _{i} \sin \varphi _{i} } \cos \psi _{i} \cos (\varphi _{i} -\varphi _{\mathrm{im}} )dA_{i} =\sigma _{\mathrm{im}} R_{i}^{2} \left[ {\cos \varphi _{\mathrm{im}} E_{12} +\sin \varphi _{\mathrm{im}} E_{22} } \right] , \end{aligned}$$

(B.2)

$$\begin{aligned} \int \limits _{A_{i} } {\cos \psi _{i} dV_{i} }= & {} \sigma _{\mathrm{im}} \int \limits _{A_{ic} } {\mu _{i} } \cos ^{2}\psi _{i} \cos (\varphi _{i} -\varphi _{\mathrm{im}} )dA_{i} =\sigma _{\mathrm{im}} R_{i}^{2} \left[ {\cos \varphi _{\mathrm{im}} E_{31} +\sin \varphi _{\mathrm{im}} E_{32} } \right] \end{aligned}$$

(B.3)

where

$$\begin{aligned} E_{11}= & {} E_{11} ({\bar{\varphi }}_{i} ,\mu _{i}^{a} ,\mu _{i}^{b} ,\varphi _{\mathrm{im}} ,\theta )=\int \limits _{A_{ic} } {\mu _{i} \cos ^{2}\varphi _{i} } \cos \psi _{i} d\varphi _{i} d\psi _{i}, \end{aligned}$$

(B.4)

$$\begin{aligned} E_{12}= & {} E_{12} ({\bar{\varphi }}_{i} ,\mu _{i}^{a} ,\mu _{i}^{b} ,\varphi _{\mathrm{im}} ,\theta )=\int \limits _{A_{ic} } {\mu _{i} \sin \varphi _{i} \cos \varphi _{i} } \cos \psi _{i} d\varphi _{i} d\psi _{i}, \end{aligned}$$

(B.5)

$$\begin{aligned} E_{22}= & {} E_{22} ({\bar{\varphi }}_{i} ,\mu _{i}^{a} ,\mu _{i}^{b} ,\varphi _{\mathrm{im}} ,\theta )=\int \limits _{A_{ic} } {\mu _{i} \sin ^{2}\varphi _{i} } \cos \psi _{i} d\varphi _{i} d\psi _{i}, \end{aligned}$$

(B.6)

$$\begin{aligned} E_{31}= & {} E_{31} ({\bar{\varphi }}_{i} ,\mu _{i}^{a} ,\mu _{i}^{b} ,\varphi _{\mathrm{im}} ,\theta )=\int \limits _{A_{ic} } {\mu _{i} \cos \varphi _{i} } \cos ^{2}\psi _{i} d\varphi _{i} d\psi _{i}, \end{aligned}$$

(B.7)

$$\begin{aligned} E_{32}= & {} E_{32} ({\bar{\varphi }}_{i} ,\mu _{i}^{a} ,\mu _{i}^{b} ,\varphi _{\mathrm{im}} ,\theta )=\int \limits _{A_{ic} } {\mu _{i} \sin \varphi _{i} } \cos ^{2}\psi _{i} d\varphi _{i} d\psi _{i}. \end{aligned}$$

(B.8)

If $\mu _{i}$ were uniform on $A_{ic}$, the integrals in Eqs. (B.4) to (B.8) would be similar to those in Eqs. (A.3) to (A.5). Instead, $\mu _{i}$ varies with $\bar{\varphi }_i$, $\theta$, $\varphi _{i}$, and $\psi _{i}$ as a step-wise function, according to Eq. (15). Consequently, the integration can still be performed similarly as in Eqs. (A.3) to (A.5), once the integration boundaries are properly redefined.

To this purpose, Eqs. (B.4) to (B.6) can be jointly expressed as

$$\begin{aligned} E_{jk} =\mu _{i}^{a} \int \limits _{A_{ic}^{a} } {f_{jk} (\varphi _{i} )} \cos \psi _{i} d\varphi _{i} d\psi _{i} +\mu _{i}^{b} \int \limits _{A_{ic}^{b} } {f_{jk} (\varphi _{i} )} \cos \psi _{i} d\varphi _{i} d\psi _{i} \end{aligned}$$

(B.9)

while Eqs. (B.7) and (B.8) as

$$\begin{aligned} E_{jk} =\mu _{i}^{a} \int \limits _{A_{ic}^{a} } {f_{jk} (\varphi _{i} )} \cos ^{2}\psi _{i} d\varphi _{i} d\psi _{i} +\mu _{i}^{b} \int \limits _{A_{ic}^{b} } {f_{jk} (\varphi _{i} )} \cos ^{2}\psi _{i} d\varphi _{i} d\psi _{i} \end{aligned}$$

(B.10)

where $f_{jk} (\varphi _{i} )$ are the various trigonometric functions of $\varphi _{i}$ appearing in Eqs. (B.4) to (B.8) and $A_{ci}^{a}$ and $A_{ci}^{b}$ are the portions of the compressed part of the $i^{th}$ interface, respectively, belonging to regions “a” and “b.”

The first integral in Eq. (B.9) can be expressed as

$$\begin{aligned}&\int \limits _{A_{ic}^{a} } {f_{jk} (\varphi _{i} )} \cos \psi _{i} d\varphi _{i} d\psi _{i} =\int \limits _{\varphi _{i}^{a-} }^{\varphi _{i}^{a+} } {f_{jk} (\varphi _{i} )} \left( {2\int \limits _{\psi _{i}^{a-} }^{\psi _{i}^{a+} } {\cos \psi _{i} d\psi _{i} } } \right) d\varphi _{i}\nonumber \\&\quad =2\int \limits _{\varphi _{i}^{a-} }^{\varphi _{i}^{a+} } {f_{jk} (\varphi _{i} )(\sin \psi _{i}^{a+} -\sin \psi _{i}^{a-} )} d\varphi _{i} \end{aligned}$$

(B.11)

where $\varphi _{i}^{a-}$, $\varphi _{i}^{a+}$, $\psi _{i}^{a-} =\psi _{i}^{a-} (\varphi _{i} )$ and $\psi _{i}^{a+} =\psi _{i}^{a+} (\varphi _{i} )$ denote the integration boundaries of the one half of $A_{ci}^{a}$, characterized by $\psi _{i} \ge$ 0 (hence the factor “2” in the right-hand side term).

With identical notation, the first integral in Eq. (B.10) can be expressed as

$$\begin{aligned} \int \limits _{A_{ic}^{a} } {f_{jk} (\varphi _{i} )} \cos ^{2}\psi _{i} d\varphi _{i} d\psi _{i}= & {} \int \limits _{\varphi _{i}^{a-} }^{\varphi _{i}^{a+} } {f_{jk} (\varphi _{i} )} \left( {2\int \limits _{\psi _{i}^{a-} }^{\psi _{i}^{a+} } {\cos ^{2}\psi _{i} d\psi _{i} } } \right) d\varphi _{i} \nonumber \\= & {} \int \limits _{\varphi _{i}^{a-} }^{\varphi _{i}^{a+} } {f_{jk} (\varphi _{i} )(\cos \psi _{i}^{a+} \sin \psi _{i}^{a+} +\psi _{i}^{a+} -\cos \psi _{i}^{a-} \sin \psi _{i}^{a-} -\psi _{i}^{a-} )} d\varphi _{i}.\nonumber \\ \end{aligned}$$

(B.12)

The second integrals in Eqs. (B.10) and (B.11) can be expressed similarly, with only the “b” superscript replacing the “a” superscript.

Once the integration boundaries are appropriately identified, the integrals in Eqs. (B.11) and (B.12) can be computed numerically, because their integrands are functions of the single variable $\varphi _{i}$. This determines first the functions $E_{jk}$ in Eqs. (B.4) to (B.8) and ultimately the integrals in Eqs. (B.1) to (B.3).

Therefore, the crucial point is now to correctly identify the integration boundaries for both $A_{ci}^{a}$ and $A_{ci}^{b}$.

To this purpose, it should be observed that in general the interface is delimited and subsequently parted (in four or less portions), by three or less characteristic lines. The four portions are regions “a” and “b,” each further divided into a “compressed” portion and a “decompressed” portion. The three lines are, respectively, the contour of the slider given by

$$\begin{aligned} \psi _{i} =\psi _{i}^{s} =\arccos \left( {\cos {\bar{\varphi }}_{i} /\cos \varphi _{i} } \right) , \end{aligned}$$

(B.13)

the contour of the inner region given by

$$\begin{aligned} \psi _{i} =\psi _{i}^{r} =\arccos [\cos {\bar{\varphi }}_{i} /(\cos \varphi _{i} \cos \theta -\sin \varphi _{i} \sin \theta )], \end{aligned}$$

(B.14)

and the neutral axis given by

$$\begin{aligned} \varphi _{i} =\varphi _{\mathrm{im}} -\mathrm{sgn}\,(\varphi _{\mathrm{im}} )\cdot \pi /2. \end{aligned}$$

(B.15)

Depending on how the three lines mutually intersect to generate the four or less portions of the interface, the integration boundaries take different values. Figure 14 shows the 7 possible cases corresponding to $\theta \ge$ 0 (the cases corresponding to $\theta < 0$ are similar and omitted for brevity). The first 6 cases refer to $0 \le \theta \le 2{\bar{\varphi }}_{i}$ (corresponding to the slider intersecting the inner region), and are ordered for increasing values of $\varphi _{\mathrm{im}}$. The $7{\mathrm {th}}$ case refers to $\theta > 2{\bar{\varphi }}_{i}$ (corresponding to the slider being entirely comprised into the outer region). Each subfigure schematically represents the inner region “a” in white color, the outer region “b” in gray color, the slider contour and the neutral axis in red lines, the compressed interface in red hatching. For brevity, only half the space is represented, corresponding to $\psi _{i} \ge 0$, coherently with the integration boundaries defined in Eqs. (B.11) and (B.12). Beside each subfigure, the corresponding integration boundaries for $A_{ci}^{a}$ and $A_{ci}^{b}$ are reported, expressed in terms of $\varphi _{i}$ and $\psi _{i}$.

With the integration boundaries of Fig. 14, all terms in Eq. (B.11) and (B.12) are known, so the respective integrals can be numerically evaluated by appropriately discretizing the $\varphi _{i}$ axis, therefore providing the first terms of Eqs. (B.9) and (B.10), referring to $A_{ci}^{a}$. The second terms of Eqs. (B.9) and (B.10), referring to $A_{ci}^{b}$, are obtained in the same way. The three integrals in Eqs. (B.1) to (B.3) are finally obtained by applying Eqs. (B.1) to (B.8).