1 Introduction

Tramway networks usually comprise different variants of track superstructures, depending on the particular requirements concerning noise and vibration mitigation; see, e.g., [1] for a respective overview which is particularly relevant for the Viennese tramway network. While those variants differ from each other in terms of the types and thicknesses of the layers building up together the track superstructure, all of them have in common an elastic layer on which the tramway rails rest. Together with the subjacent structure, this elastic layer constitutes an elastic foundation supporting the tramway rail. Unarguably, the compliance of this layered foundation influences the mechanical behavior of the rails decisively. As a matter of fact, maintenance and repair works performed on tramway rail tracks sometimes involve the replacement of whole rail sections. Such activities are likely to cause discontinuities in the elastic foundation, given that the involved materials degrade and, even more, may have partly changed entirely over the past decades. Investigating the potential effects such discontinuities may have on the elastic deformations and stresses tramway rails experience in response to practically relevant mechanical loading was the main objective of the work presented in this paper.

Understanding and predicting the effects of elastic foundations on thereon resting structures, in terms of displacements and stresses arising in response to mechanical loading, has been a long-pursued goal of the theoretical and applied mechanics community. Many consider Winkler as founding father of the field; he assumed that the deflection of an elastically founded structure is linearly related to the forces acting upon this structure via a foundation modulus [2]. In mathematical terms, the classical Winkler foundation reads as \(p=k\cdot w\), where p and w denote the pressure and the vertical displacement distributed across the foundation surface, and k denotes the material-specific foundation modulus [3]. Later, aiming for a more realistic consideration of the interactions between mechanically loaded structures and elastic foundations, the Winkler foundation was extended by additional terms, resulting in much-noticed works published by some of the most famous mechanicians active in the twentieth century, including Biot [4], Filonenko-Borodič [5], Hetényi [6], Vlasov [7], Reissner [8], or Pasternak [9]; see also the article by Kerr [3] for a comprehensive review on the subject. More recent approaches focused on refined model assumptions and consideration of additional characteristics and loading modes, including, e.g., improved consideration of boundary conditions [10], viscoelastic foundations [11], dynamic effects of moving loads [12], and torsional vibration and buckling [13,14,15]. Due to the ever-growing relevance of computational mechanics from the 1970s onwards, numerical solution strategies have found their way into the field of elastic foundations [16, 17], allowing for solution of the governing mathematical framework while investigating (more) complicated structural settings. As concerns rails, several studies have been published dealing with Vignole rails [18,19,20,21,22,23,24,25], whereas models related to tramway operation appear to be limited to investigations concerning the ground-borne noise and vibrations [26, 27]. Nevertheless, despite the considerable degree of sophistication that has been reached by now, it seems that the mechanism of restrained torsion, which affects tramway rails in a potentially substantial manner, has been disregarded so far.

In this work, we took a new path towards consideration of elastically supported beams in general, and of tramway rails in particular, tying in with the approach recently published by the present paper’s authors [28], where virtual kinematics were introduced reflecting stretching, bending, as well as primary and secondary warping deformations of a beam, and through rigorous application of the principle of virtual power [29] respective equilibrium equations and natural boundary conditions could be derived, including higher-order torsion-related force quantities. Eventually, this mathematical framework was utilized for computing displacement quantities along the longitudinal axis of the beam, and corresponding stress distributions in selected cross sections, both by means of the Finite Element method, see also [30] for further details. In order to extend this approach, elastic foundation-related traction force vectors are introduced, leading to respective extensions in the model-governing equations, see Sect. 2. Their numerical solution, based on sequentially performed one- and two-dimensional Finite Element analyses, is presented in Sect. 3. Based on numerical examples, presented in Sect. 4, the potentials and features of the new modeling approach presented in this paper are discussed in Sect. 5, containing also concluding remarks.

2 Modeling concept

2.1 A brief introduction to the principle of virtual power

The principle of virtual power (PVP) [29, 31,32,33,34] was chosen to be the fundamental theoretical vehicle of the subsequently presented work. In general format, the PVP reads as

$$\begin{aligned} {\mathcal {P}}^\text {int}+{\mathcal {P}}^\text {ext}= 0, \end{aligned}$$
(1)

where \({\mathcal {P}}^\text {int}\) is the virtual power performed by internal forces, and \({\mathcal {P}}^\text {ext}\) is the virtual power performed by external forces. Considering a three-dimensional (3D) continuum, \({\mathcal {P}}^\text {int}\) and \({\mathcal {P}}^\text {ext}\) are defined as follows:

$$\begin{aligned} {\mathcal {P}}^\text {int} = - \int _V \varvec{\sigma }({\mathbf {x}}): \hat{\mathbf{d}}({\mathbf {x}})\; \text {d}V, \end{aligned}$$
(2)

and

$$\begin{aligned} {\mathcal {P}}^\text {ext}= \int _V\mathbf{f}({\mathbf {x}})\cdot \hat{\mathbf {v}}({\mathbf {x}})\; \text {d}V + \int _S\mathbf{T}({\mathbf {x}},\mathbf{n})\cdot \hat{\mathbf {v}}({\mathbf {x}})\,\text {d}S. \end{aligned}$$
(3)

In Eqs. (2) and (3), \({\mathbf {x}}\) denotes the location vector of points throughout the continuum with volume V and surface \(S, \hat{\mathbf {v}}(\mathbf {x})\) denotes an arbitrary continuous virtual velocity field, \(\hat{\mathbf{d}}(\mathbf {x})=\nabla ^S\,\hat{\mathbf {v}}(\mathbf {x})\) denotes the virtual Eulerian strain rate tensor, \(\mathbf{f}(\mathbf {x})\) and \(\mathbf{T}(\mathbf {x},\mathbf{n})\) denote the volume and surface forces, and \(\varvec{\sigma }(\mathbf {x})\) denotes the Cauchy stress tensor. Thereby, the PVP is only confined in terms of the assumption that \(\hat{\mathbf {v}}(\mathbf {x})\) is related to geometrically compatible virtual displacements via \(\hat{\mathbf {v}}(\mathbf {x})=\dot{\hat{\mathbf{u}}}(\mathbf {x})=\partial \hat{\mathbf{u}}(\mathbf {x})/\partial t, t\) being the time variable.

2.2 Model representation of tramway rails

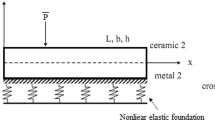
First, we stipulate that, on the one hand, the length of the beam under investigation (which is considered to be straight and of prismatic shape) is much larger than its cross-sectional dimensions, and that on the other hand, cross sections which are plain and oriented perpendicular to the beam axis in the (undeformed) reference configuration, remain, also after the application of mechanical loads, plain and oriented perpendicular to the (then deformed) beam axis—or, in other words, that the classical assumptions of a Bernoulli beam are fulfilled [35,36,37]. In order to apply the PVP, as introduced in Sect. 2.1, a virtual velocity field \(\hat{\mathbf {v}}({\mathbf {x}})\), which represents this beam reasonably well under the expected loading conditions, needs to be defined. This field is defined through components \(\hat{v}_x({\mathbf {x}}), \hat{v}_y({\mathbf {x}})\), and \(\hat{v}_z({\mathbf {x}})\), with respect to an orthonormal base frame spanned by vectors \(\mathbf{e}_x, \mathbf{e}_y\), and \(\mathbf{e}_z\), hence \({\mathbf {x}}=x\,\mathbf{e}_x +y\, \mathbf{e}_y +z\,\mathbf{e}_z \), whereby x is the coordinate in direction of the beam axis, and coordinates y and z are measured from the geometrical center (abbreviated as GC) of the cross section; hence \(\hat{\mathbf {v}}({\mathbf {x}})=\hat{v}_x({\mathbf {x}})\,\mathbf{e}_x + \hat{v}_y({\mathbf {x}})\,\mathbf{e}_y+\hat{v}_z({\mathbf {x}})\,\mathbf{e}_z\). Figure 1 shows a schematic illustration of such a beam.

Fig. 1
figure 1

External forces acting on a prismatic beam undergoing stretching, bending, shear, and torsional deformations, namely 3D continuum-specific traction vectors acting onto the lateral surface, \(\mathbf {T}(\mathbf {x},\mathbf {n}=\mathbf {n}_C)=\sum _i T_i(\mathbf {x},\mathbf {n}=\mathbf {n}_C)\cdot \mathbf {e}_i\), traction vectors acting onto the cross-sectional surfaces, \(\mathbf {T}(\mathbf {x},\mathbf {n}=\mathbf {e}_x)=\sum _i T_i(\mathbf {x},\mathbf {n}=\mathbf {e}_x)\cdot \mathbf {e}_i\) and \(\mathbf {T}(\mathbf {x},\mathbf {n}=-\mathbf {e}_x)=\sum _i T_i(\mathbf {x},\mathbf {n}=-\mathbf {e}_x)\cdot \mathbf {e}_i\), volume force vectors acting throughout the entire volume, \(\mathbf {f}(\mathbf {x})=\sum _i f_i(\mathbf {x})\cdot \mathbf {e}_i\), as well as elastic foundation-related traction force vectors acting onto the bottom surface, \(\mathbf {T}^\text {EF}(\mathbf {x},\mathbf {n}=\mathbf {n}_{C_\text {bottom}})=T_z^\text {EF}(\mathbf {x},\mathbf {n}=\mathbf {n}_{C_\text {bottom}})\cdot \mathbf {e}_z\). Note that the depicted beam is, for simplicity, of rectangular cross-sectional shape (implying \(\text {GC}=\text {CT}\)), while the model is not limited to any particular kind of cross-sectional shape

Full size image

In line with Sapountzakis [38], who presented a displacement field representative for torsion-compliant beams, we consider the virtual velocity field introduced in [28], namely

$$\begin{aligned}&\displaystyle \hat{v}_x(\mathbf {x}) = \hat{v}^\text {GC}_x(x)-\frac{ \text {d}\hat{v}_y^\text {GC}(x)}{\text {d}x}\cdot y- \frac{\text {d}\hat{v}_z^\text {GC}(x)}{\text {d}x} \cdot z+\frac{\text {d} \hat{\omega }_x(x)}{\text {d} x} \cdot \psi _\text {I}(y,z) +\frac{\text {d}^3 \hat{\omega }_x(x)}{\text {d} x^3}\cdot \psi _\text {II}(y,z), \end{aligned}$$
(4)
$$\begin{aligned}&\displaystyle \hat{v}_y(\mathbf {x})= \hat{v}^\text {GC}_y(x)- \hat{\omega }_x(x) \cdot \big (z-z_{\text {CT}}\big ), \end{aligned}$$
(5)

and

$$\begin{aligned} \hat{v}_z(\mathbf {x}) = \hat{v}^\text {GC}_z(x) + \hat{\omega }_x(x) \cdot \big (y-y_{\text {CT}}\big ), \end{aligned}$$
(6)

where \(\hat{v}^\text {GC}_x(x), \hat{v}^\text {GC}_y(x)\), and \(\hat{v}^\text {GC}_z(x)\) represent the virtual velocities of the geometrical center of the cross section (at the longitudinal coordinate x), while \(\hat{\omega }_x(x)\) stands for the angular virtual velocity with respect to the twist axis, which is the axis parallel to the beam axis passing through the center of twist (abbreviated as CT), being offset from the geometrical center by \(y_\text {CT}\) and \(z_\text {CT}\); determination of \(y_\text {CT}\) and \(z_\text {CT}\) has been demonstrated in [28]. Furthermore, \(\psi _\text {I}(y,z)\) denotes the primary warping function describing the contribution of non-restrained, Saint-Venant-type torsion, whereas \(\psi _\text {II}(y,z)\) denotes the secondary warping function, describing the effect of warping torsion. The related components of the virtual Eulerian strain rate tensor follow straightforwardly from the virtual velocity field defined by Eqs. (4)–(6), reading as follows:

$$\begin{aligned} \hat{d}_{xx}(\mathbf {x})= & {} \frac{\text {d}\hat{v}_x(\mathbf {x})}{\text {d}x}= \frac{\text {d} \hat{v}^\text {GC}_x(x)}{\text {d}x} - \frac{\text {d}^2\hat{v}_y^\text {GC}(x)}{\text {d}x^2}\cdot y- \frac{\text {d}^2\hat{v}_z^\text {GC}(x)}{\text {d}x^2}\cdot z\nonumber \\&+ \frac{\text {d}^2 \hat{\omega }_x(x)}{\text {d} x^2} \cdot \psi _\text {I}(y,z) +\frac{\text {d}^4 \hat{\omega }_x(x)}{\text {d} x^4}\cdot \psi _\text {II}(y,z), \end{aligned}$$
(7)
$$\begin{aligned} \hat{d}_{xy}(\mathbf {x})= & {} \frac{1}{2}\cdot \left[ \frac{\text {d}\hat{v}_x(\mathbf {x})}{\text {d}y}+\frac{\text {d}\hat{v}_y(\mathbf {x})}{\text {d}x}\right] = \frac{1}{2}\cdot \left\{ \frac{\text {d} \hat{\omega }_x(x)}{\text {d} x}\cdot \left[ \frac{\partial \psi _\text {I}(y,z)}{\partial y}-(z-z_{\text {CT}})\right] \right. \nonumber \\&+\left. \frac{\text {d}^3 \hat{\omega }_x(x)}{\text {d} x^3}\cdot \frac{\partial \psi _\text {II}(y,z)}{\partial y}\right\} , \end{aligned}$$
(8)

and

$$\begin{aligned} \hat{d}_{xz}(\mathbf {x})= & {} \frac{1}{2}\cdot \left[ \frac{\text {d}\hat{v}_x(\mathbf {x})}{\text {d}z}+\frac{\text {d}\hat{v}_z(\mathbf {x})}{\text {d}x} \right] = \frac{1}{2}\cdot \left\{ \frac{\text {d}\hat{\omega }_x(x)}{\text {d}x}\cdot \left[ \frac{\partial \psi _\text {I}(y,z)}{\partial z}+(y-y_{\text {CT}})\right] \right. \nonumber \\&+\left. \frac{\text {d}^3\hat{\omega }_x(x)}{\text {d} x^3}\cdot \frac{\partial \psi _\text {II}(y,z)}{\partial z} \right\} . \end{aligned}$$
(9)

Finally, the internal and external forces taken into account in Eqs. (2) and (3) must be defined. If the simplifying assumptions related to a Bernoulli beam are sufficiently fulfilled, the stress tensor components \(\sigma _{xx}(\mathbf {x}), \sigma _{xy}(\mathbf {x})\), and \(\sigma _{xz}(\mathbf {x})\) are considerably larger than the remaining components, i.e. \(\sigma _{yy}(\mathbf {x}), \sigma _{zz}(\mathbf {x})\), and \(\sigma _{yz}(\mathbf {x})\), implying

$$\begin{aligned} \begin{aligned} \varvec{\sigma }({\mathbf {x}})&=\, \left( \begin{array}{ccc} \sigma _{xx}(\mathbf {x}) &{} \sigma _{xy}(\mathbf {x}) &{} \sigma _{xz}(\mathbf {x})\\ \sigma _{yx}(\mathbf {x})=\sigma _{xy}(\mathbf {x}) &{} \approx 0 &{} \approx 0 \\ \sigma _{zx}(\mathbf {x})=\sigma _{xz}(\mathbf {x}) &{} \approx 0 &{} \approx 0 \\ \end{array}\right) \\&=\,\sigma _{xx}(\mathbf {x})\cdot \mathbf{e}_x\otimes \mathbf{e}_x+ \sigma _{xy}(\mathbf {x})\cdot \Big (\mathbf{e}_x\otimes \mathbf{e}_y+\mathbf{e}_y\otimes \mathbf{e}_x\Big )+ \sigma _{xz}(\mathbf {x})\cdot \Big (\mathbf{e}_x\otimes \mathbf{e}_z +\mathbf{e}_z\otimes \mathbf{e}_x\Big ). \end{aligned} \end{aligned}$$
(10)

In Eq. (10), symbol \(\otimes \) denotes the dyadic product. The volume force vector and the general traction force vector, both occurring in Eq. (3), are defined as follows:

$$\begin{aligned} \forall \,\mathbf {x}\text { on }V\text {:}~~~ \mathbf{f}({\mathbf {x}})= f_x({\mathbf {x}})\cdot \mathbf{e}_x + f_y({\mathbf {x}})\cdot \mathbf{e}_y + f_z({\mathbf {x}})\cdot \mathbf{e}_z, \end{aligned}$$
(11)

and

$$\begin{aligned} \forall \,\mathbf {x}\text { on }S\text {:}~~~ \mathbf{T}({\mathbf {x}},\mathbf{n})= T_x({\mathbf {x}},\mathbf{n})\cdot \mathbf{e}_x + T_y({\mathbf {x}},\mathbf{n})\cdot \mathbf{e}_y + T_z({\mathbf {x}},\mathbf{n})\cdot \mathbf{e}_z, \end{aligned}$$
(12)

where \(f_i(\mathbf {x})\) and \(T_i(\mathbf {x},\mathbf{n}), i=x,y,z\), denote the components of \(\mathbf{f}(\mathbf {x})\) and \(\mathbf{T}(\mathbf {x},\mathbf{n})\). Importantly, the definition of the traction force vector includes the unit normal vector at location \({\mathbf {x}}\) on the surface. For example, \(\mathbf{n}=\mathbf{n}_{C}\) indicates the lateral surface of the beam, \(\mathbf{n}=-\mathbf{e}_x\) its starting cross section \(S_0\) at coordinate \(x=x_0\), and \(\mathbf{n}=\mathbf{e}_x\) its end cross section \(S_1\) at coordinate \(x=x_1\), see Fig. 1.

Furthermore, as key novelty of this contribution, the effect of an elastic foundation is considered as well. To that end, one additional, elastic foundation-related traction force vector is taken into account,

$$\begin{aligned} \forall \mathbf {x}\text { on }S_\text {bottom}\text {:}~~~ T_z^\text {EF}(\mathbf {x})= -k_\text {EF}\cdot \left[ u_z^\text {GC}(x)+ \phi _x(x)\cdot \left( y-y_\text {CT}\right) \right] , \end{aligned}$$
(13)

while \(T_x^\text {EF}(\mathbf {x})=T_y^\text {EF}(\mathbf {x})=0\). In Eq. (13), \(S_\text {bottom}\) denotes the bottom surface of the beam on which it rests, \(k_\text {EF}\) denotes the foundation modulus, \(u_z^\text {GC}(x)\) denotes the actual displacement of the geometrical center, and \(\phi _x(x)\) denotes the actual rotation angle with respect to the axis that is parallel to the beam axis and passes through the center of twist. Importantly, depending on how the beam is mounted to the subgrade, an elastic foundation may represent a tensional or tensionless interaction between the structure and the subgrade. The latter case is standardly considered through setting the foundation modulus to zero at all locations where the applied mechanical loading leads to a lift-off of the beam [21, 39, 40]. Owing to the fact that the beam studied in this paper may undergo not only flexural but also torsional deformations, a different approach is pursued in order to take into account a tensionless elastic foundation. Namely, only the sections of the bottom surface of the studied beam (which is actually in contact with the subjacent elastic foundation) are considered for calculation of \(T_z^\text {EF}(\mathbf {x})\), on which the following condition for the overall displacement in z-direction is fulfilled: \(u_z(x,y)=u_z^\text {GC}(x)+\phi _x(x)\cdot (y-y_\text {CT})\ge 0\). More details on the implementation of this condition are provided in Sect. 2.3 of this paper.

2.3 Virtual powers performed by internal and external forces

Considering the virtual Eulerian strain rate tensor according to Eqs. (7)–(9), as well as the stress tensor according to Eq. (10) in Eq. (2) yields

$$\begin{aligned} {\mathcal {P}}^{\text {int}}= & {} -\int _{x_0}^{x_1}\frac{\text {d}\hat{v}^\text {GC}_x (x)}{\text {d}x}\cdot N(x)\,\text {d}x-\int _{x_0}^{x_1}\frac{\text {d}^2 \hat{v}^\text {GC}_y(x)}{\text {d} x^2}\cdot M_z(x)\,\text {d}x\nonumber \\&+ \int _{x_0}^{x_1}\frac{\text {d}^2\hat{v}^\text {GC}_z(x)}{\text {d} x^2}\cdot M_y(x)\,\text {d}x-\int _{x_0}^{x_1}\frac{\text {d}\hat{\omega }_x (x)}{\text {d}x} M_\text {T}(x)\,\text {d}x\nonumber \\&+ \int _{x_0}^{x_1}\frac{\text {d}\hat{\omega }_x (x)}{\text {d}x}\cdot M_{\text {T}}^\psi (x) \,\text {d}x+ \int _{x_0}^{x_1}\frac{\text {d}^2\hat{\omega }_x (x)}{\text {d}x^2}\cdot M^\psi _\text {II}(x)\,\text {d}x\nonumber \\&- \int _{x_0}^{x_1} \frac{\text {d}^3\hat{\omega }_x (x)}{\text {d}x^3}\cdot M^\psi _\text {III}(x)\,\text {d}x - \int _{x_0}^{x_1}\frac{\text {d}^4\hat{\omega }_x(x)}{\text {d}x^4}\cdot M^\psi _\text {IV}(x)\,\text {d}x. \end{aligned}$$
(14)

The terms on the right-hand side of Eq. (14) include a number of stress resultants provoked by the initially defined virtual beam kinematics, namely the axial force, N(x),

$$\begin{aligned} N(x)= \int _A \sigma _{xx}({\mathbf {x}})\,\text {d}A, \end{aligned}$$
(15)

where A is the cross-sectional area; the bending moments with respect to the y-axis, \(M_y(x)\), and with respect to the z-axis, \(M_z(x)\),

$$\begin{aligned} M_j(x) = \int _A \sigma _{xx}({\mathbf {x}})\cdot \beta _j\,\text {d}A, \end{aligned}$$
(16)

with \(j\in \left\{ y,z\right\} \), as well as with \(\beta _j=z\) if \(j=y\) and \(\beta _j=-y\) if \(j=z\); the classical torsional moment \(M_\text {T}(x)\),

$$\begin{aligned} M_\text {T}(x) = \int _A \sigma _{xz}({\mathbf {x}})\cdot \left( y-y_ {\text {CT}}\right) -\sigma _{xy}({\mathbf {x}})\cdot \left( z-z_ {\text {CT}}\right) \,\text {d}A; \end{aligned}$$
(17)

the primary warping-induced torsional moment \(M_\text {T}^\psi (x)\),

$$\begin{aligned} M_\text {T}^\psi (x)= -\int _A \sigma _{xy}(\mathbf {x})\cdot \frac{\partial \psi _\text {I}(y,z)}{\partial y} + \sigma _{xz}(\mathbf {x})\cdot \frac{\partial \psi _\text {I}(y,z)}{\partial z } \,\text {d}A; \end{aligned}$$
(18)

the warping-related bimoment \(M^{\psi }_\text {II}(x)\),

$$\begin{aligned} M^{\psi }_\text {II}(x) = -\int _A \sigma _{xx}({\mathbf {x}})\cdot \psi _{\text {I}} (y,z)\,\text {d}A; \end{aligned}$$
(19)

the warping-related trimoment \(M^{\psi }_\text {III}(x)\),

$$\begin{aligned} M^{\psi }_\text {III}(x)= \int _A \sigma _{xy}({\mathbf {x}})\cdot \frac{\partial \psi _\text {II}(y,z)}{\partial y} + \sigma _{xz}({\mathbf {x}})\cdot \frac{\partial \psi _\text {II}(y,z)}{\partial z} \,\text {d}A; \end{aligned}$$
(20)

and the warping-related fourth-order moment \(M^{\psi }_\text {IV}(x)\),

$$\begin{aligned} M^{\psi }_\text {IV}(x)= \int _A \sigma _{xx}({\mathbf {x}}) \cdot \psi _{\text {II}}(y,z)\,\text {d}A. \end{aligned}$$
(21)

Considering, on the other hand, the virtual velocity field according to Eqs. (4)–(6), the volume and traction force vectors according to Eqs. (11) and (12), and the elastic foundation-related traction force according to Eq. (13) in Eq. (3) yields

$$\begin{aligned} \mathcal{P}^\text {ext}&=\int _{x_0}^{x_1}n(x)\cdot \hat{v}^\text {GC}_x(x)\, \text{ d }x+ N(x)\cdot \hat{v}^\text {GC}_x(x)\,\bigg |_{x_0}^{x_1}+ \int _{x_0}^{x_1}s_y(x)\cdot \hat{v}^\text {GC}_y(x)\,\text{ d }x+ S_y(x)\cdot \hat{v}^\text {GC}_y(x)\,\bigg |_{x_0}^{x_1}\nonumber \\&\quad +\int _{x_0}^{x_1}\bigg [s_z(x)-k(x)\cdot \Delta _1y(x)\Big (u_z^\text {GC}(x)+\phi _x(x)\cdot \Delta _2y(x)\Big ) \bigg ]\cdot \hat{v}^\text {GC}_z(x)\,\text{ d }x +S_z(x)\cdot \hat{v}^\text {GC}_z(x)\,\bigg |_{x_0}^{x_1}\nonumber \\&\quad +\int _{x_0}^{x_1}m_z(x)\cdot \frac{ \text{ d }\hat{v}^\text {GC}_y(x)}{\text{ d }x}\,\text{ d }x+ M_z(x)\cdot \frac{\text{ d }\hat{v}^\text {GC}_y(x)}{\text{ d }x}\,\bigg |_{x_0}^{x_1}-\int _{x_0}^{x_1}m_y(x)\cdot \frac{\text{ d } \hat{v}^\text {GC}_z(x)}{\text{ d }x}\,\text{ d }x-M_y(x)\cdot \frac{\text{ d }\hat{v}^\text {GC}_z(x)}{\text{ d } x}\, \bigg |_{x_0}^{x_1}\nonumber \\&\quad +\int _{x_0}^{x_1}\bigg [m_\text {T}(x)-k(x)\cdot \Delta _1y(x)\cdot \Big (u_z^\text {GC}(x)\cdot \Delta _2y(x)+\phi _x(x)\cdot \Delta _3y(x)\Big )\bigg ]\cdot \hat{\omega }_x(x)\,\text{ d }x\nonumber \\&\quad +M_\text {T}(x)\cdot \hat{\omega }_x(x)\,\bigg |_{x_0}^{x_1}-\int _{x_0}^{x_1}m^\psi _\text {II}(x)\cdot \frac{ \text{ d }\hat{\omega }_x(x)}{\text{ d }x}\,\text{ d }x- M^\psi _\text {II}(x)\cdot \frac{\text{ d }\hat{\omega }_x(x)}{\text{ d }x}\,\bigg |_{x_0}^{x_1}\nonumber \\&\quad +\int _{x_0}^{x_1} m^\psi _\text {IV}(x)\cdot \frac{\text{ d}^3\hat{\omega }_x(x)}{\text{ d }x^3}\,\text{ d }x+M^\psi _\text {IV}(x) \cdot \frac{\text{ d}^3\hat{\omega }_x(x)}{\text{ d }x^3} \,\bigg |_{x_0}^{x_1}, \end{aligned}$$
(22)

with

$$\begin{aligned} \Delta _1y(x)=y_2(x)-y_1(x),~~ \Delta _2y(x)=\frac{\Delta _1y(x)}{2}-y_\text {CT},~~ \Delta _3y(x)=\frac{\Delta _1y(x)^2}{3}-y_\text {CT}\cdot \Delta _1y(x) +y_\text {CT}^2, \end{aligned}$$
(23)

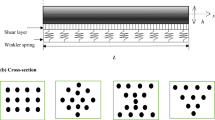
and with \(y_1(x)\) and \(y_2(x)\) as coordinates indicating the tensionless section of the beam’s bottom surface at longitudinal coordinate x, see Fig. 2.

Fig. 2
figure 2

Possible cases for the integration boundaries relating to calculation of \(T_z^\text {EF}(\mathbf {x})\), comprising a no lift-off, b partial lift-off, and c complete lift-off of the bottom surface, leading to corresponding choices of \(y_1\) and \(y_2\), compare Eq. (23); the coordinates \(y_1\) and \(y_2\), as well as \(L_\text {bottom}\), which is the contour of the bottom surface \(S_\text {bottom}\) along the y-direction, are functions of the beam axis x. Note that the depicted cross section represents profile Ri60R1 [41]

Full size image

Equation (22) includes a number of external forces, which are defined as distributed forces along the beam axis, or as forces acting onto the starting and end cross section of the beam, namely the distributed axial load per length n(x),

$$\begin{aligned} n(x)= \int _A f_x({\mathbf {x}})\,\text{ d }A + \int _C T_x({\mathbf {x}};{\mathbf{n}}= {\mathbf{n}}_C)\,\text{ d }s, \end{aligned}$$
(24)

with cross-sectional contour C; the axial forces \(N(x_i)\) acting onto the starting and end cross section of the beam,

$$\begin{aligned} N(x_i)=\int _A\beta _i\cdot T_x(x_i,y,z;{\mathbf{n}}=\beta _i \cdot {\mathbf{e}}_x)\,\text{ d }A, \end{aligned}$$
(25)

with \(i\in \left\{ 0,1\right\} \), as well as with \(\beta _i=-1\) if \(i=0\) and \(\beta _i=1\) if \(i=1\), implying, when taking into account the traction- reaction law \(\mathbf{T}({\mathbf {x}},\mathbf{n})=-\mathbf{T}({\mathbf {x}},-\mathbf{n})\),

$$\begin{aligned} N(x_i)= \int _A \sigma _{xx}(x_i,y,z)\,\text{ d }A; \end{aligned}$$
(26)

the distributed transverse (shear) loads per length in y- and z-direction, \(s_y(x)\) and \(s_z(x)\),

$$\begin{aligned} s_j(x)= \int _A f_j({\mathbf {x}})\,\text{ d }A + \int _C T_j ({\mathbf {x}};\mathbf{n}={\mathbf{n}}_C)\,\text{ d }s, \end{aligned}$$
(27)

with \(j\in \left\{ y,z\right\} \); the shear loads in y- and z-direction, \(S_y(x_i)\) and \(S_z(x_i)\), acting onto the starting and end cross section of the beam,

$$\begin{aligned} S_j(x_i)=\int _A \beta _i\cdot T_j(x_i,y,z;{\mathbf{n}}= \beta _i\cdot {\mathbf{e}}_x)\,\text{ d }A =\int _A \sigma _{xj}(x_i,y,z)\,\text{ d }A, \end{aligned}$$
(28)

with \(i\in \left\{ 0,1\right\} \) and \(j\in \left\{ y,z\right\} \); the \(\mathbf {e}_y\)- and \(\mathbf {e}_z\)-oriented distributed bending moments per length, \(m_y(x)\) and \(m_z(x)\),

$$\begin{aligned} m_j(x)=\int _A f_x({\mathbf {x}})\cdot \beta _j\,\text{ d }A + \int _C T_x ({\mathbf {x}};\mathbf{n}={\mathbf{n}}_C) \cdot \beta _j\,\text{ d }s, \end{aligned}$$
(29)

with \(j\in \left\{ y,z\right\} \), whereas \(\beta _j=z\) if \(j=y\) and \(\beta _j=-y\) if \(j=z\); the \(\mathbf {e}_y\)- and \(\mathbf {e}_z\)-oriented bending loads acting onto the starting and end cross section of the beam, \(M_y(x_i)\) and \(M_z(x_i)\),

$$\begin{aligned} M_j(x_i)=\int _A\beta _i\cdot T_x(x_i,y,z;{\mathbf{n}}= \beta _i\cdot {\mathbf{e}}_x)\cdot \beta _j\,\text{ d }A =\int _A \sigma _{xx}(x_i,y,z)\cdot \beta _j\,\text{ d }A, \end{aligned}$$
(30)

with \(i\in \left\{ 0,1\right\} \) and \(j\in \left\{ y,z\right\} \); the distributed torsional moment per length \(m_\text {T}(x)\),

$$\begin{aligned} \begin{aligned} m_\text {T}(x)&= \,\int _A f_z({\mathbf {x}})\cdot \left( y-y_\text {CT}\right) - f_y({\mathbf {x}})\cdot \left( z-z_\text {CT}\right) \, \text{ d }A\\&+ \int _C T_z ({\mathbf {x}};{\mathbf{n}}= {\mathbf{n}}_C) \cdot \left( y-y_\text {CT}\right) \,\text{ d }s\\&-\int _C T_y ({\mathbf {x}}; {\mathbf{n}}={\mathbf{n}}_C) \cdot \left( z-z_\text {CT}\right) \,\text{ d }s; \end{aligned} \end{aligned}$$
(31)

the “classical” torsional moments \(M_\text {T}(x_i)\) acting onto the starting and end cross section of the beam,

$$\begin{aligned} \begin{aligned} M_\text {T}(x_i)&= \int _A\beta _i\cdot T_z(x_i,y,z;\mathbf{n}=\beta _i\cdot {\mathbf{e}}_x) \cdot \left( y-y_\text {CT}\right) \,\text{ d }A\\&\quad -\int _A\beta _i\cdot T_y(x_i,y,z;\mathbf{n}=\beta _i\cdot {\mathbf{e}}_x) \cdot \left( z-z_\text {CT}\right) \,\text{ d }A\\&= \int _A \sigma _{xz}(x_i,y,z)\cdot \left( y-y_ {\text {CT}}\right) -\sigma _{xy}(x_i,y,z)\cdot \left( z-z_ {\text {CT}}\right) \,\text{ d }A, \end{aligned} \end{aligned}$$
(32)

with \(i\in \left\{ 0,1\right\} \); the distributed warping bimoment per length \(m^{\psi }_\text {II}(x)\),

$$\begin{aligned} m^{\psi }_\text {II}(x)= -\int _A f_x({\mathbf {x}})\cdot \psi _{\text {I}}(y,z)\,\text{ d }A +\int _C T_x ({\mathbf {x}}; {\mathbf{n}}={\mathbf{n}}_C) \cdot \psi _{\text {I}}(y,z)\,\text{ d }s; \end{aligned}$$
(33)

the bimomental loads \(M^{\psi }_\text {II}(x_i)\) acting onto the starting and end cross section of the beam,

$$\begin{aligned} M^{\psi }_\text {II}(x_i)= -\int _A\beta _i\cdot T_x(x_i,y,z;{\mathbf{n}}= \beta _i\cdot {\mathbf{e}}_x)\cdot \psi _{\text {I}}(y,z)\,\text{ d }A =-\int _A \sigma _{xx}(x_i,y,z)\cdot \psi _{\text {I}}(y,z) \,\text{ d }A, \end{aligned}$$
(34)

with \(i\in \left\{ 0,1\right\} \); the distributed fourth-order warping moment per length, \(m^{\psi }_\text {IV}(x)\),

$$\begin{aligned} m^\psi _\text {IV}(x)= \int _A f_x({\mathbf {x}})\cdot \psi _{\text {II}}(y,z)\,\text{ d }A +\int _C T_x({\mathbf {x}};{\mathbf{n}}={\mathbf{n}}_C) \cdot \psi _{\text {II}}(y,z)\,\text{ d }s; \end{aligned}$$
(35)

and fourth-order moment loads \(M^{\psi }_\text {IV}(x_i)\) acting onto the starting and end cross section of the beam,

$$\begin{aligned} M^{\psi }_\text {IV}(x_i)= \int _A\beta _i\cdot T_x(x_i,y,z;{\mathbf{n}}= \beta _i\cdot {\mathbf{e}}_x)\cdot \psi _{\text {II}}(y,z)\,\text{ d }A =\int _A \sigma _{xx}(x_i,y,z)\cdot \psi _{\text {II}}(y,z) \,\text{ d }A, \end{aligned}$$
(36)

with \(i\in \left\{ 0,1\right\} \).

2.4 Equilibrium equations and natural boundary conditions

Next, both Eqs. (14) and (22) are considered, and partial integration is applied to each integral term until the virtual velocity components, namely \(\hat{v}_x^\text {GC}(x), \hat{v}_y^\text {GC}(x), \hat{v}_z^\text {GC}(x)\), and \(\hat{\omega }_x(x)\), do not occur anymore in differential form within the respective integral term. Inserting then the such adapted formulations of \(\mathcal {P}^\text {int}\) and \(\mathcal {P}^\text {ext}\) into Eq. (1) yields a set of equilibrium equations, as well as a set of natural boundary conditions. The equilibrium equations read as

$$\begin{aligned} n(x)= & {} -\frac{\text{ d }N(x)}{\text{ d }x}, \end{aligned}$$
(37)
$$\begin{aligned} s_y(x)= & {} \frac{\text{ d}^2 M_z(x)}{\text{ d } x^2}+\frac{\text{ d } m_z(x)}{\text{ d }x}, \end{aligned}$$
(38)
$$\begin{aligned} s_z(x)= & {} -\frac{\text{ d}^2 M_y(x)}{\text{ d } x^2}-\frac{\text{ d } m_y(x)}{\text{ d }x}+k(x)\cdot \Delta _1y(x)\cdot \Big (u_z^\text {GC}(x)+\phi _x(x)\cdot \Delta _2y(x)\Big ), \end{aligned}$$
(39)

and

$$\begin{aligned} m_\text {T}(x)= & {} \, -\frac{\text{ d }M_\text {T}(x)}{\text{ d } x} +\frac{\text{ d } M_{\text {T}}^\psi (x)}{\text{ d } x} -\frac{\text{ d}^2 M^\psi _\text {II}(x)}{\text{ d } x^2} -\frac{\text{ d}^3 M^\psi _\text {III}(x)}{\text{ d } x^3} +\frac{\text{ d}^4 M^\psi _\text {IV}(x)}{\text{ d } x^4} -\frac{\text{ d } m^\psi _\text {II}(x)}{\text{ d } x} +\frac{\text{ d}^3 m^\psi _\text {IV}(x)}{\text{ d } x^3}\nonumber \\&\,+\,k(x)\cdot \Delta _1y(x)\cdot \Big (u_z^\text {GC}(x) \cdot \Delta _2y(x)+\phi _x(x)\cdot \Delta _3y(x)\Big ), \end{aligned}$$
(40)

whereas the natural boundary conditions read as

$$\begin{aligned} S_y(x_i)= & {} -\frac{\text{ d } M_z(x_i)}{\text{ d }x}-m_z(x_i), \end{aligned}$$
(41)
$$\begin{aligned} S_z(x_i)= & {} \frac{\text{ d } M_y(x_i)}{\text{ d } x}+m_y(x_i), \end{aligned}$$
(42)
$$\begin{aligned} m^\psi _\text {II}(x_i)= & {} -M_{\text {T}}^\psi (x_i)- \frac{\text{ d } M^\psi _\text {II}(x_i)}{\text{ d }x} -\frac{\text{ d}^2 M^\psi _\text {III}(x_i)}{\text{ d }x^2} +\frac{\text{ d}^3 M^\psi _\text {IV}(x_i)}{\text{ d }x^3} +\frac{\text{ d}^2 m^\psi _\text {IV}(x_i)}{\text{ d }x^2}, \end{aligned}$$
(43)

and

$$\begin{aligned} M^\psi _\text {III}(x_i)= \frac{\text{ d }M^\psi _\text {IV}(x_i)}{\text{ d }x}+ m^\psi _\text {IV}(x_i), \end{aligned}$$
(44)

with \(i\in \left\{ 0,1\right\} \).

2.5 Consideration of actual beam deformations and linear elastic constitutive behavior

The nonzero components of the linearized strain tensor \(\varvec{\varepsilon }(\mathbf {x})\) corresponding to the virtual Eulerian strain rate components defined in Eqs. (7)–(9) read as

$$\begin{aligned} \varepsilon _{xx}({\mathbf {x}})= & {} \frac{\text{ d } u^\text {GC}_x(x)}{\text{ d } x}- \frac{\text{ d}^2 u^\text {GC}_y(x)}{\text{ d }x^2}\cdot y- \frac{\text{ d}^2 u^\text {GC}_z(x)}{\text{ d }x^2}\cdot z+ \frac{\text{ d}^2 \phi _x(x)}{\text{ d } x^2}\cdot \psi _\text {I}(y,z)+\frac{\text{ d}^4 \phi _x(x)}{\text{ d } x^4}\cdot \psi _\text {II}(y,z), \end{aligned}$$
(45)
$$\begin{aligned} \gamma _{xy}({\mathbf {x}})= & {} 2\cdot \varepsilon _{xy}({\mathbf {x}})=\frac{\text{ d }\phi _x(x)}{\text{ d }x}\cdot \left[ \frac{\partial \psi _\text {I}(y,z)}{\partial y}-(z-z_\text {CT})\right] +\frac{\text{ d}^3 \phi _x(x)}{\text{ d }x^3}\cdot \frac{\partial \psi _\text {II}(y,z)}{\partial y}, \end{aligned}$$
(46)

and

$$\begin{aligned} \gamma _{xz}({\mathbf {x}})= 2\cdot \varepsilon _{xz}({\mathbf {x}}) =\frac{\text{ d }\phi _x(x)}{\text{ d }x}\cdot \left[ \frac{\partial \psi _\text {I}(y,z)}{\partial z}+(y-y_\text {CT})\right] + \frac{\text{ d}^3\phi _x(x)}{\text{ d }x^3}\cdot \frac{\partial \psi _\text {II}(y,z)}{\partial z}, \end{aligned}$$
(47)

being hence defined through the components of the actual displacement vector related to the geometrical center, \(u^\text {GC}_x(x), u^\text {GC}_y(x)\), and \(u^\text {GC}_z(x)\), as well as through \(\phi _x(x)\), which is (as defined previously, in Sect. 2.2) the actual rotation angle around the center of twist. Inserting Eqs. (45)–(47) into Hooke’s law specified for the stress state defined in Eq. (10) yields

$$\begin{aligned} \sigma _{xx}({\mathbf {x}})= & {} E\cdot \left\{ \frac{\text{ d }u^\text {GC}_x(x)}{\text{ d }x}- \frac{\text{ d}^2 u^\text {GC}_y(x)}{\text{ d }x^2}\cdot y- \frac{\text{ d}^2 u^\text {GC}_z(x)}{\text{ d }x^2}\cdot z+ \frac{\text{ d}^2\phi _x(x)}{\text{ d }x^2}\cdot \psi _\text {I}(y,z)+\frac{\text{ d}^4\phi _x(x)}{\text{ d }x^4}\cdot \psi _\text {II}(y,z)\right\} , \nonumber \\\end{aligned}$$
(48)
$$\begin{aligned} \sigma _{xy}({\mathbf {x}})= & {} G\cdot \left\{ \frac{\text{ d }\phi _x(x)}{\text{ d }x}\cdot \left[ \frac{\partial \psi _\text {I}(y,z)}{\partial y}-(z-z_\text {CT})\right] + \frac{\text{ d}^3\phi _x(x)}{\text{ d }x^3}\cdot \frac{\partial \psi _\text {II}(y,z)}{\partial y}\right\} + \sigma _{xy}^\text {bend}({\mathbf {x}}), \end{aligned}$$
(49)

and

$$\begin{aligned} \sigma _{xz}({\mathbf {x}})= G\cdot \left\{ \frac{\text{ d }\phi _x(x)}{\text{ d }x}\cdot \left[ \frac{\partial \psi _\text {I}(y,z)}{\partial z}+ (y-y_\text {CT})\right] +\frac{\text{ d}^3\phi _x(x)}{\text{ d }x^3}\cdot \frac{\partial \psi _\text {II}(y,z)}{\partial z}\right\} +\sigma _{xz}^\text {bend}({\mathbf {x}}), \end{aligned}$$
(50)

where E is the Young’s modulus of the material the beam is composed of, and G is its shear modulus. Furthermore, \(\sigma _{xy}^\text {bend}\) and \(\sigma _{xz}^\text {bend}\) are the shear stresses due to bending. The latter are not directly linked to beam axis displacements or cross-sectional rotations, but result from a boundary value problem based on the equilibrium equations for a classical 3D continuum specified for the aforementioned shear stresses and the bending-induced normal stresses. Details on how to compute \(\sigma _{xy}^\text {bend}\) and \(\sigma _{xz}^\text {bend}\) can be found in Sect. 3 of this paper and in [28].

2.6 Introduction of cross-sectional rigidities

Insertion of the virtual velocity field given in Eqs. (4)–(6), the virtual Eulerian strain rate field given in Eqs. (7)–(9), the stress tensor given in Eq. (10), and the constitutive relations given in Eqs. (48)–(50) into Eq. (2) allows for formulating \(\mathcal {P}^\text {int}\) in terms of so-called cross-sectional rigidities, see [28] for all related details. Proceeding as explained above, and considering \(\text{ d}^4\hat{\omega }_x/\text{d }x^4\approx 0\), see [28], yields

$$\begin{aligned} \mathcal {P}^\text {int}&=\, -\int _{x_0}^{x_1}\frac{\text{ d }\hat{v}^\text {GC}_x(x)}{\text{ d }x}\cdot EA\cdot \frac{\text{ d }{u}^{\text {GC}}_x(x)}{\text{ d }x}\,\text{ d }x\nonumber \\&\quad -\int _{x_0}^{x_1}\frac{\text{ d}^2\hat{v}^\text {GC}_{y}(x)}{\text{ d }x^2}\cdot \left[ \frac{\text{ d}^2 u^\text {GC}_{y}(x)}{\text{ d }x^2}\cdot EA_{yy}+ \frac{\text{ d}^2 u^\text {GC}_{z}(x)}{\text{ d }x^2}\cdot EA_{yz} \right] \,\text{ d }x \nonumber \\&\quad -\int _{x_0}^{x_1}\frac{\text{ d}^2 \hat{v}^\text {GC}_{z} (x)}{\text{ d }x^2} \cdot \left[ \frac{\text{ d}^2 u^\text {GC}_{z}(x)}{\text{ d }x^2} \cdot EA_{zz}+\frac{\text{ d}^2 u^\text {GC}_{y}(x)}{\text{ d }x^2} \cdot EA_{yz}\right] \,\text{ d }x\nonumber \\&\quad -\int _{x_0}^{x_1}\frac{\text{ d }\hat{\omega }_x(x)}{\text{ d }x}\cdot GI_\text {TI}\cdot \frac{\text{ d }\phi _x(x)}{\text{ d }x}\,\text{ d }x -\int _{x_0}^{x_1}\frac{\text{ d}^2 \hat{\omega }_x(x)}{\text{ d }x^2}\cdot EA_{\psi \psi \text {I}} \cdot \frac{\text{ d}^2{\phi }_x(x)}{\text{ d }x^2}\,\text{ d }x\nonumber \\&\quad -\int _{x_0}^{x_1}\frac{\text{ d}^3\hat{\omega }_x(x)}{\text{ d }x^3}\cdot GA_\text {R}\cdot \frac{\text{ d}^3\phi _x(x)}{\text{ d }x^3}\,\text{ d }x, \end{aligned}$$
(51)

with axial rigidity EA, bending rigidities \(EA_{yy}, EA_{zz}\), and \(EA_{yz}\), torsional rigidity \(GI_\text {TI}\), axial warping rigidity \(EA_{\psi \psi \text {I}}\), and transverse warping rigidity \(GA_\text {R}\). Furthermore, these rigidities contain area moments which are yet to be defined. In particular, \(A_{yy}, A_{zz}\), and \(A_{yz}\) are the second-order area moments,

$$\begin{aligned} A_{jk}= \int _A j\cdot k\,\text{ d }A, \end{aligned}$$
(52)

with \(j,k\in \left\{ y,z\right\} ; I_\text {TI}\) is the second-order area moment of primary torsion,

$$\begin{aligned} I_{\text {TI}} = A_{yy} + A_{zz}+A\cdot (y_\text {CT}^2 + z_\text {CT}^2) + \int _A \frac{\partial \psi _\text {I}(y,z)}{\partial z}\cdot (y-y_\text {CT})- \frac{\partial \psi _\text {I}(y,z)}{\partial y}\cdot (z-z_\text {CT})\,\mathrm {d}A; \end{aligned}$$
(53)

\(A_{\psi \psi \text {I}}\) is the second-order area moment of primary warping,

$$\begin{aligned} A_{\psi \psi {\text {I}}}= \int _A\left[ \psi _{\text {I}}(y,z)\right] ^2\,\text{ d }A; \end{aligned}$$
(54)

and \(A_\text {R}\) is the second-order area moment of secondary warping,

$$\begin{aligned} A_\text {R}= \int _A\left[ \left( \frac{\partial \psi _\text {II}(y,z)}{\partial y}\right) ^2+\left( \frac{\partial \psi _\text {II}(y,z)}{\partial z}\right) ^2\right] \, \text{ d }A. \end{aligned}$$
(55)

3 Numerical solution

The mathematical framework elaborated in Sect. 2 is solved numerically, in the form of a procedure comprising four computation steps. This strategy has been elaborated for the first time and in minute detail in [28]. In the following, a concise summary of the key aspects related to this numerical solution strategy is presented, with emphasis on the novelties of this paper.

3.1 Computation of primary and secondary warping functions

For computation of the primary and secondary warping function, as well as the coordinates of the center of twist, the shear stress components given in Eqs. (49) and (50) are split into primary shear stresses associated with \(\psi _\text {I}\) (referred to as \(\sigma _{xy}^\text {I}\) and \(\sigma _{xz}^\text {I}\)) and secondary shear stresses associated with \(\psi _\text {II}\) (referred to as \(\sigma _{xy}^\text {II}\) and \(\sigma _{xz}^\text {II}\)).

Then, as shown in [28], the following boundary value problem related to the primary shear stresses can be derived:

$$\begin{aligned} \forall \,y,z\text { on }A\text {:}~~\frac{\partial ^2 \psi ^\text {GC}_{\text {I}}(y,z)}{\partial y^2} + \frac{\partial ^2 \psi ^\text {GC}_{\text {I}}(y,z)}{\partial z^2} =0 , \end{aligned}$$
(56)

where \(\psi ^\text {GC}_{\text {I}}(y,z)\) is the primary warping function quantified with respect to the geometrical center; note that \(\psi ^\text {GC}_{\text {I}}(y,z)\) is related to \(\psi _{\text {I}}(y,z)\) via [28]

$$\begin{aligned} \psi ^\text {GC}_{\text {I}}(y,z) = \psi _{\text {I}}(y,z)-y_\text {CT}\cdot z+z_\text {CT}\cdot y+ \frac{1}{A}\cdot \int \limits _A\psi _{\text {I}}(y,z)\,\text{ d }A. \end{aligned}$$
(57)

Furthermore, requiring traction-free lateral surfaces, a boundary condition can be derived, complementing Eq. (56), reading as

$$\begin{aligned} \forall \,y,z\text { on }C\text {:}~~n_y\cdot \left[ \frac{\partial \psi ^\text {GC}_{\text {I}}(y,z)}{\partial y} -z \right] + n_z\cdot \left[ \frac{\partial \psi ^\text {GC}_{\text {I}}(y,z)}{\partial z}+y\right] =0. \end{aligned}$$
(58)

with \(n_y\) and \(n_z\) as the components of the normal vector of the lateral surface. The boundary value problem defined by Eqs. (56) and (58) can be transformed into the corresponding weak form,

$$\begin{aligned} \int _A\frac{\partial \psi ^\text {GC}_{\text {I}}(y,z)}{\partial y}\cdot \frac{\partial \Phi }{\partial y}+ \frac{\partial \psi ^\text {GC}_{\text {I}}(y,z)}{\partial z}\, \cdot \frac{\partial \Phi }{\partial z}\,\text{ d }A= \oint _C\Phi \cdot \left[ z\cdot n_y-y\cdot n_z\right] \,\text{ d }s, \end{aligned}$$
(59)

where \(\Phi (y,z)\) is a test function belonging to the Sobolev space [42].

Analogously, a boundary value problem related to the secondary shear stresses can be derived, defined by

$$\begin{aligned} \forall \,y,z\text { on }A\text {:}~~\frac{E}{G}\cdot \int _A\,\psi _\text {I}(y,z)\,\text{ d }A= -\int _A\,\frac{\partial ^2\psi _\text {II}(y,z)}{\partial y^2} +\frac{\partial ^2\psi _\text {II}(y,z)}{\partial z^2}\,\text{ d }A , \end{aligned}$$
(60)

and

$$\begin{aligned} \forall \,y,z\text { on }C\text {:}~~\oint _C\, \frac{\partial \psi _\text {II}(y,z)}{\partial y}\cdot n_y+ \frac{\partial \psi _\text {II}(y,z)}{\partial z}\cdot n_z \, \text{ d }s=0. \end{aligned}$$
(61)

The corresponding weak form reads as

$$\begin{aligned} G\,\int _A\,\frac{\partial \Phi }{\partial y}\cdot \frac{\partial \psi _\text {II}(y,z)}{\partial y} + \frac{\partial \Phi }{\partial z}\cdot \frac{\partial \psi _\text {II}(y,z)}{\partial z}\,\text{ d }A= E\cdot \int _A \Phi \cdot \psi _\text {I}(y,z)\,\text{ d }A. \end{aligned}$$
(62)

Both Eqs. (59) and (62) are solved based on a two-dimensional (2D) Finite Element (FE) analysis [43, 44], using for that purpose isoparametric four-noded quadrilateral finite elements with bilinear shape functions [30, 45], giving, eventually, access to \(\psi _{\text {I}}(y,z)\) and \(\psi _{\text {II}}(y,z)\), respectively, and to warping-related cross-sectional quantities such as the center of twist.

3.2 Computation of displacements and rotation angle along the beam axis

In order to actually compute the three displacement components, \(u_x^\text {GC}(x), u_y^\text {GC}(x)\), and \(u_z^\text {GC}(x)\), as well as the beam rotation angle, \(\phi _x(x)\), a one-dimensional (1D) FE analysis [43, 44] is employed. To that end, the beam is divided into \(n_\text {E}\) 1D finite elements \(E_m, m\in [1,n_\text {E}]\). Along each of the finite elements, the distributions of the virtual velocities are approximated through shape functions and nodal vectors. Before presenting the respective equations, we point out that for discretizing transversal virtual velocities (and displacements), cubic shape functions are used, based on so-called Hermite polynomials [46, 47]. However, such shape functions are not compatible with a nonzero deviation moment \(A_{yz}\). In order to nevertheless apply them, the transversal virtual velocities (and displacements), as well as all related quantities occurring in Eq. (51) must be expressed in a base system with the transversal base vectors coinciding with the principal axes \(\eta \) and \(\zeta \) of the cross section, see also A. Then, the element-specific virtual velocities read as

$$\begin{aligned} \hat{v}_x^{\text {GC}}(x)= & {} \mathbf{N}^\text {lin}[\xi (x)]\cdot \hat{\mathbf {v}}_x^{\text {GC},m} =\mathbf{N}^\text {lin}[\xi (x)]\cdot \nonumber \\&\Big [\hat{v}_{x,(1)}^{\text {GC},m},\,0,\,0,\,0, \,0,\,0,\,0,\, \hat{v}_{x,(2)}^{\text {GC},m},\,0,\,0,\,0,\,0, \,0,\,0\Big ]^\text {T}, \end{aligned}$$
(63)
$$\begin{aligned} \hat{v}_{\eta }^{\text {GC}}(x)= & {} \mathbf{N}^\text {cub}_\text {posD}[\xi (x)]\cdot \hat{\mathbf {v}}_{\eta }^{\text {GC},m} =\mathbf{N}^\text {cub}_\text {posD}[\xi (x)]\cdot \nonumber \\&\Bigg [0,\,\hat{v}_{\eta ,(1)}^{\text {GC},m},\, \frac{\text{ d }\hat{v}_{\eta ,(1)}^{\text {GC},m}}{\text{ d }x} ,\,0,\,0,\,0,\,0,\,0, \,\hat{v}_{\eta ,(2)}^{\text {GC},m},\, \frac{\text{ d }\hat{v}_{\eta ,(2)}^{\text {GC},m}}{\text{ d }x} ,\,0,\,0,\,0,\,0 \Bigg ]^\text {T}, \end{aligned}$$
(64)
$$\begin{aligned} \hat{v}_{\zeta }^{\text {GC}}(x)= & {} \mathbf{N}^\text {cub}_\text {neg}[\xi (x)]\cdot \hat{\mathbf {v}}_{\zeta }^{\text {GC},m} =\mathbf{N}^\text {cub}_\text {neg}[\xi (x)]\cdot \nonumber \\&\Bigg [0,\,0,\,0,\,\hat{v}_{\zeta ,(1)}^{\text {GC},m} ,\, -\frac{\text{ d }\hat{v}_{\zeta ,(1)}^{\text {GC},m}}{\text{ d }x},\,0,\,0,\,0,\,0,\,0,\, \hat{v}_{\zeta ,(2)}^{\text {GC},m},\, -\frac{\text{ d }\hat{v}_{\zeta ,(2)}^{\text {GC},m}}{\text{ d }x},\,0,\,0 \Bigg ]^\text {T}, \end{aligned}$$
(65)

and

$$\begin{aligned} \hat{\omega }_x(x)= & {} \mathbf{N}^\text {cub}_\text {posD}[\xi (x)]\cdot \hat{\varvec{\upomega }}_x^m =\mathbf{N}^\text {cub}_\text {posD}[\xi (x)]\cdot \nonumber \\&\Bigg [0,\,0,\,0,\,0,\,0,\, \hat{\omega }^m_{x,(1)},\, \frac{\text{ d }\hat{\omega }_{x,(1)}^m}{\text{ d }x},\, 0,\,0,\,0,\,0,\,0,\,\hat{\omega }^m_{x,(2)},\, \frac{\text{ d }\hat{\omega }_{x,(2)}^m}{\text{ d }x} \Bigg ]^\text {T}, \end{aligned}$$
(66)

with indices (1) and (2) denoting the two nodes of finite element \(E_m\), and \(\xi \) denoting the local coordinate (measured with respect to the center of the element), which relates to the global coordinate x via the Jacobian determinant \(|\mathbf{J}|\) and the element length \(l_m\),

$$\begin{aligned} x=\xi \cdot \frac{l_m}{2}=\xi \cdot |\mathbf{J}| \quad \text {and}\quad \frac{\text{ d }}{\text{ d }x}= \frac{2}{l_m}\cdot \frac{\text{ d }}{\text{ d }\xi }= \frac{1}{|\mathbf{J}|}\cdot \frac{\text{ d }}{\text{ d }\xi }. \end{aligned}$$
(67)

Furthermore, \(\mathbf{N}^\text {lin}, \mathbf{N}^\text {cub}_\text {posD}\), and \(\mathbf{N}^\text {cub}_\text {neg}\) denote the vectors composed of the aforementioned linear and cubic shape functions used for approximation of the virtual velocities within one finite element, see [28] for a detailed description. Importantly, the actual displacement components and the actual beam rotation angle are discretized in full analogy to Eqs. (63)–(66). Inserting Eqs. (63)–(66), the analogously defined \(u_x^\text {GC}(x), u_\eta ^\text {GC}(x), u_\zeta ^\text {GC}(x)\), and \(\phi _x(x)\), as well as the shape functions according to [28] into Eq. (51), formulated in terms of principal axes \(\eta \) and \(\zeta \), summarizing over all finite elements \(n_\text {E}\), and assembling all virtual and actual element-specific quantities into corresponding global ones (e.g., the element-specific virtual velocity vector \(\hat{\mathbf {v}}_x^{\text {GC},m}\) is assembled into one single virtual velocity vector \(\hat{\mathbf {v}}_x^{\text {GC}}\)) yields the following FE approximation of \(\mathcal {P}^\text {int}\):

(68)

with the (matrix) assembly operator . Furthermore, \(\mathbf {K}^m_{EA}, \mathbf {K}^m_{EA_{\eta \eta }}, \mathbf {K}^m_{EA_{\zeta \zeta }}, \mathbf {K}^m_{GI_{\text {TI}}}, \mathbf {K}^m_{EA_{\psi \psi \text {I}}}\) and \(\mathbf {K}^m_{GA_{\text {R}}}\) denote the element-specific stiffness matrices, see [28] for details.

Similarly, the virtual power performed by the external forces, see Eq. (22), can be expressed in terms of a corresponding FE approximation, reading as

(69)

In Eq. (69), the elastic foundation-related element matrices read as

$$\begin{aligned} \mathbf {K}_{\text {EF},1}= & {} k_\text {EF}\cdot \int _{-l_m/2}^{l_m/2} \left[ \mathbf {N}^\text {cub} _\text {posD}(x)\right] ^\text {T}\cdot \left[ \mathbf {N} ^\text {cub}_\text {posD}(x)\right] \cdot \Delta _1\eta (x)\cdot \tan \alpha \cdot \sin \alpha \,\mathrm {d}x, \end{aligned}$$
(70)
$$\begin{aligned} \mathbf {K}_{\text {EF},2}= & {} k_\text {EF}\cdot \int _{-l_m/2}^{l_m/2} \left[ \mathbf {N}^\text {cub} _\text {posD}(x)\right] ^\text {T}\cdot \left[ \mathbf {N} ^\text {cub}_\text {negD}(x)\right] \cdot \Delta _1\eta (x)\cdot \sin \alpha \,\mathrm {d}x, \end{aligned}$$
(71)
$$\begin{aligned} \mathbf {K}_{\text {EF},3}= & {} k_\text {EF}\cdot \int _{-l_m/2}^{l_m/2} \left[ \mathbf {N}^\text {cub} _\text {posD}(x)\right] ^\text {T}\cdot \left[ \mathbf {N} ^\text {cub}_\text {posD}(x)\right] \cdot \Delta _1\eta (x)\cdot \Delta _2\eta (x)\cdot \tan \alpha \cdot \sec \alpha \,\mathrm {d}x, \end{aligned}$$
(72)
$$\begin{aligned} \mathbf {K}_{\text {EF},4}= & {} k_\text {EF}\cdot \int _{-l_m/2}^{l_m/2} \left[ \mathbf {N}^\text {cub} _\text {negD}(x)\right] ^\text {T}\cdot \left[ \mathbf {N} ^\text {cub}_\text {posD}(x)\right] \cdot \Delta _1\eta (x)\cdot \sin \alpha \,\mathrm {d}x, \end{aligned}$$
(73)
$$\begin{aligned} \mathbf {K}_{\text {EF},5}= & {} k_\text {EF}\cdot \int _{-l_m/2}^{l_m/2} \left[ \mathbf {N}^\text {cub} _\text {negD}(x)\right] ^\text {T}\cdot \left[ \mathbf {N} ^\text {cub}_\text {negD}(x)\right] \cdot \Delta _1\eta (x)\cdot \cos \alpha \,\mathrm {d}x, \end{aligned}$$
(74)
$$\begin{aligned} \mathbf {K}_{\text {EF},6}= & {} k_\text {EF}\cdot \int _{-l_m/2}^{l_m/2} \left[ \mathbf {N}^\text {cub} _\text {negD}(x)\right] ^\text {T}\cdot \left[ \mathbf {N} ^\text {cub}_\text {posD}(x)\right] \cdot \Delta _1\eta (x)\cdot \Delta _2\eta (x)\cdot \sec \alpha \,\mathrm {d}x, \end{aligned}$$
(75)
$$\begin{aligned} \mathbf {K}_{\text {EF},7}= & {} k_\text {EF}\cdot \int _{-l_m/2}^{l_m/2} \left[ \mathbf {N}^\text {cub} _\text {posD}(x)\right] ^\text {T}\cdot \left[ \mathbf {N} ^\text {cub}_\text {posD}(x)\right] \cdot \Delta _1\eta (x)\cdot \Delta _2\eta (x)\cdot \sec \alpha \cdot \tan \alpha \,\mathrm {d}x, \end{aligned}$$
(76)
$$\begin{aligned} \mathbf {K}_{\text {EF},8}= & {} k_\text {EF}\cdot \int _{-l_m/2}^{l_m/2} \left[ \mathbf {N}^\text {cub} _\text {posD}(x)\right] ^\text {T}\cdot \left[ \mathbf {N} ^\text {cub}_\text {negD}(x)\right] \cdot \Delta _1\eta (x)\cdot \Delta _2\eta (x)\cdot \sec \alpha \,\mathrm {d}x, \end{aligned}$$
(77)

and

$$\begin{aligned} \mathbf {K}_{\text {EF},9}= k_\text {EF}\cdot \int _{-l_m/2}^{l_m/2} \left[ \mathbf {N}^\text {cub} _\text {posD}(x)\right] ^\text {T}\cdot \left[ \mathbf {N} ^\text {cub}_\text {posD}(x)\right] \cdot \Delta _1\eta (x)\cdot \Delta _3\eta (x)\cdot \sec \alpha ^3 \,\mathrm {d}x, \end{aligned}$$
(78)

with

$$\begin{aligned} \Delta _1\eta (x)=\eta _{2}(x)-\eta _{1}(x),~~ \Delta _2\eta (x)=\frac{\Delta _1\eta (x)}{2}- \eta _\text {CT},~~ \Delta _3\eta (x)=\frac{\Delta _1\eta (x)^2}{3}- \eta _\text {CT}\cdot \Delta _1\eta (x)+\eta _\text {CT}^2, \end{aligned}$$
(79)

and with \(\eta _{1}(x)\) and \(\eta _{2}(x)\) as the principal axes-related counterparts of \(y_1(x)\) and \(y_2(x)\), as introduced in Sect. 2.3 and Fig. 2. Furthermore, the element-specific load vectors occurring in Eq. (69) are defined as

s

$$\begin{aligned} \mathbf {F}_x^{m}= & {} {\left\{ \begin{array}{ll} \displaystyle \int \limits _{-l_1/2}^{l_1/2}\left[ \mathbf {N} ^{\text {lin}}(x)\right] ^\text {T}\cdot n(x)\,\text{ d }x- \left[ N(x_0),\,0\right] ^\text {T} &{}\text {if~~}m=1,\\ \displaystyle \int \limits _{-l_m/2}^{l_m/2} \left[ \mathbf {N} ^{\text {lin}}(x) \right] ^\text {T}\cdot n(x)\,\text{ d }x &{}\text {if~~}2\le m< n_\text {E},\\ \displaystyle \int \limits _{-l_{n_\text {E}}/2}^{l_{n_\text {E}}/2} \left[ \mathbf {N}^{\text {lin}}(x) \right] ^\text {T}\cdot n(x)\,\text{ d }x+\left[ 0,\,N(x_1)\right] ^\text {T} &{}\text {if~~}m=n_\text {E}, \end{array}\right. } \end{aligned}$$
(80)
$$\begin{aligned} \mathbf {F}_\eta ^{m}= & {} {\left\{ \begin{array}{ll} \displaystyle \int \limits _{-l_1/2}^{l_1/2}\left[ \mathbf {N} ^{\text {cubic}}_\text {posD}(x)\right] ^\text {T}\cdot s_{\eta }(x) +\left[ \dfrac{\text{ d }}{\text{ d }x}\,\mathbf {N} ^{\text {cubic}}_\text {posD}(x)\right] ^\text {T}\cdot m_{\zeta }(x) \,\text{ d }x-\left[ S_{\eta }(x_0),\,M_{\zeta }(x_0),\,0,\,0 \right] ^\text {T} &{}\text {if~~}m=1,\\ \displaystyle \int \limits _{-l_m/2}^{l_m/2}\left[ \mathbf {N} ^{\text {cubic}}_\text {posD}(x)\right] ^\text {T}\cdot s_{\eta }(x) +\left[ \dfrac{\text{ d }}{\text{ d }x}\mathbf {N}^{\text {cubic}} _\text {posD}(x)\right] ^\text {T}\cdot m_{\zeta }(x)\,\text{ d }x &{}\text {if~~}2\le m< n_\text {E},\\ \displaystyle \int \limits _{-l_{n_\text {E}}/2}^{l_{n_\text {E}}/2} \left[ \mathbf {N}^{\text {cubic}}_\text {posD}(x) \right] ^\text {T}\cdot s_{\eta }(x)+\left[ \dfrac{\text{ d }}{\text{ d }x}\mathbf {N}^{\text {cubic}}_\text {posD}(x) \right] ^\text {T}\cdot m_{\zeta }(x)\,\text{ d }x+ \left[ 0,\,0,\, S_{\eta }(x_1),\,M_{\zeta }(x_1)\right] ^\text {T} &{}\text {if~~}m=n_\text {E}, \end{array}\right. } \nonumber \\\end{aligned}$$
(81)
$$\begin{aligned} \mathbf {F}_\zeta ^{m}= & {} {\left\{ \begin{array}{ll} \displaystyle \int \limits _{-l_1/2}^{l_1/2}\left[ \mathbf {N} ^{\text {cubic}}_\text {neg}(x)\right] ^\text {T}\cdot s_{\zeta }(x) -\left[ \dfrac{\text{ d }}{\text{ d }x}\mathbf {N}^{\text {cubic}} _\text {neg}(x)\right] ^{\text {T}}\cdot m_{\eta }(x)\,\text{ d }x -\left[ S_{\zeta }(x_0),\,M_{\eta }(x_0),\,0,\,0\right] ^\text {T} &{}\text {if~~}m=1,\\ \displaystyle \int \limits _{-l_m/2}^{l_m/2}\left[ \mathbf {N} ^{\text {cubic}}_\text {neg}(x)\right] ^\text {T}\cdot s_{\zeta }(x) -\left[ \dfrac{\text{ d }}{\text{ d }x}\mathbf {N}^{\text {cubic}} _\text {neg}(x)\right] ^{\text {T}}\cdot m_{\eta }(x)\,\text{ d }x &{}\text {if~~}2\le m< n_\text {E},\\ \displaystyle \int \limits _{-l_{n_\text {E}}/2}^{l_{n_\text {E}}/2} \left[ \mathbf {N}^{\text {cubic}}_\text {neg}(x) \right] ^\text {T}\cdot s_{\zeta }(x)-\left[ \dfrac{\text{ d }}{\text{ d }x}\, \mathbf {N}^{\text {cubic}}_\text {neg}(x)\right] ^{\text {T}} \cdot m_{\eta }(x)\,\text{ d }x+\left[ 0,\,0,\,S_{\zeta }(x_1), \,M_{\eta }(x_1)\right] ^\text {T} &{}\text {if~~}m=n_\text {E}, \end{array}\right. } \nonumber \\\end{aligned}$$
(82)
$$\begin{aligned} \mathbf {M}_{x}^{m}= & {} {\left\{ \begin{array}{ll} \displaystyle \int \limits _{-l_1/2}^{l_1/2}\left[ \mathbf {N} ^{\text {cubic}}_\text {posD}(x)\right] ^\text {T}\cdot m_\text {T}(x) -\left[ \dfrac{\text{ d }}{\text{ d }x}\mathbf {N}^{\text {cubic}} _\text {posD}(x)\right] ^\text {T}\cdot m^{\psi }_\text {II}(x) +\left[ \dfrac{\text{ d}^3}{\text{ d }x^3}\mathbf {N} ^{\text {cubic}}_\text {posD}(x)\right] ^\text {T}m^{\psi } _\text {IV}(x)\cdots \\ \cdots -\left[ M_\text {T}(x_0),\,-M^\psi _\text {II} (x_0),\,0,\,0\right] ^\text {T} &{}\text {if~~}m=1,\\ \displaystyle \int \limits _{-l_m/2}^{l_m/2}\left[ \mathbf {N} ^{\text {cubic}}_\text {posD}(x)\right] ^\text {T}\cdot m_\text {T}(x) -\left[ \dfrac{\text{ d }}{\text{ d }x}\mathbf {N}^{\text {cubic}} _\text {posD}(x)\right] ^\text {T}\cdot m^{\psi }_\text {II}(x) +\left[ \dfrac{\text{ d}^3}{\text{ d }x^3}\mathbf {N} ^{\text {cubic}}_\text {posD}(x)\right] ^\text {T}m^{\psi } _\text {IV}(x) &{}\text {if~~}2\le m< n_\text {E},\\ \displaystyle \int \limits _{-l_{n_\text {E}}/2}^{l_{n_\text {E}}/2} \left[ \mathbf {N}^{\text {cubic}}_\text {posD}(x) \right] ^\text {T}\cdot m_\text {T}(x)-\left[ \dfrac{\text{ d }}{\text{ d }x}\mathbf {N}^{\text {cubic}}_\text {posD}(x) \right] ^\text {T}\cdot m^{\psi }_\text {II}(x)+\left[ \dfrac{ \text{ d}^3}{\text{ d }x^3}\mathbf {N}^{\text {cubic}} _\text {posD}(x)\right] ^\text {T} m^{\psi }_\text {IV}(x)\cdots \\ \cdots +\left[ 0,\,0,\,M_\text {T}(x_1),\,- M^\psi _\text {II}(x_1)\right] ^\text {T} &{}\text {if~~}m=n_\text {E}. \end{array}\right. }\nonumber \\ \end{aligned}$$
(83)

Inserting Eqs. (68) and (69) into Eq. (1) yields

(84)

Equation (84) can be solved for the sought-after actual displacement quantities. For realizing a tensionless elastic foundation, the following iterative approach was implemented:

  1. Step I:

    Assume, as initial guess, that the whole bottom surface of the beam undergoes a deformation in z-direction being larger than zero, relating to case (a) depicted in Fig. 2. Hence, \(\forall x:~y_2(x)-y_1(x)=L_\text {bottom}(x)\), implying corresponding values for \(\eta _2(x)\) and \(\eta _1(x)\). Consider \(y_1(x)\) and \(y_2(x)\) as reference distributions \(y_1^\text {ref}(x)\) and \(y_2^\text {ref}(x)\).

  2. Step II:

    Compute \(u_x^\text {GC}(x), u_y^\text {GC}(x), u_z^\text {GC}(x)\), and \(\phi _x(x)\), and the respective derivatives, considering for that purpose Eq. (84), as well as \(y_1^\text {ref}(x)\) and \(y_2^\text {ref}(x)\).

  3. Step III:

    Compute \(u_z(x)\) and, based on the considerations shown in Fig. 2, deduce \(y_1^\text {new}(x)\) and \(y_2^\text {new}(x)\).

  4. Step IV:

    Check if the conditions \(\forall x: y_1^\text {new}(x)=y_1^\text {ref}(x)\wedge y_2^\text {new}(x)=y_2^\text {ref}(x)\) are fulfilled. If they are, the iterative calculation of all DOFs is completed. If they are not, set \(y_1^\text {ref}(x)\) to \(y_1^\text {new}(x)\) and set \(y_2^\text {ref}(x)\) to \(y_2^\text {new}(x)\), and go back to step II.

3.3 Computation of forces along the beam axis

The computed displacement field and the rotation angle along the beam axis serve as basis for computing the corresponding force quantities. For example, inserting \(u_x^\text {GC}, u_y^\text {GC}, u_z^\text {GC}\), and \(\phi _x(x)\) into Eq. (48), and the result into Eq. (15) gives access to the normal force N(x). In similar fashion, the bending moments \(M_y(x)\) and \(M_z(x)\), the torsional moment \(M_\text {T}(x)\), the primary warping-induced torsional moment \(M_\text {T}^\psi (x)\), the warping-related bimoment \(M_\text {II}^\psi (x)\), the warping-related trimoment \(M_\text {III}^\psi (x)\), and the warping-related fourth-order moment \(M_\text {IV}^\psi \) are computed, see [28] for details.

3.4 Computation of cross-sectional stress distributions

Inserting the forces obtained as described above into Eq. (48) allows to define the bending-related share of \(\sigma _{xx}(\mathbf {x})\), termed \(\sigma _{xx}^\text {bend}(\mathbf {x})\), reading as

$$\begin{aligned} \sigma ^\text {bend}_{xx}({\mathbf {x}})= \frac{A_{yz}\cdot z-A_{zz}\cdot y}{A_{yy}\cdot A_{zz}-A_{yz}^2}\cdot M_z(x)+ \frac{A_{yy}\cdot z-A_{yz}\cdot y}{A_{yy}\cdot A_{zz}-A_{yz}^2}\cdot M_y(x). \end{aligned}$$
(85)

Additionally, we adopted the ansatz for \(\sigma _{xy}(\mathbf {x})^\text {bend}\) and \(\sigma _{xz}(\mathbf {x})^\text {bend}\) proposed by Kourtis et al. [48],

$$\begin{aligned} \sigma ^\text {bend}_{xy}(\mathbf {x})= G\cdot \left[ \frac{\partial \psi _\text {bend}(\mathbf {x})}{\partial y}-\frac{2\cdot \nu }{E}\cdot a_z(x)\cdot y \cdot z\right] , \end{aligned}$$
(86)

and

$$\begin{aligned} \sigma ^\text {bend}_{xz}(\mathbf {x})= G\cdot \left[ \frac{\partial \psi _\text {bend}(\mathbf {x})}{\partial z}-\frac{2\cdot \nu }{E}\cdot a_y(x)\cdot y \cdot z \right] , \end{aligned}$$
(87)

where \(\nu \) is the Poisson’s ratio, and \(a_y(x)\) and \(a_z(x)\) are defined as

$$\begin{aligned} a_y(x)= -\left( \dfrac{\text{ d }M_z(x)}{\text{ d }x}\cdot A_{zz}+ \dfrac{\text{ d }M_y(x)}{\text{ d }x}\cdot A_{yz}\right) \left( A_{yy}\cdot A_{zz}-A_{yz}^2\right) ^{-1} , \end{aligned}$$
(88)

and

$$\begin{aligned} a_z(x)= \left( \dfrac{\text{ d }M_y(x)}{\text{ d }x}\cdot A_{yy}+ \dfrac{\text{ d }M_z(x)}{\text{ d }x}\cdot A_{yz}\right) \left( A_{yy}\cdot A_{zz}-A_{yz}^2\right) ^{-1}. \end{aligned}$$
(89)

Equations (85)–(87), together with Eqs. (88) and (89), are inserted into a suitable equilibrium condition, and into a boundary condition reflecting traction-free lateral surfaces, both of which can be expressed in terms of a corresponding weak form, see [28] for details. The latter is again solved by means of a 2D FE analysis, using four-noded quadrilateral elements and bilinear shape functions, see [30] for details.

4 Numerical studies

4.1 Model input data

We considered a double-clamped beam of length \(l=50\,\)m, representing a tramway rail of cross section Ri60R1 [41], see Fig. 2, for which steel-typical elastic constants were chosen, namely a Young’s modulus of \(E=2.1\times 10^5\,\)N/mm\(^2\), and a Poisson’s ratio of \(\nu =0.28\). As for the elastic foundation, several scenarios were studied, ranging from a very stiff elastic foundation to a comparably compliant elastic foundation supporting the whole beam, and including also a discontinuity in the elastic foundation in the middle of the beam, representing a step-wise transition from a stiff to a compliant elastic foundation. Thereby, the upper limit of the foundation modulus was chosen according to the respective suggestions made in [49], \(k_\text {EF}^\text {max}=0.4\,\text {N}/\text {mm}^3\). The compliant (or soft) elastic foundation, in turn, was assumed to exhibit a considerably lower foundation modulus, namely \(k^\text {min}_\text {EF}=0.1\,\text {N}/\text {mm}^3\). Furthermore, an intermediate elastic foundation was also considered, exhibiting a foundation modulus of \(k^\text {med}_\text {EF}=0.25\,\text {N}/\text {mm}^3\).

4.2 Loading conditions

As for the applied loading, the loads to which the studied beams were exposed were chosen such that they reasonably represent the loads transferred from tramway wheels onto rails. In the Viennese tramway network, the maximum occurring wheel load amounts to \(P_z=59.69\) kN [50]. When assuming that the steels making up the rail and the wheel feature the same elastic constants, a simplified form of the Hertzian contact theory [51, 52] gives access to the mean contact pressure acting on a small rectangular area,

$$\begin{aligned} q_\text {mean}= \sqrt{\frac{\pi \cdot E}{64\cdot \left( 1-\nu ^2\right) }\cdot \frac{P_z}{r_\text {wheel}\cdot b_\text {cont}}}. \end{aligned}$$
(90)

In Eq. (90), \(r_\text {wheel}\) denotes the radius of the wheel in contact with the rail, and \(2\cdot b_\text {cont}\) denotes the width of the rail/wheel contact area. Furthermore, typical trams used in the Viennese tramway network exhibit a wheel radius of \(r_\text {wheel}=345\,\)mm [50] and the rail head radius of rail profile Ri60R1 [41, 52,53,54] implies \(b_\text {cont}=5\,\)mm. Evaluating Eq. (90) accordingly yields \(q_\text {mean}=622.15\) N/mm\(^2\), which corresponds to a contact area length of \(l_\text {cont}=P_z/\left( q_\text {mean}\,2\,b_\text {cont}\right) \approx 10\) mm. The respective distributed transverse load \(s_z(x)\) is obtained through multiplying the contact pressure \(q_\text {mean}\) with the width of the contact area, \(s_z(x)=6221.5\) N/mm, which was applied over the length \(l_\text {cont}\). Importantly, application of \(P_z\), and consequently of \(s_z(x)\) occurs as shown in Fig. 3, implying an offset of 16.04 mm between the line of action of those forces and the center of twist. Hence, \(P_z\) induces a torsional moment \(M_\text {T}\), which is taken into account in terms of a distributed torsional moment \(m_\text {T}(x)=99.79\) kNmm/mm, applied between \(-l_\text {cont}/2\) and \(l_\text {cont}/2\) (both with respect to the point of load application).

Fig. 3
figure 3

Point load \(P_z\), implying, due to offset with respect to center of twist, torsional moment \(M_\text {T}\), and load cases I and II. For load case II, three locations of load application are studied. Note that \(P_z\) and \(M_\text {T}\) are considered in terms of corresponding distributed transverse load \(s_z(x)\) and distributed torsional moment \(m_\text {T}(x)\), as described in Sect. 4.2

Full size image

It is emphasized that the chosen beam length of \(l=50\,\)m ensured that the bearing conditions did not have any relevant effects on the resulting forces and stress distributions.

4.3 Load case I: point load on continuous elastic foundation

One wheel load, as defined in Sect. 4.2, was applied at \(x_\text {load}=l/2\), whereby the beam was resting on a continuous elastic foundation; with the corresponding stiffness varying as defined in Sect. 4.1, see Fig. 3.

As expected, a more compliant elastic foundation leads to higher displacements \(u_y(x)\) and \(u_z(x)\), see, e.g., the two plots in the top row of Fig. 4. A similar behavior is also observed for the bending moment \(M_y(x)\) and the classical torsional moment \(M_\text {T}(x)\) minus the primary warping-related torsional moment \(M_\text {T}^\psi (x)\), see the plots in the second row of Fig. 4. The distributions along the beam of the warping-related bimoment \(M_\text {II}^\psi (x)\) and trimoment \(M_\text {III}^\psi (x)\) are depicted in the third row of Fig. 4. It is particularly interesting and instructive to compute the cross-sectional distributions of the stress tensor components \(\sigma _{xx}, \sigma _{xy}\), and \(\sigma _{xz}\). Notably, such distributions were shown in previous works [28, 30]. In this work, for the sake of conciseness, we only show the minima and maxima along the beam axis, see the plots in the fourth, fifth, and sixth row of Fig. 4. In order to allow for better comparability of the stress states along the beam axis, the von Mises stress was computed, through

$$\begin{aligned} \sigma _\text {vM}(\mathbf {x})= \sqrt{\Big [\sigma _{xx}(\mathbf {x})\Big ]^2+ 3\left\{ \Big [\sigma _{xy}(\mathbf {x})\Big ]^2+ \Big [\sigma _{xz}(\mathbf {x})\Big ]^2\right\} }. \end{aligned}$$
(91)

The respective mean and maximum values in the cross sections along the beam axis are shown in the last row of Fig. 4, confirming that a lower stiffness of the elastic foundation implies higher stresses in the rail.

Fig. 4
figure 4

Results for single wheel load, acting at \(x_\text {load}=l/2\) onto beam (with \(l=50\,\)m) supported elastically in continuous fashion, considering three foundation moduli (\(k_\text {EF}^\text {min}, k_\text {EF}^\text {med}\), and \(k_\text {EF}^\text {max}\)); namely distributions along the beam axis of transversal displacements \(u_y^\text {GC}\) and \(u_z^\text {GC}\), of bending moment \(M_y\), of the classical torsional minus the primary warping-related torsional moment \((M_\text {T}-M_\text {T}^\psi )\), the warping-related bi- and trimoments \(M_\text {II}^\psi \) and \(M_\text {III}^\psi \), as well as the minima and maxima of stress tensor components \(\sigma _{xx}, \sigma _{xy}\), and \(\sigma _{xz}\), and the maximum and mean values of the von Mises stress \(\sigma _\text {vM}\); the abscissa of all diagrams indicates the coordinate in beam direction, given in meters

Full size image
Fig. 5
figure 5

Results for single wheel load, acting at three different locations \(x_\text {load}\) onto beam (with \(l=50\,\)m) supported elastically in discontinuous fashion, with \(k_\text {EF}(x<l/2)=k_\text {EF}^\text {min}\) and \(k_\text {EF}(x>l/2)=k_\text {EF}^\text {max}\); namely distributions along the beam axis of transversal displacements \(u_y^\text {GC}\) and \(u_z^\text {GC}\), of bending moment \(M_y\), of the classical torsional minus the primary warping-related torsional moment \((M_\text {T}-M_\text {T}^\psi )\), the warping-related bi- and trimoments \(M_\text {II}^\psi \) and \(M_\text {III}^\psi \), as well as the minima and maxima of stress tensor components \(\sigma _{xx}, \sigma _{xy}\), and \(\sigma _{xz}\), and the maximum and mean values of the von Mises stress \(\sigma _\text {vM}\); the abscissa of all diagrams indicates the coordinate in beam direction, given in meters

Full size image

4.4 Load case II: point load on discontinuous elastic foundation

Again one wheel load was considered, acting onto a beam which was resting on a discontinuous elastic foundation, with a \(k_\text {EF}(x<l/2)=k_\text {EF}^\text {min}\) and \(k_\text {EF}(x>l/2)=k_\text {EF}^\text {max}\). Furthermore, three locations of load application were considered, namely \(x_\text {load}=0.45l, 0.5l, 0.55l\), see Fig. 3. The respective resulting distributions of displacements, bending moments, torsional moments, and stresses are shown in Fig. 5.

On the one hand, the qualitative trends described already in Sect. 4.3 are confirmed; hence, the stresses related to load application on a softer elastic foundation are higher than the stresses related to load application on a stiffer elastic foundation. On the other hand, it turns out that all computed quantities are clearly asymmetric, owing to the fact that they are influenced both by regions of softer and stiffer elastic foundation. This asymmetry turns out to be—not surprisingly—most pronounced for \(x_\text {load}=0.5l\).

5 Summary and conclusions

In this paper, we have presented a new approach allowing for calculating how an elastic foundation affects the force and stress distributions of beams resting thereon. The derived mathematical framework, taking the effects of restrained torsion rigorously into account, was numerically evaluated by means of a sequential, two-step Finite Element scheme, solving the equations first on the cross-sectional level in order to obtain the cross-sectional values, then in longitudinal direction of the beam, and finally again over the cross section at selected locations along the beam axis. As compared to conventional, full three-dimensional Finite Element analyses, this new approach is significantly more efficient, see also [28] for a quantitative comparison. Hence, the present paper adds a potentially valuable aspect to the growing body of scientific literature on beam theory-related Finite Element analysis; see, e.g., [55,56,57,58].

The question raised in Sect. 1 of this paper was whether discontinuities in the elastic foundation may be potential triggers of mechanical failures occurring in tramway rails. The results presented in Sect. 4.4 have not shown any particular stress peaks caused by such discontinuities themselves. However, an almost step-wise increase of stresses upon moving from a rail section resting on a stiff elastic foundation to a rail section resting on a soft elastic foundation was observed. The plots in the last row of Fig. 5 show that the maximum von Mises stress increases (for the studied jump in the foundation modulus) by more than 50 %, while the mean von Mises stress increases by more than 30 %. Hence, this study supports the hypothesis that maintenance works to which tramway networks are exposed to over the years may indeed promote the occurrence of stress peaks leading in further consequence to rail failures; especially when taking into account that materials used for elastic foundations are nowadays stiffer than in former times, while wheel loads have become higher.