Nonlinear modeling, dynamics, and chaos in a large deflection model of a rotor–disk–bearing system under geometric eccentricity and mass unbalance

Abstract

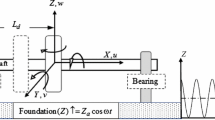
The present article treats the nonlinear dynamic analysis of a lightweight flexible rotor–disk–bearing system with geometric eccentricity and mass unbalance. A large deflection model has been derived to represent a nonlinear flexible rotor–bearing system to study the bifurcation, stability, and route to chaos. This mathematical model includes a bidirectional flexible shaft characterized by nonlinear curvature and gyroscopic effect, geometric eccentricity, a rigid disk crooked with unbalance mass, and nonlinear flexible bearings. A perturbation technique has been used to obtain a set of nonlinear algebraic equations that govern the overall dynamics of the system. The system stability has been studied by investigating the bifurcation and route to chaos upon changing the design parameters such as geometric eccentricity, mass unbalance, and disk parameters under the resonance conditions. The present system exhibits a complex behavior traveling with periodic, quasi-periodic, period doubling and chaotic behavior on a gradual change in design variables. The system loses its stability due to S–N bifurcation, which leads to a sudden jump in the response amplitude. These complex behaviors have been studied in detail with the illustration of time history, phase trajectories, bifurcation diagrams, and Poincaré’s map for each category. Qualitative assessment of bifurcation diagrams has been studied to explore the boundaries of the stable and unstable behaviors and essential dynamics of the systems. Special attention to predict its rich dynamics to highlight the route to chaos as a future diagnostic tool has been explored. The presented results offer significant understanding of the dynamic performances and its critical operating conditions of a rotor system subjected to geometric eccentricity and mass imbalance.

Appendix

The kinetic energy of the shaft and disk [7, 16] is

$$\begin{aligned} T= & {} \mathop \int \limits _0^L {\left( {m({\dot{u}}^{2}+{\dot{v}}^{2}+{\dot{w}}^{2})+I_1 \upomega _1^2 +I_2 (\upomega _2^2 +\upomega _3^2 )} \right) } {\text {d}}x\nonumber \\&+\mathop \int \limits _0^L {\left. {\left( {M({\dot{u}}^{2}+{\dot{v}}^{2}+{\dot{w}}^{2})+I_\mathrm{1d} \upomega _1^2 +I_{2d} (\upomega _2^2 +\upomega _3^2 )} \right) } \right| }_{x=L_\mathrm{d} } {\text {d}}x. \end{aligned}$$

(A.1)

The strain energy of the shaft is [19]

$$\begin{aligned} U_\mathrm{s} =\mathop \int \limits _0^L {\left( {A_{11} e\updelta e+D_{11} \rho _1 \updelta \rho _1 +D_{22} \rho _2 \updelta \rho _2 +D_{22} \rho _3 \updelta \rho _3 } \right) } {\text {d}}x. \end{aligned}$$

(A.2)

Here, $A_{11}, D_{11}$, and $D_{22}$ are the axial rigidity, torsional rigidity, and bending rigidity, respectively. The $\rho _{i}\, ({i} = 1, 2, 3)$ are components of shaft curvatures [19],

$$\begin{aligned} A_{11} =\int {E \mathrm{d}A} ,\quad D_{11} =\int G (y^{2}+z^{2})\mathrm{d}A,\quad D_{22} =\int {Ey^{2}} \mathrm{d}A=\int {Ez^{2}} \mathrm{d}A.\quad \end{aligned}$$

The kinetic energy of the mass unbalance due to both eccentricity of the rotor and the externally added unbalance mass ($m_{{\mathrm{u}}}$) can be expressed as

$$\begin{aligned} T_\mathrm {d}=&{} \varOmega \left\{ {me_v \left( {{\dot{w}}c-{\dot{v}}s} \right) +\left. {Me_v \left( {{\dot{w}}c-{\dot{v}}s} \right) } \right| _{x=L_d} +\left. {m_\mathrm {u} e_{v1} \left( {{\dot{w}}c-{\dot{v}}s} \right) } \right| _{x=L_d} } \right\} \nonumber \\&-\varOmega \left\{ {me_w \left( {{\dot{v}}c+{\dot{w}}s} \right) +\left. {Me_w \left( {{\dot{v}}c+{\dot{w}}s} \right) } \right| _{x=L_d} +\left. {m_\mathrm {u} e_{w1} \left( {{\dot{v}}c+{\dot{w}}s} \right) } \right| _{x=L_d} } \right\} . \end{aligned}$$

(A.3)

Here, c and s stand for $\cos \left( {\varOmega t} \right)$ and $\sin \left( {\varOmega t} \right)$, respectively.

The strain energy stored in the bearings can be expressed as

$$\begin{aligned} U_\mathrm{b}= & {} \frac{1}{2}\left. {\int _0^L {\left[ {\left( K_\mathrm{l} v+K_\mathrm{nl} v^{3}\right) v+\left( K_\mathrm{l} w+K_\mathrm{nl} w^{3}\right) w} \right] } } \right| _{x=0} {\text {d}}x\nonumber \\&+\left. {\frac{1}{2}\int _0^L {\left[ {\left( K_\mathrm{l} v+K_\mathrm{nl} v^{3}\right) v+\left( K_\mathrm{l} w+K_\mathrm{nl} w^{3}\right) w} \right] } } \right| _{x=L} {\text {d}}x \end{aligned}$$

(A.4)

where $K_\mathrm{l}$ and $K_\mathrm{nl}$ are linear and nonlinear bearing coefficients of the bearings, respectively. Dirac delta function has been incorporated in order to represent the bearing effect in the distributed system.

The in-extensional condition considers zero strain ($e = 0$) along the shaft length, and so, the relation between displacements u, v, and w can be expressed as [21]

$$\begin{aligned} \because {(1 + u')^2} + {v'^2} + {w'^2} = 1. \end{aligned}$$

Longitudinal displacement is expressed as $u\left( {x,t} \right) =\mathop \int \limits _0^L {\sqrt{\left\{ {1-\left( {w'^{2}+v'^{2}} \right) } \right\} }} {\text{ d }}x-L$.

Using Taylor series expansion, the longitudinal displacement can be expressed as

$$\begin{aligned} \begin{aligned} u\left( {x,t} \right) \simeq \mathop \int \limits _0^L {\left\{ {1-\left( {w'^{2}+v'^{2}} \right) +\ldots } \right\} }^{1/2}{\text{ d }}x-L\approx -\frac{1}{2}\mathop \int \limits _0^L {\left( {w'^{2}+v'^{2}} \right) } ^{1/2}{\text{ d }}x \end{aligned} \end{aligned}$$

(A.5)

where ( )’ denotes a derivative with respect to x

Using kinetic love analogy curvature ${\rho }$ can be expressed as [21]

$$\begin{aligned} \rho =\rho _1 e_1 +\rho _2 e_2 +\rho _3 e_3 \end{aligned}$$

(A.6)

Here, $\rho _1 ={\phi }'-{\psi }'\sin \theta ,\rho _2 ={\psi }'\sin \phi \cos \theta +{\theta }'\cos \phi ,\rho _3 ={\psi }'\cos \phi \cos \theta -{\theta }'\sin \phi .$

The following are the coefficients of equations of motions.

$$\begin{aligned} \kappa _1=&{} \mathop \int \limits _0^1 \left( \varphi ^{2}-\varphi {\varphi }''I_2 +\varphi _{x=d}^2 \beta _1 -\varphi _{x=d} ({\varphi }'')_{x=L_d} I_{2d} \right) {\text{ d }}x,\kappa _2 =\mathop \int \limits _0^1 \left( \varphi ^{2}+\varphi _{x=0}^2 +\varphi _{x=L}^2 \right) {\text{ d }}x, \nonumber \\ \kappa _3=&{} \mathop \int \limits _0^1 \left( {\varphi } \varphi ^{\prime \prime \prime \prime }+\varphi _{x=0}^2 K_\mathrm {l} +\varphi _{x=L}^2 K_\mathrm {l} \right) {\text{ d }}x,\kappa _4 =-\mathop \int \limits _0^1 \left( \varphi {\varphi }''I_2 +\varphi _{x=L_d}({\varphi }'')_{x=L_d} I_{2d} \right) {\text{ d }}x, \nonumber \\ \kappa _5=&{} \mathop \int \limits _0^1 \left( \varphi {\varphi }'^{2}\varphi ^{\prime \prime \prime \prime }+\varphi {\varphi }''^{3}+4\varphi {\varphi }'{\varphi }''{\varphi }'''\right) {\text{ d }}x,\kappa _6 =\mathop \int \limits _0^1 \left( \left( \varphi ^{4}\right) _{x=0} K_\mathrm {nl} +\left( \varphi ^{4}\right) _{x=l} K_\mathrm {nl} \right) {\text{ d }}x, \nonumber \\ \kappa _7=&{} \mathop \int \limits _0^1 \left( \varphi \varphi ^{\prime \prime }\int _1^x {\int _0^x {\varphi ^{\prime 2}} } {\text{ d }}x{\text{ d }}x+\beta _1 \left( \varphi \varphi ^{\prime \prime }\int _1^x {\int _0^x {\varphi ^{\prime 2}} } {\text{ d }}x{\text{ d }}x\right) _{x=L_d} \right. \nonumber \\ {}&-\left. \left( \varphi {\varphi }'\int _0^x {\varphi ^{\prime 2}} {\text{ d }}x+\beta _1 \left( \varphi {\varphi }'\int _0^x {\varphi ^{\prime 2}} {\text{ d }}x\right) _{x=L_d} \right) \right) {\text{ d }}x, \nonumber \\ c=&{} \mathop \int \limits _0^1 \left( {\varphi ^{2}} +\varphi _{x=0}^2 c_\mathrm {b} +\varphi _{x=L}^2 c_\mathrm {b} \right) {\text{ d }}x,\quad \varLambda _1 =e_v +\left( \beta _1 e_v +\beta _2 \left( e_v +e_{v1} \right) \right) |_{x=L_d} , \nonumber \\ \varLambda _2=&{} e_w +\left( \beta _1 e_w +\beta _2 \left( e_w +e_{w1} \right) \right) |_{x=L_d}. \end{aligned}$$

(A.7)