Numerical analysis of natural frequency and stress intensity factor in Euler–Bernoulli cracked beam

Abstract

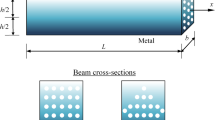
In this paper, the evaluation procedures of the natural frequency and the stress intensity factor in the opening mode are established for the Euler–Bernoulli cracked beam by using (a) a technique in the framework of the finite element method, (b) a group method of data handling (GMDH), and (c) the software ABAQUS software. In the first one, the stiffness and mass matrices of the beam are enriched according to the depth and location of the crack for the determination of the natural frequency. A discrete spring model is used to simulate the crack in the structure based on the energy release rate. The continuity conditions in a cracked element are applied to connect two sub-elements of both sides of the crack. In the second method, the natural frequency and the stress intensity factor are determined using the GMDH algorithm. Design of experiments technique is employed to create an optimum arrangement for the application in the GMDH neural network. A few case studies are examined to investigate the results of the analysis, in addition, to identify the priority and the comparison of the three methods. The procedure of the analysis explains the advantages and limitations of the finite element-based technique, the GMDH method, and ABAQUS.

Appendices

Appendix A

The components of the conversion matrix of the left sub-element:

$$\begin{aligned} D_{L}^{11}= & {} D_{L}^{22}=1 , \end{aligned}$$

(A. 1)

$$\begin{aligned} D_{L}^{12}= & {} D_{L}^{13}=D_{L}^{14}=D_{L}^{21}=D_{L}^{23}=D_{L}^{24}=0 , \end{aligned}$$

(A. 2)

$$\begin{aligned} D_{L}^{31}= & {} \frac{1}{Z}\left( l_{e}^{4}+4l_{e}^{3}\psi -3l_{e}^{2}x_{c}^{2}-12l_{e}^{2}x_{c}\psi +2l_{e}x_{c}^{3}+12l_{e}x_{c}^{2}\psi -4x_{c}^{3}\psi \right) , \end{aligned}$$

(A. 3)

$$\begin{aligned} D_{L}^{32}= & {} \frac{1}{Z}\left( l_{e}^{4}x_{c}-2l_{e}^{3}x_{c}^{2}+4l_{e}^{3}x_{c}\psi +l_{e}^{2}x_{c}^{3}-12l_{e}^{2}x_{c}^{2}\psi +12l_{e}x_{c}^{3}\psi -4x_{c}^{4}\psi \right) , \end{aligned}$$

(A. 4)

$$\begin{aligned} D_{L}^{33}= & {} \frac{1}{Z}\left( 3l_{e}^{2}x_{c}^{2}-2l_{e}x_{c}^{3}+4x_{c}^{3}\psi \right) , \end{aligned}$$

(A. 5)

$$\begin{aligned} D_{L}^{34}= & {} \frac{1}{Z}\left( -l_{e}^{3}x_{c}^{2}+l_{e}^{2}x_{c}^{3}-4l_{e}x_{c}^{3}\psi +4x_{c}^{4}\psi \right) , \end{aligned}$$

(A. 6)

$$\begin{aligned} D_{L}^{41}= & {} \frac{1}{Z}\left( -6l_{e}^{2}x_{c}+6l_{e}x_{c}^{2}-6x_{c}^{2}\psi \right) , \end{aligned}$$

(A. 7)

$$\begin{aligned} D_{L}^{42}= & {} \frac{1}{Z}\left( l_{e}^{4}-4l_{e}^{3}x_{c}+4l_{e}^{3}\psi +{3l}_{e}^{2}x_{c}^{2}-12l_{e}^{2}x_{c}\psi +12l_{e}x_{c}^{2}\psi -6x_{c}^{3}\psi \right) , \end{aligned}$$

(A. 8)

$$\begin{aligned} D_{L}^{43}= & {} \frac{1}{Z}\left( 6l_{e}^{2}x_{c}-6l_{e}x_{c}^{2}+6x_{c}^{2}\psi \right) , \end{aligned}$$

(A. 9)

$$\begin{aligned} D_{L}^{44}= & {} \frac{1}{Z}\left( -2l_{e}^{3}x_{c}+{3l}_{e}^{2}x_{c}^{2}-6l_{e}x_{c}^{2}\psi +6x_{c}^{3}\psi \right) . \end{aligned}$$

(A. 10)

The components of the conversion matrix of the right sub-element:

$$\begin{aligned} D_{R}^{33}= & {} D_{R}^{44}=1 , \end{aligned}$$

(A. 11)

$$\begin{aligned} D_{R}^{31}= & {} D_{R}^{32}=D_{R}^{34}=D_{R}^{41}=D_{R}^{42}=D_{R}^{43}=0, \end{aligned}$$

(A. 12)

$$\begin{aligned} D_{R}^{11}= & {} \frac{1}{Z}\left( l_{e}^{4}+4l_{e}^{3}\psi -3l_{e}^{2}x_{c}^{2}-12l_{e}^{2}x_{c}\psi +2l_{e}x_{c}^{3}+12l_{e}x_{c}^{2}\psi -4x_{c}^{3}\psi \right) , \end{aligned}$$

(A. 13)

$$\begin{aligned} D_{R}^{12}= & {} \frac{1}{Z}\left( l_{e}^{4}x_{c}-2l_{e}^{3}x_{c}^{2}+4l_{e}^{3}x_{c}\psi +l_{e}^{2}x_{c}^{3}-12l_{e}^{2}x_{c}^{2}\psi +12l_{e}x_{c}^{3}\psi -4x_{c}^{4}\psi \right) , \end{aligned}$$

(A. 14)

$$\begin{aligned} D_{R}^{13}= & {} \frac{1}{Z}\left( 3l_{e}^{2}x_{c}^{2}-2l_{e}x_{c}^{3}+4x_{c}^{3}\psi \right) , \end{aligned}$$

(A. 15)

$$\begin{aligned} D_{R}^{14}= & {} \frac{1}{Z}\left( -l_{e}^{3}x_{c}^{2}+l_{e}^{2}x_{c}^{3}-4l_{e}x_{c}^{3}\psi +4x_{c}^{4}\psi \right) , \end{aligned}$$

(A. 16)

$$\begin{aligned} D_{R}^{21}= & {} \frac{1}{Z}\left( -6l_{e}^{2}x_{c}-6l_{e}^{2}\psi +6l_{e}x_{c}^{2}+12l_{e}x_{c}\psi -6x_{c}^{2}\psi \right) , \end{aligned}$$

(A. 17)

$$\begin{aligned} D_{R}^{22}= & {} \frac{1}{Z}\left( l_{e}^{4}-4l_{e}^{3}x_{c}+3l_{e}^{2}x_{c}^{2}-6l_{e}^{2}x_{c}\psi +12l_{e}x_{c}^{2}\psi -6x_{c}^{3}\psi \right) , \end{aligned}$$

(A. 18)

$$\begin{aligned} D_{R}^{23}= & {} \frac{1}{Z}\left( 6l_{e}^{2}x_{c}+6l_{e}^{2}\psi -6l_{e}x_{c}^{2}-12l_{e}x_{c}\psi +6x_{c}^{2}\psi \right) , \end{aligned}$$

(A. 19)

$$\begin{aligned} D_{R}^{24}= & {} \frac{1}{Z}\left( -2l_{e}^{3}x_{c}-2l_{e}^{3}\psi +3l_{e}^{2}x_{c}^{2}+6l_{e}^{2}x_{c}\psi -6l_{e}x_{c}^{2}\psi +6x_{c}^{3}\psi \right) . \end{aligned}$$

(A. 20)

Appendix B

The polynomial equation derived from GMDH method relevant to Table 2c in the determination of the natural frequency for C-F boundary condition:

$$\begin{aligned} y_{7}=\omega _{\mathrm {C-F}}=-0.0129+0.3065y_{5}+0.6919y_{6}+1.2835y_{5}^{2}+1.2465y_{6}^{2}-2.5336y_{5}y_{6}, \end{aligned}$$

(B. 1)

in which

$$\begin{aligned} y_{5}= & {} 0.0592+0.8908 y_{1}+0.8468y_{2}+0.0697y_{1}^{2}-0.2107y_{2}^{2}-0.0178y_{1}y_{2}, \end{aligned}$$

(B. 2)

$$\begin{aligned} y_{6}= & {} 0.0651+0.2924 y_{3}+0.9679y_{4}-0.7217y_{3}^{2}-0.0584y_{4}^{2}+0.0908y_{3}y_{4}, \end{aligned}$$

(B. 3)

and

$$\begin{aligned} y_{1}= & {} -0.1146-0.5181 x_{1}-0.1048x_{4}+0.1440x_{1}^{2}-0.0740x_{4}^{2}+0.0322x_{1}x_{4}, \end{aligned}$$

(B. 4)

$$\begin{aligned} y_{2}= & {} -0.0386-0.4376 x_{2}+0.1473x_{3}+0.1467x_{2}^{2}-0.1091x_{3}^{2}-0.1009x_{2}x_{3}, \end{aligned}$$

(B. 5)

$$\begin{aligned} y_{3}= & {} 0.0106+0.0506 x_{3}-0.1148x_{4}-0.1234x_{3}^{2}+0.0162x_{4}^{2}+0.2357x_{3}x_{4}, \end{aligned}$$

(B. 6)

$$\begin{aligned} y_{4}= & {} -0.2521-0.4772 x_{1}-0.3696x_{2}+0.2319x_{1}^{2}+0.0718x_{2}^{2}+0.0345x_{1}x_{2}. \end{aligned}$$

(B. 7)

The polynomial equation derived from GMDH method relevant to Table 3c in the determination of the stress intensity factor for C-F boundary condition:

$$\begin{aligned} y_{7}=K_{{I}_{\mathrm {C-F}}}=-0.0199+0.5778y_{5} +0.5166y_{6}-0.0103y_{5}^{2}-0.0072y_{6}^{2}+0.0731y_{5}y_{6}, \end{aligned}$$

(B. 8)

in which

$$\begin{aligned} y_{5}= & {} -0.1087+0.9861 y_{1}+0.9669y_{2}+0.1940y_{1}^{2}-0.3077y_{2}^{2}-0.0769y_{1}y_{2}, \end{aligned}$$

(B. 9)

$$\begin{aligned} y_{6}= & {} -0.0332+1.6099 y_{3}+1.0231y_{4}-3.329y_{3}^{2}+0.1587y_{4}^{2}-0.0138y_{3}y_{4}, \end{aligned}$$

(B. 10)

and

$$\begin{aligned} y_{1}= & {} 0.0316+0.2490 x_{1}+0.7884x_{4}+0.0316x_{1}^{2}-0.2319x_{4}^{2}-0.1795x_{1}x_{4}, \end{aligned}$$

(B. 11)

$$\begin{aligned} y_{2}= & {} 0.0149+0.1473 x_{2}-0.2022x_{3}+0.0149x_{2}^{2}+0.0426x_{3}^{2}+0.0092x_{2}x_{3} ,\end{aligned}$$

(B. 12)

$$\begin{aligned} y_{3}= & {} 0.0084-0.0207 x_{3}-0.2191x_{4}+0.0084x_{3}^{2}+0.0801x_{4}^{2}+0.0759x_{3}x_{4}, \end{aligned}$$

(B. 13)

$$\begin{aligned} y_{4}= & {} 0.1161+0.2774 x_{1}+0.5071x_{5}-0.0096x_{1}^{2}-0.0630x_{5}^{2}-0.0581x_{1}x_{5}. \end{aligned}$$

(B. 14)

Appendix C

Modeling differences between ABAQUS and the finite element in a more accurate representation:

	ABAQUS	Finite element-based technique
Assumptions	2D analysis of the beam	1D analysis of the beam
	2D modeling of the crack	1D modeling of the crack
	Using C-Integral for the crack modeling	Using rotational spring for the crack modeling
	Plane stress state	Neglecting transverse shear deformation
Global steps	Drawing model	Using cubical Hermit functions
	Definition of material properties	Definition of strain–displacement and stress–strain relationships
	Assembling the model	Derivation of the standard stiffness and mass matrices
	Definition of the static/vibration solver	Derivation of the enriched stiffness and mass matrices
	Creating an interaction for the crack modeling	Assembling the stiffness and mass matrices and the force vector
	Applying loads and boundary conditions	Applying boundary conditions
	Meshing	Determination of displacements
	Definition of job
Advantages	Implementation of a relatively complete modeling for the beam and the crack	The short time of preparation and processing
	No need to derive equations	Flexibility in changing material and geometric characteristics and boundary conditions
	2D Graphical display of stress contours in the region around the crack tip
Disadvantages	The necessity of re-meshing and repartitioning for every new model	The decrease in the accuracy of results in crack depths higher than .8h
	Time-consuming in the preparation and processing	Un-capability in the illustration of stress contours in the region around the crack tip