Validation of Bredt’s formulas for beams with hollow cross sections by the method of asymptotic splitting for pure torsion and their extension to shear force bending

Abstract

The equations governing pure torsion of prismatic beams with thin-walled closed cross sections, known as Bredt’s formulas, are verified using the method of asymptotic splitting. In particular, the strong formulation of the Saint-Venant problem of a straight beam is expanded asymptotically. We begin by validating well-known technical assumptions for the shear stress distribution. Furthermore, the influence of a transverse force acting on the beam is considered. This shear force causes a deformation of the cross section, and therefore an adaption of Bredt’s formulas is needed. Two distinct formulations of the shear center, called the kinematic and the energetic shear center, are obtained. The latter is verified in numerical experiments.

1 Introduction

Due to their lightweight compared to the stiffness, single- and multi-cell thin-walled beams are widely used in engineering. Useful design tools for such structures are the formulas of Bredt, which in the case of a single-cell cross section read

$$\begin{aligned}&M_T= \mu \alpha J_\mathrm{T},\quad J_\mathrm{T}=4A_{\varGamma }^2 \left( \oint _{\varGamma }\frac{\mathrm{d}s}{h(s)}\right) ^{-1} \end{aligned}$$

(1)

$$\begin{aligned}&2 A_{\varGamma } \mu \alpha =\oint _{\varGamma } \tau \mathrm{d}s. \end{aligned}$$

(2)

In (1), the torque $M_T$ is expressed as a function of the shear modulus $\mu$, the torsional rigidity $J_\mathrm{T}$, and the rate of twist $\alpha$. The area enclosed by the center line $\varGamma$ is defined as $A_{\varGamma }$, and the wall thickness h(s) varies along the arc coordinate s. The formulas are derived under the engineering assumption of a constant shear stress over the thickness. As a further assumption, shear stresses orthogonal to $\varGamma$ are neglected. Equation(2) relates the shear stress $\tau$ with the deformation. In [1], the same simplifications are used to obtain the position of the shear center by using Bredt’s formulas as an approximation even in the case of combined bending and torsion. We validate the engineering assumptions by an asymptotic analysis of an arbitrary single-cell cross section. Therefore, we consider the Saint-Venant problem of a linear elastic beam. The analytical description of linear elastic beams with arbitrary, also multiply connected cross sections, was done by Eliseev [2, 3]. In the limit of small thicknesses h, represented by a formal small parameter $\lambda$, the cross section can be characterized by its center line and a small dimension orthogonal to it. The strong form of the equations is developed asymptotically to obtain the principal terms of shear stresses and related quantities. The determination of the principal terms requires the solvability conditions of the minor terms, which is intrinsic to the procedure of asymptotic splitting. This method has also been applied to the actual problem but with constant wall thickness in [3] and to the problem of constrained warping of thin open cross sections as well as plate equations in [4,5,6]. Another possibility of an asymptotic analysis is shown in [7], in which also higher terms are derived, but again only constant thickness is considered. Further asymptotic solutions of the problem were found by the authors of [8, 9], who used the weak formulation of the problem.

In the present paper, the solutions are used to verify Bredt’s formulas and to find expressions of the shear centers. There are two definitions of the shear center. The first one defines it as the point, in which a single shear force has to act such that no twisting occurs. The second one defines it as the position where the shear force and an additional applied torque do not perform work on each other’s deformations. It can be shown that for open thin cross sections these definitions are asymptotically equivalent, whereas in the case of multiply connected ones these two are distinct. In the present paper, we show that even in the case of a single-cell cross section with constant wall thickness the difference remains, a result that so far has not been reported in the literature. The analytical results are validated numerically against the formulation of Lacarbonara [10].

Fig. 1

Thin-walled single-cell cross section including vectors and the coordinate system

2 Notations and formulation of the problem

We study stresses and displacements of a Saint-Venant solution for a prismatic beam, whose axis is directed along the unit vector $\mathbf {e}_z$ with coordinate z, and with the constant cross section placed orthogonal to it in the (x, y)-plane with a position vector $\mathbf {x}=x\mathbf {e}_x+y\mathbf {e}_y$ (Fig. 1). In case of a thin-walled cross section, we describe this position vector by

$$\begin{aligned} \mathbf {x}=\mathbf {x}_0(s)+\lambda n \mathbf {e}_n, \end{aligned}$$

(3)

with the center line $\mathbf {x}_0$ as function of its arc length s, the coordinate n with $-~\frac{h}{2}~\le ~n~\le ~~\frac{h}{2}$ orthogonal to the center line(with unit vector $\mathbf {e}_n$), and $\lambda$ being a formal small parameter, representing the smallness of the thickness h.

$$\begin{aligned} \mathbf {e}_t=\frac{\partial \mathbf {x}_0}{\partial s} \end{aligned}$$

(4)

is the unit tangential vector of the center line $\varGamma$ of the thin-walled profile. With the curvature $\kappa$, we can write the normal vector

$$\begin{aligned} \mathbf {e}_n=-\kappa ^{-1}\frac{\partial \mathbf {e}_t}{\partial s}, \end{aligned}$$

(5)

which is orthogonal to $\mathbf {e}_t$. With the Frenet formula

$$\begin{aligned} \frac{\partial \mathbf {e}_n}{\partial s}=\kappa \mathbf {e}_t, \end{aligned}$$

(6)

the nabla operator is determined by

$$\begin{aligned} \nabla =\mathbf {e}_t \frac{\partial }{h_s\partial s}+\mathbf {e}_n \frac{\partial }{h_n\partial n}= (1+n\lambda \kappa )^{-1}\mathbf {e}_t\frac{\partial }{\partial s}+\lambda ^{-1}\mathbf {e}_n\frac{\partial }{\partial n}, \end{aligned}$$

(7)

with the Lamé coefficients

$$\begin{aligned} h_i^2=\frac{\partial \mathbf {x}}{\partial i}\cdot \frac{\partial \mathbf {x}}{\partial i}. \end{aligned}$$

(8)

$\nabla \mathbf {x} = \mathbf {I}_2$ holds with the identity tensor $\mathbf {I}_2$. Similar to the vectors $\mathbf {e}_t$ and $\mathbf {e}_n$ of the center line, there are a tangential vector $\mathbf {t}$ and a normal vector $\mathbf {n}$ at the boundary of the cross section. Because of the varying thickness, the directions of $\mathbf {t}$ and $\mathbf {e}_t$ as well as $\mathbf {n}$ and $\mathbf {e}_n$ are different. Note that we have $\mathbf {e}_z=\mathbf {e}_x\times \mathbf {e}_y=-\mathbf {e}_t\times \mathbf {e}_n$. Although the small parameter $\lambda$ has already been introduced, we present the general exact solution of the Saint-Venant problem. The origin $\mathbf {x}=0$ is chosen as the area center of the cross section; therefore,

$$\begin{aligned} \mathbf {x}_A=\frac{1}{A}\int _A \mathbf {x}\mathrm{d}A=0. \end{aligned}$$

(9)

Now, we briefly present the basic relations of the solution of Saint-Venant for a prismatic beam, loaded by moments $\mathbf {M}$ and forces $\mathbf {Q}$. The moment $\mathbf {M}(L)$ and force $\mathbf {Q}$ are applied at $z=L$, as well as $-\mathbf {M}(0)=\mathbf {M}(L)+L\mathbf {e}_z\times \mathbf {Q}$ and $-\mathbf {Q}$ act at $z=0$. The lateral surfaces of the beam are unloaded. We seek the stress tensor $\mathbf {T}$ in the form

$$\begin{aligned} \mathbf {T}=\sigma _z\mathbf {e}_z\mathbf {e}_z+\varvec{\tau }\mathbf {e}_z+\mathbf {e}_z\varvec{\tau }, \end{aligned}$$

(10)

with no in-plane components. The equilibrium equations for the axial component $\sigma _z$ and for the shear stresses $\varvec{\tau }$ are

$$\begin{aligned} \sigma _z=a+\mathbf {b}(z)\cdot \mathbf {x}\quad \text {and}\quad \nabla \cdot \varvec{\tau }=-\mathbf {b'}\cdot \mathbf {x}, \end{aligned}$$

(11)

a being the mean axial stress, and $\mathbf {b'}=\partial \mathbf {b}/\partial z$ determines the linear distribution of the axial stress in the cross section. We can write

$$\begin{aligned} \mathbf {b'}=\mathbf {J}^{-1}\cdot \mathbf {Q}_0,\quad \text {with } \mathbf {J}=\int _A\mathbf {x}\mathbf {x}\mathrm{d}A, \end{aligned}$$

(12)

with the tensor of the area moments of inertia $\mathbf {J}$ and the shear force $\mathbf {Q}_0$, which is the in-plane part of $\mathbf {Q}$. Furthermore, we have to satisfy the compatibility condition

$$\begin{aligned} \varDelta \varvec{\tau }=-(1+\nu )^{-1}\mathbf {b'}, \end{aligned}$$

(13)

written in the form of the Beltrami equation, with $\nu$ being Poisson’s ratio. The shear stress vector can be expressed as

$$\begin{aligned} \varvec{\tau }=\nabla \varphi +\nabla \psi \times \mathbf {e}_z \end{aligned}$$

(14)

with

$$\begin{aligned} \varDelta \varphi&=-\mathbf {b'}\cdot \mathbf {x}, \end{aligned}$$

(15)

$$\begin{aligned} \varDelta \psi&=-\nu (1+\nu )^{-1}\mathbf {b'}\times \mathbf {e}_z\cdot \mathbf {x}-2\mu \alpha \end{aligned}$$

(16)

in which $\mu$ is the shear modulus and $\alpha$ a constant. Later, we will see that $\alpha$ has the meaning of the average rate of twist of the cross section. The boundary conditions are fulfilled if

$$\begin{aligned} \varvec{\tau }\cdot \mathbf {n}=\mathbf {n}\cdot \nabla \varphi +(\mathbf {e}_z\times \mathbf {n})\cdot \nabla \psi =0. \end{aligned}$$

(17)

The first term implies that the normal derivative of $\varphi$ is zero at the boundaries, whereas the second term enforces the tangential derivative of $\psi$ to be zero. From this second expression, we conclude that $\psi$ must be constant at each closed contour of the boundary. In the case of a single-cell cross section, there are two such contours; therefore, we choose one constant to be zero, the other one is yet undetermined.

3 The method of asymptotic splitting

The asymptotic method used in this paper is based on introducing in the problem a formal small parameter $\lambda$, which is first used to obtain a serial expansion for $\lambda \rightarrow 0$, but is set equal to 1 after finishing the procedure (see also in Andrianov [11]). Assuming the order of the principal terms in the solution, we balance the leading-order terms in the equations. In general, the solution is not unique yet. Therefore, higher orders of $\lambda$ have to be considered. The method is demonstrated by considering a linear algebraic system

$$\begin{aligned} (C_0+\lambda C_1)u=f,\quad \det C_0=0,\quad \lambda \rightarrow 0, \end{aligned}$$

(18)

which becomes singular, if $\lambda$ tends to zero. Therefore, we seek u in the form of a power series in $\lambda$, starting with $\lambda ^{-1}$:

$$\begin{aligned} u=\lambda ^{-1}u^{(0)}+\lambda ^0 u^{(1)}+\lambda u^{(2)}+\cdots \end{aligned}$$

(19)

Inserting u finds the principal order ($\lambda ^{-1}$) term to

$$\begin{aligned} C_0 u^{(0)}=0 \quad \rightarrow \quad u^{(0)}=\sum a_k\varphi _k,\quad \text {with }C_0\varphi _k=0. \end{aligned}$$

(20)

The solution $u^{(0)}$ is a linear combination of the fundamental solutions $\varphi _k$, but the coefficients $a_k$ are still undetermined. Therefore, we have to consider the first minor order term ($\lambda ^0$):

$$\begin{aligned} C_0u^{(1)}=f-C_1 u^{(0)}. \end{aligned}$$

(21)

Both sides are multiplied by $\psi _i^\mathrm{T}$, and the solutions of the conjugate system $C_0^\mathrm{T}\psi _i=0$; hence, we obtain

$$\begin{aligned} 0=\psi _i^\mathrm{T}\left( f-C_1\sum a_k\varphi _k\right) . \end{aligned}$$

(22)

This further condition results in a linear system for the coefficients $a_k$. If this system is again singular, further minor terms have to be considered. For a more detailed presentation of regular and singular perturbed linear systems, see [12]. Depending on the problem, also boundary layers may arise [13]. Note that instead of introducing $\lambda$ it would be possible to nondimensionalize the equations and search for a dimensionless parameter, which is physically small. But in our opinion the introduction of $\lambda$ is, at least when searching just the principal terms, more convenient.

4 Bredt’s formulas of a single-cell cross section

First, the shear stress is determined to validate that it is constant over the thickness, and next the displacements are used to identify this constant.

4.1 Validation of the assumptions of the shear stress $\varvec{\tau }$

The equilibrium equations and the compatibility conditions are equivalent to two partial differential equations (15), (16), namely Poisson equations for the functions $\varphi$ and $\psi$. From (12), we conclude with

$$\begin{aligned} \mathrm{d}A=\lambda (1+\lambda \kappa n)\mathrm{d}n\,\mathrm{d}s \end{aligned}$$

(23)

that

$$\begin{aligned} \mathbf {b}'=\lambda ^{-1}\mathbf {b}^{(0)'}+\lambda ^0\mathbf {b}^{(1)'}+\cdots . \end{aligned}$$

(24)

Seeking the solution for $\varphi$ as

$$\begin{aligned} \varphi =\lambda ^{-1}\varphi ^{(0)}+\lambda ^0\varphi ^{(1)}+\lambda ^1\varphi ^{(2)}+\cdots , \end{aligned}$$

(25)

and inserting into (15), we find

$$\begin{aligned}&\left[ \left( (1+n\kappa \lambda )^{-1}\frac{\partial }{\partial s}\right) ^2+\lambda ^{-1}\kappa (1+\lambda \kappa n)^{-1}\frac{\partial }{\partial n}+\lambda ^{-2}\frac{\partial ^2}{\partial n^2}\right] \nonumber \\&\quad \times \left( \lambda ^{-1}\varphi ^{(0)}+\lambda ^0\varphi ^{(1)}+\lambda ^1\varphi ^{(2)}+\cdots \right) = -\lambda ^{-1}\mathbf {b}^{(0)'}\cdot \mathbf {x}_0+\cdots \text { .} \end{aligned}$$

(26)

With a series expansion in terms of $\lambda$, this equation can be arranged by orders of $\lambda ^{-3}$, $\lambda ^{-2}$ and $\lambda ^{-1}$. Hence, we obtain

$$\begin{aligned} \frac{\partial ^2}{\partial n^2}\varphi ^{(0)}&= 0, \end{aligned}$$

(27)

$$\begin{aligned} \frac{\partial ^2}{\partial n^2}\varphi ^{(1)} +\kappa \frac{\partial }{\partial n}\varphi ^{(0)}&= 0,\end{aligned}$$

(28)

$$\begin{aligned} \frac{\partial ^2}{\partial n^2}\varphi ^{(2)} +\kappa \frac{\partial }{\partial n} \varphi ^{(1)} +\frac{\partial ^2}{\partial s^2}\varphi ^{(0)}(s)&= -\mathbf {b}^{(0)'}\cdot \mathbf {x}_0(s). \end{aligned}$$

(29)

The boundary conditions on the outer and inner surface are $\mathbf {n}\cdot \nabla \varphi \big \vert _{n=\pm h/2}=0$. With

$$\begin{aligned} \mathbf {n}\bigg |_{n=\pm h/2} =\mp \frac{\mathbf {e}_z\times \partial \mathbf {x}/\partial s}{|\mathbf {e}_z\times \partial \mathbf {x}/\partial s|}=\pm \mathbf {e}_n-\frac{1}{2}\,\lambda \frac{\partial }{\partial s} h\mathbf {e}_t+\frac{\lambda }{2} h\kappa \mathbf {e}_n+\cdots , \end{aligned}$$

(30)

the boundary condition becomes

$$\begin{aligned} \left( -\frac{1}{2}\lambda \frac{\partial h}{\partial s}\frac{\partial }{\partial s}\pm \lambda ^{-1}\frac{\partial }{\partial n}+\lambda ^0\frac{h\kappa }{2}\frac{\partial }{\partial n}+\cdots \right) \left( \lambda ^{-1}\varphi ^{(0)}+\varphi ^{(1)}+\lambda \varphi ^{(2)}+\cdots \right) \bigg \vert _{n=\pm h/2}=0. \end{aligned}$$

(31)

Collecting terms of different orders in the boundary condition yields

$$\begin{aligned}&\lambda ^{-2}:\qquad \left. \frac{\partial \varphi ^{(0)}}{\partial n}\right| _{n=\pm h/2}=0, \end{aligned}$$

(32)

$$\begin{aligned}&\lambda ^{-1}:\qquad \left. \left( \pm \frac{\partial \varphi ^{(1)}}{\partial n}+\frac{h\kappa }{2}\frac{\partial \varphi ^{(0)}}{\partial n}\right) \right| _{n=\pm h/2}=0, \end{aligned}$$

(33)

$$\begin{aligned}&\lambda ^0:\qquad \left. \left( \pm \frac{\partial \varphi ^{(2)}}{\partial n}+\frac{h\kappa }{2}\frac{\partial \varphi ^{(1)}}{\partial n}-\frac{1}{2}\frac{\partial h}{\partial s}\frac{\partial \varphi ^{(0)}}{\partial s}\right) \right| _{n=\pm h/2}=0. \end{aligned}$$

(34)

Together with (27), (28), and (29), we conclude that $\varphi ^{(0)}=\varphi ^{(0)}(s)$ and $\varphi ^{(1)}=\varphi ^{(1)}(s)$, as well as

$$\begin{aligned} \varphi ^{(2)}=-\frac{n^2}{2}\left( \mathbf {b}^{(0)'}\cdot \mathbf {x}_0-\frac{\partial ^2\varphi ^{(0)}}{\partial s^2}\right) +C_1(s)n+C_2(s). \end{aligned}$$

(35)

Inserting $\varphi ^{(2)}$ into the two boundary conditions of order $\lambda ^0$ at $n=\pm h/2$ gives

$$\begin{aligned} -\frac{1}{2}\frac{\partial h}{\partial s}\frac{\partial \varphi ^{(0)}}{\partial s} +\frac{h}{2}\left( -\mathbf {b}^{(0)'}\cdot \mathbf {x}_0-\frac{\partial ^2 \varphi ^{(0)}}{\partial s^2}\right) \pm C_1(s)=0, \end{aligned}$$

(36)

such that $C_1(s)$ must vanish, and we have

$$\begin{aligned} \frac{\partial }{\partial s}\left( h\frac{\partial \varphi ^{(0)}}{\partial s}\right) +h\mathbf {b}^{(0)'}\cdot \mathbf {x}_0=0, \end{aligned}$$

(37)

from which $\varphi ^{(0)}$ can be computed. To start the asymptotics of $\psi$, it is imperative to know the order of the right-hand side terms. Therefore, we compute the torque to

$$\begin{aligned} M_z=\int _A\mathbf {x}\times \varvec{\tau }\cdot \mathbf {e}_z \mathrm{d}A=\mathbf {e}_z\cdot \int _A\mathbf {x}\times \nabla \varphi \mathrm{d}A-\left( \oint _{\partial A}\mathbf {n}\cdot \mathbf {x}\psi \mathrm{d}s-2\int _A\psi \mathrm{d}A\right) . \end{aligned}$$

(38)

Knowing the result for the special case of pure torsion of a circular ring , we conclude from (38) that the principal order of $\psi$ has to be $\lambda ^0$ and the rate of twist has to be $\alpha =\lambda ^{-1}\alpha ^{(0)}+\cdots$. Therefore, the boundary conditions are $\psi (n=+h/2)=0$ and $\psi (n=-h/2)=\lambda ^0 C^{(0)}+\cdots$. With $\psi =\lambda ^0\psi ^{(0)}+\cdots$, the asymptotic equations are

$$\begin{aligned}&\lambda ^{-1}:\qquad \frac{\partial ^2 \psi ^{(0)}}{\partial n^2}=0, \end{aligned}$$

(39)

$$\begin{aligned}&\lambda ^{0}:\qquad \frac{\partial ^2 \psi ^{(1)}}{\partial n^2}=-\kappa \frac{\partial \psi ^{(0)}}{\partial n}-2\mu \alpha ^{(0)}-\frac{\nu }{1+\nu }\mathbf {b}^{(0)'}\times \mathbf {e}_z\cdot \mathbf {x}_0, \end{aligned}$$

(40)

with the principal solution

$$\begin{aligned} \psi ^{(0)}=C^{(0)}\left( \frac{1}{2}-\frac{n}{h}\right) . \end{aligned}$$

(41)

Finally, one can insert the results into (14) to compute the shear stress vector

$$\begin{aligned} \varvec{\tau }&=\left( \mathbf {e}_t\frac{\partial }{\partial s}+\lambda ^{-1} \mathbf {e}_n\frac{\partial }{\partial n}\right) (\lambda ^{-1}\varphi ^{(0)}(s)+\lambda ^0\varphi ^{(1)}(s)+\cdots ) \end{aligned}$$

(42)

$$\begin{aligned}&\quad + \left( \mathbf {e}_t\frac{\partial }{\partial s}+\lambda ^{-1}\mathbf {e}_n\frac{\partial }{\partial n}\right) \left[ \lambda ^0C^{(0)} \left( \frac{1}{2}-\frac{n}{h}\right) +\cdots \right] \times \mathbf {e}_z \end{aligned}$$

(43)

$$\begin{aligned}&=\lambda ^{-1}\mathbf {e}_t\frac{\partial \varphi ^{(0)}}{\partial s}-\lambda ^{-1}\mathbf {e}_n\times \mathbf {e}_zC^{(0)}/h+\cdots . \end{aligned}$$

(44)

Hence, the principal term of the shear stress vector,

$$\begin{aligned} \varvec{\tau }=\lambda ^{-1} \left( \frac{\partial \varphi ^{(0)}}{\partial s}+\frac{C^{(0)}}{h}\right) \mathbf {e}_t+\cdots =\lambda ^{-1} \tau (s) \mathbf {e}_t+\cdots , \end{aligned}$$

(45)

is constant through the thickness and tangential to the center line. With $\mathbf {b}=0$ in pure torsion, $\varphi ^{(0)}=0$ holds. Setting $\lambda =1$, the shear stress vector is $\varvec{\tau }h=C^{(0)}\mathbf {e}_t$, and $C^{(0)}$ is computed from the circulatory theorem

$$\begin{aligned} \frac{1}{\mu \alpha }\oint \tau \mathrm{d}s=2A_{\varGamma }. \end{aligned}$$

(46)

With the shear flow $T=\tau h=C^{(0)}$ Bredt’s formulas are obtained. In this paper, we are further interested in the extension of Bredt’s formulas to account for shear forces. With the definition of the shear flow

$$\begin{aligned} T(s)=\int _{-h/2}^{+h/2} \tau \mathrm{d}n, \end{aligned}$$

(47)

the integration of $\tau$ across the thickness yields

$$\begin{aligned} h\frac{\partial \varphi ^{(0)}}{\partial s}=\tau h-C^{(0)}=T-C^{(0)}. \end{aligned}$$

(48)

Inserting this formula into (37) yields the known equations

$$\begin{aligned}&\frac{\partial T}{\partial s}+h\mathbf {b}^{(0)'}\cdot \mathbf {x}_0=\frac{\partial T}{\partial s}+h\frac{\partial \sigma _{z}}{\partial z}=0, \end{aligned}$$

(49)

with $\mathbf {b}^{(0)'}\cdot \mathbf {x}_0=\partial \sigma _{z}/\partial z$ , from which we find the shear flow

$$\begin{aligned} T(s)=T_0-\int _0^s h\mathbf {b}^{(0)'}\cdot \mathbf {x}_0 \mathrm{d}s. \end{aligned}$$

(50)

Next, we establish a further condition to evaluate $T_0=T(s=0)$, which follows from the continuity of the displacements.

4.2 Consideration of the displacements

Due to the absence of in-plane stresses in the cross-sectional plane, the in-plane strains $\varvec{\varepsilon }_0=(\nabla \mathbf {u}_0)_\mathrm{sym}=-\nu \mathbf {I}_2\varepsilon _z$ are caused only by the Poisson effect, with the 2D identity tensor $\mathbf {I}_2$ and the axial strain $\varepsilon _z$. The resulting displacements $\mathbf {u}=\mathbf {u}_0+u_z\mathbf {e}_z$ according to Hooke’s law applied to the principal strains and the axial stress $\sigma _z$, including an additional in-plane rigid body motion $\mathbf {U}_0+\omega \mathbf {e}_z\times \mathbf {x}$ as well as an additional axial displacement $U_z(\mathbf {x})$, are

$$\begin{aligned} \mathbf {u_0}&=-(\nu /E)(a\mathbf {x}+\mathbf {b}\cdot \mathbf {xx}-\frac{1}{2}\mathbf {b x\cdot x})+\mathbf {U}_0(z)+\omega (z)\mathbf {e}_z\times \mathbf {x}, \end{aligned}$$

(51)

$$\begin{aligned} u_z&=1/E(az+[\mathbf {b}(L)z-(Lz-z^2/2)\mathbf {b'}]\cdot \mathbf {x})+U_z(\mathbf {x}). \end{aligned}$$

(52)

For details of this classical result, see [2]. The displacement $U_z(\mathbf {x})$ may be used, too, to obtain the solution, but as seen below, usage of the stresses $U_z(\mathbf {x})$ is not needed. The displacements are inserted into Hooke’s law,

$$\begin{aligned} \varvec{\tau }(\mathbf {x})/\mu =\partial _z\mathbf {u}_0+\nabla u_z. \end{aligned}$$

(53)

If we insert the displacements as well as $\psi$ and $\varphi$ into Hooke’s law and take the rotor $\nabla \times$, we find $\alpha =\omega '$; see Eliseev [2]. This is the proof of the above statement that $\alpha$ is the mean rate of twist. It should be mentioned that because of Poisson’s ratio the rate of twist is not constant within the cross section. The resulting equation splits into a part, which depends on z and one part, which is independent of z. Both must hold on their own. The part dependent of z is

$$\begin{aligned} 0=\mathbf {U}_0'+E^{-1}[\mathbf {b}(L)z-(Lz-z^2/2)\mathbf {b'}]. \end{aligned}$$

(54)

In the following, we consider only the part of the equation which is independent of z, which reads

$$\begin{aligned} \varvec{\tau }/\mu =\nabla U_z+\frac{\nu }{E}\mathbf {b'}\cdot \left( -\mathbf {xx}+\frac{1}{2}\mathbf {I}_2\mathbf {x\cdot x}\right) +\alpha \mathbf {e}_z\times \mathbf {x}. \end{aligned}$$

(55)

Next we take the principal terms of the equation and integrate along the center line $\varGamma$,

$$\begin{aligned} \oint _{\varGamma }\tau \mathrm{d}s/\mu&=\oint _{\varGamma }\mathbf {e}_t\cdot \varvec{\tau }\mathrm{d}s/\mu \nonumber \\&=\alpha ^{(0)} 2A_{\varGamma }+\underbrace{\oint _{\varGamma }\mathbf {e}_t\cdot \nabla U_z \mathrm{d}s}_{0}+\frac{\nu }{E}\mathbf {Q}_0\cdot \left( \mathbf {J}^{(0)}\right) ^{-1}\cdot \oint \left( -\mathbf {e}_t\cdot \mathbf {x}_0 \mathbf {x}_0+\frac{1}{2}\mathbf {e}_t(\mathbf {x}_0\cdot \mathbf {x}_0)\right) \mathrm{d}s, \end{aligned}$$

(56)

with $A_{\varGamma }$ being the area enclosed by the center line. With $\partial \mathbf {x}_0/\partial s=\mathbf {e}_t$ and integration by parts, we find

$$\begin{aligned} \oint _{\varGamma }\tau \mathrm{d}s=2\alpha ^{(0)} A_{\varGamma }\mu +\frac{\nu }{2(1+\nu )}\mathbf {Q}_0\cdot \left( \mathbf {J}^{(0)}\right) ^{-1}\cdot \oint _{\varGamma }\mathbf {e}_t(\mathbf {x}_0\cdot \mathbf {x}_0)\mathrm{d}s, \end{aligned}$$

(57)

where we already can see (2) in the case of pure torsion ($\mathbf {Q}_0=0$). According to the Stokes theorem,

$$\begin{aligned} \oint _{\partial A_{\varGamma }}\mathbf {v}\cdot \mathrm{d}\mathbf {x}=\int _{A_{\varGamma }} \nabla \times \mathbf {v}\cdot \mathbf {e}_z \mathrm{d}A_{\varGamma }, \end{aligned}$$

(58)

the integral on the right-hand side can be transformed to an area moment of first order, which does not vanish, because the coordinate system was set in the gravity center of the cross section, which is not the gravity center of the embedded area. This leads finally to an expression for the remaining unknown $C^{(0)}$,

$$\begin{aligned} C^{(0)}\oint _{\varGamma }\frac{\mathrm{d}s}{h}=\oint _{\varGamma }\tau \mathrm{d}s=2\alpha ^{(0)} A_{\varGamma }\mu -\frac{\nu }{1+\nu }\mathbf {b}^{(0)'}\cdot \mathbf {x}_{\varGamma }A_{\varGamma }\times \mathbf {e}_z, \end{aligned}$$

(59)

with $A_{\varGamma }\mathbf {x}_{\varGamma }=\int _{A_{\varGamma }} \mathbf {x} \mathrm{d}A_{\varGamma }$. According to Eliseev[3], the work conjugate of the moment $M_z$ is

$$\begin{aligned} \theta _z'=\alpha ^{(0)} -\frac{\nu }{E}\mathbf {b}^{(0)'}\cdot \mathbf {x}_{\varGamma }\times \mathbf {e}_z. \end{aligned}$$

(60)

Inserting $\theta _z'$ into the above equation results in

$$\begin{aligned} C^{(0)}\oint _{\varGamma }\frac{\mathrm{d}s}{h}=\oint _{\varGamma }\tau \mathrm{d}s=2A_{\varGamma }\mu \theta _z'. \end{aligned}$$

(61)

Further, by inserting $\tau =T/h$, we obtain $T_0$ as

$$\begin{aligned} T_0= \left( \oint _{\varGamma }\frac{\mathrm{d}s}{h}\right) ^{-1}\left[ 2A_{\varGamma }\mu \theta _z'+\oint _{\varGamma }\frac{1}{h}\left( \int _0^s \mathbf {b}^{(0)'}\cdot \mathbf {x}_0h\,\mathrm{d}s\right) \mathrm{d}s\right] . \end{aligned}$$

(62)

With (48), we can write the leading order $\lambda ^0$ of the torque as

$$\begin{aligned} M_z&=\mathbf {e}_z\cdot \int \mathbf {x}\times \varvec{\tau }\mathrm{d}A=\mathbf {e}_z \cdot \oint _{\varGamma }\mathbf {x}_0\times \mathbf {e}_t \tau (s) h \mathrm{d}s\nonumber \\&=2A_{\varGamma }T_0-\mathbf {b}^{(0)'}\cdot \oint _{\varGamma }\left( \int _0^s\mathbf {x}_0 h \mathrm{d}s\right) p\mathrm{d}s\nonumber \\&=\mu J_\mathrm{T}\theta _z'+\oint _{\varGamma } \left( 2A_{\varGamma }\left( \oint _{\varGamma }\frac{\mathrm{d}s}{h}\right) ^{-1}\frac{1}{h}- p\right) \left( \int _0^s \mathbf {b}^{(0)'}\cdot \mathbf {x}_0h\,\mathrm{d}s\right) \mathrm{d}s \end{aligned}$$

(63)

with $p=\mathbf {e_n\cdot x_0}$. Integrating by parts and noting $\oint x_0 h \mathrm{d}s=0$, we obtain

$$\begin{aligned} M_z=&\mu J_\mathrm{T}\theta _z'+\mathbf {b}^{(0)'}\cdot \oint _{\varGamma }\left( -2A_{\varGamma }\left( \oint _{\varGamma }\frac{\mathrm{d}s}{h}\right) ^{-1}\int _0^s\frac{1}{h}\mathrm{d}\bar{s}+\int _0^s p\, \mathrm{d}\bar{s}\right) \mathbf {x}_0 h\,\mathrm{d}s. \end{aligned}$$

(64)

With the abbreviations

$$\begin{aligned} 2a(s)=\int _0^s p\,d\bar{s},\quad b(s)=\int _0^s \frac{d\bar{s}}{h},\quad B=\oint \frac{\mathrm{d}s}{h}, \end{aligned}$$

we have

$$\begin{aligned} M_z= \mu J_\mathrm{T}\theta _z'+\mathbf {b}^{(0)'}\cdot \oint _{\varGamma }\left( 2a(s)-\frac{2A_{\varGamma }}{B}b(s)\right) \mathbf {x}_0 h\,\mathrm{d}s. \end{aligned}$$

(65)

The terms in the brackets represent the principal term of the warping function W from pure torsion; therefore, we can write

$$\begin{aligned} M_z= \mu J_\mathrm{T}\theta _z'+\mathbf {b}^{(0)'}\cdot \oint _{\varGamma }W\mathbf {x}_0 h\,\mathrm{d}s. \end{aligned}$$

(66)

If we assume pure torsion ($\mathbf {b'=0}$), the rate of twist $\alpha ^{(0)}$ is equal to $\theta _z$, and we get

$$\begin{aligned} M_T=M_z\bigg |_{\mathbf {b}^{(0)'}=0}=\mu \alpha ^{(0)} J_\mathrm{T}, \end{aligned}$$

(67)

which validates (1). Repeating (61), the adapted second formula of Bredt including shear forces is

$$\begin{aligned} \oint _{\varGamma } \tau \mathrm{d}s=2 A_{\varGamma } \mu \theta _z' . \end{aligned}$$

In the case of pure torsion, with $\theta _z'=\alpha ^{(0)}$, we recover (2).

4.3 Shear center

The kinematic shear center $\mathbf {x}^*$ is defined as the point where a shear force $\mathbf {Q}_0$ causes no twisting of the beam ($\alpha =0)$. The torque resulting from the shear stresses $\varvec{\tau }$ has to compensate the torque caused by the shear force, that is,

$$\begin{aligned} M_z\bigg \vert _{\alpha =0}=\mathbf {e}_z\cdot \mathbf {x}^*\times \mathbf {Q}_0=\mathbf {Q}_0 \cdot \mathbf {e}_z\times \mathbf {x}^*. \end{aligned}$$

(68)

Next, we substitute $M_z$ considering $\alpha =0$ and get

$$\begin{aligned} \mathbf {Q}_0\cdot \mathbf {e}_z\times \mathbf {x}^*=&-J_\mathrm{T}\frac{\nu }{2(1+\nu )}\mathbf {b}^{(0)'}\cdot \mathbf {x}_{\varGamma }\times \mathbf {e}_z +\mathbf {b}^{(0)'}\cdot \oint _{\varGamma }W\mathbf {x}_0 h\,\mathrm{d}s. \end{aligned}$$

We substitute $\mathbf {b'}^{(0)}$ from (12), cancel $\mathbf {Q}_0$, and multiply the resulting equation with $\times \mathbf {e}_z$. The resulting equation is

$$\begin{aligned} \mathbf {x}^*=\left( \mathbf {J}^{(0)}\right) ^{-1}\left( J_\mathrm{T}\frac{\nu }{2(1+\nu )}\mathbf {x}_{\varGamma } +\oint _{\varGamma }W\mathbf {x}_0 h\,\mathrm{d}s\times \mathbf {e}_z\right) . \end{aligned}$$

(69)

Expressions for the coordinates of the shear center can be written in a simple form if the principal axes of inertia coincide with the axes of the coordinate system, because $\mathbf {J}=J_y\mathbf {e}_x\mathbf {e}_x+J_x\mathbf {e}_y\mathbf {e}_y$, and therefore also its inverse is diagonal. For the x-component, we then write

$$\begin{aligned} x^*=\mathbf {e}_{x}\cdot \mathbf {x^{*}}&=\frac{1}{J_x}\oint _{\varGamma }yWh\mathrm{d}s+\frac{\nu }{1+\nu }\frac{J_\mathrm{T}}{2J_x}x_{\varGamma }. \end{aligned}$$

(70)

In contrast to the kinematic shear center, the energetic shear center $\mathbf {x}^{**}$ is defined at the point where an acting shear force has no influence in the work conjugate of the torque $M_z$, which implies that $\theta _z'$ has to be zero. This results in

$$\begin{aligned} \mathbf {x}^{**}=\mathbf {J}^{-1}\cdot \oint _{\varGamma } W\mathbf {x}_0 h \mathrm{d}s\times \mathbf {e}_z, \end{aligned}$$

(71)

respectively, the x-coordinate

$$\begin{aligned} \mathbf {e}_{x}\cdot \mathbf {x^{**}}=\frac{1}{J_x}\oint _{\varGamma }yWh\mathrm{d}s. \end{aligned}$$

(72)

The two shear centers only differ in the term containing $\nu$. They coincide if $x_{\varGamma }=x_A(=0)$. The difference also disappears if $\nu =0$, which represents rigidity of the projection of the cross section onto the cross-sectional plane.

Fig. 2

Specific cross sections with $\mathbf {x}_{\varGamma }\ne \mathbf {x}_A$ (both are symmetric to the x-axis)

5 Numerical example

Next, the above theoretical considerations are validated numerically. We consider two cross sections symmetric to the x-axis (Fig. 2). The first one is a thin hollow square profile with the right wall being $\beta h$ thick and the other three walls being h thick. The second one has the shape of a hollow C-profile with a constant wall thickness. For the first one, we study the convergence of the asymptotic solution; the second example was chosen to proof the statement that for thin single-cell cross sections with constant thickness the difference of the two shear centers vanishes is wrong [14]. The computation is done by the above analytical formulas as well as numerically. We approach the exact three-dimensional solution by using the method of finite differences. The numerical solution makes no assumption about the thickness of the cross section. Instead of solving the above Laplace equations for the stress functions (15) and (16), the basis of the finite difference scheme are the equations established by Lacarbonara [10] (only the x-component is needed in the two symmetric examples):

$$\begin{aligned} \varDelta W_2&=-2\frac{y}{J_x}, \end{aligned}$$

(73)

$$\begin{aligned} \mathbf {n}\cdot \nabla W_2\bigg |_{\partial A}&=-\frac{\nu }{J_x}\left[ \frac{1}{2}(x^2-y^2)n_y-xyn_x\right] , \end{aligned}$$

(74)

$$\begin{aligned} \mathbf {e}_x\cdot \mathbf {x^*}=x^*&=-\frac{1}{2(1+\nu )}\oint _{\varGamma }W_2\mathbf {x}\cdot \mathrm{d}\mathbf {s}+\frac{\nu }{4(1+\nu )J_x}\int _A x (\mathbf {x}\cdot \mathbf {x}) \mathrm{d}A. \end{aligned}$$

(75)

This approach is called the displacement approach, because it is based on computing the divergence of both sides of (55) and representing the displacement $U_z(\mathbf {x})$ as a superposition of three warping functions $W_1$, $W_2$, and W:

$$\begin{aligned} \varDelta {U_z}=-2 E^{-1}\mathbf {b'}\cdot \mathbf {x}=\frac{Q_{0x}}{E}\varDelta W_1+\frac{Q_{0y}}{E}\varDelta W_2+\alpha \varDelta W. \end{aligned}$$

(76)

It can be seen easily that W is the well-known ”ordinary” warping function from the problem of pure torsion. It should be noted that the above equations for $W_2$ are only valid if the coordinate axes are principal axes of inertia. The advantage of the displacement approach of Lacarbonara compared with equations (15) and (16) is that the boundary condition is a Neumann one, which is known at all boundaries, whereas the above formulation uses the Prandtl stress function, which is constant at the different boundaries, but a priori unknown and has to be calculated with compatibility conditions (see above for $C^{(0)}$).

5.1 Finite difference scheme

The numerical solution is obtained by discretizing the Laplace equation in the two-dimensional domains (Fig. 2) using the finite difference method. To keep it simple, the differences $\varDelta x$ and $\varDelta y$ are constant. In the case of a node (i, j) inside the domain, the scheme requires five points and reads

$$\begin{aligned} \frac{W_2^{i+1,j}-2W_2^{i,j}+W_2^{i-1,j}}{\varDelta x^2}+\frac{W_2^{i,j+1}-2W_2^{i,j}+W_2^{i,j-1}}{\varDelta y^2}=-\frac{2 y_i}{J_x}. \end{aligned}$$

(77)

At the boundaries, the scheme has to be adapted. In our case, the normal vectors are only horizontal or vertical which simplifies this process. Therefore, we have four different kinds of boundary conditions, depending on the direction of the normal vector. For example, the boundary conditions at a straight boundary with constant $x=x_{i_{BC}}$ and $n_y=0$ are

$$\begin{aligned} n_x \frac{\partial W_2}{\partial x}=+\frac{\nu }{J_x} xy n_x\quad \rightarrow \quad \frac{\partial W_2}{\partial x}=\frac{\nu }{J_x} xy. \end{aligned}$$

(78)

As we can see, the component and the sign of $n_x$ are not important in this equation. The discretized form is

$$\begin{aligned} \frac{W_2^{i_{BC}+1,j}-W_2^{i_{BC}-1,j}}{2\varDelta x}=\frac{\nu }{J_x}x_{i_{BC}}y_j. \end{aligned}$$

(79)

Analogous relations are obtained for the other boundaries as well. Hence, the numerical scheme is complete. At a certain boundary, the appropriate node is substituted by one of the boundary conditions. If the middle node (i,j) is a convex corner, two points have to be replaced. Concave corners are treated like inner nodes. Because there are only Neumann boundary conditions, the solution is determined up to an additive constant, and the solution for an arbitrary point is set to zero, e.g., the left-low corner $W_2^{0,0}=0$. Note that in (75) the term

$$\begin{aligned} \oint _{\varGamma }W_2^{0,0} \mathbf {x}\cdot \mathrm{d}\mathbf {s}=\frac{W_2^{0,0}}{2}\oint _{\varGamma }\nabla (x^2+y^2)\cdot \mathrm{d}\mathbf {s}=0, \end{aligned}$$

(80)

vanishes, which confirms the arbitrariness of $W_2^{0,0}$.

5.2 Numerical results

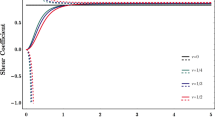
The solution is obtained for parameters $\nu =0.3$, $a=1$, $\beta =2$ and different thickness values h. We choose $\varDelta x=\varDelta y$ and at least six points per wall thickness of the thinner walls. Then, the convergence is tested by repeated reduction of $\varDelta x$ and $\varDelta y$ by the factor 2. As we can see in Fig. 3, for small wall thicknesses (large ratios a / h), the two centers, measured from the left outer edge, remain distinct, and the numerical solutions tend toward the asymptotic expressions. Note that $x^*$ and $x^{**}$ are computed from (70) and (72), added by $\mathbf {x}_A$, measured from the left edge.

Fig. 3

Analytical and numerical solutions of kinematic and energetic shear centers of the square cross section with $\beta =2$ (left) and the hollow C-section (right)

Next, the error due to variable thickness of the cross section is discussed. Therefore, the energetic shear center $x^{**}$ of the quadratic cross section is presented as a function of the wall thickness ratio $\beta$. Three thickness values $h=\frac{a}{500},$$\frac{a}{100},$$\frac{a}{20}$, with $a=1$ are considered. In Fig.4, the asymptotic results are compared with the numeric ones. For $\beta =1$, the cross section is double-symmetric, and therefore both solutions are independent of h exactly at the center of the cross section, a fact which would count for the kinematic shear center, too. With increasing $\beta$, the shear center at first shifts to the right up to a maximum value and decreases again. The maximum value of the shear center of the curve $h/a=0.05$ is at a point at which the thickness of the wall is about $25\%$ of the square’s length.

Fig. 4

Energetic shear center $x^{**}$ of the hollow quadratic cross section

After this numerical validation of the asymptotic equations for the shear centers, we proceed with a further instructive example, showing that also for a warping-free cross section $\mathbf {x}_{\varGamma }\ne \mathbf {x}_A$ is possible. It is well known that cross sections with constant thickness, which represent tangential polygons, are warping-free. Therefore, we consider an isosceles triangle, with basis c, height H and the angle $\gamma$ opposite to c, with the x-axis being the axis of symmetry. Then, the positions of $\mathbf {x}_{\varGamma }$ and $\mathbf {x}_A$ in the limit $h\rightarrow 0$, counted from the basis, are

$$\begin{aligned} x_{\varGamma }&=\frac{H}{3} \end{aligned}$$

(81)

$$\begin{aligned} x_{A}&=\frac{H}{2(1+\sin {\frac{\gamma }{2}})}. \end{aligned}$$

(82)

We can see that only in the case of $\gamma =\frac{\pi }{3}$, which represents an equilateral triangle, the two expressions are equal.

6 Conclusions

In this paper, we studied the asymptotic behavior of the solutions of the Saint-Venant problem for a linear elastic beam with a hollow cross section under the action of torsion and shear force bending. Assuming thin-walled cross sections, we introduced the small parameter $\lambda$, representing the thinness of the walls. After expressing the strong form of the equations in terms of $\lambda$ and merging terms of equal order, we first managed to validate the engineering assumptions. Further, we got well-known formulas, like for the shear flow and finally Bredt’s formulas for the torsion of rods. We noticed that if the Poisson effect is not neglected within the cross section, the second formula of Bredt has to be adapted by using the energetic twist rate $\theta _z'$ instead of the kinematic one. The leading-order terms of the kinematic and energetic shear centers were derived assuming a variable thickness of the cross section. In the final numerical investigation of two hollow cross sections, the exact location of the shear centers was calculated for different thickness values. A good agreement with the obtained asymptotic formulas was observed when the thickness is small. Furthermore, it has been shown that the energetic and kinematic shear centers are in general distinct even in the case of a single-cell hollow cross section with a constant small thickness. The opposite statement, which is sometimes met in the literature [14], is thus proven to be incorrect.