Abstract
Matrix-inclusion composites are known to exhibit interaction among the inclusions. When it comes to the special case of inclusions in form of flat interfaces, interaction among interfaces would be clearly expected, but the two-dimensional nature of interfaces implies quite surprising interaction properties. This is the motivation to analyze how interaction among two different classes of microscopic interfaces manifests itself in macroscopic creep and relaxation functions of matrix-interface composites. To this end, we analyze composites made of a linear elastic solid matrix hosting parallel interfaces, and we consider that creep and relaxation of such composites result from micro-sliding within adsorbed fluid layers filling the interfaces. The latter idea was recently elaborated in the framework of continuum micromechanics, exploiting eigenstress homogenization schemes, see Shahidi et al. (Eur J Mech A Solids 45:41–58, 2014). After a rather simple mathematical exercise, it becomes obvious that creep functions do not reflect any interface interaction. Mathematical derivation of relaxation functions, however, turns out to be much more challenging because of pronounced interface interaction. Based on a careful selection of solution methods, including Laplace transforms and the method of non-dimensionalization, we analytically derive a closed-form expression of the relaxation functions, which provides the sought insight into interface interaction. The seeming paradox that no interface interaction can be identified from creep functions, while interface interaction manifests itself very clearly in the relaxation functions of matrix-interface materials, is finally resolved based on stress and strain average rules for interfaced composites. They clarify that uniform stress boundary conditions lead to a direct external control of average stress and strain states in the solid matrix, and this prevents interaction among interfaces. Under uniform strain boundary conditions, in turn, interfacial dislocations do influence the average stress and strain states in the solid matrix, and this results in pronounced interface interaction.
Article PDF
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Abbreviations
- a :
-
Coefficient of ordinary differential equation in γ
- a 1 :
-
Radius of first interface family
- a 2 :
-
Radius of second interface family
- A I :
-
Relaxation capacity associated with characteristic time τrelax,I
- A II :
-
Relaxation capacity associated with characteristic time τrelax,II
-
 :
: -
Third-order strain-to-dislocation downscaling tensor, quantifying the concentration of macroscopic strain into the average dislocation encountered across the interfaces; j = 1, 2 refers to the two interface families
-
 :
: -
Third-order influence tensor describing the influence of macroscopic stress on the dislocation of interfaces; j = 1, 2 refers to the two interface families
- b :
-
Coefficient of ordinary differential equation in γ
-
 :
: -
Third-order influence tensor describing the influence of interface traction on the macroscopic stress; j = 1, 2 refers to the two interface families
-
 :
: -
Third-order influence tensor describing the influence of interface traction on the macroscopic strain; j = 1, 2 refers to the two interface families
- c j :
-
Constant used in Laplace transformation method, related to dislocation of interface family j = 1, 2
- C j :
-
Integration constant used in the elimination-non-dimensionalization method, related to the dislocation of interface family j = 1, 2
- C̄1 :
-
Constant appearing in relaxation function
- C̄2 :
-
Constant appearing in relaxation function
- \({\mathcal{C}_j}\) :
-
Domain of interface belonging to interface family j = 1, 2
-
 :
: -
Fourth-order elastic stiffness tensor of solid
-
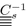 :
: -
Inverse of

-
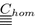 :
: -
Fourth-order homogenized stiffness tensor of matrix-interface composite
-
 :
: -
Inverse of
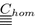
- d j :
-
Interface density parameter of interface family j = 1, 2
- D j :
-
Integration constant used in the elimination-non-dimensionalization method, related to dislocation of interface family j = 1, 2
- D̄1 :
-
Constant appearing in relaxation function
- D̄2 :
-
Constant appearing in relaxation function
- e j :
-
Constant used in Laplace transformation method, related to the dislocation of interface family j = 1, 2
-
 :
: -
Unit base vectors of Cartesian coordinate system
-
 :
: -
Second-order tensor of macroscopic strain
- E xz :
-
Shear component of

- E s :
-
Young’s modulus of the solid
- j :
-
Index for interface phase (family)
-
 :
: -
Symmetric fourth-order identity tensor
-
 :
: -
Deviatoric part of

-
 :
: -
volumetric part of

- J xzxz :
-
Creep function
- \({\mathcal{L}}\) :
-
Laplace transformation operator
- \({\mathcal{L}^{-1}}\) :
-
Back transformation operator from Laplace space to time domain
- \({ \mathcal{N}_j }\) :
-
Number of interfaces per unit volume of a matrix-interface composite; j = 1, 2 refers to the two interface families
-
 :
: -
Outward unit normal at any point of the boundary of the volume element representing the composite material
-
 :
: -
Unit vector oriented orthogonal to the interface family j = 1, 2
- R xzxz :
-
Relaxation function
- s :
-
As subscript: index for solid phase
- s :
-
As variable: Laplace space parameter
-
 :
: -
Interface traction vector acting on interface phase j = 1, 2
-
 :
: -
Fourth-order morphology tensor for 2D interface inclusion (“sharp crack” morphology)
- T j,x :
-
Shear component in x-direction, of traction vector

- T j,y :
-
Shear component in y-direction, of traction vector

- x, y, z :
-
Cartesian coordinates
-
 :
: -
Position vector
- γ:
-
Macroscopic engineering strain (related to E xz )
- γ j :
-
Strain-like variable related to dislocation of interface family j = 1, 2
- γ j,h :
-
Solution of homogeneous differential equation in γ j
- γ j,p :
-
Particular solution of non-homogeneous differential equation in γ j
- γ j :
-
Laplace transform of function γ j
- δ:
-
Kronecker delta
- Δμ :
-
Loss of effective stiffness during relaxation test
-
 :
: -
Second-order tensor of microscopic linear strain
- η i,j :
-
Viscosity of interface family j = 1, 2
- η j :
-
Differential equation-related “viscosity constant” related to interface family j = 1, 2
- μ s :
-
Shear modulus of isotropic solid matrix
- μ j :
-
Differential equation-related “stiffness constant” related to interface family j = 1, 2
- ν s :
-
Poisson’s ratio of isotropic solid matrix
-
 :
: -
Displacement vector
-
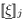 :
: -
(average) Dislocation vector of interface phase j = 1, 2
- [[ξ]] j , x :
-
Shear component of
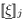
- [[ξ]] j , z :
-
Normal component of
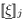
-
 :
: -
Second-order tensor of microscopic Cauchy stresses
-
 :
: -
Second-order tensor of macroscopic Cauchy stresses
- Σ xz :
-
Shear component of

- τcreep,j :
-
Characteristic creep time related to dislocation in interface family j = 1, 2
- τrelax,I :
-
First characteristic relaxation time of material system comprising two interface families
- τrelax,II :
-
Second characteristic relaxation time of material systme comprising two interface families
- Ω :
-
Volume of the matrix-interface composite
- Ω s :
-
Volume occupied by the solid phase
- ∂:
-
Partial derivative
- ::
-
Second-order tensor contraction
- \({\dot{\bullet}}\) :
-
Partial derivative with respect to time (“rate”), of quantity “•”
- \({\otimes }\) :
-
Dyadic product
References
Benveniste Y.: A new approach to the application of Mori–Tanaka’s theory in composite materials. Mech. Mater. 6, 147–157 (1987)
Zaoui A.: Continuum micromechanics: survey. J. Eng. Mech. (ASCE) 128, 808–816 (2002)
Luciano R., Willis J.R.: FE analysis of stress and strain fields in finite random composite bodies. J. Mech. Phys. Solids 53, 1505–1522 (2005)
Gruescu C., Giraud A., Homand F., Kondo D., Do D.P.: Effective thermal conductivity of partially saturated porous rocks. Int. J. Solids Struct. 44, 811–833 (2007)
Mercier S., Molinari A.: Homogenization of elastic-viscoplastic heterogeneous materials: self-consistent and Mori–Tanaka schemes. Int. J. Plast. 25, 1024–1048 (2009)
Lin P.J., Ju J.W.: Effective elastic moduli of three-phase composites with randomly located and interacting spherical particles of distinct properties. Acta Mech. 208, 11–26 (2009)
Zheng Q.-S., Du D.-X.: An explicit and universally applicable estimate for the effective properties of multiphase composites which accounts for inclusion distribution. J. Mech. Phys. Solids 49, 2765–2788 (2001)
Sevostianov I., Kachanov M.: Normal and tangential compliances of interface of rough surfaces with contacts of elliptic shape. Int. J. Solids Struct. 45, 2723–2736 (2008)
Sevostianov I., Kachanov M.: Homogenization of a nanoparticle with graded interface. Int. J. Fract. 139, 121–127 (2006)
Kachanov M.: Elastic solids with many cracks: a simple method of analysis. Int. J. Solids Struct. 23, 23–43 (1987)
Kachanov M.: Effective elastic properties of cracked solids: critical review of some basic concepts. Appl. Mech. Rev. 45, 304–335 (1992)
Vlahinić, I., Thomas, J.J., Jennings, H.M., Andrade, J.E.: Transient creep effects and the lubricating power of water in materials ranging from paper to concrete and Kevlar. J. Mech. Phys. Solids 60, 1326–1350 (2012)
Manzano H., Moeini S., Marinelli F., Van Duin A.C.T., Ulm F.J., Pellenq R.J.M.: Confined water dissociation in microporous defective silicates: Mechanism, dipole distribution, and impact on substrate properties. J. Am. Chem. Soc. 134, 2208–2215 (2012)
Eberhardsteiner L., Hellmich C., Scheiner S.: Layered water in crystal interfaces as source for bone viscoelasticity: arguments from a multiscale approach. Comput. Methods Biomech. Biomed. Eng. 17, 48–63 (2014)
Shahidi M., Pichler B., Hellmich C.: Viscous interfaces as source for material creep: a continuum micromechanics approach. Eur. J. Mech. A Solids 45, 41–58 (2014)
Pichler B., Hellmich C.: Estimation of influence tensors for eigenstressed multiphase elastic media with nonaligned inclusion phases of arbitrary ellipsoidal shape. J. Eng. Mech. 136, 1043–1053 (2010)
Hashin Z.: Analysis of composite materials—a survey. J. Appl. Mech. Trans. ASME 50, 481–505 (1983)
Budiansky B., O’Connell R.J.: Elastic moduli of a cracked solid. Int. J. Solids Struct. 12, 81–97 (1976)
Alizadeh R., Beaudoin J.J., Raki L.: Viscoelastic nature of calcium silicate hydrate. Cem. Concr. Compos. 32, 369–376 (2010)
Kalinichev A.G., Wang J., Kirkpatrick R.J.: Molecular dynamics modeling of the structure, dynamics and energetics of mineral–water interfaces: application to cement materials. Cem. Concr. Res. 37, 337–347 (2007)
Barenblatt G.I.: Scaling, Self-similarity, and Intermediate Asymptotics. Cambridge University Press, Cambridge (1996)
Qu T., Verma D., Shahidi M., Pichler B., Hellmich C., Tomar V.: Mechanics of organic–inorganic biointerfaces—implications for strength and creep properties. MRS Bull. 40, 349–358 (2015)
Mori T., Tanaka K.: Average stress in matrix and average elastic energy of materials with misfitting inclusions. Acta Metall. 21, 571–574 (1973)
Sevostianov I., Kachanov M.: On some controversial issues in effective field approaches to the problem of the overall elastic properties. Mech. Mater. 69, 93–105 (2014)
Kachanov M., Tsukrov I., Shafiro B.: Effective moduli of solids with cavities of various shapes. J. Appl. Mech. Rev. 47, 151–174 (1994)
Pensée V., Kondo D., Dormieux L.: Micromechanical analysis of anisotropic damage in brittle materials. J. Eng. Mech. 128, 889–897 (2002)
Pichler B., Hellmich C., Mang H.A.: A combined fracture-micromechanics model for tensile strain-softening in brittle materials, based on propagation of interacting microcracks. Int. J. Numer. Anal. Methods Geomech. 31, 111–132 (2007)
Castañeda P.P., Willis J.R.: The effect of spatial distribution on the effective behavior of composite materials and cracked media. J. Mech. Phys. Solids 43, 1919–1951 (1995)
Pellenq R.J.M., Kushima A., Shahsavari R., Van Vliet K.J., Buehler M.J., Yip S., Ulm F.J.: A realistic molecular model of cement hydrates. Proc. Natl. Acad. Sci. USA 106, 16102–16107 (2009)
Prostak K.S., Lees S.: Visualization of crystal-matrix structure. In situ demineralization of mineralized turkey leg tendon and bone. Calcif. Tissue Int. 59, 474–479 (1996)
Schmidt S.R., Katti D.R., Ghosh P., Katti K.S.: Evolution of mechanical response of sodium montmorillonite interlayer with increasing hydration by molecular dynamics. Langmuir 21, 8069–8076 (2005)
Bronstein, I.N., Semendjajew, K.A., Musiol, G., Mühlig, H.: Taschenbuch der Mathematik, 6 edn [Handbook of Mathematics]. Verlag Harri Deutsch (2005) (In German)
Fritsch A., Hellmich C., Young P.: Micromechanics-derived scaling relations for poroelasticity and strength of brittle porous polycrystals. J. Appl. Mech. Trans. ASME 80, 020905-1 (2013)
Katz J.L., Ukraincik K.: On the anisotropic elastic properties of hydroxyapatite. J. Biomech. 4, 221–227 (1971)
Hill R.: Elastic properties of reinforced solids: some theoretical principles. J. Mech. Phys. Solids 11, 357–372 (1963)
Nguyen S.T., Dormieux L., Pape Y.L., Sanahuja J.: A Burger model for the effective behavior of a microcracked viscoelastic solid. Int. J. Damage Mech. 20, 1116–1129 (2011)
Dormieux L., Kondo D.: Micromechanical approach to the coupling between permeability and damage. C. R. Mec. 332, 135–140 (2004)
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Shahidi, M., Pichler, B. & Hellmich, C. How interface size, density, and viscosity affect creep and relaxation functions of matrix-interface composites: a micromechanical study. Acta Mech 227, 229–252 (2016). https://doi.org/10.1007/s00707-015-1429-9
Received:
Revised:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00707-015-1429-9





 :
: :
: :
: :
: :
: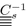 :
: :
: :
: :
: :
: :
: :
: :
: :
: :
: :
: :
: :
: :
: :
: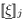 :
: :
: :
: