Skip to main content
SpringerLink
Log in

Stochastic shape functions and stochastic strain–displacement matrix for a stochastic finite element stiffness matrix

  • Published:
Acta Mechanica Aims and scope Submit manuscript

Summary

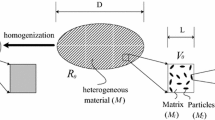
For conventional finite element problems, element geometry is adequate to determine shape functions. However, to account for secondary effects due to material randomness, conventional shape functions need to be modified according to the spatial fluctuation of constitutive variables in each Monte Carlo sample. This paper develops a method to compute stochastic shape functions based on local equilibrium criteria when each simulated sample complies with the same order of accuracy as designated for the associated deterministic problem. The resulting stochastic stiffness matrix is then calculated via the stochastic strain–displacement matrix based on those stochastic shape functions. In order to attain high accuracy, which is the characteristic of the boundary element method, rational polynomial shape functions are used in this paper. The proposed formulation is indispensable when secondary effects (due to nano size and time scale in modern technology, fiber randomness in composites, thermodynamic interactions in biological tissues, to name a few) demand a high accuracy finite element formulation. The elasto-plastic deformation that introduces concavity motivated the numerical example elaborated here. An example of a concave quadrilateral element with spatial randomness for the modulus of elasticity is illustrated. Since isoparametric shape functions for concave quadrilaterals do not exist, the Wachspress rational polynomial shape functions with irrational terms are used. The computer algebra environment Mathematica is employed here.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Zienkiewicz, O.C., Taylor, R.L.: The Finite Element Method, vol. 2. Solid Mechanics, 5th edn. Elsevier, New York (2000)

  2. Ditlevsen O. and Madsen H.O. (1996). Structural Reliability Methods. Wiley, New York

    Google Scholar 

  3. Kelly, J.M., Sackman, J.L.: Equipment–structure interaction at high frequencies. Technical Report No. DNA 4298T, Defense Nuclear Agency (1977)

  4. Igusa, T., Der Kiureghian, A., Sackman, J.L.: Modal decomposition method for stationary response of non-classically damped systems. Earthquake Engng. Struct. Dyn. 12 (1984)

  5. Ziegler, F.: The tuned liquid column damper as the cost-effective alternative of the mechanical-damper within vibration prone civil engineering structures, 2006. Keynote address: ICSV13, 3–7 July, 2006. In: 13th International Congress on Sound and Vibration Vienna University of Technology

  6. Höllinger, F., Ziegler, F.: A random interaction problem: Dam reservoir system excited by earthquakes. In: Casciati, F., Faravelli, L., (eds.) Stochastic Methods in Structural Mechanics. Se.A.G., Proc. Int. Workshop (1983)

  7. Milton E. (1987). Harr: Reliability Based Design in Engineering. McGraw Hill, New York

    Google Scholar 

  8. Haldar A. and Mahadevan S. (2000). Probability, Reliability and Stastitical Methods in Engineering Design. Wiley, New York

    Google Scholar 

  9. Boley B.A. and Weiner J.H. (1997). Theory of Thermal Stresses. Dover, New York

    Google Scholar 

  10. Ziegler F. (1995). Mechanics of Solids and Fluids, 2nd edn. Springer, New York

    Google Scholar 

  11. Irschik, H., Hayek, H., Ziegler, F.: Random vibrations of discrete and continuous inelastic structures. In: Ang, A.H.S., Shinozuka, M., Schueller, G.I. (eds.) Structural Safety & Reliability II. In: ASCE, Proceedings of ICOSSAR 89, San Francisco (1987)

  12. Ziegler, F., Irschik, H.: Thermal stress analysis based on Maysel’s formula. In: Hetnarski, R.B. (ed.) Thermal Stresses II. North-Holland, Amsterdam (1987)

  13. Ziegler, F., Rammerstorfer, F.G.: Thermoelastic stability. In: Hetnarski, R.B. (ed.) Thermal Stresses III. North-Holland, Amsterdam (1989)

  14. MacNeal R.H. (1994). Finite Elements: Their Design and Performance. Marcel Dekker, New York

    Google Scholar 

  15. Keller, J.B., McKean, H.P.: Siam-ams proceedings. In: Stochastic Differential Equations, vol. VI. American Mathematical Society, Providence, RI (1973)

  16. Deb M.K., Babuka I.M. and Tinsley Oden J. (2001). Solution of stochastic partial differential equations using Galerkin finite element techniques. Comput. Methods Appl. Mech. Engng. 190: 6359–6372

    Article  MATH  Google Scholar 

  17. Ziegler F. (1994). Mean waves in laminated random media. Int. J. Solids Struct. 5: 893–914

    Article  Google Scholar 

  18. Kleiber M. and Hien T.D. (1992). The Stochastic Finite Element Method. Wiley, London

    MATH  Google Scholar 

  19. Dasgupta, G., Yip, S.-C.: Nondeterministic shape functions for finite elements with stochastic moduli. In: Schuëller, G.I. (ed.) Structural Safety and Reliability 1989. In: International Association of Structural Safety and Reliability, San Francisco, June 1989. American Society of Civil Engineers (1989)

  20. Barrère R. (1977). A heuristic method for the resummation of perturbation series. In: Keränen, V. and Mitic, P. (eds) Innovation in Mathematics: Proceedings of the Second International Mathematica Symposium, pp. Computational Mechanics Publications, Southampton, Boston

    Google Scholar 

  21. Yamazaki F., Shinozuka M. and Dasgupta G. (1988). Neumann expansion for stochastic finite element analysis. J. Engng. Mech. 114(8): 1335–1354

    Google Scholar 

  22. Wolfram S. (2003). The Mathematica Book, System 5. Wolfram Media, NY

    Google Scholar 

  23. Dasgupta G. (2003). Integration within polygonal finite elements. J. Aerosp. Engng. ASCE 16(1): 9–18

    Article  Google Scholar 

  24. Shinozuka M. (1972). Monte Carlo solution of structural dynamics. Int. J. Comput. Struct. 2: 855–874

    Article  Google Scholar 

  25. Ziegler, F.: Plane wave propagation in the semi-space with random excitation and coupling between stress and temperature. Technical Report, Institut für Angewandte Mechanik, Contract 61 (052) - 645, October 1966. Final Scientific Report Snapping of Shallow Shells and Thermal Stresses from Stochastic Fields, 1 November, 1963–31 October 1966

  26. Ziegler, F.: The elastic-viscoelastic correspondence in case of numerically determined discrete elastic response spectra. ZAMM – J. Appl. Math. Mech./Z. Angew. Math. Mech. 63, 135–137 (1983). (Sonderheft GAMM-Tagung Budapest 1982)

  27. Pian T.H.H. (1978). A historical note about hybrid elements. Int. J. Numer. Methods Engng. 12: 891–892

    Article  Google Scholar 

  28. Dasgupta G., Papusha A.N. and Malsch E.A. (2001). First order stochasticity in boundary geometry: a computer algebra BE development. Engng. Anal. Boundary Elements 25: 741–751

    Article  MATH  Google Scholar 

  29. Wachspress E.L. (1975). A rational finite element basis. Academic Press, London

    MATH  Google Scholar 

  30. Gout, J.-L.: Elements finis polygonaux de Wachspress. Ph.D. thesis, L’université de Pau et des pays de l’adour, 6 June, 1980. Thèse de doctorat d’état es-sciences mathématiques, le grade de Doctoeur-es-sciences

  31. Beltz G.E., Rice J.R., Shih C.F. and Xia L. (1996). A self-consistent model for cleavage in the presence of plastic flow. Acta Mater. 44: 3943–3954

    Article  Google Scholar 

  32. Fotiu P.A. and Ziegler F. (2001). A micromechanical model for polycrystalline creep with grain boundary cavitation. Arch. Appl. Mech. 8: 110–122

    Google Scholar 

  33. Irschik H. and Ziegler F. (1977). Thermal shock loading of elastoplastic beams. J. Thermal Stresses 8: 53–69

    Article  Google Scholar 

  34. Ziegler F. and Irschik H. (1985). Dynamic analysis of elastic-plastic beams by means of thermoelastic solutions. Int. J. Solids Struct. 21(7): 819–829

    Article  MATH  Google Scholar 

  35. Wachspress, E.L.: Rational basis functions. In: Noor, A.K., Pilkey, W.D. (eds.) State-of-the-Art Survey of the Finite Element Method. ASME. A Special ASME Publication, New York (1981)

  36. Wachspress, E.L.: A Rational Basis for Function Approximation. In: Lecture Notes in Mathematics, vol. 228. Springer, Heidelberg (1971)

  37. Dasgupta G. (1992). Approximate dynamic responses in random media. Acta Mech. 3: 99–114

    Google Scholar 

  38. Werner, H., Bünger, H.J. (eds.): Padé Approximation and its Applications. Lecture Notes in Mathematics, vol. 1071. Bad Honnef, Germany. Springer, New York (1983)

  39. Shinozuka, M.: Digital simulation of random processes and its applications. J. Sound Vib. 25 (1972)

  40. VanMarcke E. (1983). Random Fields: Analysis and Synthesis. MIT Press, Cambridge

    Google Scholar 

  41. Shinozuka, M.: Digital simulation of random processes in engineering mechanics with the aid of FFT technique. University of Waterloo Press (1974)

  42. Keller, J.B.: Stochastic equations and wave propagation in random media. In: Symposium on Applied Mathematics, vol. 16. American Mathematical Society, Providence, RI (1964)

  43. Molyneux J.E. (1968). Analysis of dishonest methods in the theory of wave propagation in a random medium. J. Opt. Soc. Am. 58: 951–957

    Google Scholar 

  44. Dasgupta, G.: A computational scheme to analyze nonlinear stochastic dynamic systems by finite elements. Research Report, Columbia University, April 1987. Presented at the IUTAM Symposium, Igls, Austria, June (1987)

  45. Nakagiri, S., Hisada, T.: An Introduction to Stochastic Finite Element Method. Bai Fu Kan (1985). (in Japanese)

  46. Nayfeh A.H. (1973). Perturbation Methods. Wiley-Interscience, New York

    MATH  Google Scholar 

  47. Nakagiri, S., Hisada, T.: Notes on stochastic finite element method. Res. J. Inst. Ind. Sci. pp. 32–35 (in eight parts) (1980)

  48. Dasgupta, G.: First order perturbation economizing integration/differentiation. In: Demidov, V., Kernen, V. (eds.) International Arctic Seminars (Physics and Mathematics), pp. 9–16. State Pedagogic Institute, Murmansk University of Technology, May (1998)

  49. Sobczyk K. (1985). Stochastic Wave Propagation. Elsevier, New York

    MATH  Google Scholar 

  50. Spanos P.D. and Zeldin B.A. (1998). Monte Carlo treatment of random fields: A broad perspective. Appl. Mech. Rev. 51(3): 219–237

    Article  Google Scholar 

  51. Strang G. and Fix G.J. (1973). An Analysis of the Finite Element Method. Prentice-Hall, Englewood Cliffs

    MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Civil Engineering and Engineering Mechanics, Columbia University, New York, NY, U.S.A.

    Gautam Dasgupta

Authors
  1. Gautam Dasgupta
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Gautam Dasgupta.

Additional information

Dedicated to Professor Franz Ziegler on the occasion of his 70th birthday

Rights and permissions

Reprints and permissions

About this article

Cite this article

Dasgupta, G. Stochastic shape functions and stochastic strain–displacement matrix for a stochastic finite element stiffness matrix. Acta Mech 195, 379–395 (2008). https://doi.org/10.1007/s00707-007-0569-y

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00707-007-0569-y

Keywords

Search

Navigation