Stochastic local FEM for computational homogenization of heterogeneous materials exhibiting large plastic deformations

Abstract

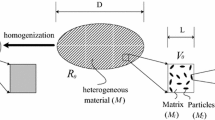
Computational homogenization is a powerful tool allowing to obtain homogenized properties of materials on the macroscale from simulations of the underlying microstructure. The response of the microstructure is, however, strongly affected by variations in the microstructure geometry. In particular, we consider heterogeneous materials with randomly distributed non-overlapping inclusions, which radii are also random. In this work we extend the earlier proposed non-deterministic computational homogenization framework to plastic materials, thereby increasing the model versatility and overall realism. We apply novel soft periodic boundary conditions and estimate their effect in case of non-periodic material microstructures. We study macroscopic plasticity signatures like the macroscopic von-Mises stress and make useful conclusions for further constitutive modeling. Simulations demonstrate the effect of the novel boundary conditions, which significantly differ from the standard periodic boundary conditions, and the large influence of parameter variations and hence the importance of the stochastic modeling.

1 Introduction

Computational homogenization is a widely used technique due to the fact that it can be equally applied without any modifications to both linear and nonlinear problems, arbitrary complex geometries, and any types of physical problems—elasticity, plasticity, electromagnetism, etc. This technique consists of three steps. Firstly, we need to design a suitable model of the microstructure and transfer macroscopic loads and deformations to the microscale. This is done using the Hill-Mandel [14, 23, 44, 45, 54] condition which states that the virtual work performed by microscopic stresses at microscopic deformation gradients must be equal to the virtual work performed by macroscopic (homogenized) stresses at macroscopic (homogenized) deformation gradients. The second step is to simulate the response of the micromodel. This step is the most challenging due to the high computational costs of a high resolution FEM model [35, 36, 38]. The third step is the transfer of homogenized quantities back to the macroscale, which is also determined by the Hill-Mandel condition.

Computational homogenization is a well developed technique, however there are still some open questions, e.g. the design of a suited representative volume element (RVE) of the microstructure in case that uncertainties (randomness) in the microstructure are present. The effect of uncertainties in the microstructure is the crucial aspect in this paper. Here we follow our work [39], where an ergodicity assumption and boundary conditions for a non-deterministic (stochastic) problem were analyzed. The purpose of this work is to increase the overall realism of the presented approach by extending it to the realm of large deformation plasticity.

Stochastic plasticity was already intensively studied in works of Rosic [40,41,42,43], and many problems in stochastic plasticity are considered as solved. However, random geometry and hence random boundaries and interfaces, which are the topic of interest for us, provide a new dimension of complexity. For example the application of the common polynomial chaos expansion and related methods becomes inefficient [33, 34].

The most widely used approach towards computational homogenization of random media is to run large simulations with a sufficiently large number of randomly generated inclusions or voids (non-ergodic approach). This approach is presented in particular in [1, 5, 11, 15, 21,22,23, 25, 26, 30, 51]. Specifically, plasticity is studied within this approach in [7, 16, 19, 20]. The effect of the scale of an RVE is studied in detail in [29]. This work also highlights the differences between a fully representative volume element and a statistical volume element and thus builds a necessary bridge to the ergodic approach.

The ergodic approach is another possibility in the treatment of random media. It uses some parameterized model together with a sophisticated non-deterministic modeling technique [2,3,4, 8,9,10, 17, 18, 24, 47,48,49, 52, 53]. In the extreme case the model of the microstructure is fully replaced by some statistically similar volume element [50]. Particular questions regarding the design of the representative volume element of the microstructure are discussed in [29]. The approach presented in this work is also classified as extreme ergodic. Using results from [39, 56] we reduce a model with randomly distributed inclusions to a simple parametric model with only one single inclusion possessing random geometry. This reduction results however in a highly sophisticated stochastic problem with discontinuous random fields. It is worth to notice that a similar approach towards the homogenization of elasto-plastic materials with random microstructure was recently developed in [54].

In order to simulate a non-deterministic RVE we use the recently proposed stochastic local FEM (SL-FEM) [34, 37]. This method was originally developed for problems with only a few random parameters, but these parameters can affect the geometry of an RVE, cause random interfaces and boundaries, and, as a consequence, the microscopic displacements and stresses exhibit strongly nonlinear and discontinuous dependencies on random parameters. This technique was also used for more general fuzzy-stochastic problems [31, 32]. Our simulations demonstrate that the SL-FEM can be applied without any modifications also to fuzzy and interval problems: since a local formulation is used, the nature of uncertain parameters is not important for the solution procedure, but only for the postprocessing [37].

Another advantage of the SL-FEM is that it reduces any parametric (stochastic, fuzzy, interval) FEM model to an n-dimensional deterministic FEM model. As a result, plastic or any other complex material response is implemented in the same way as for the common FEM—no modifications are required. A subroutine written for a standard FEM code can be directly used in a SL-FEM code.

The structure of this paper is as follows. Section 2 describes the method which is used in simulations. Section 3 schematically depicts our approach towards the design of an RVE and provides parameters used for simulation. Section 4 provides a brief validation of the ergodic RVE design. Section 5 contains simulation results. Finally, Sect. 6 concludes the paper.

2 Stochastic local FEM

In this section we introduce the basic idea of the stochastic local FEM. Similar to the common deterministic FEM, the SL-FEM is a special case of the Galerkin method. To start with let us consider the physical space $\mathbb {E}$, i.e. the Euclidean space with coordinates $\varvec{{x}}\in \mathbb {R}^3$ augmented by a corresponding algebra, and the stochastic space (space of parameters) $\mathbb {S}$ with coordinates (parameters) $\varvec{{\theta }}\in \mathbb {R}^n$. Note that we consider here only the stochastic approach, however any problem can be treated using the non-probabilistic methods evolved from interval arithmetic and fuzzy set theory [12, 13]. In case of non-probabilistic or mixed treatment the fuzzy space or some generic parameter spaces can be introduced with only small changes in definitions [37].

The solution of the deterministic FEM belongs to the physical Hilbert space of functions $\varvec{\mathcal {H}}$ defined over the physical domain $\mathcal {D} \subset \mathbb {E}$. Analogously, we introduce the stochastic Hilbert space of functions $\varvec{\mathcal {Q}}$ defined over the stochastic domain $\mathcal {S}\subset \mathbb {S}$. The solution of the stochastic (or general parametric) FEM belongs to the space $\varvec{\mathcal {H}} \times \varvec{\mathcal {Q}}$.

Next, let us introduce some random differential operator

$$\begin{aligned} \mathrm {D}(\varvec{{x}},\varvec{{\theta }})\varvec{{y}}(\varvec{{x}},\varvec{{\theta }})=f(\varvec{{x}},\varvec{{\theta }}), \end{aligned}$$

(1)

where $f(\varvec{{x}},\varvec{{\theta }})$ is the (random/parameterized) loading. Its solution

$$\begin{aligned} \varvec{{y}}(\varvec{{x}},\varvec{{\theta }})=\sum _{i=1}^{\infty } \varvec{{y}}_i \varphi _i(\varvec{{x}},\varvec{{\theta }})\end{aligned}$$

(2)

belongs to the space $\varvec{\mathcal {H}} \times \varvec{\mathcal {Q}}$, with $\varphi _i(\varvec{{x}},\varvec{{\theta }})$ representing some basis in $\varvec{\mathcal {H}} \times \varvec{\mathcal {Q}}$. If we consider only a finite number of terms N in (2), the function $\varvec{{y}}(\varvec{{x}},\varvec{{\theta }})$ will approximate the exact solution. Then the basic idea of the Galerkin method is to project not only the unknown function $\varvec{{y}}(\varvec{{x}},\varvec{{\theta }})$ but also the differential operator $\mathrm {D}(\varvec{{x}},\varvec{{\theta }})$ onto the basis $\varphi _i(\varvec{{x}},\varvec{{\theta }})$:

$$\begin{aligned} \begin{aligned}&\left\langle \left[ \mathrm {D}(\varvec{{x}},\varvec{{\theta }})\varvec{{y}}(\varvec{{x}},\varvec{{\theta }})-f(\varvec{{x}},\varvec{{\theta }})\right] \varphi _i(\varvec{{x}},\varvec{{\theta }})\right\rangle =0,\\&\qquad \forall i=1,~...~,~N. \end{aligned} \end{aligned}$$

(3)

The key ingredient here is the Galerkin projection $\langle {\,}\rangle$ which coincides with the inner product in the physical-stochastic space $\varvec{\mathcal {H}} \times \varvec{\mathcal {Q}}$:

$$\begin{aligned} \left\langle g_1(\varvec{{x}},\varvec{{\theta }})g_2(\varvec{{x}},\varvec{{\theta }})\right\rangle :=\int \limits _{\mathcal {D}}\int \limits _{\mathcal {S}} g_1(\varvec{{x}},\varvec{{\theta }})g_2(\varvec{{x}},\varvec{{\theta }})f_{\varvec{{\theta }}} \mathrm {d}\varvec{{\theta }}\mathrm {d}\varvec{{x}}, \end{aligned}$$

(4)

where $f_{\varvec{{\theta }}}$ is the joint probability density function of the random parameters $\varvec{{\theta }}$.

For a geometrically nonlinear problem with nonlinear constitutive equations the differential operator reads explicitly as

$$\begin{aligned} \begin{aligned}&\mathrm {D}(\varvec{{x}},\varvec{{\theta }})\varvec{{y}}(\varvec{{x}},\varvec{{\theta }}):=-{{\,\mathrm{Div}\,}}\varvec{\mathrm {F}} \varvec{\mathrm {S}}(\varvec{\mathrm {C}} ),\\&\varvec{\mathrm {C}}=\varvec{\mathrm {F}}^t\varvec{\mathrm {F}},\\&\varvec{\mathrm {F}}={{\,\mathrm{Grad}\,}}\varvec{{y}}(\varvec{{x}},\varvec{{\theta }}),\\&f(\varvec{{x}},\varvec{{\theta }}):=\varvec{{f}}(\varvec{{x}},\varvec{{\theta }}), \end{aligned} \end{aligned}$$

(5)

where $\varvec{{y}}(\varvec{{x}},\varvec{{\theta }})$ corresponds to the non-deterministic deformation map describing the position of material points in the spatial configuration, $\varvec{{f}}(\varvec{{x}},\varvec{{\theta }})$ denotes the non-deterministic body force density, $\varvec{\mathrm {F}}$ denotes the deformation gradient, $\varvec{\mathrm {S}}$ and $\varvec{\mathrm {C}}$ represent the Piola-Kirchhoff stress tensor and the Cauchy-Green strain tensor, respectively. Note that the ${{\,\mathrm{Grad}\,}}$ and ${{\,\mathrm{Div}\,}}$ operators involve differentiation only with respect to the physical coordinates $\varvec{{x}}$ in the material configuration.

Expression (3) provides the residual vector $\varvec{{R}}_i$ which is then minimized using, e.g. the Newton iterations.

The FEM formulation is obtained by considering that $\varvec{{y}}_i$ are nodal values of the unknown function $\varvec{{y}}(\varvec{{x}},\varvec{{\theta }})$ and the basis functions $\varphi _i(\varvec{{x}},\varvec{{\theta }})$ are piece-wise continuous and defined locally over elements. In contrast to the common polynomial-chaos based stochastic FEM, $\varphi _i(\varvec{{x}},\varvec{{\theta }})$ are piece-wise continuous and local not only in the physical space, but also in the stochastic (parameter) space. As a result, we discretise the parameter domain using FE shape functions as common in the physical domain.

Both the common deterministic FEM and the SL-FEM utilize the isoparametric concept. Therefore we can switch to isoparametric coordinates $\varvec{{\xi }}$ and represent the solution element-wise as

$$\begin{aligned} \begin{bmatrix} \varvec{{x}}^e\\ \varvec{{\theta }}^e \\ \varvec{{y}}^e(\varvec{{x}},\varvec{{\theta }})\end{bmatrix} = \sum \limits _{i\in I^e} \begin{bmatrix} \varvec{{x}}_i\\ \varvec{{\theta }}_i \\ \varvec{{y}}_i \end{bmatrix} \varphi ^e_i(\varvec{{\xi }}), \end{aligned}$$

(6)

with

$$\begin{aligned} \begin{aligned}&\dim (\varvec{{\xi }})=\dim (\varvec{{x}})+\dim (\varvec{{\theta }}),\\&\varvec{{\xi }}\in [-1,~1]^{n+3}, \end{aligned} \end{aligned}$$

where $\varvec{{\xi }}$ are local (isoparametric) coordinates, n is the number of random variables/parameters, $\varphi ^e_i$, $\varvec{{x}}^e$, $\varvec{{\theta }}^e$, and $\varvec{{y}}^e$ are the basis functions, the physical and stochastic coordinates, and the unknown function defined over element e, respectively, and $I^e$ is a set of indices associated with a current element.

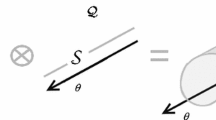
This method becomes advantageous in case of random interfaces and boundaries, where the physical-stochastic domain cannot be obtained as the tensor product of the physical domain and the stochastic domain due to curvilinear boundaries, and thus meshes in the physical and the stochastic spaces are not independent [34, 37]. This is demonstrated schematically in Fig. 1 demonstrating a 2D problem in the physical space (x, y). The third dimension $\theta$ depicts some random parameter. Figure 1 left demonstrates the model build as the tensor product of the FEM mesh in the physical domain and the traditional polynomial chaos expansion in the stochastic domain. It is not suitable for problems with random interfaces (like Fig. 1 right). Figure 1 right demonstrates an isoparametric local mesh generated originally in the general n-dimensional physical-stochastic space.

Fig. 1

Schematic FEM models generated as the tensor product of a FEM mesh in the physical space (x, y) and the polynomial chaos expansion along some stochastic parameter $\theta$ (left), and an isoparametric local FEM mesh as utilized in SL-FEM (right)

The local formulation is also highly compatible with various order reduction and hyperreduction techniques [36].

3 Representative volume element

3.1 Design of the RVE for non-overlapping inclusions

This section shortly reassembles the approach developed in [31, 32, 34, 39]. In our work we study materials with non-overlapping randomly distributed circular inclusions, which radii are also random. The basic idea is to replace the large randomly generated sample of material with a huge number of inclusions (non-ergodic model) by some simple parametric model with only one inclusion (ergodic model). The replacement (ergodic model) must be statistically similar to the original model in some sense [50].

The main questions are: which properties must be captured by the reduced model and how to perform model reduction? The answer to the first question comes directly from the huge experience gained by material scientists in recent decades. We know now that the main factor defining homogenized properties of heterogeneous materials is the global volume fraction of inclusions. Two models with a very different number of inclusions but the same global volume fraction exhibit very close homogenized stresses [56]. This is also the main quantity in analytical homogenization methods [44] like the Mori-Tanaka scheme, etc. On the microscale the most important quantity is the distance between neighboring inclusions [10]. It defines fluctuations of the microscopic stresses. The distance between neighboring inclusions can be estimated using the Delaunay triangulation [31]. Taken together, we thus keep our reduced ergodic model statistically similar to the original non-ergodic model in terms of the global volume fraction and the interparticle distances.

The second question is how to perform the reduction to the simplified ergodic model. To give an answer, we refer to the concept closely related to the Delaunay triangulation, namely the Voronoi tessellation. The Delaunay triangulation and the Voronoi tessellation are dual and unique. The Voronoi tessellation divides the material sample into cells such that each cell contains only one inclusion. The Voronoi cell $C_i$ is the set of points which are closer to the inclusion i than to any other inclusion. It can be understood as the region of predominant influence of the given inclusion. The volume fraction of the Voronoi cell is called the local volume fraction $v_f$. It depends on interparticle distances, the size of inclusions, and the number of neighbors to the inclusion. Thus, it reassembles a huge amount of statistical information regarding the microstructure. Furthermore, the local volume fraction determines the global volume fraction. Hence we can create a statistically similar ergodic model by preserving only one quantity—the local volume fraction.

The procedure is schematically illustrated in Fig. 2. Firstly, the large non-ergodic sample is divided into Voronoi cells. Next, the areas and local volume fractions of the Voronoi cells are computed. After that all Voronoi cells are reduced to rectangular unit cells, however, keeping the same values of the local volume fraction. The last step is the rearrangement of unit cells into the parametric model. Unit cells are re-scaled at this step, however, their areas are not lost, they become weight factors in the new model and thereby are included into the statistics. The detailed description of this procedure and a statistical comparison of the ergodic and non-ergodic models is presented in [39].

Fig. 2

Reduction of a non-ergodic model to a simple ergodic model: division into Voronoi cells, reduction into rectangular cells with the same local volume fraction, and further rearrangement into a parametric model

Remark

The probability density function of the inclusion radius r in the ergodic model reflects the inclusion distribution in the non-ergodic model. Thus, different distributions, the effect of clustering, etc. are included into the simulation through the probability density function. Figure 1 right depicts the model with variable inclusion radius. The dependency $r(\theta )$ and correspondingly the shape of the inclusion in Fig. 1 are uniquely evaluated from the probability density function of r [32].

3.2 Example of the ergodic RVE design

In this section we provide a simple example of the ergodic RVE design for the purpose of illustration. In order to show how interparticle distances are included into the ergodic RVE, we consider inclusions of one size. Note that there will be still only one variable in the ergodic model—the inclusion radius.

To start with, we generate one large non-ergodic random sample with 35 000 inclusions and use it to collect statistical information. Inclusions are distributed using the random number generator. Overlapping inclusions are removed from the sample and regenerated. For purpose of convenience we locate all inclusions within bounding boxes and enforce that the bounding boxes are also non-overlapping. This is done for two reasons: firstly, we guarantee some minimal distance between inclusions and simplify the meshing for a further simulation; secondly, we induce anisotropy in the non-ergodic sample. The ergodic RVE is anisotropic due to its rectangular shape, which is a well-known issue and can be fixed using some novel RVE types like the circular RVE [6]. Since we rely on the classical rectangular RVE, we need to make the non-ergodic RVE also anisotropic for a fair comparison of two models.

Since we use bounding boxes, we check distances not between inclusions, but between boxes. Mathematically this is equivalent to the distances between inclusions measured not in the Euclidean metric, but in the max value metric.

After the non-ergodic sample is generated, the interparticle distances between neighbor inclusions and the number of neighbors for each inclusion is measured. This is done using the Delaunay triangulation.

An ergodic model with variable inclusion radius can reproduce a variable interparticle distance. Under consideration of the PBC the distance to the neighbor inclusion is twice the distance from the inclusion interface to the boundary of the RVE. Therefore the ergodic model is capable to replicate the interparticle distances simply by choosing the correct radii distribution. Theoretically this can be done immediately at this stage, but the general procedure is developed for a more complicated example and requires some further transformations.

The next step is to compute the Voronoi tessellation and to evaluate Voronoi cell areas (the main statistical information for an ergodic model). It is expected that the area distribution is close to the log-normal distribution: Area is strictly positive, has no upper limit, and results from a fully random sequence. Another reason for using the log-normal distribution to approximate statistical data is that division and multiplication of log-normal variables yield a log-normal variable.

The quantity of interest is now the normalized radius evaluated from the non-ergodic sample. This is the relation of the inclusion radius (fixed value) to the square root of the cell area. It is also expected to be close to a log-normal distribution. The original distribution of the normalized radii in the non-ergodic sample and its log-normal fit are depicted in Fig. 3. The presented theoretical distribution (fitting curve) is then incorporated into the ergodic RVE. For the purpose of convenience we truncate the log-normal distribution in a way that the smallest radius value is exactly 0.25 and the largest radius value does not exceed 0.6. This is the radii distribution we use in ergodic simulations.

Fig. 3

The cumulative distribution function of the normalized radius in the sample with 35,000 inclusions and its log-normal fit

The non-ergodic sample with 35 000 inclusions is however far too large and computational costs required for a FEM simulation of this sample exceed our capabilities. Thus we need samples of a more modest size for simulations. Reasonable computational time can be achieved if non-ergodic samples contain only 128 inclusions.

In order to improve the quality of non-ergodic samples with 128 inclusions we generate a large number of them (100) and select the ten samples demonstrating statistical properties closest to those depicted in Fig. 3. Figure 4 shows the normalized radii distributions for the ten best samples with 128 inclusions and the normalized radii distribution obtained for 35 000 inclusions. The selected ten samples are used for a comparison with the ergodic model in the sequel.

Fig. 4

The cumulative distribution function of the normalized radius in the sample with 35,000 inclusions and in ten samples with 128 inclusions

The last step is the generation and meshing of the ergodic sample with the given radii distribution. Information on interparticle distances is included into the model through the variable radius, however the information on the number of neighbors and many-point probability distributions are captured only partially and indirectly (they also affect the areas of Voronoi cells and thus the normalized radii).

The statistical study of the non-ergodic sample shows [39] that the average number of neighbors in the presented non-ergodic model equals six. The rectangular shape of the ergodic RVE prescribes the existence of only four neighbors in ergodic model. This disagreement is significant. The number of neighbors is related to 3- and higher-point distributions. The ergodic model can be further improved by using arbitrary-sided or even circular RVEs, but this is the subject of a separate study.

3.3 Boundary conditions

The accuracy of the presented model depends strongly on the proper choice of boundary conditions (BC) since by switching to the ergodic model we increase their influence. For a sufficiently large non-ergodic sample the effect of boundary conditions is negligible. In contrast, varying the boundary conditions in an ergodic model can even double the microscopic stress values [48, 56].

All BC applied to the microstructure must satisfy the Hill-Mandel condition, which states the equality between the microscopic and macroscopic energy increments. The quantities involved in the Hill-Mandel condition are often understood as incremental internal energies or as virtual work of internal forces on the macroscale and on the microscale. In classical (deterministic) computational homogenization there are only three types of BC satisfying the Hill-Mandel condition: the Dirichlet BC (DBC), the periodic BC (PBC), and the traction BC (TBC). The recently introduced novel weak PBC [46] and other advanced techniques still belong to one of the three classical types of BC from this perspective. It is well-known that the DBC overestimate stresses, while the TBC underestimate them [6, 44, 45, 48, 55, 56]. The most reliable results even in case of random materials are obtained using the PBC, which is however often criticized in literature since random samples are not periodic.

In our previous study [39] we addressed this criticism and proposed a novel type of boundary conditions for stochastic problems, namely the soft PBC. Note that the soft PBC reduce to the classical strong PBC in the deterministic case. To set the stage, let us define two spaces: the physical space $\mathbb {E}$, i.e. the Euclidean space with coordinates $\varvec{{x}}\in \mathbb {R}^3$ augmented by a corresponding algebra, and the stochastic space (space of parameters) $\mathbb {S}$ with coordinates (parameters) $\varvec{{\theta }}\in \mathbb {R}^n$. Let us consider the physical domain $\mathcal {D} \subset \mathbb {E}$ associated with the space occupied by a body in its undeformed state and the stochastic domain $\mathcal {S}\subset \mathbb {S}$ associated with uncertain parameters. The soft PBC are introduced as follows:

$$\begin{aligned} \begin{aligned}&\frac{1}{V_0}\int \limits _{\mathcal {D}}\varvec{\mathrm {F}}(\varvec{{x}},\varvec{{\theta }})~\mathrm {d}\varvec{{x}}=\bar{\varvec{\mathrm {F}}}^\theta ,&\exists \bar{\varvec{\mathrm {F}}}^\theta \ne \bar{\varvec{\mathrm {F}}},\\&\int \limits _{\mathcal {S}}\bar{\varvec{\mathrm {F}}}^{\theta } f_{\varvec{{\theta }}} \mathrm {d}\varvec{{\theta }}=\bar{\varvec{\mathrm {F}}},\\&\frac{1}{V_0}\int \limits _{\mathcal {D}}\varvec{\mathrm {P}}(\varvec{{x}},\varvec{{\theta }})~\mathrm {d}\varvec{{x}}=\bar{\varvec{\mathrm {P}}}^\theta ,&\exists \bar{\varvec{\mathrm {P}}}^\theta \ne \bar{\varvec{\mathrm {P}}},\\&\int \limits _{\mathcal {S}} \bar{\varvec{\mathrm {P}}}^\theta f_{\varvec{{\theta }}} \mathrm {d}\varvec{{\theta }}=\bar{\varvec{\mathrm {P}}},\\&\frac{1}{V_0}\int \limits _{\partial \mathcal {D}}\delta \varvec{{w}}^\theta \cdot [\varvec{\mathrm {P}}^\theta \cdot \varvec{{N}}]~\mathrm {d}A=0, \quad \forall \theta . \end{aligned} \end{aligned}$$

(7)

where $V_0$ is the physical volume of the RVE, $\varvec{\mathrm {F}}$ and $\varvec{\mathrm {P}}$ are the microscopic deformation gradient and the microscopic Piola stress tensor, $\bar{\varvec{\mathrm {F}}}^\theta$ and $\bar{\varvec{\mathrm {P}}}^\theta$ are quantities averaged over the physical volume (but still functions of the random parameters), and $\bar{\varvec{\mathrm {F}}}$ and $\bar{\varvec{\mathrm {P}}}$ are the macroscopic (homogenized) deformation gradient and the macroscopic (homogenized) Piola stress tensor, $\delta \varvec{{w}}^\theta$ is the variation of the displacement at a fixed $\theta$, $\varvec{{N}}$ is the unit normal vector to the boundary $\partial \mathcal {D}$. The last equation implies that the displacements are periodic, and stresses are antiperiodic on the boundary of the RVE for each value of $\theta$. By considering condition (7) we apply some sort of weakened Hill-Mandel condition and thus allow local fluctuations of $\bar{\varvec{\mathrm {F}}}^\theta$ and $\bar{\varvec{\mathrm {P}}}^\theta$, whereby only the parameter averages of $\bar{\varvec{\mathrm {F}}}^\theta$ and $\bar{\varvec{\mathrm {P}}}^\theta$ must coincide with their macroscopic counterparts $\bar{\varvec{\mathrm {F}}}$ and $\bar{\varvec{\mathrm {P}}}$. In contrast, in the classical PBC the following strong relations are enforced $\bar{\varvec{\mathrm {F}}}^\theta =\bar{\varvec{\mathrm {F}}}$ and $\bar{\varvec{\mathrm {P}}}^\theta =\bar{\varvec{\mathrm {P}}}$.

Simulations considered in this paper are performed using either the strong PBC or the soft PBC. For the purpose of comparison, the macroscopic deformation gradient applied to the microstructure corresponds to 10% uniaxial extension or to 10% simple shear:

$$\begin{aligned} \bar{\varvec{\mathrm {F}}} ~\widehat{=}~ \begin{bmatrix} 1.1 &{} ~0~ \\ 0 &{} 1 \end{bmatrix}, \quad \quad \quad \bar{\varvec{\mathrm {F}}} ~\widehat{=}~ \begin{bmatrix} ~1~ &{} 0.1 \\ 0 &{} 1 \end{bmatrix}. \end{aligned}$$

(8)

3.4 Elasto-plastic material model

For the sake of demonstration, the considered material model is isotropic. We use finite additive von-Mises plasticity in the logarithmic strain space with a saturation-type nonlinear isotropic hardening [27, 28]. Let us consider the right Cauchy-Green strain tensor $\varvec{\mathrm {C}}=\varvec{\mathrm {F}}^t\cdot \varvec{\mathrm {F}}$ and its dual the Piola-Kirchhoff stress tensor $\varvec{\mathrm {S}}=\varvec{\mathrm {F}}^{-1}\cdot \varvec{\mathrm {P}}$, where $\square ^t$ and $\square ^{-1}$ denote transposition and inversion, respectively. Within this approach the Hencky strain $\varvec{\mathrm {E}}:=\frac{1}{2}\mathrm {ln}\varvec{\mathrm {C}}$ is additively decomposed into elastic $\varvec{\mathrm {E}}^e$ and plastic $\varvec{\mathrm {E}}^p$ parts. Since the elastic and plastic strains are decomposed additively, relations known from small strain plasticity can be used further. Let us consider the stress $\varvec{\mathrm {T}}$ dual to the Hencky strain. The stress $\varvec{\mathrm {T}}$ is evaluated using a standard (small-strain) constitutive model [27], e.g. linear isotropic von-Mises plasticity with nonlinear hardening:

$$\begin{aligned} \begin{aligned}&\varvec{\mathrm {E}}=\varvec{\mathrm {E}}^e+\varvec{\mathrm {E}}^p,\\&\varvec{\mathrm {T}}^{vol}=3 k \varvec{\mathrm {E}}^{e,vol},\quad \quad \varvec{\mathrm {T}}^{dev}=2\mu \varvec{\mathrm {E}}^{e,dev},\\&\Phi =\Vert \varvec{\mathrm {T}}^{dev}\Vert -\sqrt{\frac{2}{3}}[y_0-\beta ]\le 0,\\&\dot{\varvec{\mathrm {E}}^p}={\dot{\lambda }}\varvec{\mathrm {T}}^{dev}/\Vert \varvec{\mathrm {T}}^{dev}\Vert ,\\&{\dot{\alpha }}={\dot{\lambda }}\sqrt{\frac{2}{3}},\\&{\dot{\lambda }}\ge 0,\quad \quad \Phi \le 0, \quad \quad {\dot{\lambda }} \Phi = 0,\\&\dot{\varvec{\mathrm {T}}}=\varvec{\mathrm {J}}^{ep,log}:\dot{\varvec{\mathrm {E}}}, \end{aligned} \end{aligned}$$

(9)

where ${\dot{\square }}$ is the time derivative, $\square ^{vol}$ is the volumetric part of a tensor, $\square ^{dev}$ is the deviatoric part of a tensor, $\varvec{\mathrm {J}}^{ep,log}$ is the elasto-plastic tangent modulus in the logarithmic strain space, k and $\mu$ are the bulk modulus and the shear modulus, $\lambda$ is the plastic multiplier, $\alpha$ is the internal variable, $\beta$ is the hardening stress, and $\Phi$ is the yield function [27]. The saturation type isotropic hardening is defined by

$$\begin{aligned} \beta =-h\alpha -[y_\infty -y_0][1-\exp (-\omega \alpha )], \end{aligned}$$

where $\omega$ is the saturation parameter, h is the hardening parameter, $y_0$ and $y_\infty$ are the initial yield stress and the limit yield stress.

Once the stress $\varvec{\mathrm {T}}$ and tangent modulus $\varvec{\mathrm {J}}^{ep,log}$ in the logarithmic strain space have been obtained from the constitutive model, they are mapped back into the Piola-Kirchhoff stress

$$\begin{aligned} \varvec{\mathrm {S}}=\varvec{\mathrm {T}}:\mathbb {P}^1 \end{aligned}$$

and the elasto-plastic tangent modulus

$$\begin{aligned} \varvec{\mathrm {J}}^{ep}=[\mathbb {P}^1]^t:\varvec{\mathrm {J}}^{ep,log}:\mathbb {P}^1+\varvec{\mathrm {T}}:\mathbb {P}^2, \end{aligned}$$

where $\mathbb {P}^1=\frac{\partial \varvec{\mathrm {E}}}{\partial \varvec{\mathrm {C}}}$ and $\mathbb {P}^2=\frac{\partial ^2 \varvec{\mathrm {E}}}{\partial \varvec{\mathrm {C}}^2}$ are some projection tensors. A detailed outline of the projection tensors is given in [28].

The following values of material parameters of a matrix are considered for all simulation presented in the sequel: the bulk modulus $k=17.33$, the shear modulus $\mu =8$, the saturation parameter $\omega =20$, the hardening modulus $h=1$, the initial and limit yield stresses $y_0=1$ and $y_\infty =1.2$. The inclusion is ten times stiffer than the matrix material ($k=173.3$, $\mu =80$). The hyperelastic material model, which is used for comparison, is obtained by considering an infinite yield stress but keeping the same bulk modulus and shear modulus [27].

The plastic hysteresis curve under uniaxial loading is depicted for the specified material model in Fig. 5. Here the Cauchy stress is plotted versus the Biot strain $\sqrt{\varvec{\mathrm {C}}}-\varvec{\mathrm {I}}$, where $\varvec{\mathrm {I}}$ is the second order identity tensor.

Fig. 5

The Cauchy stress plotted versus the Biot strain for the idealized uniaxial tension experiment. Hysteresis curve obtained using the specified material properties

4 Validation of the ergodic RVE

The validation of the ergodic RVE design is performed in [39] for elastic problems. The application of the ergodic RVE design for plastic problem can result in higher errors due to the increased role of the 3- and higher-point distributions. In this section we provide the comparison of the ergodic RVE described in Sect. 3.2 with ten non-ergodic samples including 128 inclusions each (see also Sect. 3.2). Due to high computational costs of the non-ergodic models, simulations with higher number of inclusions are not performed. The FE mesh is also restricted to linear finite elements. A fragment of the mesh used in the non-ergodic simulations is depicted in Fig. 6.

The non-ergodic simulations are performed with the classical PBC, the ergodic simulation is repeated twice with the strong PBC and the soft PBC. We apply a macroscopic deformation gradient which corresponds to 10% uniaxial tension. Material properties are presented in Sect. 3.4. The inclusions remain elastic, their bulk and shear modulus are ten times higher than those of the matrix.

Fig. 6

Fragment of the mesh generated for the non-ergodic model with 128 inclusions

The microscopic stress distribution over the volume of the non-ergodic RVE at maximum tension of 10% is depicted in Fig. 7. The microscopic equivalent plastic strain distribution over the volume of the non-ergodic RVE is depicted in Fig. 8. For comparison the distribution of the microscopic equivalent strain within the ergodic RVE with the soft PBC is presented in Fig. 9. A detailed analysis and discussion on the ergodic RVE is presented in Sect. 5.

Fig. 7

Stress distribution within the non-ergodic sample: the first component of the stress tensor (left), the microscopic von-Mises stress (right)

Fig. 8

The equivalent microscopic plastic strain $\alpha$ distributed over the volume of the non-ergodic RVE

Fig. 9

The equivalent microscopic plastic strain $\alpha$ distributed over the volume of the ergodic RVE with the soft PBC

In this section only the microscopic quantities are compared, because they are shared by both the ergodic and the non-ergodic models. Macroscopic quantities cannot be compared directly (except of homogenized stress values), because the ergodic RVE is a stochastic RVE and all quantities are computed not as single values but as probability distributions.

Here we compare the following statistical moments of microscopic quantities: the mean value (the mean microscopic stress equals the macroscopic/homogenized stress), standard deviation of the microscopic quantities, higher order standardized moments like skewness (3rd order moment) and kurtosis (4th order moment), and $\min$ and $\max$ values over the volume.

Considering some scalar $\sigma$ as quantity of interest, the mean value is evaluated as:

$$\begin{aligned} \mathrm {mean} \sigma= & {} \frac{1}{V_0}\int \limits _{\mathcal {D}}\int \limits _{\mathcal {S}}\sigma (\varvec{{x}},\varvec{{\theta }})f_{\varvec{{\theta }}} \mathrm {d}\varvec{{\theta }}~\mathrm {d}\varvec{{x}}, \end{aligned}$$

(10)

$$\begin{aligned} \mathrm {mean} \sigma= & {} \frac{1}{V_0}\int \limits _{\mathcal {D}}\sigma (\varvec{{x}})~\mathrm {d}\varvec{{x}}, \end{aligned}$$

(11)

for an ergodic model and for a non-ergodic models, respectively.

The standard deviation is evaluated for an ergodic model and for a non-ergodic models as:

$$\begin{aligned} \mathrm {std} \sigma= & {} \sqrt{\frac{1}{V_0}\int \limits _{\mathcal {D}}\int \limits _{\mathcal {S}}[\sigma (\varvec{{x}},\varvec{{\theta }})-\mathrm {mean}\sigma ]^2 f_{\varvec{{\theta }}} \mathrm {d}\varvec{{\theta }}~\mathrm {d}\varvec{{x}}}, \end{aligned}$$

(12)

$$\begin{aligned} \mathrm {std} \sigma= & {} \sqrt{\frac{1}{V_0}\int \limits _{\mathcal {D}}[\sigma (\varvec{{x}})-\mathrm {mean}\sigma ]^2~\mathrm {d}\varvec{{x}}}. \end{aligned}$$

(13)

Standardized n-th order moments are given as:

$$\begin{aligned} {\mu }^n \sigma= & {} \frac{\frac{1}{V_0}\int \limits _{\mathcal {D}}\int \limits _{\mathcal {S}}[\sigma (\varvec{{x}},\varvec{{\theta }})-\mathrm {mean}\sigma ]^n f_{\varvec{{\theta }}} \mathrm {d}\varvec{{\theta }}~\mathrm {d}\varvec{{x}}}{[\mathrm {std}\sigma ]^n}, \end{aligned}$$

(14)

$$\begin{aligned} {\mu }^n \sigma= & {} \frac{\frac{1}{V_0}\int \limits _{\mathcal {D}}[\sigma (\varvec{{x}})-\mathrm {mean}\sigma ]^n~\mathrm {d}\varvec{{x}}}{[\mathrm {std}\sigma ]^n}. \end{aligned}$$

(15)

Since the reference solution obtained with ten non-ergodic samples demonstrates some spread, the relative error is estimated as the normalized distance between the reference interval and the ergodic solution:

$$\begin{aligned} \begin{aligned}&M=\max (\sigma ^{non-ergo}),\\&N=\min (\sigma ^{non-ergo}),\\&A=\mathrm {average} (\sigma ^{non-ergo}),\\&\mathrm {error}=\left\{ \begin{aligned}&0,&\sigma ^{ergo}\in [N,~M]\\&\frac{\sigma ^{ergo}-M}{|A|},&\sigma ^{ergo}> M \\&\frac{\sigma ^{ergo}-N}{|A|},&\sigma ^{ergo}< N \end{aligned} \right. . \end{aligned} \end{aligned}$$

(16)

Note that the error is set to zero if the ergodic solution fits into the reference interval.

Figures 10, 11 and 12 demonstrate comparison of statistical moments for the first component of the stress tensor $\sigma _{11}$, for the second normal stress $\sigma _{22}$, and for the equivalent plastic strain $\alpha$, respectively.

Fig. 10

Comparison of statistical moments for the first component $\sigma _{11}$ of the microscopic stress tensor

Fig. 11

Comparison of statistical moments for the second normal stress $\sigma _{22}$ of the microscopic stress tensor

Fig. 12

Comparison of statistical moments for the microscopic equivalent plastic strain $\alpha$

The ergodic RVE with the soft PBC performs better than the ergodic RVE with the strong PBC in terms of skewness and kurtosis. Highest disagreement is observed for the second normal stress. The error of the ergodic model is much higher for plastic materials than for hyperelastic materials [39], but is still reasonable. The main contribution to the error is most probably associated with the model simplifications, namely the loss of information regarding the number of neighbors in the non-ergodic model (Sect. 3.2). It is worth to mention however that some ergodic model inaccuracy is caused by the fitting error (Fig. 3). Our previous study shows that up to 2% disagreement in homogenized stresses is associated with fitting error [32].

The simulation is performed with 10 load steps. For each step we increase the applied macroscopic Biot strain by 1% until the maximum strain of 10% is obtained. The evolution of the macroscopic von-Mises stress plotted versus the macroscopic Biot strain (for different load steps) is depicted in Fig. 13. The non-ergodic samples demonstrate only a very small spread, that is why it is depicted schematically by red bars. Numbers near red bars give the exact size of the spread. Note that the spread is temporally decreased in the transition region between the fully elastic and the fully plastic macroscopic response (4-6% strain).

Fig. 13

Evolution of the macroscopic von-Mises stress in ergodic and non-ergodic models plotted versus Biot strain

Note that the soft PBC perform clearly better in the elastic region. However in the plastic region of the diagram both types of PBC yield a regular error about 4%. In the plastic region the soft PBC seems to be better in terms of higher order moments (Fig. 10). Further comprehensive discussion and comparison of the strong and the soft PBC is given in Sect. 5.

The main conclusion is that the ergodic model performs well for elastic problems, is still reasonably accurate for plastic problems, and can be further improved by including the 3- and higher-point distributions. The 4% regular error in stresses in the current example is the price for model simplification in the ergodic RVE design.

4.1 Computational costs of ergodic model

The stochastic FEM is known for high computational costs. Furthermore most of stochastic methods are sensitive to the curse of dimensionality, i.e. the exponential growth of the problem complexity with an increase of number of parameters.

The presented design of the ergodic RVE allows to overcome the curse of dimensionality by reducing the problem to only one random parameter. Even if further noise and error terms are added to the model to reflect the fitting error and measurement imprecision in case of experimental data taken from a lab, the dimension reduction presented in [37] allows to avoid additional parameters in the simulation. The stochastic model with only one parameter is in general very cheap.

Already medium-precision RVE with 128 inclusions require 10 times more computational time than the ergodic RVE. Furthermore the convergence of the non-ergodic model is the typical convergence of the Monte-Carlo simulation with fully random input sequence. It is theoretically estimated as the square root of the number of inclusions.

The ergodic RVE design permits for use of highly precise stochastic methods like the stochastic collocation method or the spectral Galerkin method, which demonstrate from polynomial up to exponential convergence rate. The random generator used in the non-ergodic approach produces unstructured data sequence, while the ergodic approach utilizes the well-structured uncorrelated parameterized random variables, which allows for an optimized sampling strategy.

Another possibility to reduce the computational costs of the ergodic simulation is the reduced order modeling. Very good results are achieved for elastic problems by using the combination of the proper orthogonal decomposition (POD) and the discrete empirical approximation [36]. However the standard sampling based order reduction (like POD) fails for plastic problems due to the existence of internal variables and thus material memory. Up to our knowledge, the application of the POD for plasticity is still under consideration.

5 Simulation results

In this work we compare ergodic stochastic FEM simulations performed with four different models. In the first example we consider a single unit cell with a randomly oriented elliptic inclusion. This model is simply used to compare the elastic and plastic material models and also to demonstrate the significant influence of the uncertain (random) parameter on the simulation results.

In the second example we consider a circular inclusion with random radius. This RVE model is based on the approach described in 3.1. The second example is provided to demonstrate the effect of the novel soft PBC in comparison to the standard strong PBC.

The third example focuses on macroscopic plasticity signatures such as the macroscopic von-Mises stress (von-Mises stress of the homogenized stress tensor). Here, the RVE model is similar to the previous one, however, here we consider two random parameters: the inclusion radius and the limit yield stress. These simulations provide additional data for further constitutive modeling on the macroscale.

The fourth example is similar to the third example, but it considers that the yield stress for the soft matrix and for the stiff inclusion are the same, which is a very rare situation in practice. This example has rather academic interest. It is particularly interesting because it shows that the macroscopic von-Mises stress can be a misleading signature of plasticity on the microscale.

Remark

The inclusion orientation and the radius variation reflect some actually observed property fluctuations over the volume of the non-ergodic RVE. This type of uncertainty is called in the dedicated literature an aleatoric uncertainty. Corresponding simulations (the first and second examples) are performed with both the soft PBC and the strong PBC. In contrast, the variation of the limit yield stress in the third example represents only our doubts (lack of knowledge) regarding some simulation constants. Here, we do not consider the property fluctuations over the volume (a classical example of an aleatoric random field), but only the unknown/imprecisely measured value. This type of uncertainties is called epistemic. The soft PBC are designed only for aleatoric uncertainties (representing volume fluctuations), hence they cannot be used in the third example, where the effect of epistemic uncertainty is studied.

5.1 Example I: stochastic RVE with an elliptic inclusion

To start with, we consider a simple model of heterogeneous materials with periodic microstructure consisting of a soft matrix and stiff elliptic randomly oriented inclusions. The inclusions possess higher yield stress and stay elastic during the entire simulation. The orientation angle $\varphi$ is the only random parameter in the RVE (see Fig. 14). Due to periodicity it is sufficient to model only a single unit cell. This problem was studied in [39] for purely elastic materials. The soft PBC are applied, however the previous study [39] demonstrated that there is only a very small effect of the soft PBC in comparison to the classical strong PBC for this model. Material properties and the macroscopic deformation gradient are introduced in Sect. 3.4.

Fig. 14

A single unit cell with a randomly oriented elliptic inclusion

Fig. 15

The microscopic von-Mises stress distribution for an RVE with a single randomly oriented elliptic inclusion. The third dimension is the parameter $\theta$. Elastic material model

Fig. 16

The microscopic von-Mises stress distribution for an RVE with a single randomly oriented elliptic inclusion. The third dimension is the parameter $\theta$. Plastic material model

Fig. 17

The distribution of the equivalent microscopic plastic strain $\alpha$ within the RVE. The third dimension is the parameter $\theta$. Plastic material model

Note that the physical model is 2D. The third dimension is the parameter $\theta$. This parameter is linked to the orientation angle of the elliptic inclusion. For the sake of convenience the random variable $\theta$ is modeled as a truncated Gaussian random variable with zero mean and unit variance. This implies that the parameter is specified in the range $\theta \in [-3,~3]$.

In this example the parameter $\theta$ is related to the orientation angle $\varphi$ through the expression:

$$\begin{aligned} \varphi (\theta )=\frac{\pi }{4}+\frac{\pi }{12}\theta , \end{aligned}$$

(17)

where $\theta \in [-3,~3]$ and consequently $\varphi \in [0,~\pi /2]$.

Figures 15 and 16 demonstrate the micromechanical von-Mises stress distribution within the unit cell for a purely elastic material model (Fig. 15) and for a plastic material model (Fig. 16). The distribution of the equivalent plastic strain within the RVE is plotted in Fig. 17, different colors depict the plastic strain intensity. Note that nearly the entire RVE exhibits plastic strains.

These figures demonstrate that (1) the effect of the parameter variation is significant (Fig. 16), (2) the unit cell exhibits large strain plasticity with most of material being plastified (Fig. 17), and 3) plasticity strongly changes the microscopic stress distribution (Figs. 15, 16). This is also a suited example to demonstrate the methodology.

Remark

Any output in the parametric simulation (stress, displacement, etc.) is a function of a parameter. If the model parameter is a random variable, the output becomes also a random variable with some probability distribution and probabilistic moments. The parametric simulation does not return however the probability density of the output, instead the mapping function is evaluated. This is a function which maps input (random parameter) into the output (Fig. 18). Let us consider the output quantity $\sigma$ (a random variable) with the probability density function $f_\sigma (\sigma )$, $\sigma (\theta )$ is the mapping function, $\theta$ is the input parameter with the predefined probability density function $f_\theta (\theta )$. For the sake of simplicity, let us consider only the monotonic mapping function $\sigma (\theta )$, then the probability density $f_\sigma (\sigma )$ is obtained from the expression:

$$\begin{aligned} f_\sigma (\sigma ) \mathrm {d}\sigma = f_\theta (\theta ) \mathrm {d}\theta , \quad \sigma =\sigma (\theta ). \end{aligned}$$

(18)

In fact the two probability density functions $f_\sigma (\sigma )$ and $f_\theta (\theta )$ are connected through the derivative $\frac{\mathrm {d}\sigma (\theta )}{\mathrm {d}\theta }$. Any probabilistic moments of the output can be indeed estimated using the mapping function only, for instance, the mean value reads as

$$\begin{aligned} \mathrm {mean}(\sigma )=\int \limits _{\mathrm {min}\sigma }^{\mathrm {max}\sigma }\sigma f_\sigma (\sigma ) \mathrm {d}\sigma =\int \limits _{\mathrm {min}\theta }^{\mathrm {max}\theta }\sigma (\theta ) f_\theta (\theta ) \mathrm {d}\theta . \end{aligned}$$

(19)

Fig. 18

The output of the parametric simulation is the function which maps the input parameter $\theta$ into some quantity of interest $\sigma$. The input $\theta$ has predefined probability density, the probability density of $\sigma$ can be uniquely obtained from the mapping function according to Eq. (18)

Fig. 19

The macroscopic von-Mises stresses for an elastic RVE model (top red) and for an elasto-plastic RVE model (bottom green) as function of the orientation angle $\varphi$. The blue area depicts schematically the pdf of the angle $\varphi$. All probabilistic moments of the macroscopic von-Mises stress can be evaluated form the mapping function $\sigma (\varphi )$ according to Eq. (19). (Color figure online)

Figure 19 depicts the macroscopic von-Mises stress $\sigma (\varphi )$ (the von-Mises stress obtained from the homogenized stress tensor) as function of the orientation angle $\varphi$ for the purely elastic (the top red curve) and elasto-plastic (the bottom green curve) material models. The blue area depicts schematically the pdf $f_\varphi (\varphi )$ of the input variable $\varphi$. The input pdf will be skipped in subsequent figures for the sake of simplicity. Stress mean values are obtained from (19) by integrating $\sigma (\varphi )$ with the input pdf $f_\varphi (\varphi )$. Note that both curves $\sigma (\varphi )$ are nearly straight. This is due to the soft PBC, which redistribute the loading between different unit cell configurations (RVE sections which correspond to different parameter values) in a way that the total mechanical energy is minimized. The effect of the soft PBC is similar to connecting springs sequentially: all springs possess the same stress but different strains. In contrast, the strong PBC are similar to springs connected in parallel: all springs possess the same strain but different stresses.

The behavior implemented through the soft PBC is more realistic due to interaction between separate unit cells, as it happens in the non-ergodic models. Also the stress standard deviation is strongly reduced in case of the soft PBC. Note that the only quantity transferred to the macroscale is the mean value of the stress. The stress standard deviation, higher order moments, as well as the upper and lower stress bounds are relevant mostly in case of non-perfect scale separation, for the mesoscale simulations, for damage models, and as plasticity signatures on the macroscale. Too large standard deviation means that model is not reliable, it is too sensitive to parameter variation, and the mean value can be calculated with significant error. In some sense the soft PBC stabilize model response.

5.2 Example II: stochastic RVE with variable size of inclusion

The second example investigates a heterogeneous material consisting of a soft matrix and non-overlapping randomly distributed circular inclusions, which radii are also random. The design of a simple stochastic ergodic RVE for this type of materials is briefly introduced in Sect. 3.1. Material properties are the same as in the previous example (see Sect. 3.4). The soft PBC (Sect. 3.3) are applied since they are found to be the most accurate for this model in the purely elastic case [39].

The purpose of this example is to apply the plastic constitutive relation within the homogenization framework developed earlier and to study microscopic and macroscopic plasticity signatures (von-Mises Stress). It suits also for the comparison of the soft PBC and the strong PBC in case of large deformation plasticity.

The physical microstructure is modeled as a 2D unit cell. The third dimension in these figures is the parameter $\theta$. The random parameter $\theta$ is related to the inclusion radius r through the expression:

$$\begin{aligned} r(\theta )=\exp (r_{mean}+r_{var}\theta ), \end{aligned}$$

(20)

where $\theta \in [-3,~3]$ and $r\in [0.25,~0.6]$. Note that the radius is here a truncated log-normal random variable and possesses a corresponding truncated log-normal probability distribution.

For the sake of demonstration we plot firstly the micromechanical von-Mises stress distribution within the RVE for a purely elastic model (Fig. 20) and for a plastic model (Fig. 21) under uniaxial tension (Sect. 3.3).

Fig. 20

The von-Mises stress distribution for an ergodic RVE which corresponds to randomly distributed circular inclusions. The third dimension is the parameter $\theta$. Elastic material model, the soft PBC

Fig. 21

The von-Mises stress distribution for an ergodic RVE which corresponds to randomly distributed circular inclusions. The third dimension is the parameter $\theta$. Plastic material model, the soft PBC

Figure 22 shows the macroscopic von-Mises stress (the von-Mises stress obtained from the homogenized stress tensor) as function of the inclusion radius $r(\theta )$ for the elastic (the top dashed curve) and plastic (the bottom solid curve) material models. These curves are obtained at 10% uniaxial tension. Stress mean values are obtained by integrating the stress curves with the input pdf according to (19). The first interesting result is that the macroscopic von-Mises stress in the elastic model decreases while the inclusion radius is increased. Normally we would expect higher stresses for larger radii, since the cell is getting stiffer. This effect is fully explained by the soft PBC, which redistribute the loading between different RVE sections (different radii). A larger radius causes a higher stiffness of the unit cell and has a very low probability of appearance according to the log-normal distribution (20). The minimization of the total mechanical energy is achieved if these rare and stiff unit cells are less loaded than the rest. In the elasto-plastic material model the plasticity also causes some load redistribution and the corresponding stress curve monotonically increases.

The strong PBC (Fig. 23) do not imply this behavior: a higher radius corresponds to a stiffer unit cell and causes larger von-Mises stress. Obviously, the plastic curve (bottom solid) demonstrates a smaller spread and significantly lower absolute stress values than the elastic curve (top dashed). The soft PBC (Fig. 22) yield much lower curve slopes than the strong PBC (Fig. 23) in all simulations. In these simulations we considered only uniaxial tension. Analogous results for 10% simple shear are depicted in Fig. 24.

Fig. 22

The macroscopic von-Mises stresses for an elastic model (top dashed) and for a plastic model (bottom solid) as function of the inclusion radius. Uniaxial tension, the soft PBC

Fig. 23

The macroscopic von-Mises stresses for an elastic model (top dashed) and for a plastic model (bottom solid) as function of the inclusion radius. Uniaxial tension, the strong PBC

Fig. 24

The macroscopic von-Mises stresses for a plastic model with the strong PBC (red curve) and with the soft PBC (green curve) as function of the inclusion radius. Shear loading. (Color figure online)

In summary, the RVE with the classical strong PBC and the RVE with the soft PBC demonstrate significantly different stress distributions.

Next we study the evolution of the macroscopic von-Mises stress while increasing the uniaxial loading. The simulation is performed with 10 load steps. For each step we increase the applied macroscopic Biot strain by 1% until the maximum strain of 10% is obtained. Figures 25 and 26 depict the evolution of the macroscopic von-Mises stress plotted versus the macroscopic Biot strain (for different load steps). Figure 25 is obtained for the soft PBC, while Fig. 26 is obtained for the strong PBC. The two dashed lines in each figure correspond to the maximum and minimum stresses (upper and lower bounds). The dependency on the random parameter is not depicted, but the parameter variation causes some spread of the macroscopic stresses. The stress spreads at 10% strain in Figs. 25 and 26 coincide with the lower curves in Figs. 22 and 23, respectively.

Fig. 25

The evolution of the macroscopic von-Mises stress plotted versus the macroscopic Biot strain. The soft PBC

Fig. 26

The evolution of the macroscopic von-Mises stress plotted versus the macroscopic Biot strain. The strong PBC

Figure 26 demonstrates the proportionally increasing spread in macroscopic stresses, while the load increases, but only up to 3% strain. After this point the stress spread is even reduced. This is the signature that plasticity started in the most stiff cells. After approximately 6–7% strain all cells exhibit plastic deformations and the spread in macroscopic stresses starts to increase proportionally again. In general, when plasticity starts, the spread is reduced. At the strain of 10% all unit cells exhibit massive plastic deformations and the spread in macroscopic stresses is smaller than at the strain of 3%, when all cells are elastic.

Figure 25 demonstrates a behavior similar to Fig. 26, however with much smaller spread in stresses. This is related to the load redistribution between unit cells. Similarly to Fig. 26, there is a bottle-neck in stress spread at 7% loading. At this point all unit cells start to deform plastically and the macroscopic stress curve (see Fig. 22) flips from the dashed-curve-like shape to the solid-curve-like shape in Fig. 22.

The spread of the macroscopic von-Mises stresses is an important quantity for further macroscale simulations. Thus the effect of the soft PBC is very important.

It is always hard to say when plastic deformations on the macroscale appear. From the moment when first plastic deformations are indicated on the microscale, until the microscale is massively plastic deformed, the stress curve on the macroscale slowly changes from the typically elastic behavior to the typically plastic behavior. There is no clear sharp transition between elastic and plastic regions on the macroscale. In case of a parametric simulation (as the one presented here), the stress spread is an additional indicator. In case of the soft PBC its signals are vague, but still can indicate the end of the transition region.

5.3 Example III: stochastic RVE with variable size of inclusion and variable material parameters

In the following example we add an additional random variable $\theta _y$ that relates to the limit yield stress in Eq. (9). Therefore the parameter variation $\theta _y$ does not affect elastic deformations of the body. Note that we do not consider here the empirically measurable property fluctuations over the volume. The additional random variable reflects another source of uncertainty: measurement imprecision due to poor experimental data, poor measurement tool accuracy, etc. Similarly to the previous simulations we consider the truncated Gaussian random variable $\theta _y$ as the additional parametric dimension to the problem. The limit yield stress is then given by:

$$\begin{aligned} y_{\infty }=1.2+\frac{0.1}{3}\theta _y, \end{aligned}$$

(21)

where $\theta _y\in [-3,~3]$ and $y_{\infty }\in [1.1,~1.3]$.

The simulation is performed using material properties given in Sect. 3.4. The RVE design is presented in Sect. 3.1. In contrast to the previous example we apply only the strong PBC, since the variation of the material parameters is a typical example of the so-called epistemic uncertainty. The epistemic uncertainty results not from a natural variation of some system properties which is observed in reality, but from our lack of knowledge. It has no physical background, we cannot treat it in a way presented in Sect. 3.3, hence the soft PBC are not applicable to epistemic uncertainties.

Due to the obvious difficulty to visualize a 4D model we do not show the parameter dimension related to the radius variation, instead we plot separate models for three different radii: $r=0.25$—the smallest radius (Fig. 27), $r=0.4$—the rounded mean value (Fig. 28), and 0.6—the largest radius (Fig. 29).

Fig. 27

The von-Mises stress distribution for an ergodic model with limit yield stress variation. The third dimension is the parameter $\theta _y$. Radius of the inclusion $r=0.25$, plastic material model

Fig. 28

The von-Mises stress distribution for an ergodic model with limit yield stress variation. The third dimension is the parameter $\theta _y$. Radius of the inclusion $r=0.4$, plastic material model

Fig. 29

The von-Mises stress distribution for an ergodic model with limit yield stress variation. The third dimension is the parameter $\theta _y$. Radius of the inclusion $r=0.6$, plastic material model

The dependence of the macroscopic von-Mises stress on the limit yield stress under uniaxial tension is depicted in Fig. 30. A larger limit yield stress corresponds to a stiffer unit cell and thus results in higher homogenized stresses. The middle points in the upper, middle, and lower curves in Fig. 30 coincide with the far right, middle, and far left points in the solid curve in Fig. 23, respectively. These are points where both diagrams intersect. Analogous results for the shear loading are depicted in Fig. 31. The middle points in curves in Fig. 31 coincide with the far right, middle, and far left points in the red curve in Fig. 24.

Fig. 30

The macroscopic von-Mises stresses for a plastic model with variable limit yield stress and three different inclusion’s radii. Uniaxial tension, the strong PBC

Fig. 31

The macroscopic von-Mises stresses for a plastic model with variable limit yield stress and three different inclusion’s radii. Shear loading, the strong PBC

Figure 32 demonstrates the evolution of the macroscopic von-Mises stress while increasing the Biot strain. For the purpose of visualization we plot separately curves for three selected radii.

Fig. 32

The evolution of the macroscopic von-Mises stress plotted versus the macroscopic Biot strain. The variable parameter is $y_\infty$. The strong PBC

Since the variation of $y_\infty$ does not affect the elastic deformations, elastic stresses show no spread. The point when the spread in stresses starts to grow indicates the start of plastic deformations. Softer cells with smaller inclusions start to deform plastically a bit later, this cause the transition region [3%–6%], where part of the unit cells exhibits still elastic deformations only. The spread between the red and blue curves in Fig. 32 coincides with the diagram in Fig. 26.

5.4 Example IV: stochastic RVE with plastic inclusion

In this example we consider an RVE very similar to the one in the previous example. The only difference is that the yield stress (and also the hardening, the limit yield stress, and the saturation parameter) for the soft matrix and for the stiff inclusion is the same, which is a very rare situation in practice. Thus, this example has rather academic interest to demonstrate the disagreement between quantities observed on the macroscale and microscopic effects.

Let us consider firstly the RVE with only one random parameter—the inclusion radius. The macroscopic von-Mises stress in case of 10% uniaxial tension and the soft PBC is presented in Fig. 33 (blue curve). For the purpose of comparison we also present here results for a purely elastic model (dashed green curve), and a realistic model with elastic inclusion (solid green curve) from example II. Analogous results but for the strong PBC are presented in Fig. 34.

Fig. 33

The macroscopic von-Mises stresses for a purely elastic model (dashed green), for a plastic model with elastic inclusion (solid green), and for a plastic model with plastic inclusion (bottom blue) as function of the inclusion radius. Uniaxial tension, the soft PBC. (Color figure online)

Fig. 34

The macroscopic von-Mises stresses for a purely elastic model (dashed red), for a plastic model with elastic inclusion (solid red), and for a plastic model with plastic inclusion (bottom blue) as function of the inclusion radius. Uniaxial tension, the strong PBC. (Color figure online)

Note that the blue curve in Fig. 34 is nearly horizontal but still slightly decreasing. This is unexpected and cannot be explained by the load redistribution, since the strong PBC are applied. This effect is observed only for uniaxial tension. The corresponding simulations under shear loading do not exhibit this behavior (Fig. 35).

Fig. 35

The macroscopic von-Mises stresses for a plastic model with the strong PBC (red curve) and with the soft PBC (green curve) as function of the inclusion radius. Dashed lines correspond to the model with plastic inclusion. Shear loading. (Color figure online)

For further analysis of this problem let us consider the second random parameter—the limit yield stress. Similar to example III, we plot the macroscopic von-Mises stress as function of the limit yield stress for three different inclusion radii (Fig. 36). This diagram clearly indicates the behavior we have reported in Fig. 34: unexpected decrease of the macroscopic von-Mises stress, while the inclusion radius and hence the cell stiffness increase. This observation contradicts our intuitive picture. A larger inclusion radius corresponds to a higher unit cell stiffness and must increase the macroscopic stresses. However we see the opposite situation. This simulation is performed using the strong PBC, thus there is no load redistribution.

Fig. 36

The macroscopic von-Mises stresses as functions of the limit yield stress plotted for different inclusion radii. The RVE with plastic matrix and inclusion, uniaxial tension, the strong PBC

Figure 37 demonstrates the evolution of the macroscopic von-Mises stress while increasing the Biot strain. Note that the unexpected behavior of the macroscopic von-Mises stress is observed only in the plastic region of the diagram. When the macroscopic strain reaches 6% the red, green and blue curves switch order : the top curve in the elastic region corresponds to the largest radius, it becomes the lowest curve in the plastic region.

Fig. 37

The evolution of the macroscopic von-Mises stress plotted versus the macroscopic Biot strain. The variable parameter is $y_\infty$. The strong PBC

In order to explain this paradox, we need to look closer at the macroscopic stress. In case of the smallest radius $r=0.25$ and the maximum uniaxial tension of 10% the mean macroscopic Cauchy stress reads:

$$\begin{aligned} \varvec{\bar{\sigma }}_{0.25}\widehat{=}\begin{bmatrix} 2.2294&{}0.000&{}0.000\\ 0.000&{}1.2473&{}0.000\\ 0.000&{}0.000&{}1.2567 \end{bmatrix}. \end{aligned}$$

(22)

Since the problem is 2D, the first and the second indices in the stress tensor correspond to x and y axes, and the third index is related to the out-of-plain stress evaluated based on the plane strain assumption.

In case of the largest radius $r=0.6$ the mean macroscopic Cauchy stress tensor reads:

$$\begin{aligned} \varvec{\bar{\sigma }}_{0.6}\widehat{=}\begin{bmatrix} 2.6625&{}0.000&{}0.000\\ 0.000&{}1.6757&{}0.000\\ 0.000&{}0.000&{}1.7325 \end{bmatrix}. \end{aligned}$$

(23)

As expected, in case of a larger inclusion all stress components are also larger. However, the von-Mises stress is evaluated using only the deviatoric component of the stress tensor, and in case of the larger radius it becomes smaller for some reasons.

Furthermore, it is known that the von-Mises stress evaluated from the homogenized stress (macroscopic von-Mises stress) is not the same as the homogenized von-Mises stress (average micromechanical von-Mises stress). The first option is the stress which can be observed and studied on the macroscale, while the second option is related to the intensity of plastic deformations but loses the connection to stresses observed on the macroscale. For the purpose of comparison, both quantities are evaluated (Table 1). Note that the averaged microscopic von-Mises stress grows with increasing inclusion size, indicating thereby the increased plastic deformation. At the same time the macroscopic von-Mises stress decreases. This table clearly indicates that the macroscopic von-Mises stress does not correctly represent the intensity of plastic deformations in heterogeneous materials.

Table 1 Comparison of the mean macroscopic von-Mises stress and the averaged microscopic von-Mises stress for two inclusion radii

From the simulation results we can conclude that neither the RVE with elastic inclusion nor the RVE under shear loading display the macroscopic von-Mises stress decay. Thus this effect is observed in one academic example only. This is however a bad sign telling us that the macroscopic von-Mises stress is not directly linked to processes on the microscale and can be potentially a misleading indicator of the plastic yielding. These observations are important for a further design of macroscopic constitutive models of heterogeneous materials.

The second conclusion is that the effect of the soft PBC is still significant and, as expected, fixes the entire stress curve near some averaged value.

6 Conclusions

In this paper we perform the non-deterministic computational homogenization of heterogeneous materials which exhibit large plastic deformations. We utilize a simplified parametric ergodic model of materials with randomly distributed non-overlapping inclusions and the recently proposed novel soft periodic boundary conditions for non-deterministic problems. Following our previous works, we compare the new soft periodic boundary conditions with the standard strong periodic boundary conditions. Furthermore, we estimate the effect of parameter variations on homogenized stresses in case of large plastic deformations. The non-deterministic (stochastic) solutions are obtained using the recently developed stochastic local FEM (SL-FEM). Thereby we extend to and examine the earlier proposed homogenization framework in case of large deformation plasticity.

On the basis of the performed simulations we conclude that the effect of the soft PBC compared to the strong PBC is significant for materials with non-periodic microstructure. The soft PBC redistribute load between parameter realizations (samples) and minimize the overall mechanical energy of the parameterized system. As a consequence, the spread in macroscopic stresses (which are functions of random parameters) is strongly reduced. Dependent on the weight factor (probability density function of random variable) the redistribution can even cause counterintuitive material response, where stiffer unit cells with large inclusions possess lower stresses than softer unit cells.

Plastic constitutive relations have a similar effect and reduce the spread in homogenized stresses. However, in case of the soft PBC the effect of plasticity on the stress spread is not significant. The stress redistribution caused by the boundary conditions clearly dominates.

Also there is a clear difference between the strong PBC and the soft PBC in predicting macroscopic yielding. An interesting result is that the macroscopic stress spread can be considered as an indicator for yielding on the microscale.

The response of the parameterized model cannot be obtained as a simple rescaling of the response of only one single deterministic model. Thus, the parametric simulation provides much more realistic results and must be preferred for the simulation of the material microstructure.

An unexpected stress response is observed while studying materials with plastic inclusions under uniaxial loading. Stiff unit cells displaying larger plastic strains and larger microstructural stresses exhibited smaller macroscopic von-Mises stresses (the von-Mises stress evaluated from the homogenized stress tensor). Interesting is also that the averaged microscopic von-Mises stress does not show this effect. Also, this is observed neither in case of shear nor in more realistic setting with stiff elastic inclusion. So, this effect is observed in only one academic example, but this shows that the macroscopic von-Mises stress is not necessarily a good representative for mechanical effects on the microscale. This is important for later constitutive modeling of heterogeneous materials and for formulating the yield criterium based on macroscopic indicators.

Note that the mentioned von-Mises stress decrease is related only to uncertain parameters affecting the geometry. Thus the significance of the accurate modeling of geometrical uncertainties for large deformation plasticity becomes undeniable.

Finally, we conclude that the application of advanced techniques like the SL-FEM, non-deterministic homogenization, the soft PBC and large strain plasticity increases the overall realism of simulations and allows to harvest important and non-trivial data for further constitutive modeling of heterogeneous materials.