1 Introduction

Rainfall is the most important climatic variable for establishing the availability of water resources, which, in turn, contributes to the long-term socioeconomic growth of a country (Bates et al. 2008). However, as a consequence of global climate change, rainfall is subject to variability, and is closely linked to instances of floods and droughts (Wu et al. 2013; Nicholson 2016; Wang et al. 2020). Studies conducted so far suggest that spatiotemporal inconsistencies characterize this change in rainfall patterns, particularly in southern Africa. For instance, despite the fact that the majority of studies generally indicate a drop in annual rainfall across this region, some areas, including the north and east, have experienced an increase during the past century (Shongwe et al. 2009; Jury 2013; Marumbwa et al. 2019). Regarding seasonal variations, records confirm that many areas of southern Africa, notably the western regions, had a general decline in austral summer (i.e., December-January–February) rainfall in the second half of the twentieth century (New et al. 2006). Nonetheless, increased December-January–February seasonal rainfall trends have also been observed in some sections of this region (Ngongondo et al. 2011; Daron 2014).

Owing to the profound consequences that rainfall discrepancies have on the living conditions of mankind, in recent years, climate change studies have been of great concern to the scientific community, policy makers, and the general public. In this context, accurate estimation of long-term trends offers important information for regional water resources planning and management, so as to minimize the ruinous effects of such disparities in rainfall amounts (Sun et al. 2018; Yang et al. 2019; Mallick et al. 2021; Wu et al. 2022). The commonly used trend analysis approaches for hydro-climatic time series are classified as either parametric or non-parametric (Huth and Pokorná 2004). Non-parametric tests are generally less effective than their parametric analogs, but considered more popular since they do not require data that conforms to stationarity and normal distribution. Additionally, the latter approaches are more tolerant to outliers, which are prevalent in hydro-climatological time series (Mirabbasi et al. 2020).

The Mann–Kendall (MK) and Spearman’s rho (SMR) tests are well-known non-parametric tests that have been utilized for trend detection in studies all around the world, including Yue et al. (2002a), Shadmani et al. (2012), Some'e et al. (2012), Duhan and Pandey (2013), Westra et al. (2013), Sayemuzzaman and Jha (2014), and Zuzani et al. (2019). In most studies, the SMR has frequently been used together with the MK test for comparative reasons, and their findings consistently demonstrate the same power in identifying trend (Shadmani et al. 2012; Ahmad et al. 2015). Although these classical methods are popular, the presence of serial correlation increases the probability of the tests to detect a significant trend in a time series when none actually exists (von Storch 1995). This is especially true for the MK test. Moreover, these techniques are purely statistical and do not provide the graphical exploratory aspects of the analysis, consequently leading to meaningless results in some cases (Kundzewicz and Robson 2000; Cohn and Lins 2005). In the same vein, Cengiz et al. (2020) showed that when visuals in the form of graphs are combined with statistical analysis techniques, a more thorough and comprehensive depiction of regional hydrological changes can be obtained. Thus, it becomes vital to grasp the hidden sub-trends in long-term series of hydro-climatic data, and this can only be done if the trends are visualized. Furthermore, the combined use of various methods for assessing hydro-climatologic trends provides reliable uncertainty estimations (Onyutha 2016c, 2021), hence eliminating the influence of choice of method used.

In pursuit of addressing the need for visual quantitative trend detection, two graphical methods such as the Onyutha trend (OT) test (Onyutha 2016a, 2021) and the innovative trend analyses (ITA) (Şen 2012) have been developed and used over the years (Onyutha 2016c; Gedefaw et al. 2018; Caloiero 2020; Cengiz et al. 2020; Wang et al. 2020). Of the two methods, the ITA has been applied the most on observed time series and this is well reported in hydro-climatological literature (Gedefaw et al. 2018; Wu et al. 2022). Developed much more recently, the OT test has also proven to be capable of providing more meaningful results than when the purely statistical methods are applied. In fact, when applied together or against the popular MK and SMR trend tests, the ITA and OT methods tend to yield comparable results, particularly if the data has no irregularities, e.g., ties or autocorrelation. According to the studies reported by Dabanlı et al. (2016) and Kisi (2015), employing the ITA to uncover hidden trends has certain advantages over just performing the MK or SMR tests. Cengiz et al. (2020) and Onyutha (2016a) demonstrated that not only are the results of the MK, ITA, and OT methods fairly comparable but also the graphical explorations by the ITA and OT disclose interesting results about the dataset and may be applied for further research. The ITA test, for instance, demonstrates the ability to detect trends in various types of precipitation, including low, medium, and high levels (Şen 2014), whereas the OT test not only detects trends but also recognizes climatic variability (Onyutha 2021).

The Shire River Basin (SRB) is one of the most important river basins in Malawi and southern Africa, accounting for 12% of Zambezi River flow (Hamududu and Killingtveit 2016). Accordingly, regional rainfall variability and human-induced activities have a great impact on the surface runoff (Adhikari and Nejadhashemi 2016; Zuzani et al. 2019) as well as the occurrence of droughts (Mtilatila et al. 2020) and floods (Coulibaly et al. 2015) in the area. Previous research on rainfall trends in the SRB has mainly examined general temporal variations (Mtilatila et al. 2020) and the frequency of extreme events (Zuzani et al. 2019), both of which have been conducted on an annual basis and using a single trend analysis technique. Yet, given the significance of the SRB to Malawi’s developmental sector, a more detailed study that integrates various trend analyses, both statistical and graphical, is encouraged for a better understanding and validation of the results. Therefore, in this study, four rank-based tests, namely the MK, SMR, OT, and ITA, are applied to historical rainfall time series (1976–2005) in order to determine seasonal and annual trend changes in the SRB, Malawi.

2 Study area and data used

2.1 Study area description

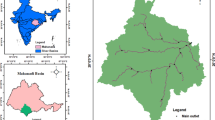
The Shire River is Malawi’s largest river and the sole outlet from Lake Malawi. Flowing over a distance of 700 km until its confluence with the Zambezi, the Shire River has a dense network of sub-catchments with surface area coverage of ~ 19,248 km2 (see Fig. 1). The SRB is thus a sub-basin of the Zambezi River Basin (ZRB), which, combined with other sub-basins, forms Africa’s fourth largest river basin and the largest in Southern Africa (Jury and Gwazantini 2002). The eastern portion of the basin is dominated by mountains, including the Mulanje Massif, while a low-lying flood plain known as the Lower Shire valley occupies the south of the region. Having a subtropical climate, the SRB has a distinct rainy season that is experienced between November and April and this is when roughly 80% of the rainfall occurs. Rainfall is season dependent and mostly influenced by the north–south migration of the intertropical convergence zone (ITCZ), which collaborates with the Congo air boundary. The proximity to the Lake Malawi and altitude are the major drivers of local rainfall patterns and variability (Kumbuyo et al. 2015).

Fig. 1
figure 1

Digital elevation model of the SRB along with the distribution of rivers and meteorological stations

Full size image

Based on the acquired time series, the mean annual rainfall recorded in the SRB between 1976 and 2005 ranged from 750 mm at N’gabu to 1618 mm at Mimosa, with an overall average of 1039 mm (Table 1). The standard deviation varied between 222.6 and 338.3 mm for Chileka and Mimosa, respectively. It is seen that the CV ranges from 0.21 to 0.30, indicating that the areas with usually heavy rainfall have the least variability as compared to areas that receive low rainfall. The measure of asymmetry in the frequency distribution as shown by skewness varied between − 0.82 and 0.74, exhibiting a predominant positive skewness with an average of 0.22. In other words, the annual rainfall during the period in question is asymmetric, falling to the right of the mean across most stations.

Table 1 Location and annual rainfall characteristics (Xmean, mean annual rainfall; SDev, standard deviation; CV, coefficient of variation; CSX, coefficient of skewness) for the twelve stations in the SRB
Full size table

2.2 Data set description

Daily rainfall data collected by the Department of Climate Change and Meteorological Services (MDCCMS) at 12 weather stations across the SRB from January 1976 to December 2005 were used for this study (Fig. 1 and Table 1). Meteorological data quality control is a fundamental step in weather and climate analyses; however, the data were already checked for errors and gaps by the department. Therefore, no gap filling method was necessary. Additionally, it is important to note that this study involved the use of non-parametric rank-based tests; thus, it was also deemed irrelevant to detect outliers, as these approaches are robust against such. The seasons used in this study are defined as follows: December-January–February (DJF), March–April-May (MAM), June-July–August (JJA), and September–October-November (SON).

To evaluate the homogeneity of the rainfall time series data at each station, the standard normal homogeneity test (SNHT) (Alexandersson 1986; Alexandersson and Moberg 1997) and Buishand’s range (BR) test (Buishand 1982) were applied at a 5% significance level. According to these authors, the time series is considered homogeneous if the SNHT statistic (To) is less than 9.17 while the BR statistics are less than 1.22 (\(Q\sqrt{n})\) and 1.55 (\(R\sqrt{n})\). The findings in Table 2 reveal that all the time series were homogeneous. Furthermore, all time series were checked for serial correlation using Lag-1 autocorrelation at 1%, 5%, and 10% to rule out its influence on some of the trend tests used in this study (Yue et al. 2002b). Since the time series were confirmed to be serially independent, all the trend tests were applied on original data.

Table 2 Homogeneity test results for annual rainfall time series at the twelve stations in the SRB
Full size table

3 Methodology

In this study, the non-parametric approach is chosen to detect trend in annual and seasonal rainfall for the SRB. This is accomplished in two steps. The first is to identify trend direction by using two purely statistical methods, namely the Mann–Kendall (MK) and Spearman’s rho (SMR) tests. The Thiel-Sen approach is also utilized in the first step to estimate the magnitude of the slope of the identified trends by the MK and SMR methods. However, since this study is also about the analyses of trends and sub-trends using statistical-graphical methods, Onyutha’s trend (OT) test and the innovative trend analysis (ITA) are employed in the second step.

3.1 Statistical tests

3.1.1 The Mann–Kendall (MK) test

Due to its prominence in the literature, the Mann–Kendall (Mann 1945; Kendall 1975) monotonic trend test is used to identify changes in rainfall data for this study. To execute this task, the test statistic S (as shown in Eq. 1) is calculated using the sign function \(sgn\) (\({x}_{j}-{x}_{i})=sgn (\theta )\), which is derived by comparing the provided time series data \(x({x}_{1},{x}_{2},\dots .{x}_{n})\) in turn.

$$S=\sum_{i=1}^{n-1}\sum_{j=i+1}^{n}sgn ({x}_{j}-{x}_{i})$$
(1)

where \({x}_{j}\) and \({x}_{i}\) are the sequential data values and if \(\theta\) is greater than, equal to, or less than zero, then \(sgn(\theta )\) is equivalent to 1, 0, and − 1, respectively. It is important to note that the variance of \(S\) is calculated as follows:

$$Var\left(S\right)=\left\{n\left(n-1\right)\left(2n+5\right)-\sum\nolimits_{i=1}^{m}{t}_{i}({t}_{i}-1)({2t}_{i}+5)\right\}/18$$
(2)

where \(m\) and \({t}_{i}\) are the number of tied groups (a tied group is a set of sample data having the same value) and the number of data points in the \({i}^{th}\) group, respectively. Ultimately, the standardized Mann–Kendall test statistic, denoted by \({Z}_{MK}\), is calculated as:

$${Z}_{MK}=\left\{\begin{array}{c}\frac{S-1}{\sqrt{Var }\left(S\right)}, if S>0\\ 0, if S=0 \\ \frac{S+1}{\sqrt{Var} \left(S\right)}, if S<0\end{array}\right.$$
(3)

Since the values of \({Z}_{MK}\) are considered approximately normally distributed, the null hypothesis \(({H}_{0})\) of no trend is accepted if the Z test statistic is not statistically significant, i.e., \({-Z}_{\alpha /2}<Z<{Z}_{\alpha /2}\), where \({Z}_{\alpha /2}\) is a standard normal deviate. In this equation, the positive and negative values of Z indicate an upward and downward trend, respectively.

3.1.2 The Spearman rho (SMR) test

Similar to the MK method, the Spearman rho (Lehmann 1975; Sneyers 1990) is another non-parametric test that is rank based and commonly used to analyze monotonic trends within a time series (Shadmani et al. 2012; Ahmad et al. 2015). Since this method relies on the existence of correlation between two classifications of the same set of observations; this approach is considered quick and simple. To apply this test for identifying the rainfall trend in this study, the SR correlation coefficient \((D)\) and its test statistic \(({Z}_{SMR})\) were determined as follows (Yue et al. 2002a):

$$D=1-\frac{6\sum_{i=1}^{n}{\left({R}_{i}-i\right)}^{2}}{n\left({n}^{2}-1\right)}$$
(4)
$${Z}_{SMR}=D\sqrt{\frac{n-2}{1-{D}^{2}}}$$
(5)

where \({R}_{i}\) is the rank of the \({i}^{th}\) observation \({X}_{i}\) in the time series, and \(n\) is the total length of the time series data. Positive and negative values of \({Z}_{SMR}\) indicate an increasing and decreasing trend across the time series, respectively. In instances when |\({Z}_{SR}\)|\({>t}_{(n-2, 1-\alpha /2)}\), the null hypothesis is rejected, meaning a significant trend in the time series exists. \({t}_{(n-2, 1-\alpha /2)}\) is defined as the critical value of t from the student’s t-distribution table, at a 5% significant level.

3.1.3 The Theil-Sen approach

The Theil-Sen approach (Theil 1950; Sen 1968) is used to estimate the magnitude of the trends identified by MK and SMR. Trend magnitude (also known as trend slope) is defined as the amount by which a variable is anticipated to change linearly over unit time of the observation. This linear change in slope (m) is computed using the following equation:

$$\begin{array}{ccc}m=Median\frac{X_j-X_i}{j-i}&\mathrm{for}\;\mathrm{all}&i<j\end{array}$$
(6)

where \({X}_{j}\) and \({X}_{i}\) are the sequential data values of the time series in the years \(j\) and \(i\), and \(m\) is the estimated magnitude of the trend slope in the data series.

3.2 Graphical-statistical test

3.2.1 Onyutha trend test

Trend analysis based on Onyutha’s method comprises both graphical diagnosis and statistical tests (Onyutha 2016b), hence the rationale for its use in this study. Moreover, as already stated in Sect. 1, previous studies indicate that its performance is quite comparable to both the ITA and the MK tests (Onyutha 2016a; Cengiz et al. 2020). Onyutha’s technique of change detection addresses the non-parametric rescaling of a given time series. To execute this method, the independent and dependent variables are denoted by \(X\) and \(Y\), respectively. Given that the sample size of \(X\) or \(Y\) is n, these two variables can possibly be rescaled into series \({d}_{x}\) and \({d}_{y}\), respectively, using the equation:

$$d_{y,i}={n-w}_{y,i}-{2t}_{y,i}\;\mathrm{and}\;d_{x,i}={n-w}_{x,i}-{2t}_{x,i}\mathrm{for}1\leq i\leq n$$
(7)

where \({t}_{y,i}\) and \({t}_{x,i}\) are the number of times the \({i}^{th}\) observation exceeds other data points in \(X\) and \(Y\), respectively. In a similar vein, \({w}_{x,i}\) and \({w}_{y,i}\) are the number of times the \({i}^{th}\) data point appears within \(X\) and \(Y\), respectively.

Series \({d}_{y}\) and \({d}_{x}\) can be normalized to obtain series \({e}_{y}\) and \({e}_{x,}\), respectively, using:

$$\begin{array}{c}{e}_{y,i}={d}_{y,i}\times \sqrt{\left(n-1\right)\times ({{c}_{y})}^{-1} } \mathrm{and}\\ {e}_{x,i}={d}_{x,i}\times \sqrt{\left(n-1\right)\times ({{c}_{x})}^{-1} }\mathrm{ for} 1\le i\le n\end{array}$$
(8)

where

$${c}_{y}={\sum }_{i=1}^{n}({{d}_{y,i})}^{2} and {c}_{x}={\sum }_{i=1}^{n}({{d}_{x,i})}^{2}$$
(9)

In a situation when the data points \(y\) or \(x\) are tied n times, each value of \({d}_{y}\) or \({d}_{x}\) will become zero.

The trend statistic \(T\) using Onyutha’s method can then be calculated as follows:

$$T={\sum }_{j=1}^{n}{\sum }_{i=1}^{j}{e}_{y,i}$$
(10)

When \(T\) > 0, the series displays a positive trend, while when \(T\) < 0, it exhibits a negative trend.

The mean of \(T\) is zero, and the distribution of \(T\) is approximately normal for large \(n\), with the variance of \(V(T)\) which is characterized by:

$$V(T)=\frac{n({n}^{2}-1)}{12}$$
(11)

The \(V(T)\) equation applies for independent data, but it is affected by the kind of persistence in the data for dependent data. In addition, data with persistence consists of long-term series. Sub-trends can also develop over long periods, such as more than 10 years. In such circumstances, \(V\left(T\right)\) can be further adjusted for autocorrelation influence using the approach in Onyutha (2016b).

Ultimately, the computation of the standardized test statistic \(Z\) is done using the following equation:

$$Z=\frac{T}{\sqrt{{V}^{F}(T)}}$$
(12)

where \({V}^{F}(T)\) is the version of \(V(T)\) adjusted for the influence of autocorrelation (refer to Onyutha 2016a, b, c, d for procedure). Suppose Zα/2 is the standard normal variate at a selected α, the null hypothesis H0 (no trend) at the significance level α% is rejected if |\(Z\)|> Zα/2 at α; alternatively, H0 is rejected.

For graphical diagnosis of sub-trends using the OT test, it is considered necessary to obtain \({a}_{j}\) and \({q}_{k}\) series (Onyutha 2021). Series \({a}_{j}\) is determined through the accumulation of \({e}_{y}\) sequentially as follows:

$${a}_{j}=\sum_{i=1}^{j}{e}_{y,i} \mathrm{ for} 1\le i\le n$$
(13)

The \({a}_{j}\) series generated above is used to indicate sub-periods across which the cumulative effect of temporal change in the time series is consistently positive or negative. Therefore, in order to detect sub-trends graphically, \({a}_{j}\) is plotted against the observation period j and this referred to as a sub-trend plot.

Series \({q}_{k}\) is used for additional graphical diagnostics, such as determining/confirming the significance of a trend. In order to generate \({q}_{k}\), a stepwise summation is applied to \({a}_{j}\). This can be done for the entire data period or for the identified sub-trends. Thus \({q}_{k}\) is plotted against the time of observations \(k\).

$${q}_{k}=\sum_{j=1}^{j}{a}_{j} \mathrm{ for} 1\le k\le n$$
(14)

Hence, the H0 (no sub-trend) is tested by adding 100 (1 α) % confidence interval limits (CILs) to the plot of \({q}_{k}\) versus \(k\) using:

$${CIL}_{s}=\pm \left|{z}_{\alpha /2}\right| \times \sqrt{{V}^{F}(T)}$$
(15)

If any scatter points exceed the 100–α %\({CIL}_{s}\), the H0 (no trend) is rejected; otherwise, the H0 is not rejected.

3.2.2 The innovative trend analysis (ITA)

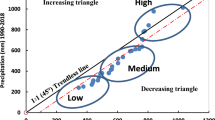
Sen’s innovative trend analysis (ITA) is also utilized in this article because of its capacity to find trend both visually and statistically (Şen 2012, 2017). This method for investigating changes in time series is based on the concept that if two time series are identical to each other, their plot against each other reveals a dispersion of points along a 1:1 (45°) line on the Cartesian coordinate system. The scatter points are generated by arranging the data in the first and second half of the time series in either descending or ascending order, and then plotting them on the X and Y axes, respectively. The 1:1 straight line forms two triangles at its top and bottom, and the scatter points above and below it reflect an increasing and decreasing monotonic trend respectively. When analyzing a non-monotonic trend in a time series, the trends in high (> 10th percentile), medium (10th–90th percentile), and low (< 10th percentile) values are examined independently (Brunetti et al. 2004).

For the statistical analysis portion of the ITA approach, the linear slope \((s)\) was calculated as follows (Şen 2017):

$$s=\frac{2({\overline{y} }_{2}-{\overline{y} }_{1})}{n}$$
(16)

where \({\overline{y} }_{1}\) and \({\overline{y} }_{2}\) are averages of two sub-series \({y}_{1}\) and \({y}_{2}\). To test the significance of the trend slope \(s\), the null hypothesis H0 (no trend) is accepted if the estimated slope value,\(s\), is less than a critical value, \({S}_{cri}\). Otherwise, the alternative hypothesis, Ha, is accepted when \(s\) is greater than the critical value, \({S}_{cri}\), indicating the sequence has a significant trend.

Since \({\overline{y} }_{1}\) and \({\overline{y} }_{2}\) are stochastic variables and of the same length, the expectations of these two sub-sequences are used to calculate the first-order matrix of slope \(s\) as follows:

$$E\left(s\right)=\frac{2}{n}[E({\overline{y} }_{2})-E\left({\overline{y} }_{1}\right]$$
(17)

In the absence of a trend, the centroid point lies on the 1:1 line, and \(E\left({\overline{y} }_{2}\right)=E({\overline{y} }_{1})\), resulting in \(E\left(s\right)=0\). Apart from that, the variation in the slope is given by the difference between the expectations of both sides:

$${\sigma }_{s}^{2}=E\left({s}^{2}\right)-E\left({s}^{2}\right)=\frac{4}{{n}^{2}}\left[E\left({\overline{y} }_{2}^{2}\right)-2E\left({\overline{y} }_{1}{\overline{y} }_{2}\right)+E\left({\overline{y} }_{1}^{2}\right)\right]$$
(18)

As \(E\left({\overline{y} }_{1}^{2}\right)=E\left({\overline{y} }_{2}^{2}\right)\), the equation above can be converted in the following way:

$${\sigma }_{s}^{2}=\frac{8}{{n}^{2}}\left[E\left({\overline{y} }_{2}^{2}\right)-E\left({\overline{y} }_{1}{\overline{y} }_{2}\right)\right]$$
(19)

The following equation is used to calculate the correlation coefficient between the two averages in the random process:

$${\rho }_{{\overline{y} }_{1}{\overline{y} }_{2}}=\frac{E\left({\overline{y} }_{1}{\overline{y} }_{2}\right)-E({\overline{y} }_{1})E({\overline{y} }_{2})}{{\sigma }_{{\overline{y} }_{1}}{\sigma }_{{\overline{y} }_{2}}}$$
(20)

As \({\sigma }_{{\overline{y} }_{2}}={\sigma }_{{\overline{y} }_{1}}=\sigma /\sqrt{n}\), substituting this equation and Eq. (20) into Eq. (21), the variance of the slope can be obtained as follows:

$${\sigma }_{s}^{2}= \frac{8}{{n}^{2}}\frac{{\sigma }^{2}}{n}\left(1-{\rho }_{{\overline{y} }_{1}{\overline{y} }_{2}}\right)$$
(21)

Ultimately, the confidence limit (CL) of the standard normal distribution probability density function (PDF) with a zero mean and standard deviation is \({S}_{cri}\); thus, the trend slope’s confidence limit (CL) at a \(\alpha\) significant level is as follows:

$${CL}_{(1-\alpha )}=0\pm {S}_{cri}\times {\sigma }_{s}$$
(22)

where \({\sigma }_{s}\) is the standard deviation of the slope and is given as:

$${\sigma }_{s}= \frac{2\sqrt{2}}{n\sqrt{n}}\sigma \sqrt{1-{\rho }_{{\overline{y} }_{1}{\overline{y} }_{2}}}$$
(23)

If the trend slope, s, of a time series falls outside the confidence limits, it is statistically significant. Since all of the slope variable’s odd-order moments are equal to zero, the slope PDF follows a Gaussian PDF with a zero mean and the standard deviation.

4 Results

4.1 Annual trends

The monotonic trend results of the statistical MK and SMR tests that were applied on annual rainfall time series (at a 1% and 5% significance level) between 1976 and 2005 at 12 stations in the SRB are summarized in Table 3. The associated trend magnitudes are displayed in Table 4. From the examined time series, it is noticeable that the results of both tests were comparable and that the statistics are dominated by negative trends (75%), most of which are insignificant. However, of the three stations that exhibited positive trends, only Makhanga station (with a trend magnitude of 8.09 mm/year) showed significance at the confidence level of 95%, and this applies to both tests.

Table 3 Statistical results of the MK and SMR tests for annual and seasonal rainfall time series at study stations
Full size table
Table 4 Magnitude (mm/year) of trends for annual and seasonal rainfall at the study stations
Full size table

The monotonic trend statistics for annual rainfall at the selected stations in the SRB using Onyutha’s trend technique are shown in Table 5. The findings from the analysis demonstrate that the OT statistic of annual rainfall is characterized by negative trends (9 of 12 stations) and are all insignificant at a 95% confidence level. Nonetheless, when the significance level for the remaining three stations identified as having positive trends was evaluated, only Makhanga demonstrated significance at the 95% confidence level. The trend results identified by this statistic, in terms of both trend direction and significance, are consistent with those detected by the MK and SMR tests. The decreasing trend of annual rainfall is also clearly seen in Fig. 2, which depicts the cumulative effect of temporal fluctuations in rainfall using sub-trend plots. From the plots, it is undeniably visible that annual rainfall at the Makhanga station trended upward, while the Mimosa and Neno stations definitely showed a downward trend. Similarly, it should be emphasized that the existence of both positive and negative sub-trends of varied lengths is apparent at the remaining stations. Even so, when the overall trend in a given series is considered, it is clear that some stations are dominated by either positive or negative trends. In addition, Chichiri and Chileka stations exhibited a distinct negative sub-trend that spanned the years 1976–1993. Figure 3 graphically shows the significance of trends in annual rainfall at the study stations. Annual rainfall trends (both positive and negative) and their significance can be depicted using this figure, where the H0 (no trend) was rejected in terms of rainfall only for Makhanga.

Table 5 Statistical results of the OT test for annual and seasonal rainfall time series at study stations
Full size table
Fig. 2
figure 2

Sub-trend plots for annual rainfall at the twelve stations selected across the SRB

Full size image
Fig. 3
figure 3

OT method graphical diagnoses of the trend significance for annual rainfall at twelves stations across the SRB

Full size image

The trends in annual rainfall detected by the ITA technique are summarized in Table 6. The slope (s) of annual rainfall is dominated by negative values (accounting for 83%), and there are 10 stations that exhibit a significant trend at 95% significance level. The associated graphical results showing the decline in annual rainfall can also clearly be seen in Fig. 4, where for most stations, the blue points fall below the 1:1 line, thus supporting the findings in Table 6. Furthermore, the red, yellow, and green dots, which denote the centroid points of the low, medium, and high rainfall clusters, showed that all stations except Makhanga and Neno had a decreasing tendency for low rainfall. For medium rainfall, all of the stations indicate a negative trend, except for Bvumbwe, Makhanga, Mangochi, and Thyolo stations. High rainfall at all stations also showed a downward trend with the exception of Bvumbwe, Chichiri, N’gabu and Thyolo stations. What cannot be overlooked is that the trend aspects of each station in the three rainfall categories appear to be relatively unique. For instance, low and medium rainfall at Mwanza station were < 5 mm/year, whereas high rainfall was > 12 mm/year. At Neno station, a strong increase was observed in the low category while medium and high rainfall had a relatively stronger decrease.

Table 6 Statistical results for the slope (s) of annual rainfall using the ITA approach
Full size table
Fig. 4
figure 4

Trend graphs for annual rainfall at twelve stations in the study area using the ITA approach (red, yellow, and green points illustrate mean centroid points of low, medium, and high rainfall, respectively)

Full size image

4.2 Seasonal trends

The rainfall trend statistics identified by the MK and SMR tests for the four seasons over the study period (1976–2005) are summarized in Table 3. Table 4 shows the accompanying trend magnitudes. Much like annual rainfall, results for both statistical tests were in agreement with one another. DJF seasonal rainfall is dominated by positive trends; however, all but the Makhanga station (with an associated magnitude of 6.05 mm/year) are insignificant. Rainfall in the MAM season at nearly all the stations showed a downward trend, but none of these trends is significant. The JJA season showed significant negative trends at the Chichiri and Mimosa stations but had a significant positive trend at the Thyolo station. In terms of the SON season, the findings showed that no significant trends were found at any station.

The rainfall trend statistics for the 4 seasons by the OT approach have also been provided in Table 5. Similar to annual rainfall, both positive and negative trends were detected. However, positive trends predominated throughout the DJF and SON seasons, with rises at 75% and 67% of the selected stations, respectively. Makhanga is the only station that achieved significant results. On the other hand, the MAM and JJA seasons were primarily characterized by a downward trend in rainfall, with declines occurring at 67% of the stations for the JJA season and across the entire study region for MAM. Nonetheless, significant trends were spotted at Chichiri and Thyolo for JJA. The results of further investigation into the DJF seasonal rainfall trends based on sub-trend plots are presented in Fig. 5. Due to limited space, CSD plots for the MAM, JJA, and SON season are not shown, but nevertheless, readers can refer to Table 5 for the overall station level trends. According to this figure, rainfall at the Makhanga station is primarily driven by a monotonic increase during the whole data period. The remaining stations exhibit sub-periods with both increasing and decreasing trends at various points throughout the data period. However, it is apparent that the majority of the sub-trends are positive at stations like Bvumbwe, Chichiri, Makoka, Mimosa, Mwanza, N’gabu, and Thyolo, while Chileka and Neno stations are dominated by negative sub-trends. On the other hand, it appears that the Mangochi and Nsanje stations have an overall trend that is graphically inconclusive. The visual diagnosis in Fig. 6 makes it evident that throughout DJF season, positive tendencies predominate, with Makhanga indicating significance.

Fig. 5
figure 5

Sub-trend plots for DJF seasonal rainfall at the twelve stations selected across the SRB

Full size image
Fig. 6
figure 6

OT method graphical diagnoses of the trend significance for DJF rainfall at twelves stations across the SRB

Full size image

The statistical findings of applying the ITA to detect seasonal rainfall changes are listed in Table 7. For 67% of the stations, the DJF season slope (s) is found to be positive, and there are eight stations that exhibited trends at 95% level of significance. The remaining three seasons are dominated by negative trends; the MAM season exhibited significant trends all across the basin at the 95% level, while the JJA and SON seasons recorded a 99% significance level of trend at nine stations, respectively. The visual-graphical results for the DJF season (Fig. 7) reveal a clear dominating increasing tendency for rainfall during this season, where the blue scatter points for majority of the stations fall above the 1:1 line of the Cartesian coordinate system. This figure also depicts the DJF season trend plots in respect to the three clusters; declining trends are observed for low rainfall at most stations, medium rainfall shows a modest increasing trend, and high rainfall detects a strong upward trend at most stations.

Table 7 Statistical results for the slope (s) of seasonal rainfall using the ITA approach
Full size table
Fig. 7
figure 7

Trend graphs for DJF seasonal rainfall at twelve stations in the study area using the ITA approach (red, yellow, and green points illustrate mean centroid points of low, medium, and high rainfall, respectively)

Full size image

5 Discussions

Rainfall in the SRB fluctuates considerably both seasonally and annually, and climate change is causing this variability to become increasingly irregular and uneven. The basin receives between 750 and 1618 mm of rain each year, with more than 60% of the rainfall concentrated in the DJF season. Hence, an in-depth understanding of both long-term trends as well as the hidden sub-trends within the overall rainfall changes across the SRB is essential for better management of water resources and the mitigation of natural hazards. However, previous studies on rainfall trends in the basin have mostly focused on total rainfall (Mtilatila et al. 2020) and the frequency of extreme rainfall events (Zuzani et al. 2019), neither of which indicate seasonal rainfall features. Aside from the use of purely statistical analysis to detect these variations in rainfall, no visual quantitative study that represents trends in sub-series has been conducted. In accordance to the observed knowledge gap, this study integrated statistical and graphical approaches to analyze overall trends and sub-trends of rainfall for the SRB at seasonal and annual timescales.

The results of this study revealed decreasing trends for annual rainfall over nearly the entire study area. Similar statistical findings are reported by Mtilatila et al. (2020) for the SRB. These results are also evidenced by Ngongondo et al. (2011), Ngongondo et al. (2015), and Tadeyo et al. (2020), wherein they observed a decline in annual rainfall for most parts of Malawi. Our research showed increasing DJF season trends, particularly for sites in the south of the basin. These results also support the findings by Ngongondo et al. (2011) for the whole Malawi. The frequent occurrence of tropical cyclones from the western Indian Ocean, which generally occur in December, January, or February, might be one of the explanations for the increase during DJF season. These cyclones are associated with wet spells, i.e., large amounts of rain in a short period of time (Otto et al. 2022); examples include cyclones Delfina and Ernest that occurred during the study period (Sithole and Murewi 2009). On the other hand, declining trends for the JJA and MAM seasonal rainfall were observed. As to what concerns the SON season, the trend results were rather inconclusive. These rainfall trends in Malawi and indeed southern Africa can be linked to the abnormal shifts of the sea surface temperature (SST) in the Indian Ocean and the El Niño (La Niña) phenomenon (Ratnam et al. 2014; Haghtalab et al. 2019).

To further validate the findings, the four statistical trend analysis techniques were compared, and the summaries of the annual and seasonal results are displayed in Fig. 8. It is evident that all approaches have demonstrated the presence of comparable trends over all time scales, with the exception of the SON season. However, for the 60 annual and seasonal time series studied, significant trends are detected in 5, 4, 4, and 52 time series by the MK, SMR, OT, and ITA tests, respectively. Moreover, the ITA approach detects all significant trends identified by the MK, SMR, and OT tests. These findings align with the results reported by Bouizrou et al. (2022), who evaluated the two traditional techniques along with the OT test and found that these methods exhibited similar power in detecting monotonic trends. This is a noteworthy observation as it suggests that the OT test can provide a certain level of accuracy in trend analysis. Indeed, as highlighted by Wang et al. (2020) and Alifujiang et al. (2020), the ITA approach has the advantage of uncovering more meaningful variation trends in rainfall series than the MK. Building upon this, our findings indicate that ITA may indeed have similar benefits over SMR and OT test. Furthermore, these statistical findings partially confirm the comparability of most non-parametric methods, particularly when the data set employed is free of irregularities such as ties and autocorrelation (Huth and Pokorná 2004). The variations in trend direction as well as the capacity for ITA to identify more significant trends than the other methods reveal the complexity of the trend phenomena. Besides, the disparities in the results from the various methods generally emphasize the potential uncertainty in the findings. Consequently, if such techniques are to be taken into account to assist in the development of watershed management strategies in the SRB and anywhere in the world, careful statistical inference is required.

Fig. 8
figure 8

Comparison of the results of the MK, SMR, OT, and ITA methods in the SRB; a–e, f–j, k–o, and p–t represent annual DJF, MAM, JJA, and SON rainfall trend results based on MK, SMR, CSD, and ITA, respectively

Full size image

The integrated use of statistical and graphical trend detection methods performed in this study was particularly crucial since, as Kundzewicz and Robson (2000) pointed out, relying solely on statistical approaches for trend analysis could produce results that are in some cases meaningless. Incorporating visual quantitative techniques of analyzing trend can reveal influential information, suggesting further research to enhance knowledge of the data (Onyutha 2016a; Caloiero 2020). It should be said that the sub-trend plots by OT method benefit for disclosing step jumps in the mean of the data at some stations in the SRB. As a result, while significant long-term trends were only detected in 4 time series, separate investigations on the sub-trends (Onyutha 2021) could reveal significant patterns necessary to consider for environmental management techniques. Additionally, other studies have used OT method further to assess significance of temporal variability based on sub-trends (Onyutha 2021; Bouizrou et al. 2022; Koycegiz and Buyukyildiz 2023; Mubialiwo et al. 2023), establishing its importance in environmental management. In contrast, the ITA technique graphically presents all data ranges on a Cartesian coordinate system, allowing for detailed information regarding trends in terms of evaluation of low, medium, and high rainfall clusters. This trend categorization feature illustrates the SRB’s propensity for droughts and floods in various sections of the study area, most notably the DJF season floods. A study by Zuzani et al. (2019) also suggested the potential worsening of droughts in the basin, but our work reveals additional insight into the frequency of floods because it was conducted at both annual and seasonal timeframes. In order to achieve an effective and ideal management of water resources, the completely different aspects offered by the visually oriented methods complement the purely monotonic trend detection methods.

6 Conclusion

In the present study, purely statistical approaches of MK and SMR were integrated with the statistical-graphical methods of OT and ITA to examine seasonal and annual rainfall variations across the SRB during 1976–2005. The main conclusions of this investigation are summarized as follows:

  1. 1)

    Declining annual rainfall trends were detected at most stations in the SRB, thus indicating that the study area is likely to become drier. On seasonal basis, increasing trends were observed for the DJF season, and these are concentrated in the lower parts of the basin. Rainfall in the MAM and JJA season exhibited decreasing trends, while for the SON season, the trends were rather unclear.

  2. 2)

    The statistical results for the four methods demonstrated partial conformity, particularly in terms of trend inclination. However, the ITA approach produced the maximum number of significant trends for both annual and seasonal rainfall series, followed by the MK, SMR, and OT tests, which gave the closest agreement of results in terms of both trend direction and significance. This suggests that the three methods are well aligned and that the ITA method exhibits a more defined significant pattern. These disparities in the results of the four statistical approaches in question highlight the complexities of applying various techniques independently for trend analysis. Hence, this necessitates a more cautious statistical inference if these methods are to be applied in water resources planning and management programs for the study area and beyond.

  3. 3)

    The statistical-graphical approaches offer several benefits over the traditional analysis techniques. These methods detect both monotonic and non-monotonic trends, revealing not only the general tendencies of rainfall as a variable, but also hidden sub-trends in the overall time series. With their visual-graphical properties, the OT and ITA tests can disclose additional information on rainfall variability including short-durational fluctuations in the series and an area’s sensitivity to severe occurrences. For instance, our analysis highlighted the SRB’s susceptibility to flooding, especially during the DJF season. Nevertheless, for a much thorough depiction of hydro-climatologic changes, the integrated use of graphical approaches to complement the purely arithmetic methods is encouraged.

Hence, it is hoped that this study could provide relevant information to help understand rainfall trends in the SRB. The findings are valuable to water resources managers involved in predicting and mitigating hazards associated with floods and droughts in the study area. Furthermore, this study also makes contribution to the graphical OT and ITA methods and this is by quantitatively evaluating trends in sub-series.