1 Introduction

There are two sets of characteristics that govern ocean variability and show global teleconnection patterns. One is the cycle periods (CP) or frequencies that describe variability for single ocean variability series (Saenko et al. 2004; Chen and Wallace 2016; Wills et al. 2018; Gong et al. 2020). The second characteristics is the changes in the lead-lag (LL) relations between paired ocean variabilities.

To identify lead-lag (LL) relations between pairs of five climate time series, we use a high-resolution LL (HRLL) method. Teleconnection patterns for the LL relations between paired ocean variabilities have been noticed in several studies (Wu et al. 2011a, b, Meehl et al. 2013, Chylek et al. 2014 a, Delworth et al. 2017, Seip and Gron 2019), but they have not been given a well-defined role in global warming. When LL relations are established, studies often compare variability in two ocean regions, like the North Atlantic Ocean and the Pacific Ocean, over multidecadal time spans (d’Orgeville and Peltier 2007; Zhang et al. 2011). Quantification of LL relations between cyclic climate variables has, with some exceptions, e.g., Kestin et al. (1998), been made for the whole length of the available series, often assuming that the series are semi-stationary.

The three most prominent ocean candidates for heat redistribution between upper and lower ocean layers are the Atlantic Ocean, the Pacific Ocean and the Southern Ocean (South of 35 oS) (Meehl et al. 2011; Cheng et al. 2017; Stolpe et al. 2017; von Kanel et al. 2017; Yao et al. 2017). Meehl et al. (2011, p. 361) show in a model study that the lower ocean layers that receive heat during the hiatus periods have an upper limit of about 300 to 700 m. The contributions from the Pacific decadal oscillation (PDO) and the Atlantic meridional overturning circulation (AMOC) to ocean heat uptake are discussed by, e.g., Chen and Tung (2018), Caesar et al. (2021) and Oldenburg et al. (2021). Furthermore, the atmosphere also transports heat and the partitioning of heat transport between the ocean and the atmosphere depends upon latitude. (Czaja and Marshall 2006).

Our hypothesis is that there are teleconnected and synchronized changes in LL relations between superimposed (stacked) ocean variabilities (∑LL) and that the synchronized changes and the change in global temperature anomaly (∆GTA) have a reciprocal impact on each other, ∑LL ↔ ∆GTA. (The ΣLL will be explained further in the method section). The hypothesis can be tested using the time series from about 1880 to present. The older part of the series may not be directly instrumentally observed but has been reconstructed by the observation of proxies or by modeling.

The rationale is that when ocean variabilities in a basin persistently drive synchronous, but delayed variabilities in another basin and this influence ceases and turns around, there are likely “bridges” between the oceans and between ocean layers during such periods (Newman et al. 2016). Changes in ocean variability generally affect the atmosphere and ocean heat distributions (Dai et al. 2015; Chen and Tung 2018; Gong et al. 2020; Liu et al. 2020) and thereby GTA (Wu et al. 2019). Strong movements of ocean waters may also affect carbon dioxide (CO2) sequestration (Guallart et al. 2015) and thereby indirectly GTA. Furthermore, since oceanic heat distribution has been shown to affect the climate over land (McCabe et al. 2004, Sutton and Hodson 2005, Chylek et al. 2014 a, Liu et al. 2020), the combined impact may strengthen the land component of GTA. We here focus on an analysis of the observational data and not upon physical mechanisms. The question of the influence of external forcing as a potential driver of coherent shifts is outside the scope of the present work, but we comment on some suggestions for possible mechanisms.

This paper is organized as follows. In Sect. 2, we give key characteristics of the climate data used in the study. In Sect. 3, we give an outline of the methods used, but with emphasis on the high-resolution LL (HRLL) method. In Sect. 4, we show the results for the three ocean time series, the ∆GTA, and the CO2, and the stacked LL relations for ten pairs of climate variables, ΣLL (10), that can be formed from the five series. We discuss the results in Sect. 5 with some emphasis on the empirical patterns we identify and some unresolved questions. In Sect. 6, we draw conclusions.

2 The data

We examine two variables that are closely related to climate variability in the Pacific Ocean and one variable that is related to the Atlantic Ocean. The first time series is the Southern Oscillation Index (SOI) from Ropelewski and Jones (1987), Allan et al. (1991), Konnen et al. (1998). The second is the Pacific decadal oscillation (PDO) from Mantua et al. (1997). The third is the Atlantic meridional overturning circulation (AMOC). The AMOC series is an extended series supplied by Caesar et al. (2021). The AMOC series is supported by proxy observations that are not expressed as temperatures. The instrumental AMOC series started in 2004. Characteristics for the series and their references are listed in Table 1.

Table 1 Data on climate variability series. AMOC is the Atlantic meridional overturning circulation, PDO is the Pacific decadal oscillation, and SOI is the Southern Oscillation Index. Detrending is either linear or made with a 2nd order polynomial function. “St.Dev. raw series” is the standard deviation of the numerical values for the raw series and “St.Dev. LOESS series” is the corresponding values for the LOESS (0.3) smoothed series. CO2 is additionally smoothed
Full size table

The AMOC measures volume transport (Sv) due to overturning between surface and deep-water currents in the Atlantic Ocean. From 2004 the AMOC is identified in two versions, as depth limited and as density limited. The PDO index is a standardized value of the leading principal component (PC) time series for the North Pacific SST mode (20O–70ON). The SOI measures sea level pressure differences between Tahiti and Darwin, Australia, as a proxy for tropical Pacific “ocean variability.” The AMOC and SOI were chosen, because both AMOC and SOI have been candidates for explaining changes in ocean heat transport (Jackson et al. 2015; Chen and Tung 2018).

Global-mean temperature anomaly, GTA

We use the global land–ocean temperature index from the National Aeronautics and Space Administration (NASA) Goddard Institute for Space Studies (GISS) for GTA. The data are updated every month and may change within their margin of error (Lenssen et al. (2019), Ruedy, NASA Goddard Space Flight Center, personal communication).

The hiatus periods

The global-mean temperature has showed a rising trend during the last centennial. However, since 1880s, there have been three slowdowns in global warming (hiatus periods) that have been associated with changes in ocean dynamics (Wu et al. 2019). A recent study shows that volcanic eruptions have been closely associated with cold periods on a multidecadal scale (Buntgen et al. 2020). We define the hiatus periods as the portions of the GTA time series where the slopes (∆GTA) during the hiatus periods are less than 1/20 of the range of the slopes. By examining the running average slope (n = 20) of a detrended GTA series, the hiatus periods are found to be from 1894 to 1912, from 1943 to 1975, and from 1998 to 2014. The hiatus periods last 16 to 32 years. For a comparison, slope values calculated by Yao et al. (2017) were in a range of zero to 0.014°C yr−1 for decadal time windows for the period 1900 to 2014. The GTA time series measure the surface temperatures, which can be a slowdown in the warming of the whole earth climate system because heat may be stored in deep ocean layers (Yan et al. 2016; Chen and Tung 2018).

Carbon dioxide CO2

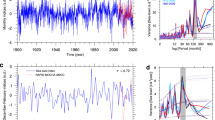
The data were downloaded from the NOAA web page, which also contains the references. The series were extended with recent CO2 data from Scripps Institute of Oceanography, which were averaged from monthly data (Table 1). All time series are normalized to unit standard deviation in Fig. 1a and detrended and LOESS (0.3) smoothed in Fig. 1b; see Methods for LOESS parameters. We will discuss the droplines in Fig. 1b in the discussion section.

Fig. 1
figure 1

Data series. a) Raw series normalized to unit standard deviation and shifted vertically for display purposes. b) Series detrended, centered, normalized to unit standard deviation and LOESS (0.3) smoothed. Blue droplines show dates for synchronized changes in lead-lag relations for ten pairs of climate variables. The dashed line shows an additional sign-change for PDO (Wills et al. 2018). Red horizontal lines denote hiatus periods. c) Power spectral analysis for the full raw time series of the AMOC, the SOI and the PDO and six partial series, from the beginning to 1950 and from 1951 to the end. Peaks above the 95% confidence limit are at 3–4 years, 12 years, 15 years, 21 years, 23–24 years, 29 years, and 36–37-38 years. See text for details. d) Power spectral analysis for the LOESS(0.3) smoothed time series in (b) with peaks above the 95% confidence limit at 3 years, 6 years, 21–23 years, and 28–29 years

Full size image

3 Methods

We first describe the detrending and smoothing of the data, thereafter the method for calculating high-resolution LL relations. All calculations were made either in Excel or with functions in the program package SigmaPlot©. All data, all calculations, and the numerical data supporting the figures are available from the authors.

3.1 Detrending and smoothing of raw data

For the GTA and the CO2 series, we used a second order polynomial function since the series show a progressively increasing trend. For CO2 we found that a 70-year long cycle dominates its variability. We therefore smoothed the polynomial series strongly using the LOESS local smoothing algorithm with parameters f = 0.8 and p = 2 and let the residual from the smoothed curve represent the multi-decadal CO2 variation. The parameter (f) determines the local domain as a fraction of the whole series, and the parameter (p) determines the degree for a polynomial fitting. We always use p = 2 in this study and therefore use the nomenclature LOESS (f) in the following. The three hiatus periods last several decades, as the positive (+ , warm, relative to the average) and negative (-, cold) phases do in ocean variability series. Therefore, we are interested in the mechanisms that act on multi-decadal time scales. We LOESS (0.3) smoothed the ocean variability series to separate decadal variability from multidecadal variability. We will discuss further the effects of detrending and smoothing in the discussion section.

Since the data are measured in different units and show different order of magnitudes, they can be normalized by dividing with unit standard deviation without loss of information. It is an added advantage that the measurement units have no influence on the calculations. To see how smoothing would emphasize long cycles in the PDO, the AMOC and the SOI, we applied power spectrum density (PSD) algorithm to the raw data and to the LOESS (0.3) smoothed data. The results show that, except for very short cycles (< ≈ 5 yrs.), only long cycles (> 20 yrs.) break the 95% confidence interval after smoothing, as shown in Fig. 1c and d.

3.2 The high-resolution LL method

The HRLL method is a technique for calculating running average LL relations. It is based on a dual representation of pairs of time series x(t) and y(t). Presentation of the method follows closely that of Seip and McNown (2007) and Seip et al. (2018), but recently Krüger (2021) has described a method related to wavelet analysis that is based on similar principles. Alternative group of methods are cross correlation methods and Power spectrum density (PSD) methods. PSD are discussed in (Kestin et al. 1998), but those methods as well as the cross correlation methods require long quasi stationary series, ≥ 30 years to give good results. Figure 2a shows both series plotted on the y-axis and with time as the x-axis. In Fig. 2b, the series are plotted in a phase space with x(t) on the x-axis and y(t) on the y-axis. Two perfect sine functions would show an ellipse with the major axis in the 1:1 or the 1: -1 direction. The two series in Fig. 2a shift in being leading and lagging and the direction of the rotation of the trajectories in Fig. 2b, clockwise or counterclockwise, determines which series is leading and which is lagging. We quantify the rotational patterns in the phase plot by the angle, θ,Footnote 1

$$\theta =sign\left(\overline{v }1\times \overline{{v }_{2}}\right)\bullet A \mathrm{cos}\left(\frac{\overline{{v }_{1}} \bullet \overline{{v }_{2}}}{\left|\overline{{v }_{1}}\right|\bullet \left|\overline{{v }_{2}}\right|}\right)$$
(1)

where \(\overline{{v }_{1}}\) and \(\overline{{v }_{2}}\) are two vectors formed by two sequential trajectories between three sequential points in the phase plot. The angles, θ, result in a time series for a set of paired cyclic series, N-2 time steps long.

Fig. 2
figure 2

Method example. Calculating lead-lag (LL) relations and LL – strength. a) Two sine functions: the smooth curve is a simple sine function, sin (0.5t), the dashed curve has the form: sin (0.5t + ϕ × RAND()) where ϕ =  + 0.785 for t = 1–10 and ϕ = -0.785 for t = 11–20. RAND() is the Excel random generator. Both x and y are centered and normalized to unit standard deviation, SD. Bold part of the simple sine function, xSD, shows that it leads ySD. b) In a phase plot with sin (0.5t) on the x- axis and the sin(0.5t + ϕ RAND()) on the y-axis, the time series rotates first clockwise (1 to 10, negative by definition) then counterclockwise 11 to 20; θ is the angle between two consecutive trajectories. The wedge suggests the angle between the origin and lines to observations 0 and 1. See text for details. c) Angles between successive trajectories (light gray bars) and LL—strength (black bars). Dashed lines suggest confidence limits for persistent rotation in the phase plot and persistent leading or lagging relations in the time series plot. Figure redrawn after Seip et al. (2018). d) The LL relation and the correlations between cyclic time series with common cycle period, λ, as a function of the phase shifts, ϕ, between the paired series

Full size image

LL- strength. From the angles, we define a lead-lag strength as:

$$\mathrm{LL}=\left({\mathrm{N}}_{\mathrm{pos}}-{\mathrm{N}}_{\mathrm{neg}}\right)/\left({\mathrm{N}}_{\mathrm{pos}}+{\mathrm{N}}_{\mathrm{neg}}\right)$$
(2)

where Npos and Nneg are the numbers of positive and negative rotations in a sample of N tot = Npos + Nneg rotations. The variable LL ranges between -1 (the y-variable leads the x -variable) and + 1 (the y-variable lags the x- variable). The LL values are depicted as the black bars in Fig. 2c. We calculate the 95% confidence interval (dashed lines in Fig. 2c and Fig. 3d) by calculating the persistence of rotational directions for two uniformly random series with length 9. The number nine is a tradeoff between using a short time window to identify changes in LL- strength and the ability to calculate confidence interval (CI). However, with smoothed series the probability to detect θ values that have the same sign increases. Thus, the CI does not strictly apply for smoothed series, and we use the term “pseudo significant” for CI lines as long as the LL values do not reach their maximum values of ± 1.0. (For short series, arcsine transformation does not well approximate a normal distribution.)

Fig. 3
figure 3

Statistics for climate variables. a) The absolute value of the stacked LL relations for the ten sets of paired climate variables, ΣLL (10), the stacked LL relations for the three paired ocean variables: ΣLL(3)O and the stacked series for three pairs of series where the ocean variables are paired to GTA. ΣLL(3)GTA. The six lowest values in the graph are at the years 1900, 1926, 1965, 1977 1997 and 2013. b) ∆GTAS and ∑LL(10); upper two series: ∑LL(10) and ∆GTAS. LOESS(0.4, Residuals) and LOESS(0.1) smoothed; regression:1880–1955: r = 0.35, p < 0.001. Lower two series: ΣLL(10) and ∆GTA. LOESS(0.4) smoothed, r =—0.39, p < 0.001. Red horizontal lines denote hiatus periods in (b). Open circles show date for the troughs in (a). c) LL relations between global temperature change ΔGTA and all ten pairs of interaction series ∑LL(10) Residual after detrending with LOESS (0.4). The five climate variables are AMOC, SOI, PDO, CO2, and GTA. Open circles show years when the bold curve crosses or touches the zero line. d) LL relations between global temperature change ΔGTA and all ten pairs of interaction series ∑LL(10), the LOESS(0.4) smoothed line. Red droplines delimit the period 1926 to 1946. e) Phase plot for the pair ΣLL(10) and ∆GTA LOESS(0.4) residuals and LOESS(0.1) smoothed during the period 1926–1946. f) Phase plot for the pair ΣLL(10) and ∆GTA, LOESS(0.4) residuals and LOESS(0.1) smoothed. Black dots correspond to transition points between positive and negative LL relations in Fig. 3d

Full size image

We apply this method to the detrended, smoothed, and normalized data in Fig. 1b. Thus, it is possible to identify the length of time windows where one series leads another, and when they shift in being leading or lagging. In addition to the LL relation between paired cyclic time series, we also calculate an ordinary linear regression (OLR) between the series. If the β—coefficient (the slope) are positive, the two series are said to be pro-cyclic. If the coefficient is negative, the two series are said to be countercyclic. Figure 2d shows how LL relations and the β -coefficient depend on the shift between the paired sine functions. If the shift, φ, between two series x(t- φ) and y(t) are less than ¼ of their common cycle period, series x(t) is leading series y(t) and the two series are pro-cyclic. However, most cyclic series do not satisfy the formal conditions for OLR (Pyper and Peterman 1998). Furthermore, if two paired series have causal relations to each other, the cause would be shifted backwards relative to the other but could still be closely similar to the first. We here do not shift the series relative to each other because the sign of the LL relations as well as its shift, φ, may change with time. The OLR test statistics therefore only suggest the strength of the association between the two time series.

3.3 Stacking LL relations

If there are teleconnections that govern the LL relations between global ocean variability series, then when the LL strength series LL(x,y) are stacked (superimposed) the periods with high strength should reinforce each other, and periods where the LL relations change should cancel each other. (When the LL relations change, their values will be close to zero because half of the angles, θ, in the expression for LL are positive and the other half is negative.) Therefore, if we see troughs in the stacked LL relations, they would distinguish a weakening of LL relations or global turning points for LL relations. The method we use is a version of the multiple window spectrum (MWS) method, (Johnson et al. 1996).

3.4 Stacking cycle periods

We identify cycle periods with three methods. First, we apply the PSD algorithm to the time series. The PSD produces a time series for the strength of the cycle periods in time series. As with the LL- series, we stack PSDs for several climate time series. The assumption is that cycle periods that are common for several series will reinforce each other, whereas other cycle periods will cancel each other. Second, we identify the series crossings with the zero line for the series that first have been detrended, centered and normalized to unit standard deviation. The third method depends on the dual presentation of cyclic series. A common cycle period for two series x (t) and y(t) will give a closed curve when the series are plotted on the x- and y- axes of a phase diagram for the two series. This last method is called the cumulative angle method.

4 Results

The time series of the five variables and the detrended and LOESS (0.3) smoothed time series are shown in Fig. 1a and b, respectively. In Fig. 1b, we also show the time series for ∆GTA. We first show the result of LOESS smoothing on the identification of cycle periods, then the LL relations and last, the relation between ∆GTA, CO2 and the stacked LL series.

4.1 Cycle periods

The PSD graph of the smoothed series can be compared to that of the raw series (Fig. 1c and d). By smoothing, the peaks that show decadal variations (12–15 years) become non-significant. The smoothed series are dominated by cycle periods 21–23 and 28–29 years long. However, the cycles identified in Fig. 1c are still present in Fig. 1d. The peaks at very short oscillations (< 5 years) are probably due to stochastic variations because two uniform stochastic distributions will show a high frequency of oscillations less than 5 years long (Seip et al. 2019a, b).

4.2 LL relations

The five variables, AMOC, SOI, PDO, GTA, and CO2, will give ten pairs of LL relations that vary with time in the period 1880 to 2017 (PDO from 1900). Figure 3a shows stacked series of the absolute value of the three pairs that can be formed from the three ocean variables, ΣLL (3)O, the three series where the ocean variables are paired with GTA, ΣLL(3)GTA; and the 10 LL- pairs that can be formed from all five variables, ΣLL (10). During periods with peaks in the series, there are persistent LL relations. During the shorter periods with troughs, several series change the direction of LL relations simultaneously or the LL relations become weak (close to zero). It is seen that peaks and troughs occur at about the same time in the 10- and the 3- series. The climate indices changed direction synchronously in 1900, 1926, 1965, 1977, 1997, and 2013, with the change in 1997 as a strong event. The years for synchronous changes correspond with the beginning and end of the 1943–1975 and the 1997/8—2013 hiatus periods. We examined closely the LL directions between the five variables 5 years before and after the 1997 hiatus period. In the sequences below, the arrows point from the leading series to the target series. The most pronounced changes were that we had the LL relations: GTA → AMOC → PDO five-years before 1997, but PDO → AMOC → GTA five years later, in 2003. We found the AMOC → PDO before and the PDO → AMOC after also the 1943–1975 hiatus, but the 1894–1912 hiatus shoved only weak and non-significant LL relations.

4.3 The ∆GTA, atmospheric CO 2, ocean interactions, ΣLL (10)

To compare ∆GTA with the resulting LL relations, ΣLL (10) on a bi-decadal scale, we disentangle bi-decadal variation from variations with longer periods. We did this by LOESS (0.4) smoothing the series strongly and calculating the residuals as an expression for bi-decadal cycles. The results are shown in Fig. 3b. The open circles designate the years with troughs in the ΣLL(10). Figure 3c shows that oceanic and atmospheric interactions, ∑LL (10), both lead and lag ΔGTA on a decadal scale. The open circles suggest shifts in LL relations. Periods with persistent LL relations are about ten years. The LL relations for the strongly smoothed time series in Fig. 3b (lower two series) are shown in Fig. 3d.

In Fig. 3e, we show a phase plot of the bi-decadal series from 1926 to 1946. A phase plot for cyclic series allows us to make two interpretations. i) We will see if there is positive or negative association between the two series, and ii) the rotational direction of trajectories in the plot allows us to see which of the series is leading the other. From 1926 to 1940, the rotation is clockwise and ∆GTA relatively persistently leads ΣLL(10). From 1940 to 1946 rotations are counterclockwise and ΣLL(10) leads ∆GTA. It requires 17 years to close a curve in the phase plot. This shows that there is a common cycle period of 17 years for the two series ΣLL(10) and ∆GTA. Figure 3f shows a phase plot for the low frequency component of ∆GTA and ΣLL(10). Years are shown in the figure when the rotational direction changes. The years correspond to changes in LL relations in Fig. 3d.

4.4 Structural break in 1960

The residual series (upper two series) are pro cyclic until 1960 (r = 0.25, p < 0.05, n = 72) and the common cycle period is 21.1 ± 1.8 yrs. (Cumulative angle method). The strongly smoothed series are counter cyclic (r =—0.51, p < 0.001, n = 119) and show common cycle periods of 65.3 ± 10.9 yrs. (Zero-crossings method).

5 Discussion

We find distinct timing of persistent LL relation between 10 pairs that can be constructed from five variable: three ocean variables, the rate of change of GTA, ∆GTA, and atmospheric CO2. The changes in ΣLL(10) coincide with major phase shifts in PDO (shifts between warm and cold periods), and both starts and ends of the changes correspond well with the beginning and ending of the last two hiatus periods in global warming, Fig. 1b.

5.1 Cycle periods

An analysis of oscillations in the AMOC, the SOI and the PDO with the PSD method suggests that the series are superpositions of distinct components of ocean oscillations with specific cycle periods. For PDO (or Pacific decadal variability, PDV), Newman et al. (2016, p. 4402) show that the series describe several distinct mechanisms and time scales.

Detrending and smoothing

To disentangle component time series in the observed variability series, time series are often detrended, smoothed and normalized in some way. We smoothed the raw time series to more closely describe multidecadal variations. Oscillations of 21–23 years and 28–29 years dominate the smoothed time series in the PSD graphs, and bi-decadal cycles are identified as common cycle periods for ∆GTA and ΣLL (10) for the residual series in Fig. 3b, upper two series. The oscillations of 21–23 years correspond to the interdecadal variations of 21.39 ± 1.34 years identified by Wei et al. (2019), and were proposed by the authors to partially cause the last hiatus period 1998- 2013. Wills et al. (2018, p.2491–2) found variabilities on the 10–20-year time scales that contribute to the variability of their PDO series. However, Meehl et al. (2021, p. 41) suggest that the AMO and PDO series are not cyclic and that the variability varies between about 10 and 30 years. We found with the cumulative angle method the average cycle periods to be 21 years and with a standard deviation of 9%. We use the term cycle—series, but do not require that the cycles are stationary.

5.2 LL relations between ∆GTA, atmospheric CO 2 , and ocean variables

We first show our major results, then we list findings that may contribute to an explanation of the results. Third, we compare our results to observations reported in the literature.

We found that there is a concerted global change in the LL relations between pairs of five climate variables, ΣLL(10). The timing of the changes was identified by troughs in the time series for ΣLL(10). In Fig. 3a, we added droplines that correspond to the troughs. Four of the dates for pronounced changes in the ΣLL(10) relations were also found as major phase shifts for a PDO—like mode by Newman et al. (2016, Fig. 6) and by Wills et al. (2018 p. 2491), i.e., in 1925–26; 1977, 1997–1998, and 2013–2014. There is one exception, the years 1946–1947 showed a shift in PDO, but no distinct trough in the ΣLL(10) series.

The patterns in Fig. 3a suggest that the LL relations between the ocean variables, ΣLL(3)O compare well with the patterns between all LL relations for all five variables:

$$\sum L\mathrm{L}\left(10\right)=2.17\times \sum \mathrm{LL}\left(3\right)+2.15, {\mathrm{R}}^{2}=0.59,\mathrm{ p}<0.001,\mathrm{ n}=130$$
(3)

The 1997–98 change was most pronounced. Five years before, the year 1992, was a year when PDO had a positive, warm phase and AMOC (unit Sv) a high value in its cyclic component. In 1992, we obtained the LL relation GTA → AMOC → PDO. In the year 2003, 5 years after 1997, PDO had a cold phase and the LL relation had switched to PDO → AMOC → GTA. In addition, the LL relation AMOC → CO2 changed sign around 1997 to CO2 → AMOC. There are also direct LL relations between PDO and GTA, but they were not so well synchronized with the LL- changes in 1997. Other studies also examine LL relations between the AMOC, the AMO, the North Atlantic Oscillation (NAO) and PDO. However, most studies use autocorrelation techniques that apply to the full time series, e.g., Sun et al. (2021, AMOC time series 1871–2018) and Nigam et al. (2020, time series 1900–2018). Thus, their LL relations will probably be an average relative to ours.

In the literature, several other events around 1997 were reported. In 1997, the last hiatus phase was initiated. In 1998 El Niño was in a warm phase, the Pacific cross equatorial wind index (m s−1) was low, and Pacific precipitation anomalies were high, Hu et al. (2014, Figs. 1 and 2). Concurrent with changes in the AMOC around 1997, the Atlantic multidecadal oscillation (AMO) changed from a negative, cold phase, to a warm phase and this change was accompanied with a change in the zonal mean meridional stream function across equator in the Pacific (5oS, 5° N), Gong et al. (2020, Fig. 9). However, the physical processes connecting LL relations and variabilities in PDO, the AMOC (units Sv) and the AMO (units oC for sea surface temperature) need to be analyzed further, (Yuhan Gong, School of Atmospheric Science, Nanjing University of Information Science & Technology, Nanjing 210044, China, personal communication.)

5.3 Cycle periods, LL- periods, and a structural break around 1960

Several studies refer to internal ocean mechanisms for ocean variabilities and some studies directly or implicitly assume that there are changing LL relations between ocean basins. An overview of research that examines how different physical processes contribute to PDO variability is given in Newman et al. (2016).

5.3.1 The short, ≈ 20 years cycles

Internal ocean mechanisms

Recently, Arzel et al. (2018, p. 6418) show that inter-decadal oscillations (≈ 20 years) are driven by a hydrodynamic (baroclinic) instability of the North Atlantic Current and no changes in the surface forcing (wind or heat flux) are needed. The energy source for the variability originates from the baroclinic instability. With increasing eddy diffusivity, K, the cycle period moves into the multidecadal scale and increases up to about 50 years. Seip and Grøn (2019) found that when two oscillating time series interact, they will result in distinct cycle periods. Both studies may point to properties of stochastic series that interact, and the finding that shuffling a card deck seven times gives a random distribution (Bayer and Diaconis 1992) may serve as a metaphor for the existence of distinct cycles resulting from interactions between stochastic series.

Heat exchange mechanisms

A second group of explanations refer to heat exchange mechanisms between ocean basins that require time to take place. The causes for the variabilities may be related to sequential interactivity between the Pacific and the Atlantic through the atmospheric Walker circulation and teleconnections (Meehl et al. (2021, p. 41), or sea surface temperature warming by long range radiation caused by warmer water and higher concentration of water vapor in the troposphere (Yao et al. 2022).

External mechanisms

Volcanism has been suggested as a source for climate variability (Huybers and Langmuir 2009, 2017; Birkel et al. 2018; Buntgen et al. 2020). In particular, the little ice ages during the last 2000 years have been associated with volcanism, but association with hiatus periods is, to our knowledge, absent.

Pro and counter cyclisity

The interaction between the Pacific and the Atlantic takes time causing the temperature variabilities to be shifted relative to each other, (but less than ½ variability length ≈ cycle period) and thus give the signature of pro-cyclicity. The time argument apply also if it is the Arzel et al. (2018) or the Seip and Grøn (2019) mechanisms that govern the cyclic behavior.

To our knowledge, no studies associate weak LL relations with hiatus periods. If the hiatus period is (partially) caused by the upper ocean layers being colder (or heat being transported to deep ocean layers < 300 m), then both the Atlantic and the Pacific Ocean’s surface waters should cease to warm, or become colder (von Kanel et al. 2017; Yao et al. 2017; Wu et al. 2019). Our results also suggests that there are persistent cycles within a narrow range of cycle period durations. Thus, based on the cold ocean temperatures in both the Atlantic and the Pacific oceans required by the hiatus theory (Wu et al. 2019) and on the regular periodicity of the ocean series we suggest that internal ocean mechanisms are the most likely explanation for the PDO’s and AMO’s oscillating behavior.

5.3.2 The long ≈ 60 years cycles

There is a superimposed longer temperature variation in ∆GTA which lasts for about 65 years, and which is counter cyclic to ΣLL (10), R =—0.50, p < 0.001, Fig. 3b. The amplitude of the long temperature variation, A, is about twice the amplitude of the short variations, a, with a/A = 0.48. We do not know the origin of the 65 years cycle and multidecadal long-term cycles are also difficult to identify because long-term climate time series are based on proxy data and therefore uncertain. However, there is strong evidence that long-term multidecadal to centennial variabilities occur, although it is uncertain if they belong to a series with pseudo-cyclic characteristics. For example, long-term climate variability of 40 years was reported for AMOC (Latif et al. 2022) and 50–70 years climate oscillations were reported over the North Pacific and North America (Minobe 1997).

Internal ocean mechanisms

Also, the long cycle periods, ≈ 40–70 years., may be generated by the mechanisms suggested by Arzel et al. (2018) or Seip and Grøn (2019).

Heat exchange mechanisms

Cheng et al. (2015) suggest that there are global water column depths that change in being cool and warm and that may have impacted the recent surface warming slowdown, but also contributed to a 60-year cycle period. The AMOC is suggested to deliver heat to the deep Atlantic Ocean (Chen and Tung 2018; Wei et al. 2019) and if the heat transport changes direction, cycle-like variabilities may occur. A survey of possible “bridges” between oceans and the atmosphere and between ocean basins is given in Wei et al. (2019). D’Asaro et al. (2011) link ocean-fronts to downward propagating internal waves, again being a possible cause for cycle variability on short and long timescales.

External mechanisms

Volcanic eruptions may lead to multidecadal to centennial cold periods, by first instigating cold spells lasting for 2–4 years that then are followed by cascades of mechanisms that lengthen the cold period (Marshall et al. 2022). However, the impact of volcanism is studied over long time spans, say during the last 2000 years (Buntgen et al. 2020, the Common Era), whereas hiatus periods are only identified in temperature series from about 1880. So applying volcanism arguments to the recent industrial era are uncertain. The counter cyclic nature of the long cycles would indicate that the mechanisms that cause temperature variabilities use longer than ½ cycle common period to generate the temperature variability.

5.3.3 LL- periods and PDO

Most studies on the LL relations use cross-correlation techniques where the skill of the LL characteristics improves for long stationary series. Thus, the studies only identify lead or lag relations that apply to the full series. In a study that compared modeling results (HadGEM2-ES), Seip and Wang (2018, Fig. 3) found similarities between LL relations for El Niño and PDO that would indicate that the model contains constructs that would be sufficient to identify causes for cycles in LL relations. However, they did not make further analyses.

Here, we found an almost perfect connection between the dates for weakening of the LL relations, ΣLL(10), and the dates when PDO shift between negative (-) and positive ( +) phases (There is one exception). One event could cause the other event, but the metaphor for what comes first, the “hen” or the “egg” may so far apply. We do not know if temperature changes in PDO drives LL changes in the oceans, or if it is the events with weakening of the ocean oscillations that changes temperatures in the PDO.

5.3.4 The hiatus periods

To our knowledge, there is no consensus on the ultimate cause of the hiatus periods in global warming. A train of causes and effects may be as follows. Starting from the observations of the hiatus periods, they seem to be linked to cold-water phases in ocean variabilities, e.g., Dai et al. (2015), Yao et al. (2017) and Wu et al. (2019). The cold-water phases are linked to warm and cold phases at deep waters (Cheng et al. 2015) caused by transport of heat to large depths (Wu et al. 2019). If the pronounced troughs in ΣLL(10) can be associated with water movements and heat transport, then changing LL relations may contribute to the hiatus periods, Fig. 1b. However, several smaller changes in ΣLL (10) do not appear to be related to the hiatus periods. Thus, our hypothesis that the teleconnected changes in LL relations and ∆GTA have reciprocal impact on each other, ΣLL ↔ ∆GTA are supported, but we do not know the importance of the reciprocal impact for the creation of hiatus periods. One hypothesis based on the LL relations found before and after the 1943 and the 1997/8 hiatus periods may be that changes in AMOC instigate a hiatus period whereas changes in PDO terminate it.

5.3.5 Structural break round 1960

The structural break in 1960 may be associated with a response to increasing atmospheric CO2 and a weakening of the AMOC (Thornalley et al. 2018). There is also an increasing trend in the CO2 flux from the atmosphere to the oceans around 1960 (Le Quere 2016their Fig. 4d).

5.4 Robustness

The very good correspondence between ΣLL(10) and the major phase shifts in PDO strengthens the finding that there are both concerted changes in LL relations across the globe and the correctness and relevance of the PDO.

The PDO is assumed to be a superposition of several series that are generated by different mechanisms (Newman et al. 2016). Therefore, to make interferences about causal effects the series must be disentangles. There is no canonical way to choose the LOESS smoothing parameters since the chance is always that there are peaks caused by dynamic chaos (Sugihara and May 1990; Tømte et al. 1998) or by interactions between the embedded series (Seip and Pleym 2000). However, several methods are employed to disentangle component series. Moving average n-year periods is used by several authors, Chylek et al. (2014 a n = 5), Wu et al. (2019, n = 9 and 21). Wu et al. (2011a, b) used the so-called ensemble empirical mode decomposition to identify the multidecadal variability.

5.4.1 Empirical results for the LL- method

In Fig. 3e, we plotted the time series for ΣLL(10) and ∆GTA from the years 1926 to 1946 in a phase plot. The trajectories correspond well to the time series pattern seen in Fig. 3b. In Fig. 3f, we see that the leading and lagging relations in Fig. 3d show up as counter- clockwise and clockwise rotations in the phase plot.

To further examine the robustness of the LL relation, we applied the LL-method to the ∆GTA LOESS(0.3) smoothed series and examined the LL relation between this series and the same series shifted five years forward. The result showed that the series not shifted forward was leading the forward shifted series 100% of the time. Another empirical example, from economics, showed that a predictive sentiment index that per definition should be a leading index to industrial production (IP) was leading IP 78% of the time. When it was not leading, the economy was abnormal (Seip et al. 2019a, b).

Although we focus on the relations between the AMOC and the PDO, our study extends the relation between PDO and LL relations to the variables CO2, GTA and SOI. The results for the latter variables were less strong than for the AMOC/ PDO pair and would need extended background theories for reasonable interpretations.

5.5 Future work

Our empirical study leaves several open questions. We do not know which of the suggested mechanisms that cause regular bi-decal cycles during the studied period. We do not know why the bi-decal cycles show pro cyclisity for ∆GTA and ∆LL (10) or why the multidecadal series tend to show counter cyclicity. The results are empirical, and we suggest that further explanations than we can give here need to be explored in modeling studies. One could corroborate the modelling results by applying the HRLL method to the series generated by the model.

6 Conclusion

A relatively novel technique allows us to identify lead-lag (LL) relations over short periods. By applying this technique to ten pairs that can be formed from the five variables: AMOC, SOI, PDO, CO2 and GTA, we identify synchronous timing of changes in LL relations during the years 1900, 1926, 1965, 1977, 1997, and 2013. The years correspond almost exactly two years when PDO changes between warm and cold phases. The stacked LL relations, ΣLL(10), and the rate of change in GTA, ∆GTA, showed pro-cyclic, bi-decadal (≈ 20 years) variability until about 1960. From 1960 to 2015, both series still showed bi-decadal variability, but not with synchronous movements. The pronounced 1997 change in global LL relations coincided with a change from GTA → AMOC → PDO to the opposite LL relation PDO → AMOC → GTA, and the PDO changed from a warm to a cold phase and GTA showed a hiatus period.