1 Introduction

The disparity, D, proposed by Martín-Vide (1986, 1987), is a well-defined concept and a good mathematical application to quantify the rainfall irregularity at monthly and annual scales, being an alternative or a complement, to other indices involving quotients or differences between consecutive monthly or annual rainfall amounts (García-Barrón et al. 2011) and other simpler, as for instance, the well-known coefficient of variation CV. This coefficient CV is commonly used for this quantification, despite its known weaknesses such as its dependence on the mean and the series length, as well as its inability for assessing any temporal structure of the time series since the chronological order of the values is not considered in its calculation. Instead, D uses the average of the logarithmic ratios obtained for each pair of consecutive quantities, taking into account temporal or chronological variations. Also, it can be deduced from the formulation of D that the disparity values will be independent of the mean of the time series, being its robustness in relation to series length is also expected, so it certainly offers a better quantification of rainfall irregularity. Lana and Burgueño (2000) and Martín-Vide et al. (2022) are two examples of previous studies performed along a section of the Mediterranean coast and the Iberian Peninsula respectively, analysing the rainfall disparity. Also, López-Bustins and Lemus-Cánovas (2020) studied the statistical relationship between the Western Mediterranean Oscillation index (WeMOi) and rainfall disparity indices at the seasonal and annual timescales. Fernández-Martínez et al. (2018) analysed the disparity in ecological processes as fruit production for several trees, birds population and rodent captures and simulated a thousand-time series for different statistical distributions and temporal autocorrelations to compare different irregularity indices, the disparity between them. García-Barrón et al. (2015, 2018) used the disparity index to evaluate a new environmental indicator in the Iberian Peninsula directly related to the physical effects of rainfall on erosion soil, associated with the incidence of torrents, floods and landslides. Wasee et al. (2020) also considered the consecutive disparity in their investigation of spatio-temporal precipitation trends from a climate change perspective in the southwest arid region of Pakistan. The disparity index was also used for trend analysis in India by Saini et al. (2020). Siqueira and Nery (2021) analysed the spatial and temporal variability of the precipitation concentration in north-eastern Brazil and associated the observed rainfall irregularity with the occurrence of El Niño and La Niña and Tropical Atlantic Oscillation patterns. Xie et al. (2023) also used the concept of the consecutive disparity in their investigation of the generalizable patterns of how intra-annual precipitation patterns affect the productivity and community structures of ecosystems. Other methods to quantify rainfall irregularity are those based on fractal structures at different scales. In the monofractal approach (Menabde et al. 1999; Yu et al. 2004; Bara et al. 2010; Casas-Castillo et al. 2018b), the scaling fractal parameter β that appears in scaling relationships between distributions of rainfall intensity at different time scales has been proven to be related to the characteristics of the rainfall pattern over the studied area as a good indicator of rainfall irregularity (Innocenti et al. 2017; Rodríguez-Solà et al. 2017; Casas-Castillo et al. 2018a, 2022).

In line with other previous works, the motivation of the present study is to continue deepening the analysis of rainfall in Catalonia in search of a more detailed knowledge of its complex characteristics. In particular, the objective of this study is to obtain a detailed information of the time and spatial monthly rainfall irregularity in Catalonia with the aim of future improvement of rainfall forecasting. To this end, the concept of disparity proposed by MartÍn-Vide (1986) has been considered at the present analysis as an irregularity indicator calculated to every one of the twelve monthly calendar amounts series and to the whole series of consecutive monthly data. The spatial and temporal evolution of the different rainfall irregularity levels in Catalonia (NE Spain) is notably affected by the complex topography, presented in Section 2.

The second section (Section 2) details the main characteristics of the pluviometric network of 97 rain gauges, including data quality and the algorithms used to substitute a few missing data. The concept of disparity is developed in the third section, including the possible computational alternatives when a monthly data cannot be recovered or its guarantee is doubtful. The fourth section shows the obtained irregularity at a monthly scale and extreme irregularity maps, as well as the results concerning the influence of the vicinity to the Mediterranean littoral and the altitude above sea level of every rain gauge. The fifth section (Section 5) details the most relevant results on the NE Spain and the advantages of bearing in mind the monthly calendar disparities, causing monthly rainfall irregularity and, at the same time, probably affecting the forecasting of forthcoming monthly amounts, which would eventually finish long drought episodes. Some characteristics of this research are also compared with the rainfall disparities for all peninsular Spain, obtained by Martín-Vide et al. (2022). Finally, Section 6 summarises the most relevant results of the disparity in the NE Spain and suggests some possible improvements on the results concerning forthcoming monthly rainfall amounts related to drought episodes, which use to be quite common in the Mediterranean domain.

2 Area of study and database

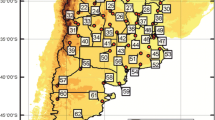
The orography of Catalonia is quite complex (Fig. 1a), with altitudes varying from close to 3000 m in some areas of the Pyrenees to 2000 m in the Pre-Pyrenees, between 900 and 1500 m in the Pre-Littoral chain, close to 500–600 m in the Central Basin and only a few hundred metres along the Littoral chain. A climatic diversity is consequently generated, which is manifested from the point of view of rainfall patterns by notable spatial changes on monthly and annual amounts, and remarkable irregularities at annual and monthly scales, being then necessary for a dense pluviometric network. A set of 97 monthly rainfall series were obtained from Servei Meteorològic de Catalunya (SMC, www.meteo.cat), the meteorological agency of Catalonia, complemented with records from two other scientific organisations: Fabra Observatory (Reial Acadèmia de Ciències i Arts, RACA, Barcelona) and Ebre Observatory (Ramon Llull University, URL, and Consejo Superior de Investigaciones Científicas, CSIC, Spanish Government). The same dataset has been used (Lana et al. 2020, 2021a, 2021b) to study several questions concerning rain amounts multifractal complexity and forecasting at a monthly scale, with the aim of preventing droughts episodes.

Fig. 1
figure 1

Schematic geographic description of a Catalonia (NE Spain) and b rain gauge network

Full size image

The 97 selected series were chosen according to their performance in the quality control and homogeneity checks. The quality control of this dataset was performed following the quality control procedure developed by Llabrés-Brustenga et al. (2019); series have at least 40 years of monthly rainfall data in the period 1950–2016, each year scoring a minimum value of 80 in a global Quality Index (Llabrés-Brustenga et al. 2019) with a maximum of 1% of days with missing data or marked as not valid data in the automatic quality control. The ACMANT3 procedure was applied to detect homogeneity breaks in monthly precipitation series. As explained by Domonkos and Coll (2016), ACMANT3 is a software package composed by six programs that incorporate 174 sub-routines in total. In particular, the executable used in the present work is ACMANP3month, which allows an automatic detection and correction at monthly resolution of precipitation data. The choice of the homogenisation procedure has been made because of the reported good performance of ACMANT, valuing also its complete automation and specific design for precipitation. Additionally, the Mann-Kendall rank test applied to the dataset confirmed that significant time trends were not detected. Figure 1b details the spatial distribution of the 97 rain gauges. Very short data lags of a few days were substituted by those generated by a kriging interpolation process (Stein 1999; Press et al. 2007; Llabrés-Brustenga et al. 2019) based on available daily records close to a gauge with a few lost data, as well as on the topography of the area around this place. In this way, good quality data of at least 40 years in length are obtained, corresponding to the period 1950–2016, thus assuring low uncertainty on the corresponding disparity coefficients.

3 Methodology

The degree of disparity, D, for positive time series {xi(t), i=1, 2, …, N} could be easily quantified by Eq. (1):

$$D=\frac1{N-1}\sum\nolimits_{i=1}^{N-1}\left|\ln\frac{x_{i+1}}{x_i}\right|$$
(1)

D being the consecutive disparity index (Martín-Vide 1986; Burgueño 1991), equal to 0 for the absolute regularity {xi(t)= x0, i=1, 2, …, N}, which is its minimum value. The greater the irregularity, with consecutive data xi(t) increasingly different from each other, the higher disparity values are found. The theoretically maximum value of D attending to Eq. (1) is infinity (López-Bustins and Lemus-Cánovas 2020), and the quantification of a possible empirical maximum value of D in a place is complex as it depends on the physical/mathematical structure (atmospheric dynamics in this case) of the analysed phenomenon. Nevertheless, it can be estimated by simulating a series of alternate consecutively monthly amounts between the resolution amount (1 mm) and the maximum value registered at the place, as it is presented in Section 5 (Discussion of the results). Section 5 also describes the generation of some random and Gaussian series of monthly amounts that permits a comparison of their disparities with those corresponding to real monthly amounts. López-Bustins and Lemus-Cánovas (2020) presented several hypothetical rainfall series showing different degrees of variability and the adequacy of the disparity value to characterise them.

A question to be considered is how the presence of null data along the analysed series could be solved. A null record of monthly rainfall series could be due to lost data or null amounts due to heavy drought episodes (long dry spells), which are not so rare in Mediterranean domains. In these cases, several rules are possible to prevent the computational error in Eq. (1). If xi is one of the affected monthly data, quotients xi/xi−1 and xi+1/xi are removed when computing Eq. (1), and N is substituted by N-2. Alternatively, xi could be substituted by 1.0 mm/month, 0.01 times the monthly mean of the analysed series, or adding 1.0 mm/month to every monthly amount to smooth some null monthly amount (Fernández-Martínez et al. 2018).

At the present case, bearing in mind that short lost data sections were substituted by monthly amounts obtained by kriging methods (Section 2 and Llabrés-Brustenga et al. 2019), the computational problems caused by a real monthly null amount xi has been discarded removing the quotients xi/xi−1 and xi+1/xi on Eq. (1) and substituting N by N-2 for every detected real null amount. The number of these strictly null amounts is rather small: considering a total of 62.689 months-station values, a global 3.3 % has been found, which means, on average, one month with null precipitation every two and a half years in any station. It is assumed that the uncertainty on the disparity due to these shortcomings is expected to be very low.

A correlation analysis between D and geographic features as altitude and continentality (distance to the sea), as well as with the amount of average annual precipitation, has been performed, being its results described in the next section.

4 Results

4.1 Spatial distribution and histograms

The evolution of the disparity in the NE Spain is relatively complex bearing in mind that the pluviometric regime at a monthly scale is quite different along the 12 calendar months and, additionally, the quite intricate orography and the vicinity or remoteness to the Mediterranean coast and the Pyrenees chain (Fig. 1a and b) also contribute to different rainfall regimes (Casas et al. 2007; Martín-Vide and Raso-Nadal 2008; Casas-Castillo et al. 2018a; Lana et al. 2021a) and consequently, to different disparity values. Additionally, the spatial distribution of high irregularity nuclei is relatively complicated, especially for October, November and December, characterised by several dispersed high and low values of D. Figure 2 describes the spatial distribution of D for every calendar month. The highest values of D have been obtained for winter months (December, January and February), being found the lowest for April and May.

Fig. 2
figure 2

Geographic distribution of the consecutive disparity index D for every calendar month

Full size image

The spatial distribution of these disparity values at a monthly scale is a bit complex; the distribution of high irregularity, especially for October, November and December, is characterised by several dispersed nuclei of high and low values of D, while from June to September, a clear increment of the rainfall irregularity is observed from the North (Pyrenees) to the Southern Mediterranean coast. It is also relevant to remember that the lowest values of disparity correspond to calendar months with minor oscillations on the consecutive amounts. October, for example, could be qualified as relatively copious amounts in comparison with other months. Nevertheless, the disparity (in fact, irregularity along the years) manifests in many places of the analysed domain notable oscillations year after year in comparison with the spatial distribution of D for August, a calendar month with notably lower, but many times more regular, rainfall amounts every year. Even though August rainfall could seem variable at a daily scale, with sudden local and intense storms, the situation is similar each August of every year, so the disparity ends up being low at a monthly scale.

With respect to the disparity for the consecutive series of monthly amounts (Fig. 3a), an evident increase of the rainfall irregularity is observed from NE to SW, being also very notable the minimum values of D for almost all the Pyrenees, especially for areas covering the West and North faces of the Catalan Pyrenees. On the contrary, the highest disparities are clearly detected at the southwest extreme, including the southern Mediterranean coast and a portion of the Central basin and the values of D for the consecutive months vary from 0.7 to 1.6. With respect to Fig. 3b, the spatial distribution of extreme disparities (maximum disparity obtained for every rain gauge) presents quite different patterns to those described in Fig. 3a, being more similar to some of the monthly spatial distributions. It is noticeable that notable extreme disparities have been observed in the Southern Mediterranean Littoral, together with some areas close to the Eastern and Western Catalan Pyrenees. The North face of the Western Catalan Pyrenees depicts the lowest extreme disparities, this fact suggesting that the Eastern Pyrenees, relatively close to the Mediterranean coast, shows an evident different disparity with respect to the western Catalan Pyrenees, given that in this last case, the pluviometric regime would be more conditioned by the Atlantic atmospheric circulation. It is also notable that the Central Basin (Western Catalonia) and a small domain of the Central Mediterranean coast (near the city of Barcelona) are characterised by moderate extreme disparity, in comparison with other extreme values. These results concerning the spatial distribution of extreme disparities vary from 1.0 to 2.0.

Fig. 3
figure 3

Geographic distribution of the disparity index D for a consecutive monthly data without distinguishing calendar months and b extreme disparity defined as the maximum value of calendar months D for every rain gauge

Full size image

The empirical statistical distribution of disparity for every calendar month and series of consecutive months is described by the histograms in Fig. 4. Besides January, March, April, October and November, with some characteristics suggesting a few signs of a normal distribution, (nevertheless, without accomplishing the Kolmogorov-Smirnov test) an approach to a Gaussian distribution for the other seven histograms is absolutely discarded, with clear asymmetries. The amplitude of disparities for all the calendar months is very similar (1.0–1.2) with the single exception of September, with an interval of 1.4 units. The highest values of the standard deviation of D are detected along the summer (0.29 to 0.32) and December (0.29), with notable differences in the spatial distribution of disparities. It is also relevant that December not only depicts one of the highest standard deviation, but also one of the highest average disparities (1.54). A similar average disparity is obtained for January (1.57), but with one of the narrowest standard deviations. Additionally, the spring season (especially April and May) is characterised by the lowest average disparities (0.97 and 0.93) and small standard deviations, especially for April, with the lowest value (0.18). The histogram corresponding to the consecutive monthly amounts could depict some signs of possible Gaussian distribution. Nevertheless, the asymmetry of the histogram and the Kolmogorv-Smirnov test permit to discard this theoretical distribution. Additionally, the average disparity of the consecutive monthly amounts (1.25) and the corresponding standard deviation (0.20) are quite similar to those obtained for October at a monthly scale.

Fig. 4
figure 4

Disparity histogram for every calendar month and the consecutive monthly series. Averages and standard deviations for the 13 histograms are summarised in Table 1

Full size image

4.2 Dependence of D on altitude, distance to the Mediterranean coast and rainfall amount

Another relevant question to be analysed is a possible dependence of D on the altitude above sea level, Z, for every one of the 97 rain gauges. Figure 5 depicts the negative slopes of D with the increasing altitude of the rain gauges. Table 1 summarises the 12 slopes (monthly calendar scale), being remarkably the highest negative values detected for the end of spring (May) and summer (June, July and August), depicting an evident decrease with the altitude. Consequently, the strongest influence on D is detected for these cited four months, being also manifested an evident influence of the altitude on the rainfall disparity for all calendar months. It is also noticeable the clearest dependence of D on altitude (Fig. 5), usually detected for Z approximately equalling to or exceeding 800 m.

Fig. 5
figure 5

Dependence of the twelve calendar months and consecutive month disparities on Z (altitude above sea level). The slopes of the linear fits are listed in Table 1

Full size image
Table 1 Slopes of the linear fits of Figs. 5, 6 and 7 showing the dependence of the monthly calendar and consecutive monthly records disparity on altitude above sea level (Z), distance to the Mediterranean coast (dc), and average monthly rainfall (MR). Values of the average <D> and the standard deviation of the disparity σ(D) for histograms of Fig. 4. The highest slopes, average disparities and standard deviations are written in bold types
Full size table

Figure 6 and Table 1 also describe the dependence of D with respect to the distance to the Mediterranean coast. It is noticeable that the highest negative dependence of the disparity with respect to the distance to the Mediterranean coast is detected at the end of spring (May, −2.99×10−3 km−1), the whole summer (from −3.28×10−3 km−1 to −3.87×10−3 km−1) and December (−2.92×10−3 km−1). More moderate negative dependencies are detected for the other calendar months, especially for those corresponding to the cold period of the year (January and March). Nevertheless, February (−3.16 × 10−3 km−1), in the middle of the winter season, depicts a tendency very close to that detected in June. Consequently, in spite of some of the highest tendencies are detected in summer, quite similar ones are detected in December, February (winter season) and May (at the end of the spring season). From the point of view of all the consecutive monthly amounts, the tendency is very notable (−3.97 ×10−3 km−1), reinforcing the rainfall disparity reduction as longer the distance to the Mediterranean littoral is.

Fig. 6
figure 6

Dependence of the disparity index D with the distance to the Mediterranean coast for every calendar month and for all the consecutive monthly data. The slopes of the linear fits are listed in Table 1

Full size image

Finally, a question to be analysed is the possible relationship between disparity and average amounts for every calendar month and for the whole set of monthly amounts. Figure 7 depicts the evolution of these pairs of variables at a monthly scale, being noticeable the reduction on March, May, June, July, August and December (Table 1) of D with the increasing amounts. In agreement with these results, the highest linear decrease of the disparity from May to August, as well as for January, is notable. Consequently, the strongest linear relationship between average monthly amounts and low disparities would correspond to the end of spring, usually a quite humid season for all Catalonia, summer, characterised by a notably hot and dry season excepting for the Pyrenees area, and an isolated month (December) at the end of autumn and beginning of winter. Conversely, October does not depict clear signs of dependence of the disparity on the average monthly amount, and for the remaining calendar months, these dependences are much more moderate. With respect to the consecutive monthly rainfall (Table 1 and Fig. 7) a negative trend, more moderate in comparison with those corresponding to calendar monthly data, is also detected. This smoother negative tendency could be a direct consequence of substituting every characteristic at monthly calendar scale by the combined effects of 12 different monthly rainfall characteristics. Nevertheless, the negative slope is quite evident.

Fig. 7
figure 7

Relationship between the calendar month and consecutive disparity indexes D on average monthly rainfall. The slopes of the linear fits are listed in Table 1

Full size image

5 Discussion of the results

The disparity values found in the present study are in accordance with those obtained in previous analysis (Burgueño 1991; Lana and Burgueño 2000). In the case of annual rainfall series, López-Bustins and Lemus-Cánovas (2020) and Martín-Vide et al. (2022) found disparity values ranging between 0.15 and 0.40, while for seasonal rainfall, they obtained values from 0.3 to 1.2. In the case of consecutive monthly rainfall, the disparity values found by Martín-Vide et al. (2022) ranged between 0.6 and 1.7 for the Iberian Peninsula, similarly to the interval (0.7–1.6) observed in the present study for Catalonia. For calendar months, the observed disparity ranges from 0.4 and 2.0 as it was found by Martín-Vide et al. (2022), even though the values displayed for Catalonia in that study had a narrower range, probably due to the smoothing and the interpolation method applied to elaborate their maps.

The comparison with the results of previous studies is not only convenient but essential, given the very nature of this index, which does not mean nothing but itself and must be compared with the values obtained in other stations. A station record is more or less irregular in relation to other station records; the closer the disparity gets to 0, the more regular the rainfall record is. As an example, a specific value of D=1, considered a moderate value in the quantification scale of Fig. 2, would be a low value if registered in October at a southern station and a high value in May at a northern station. Instead, a value of D of 0.2 is a very low value in Catalonia for both October and May, whether in a mountainous or in a coastal area. Also, the disparity values depend on the record resolution; for instance, it is not the same calculated from monthly than from annual records.

The possible empirical maximum value of D in a specific place can be estimated by simulating an extremely irregular series of alternate consecutively monthly amounts between the resolution amount (established as 1 mm) and the maximum value registered at the place. For instance, at two of the stations contributing most to the map of maximum disparities of Fig. 3, one in the Pre-Pyrenees (D=1.7, for January) and the other one in the south (D=1.9, for December), the maximum monthly amounts registered were 200 mm and 359 mm. Simulated series of consecutively monthly amounts alternating the minimum (1 mm) and the maximum monthly amounts in both places resulted in disparity values of 5.3 and 5.9, respectively. Carrying out the same simulation for the rest of stations, a range of extreme maximum disparity values between 4.9 and 6.6 has been obtained, with an average value of 5.8.

The disparity values obtained for the twelve calendar months could be also compared with disparities simulated by random and Gaussian distributions. In the first case, a random rainfall distribution would be characterised by a disparity of 0.95, taking as reference 250 random samples {x1} on the (0.0, 1.0) interval. In the second case, a Gaussian distribution, with the same number of samples, derived from two different segments of random series {x1} and {x2}, can be generated according to Box and Muller (1958) and Papoulis (1991) using equation (2).

$$z={\left\{-2\mathit{\ln}\left({x}_1\right)\right\}}^{1/2}\cos \left(2\uppi {x}_2\right)$$
(2)

The simulated Gaussian series would be characterised by D equal to 0.52. After revising again the Figs. 2 and 4 of disparity maps and histograms, some areas of Catalonia (NE Spain) could be related to the Gaussian distribution of monthly rainfall amounts, given that for April, May, June, August, September and November, low disparity levels close to 0.5 are detected. Nevertheless, the above-mentioned Kolmogorov-Smirnov test does not verify this Gaussian structure. With respect to a possible random distribution of monthly rainfall amounts, it is notable that for all the calendar months some areas are associated with disparities close to 0.9, consequently suggesting a random structure. Additionally, many other places of the analysed area, for every one of the calendar months, also depict disparities not coincident with random levels. It could then be assumed that the atmospheric circulation, combined with the altitude above sea level and the vicinity to the Mediterranean littoral and the Pyrenees and Littoral and Pre-Littoral chains, should be relevant factors for the calendar monthly rainfall disparity, having a very moderate role a possible random distribution of monthly amounts. Additionally, the obtained values of D by means of the whole series of monthly amounts (Fig. 3a) are absolutely disassociated with Gaussian structures, and only some places of the western Pyrenees and the north face of the Catalan Pyrenees depict disparities close to 0.7, with some signs of Gaussian distribution of monthly amounts along the recording period. With respect to the spatial distribution of the extreme (maximum) disparities (Fig. 3b), these values are not included within the 0.5–0.9 levels. On the contrary, they exceed or are close to 1.0, being to be probably associated, in some cases, with random structures. These structures would correspond with the Hurst exponents relatively close to 0.5, identifying randomness behaviour, obtained for the same rain gauge network used in this work (Lana et al. 2020). In the just mentioned research, a notable percentage of rain gauges were characterised by Hurst values within the 0.4–0.6 interval, with evident signs of randomness, and only a small set of rain gauges depicted signs of moderate persistence, with values of H within the 0.6–0.7 interval.

The spatial distribution of the disparity D for consecutive months (Fig. 3a), with its lowest values at the most north-western corner of Catalonia and a soft gradient towards the south and the east until reaching its highest values at its southern end, is in great agreement with the distribution of a scaling fractal parameter β calculated using monthly rainfall series (Lana et al. 2021a). This parameter is an exponent that appears in scaling relationships between distributions of rainfall intensity at different time scales in the monofractal approach (Menabde et al. 1999; Yu et al. 2004; Bara et al. 2010; Casas-Castillo et al. 2018b). This scaling parameter β has been proven to be a good indicator of rainfall irregularity (Rodríguez-Solà et al. 2017; Casas-Castillo et al. 2018a, 2022; Lana et al. 2021a). The values of β calculated for the maximum monthly rainfall series of Catalonia range from the lowest values of around −0.3 at the northern area to values around −0.6 at the south, showing a negative gradient towards the south and the east (i.e. towards more irregularity), similar to that found for the disparity D of the consecutive months. One of the differences between both distributions is a low value of β obtained at the most northeastern area (around −0.6 as at the south) compatible with some of the monthly distributions of Fig. 2 (April, May, July).

It is also relevant to the different disparity values associated with rainfall regimes more affected by Atlantic or by Mediterranean atmospheric circulations. The area of the Eastern Pyrenees, and especially the North face of the Western Catalan Pyrenees, is characterised by very different topographic elements in comparison with the Littoral and Pre-littoral chains. Additionally, the Central Basin, with a very moderate altitude, is at a not negligible distance of the Mediterranean littoral. Consequently, a single common Mediterranean climate and, particularly, a single pluviometric regime would not be expected for NE Spain. In agreement with the Köppen-Geiger climate classification system (Melvin 2016; McVicar et al. 2018), four different domains, all of them classified as temperate, should be considered: first, a domain, with dry and hot summer (CSa code), which would be associated with the Littoral and Pre-Littoral chains, and the Western Basin; second, two domains without dry season and hot summer (Cfa code) and warm summer (Cfb code), both assigned to the areas delimited by the Pre-littoral chain and the beginning of the Pyrenees structures; and finally, a fourth domain with cold summer and without dry season (Cfc code), covering the Pyrenees region.

In agreement with the different Köppen-Geiger classifications and the complex topography and vicinity to the Mediterranean Sea, different rainfall disparity intervals have been finally obtained, being then detected different variations on the pluviometric regime irregularity for every calendar month. It is relevant to remember that most of the calendar months are associated with disparity intervals of amplitudes 1.2 and maximum disparities equalling or exceeding 1.7, up to 2.1 and 1.9 for January and December. Conversely, two months of the spring season (April and May) are respectively characterised by interval amplitudes of 1.0 and 1.2, also achieving the lowest maximum disparities, 1.5 and 1.6. From this point of view, a good part of the spring could be assumed as the less irregular rainfall season in Catalonia. It is also worth mentioning that a continuous smooth evolution of the disparity along the calendar months is not detected for the four seasons. For example, whereas disparity maps for July, August and September (summer) depict relatively similar geographic structures, those corresponding to January, February and March (winter) are quite different, with different ranges of D and geographic distribution.

It is also worth mentioning that the lowest disparities are detected in April and May, in agreement with the results of a global analysis for all the peninsular Spain (Martín-Vide et al. 2022). Conversely, June and July, one more time in agreement with the just-cited global research, depict higher disparities. Some differences are detected bearing in mind that in the SW of Spain, July and August are characterised by the highest disparities. Nevertheless, in this analysed database, the disparity of August is exceeded by June and July. Additionally, in comparison with the cited research of Martín-Vide et al. (2022), the high disparity obtained for December, ranging from 0.7 to 1.9, is quite different. Consequently, some rainfall disparity patterns could be very similar to the whole of peninsular Spain, but others would change on some areas of NE Spain, possibly due to the vicinity to the Pyrenees chain and the Mediterranean Sea. The area covered in the present manuscript is restricted to a reduced section of NE Spain, with a high enough density of rain gauges, and the detected changes of D at a smaller scale would not be necessarily opposite to the results obtained by Martín-Vide et al. (2022) who included the whole Spanish territory in their research. The high density of rain gauges has permitted to observe several relationships between disparity values and geographic and orographic structures, perhaps a bit more difficult to detect at larger geographic scales.

The disparity analysis for a complex Mediterranean rainfall area could be a new point of view to complement the forecasting of the length and intensity of monthly drought episodes. In fact, the higher the monthly disparity (irregularity) of a recorded monthly series, the more difficult it could be to make a good forecasting of the next monthly amount recorded. These complements on forecasting improvements should contribute to decide the best way of water distribution for agriculture, cattle raising, industrial activity and drinking water supply, among other relevant questions, for Mediterranean regions where drought episodes, sometimes long, are quite usual, and negative rainfall amount trends at annual and seasonal scales, as well as long dry spells, (Brunetti et al. 2002; Anagnostopoulou et al. 2003; Serra et al. 2006; Lana et al. 2006; Cindrić et al. 2010, among others) are detected.

Finally, it is also relevant to observe that the four months corresponding to the end of spring and the almost complete summer (May, June, July and August) depict the common property of high negative slopes of disparity with increasing distances to the Mediterranean coast, altitude above sea level and average monthly amounts. Consequently, lower monthly rainfall disparities should be expected for rain gauge emplacements characterised by notable altitude and distance to the Mediterranean coast, as well as high average monthly amounts. These characteristics could also contribute to facilitate monthly rainfall forecasting.

6 Conclusions

The concept of disparity, and the available dense rain gauge network, permits the detailed detection of the different irregularities on the rainfall regime of Catalonia (NE Spain), characterised by a complex orography, and the influence of Mediterranean and Atlantic atmospheric circulations. These irregularity patterns usually change from one calendar month to the next and sometimes are relatively different for calendar months belonging to the same season. In agreement with the obtained disparity maps at a calendar monthly scale, two relevant results for future better rainfall amounts forecasting are obtained: on the one hand, the extreme irregularity for every one of the 97 rain gauges, a question which could be considered a first calibration of the monthly amounts forecasting difficulty, and on the other hand, a more detailed disparity for every gauge and calendar month, which should be a contribution to improve the forecasting of consecutive monthly rainfall amounts, which have been obtained (Lana et al. 2021b) by means of the reconstruction theorem, fractal theory (Diks 1999) and the ARIMA algorithm (Box and Jenkins 1976). Improvements on the monthly rainfall forecasting would be relevant, bearing in mind that long dry spells at a monthly scale are usually detected in Europe and especially in the Mediterranean area. In short, a more accurate quantification of forthcoming monthly amounts, with the contribution of the monthly rainfall parameter D, would be relevant to detect the expected end of a long drought episode.