Multi-depth daily soil temperature modeling: meteorological variables or time series?

Abstract

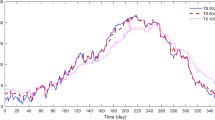
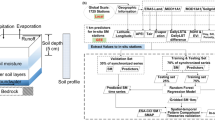
This study presents the first-time application of a novel emotional neural network (ENN) for soil temperature modeling. Two scenarios were considered for soil temperature forecasting: (i) meteorological variable-based modeling and (ii) time series-based modeling. For the first scenario, meteorological variables, including average air temperature, average wind speed, and total solar radiation, were considered as the inputs of a predictor model, while for the second one, the time delays of the soil temperature time series were considered as input(s) for forecasting future time-step soil temperature profiles. The multi-depth daily soil temperature datasets from Springfield and Champaign stations, located in Illinois, USA, were collected at the 10-cm and 20-cm depths to evaluate the proposed model. Moreover, the proposed ENN model was compared with other popular modeling techniques, including generic programming (GA), least square support vector machine (LSSVM), and multivariate adaptive regression splines (MARS). These case studies indicate the superior performance of the ENN compared to other popular modeling techniques for soil temperature applications. The mean relative error of scenario 2 was in the 5–7% range, while it was more than 40% for scenario 1.

Appendix

Multivariate adaptive regression splines.

The main goal of MARS is to capture the relationship between the output variable and the input variable from the data. In general, the basic equation of MARS is given below:

$$y=\stackrel{\wedge }{f}(x)={a}_{0}+\sum_{m=1}^{M}{a}_{m}{B}_{m}^{(q)}(x)$$

(A1)

where a₀ expresses the coefficient of the constant basis function or the constant term;${\left\{{a}_{m}\right\}}_{1}^{M}$ denotes the vector of coefficients of the non-constant basis functions, m = 1, 2, …, M;${B}_{m}^{\left(q\right)}$ are the basic functions that are selected for inclusion in the model of qth order:

$${B}_{m}^{(q)}(x)=\prod_{k-1}^{{k}_{m}}{[{s}_{km}.({x}_{v(k,m)}-{t}_{km})]}_{+}^{q}$$

(A2)

where ${B}_{m}^{\left(q\right)}\left(x\right)$ is the vector of non-constant (truncated) basis functions, or the tensor product spline basis, m is a number of non-constant basis functions (1, 2, …, M), q represents the power to which the spline is raised in order to control the degree of smoothness of the resultant function estimate, which in this case is equal to 1, and + denotes that only positive results of the right-hand side of the equation are considered; otherwise, the functions evaluate to 0. Thus, the term truncated (S_km) indicates the (left/right) sense of truncation, which assumes only two values (± 1), representing the standard basis function and its mirror image. For S_km equal to + 1, the basis function will have a value x − t if x > t and 0 if x ≤ t. If it is − 1, the basis function will have a value t − x when x < t, while 0 if x ≥ t, x_ν(k,m) is the value of the predictor, ν(k,m) expresses the label of the predictor $\left(1\le \nu \left(k,m\right)\le n\right)$, n is the number of predictors, t_km denotes “knot” location on the corresponding predictor space or region or value that defines an inflection point along the range of the predictor, K is maximum level or order of interaction, or the number of factors, in the mth basis function (1, 2, …, K_m).

Forward and backward steps are involved in constricting the MARS model. In the forward step, basis functions are introduced to define Equation (A1). Overfitting can occur due to a large number of basis functions. Craven and Wahba (1978) proposed generalized cross-validation (GCV) criterion for preventing overfitting. The expression GCV is given below:

$$GCV=\frac{\frac{1}{N}\sum\limits_{i=1}^{N}{\left[{y}_{i}-\stackrel{\wedge }{\underset{M}{f}}({x}_{i})\right]}^{2}}{{\left[1-\frac{C(M)}{N}\right]}^{2}}$$

(A3)

where N is observations, C(M) is cost penalty measures of the model, and M is basis functions, f_m(x_i) is the basis function model.

Least square support vector machine (LSSVM).

Let us consider the following dataset (D).

$$\begin{array}{cc}D={\{{x}_{k},{y}_{k}\}}_{k=1}^{N};& {x}_{k}\in {R}^{N}{y}_{k}\in r\end{array}$$

(A4)

where x is input, y is output, R^N is the N-dimensional vector space, and r is the one-dimensional vector space. LSSVM adopts the following equation for the prediction of y.

$$y(x)={w}^{T}\phi (x)+b$$

(A5)

where the non-linear mapping φ(.) maps the input data into a higher dimensional feature space, $w\in {R}^{n}$, $\mathrm{b}\in \mathrm{r}$; w expresses an adjustable weight vector; b denotes the scalar threshold.

The value of w and b is determined by solving the following optimization problem.

Minimize:$\frac{1}{2}{w}^{T}w+\gamma \frac{1}{2}\sum\limits_{k=1}^{N}{e}_{k}^{2}$

$$\mathrm{Subjected to}: y\left(x\right)={w}^{T}\phi \left({x}_{k}\right)+b+{e}_{k},k=1,\cdots ,N$$

(A6)

where γ is the regularization parameter, determining the trade-off between the fitting error minimization and smoothness, and e_k is the error variable.

Lagrange multipliers solve the above optimization problem (Eq. A6). So, the Lagrangian ($L\left(w,b,e,\alpha \right)$) is given below:

$$L(w,b,e;\alpha )=\frac{1}{2}{w}^{T}w+\gamma \frac{1}{2}\sum_{k=1}^{N}{e}_{k}^{2}-\sum_{k=1}^{N}{\alpha }_{k}\{{y}_{k}[{w}^{T}\phi ({x}_{k})+b]-1+{e}_{k}\}$$

(A7)

with α_k expresses Lagrange multipliers. The following equations are used for the condition of optimality.

$$\frac{\partial L}{\partial w}=0\Rightarrow w=\sum_{k=1}^{N}{\alpha }_{k}\phi ({x}_{k})$$

(A8)

$$\frac{\partial L}{\partial b}=0\Rightarrow \sum_{k=1}^{N}{\alpha }_{k}=0$$

(A9)

$$\frac{\partial L}{\partial {e}_{k}}=0\Rightarrow {\alpha }_{k}=\gamma {e}_{k}, k=1,\cdots ,N$$

(A10)

$$\frac{\partial L}{\partial {\alpha }_{k}}=0\Rightarrow {w}^{T}\phi \left({x}_{k}\right)+b+{e}_{k}-{y}_{k}=0,k=1,\cdots ,N$$

(A11)

The above equations can be written in the following way:

$$\left[\begin{array}{cc}0& {1}^{T}\\ 0& \Omega +{\gamma }^{-1}I\end{array}\right]\left[\begin{array}{c}b\\ a\end{array}\right]=\left[\begin{array}{c}0\\ y\end{array}\right]$$

(A12)

where $y=\left[{y}_{1},\dots ,{y}_{N}\right]$,$1=\left[1,\dots ,1\right]$, $\alpha =\left[{\alpha }_{1},\dots ,{\alpha }_{N}\right]$ and Ω matrix, $\Omega =\phi {\left({x}_{k}\right)}^{T}\phi \left({x}_{l}\right)=k\left({x}_{k},{x}_{l}\right)$, k,l = 1,…, N.where $k\left({x}_{k},{x}_{l}\right)$ denotes the kernel function. Choosing γ > 0, ensures the matrix. $\Phi =\left[\begin{array}{cc}0& {1}^{T}\\ 1&\Omega +{\gamma }^{-1}I\end{array}\right]$ is invertible. Then, the analysis of α and b is given by the following expression.

$$\left[\begin{array}{c}b\\ \alpha \end{array}\right]={\Phi }^{-1}\left[\begin{array}{c}0\\ y\end{array}\right]$$

(A13)

The final LSSVM model for prediction output is given below

$$y\left(x\right)=\sum_{k=1}^{N}{\alpha }_{k}K\left(x,{x}_{k}\right)+b$$

(A14)