1 Introduction

The Qinghai-Tibet Plateau is a large terrain with the highest average altitude and the most complex underlying surface of any region in the world. Its dynamic and thermal effects have undoubtedly influenced the Asian monsoon, global energy and water cycles (Manabe and Terpstra 1974; Xu et al. 2008; Wu et al. 2012). The Tibetan Plateau Vortex (hereafter referred to as TPV) is a low-level (500 hPa) mesoscale weather system generated under a dynamic and thermal background unique to the TP. Its horizontal scale is approximately 500 km, its vertical thickness is approximately 2–3 km, and its life cycle is approximately 1–3 days (Yeh 1957; Lhasa Group for Tibetan Plateau Meteorology Research 1981). The TPV is not only the most important factor in the plateau’s disastrous weather system but also the driving factor of the SWV and one of the precipitation inducers in the middle and lower reaches of the Yangtze River. Its generation, dissipation, development and water cycle processes have a profound impact on the weather and climate patterns on the plateau, China and even throughout Asia (Tao and Ding 1981; Wang 1987; Yu et al. 2014). Hence, since the concept of the TPV was proposed, it has been a popular topic in the field of meteorology in China and worldwide.

At present, many scholars have carried out much research on the structural characteristics, generation, dissipation and development of TPVs based on observation data and numerical simulations. Previous studies have noted that most TPVs are warm structures and low-pressure cyclones with asymmetric warmth and humidity, with a spiral cloud system very similar to that of tropical cyclones; this view has also been confirmed by its dynamics (Lhasa Group for Tibetan Plateau Meteorology Research 1981; Wang 1987; Qiao and Zhang 1994; Li and Jiang 2000; Li et al. 2002). The occurrence and development of TPVs are not only related to large-scale systems such as the South Asian high, the Western Pacific subtropical high and the upper westerly jet (Yu and Gao 2008; Yu et al. 2016) but are also closely related to diabatic heating and atmospheric energy. The release of ground sensible heat and latent heat can produce a thermal environment conducive to the development of TPVs (Luo et al. 1991; Luo and Yang 1992; Li et al. 2002); shortwave radiation and cloud radiation effects also have important impacts on the development and removal of TPVs (Dell’Osso and Chen 1986; Li and Fan 2020; Chen and Fan 2022).

The water cycle process connects all spheres of the climate system; it both forms and restricts weather and climate change (Dai and Deser 1999). The plateau vortex is located in the Qinghai-Tibet Plateau, which is in the Asian monsoon region; it is one of five global experimental areas of the energy and water cycle. The characteristics of its water cycle are distinct, and its mechanism is complex. Therefore, researchers from China and other parts the world have implemented many scientific experiments on the Qinghai-Tibet Plateau and water cycle, thus generating many data (Chahine 1992; Lawford 1999; Sorooshian et al. 2005; Zhao et al. 2019). Existing studies have shown that due to the unique geographical location and climate background of the Qinghai-Tibet Plateau, water cycle processes associated with TPV have their own, clearly local characteristics. A self-circulation process of water vapour supply in convection activities occurs on the Qinghai-Tibet Plateau, in which ground evaporation plays an important role; this process is significantly different from that of the plain area (Li et al. 2019a). The formation and movement of convective clouds and the physical process of cloud precipitation accompanied by the occurrence and development of the TPV also play an important feedback role in the water cycle of the TPV (Li et al. 2016). At a larger scale, the energy and water vapour transport anomalies caused by the intersection of multiple monsoons can lead to changes in the vortex water cycle on the plateau, resulting in anomalies in the plateau and surrounding areas, and can react on the plateau and atmospheric circulation (Yu and Gao 2008; Li et al. 2014; Yu et al. 2016).

There are complex feedbacks between the change in the water cycle and the climate system, and only considering a single factor cannot fully explain the evolution of the water cycle. At present, most of the research on the TPV water cycle analyses individual cases or single water cycle factors such as precipitation recycling rate and the precipitation efficiency. However, they ignored the overall characteristics of the TPV water cycle and do not describe the water components of the TPV water cycle. Especially in the context of global warming, the global water cycle also changes dramatically, and research on the change trend of the long-term series of the TPV water cycle is even less common. Therefore, this paper focuses on the TPV weather system, which is different from previous studies on the fixed regional water cycle. It does research on the climate characteristics and changes of the atmospheric process of the TPV water cycle, also compares and analyses the atmospheric circulation in the active and inactive years of the TPV to explore the reasons that may effect the changes of the TPV water cycle. The resulting data are of great significance for revealing the general law of the TPV water cycle and further understanding the nature and characteristics of TPV and its impact on the plateau and even global climate change.

2 Data and method

2.1 Data

The atmospheric circulation data are ERA-Interim, a reanalysis dataset of the European Centre for Medium-Range Weather Forecasts (ECMWF; https://apps.ecmwf.int/datasets/data/interim-full-daily/levtype=sfc/), which includes wind, geopotential height, specific humidity, temperature, divergence, etc., with a spatial resolution of 0.5° × 0.5° and a time interval of 6 h. These reanalysis data are widely used on the plateau and perform better than other data (Li et al. 2012; Gao et al. 2020). TPV data are obtained from the TPV datasets objectively identified by Lin (2015) using ERA-Interim reanalysis data. Compared with the plateau vortex dataset objectively identified by NCEP FNL reanalysis data (Lin et al. 2013), the ERA-Interim reanalysis data are of a longer duration and more complete nature, with a time interval of 6 h. The precipitation data adopt the East Asian monsoon sub daily dataset of APHRODITE (Asian Precipitation-Highly Resolved Observational Data Integration Towards Evaluation of Water Resources; http://aphrodite.st.hirosaki-u.ac.jp/product/) (Yatagai et al. 2012). The time series is 1979–2015, and the spatial resolution is 0.5° × 0.5°. These data are suitable for studying the characteristics of plateau climate change because of their high accuracy and long time series (Dong et al. 2016; Li et al. 2018; Tan et al. 2020). Evaporation data are 3-h data from GLDAS (Global Land Data Assimilation System) (https://doi.org/10.5067/L0JGCNVBNRAX of 1° × 1°. Among the widely used global reanalysis products, the surface variables of GLDAS perform well on the plateau (Wang and Zeng 2012; Zhang et al. 2019).

2.2 Method

2.2.1 Definition of precipitation value of TPV

According to the structure and precipitation characteristics of the TPV (Jiang et al. 2015; Li et al. 2019b; Quan et al. 2019), the precipitation within 500 km from the centre of the TPV is usually defined as TPV precipitation. Therefore, in this study, the daily precipitation for which the vortex centre is at the centre of a circle with a diameter of five longitudes and latitudes (5° × 5°) is recognized as TPV precipitation (Fig. 1), and the total precipitation of each TPV is the sum of grid values within the range. The low vortices that originated outside the main body of the plateau and moved out of the plateau area in the TPV datasets were removed.

Fig. 1
figure 1

Value range of plateau vortex precipitation (the centre of the circle represents the plateau vortex centre)

Full size image

2.2.2 Calculation method of the water cycle coefficient

The water cycle process is very complex. To quantitatively describe the characteristics and changes in the TPV water cycle, five water cycle coefficients proposed by Liu (1997) are used to describe the characteristics of the TPV water cycle. This conceptual model of the water cycle is based on relevant methods at home and abroad and on research on China’s hydrological cycle. He believes that the following five coefficients have clear physical meanings and sensitive description effects:

  1. (1)

    Hydrological external circulation coefficient (KI)

    $$K_{I} = \frac{N}{{P_{I} }}$$
    (1)

    The hydrological external circulation coefficient (KI) is the ratio of the net water vapour input outside the region (N) to the precipitation formed by external water vapour in the region (PI); it reflects the contribution of overseas water vapour input to the precipitation in the region.

  2. (2)

    Hydrological internal circulation coefficient (KE)

    $$K_{E} = \frac{{P_{E} }}{E}$$
    (2)

    The hydrological internal circulation coefficient (KE) is the ratio of precipitation formed by internal evaporation in the region (PE) to the water vapour evaporated in the region (E), reflecting the contribution of evaporation in the region to the hydrological cycle in the region.

  3. (3)

    Hydrological circulation coefficient (K)

    $$K = \frac{{P_{I} }}{P}$$
    (3)

    The hydrological cycle coefficient (K) is the ratio of precipitation formed by external water vapour in the region (PI) to the total precipitation in the region (P), indicating the contribution of externally transmitted water vapour to precipitation in the region. (1 − K) reflects the contribution of precipitation formed by local evaporation to the total precipitation in the region, also known as the precipitation recycling rate.

  4. (4)

    Water vapour retention coefficient (τ)

    $$\tau = \frac{W}{P}$$
    (4)

    The water vapour retention coefficient (τ) is the ratio of the precipitable water vapour (W) over the region to the total precipitation in the region (P), indicating the time required for the atmospheric water vapour content over the region to be completely replaced (converted to precipitation). The larger the retention coefficient of water vapour is, the slower the renewal rate of water in the atmosphere. In contrast, the smaller the retention coefficient of water vapour is, the faster the renewal rate of water in the atmosphere.

  5. (5)

    Water vapour utilization coefficient (J)

    $$J = \frac{P}{W}$$
    (5)

The water vapour utilization coefficient (J) is the ratio of the total precipitation (P) to the precipitable water vapour (W) in the region; it indicates the efficiency of water vapour conversion into precipitation over the region, also known as the precipitation efficiency or the efficiency coefficient. The larger the water vapour utilization coefficient is, the faster the water vapour renewal speed and the higher the utilization efficiency; otherwise, the utilization efficiency is low.

It is assumed that the total precipitation (P) is composed of precipitation formed by external water vapour in the region (PI) and precipitation formed by internal evaporation in the region (PE). The distribution of precipitation, evaporation, atmospheric water vapour and water vapour transport flux change linearly in the study area. The water vapour input from outside the region and evaporated from within the region can be fully mixed over the region, so there is an equal opportunity to form precipitation. I represents the regional average of total water vapour input.

$$P={P}_{I}+{P}_{E}$$
(6)
$${P}_{I}=\frac{P}{1+\frac{E}{2I}}$$
(7)
$${P}_{E}=\frac{P}{1+\frac{2I}{E}}$$
(8)

When the water vapour input in the region is zero, the KI and PI are zero. During calculation, the precipitable water vapour is integrated from the ground to 200 hPa. The water vapour input and output boundary is a rectangular box in which the TPV is centred with five longitudes and latitudes as the side length (Fig. 1). The specific calculation method refers to hydrological cycle atmospheric process (Liu 1997).

This work is mainly to study the macroscopic budget of the atmospheric water cycle of TPV. When the evaporation water vapour outside the region rises to the air and enters the boundary of the TPV precipitation box along with the air transport, it participates in the calculation of the water vapour budget. If the water vapour in the region is transported to the outside of the region, it also participates in the calculation of the boundary water vapour budget. However, the water vapour transport within 500 km mainly participates inside the TPV water cycle, which involves cloud microphysical processes and changes the phase transition and distribution state of water vapour in the region. It does not change the total amount of water vapour in the region and does not affect the calculation of water vapour budget. In the process of each TPV centre movement, the value of five coefficients in this study area (5° × 5°) was calculated every 6 h (according to data temporal resolution), and an average value of all TPVs was obtained in 1 year. The calculation area is a constantly moving and non-fixed area, so there is no spatial distribution.

3 Characteristics and changes in the TPV water cycle

3.1 Climate characteristics of the TPV water cycle

According to the average value of the TPV water cycle coefficient in Table 1, the average value of KI is 4.02; the calculated average value of KE is 1.93, which is higher than that of the Qilian Mountain Region in the northeast of the Qinghai-Tibet Plateau calculated by predecessors (Zhang et al. 2014), indicating that the internal circulation in the south of the plateau is more active than that in the northeast of the plateau. K reflects the contribution of external input water vapour to the total precipitation in the region, with an average value of 0.74; that is, the precipitation caused by external water vapour input accounts for 74% of the total precipitation, indicating that the precipitation of the TPV is mainly caused by overseas water vapour input, and the hydrological external cycle of the TPV is very active compared with the internal cycle. The precipitation recycling rate (1 − K) is the contribution of precipitation caused by evaporation to the total precipitation in the region and accounts for 26% of the total precipitation, which is higher than the previous study of the maximum annual precipitation recycling rate of 20% on the plateau (van der Ent et al. 2010; Guo and Wang 2014; Zhang et al. 2017; Yang et al. 2022), indicating that the precipitation recycling rate of the convective system, such as the TPV, is greater.

Table 1 Average value of the TPV water cycle coefficient from 1979 to 2015
Full size table

The above three coefficients characterize the TPV water cycle using contributions from the water vapour input outside the region, the water vapour evaporated locally and the precipitation. J and τ can be further supplemented based on these contributions to the water cycle. During the analysis, the water cycle coefficient of each TPV process is calculated first, and then the average value is calculated. Therefore, the value of J is not directly equal to the reciprocal of τ, which is more a reflection of the change in precipitation efficiency. The physical meaning of τ is the time required in days for all atmospheric water vapour in the air to convert into precipitation, with an average value of 0.32 day, indicating that it takes 0.32 day to convert the water vapour in the air over the region into precipitation; that is, 3.125 water cycles per day are needed to meet the precipitation required by the TPV.

3.2 Trend analysis of the TPV water cycle

To illustrate the interannual variation in the TPV water cycle, the time series (solid line) and trend line (dotted line) of each water cycle coefficient are calculated, and the time series of each water cycle coefficient are tested by the M–K catastrophe test (Mann 1945; Kendall 1975). In Fig. 2a, it can be seen that KI generally shows a significant upwards trend (p < 0.05). According to formula (4) KI = N/PI, when N is constant, the large the PI is, the more precipitation is formed by the external cycle. At this time, the closer PI is to N, the smaller the KI value is. And the correlation coefficient between J and KI was calculated (R =  − 0.66, p < 0.01), so KI is negatively correlated with activity of TPV. Therefore, the upwards trend shows that the contribution of water vapour input outside the region to the water cycle in the TPV precipitation region decreases, and the activity of the external cycle decreases. In Fig. 2b, KE shows a decreasing trend (p < 0.05), indicating that the activity of the plateau vortex internal circulation decreases; K has a significant upwards trend (p < 0.05), whereas the precipitation recycling rate (1 − K) is decreasing. This indicates that although the activity of water circulation inside and outside the TPV decreases, the contribution of water vapour input outside the region to the precipitation of the TPV increases, and the contribution of evaporation to the precipitation of the region decreases.

Fig. 2
figure 2

Interannual variation in the hydrological cycle coefficient in the TPV region from 1979 to 2015

Full size image

The water vapour retention coefficient (τ) shows an upwards trend, while the water vapour utilization coefficient (J) shows a significant downwards trend (p < 0.05) (Fig. 2d and e), indicating that the TPV water cycle has become more inactive overall in the past 37 years. However, it is clear that the trend of each coefficient has a turning point in the late 1990s and early 2000s. The hydrological external circulation coefficient (KI) changed from + 0.09 times/a in 1979–2000 to − 0.16 times/a after 2000 (p < 0.05), and the hydrological external circulation coefficient (KE) changed from − 0.06/a to + 0.06/a (p < 0.05). The other coefficients also have positive and negative changes in the rate of change, and all have passed the 95% significance test. These results, combined with the results of the M–K mutation test, show that there is a mutation in each water cycle coefficient in the mid- or late 1990s, indicating that the TPV water cycle indeed changed significantly in this period. Although the overall activity of the TPV water cycle has been lower in the twenty-first century than in the last century, due to the intensification of climate change since 2000, the external water vapour input and evaporation in the TPV water cycle have developed increasing trends. The activity of the overall water cycle has increased significantly, and the time required for the formation of precipitation in TPV has shortened.

4 Spatial and temporal characteristics of TPV precipitation and its relationship with the TPV water cycle

As one of the important outputs of the TPV water cycle, TPV precipitation garners much attention. This paper separately analyses the spatial and temporal characteristics of TPV precipitation and its relationship with the TPV water cycle.

4.1 Average spatial distribution of precipitation in the TPV

The TPV datasets from 1979 to 2015 were matched with the precipitation data, and the spatial distribution of the average annual precipitation of the TPV was obtained by time averaging (Fig. 3). The TPV precipitation is mainly distributed between 25–35°N and 78–105°E, and the centre of the maximum value is mainly located in Shuanghu, Ando and Nagqu in the central part of the plateau; the maximum annual precipitation is 304.4 mm. On the whole, TPV precipitation has a decreasing distribution trend with a large value centre in the middle, and it protrudes to the east. By comparing and analysing the origin and track distribution of TPVs in previous studies (Lin 2015), it was found that the precipitation of TPVs is mainly distributed southeast of the vortex centre and TPV track. This is roughly the same as the precipitation distribution of the TPV analysed by predecessors using the station precipitation data (Quan et al. 2019), but the difference is that the precipitation value in this study is larger. The reason may be that this study selects precipitation reanalysis data, which makes up for the shortcoming of “more in the east and less in the west” of the plateau stations and better reflects the distribution pattern of plateau vortex precipitation.

Fig. 3
figure 3

Spatial distribution of the annual average precipitation of TPV from 1979 to 2015 (unit: mm)

Full size image

4.2 Trend analysis of TPV precipitation

To reveal the spatial and temporal changes in TPV precipitation, the spatial linear trend and regional average time series from 1979 to 2015 are calculated. The results are shown in Fig. 4. It can be seen that there are certain spatial differences in the changes in TPV precipitation (Fig. 4a). The TPV precipitation in most regions shows an upwards trend, especially in the large-value area in the middle of the plateau, which increases significantly; the maximum change rate is + 5.87 mm/a. The dotted area reaches a significance level of 0.05, indicating that the change trend of TPV precipitation becomes increasingly significant with time. The area of precipitation reduction is less, mainly distributed in the south of the plateau and the southern foothills of the Himalayas. Some scholars have pointed out that the water vapour budget of major water vapour channels, such as the Yarlung Zangbo River Valley, has decreased in recent years (Gao et al. 2020), which may explain the decrease in precipitation over the TPV in this region. Based on the analysis of the multiannual mean distribution of TPV precipitation (Fig. 3), the regions with large change rates are consistent with the large value regions of TPV precipitation, showing that the regions with more precipitation have relatively high climatic tendencies, indicating that the spatial change in TPV precipitation is very obvious.

Fig. 4
figure 4

Spatial distribution trend (unit: mm/a) (a) and regional average time series (b) of annual mean precipitation of TPV from 1979 to 2015. The dotted area is significant at α = 0.1

Full size image

From the perspective of interannual changes, the annual average precipitation of TPV has obvious fluctuations, of which the highest is 135.7 mm in 1999 and the lowest is 71.7 mm in 2009; it has shown an increasing trend over 37 years (Fig. 4b), with a change rate of 0.1 mm/a, which is basically consistent with previous research results (Quan et al. 2019). The precipitation of the plateau vortex has shown a fluctuating upwards trend since 1979. In addition, the M–K mutation test (figure omitted) is carried out on the time series in Fig. 4b, and the results show that there is no significant mutation point in the annual average TPV precipitation and thus no obvious mutation phenomenon in the TPV precipitation.

4.3 Analysis of the relationship between TPV precipitation and the TPV water cycle

As a part of the water cycle, TPV precipitation is inseparable from the TPV water cycle. To explore how the change in the TPV water cycle affects TPV precipitation, the correlation coefficients of the time series of the water cycle coefficients in Fig. 2 and the time series of TPV precipitation in Fig. 4b are calculated; the results are shown in Table 2. KI is negatively correlated with precipitation, r =  − 0.14, indicating that the greater the precipitation of TPV is, the shorter the precipitation times formed by external water vapour are. KE is significantly positively correlated with precipitation, r = 0.45, indicating that the greater the precipitation in TPV is, the more active the internal circulation is. The precipitation of TPV is negatively correlated with τ (r =  − 0.21) and significantly positively correlated with J (r = 0.57), indicating that the greater the precipitation of TPV is, the faster the water vapour in the air needs to be converted into precipitation, and the shorter the retention time of water vapour in the air, the higher the utilization coefficient of water vapour, the faster the water renewal speed, and vice versa. Since the water vapour utilization coefficient (J) can comprehensively represent the activity of the TPV water cycle, the spatial correlation between the time series of J and the precipitation distribution of TPV is calculated separately (Fig. 5). It is of clear physical significance to calculate the correlation between the time series of J and the annual precipitation of TPV in the same period. It can be seen that there is a significant positive correlation between J and the TPV annual precipitation outside the eastern boundary of the plateau. The higher the water vapour utilization efficiency, the greater the precipitation outside the main body, indicating that when the atmospheric water cycle of TPV is more active, the TPV is more likely to move out of the main body of the plateau and generates precipitation. On the other hand, there is a significant negative correlation between J and the TPV annual precipitation in the main body of the plateau. The lower the water vapour utilization efficiency is, the greater the precipitation in the main body is. This shows that the TPV is less likely to move when the TPV water cycle is not active, and precipitation is mainly generated in the main body of the plateau.

Table 2 Correlation coefficient between the TPV water cycle coefficient and TPV precipitation time series from 1979 to 2015 (** indicates that the t-test value reaches the significance level of 0.05)
Full size table
Fig. 5
figure 5

Correlations between the time series of the water vapour utilization coefficient of the TPV and the annual precipitation of the TPV from 1979 to 2015. The dotted area is significant at α = 0.05

Full size image

5 The relationship between the TPV water cycle and atmospheric circulation

The close relationship between TPV precipitation and its water cycle coefficient shows that precipitation is a key part of the TPV water cycle. To study the factors that may affect the TPV water cycle, the time series of TPV precipitation in Fig. 4b is used for standardization, and the years with a standardized series greater than 1 are taken as the active years of the TPV water cycle, resulting in 5 years in total: 1983, 1988, 1991, 1994 and 2014. The years less than − 1 are taken as the inactive years of the TPV water cycle, resulting in 7 years in total: 1982, 1986, 1989, 1992, 1997, 2001 and 2003. The possible reasons for the changes in the TPV water cycle are discussed through the synthetic analysis of atmospheric circulation.

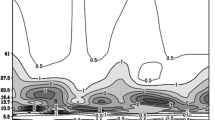
Figure 6 shows the distribution of the difference between the average wind field and the geopotential height field at 200, 500 and 850 hPa in the active and inactive years of the TPV water cycle. Figure 6a shows that there is an abnormal anticyclonic circulation over the Qinghai-Tibet Plateau at 200 hPa, and the potential height difference is positive; that is, the intensity of the South Asian high is stronger in the active years than in the inactive years; its position is north by east. The TPV is closer to the ridge of the South Asian high, and the intensity of the upper westerly jet is stronger. Combined with the analysis of the vertical profile difference of the wind field and temperature field in active and inactive years (Fig. 7), when the TPV water cycle is more active, the intensity of the South Asian high within the range of 10–35°N in the plateau is significantly stronger than that in inactive years and thus is conducive to strengthening the horizontal divergence of the high-level plateau. The vertical upwards movement over the main body of the plateau is significantly stronger, and the temperature is higher. Such a warm upwards region is conducive to the convergence of near-surface air flow, provides dynamic conditions for the occurrence and development of TPVs and is conducive to the active circulation of TPV water. Some predecessors also pointed out that when the South Asian high is stronger, it is conducive to the TPV moving eastward out of the plateau boundary (Yu and Gao 2008). Combined with the correlation between J and TPV precipitation in “Sect. 4.3”, it can be further proven that when the South Asian high is stronger, the water vapour utilization efficiency is higher, the TPV water cycle is more active, and the TPV more easily moves eastward and produces precipitation.

Fig. 6
figure 6

The composite difference distributions of a 200 hPa, b 500 hPa and c 850 hPa wind fields (vector, unit: m·s−1) and geopotential height fields (contour, unit: dagpm) based on active minus inactive TPV water cycle years. The areas passing the 0.05 significance level are shaded

Full size image
Fig. 7
figure 7

The composite meridional vertical profile difference distribution of wind (vector, horizontal wind: m·s−1, vertical motion: 10−2·Pa·s−1) and temperature (contour, unit: K) fields averaged along 70–105°E based on active minus inactive TPV water cycle years. The areas passing the 0.05 significance level are shaded

Full size image

From the perspective of 500 hPa in the middle troposphere (Fig. 6b), there is a significant cyclonic circulation north of the Qinghai-Tibet Plateau. The main body of the plateau is located in the low-pressure trough at the bottom of the cyclone. At the same time, there is a low-pressure cyclone in India, which makes it easier for tropical water vapour from the south of the plateau to enter the hinterland of the plateau. The intensity of the Western Pacific subtropical high is stronger, and its location is closer to China. The water vapour in the Western Pacific in the lower troposphere continues to be transported to China and converges to the hinterland of the plateau, which is conducive to the maintenance and eastward movement of the TPV. Combined with the spatial distribution of the 500 hPa divergence climate anomaly in active and inactive years (Fig. 8), the overall divergence of the main body of the plateau in active years is significantly weaker, that is, the convergence is stronger, which causes the TPV water cycle to be more active and is conducive to the generation of TPV precipitation. The inactive annual divergence is obviously stronger and thus not conducive to TPV occurrence and development or to an intense water cycle, resulting in the reduction of precipitation in the TPV.

Fig. 8
figure 8

Average anomaly distribution of 500 hPa divergence in active (a) and inactive (b) years of the TPV water cycle. Unit: × 10−6 s−1. The dotted area is significant at α = 0.1

Full size image

For 850 hPa in the lower troposphere (Fig. 6c), when the TPV water cycle is active, the anticyclone circulation in the Western Pacific is stronger, resulting in the southeast wind also being enhanced and transported to China. At the same time, there is a strong southerly air flow in the northern Arabian Sea, the southeast wind in the western Pacific converges on the southern side of the Qinghai-Tibet Plateau, and a large amount of water vapour is transported to the plateau. Combined with the analysis of the 850 hPa average water vapour transport difference between the active and inactive years of the TPV water cycle (Fig. 9), there is a significant positive anomaly area of water vapour flux from the northern Indian Ocean to the southern foothills of the Himalayas. The positive anomaly value of the water vapour flux from the Western Pacific to the southern part of China is also strong, which further explains why the strengthening of the southerly wind on the southern and southeastern sides of the plateau is conducive to the centralized transport of water vapour from the ocean to the plateau. Thus, the TPV water cycle becomes more active, providing sufficient water vapour conditions for TPV precipitation, which is conducive to the TPV water cycle.

Fig. 9
figure 9

The composite difference distributions of 850 hPa water vapour flux (g·s−1·hPa−1·cm.−1) based on active minus inactive TPV water cycle years. The dotted area is significant at α = 0.05

Full size image

In summary, the South Asian high with a stronger intensity has a northeastern location and the West Pacific subtropical high has a strong intensity and a western location; the two have an interactive trend of “approaching each other”, with better water vapour transmission conditions in the lower layer, thus enabling the TPV water cycle to more active, greater water vapour utilization efficiency and the TPV to more easily move out of the plateau and produce precipitation. In contrast, the South Asian high with a weaker intensity has a western location and the West Pacific subtropical high retreats to the ocean surface in the east; when the two tend to be “far away from each other”, and the low-level water vapour transmission conditions are insufficient, the TPV water cycle is not active, it does not easily move out of the plateau, and the precipitation is correspondingly less.

6 Summary and discussion

As an important disastrous weather system on the Qinghai-Tibet Plateau, the Tibetan Plateau Vortex (TPV) has distinct characteristics of atmospheric water cycle processes, which have a profound impact on the weather and climate of the plateau and the downstream areas. In this work, TPV datasets from 1979 to 2015 are selected, then the climatic characteristics of the TPV water cycle are studied via statistical analysis methods. Simultaneously, the differences between the atmospheric circulation in the active and inactive years of the TPV water cycle and its possible impact on the TPV water cycle are analysed, and the following conclusions are drawn:

  1. (1)

    In the TPV water cycle, precipitation is mainly caused by water vapour input outside the region, which accounts for 74% of the total precipitation, and the remaining 26% is caused by evaporation. The contribution of external circulation has increased, and the contribution of water circulation in the region has decreased. Overall, the water vapour utilization efficiency of the TPV water cycle first decreased and then increased, and the activity first decreased and then increased. Sudden changes occurred in the middle and late 1990s.

  2. (2)

    The precipitation of the TPV is mainly distributed in the middle and south of the plateau (25–35°N, 78–105°E), showing a decreasing distribution trend from the middle to the surroundings. The high value centre is mainly located in the Shuanghu, Ando and Nagqu areas in the middle of the plateau, with a maximum value of 304.4 mm. The annual precipitation shows an upwards trend of fluctuating changes, especially since the twenty-first century. Spatially, it shows a significant increasing trend in most areas of the plateau; there is a good correlation between TPV precipitation and the TPV water cycle. The more active the TPV water cycle is, the easier it moves eastward, and the more precipitation is generated outside the main body, and vice versa.

  3. (3)

    In the year of an active TPV water cycle, the intensity of the high-level South Asian high is stronger in the Qinghai-Tibet Plateau, the West Pacific subtropical high advances westward, and the two “approach each other”. There is a warm rising area over the main body of the plateau, with vigorous vertical movement. On the subtropical ocean surface, the low-level southerly airflow is strong, which shows a positive anomaly of water vapour flux; the circulation situation is opposite in the inactive years of the TPV water cycle.

Due to the complex topography of the underlying surface of the TPV area and many influencing factors, this paper only uses statistical methods to analyse the characteristics of the TPV water cycle and the relationship between the atmospheric circulation and the TPV water cycle, but these methods alone are not enough to prove that the anomaly of the atmospheric circulation causes the change in the TPV water cycle; in the future, we plan to conduct numerical simulations to further verify the role of atmospheric circulation and study the microscopic characteristic of water cycle inside the TPV. Furthermore, we will study how the enhanced evaporation caused by climate change specifically affects the atmospheric water cycle of TPV. In addition, it is worth mentioning that in recent years, the number of TPVs has decreased throughout the year, though the number of TPVs is increasing in summer. It is proposed that the enhancement or weakening of the water cycle is limited by small changes in the latent heat flux, and the change rate is less than that of water vapour (Held and Soden 2006; Richter and Xie 2008), which will increase the time that water vapour stays in the atmosphere. Therefore, the convective mass flux must be reduced, and the atmospheric circulation needs to be slowed down. Is this related to the decline in the overall number of TPVs? On the other hand, due to the influence of climate change, the surface wind speed, temperature, sensible latent heat and surface evaporation in the plateau have changed dramatically and suddenly to varying degrees. Are these changes related to the phenomenon of TPV concentration “approaching” in summer, and is this trend also affected by the transformation of TPV water cycle characteristics that has occurred since the start of the twenty-first century? These are topics worthy of further study.