Abstract
Air temperature inversions are common features in Antarctica, especially in the interior where they are observed nearly year-round. Large temporal variability of air temperature inversion incidence is typical for the coastal areas and little is known about its occurrence in the Antarctic deglaciated areas. Here we present a 12-year-long time series of near-surface air temperature inversion derived from two automatic weather stations situated at different altitudes (10 and 375 m a.s.l.) in ice-free part of northern James Ross Island (Antarctic Peninsula). The highest monthly relative frequency of temperature inversions during 2006–2017 was observed in July (38%) when the range between minimum and maximum monthly frequencies reached 34%. Both the lowest monthly relative frequency of temperature inversions and the range were found in December with values of 7% and 15%, respectively. The correlation between mean lapse rate and selected mesoscale flow characteristics were tested. The highest correlations were found between lapse rate and specific humidity for the yearly means (0.69 in the 925 hPa pressure level). Negative correlation coefficients were established between lapse rate and air temperature in summer (− 0.65 in the 500 hPa pressure level). Finally, we also used the Weather and Research Forecasting (WRF) model to ascertain its ability to simulate situations as complicated as near-surface air temperature inversion formation in complex terrain. For a strong winter air temperature inversion, simulated air temperature was compared with in situ observations to assess the model performance.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Polar boundary layer is often distinguished as one of the types of boundary layers due to its specific characteristics. Boundary layer in polar regions is almost permanently stable, because of the combination of the reflection of shorter wavelengths from the snow and ice at low sun angles and infrared radiation emitted from the surface (Anderson and Neff 2008). Further contributing factors are low absolute humidity of the atmosphere and frequent cloud-free conditions, enhancing the net loss of radiative energy from the surface. Since there is no diurnal cycle closer to the poles, the boundary layer is modified primarily by synoptic scale weather systems. Yet, the reaction of very stable boundary layer to surface forcing can be slower than an hour used by Stull (1988) for the definition boundary layer (Anderson and Neff 2008). Low temperatures in polar regions lead to the substantial coupling between the atmosphere and different cryospheric parts, for instance, sea ice, snow or permafrost (Esau and Sorokina 2010). As a result of this coupling, an atmospheric response is generated on different scales, from teleconnections in the atmospheric circulation patterns (Adachi and Yukimoto 2006) to near-surface inversions.
Temperature inversions in the polar regions are of special importance for climate since due to their strong vertical stability the depth of vertical mixing of sensible and latent heat is limited (Serreze and Barry 2005; Vihma et al. 2009). On the other hand, they also reduce further infrared cooling of the layers below the inversion (Bintanja et al. 2011; Pithan and Mauritsen 2014). Stable boundary layers are still rather poorly understood, even though progress in observations and modelling of polar boundary layers are required to improve numerical models and raise certainty of climate predictions.
There are different types of air temperature inversions in polar regions. The air temperature inversions close to the surface are often a result from a near-surface cooling, which can lead to an inversion strength of 35 K (e.g. Pietroni et al. 2014). Near-surface air temperature inversions of this kind occur in East Antarctica close to 100% of the time in winter (Zhang et al. 2011). Nearby to the Antarctic coasts and over the ice-covered sea, air temperature inversion close to the surface can be formed due to warm air advection, either when the ground surface is much colder or in combination with blocking (King et al. 2008). Stable boundary layer can be formed over larger areas or can further intensify in anticyclonic conditions due to subsidence (Schwerdtfeger 1970; Baas et al. 2019). Nygård et al. (2017) showed that both cold-air advection and long-wave radiative cooling can contribute to development and strengthening of surface-based inversion layer in Dronning Maud Land (Antarctica).
The knowledge on air temperature inversions in deglaciated areas is important, as they can influence active layer degradation (Zhang et al. 1997), glacier melt (Mernild and Liston 2010) or availability of liquid water for living organisms. The air temperature inversion frequency in the Arctic can be over 80% year-round even in the deglaciated areas (Wang et al. 2021); however, the seasonal variation in frequency shows remarkable spatial variability (Ambrožová and Láska 2017; Wang et al. 2021). The occurrence of air temperature inversions in deglaciated areas of Antarctica is not well-examined. Near-surface air temperature inversions on the eastern side of the Antarctic Peninsula (AP) can have a relative frequency of 61% even in summer and can occur up to 10 times more often than on the western side (Rau 2004). Ambrozova et al. (2019) suggested that near-surface lapse rates as well as the air temperature inversion relative frequency can differ from year to year; yet, the interannual variability of air temperature inversions occurrence in AP Region has not been properly investigated. Kejna (2008) related summer air temperature inversions on King George Island with fog occurrence and differences in incoming solar radiation. In a case study from northern JRI, Ambrozova et al. (2019) suggested that winter air temperature inversions can be connected to cold-air pool formation.
Here we aim to contribute to a better understanding of the conditions of near-surface air temperature inversions (TI) formation in the AP Region and how they are represented in the Weather and Research Forecasting (WRF) model, a numerical weather prediction model. In the first part of the results, we examine the climatology of TI on James Ross Island (JRI) with an emphasis on interannual variability. In the second part, we determine how mesoscale atmospheric conditions were connected to TI occurrence in the area. The third part contains a simulation of one of the strongest observed TI on JRI.
2 Methods
2.1 Study area
JRI is situated in the north-western Weddell Sea near the tip of the AP (Fig. 1). The observations come from the Ulu Peninsula, which is an ice-free region with the area of 312 km2 (Kavan et al. 2017) in the northern part of the island. Apart from the southwest, the Ulu Peninsula is surrounded by the sea, which has usually been ice-free from December to March. The Prince Gustav Channel separates JRI from the AP, lying approx. 14 km away. The mountain range of the AP causes significant blocking of air masses from the west and lead to recurrent barrier winds (King et al. 2013). The advected cold air can be subject to channelling in the Prince Gustav Channel and affect lower-lying areas more than the higher-elevated sites and free atmosphere. On the other hand, the eastern side of the AP where JRI is located is occasionally affected by strong foehn winds leading to significant low-level warming. Foehn occurrence could dramatically change the surface energy balance and lead to rapid melting of snow or ice (Kuipers Munneke et al. 2018). At Cabinet Inlet (66°24′S) on the Larsen C ice shelf, 45% of total surface melt happened under foehn conditions despite they lasted only 15% of time (Elvidge et al. 2020).
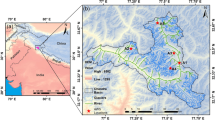
Regional map showing the northern part of the Antarctic Peninsula Region and the nested domain set-up used for the WRF model simulations (left): the 6.3 km domain (d01), the 2.1 km domain (d02) and the 0.7 km domain (d03). The location of the two automatic weather stations used in this study (Bibby and Mendel) inside domain d03 (right). The topography is based on Norwegian Polar Institute’s Quantarctica package (Matsuoka et al. 2018)
The Ulu Peninsula is partly covered by ice domes and valley glaciers; however, near the observation sites the land cover is mostly bare soil and sedimentary rocks. The mean annual air temperature (2013–2016) in the Ulu Peninsula ranges between − 6.3 °C at the sea level and below − 7.5 °C in the higher elevated regions (Ambrozova et al. 2019). The northern coast of the Ulu Peninsula is surrounded by mesas, from where snow is frequently blown away and cold air slides down the steep slopes towards the coast.
Continuous snow cover on the Ulu Peninsula usually occurs from the second half of March until the second half of September (Hrbacek et al. 2016), but the distribution of snow cover is greatly affected by the prevailing south to south-westerly winds (Kavan et al. 2020). Mean sea ice fraction around JRI was 0.12 in austral summer and 0.33 in austral winter (Ambrozova et al. 2019) with a usual sea ice break-up around 17 December (Ambrožová et al. 2020).
2.2 Observations and statistical analysis
Air temperature data were measured at two sites. The first, Mendel, is situated at 10 m a.s.l. on a Holocene marine terrace approx. 100 m to the south-east from the Johann Gregor Mendel Station (Fig. 1). The nearest seashore is located 150 m to the north. The second site, Bibby, is located at an altitude of 375 m a.s.l. about 2 km to the west of the Johann Gregor Mendel Station (Fig. 2). Close to the measurement site, the topography falls very steeply towards the sea in the north and west.
a Local map showing the northern part of the Ulu Peninsula with the two automatic weather stations used in this study (Bibby and Mendel). The topography is based on map by Czech Geological Survey (2009). b Meteorological mast at Mendel site. c Automatic weather station at Bibby site
The instruments were installed at a height of 2 m above the ground and the sensors are kept in naturally ventilated radiation shields. The air temperature was measured with a Minikin TH air temperature and humidity sensor (EMS Brno, Czech Republic) with an accuracy of ± 0.15 K. The sensors were calibrated before installation and every summer in a standard laboratory calibration procedure (EMS Brno) by comparison with a reference instrument. Both sites have nearly continuous measurements for the period 2006–2017 with a time resolution of 1 h. Due to instruments failure, 0.9% of observations at Mendel and 0.6% of observations at Bibby have been filled in by regression analysis with data from the nearest automatic weather station. For Mendel, the closest measurement site is situated on the slope of Berry Hill 2.2 km to the east with altitude higher by 46 m. Similarly, for Bibby, the closest measurement site lies on the Johnson Mesa 2 km to the south-east and its altitude is just 35 m lower. Ambrozova et al. (2019) showed that the mean differences between the time series at Mendel and Berry Hill and at Bibby and Johnson Mesa during 2013–2016 were 0.4 K and 0.3 K, respectively. We have found the correlation coefficients between the hourly values (Mendel vs. Berry Hill and Bibby vs. Johnson Mesa) in this period to be > 0.98.
Near-surface lapse rate (Γ) was calculated as the hourly air temperature difference between Mendel and Bibby divided by the difference in their altitudes and multiplied by 100 to get the Γ in K·100 m−1. TI was defined as hourly Γ < 0 K·100 m−1. Similar definitions of Γ and TI were used by Ambrozova et al. (2019) for the possibility of comparison with other studies from the AP Region. The Γ would deviate from lapse rate in the free atmosphere as air temperature at 375 m close to a surface would be warmed by the surface in summer and cooled in winter. Moreover, we are aware that using the temperature difference at two levels might have led to underestimation of TI frequency.
For the purpose of examining if TI characteristics would be different for the TI that lasted extremely long or when the Γ reached extremely low values for JRI, TI episode was defined. TI episode represents 1 or more hours long period, during which Γ ≤ 0 K·100 m−1 without interruption. Therefore, an TI episode was defined as the strongest TI episode if the minimum Γ occurring anytime during the TI episode duration was within the first decile of hourly Γ measured on JRI during 2006–2017 (− 2.28 K·100 m−1 and less). Correspondingly, an TI episode belonged to the category of the longest TIs if its length (represented by the number of hours) was above the ninth decile of lengths measured on JRI (more than 16 h).
Basic descriptive statistics such as mean and standard deviation were calculated in order to study the interannual variability of Γ and TI episodes. Moreover, Spearman’s rank correlation (McClave and Dietrich 1991) was used to analyse the relationship between Γ and the influence of mesoscale atmospheric circulation described by a set of variables (specified further in the paragraph). The relationship was considered significant when the p-value for the correlation coefficient was below the significance level of 0.05. To study the influence of mesoscale atmospheric circulation, the following variables were extracted from ERA5 Reanalysis (Copernicus Climate Change Service 2017): geopotential height (geop), air temperature (temp), vertical velocity (vert) and wind speed (ws). The data come from three pressure levels (925 hPa, 850 hPa and 500 hPa) and were averaged over the area of approx. 0.6 × 0.6° around JRI.
2.3 WRF simulations
For the simulations, we used the WRF Model, version 3.9.1.1 (Skamarock et al. 2008) with 3 one-way nested domains at 6.3, 2.1 and 0.7 km horizontal resolution (Fig. 1a). The domains were centred over the Ulu Peninsula (63.9° S, 58.0° W) and had 281 × 221, 241 × 241 and 148 × 157 grid points for the domains d01, d02 and d03, respectively. In the vertical direction, 73 eta levels were used with 9 eta levels (including one at the surface) having their base-state altitude within the lowermost 100 m. For the land surface model (LSM) in WRF, the Noah multi-physics LSM (Niu et al. 2011) was used, while for cloud microphysics the Thompson et al. scheme (Thompson et al. 2004) was applied. The longwave and shortwave radiation fluxes were calculated using the scheme from the Rapid Radiative Transfer Model for GCM Applications (RRTMG; Iacono et al. 2008). The planetary boundary layer (PBL) is simulated with the QNSE PBL scheme (Sukoriansky et al. 2005b), which was designated for stable boundary layers (Sukoriansky et al. 2005a) and was found suitable for simulating air temperature under stable boundary layer conditions (Claremar et al. 2012; Tastula et al. 2015; Láska et al. 2017). Moreover, the eddy diffusivity mass flux option was turned on. Cumulus cloud schemes were turned off in all three domains due to the chosen fine resolution of the model.
The lateral boundary conditions were derived from ERA5 with about 0.28° resolution (Copernicus Climate Change Service 2017). The simulation ran between 13 and 26 August 2013; however, the first two days were discarded as a spin-up period. Due to the complex topography, the Reference Elevation Model of Antarctica (REMA; Howat et al. 2019) was used for surface elevation, while the Antarctic sea ice concentration dataset derived from Advanced Microwave Scanning Radiometer (AMSR2) by the University of Bremen (Spreen et al. 2008; Melsheimer and Spreen 2019) was utilised for sea ice, as good sea ice data are assumed to be crucial for appropriate air temperature representation in the models in Western Antarctica (Deb et al. 2016). The basis for the land cover dataset were the map of the Czech Geological Survey (2009) and the shapefiles of Rock outcrop-medium resolutions, Rock outcrop-high resolution from Landsat 8 and Coastline–high resolution polygons from the Antarctic Digital Database (British Antarctic Survey 2016).
3 Results
3.1 Occurrence of air temperature inversions
Relative frequency of TI on JRI was derived from Γ (Fig. 3) between Mendel and Bibby (Fig. 2). Mean winter Γ was − 0.07 K·100 m−1, compared with 0.38 K·100 m−1 in spring, 0.63 K·100 m−1 in summer and 0.34 K·100 m−1 in autumn. The standard deviation in winter (0.39 K·100 m−1) was, on the other hand, by 0.26 K·100 m−1 larger than in summer. The lowest mean monthly Γ was observed in July 2008, when the value dropped down to − 1.42 K·100 m−1. Other months with mean monthly Γ below − 0.5 K·100 m−1 were August 2009, June 2014, July 2015 or May 2016. In summer, unusually low Γ (below 0.5 K·100 m−1) were observed in January and February 2006, January and December 2007, February 2013 and January 2015.
The monthly histograms of hourly Γ (Fig. 4) revealed the absence of Γ < − 3.5 K·100 m−1 from November to March. Furthermore, the relative frequency of the interval from 0.5 to 1 K·100 m−1 decreased from 61% in March and April to 44% in August. The annual cycle in Γ, apparent from Figs. 3 and 4, is well reflected in the annual cycle of relative frequency of air temperature inversions (Fig. 5). The median of the relative frequency was the highest in July (38%), August (33%) and May (29%). Interestingly, a drop of relative frequency down to 23% is typical between May and June. High relative frequency of air temperature inversions can be attributed to prevailing long-wave radiation loss from snow and ice-covered coastal areas during winter period with almost no daylight.
The median of the relative frequency was only 7% in December, 8% in January and 7% in February, which agrees well with the increase of Γ in summer (Fig. 3). Increase of the amount of incoming shortwave radiation in summer leading to positive thermal balance and enhanced air mixing explains a decrease of air temperature inversion frequency in summer. The highest range of 34% was observed in July, the lowest in December (15%). The highest monthly relative frequency was observed in July 2015 and May 2016, when the frequency reached 53%. In both cases Γ was very low, however, it was by 0.23 K·100 m−1 lower in July 2015 than in May 2016 (Fig. 3). On the other hand, for July 2008, when the lowest mean monthly Γ was measured, the relative frequency was 50%, suggesting that the Γ in TI in July 2008 must have reached lower values than in July 2015 or May 2016. Consequently, it is clear that the values of mean monthly Γ correspond well to relative frequency of TI, yet in some cases stronger but shorter inversions occur. In December, the month with the lowest median of relative frequency, the highest monthly relative frequency of 17% occurred in the year 2007.
3.2 Longest and strongest air temperature inversions
While short TI (Γ ≤ 0 K·100 m−1 for just 1–2 h) can be caused by random microscale phenomena such as turbulence, longer air temperature inversion would more likely be connected to mesoscale atmospheric circulation. To reveal the origin and main features of TI, the longest and strongest TI were studied over the period 2006–2017.
In July, 19% of the longest TI was observed and it even reached 22% for the strongest TI (Fig. 6). Out of those TI, 15% were both the longest and the strongest. From May until September, the relative frequency of the strongest TI exceeded 15%, apart from June, when it only reached 14%. None of the strongest TI was observed in December. The longest TI were spread more equally throughout the year with relative frequencies of at least 2% in each month. The relative frequency of both the longest and the strongest TI was the lowest in 2010 when it was only 5 and 6%, respectively. While 11% of the strongest TI were observed in 2007 and 2014, 10% of the longest TI occurred in 2011 and 2013.
3.3 Mesoscale atmospheric influence on air temperature inversions
The relationships between Γ and variables indicating influence of mesoscale atmospheric circulation were mostly statistically significant (p = 0.05) on a yearly basis (Table 1). The strongest and most consistent relationships were found with specific humidity (q) which had Spearman’s rank correlation coefficients of 0.64, 0.66 and 0.69 for pressure levels 500 hPa, 850 hPa and 925 hPa, respectively. Interestingly, the relationships between Γ and specific humidity were positive between autumn and spring, while they were negative in summer and only statistically significant in the pressure level of 500 hPa. It can be expected that water vapour in the air masses absorbed outgoing longwave radiation, lost by the ground surface. That would lessen the thermal loss of the boundary-layer in the coastal area and increase the Γ. Similar behaviour was observed for air temperature (temp). On a yearly basis, the correlation coefficients varied between 0.43 and 0.55 in the three levels, yet they were between − 0.58 and − 0.65 in summer and mostly insignificant in the rest of the year. Considering the strength of the relationships, it seems that air temperature has the largest influence on Γ in summer, while during the rest of the year, specific humidity is more important.
The geopotential height (geop) had the Spearman’s rank correlation coefficients with Γ mostly negative (Table 1). For the 850 and 925 hPa levels, the values were − 0.27 and − 0.36, respectively, on an annual basis and they were even lower (between − 0.37 and − 0.49) between autumn and spring. For summer, the only statistically significant relationship of Γ was with geopotential height at the 500 hPa pressure level, when it was − 0.55. The correlation coefficients between Γ and wind speed (ws) were between − 0.25 and − 0.38 (all statistically significant) for the whole year, yet statistically significant negative relationships were ascertained only in summer for the 500 hPa pressure level and in spring for the 925 hPa pressure level. On the other hand, wind speed was also connected to Γ in winter, when the correlation coefficients at the 850 hPa and 925 hPa pressure levels was 0.50 and 0.48, respectively (both statistically significant). Finally, there was also a relationship found in winter between Γ and vertical velocity (vert) at all three levels. However, the Spearman’s rank correlation coefficients were 0.40 and 0.37 for the 925 hPa and 850 hPa pressure levels, yet it was − 0.34 for the 500 hPa pressure level. In order to link the relationships presented in Table 1 with specific atmospheric circulation around the AP Region, the horizontal fields of selected variables are presented for the winter and summer month with the highest measured monthly relative frequency of TI. The variables (geopotential height at 500 hPa level and geopotential height, air temperature and wind vectors at 925 hPa level) were mostly chosen due to their relatively strong relationships with Γ either in winter, or in summer (Table 1). In July 2015, the mean monthly pressure field at the 500 hPa pressure level resembled a nearly zonal transition from higher pressure over mid-latitudes towards lower pressure over Antarctica (Fig. 7a). At the 925 hPa level, the mean monthly pressure field indicated an area of lower pressure both in the southern Weddell Sea and the south-western Bellingshausen Sea, while over the AP and JRI there was a noticeable high-pressure ridge. The wind was south-westerly at 925 hPa pressure level with a speed up to 6 m s−1 on the northern coast of JRI (Fig. 7b), lower than on the western side of the AP at the same latitude. That was likely due to a combination of blocking of westerlies from the other side of the AP and barrier wind blowing from the south along the AP towards JRI. The air temperature at 925 hPa level was between 260 and 262 K over JRI, showing the influence of the south-westerly wind.
In December 2007, the mean monthly fields of geopotential height at 500 hPa and 925 hPa pressure levels (Fig. 8a) appeared similar to those in July 2015. At the 500 hPa level, a zonal circulation with a weak high-pressure ridge was located over the northern part of the AP. The high-pressure ridge was even clearer at 925 hPa, complemented by areas of lower pressure over both the eastern Bellingshausen Sea and the north-western Weddell Sea. The mean wind speed at 925 hPa over JRI (Fig. 8b) was also below 6 m s−1 with a prevailing wind direction from the west. Finally, the mean monthly air temperature over JRI was between 270 and 272 K, which is fairly high considering that the highest mean monthly air temperature at this level over JRI during 2006–2017 was 272.9 K.
3.4 Air temperature inversion simulation with WRF
In “The whole simulation” subsection, the simulation as a whole is analysed. Subsections “The high wind episode” and “The air temperature inversion episode” contain detailed description of two episodes of the simulation: 19–21 August with a high near-surface wind speed and 22–25 August, when TI was observed over northern JRI. These two distinguished periods were chosen to evaluate model performance under different meteorological conditions.
3.4.1 The whole simulation
The simulation spans between 15 and 25 August 2013 (Fig. 9). At the beginning, the air temperature on the coast of JRI was gradually decreasing from 255 to 249 K at 1200 UTC on 23 August, when it started increasing up to 278 K at 0300 UTC on 25 August. The mean air temperature at the coastal station Mendel was 256.9 K (Table 2) for the whole simulation period. At Bibby, located at a 350 m a higher altitude, it was, with 249.8 K, 3.3 K colder, indicating an on average close to dry adiabatic temperature gradient. The mean bias in air temperature was 5.2 K for Mendel, but only 1.9 K for Bibby. Correspondingly, the Spearman’s rank correlation coefficient was 0.94 for Bibby, but by 0.33 lower for the Mendel site. Observed mean Γ between Mendel and Bibby was − 0.34 K·100 m−1 with a bias of 0.92 K·100 m−1 and a Spearman’s rank correlation coefficient of 0.74. The mean wind speed, measured at Mendel, was 8.6 m s−1 and the mean bias was − 0.4 m s−1.
Observed and simulated variability of air temperature (a), lapse rates (b), wind speed (c) and wind direction (d) for James Ross Island during 15–25 August 2013. Simulation sea-ice indicates a lapse rate between Mendel SI and Bibby. The dark-shaded rectangle highlights the high wind episode, the light-shaded rectangle highlights the air temperature inversion episode.
3.4.2 The high wind episode
Between 19 and the end of 21 August, mean wind speed reached 16.8 m s−1 with a maximum of 24.1 m s−1 at 1800 UTC on 20 August. The wind direction was also mostly from south-south-west with westerly wind just before 0000 UTC on 19 August and around midnight on 22 August. Air temperature both at Mendel and Bibby was decreasing more steeply than before 19 August (Fig. 8b) and the Γ was between 0.45 and 1.13 K·100 m−1. However, the Γ rose concurrently with the wind speed increase during the first 9 h and then varied above 0.9 K·100 m−1 until 1200 UTC 21 August, synchronously with the period of the highest wind speeds. The Spearman’s rank correlation coefficient between the model and the observed lapse rate was only 0.09 due to very stable values with only slight and unpredictable fluctuations.
For Bibby site, there was a warm bias of 2.8 K (Table 2). The difference between the model and the observations were between 1.4 and 4.5 K, but the model mostly followed the general decrease of air temperature (Spearman’s rank correlation coefficient 0.76). The warm bias was the same for air temperature at Mendel (Table 2), but the differences between the model and the observations were between − 0.5 and 5.6 K. Moreover, the model air temperature developed slightly different (Fig. 9a), as the Spearman’s rank correlation coefficient of 0.34 indicates. The mean wind speed in the simulation was also 2.5 m s−1 lower than observed.
3.4.3 The air temperature inversion episode
On 22 August at 0300 UTC, the modelled air temperature at Mendel decreased to 249.4 K which led to a drop of the Γ to − 0.16 K·100 m−1. While the observed air temperature at Bibby site started increasing at 0900 UTC and the rise continued until 1500 UTC on 24 August, the observed air temperature at Mendel did not start increasing before 1200 UTC on 23 August. Consequently, the difference in observed air temperature between Mendel and Bibby reached − 21.3 K at 1200 UTC on 24 August, generating a Γ of − 5.93 K·100 m−1. In contrast, the Γ from the simulation stayed very close to 0 K·100 m−1. The observed TI continued until 0300 UTC on 25 August, when air temperature at Mendel finally rose to 278.1 K. The mean wind speed between 22 and 25 August was only 2.9 m s−1 with a variable wind direction (Fig. 9d).
The air temperature development at Bibby was caught extremely well, with a cold bias of only − 0.3 K and the Spearman’s rank correlation coefficient of 0.93 (Table 2). The model temperatures for Mendel were very closely following the ones for Bibby (the largest difference of air temperature between Mendel and Bibby was only − 3.5 K) and did not show the observed delay by ca. 30 h in the start of the temperature increase. This led to a mean bias of 8.9 K between model and observations at Mendel. As the simulated Γ mostly varied between ± 0.98 K·100 m−1, the TI was simulated only for short periods (1–3 h). Spearman’s rank correlation coefficient for the lapse rate was actually higher during 22–25 August (0.65) than during the high-wind speed period.
Since the TI was captured so poorly at the coast, it was inquired if it would be more pronounced in the model more over the sea ice, 4.2 km north of Mendel inside the Prince Gustav Channel (point “Mendel SI”). The mean bias between modelled air temperature at point Mendel SI (Fig. 1) and observed air temperature at Mendel during 22–25 August was 4.6 K and also the mean bias in Γ between Bibby and the point on the sea ice was only 1.36 K·100 m−1. It is clear from Fig. 8a that the TI with the sea ice point had almost the same length as in observations (just started 1 h later). The Γ bias for the 22 August and 24 August was even 1.07 K·100 m−1, as the modelled Γ followed variation of the observation fairly well. In the middle of the TI, intensive warming over the sea ice was simulated after 0000 UTC 23 August, which was not only too strong, but also earlier than observed at the Mendel site.
4 Discussion
In this study, 12 years observations on TI from an ice-free area on JRI are presented. The seasonal and interannual variability of both Γ and TI on JRI was larger in winter than in summer. The annual cycle of TI relative frequency showed an increase from summer to winter, apart from May, which had higher monthly mean frequency than June. The yearly mean Γ showed statistically significant positive correlation with specific humidity and air temperature for the 925 hPa level. In a case study of TI in WRF from August 2013, no TI was actually simulated between Mendel and Bibby. The error in modelled air temperature was partly attributed to the specific surface conditions, as there was an TI simulated between Bibby and a sea-ice covered point situated north of Mendel.
The wintertime relative frequency of TI at the Neumayer station (Ekström Ice Shelf in Queen Maud Land, 2200 km from JRI) was more than twice the relative frequency observed by us at JRI. Over western Weddell Sea, autumn to winter relative frequency of TI even reached 96% (Andreas et al. 2000). Furthermore, in summer the frequency at the Neumayer Station (Zhang et al. 2011) was more than 4 times higher than at JRI. The much lower relative frequency in this study can be partly explained by different surface conditions, since the Neumayer station is situated on an ice shelf and the Weddell Sea south of JRI had a sea ice index over 50% during the study by Andreas et al. (2000). Accordingly, the difference in relative frequency would be lower in winter, when there was snow cover on JRI and the surrounding Prince Gustav Channel was ice-covered.
Another important factor influencing the relative frequency was the use of radio sounding in other studies, which enables better vertical resolution. Nygård et al. (2017) used tethersondes over Aboa (Queen Maud Land) to study summertime TI and mostly detected several thin inversion layers with a vertical extension of less than 100 m. Consequently, it is likely that in our observations from 8 to 375 m a.s.l., we actually detected the base of one inversion layer and the top of another one above the surface-based TI. However, as the primary aim of this study was to reveal interannual variability, the length of the study period had a priority.
The increases of interannual variability of Γ and the TI relative frequencies on JRI in winter are in agreement with radio sounding from Dome C station (Tomasi et al. 2012), where an increase of both seasonal and interannual variability of Γ in TI was reported during March-October. Even though the TI development depends considerably on micro and mesoscale processes, the relationships between the mesoscale atmospheric circulation indices and Γ can partly explain the interannual variability. From the Spearman rank correlation coefficients between yearly Γs, air temperature and specific humidity (in all three levels) it might be assumed that during the years with lower Γs, leading to higher TI relative frequency, the air masses over JRI were colder and drier than on average. However, looking at individual seasons showed a more complicated feature. In summer, warmer air masses were actually connected to lower Γs, consistently with the 925 hPa air temperature field from December 2007, and cold air masses associated with higher Γs. Therefore, it might be assumed that in years with less TI in summer, cold air mass advection over warm ice-free areas promoted more frequent convection. From autumn to spring, however, negative correlations between Γ and the geopotential heights at 850 and 925 hPa, respectively, suggested the tendency of low-level high-pressure areas to support TI formation. That was confirmed by the 925 hPa pressure field from July 2015 (Fig. 7a). Conversely, an approach of a winter cyclone would increase horizontal wind speed and lead to turbulent mixing and Γ increase, as the positive relationships between Γ and wind speed and vertical velocity at 850 and 925 hPa, respectively, indicated. The positive relationships between Γ and specific humidity (at all three levels) between autumn and spring, might suggest that sufficient moisture in air masses could be an indicative of cloud cover present in the atmosphere, which might have turned the net radiative flux at the surface positive and thus prevented TI formation (Nygård et al. 2017). However, as even the highest correlation coefficients only reached 0.6–0.7, the explained interannual variability of TI relative frequency on JRI was less than 50%.
The unexplained variability in both seasonal and interannual Γ can be attributed to microscale phenomena, especially surface thermal balance. Negative radiation and thermal balance are typical features in polar regions (Van den Broeke et al. 2004) and in the northern AP Region mean net radiation is negative from April to September (Soares et al. 2019). As the snow or ice-covered surface cools via long-wave radiation loss, it also cools the above-lying air layers, which are consequently colder than the higher layers (e.g. King and Turner 1997). Even though the air temperature measurement in the higher air layer in this study comes from automatic weather station, the terrain around Bibby Hill falls steeply and so it would not be as affected by the surrounding ground as Mendel.
A decrease in TI frequency was observed in June on JRI in comparison with May and July (Fig. 5), yet not in all the observed years. Pietroni et al. (2014) have also noticed weakening of surface-based TI (below 205 m) in June over Dome C and attributed it to frequent warming events (Astapenko 1964). Warming events cannot be the factor over JRI, as their occurrence in June during 2006–2017 was not higher than in May or July. Nor were relationships found between inversion relative frequency and the sea ice fraction around JRI, the Southern Annular Mode or the El Niño-Southern Oscillation, in the period May to July. Due to the statistically significant difference in mean May wind speed at 925 hPa between the years when the relative frequency of TI was lower in June than in May and July (anomaly years: 2007, 2010, 2011, 2012, 2015, 2016) and the rest of the years, the mean geopotential field around the AP was compared for May and June for these two sets of years (Fig. 10). The mean 925 hPa field around the AP both in June with the anomaly (Fig. 10a) and without the anomaly (Fig. 10b) was characterised by a low-pressure band elongated in east–west direction. From the difference field (Fig. 10c), however, it is clear that during years with the anomaly the geopotential height above the northern part of the AP was by more than 30 m lower than without the anomaly. In other words, there was a stronger or more frequent cyclonic influence in the north-western Weddell Sea, resulting in more intensive flow of warmer air mass from south-west towards JRI, higher wind speed and thus enhanced turbulent mixing destroying the TI. There is no obvious difference between the mean 925 hPa fields for May with the anomaly (Fig. 10d) and without the anomaly (Fig. 10e), but the difference map (Fig. 10f) reveals that during the years with the anomaly, the geopotential height just to the west of the AP was by more than 50 m higher than without the anomaly. That could indicate that the warm westerly airflow towards JRI was likely less intensive with a less deep or frequent cyclone in the Bellingshausen Sea, yielding the space to high-pressure ridges, which frequently occur in the AP Region in winter (Ambrožová et al. 2020).
The mean geopotential height of the 925 hPa pressure level (m) in the AP Region for June in the anomaly years, when TI relative frequency was lower than in May and July (a) (2007, 2010, 2011, 2012, 2015, 2016), for the rest of the years (b) 2006, 2008, 2009, 2013, 2014, 2017) and the resulting difference field (c). The mean geopotential height of the 925 hPa pressure level (m) in the AP Region for May in the anomaly years, when TI relative frequency in June was lower than in May and July (d), for the rest of the years (e) and the resulting difference field (f)
The air temperature bias in the WRF simulation in this study was comparable to July simulations from the coast of Pine Island Bay (Deb et al. 2016). In their case, however, air temperature was underestimated by − 2.8 (312 m a.s.l.) to − 4.5 K (188 m a.s.l.). The air temperature was also overestimated by 0.5–1.6 K over Larsen Ice Shelf in May (Turton et al. 2017). The much lower bias can be attributed to the flatness of the ice shelf. The lower bias at the higher-elevated Bibby site confirms the significance of spatial heterogeneity on the model performance, which even the 700-m horizontal resolution was not able to overcome.
During the high-wind speed event, the mean bias in air temperature was the same, both at Bibby and Mendel. Since the wind speed was underestimated by 2.5 m s−1, it is likely that less turbulent mixing with the cold air mass advected from the south, took place in the model performance. Interestingly, due to the identical overestimation of air temperature both at Bibby and Mendel sites, the mean bias in Γ was only − 0.02 K. Nevertheless, the random fluctuations due to small-scale eddies passing could hardly have been resolved, which explains the Spearman rank correlation coefficient close to zero.
While the model performance during the TI episode improved significantly with respect to air temperature at Bibby, it was nearly three times worse for Mendel. The good model performance at the higher-elevated site indicates that synoptic situation was likely well-represented in the model which suggests also a good quality of the forcing ERA5 reanalysis. However, the resolution of the model grid was not sufficient to contain an indication of TI over the complex topography of JRI. In series of model simulations from the western Weddell Sea, Tastula and Vihma (2011) found that the model slightly overestimated the TI frequency (depending on a PBL scheme). However, when a PBL scheme with higher (and closer to observations) sea-ice concentration was used, lower-than-observed TI frequency was simulated over western Weddell Sea. Consequently, their results do not support the hypothesis that insufficient snow or sea-ice cover affected the boundary layer stratification during JRI simulations.
It is, therefore, more likely that small scale terrain features not represented in the model were behind the differences between simulated and observed air temperature at Mendel during the TI episode. The terrain on the north-eastern coast of JRI is very heterogenous, as for instance the Bibby site is located on an edge of a steep cliff falling directly into the Prince Gustav Channel. Such sharp topographic differences could not have been captured even with horizontal resolution of 700 m, which would especially impact the wind field. Consequently, the positive wind speed bias likely led to too much turbulent mixing in the stable boundary layer (Bromwich et al. 2013). According to NCEP reanalysis, high-pressure ridge from the north prevailed over the northern tip of the AP during 22–25 August 2013, leading to south-westerly wind. The air temperature increase at Bibby was likely connected to foehn phenomena on the eastern side of the AP (Elvidge et al. 2015), whose proper representation in areas with complex topography requires higher model resolution (Turton et al. 2017). The delay of warming observed at Mendel compared with Bibby (Fig. 9) indicates potential channelling effects between the AP and JRI, which blocked the air flow from the south of Mendel (Fig. 1).
It is also possible that the ability of the numerical schemes in the model to capture the observed boundary layer stratification and sharp near-surface temperature gradients was strongly reduced in the grid resolution of 700 m. This possible effect is also supported by better model performance over the sea ice further from the elevations around Mendel.
5 Conclusions
In this study, we analysed the seasonal and interannual variability of air temperature inversions (TI) on James Ross Island (JRI) during 2006–2017. Furthermore, the influence of the mesoscale-atmospheric circulation on the lapse rate (Γ) on JRI was investigated and a 10-day-long winter simulation from JRI is presented. The main findings were the following:
-
Both the seasonal and interannual variability of Γ and TI on JRI was larger in winter than in summer. The standard deviation of hourly Γ was 0.39 K·100 m−1 in winter and 0.13 K·100 m−1 in summer, while the range of monthly TI relative frequency reached 34% in July and just 15% in December.
-
The annual cycle of TI frequency resembled a smooth increase from summer to winter, apart from June, when the monthly mean frequency was lower than in May. Analysis of the 925 hPa geopotential height field revealed more cyclonic conditions in the north-eastern AP Region during those months of June when a drop in TI relative frequency occurred.
-
The yearly mean Γ showed statistically positive correlation with specific humidity and air temperature with the highest Spearman’s rank correlation coefficients for the 925 hPa level (0.69 for specific humidity and 0.55 for air temperature). The monthly mean Γ was negatively correlated with air temperature (highest correlation coefficient − 0.65 at 500 hPa level) in summer, and it was negatively correlated with geopotential height during the rest of the year (highest correlation coefficient of − 0.49 for the 925 hPa level in spring). All correlations mentioned in this paragraph were statistically significant.
-
In the simulation from August 2013, the mean bias of air temperature at the higher-elevated site (Bibby) was 2.8 K during the high-wind speed episode and 2.5 K lower during the simulated TI. The mean bias of the air temperature at the site situated on the coastal site was the same as at Bibby during the high-wind speed episode, but it was by 6.1 K higher during the TI, and no TI was actually simulated. The error in air temperature was partly attributed to limited spatial resolution in the model in combination with local complex topography, as there was TI simulated between Bibby and a sea-ice covered grid point situated in the Prince Gustav Channel 4.2 km off the coast line.
Data availability
Data are available upon reasonable request.
Code availability
Code is available upon reasonable request.
References
Adachi Y, Yukimoto S (2006) Influence of sea ice thickness on the atmosphere in the winter Arctic region in an atmospheric general circulation model. SOLA 2:76–79. https://doi.org/10.1002/joc.5832
Anderson PS, Neff WD (2008) Boundary layer physics over snow and ice. Atmos Chem Phys 8(13):3563–3582. https://doi.org/10.5194/acp-8-3563-2008
Ambrožová K, Láska K (2017) Air temperature variability in the vertical profile over the coastal area of Petuniabukta, central Spitsbergen. Pol Polar Res 38(1):41–60. https://doi.org/10.1515/popore-2017-0004
Ambrozova K, Laska K, Hrbacek F, Kavan J, Ondruch J (2019) Air temperature and lapse rate variation in the ice-free and glaciated areas of northern JRI, Antarctic Peninsula, during 2013–2016. Int J Climatol 38(2):643–657. https://doi.org/10.1002/joc.5832
Ambrožová K, Láska K, Kavan J (2020) Multi-year assessment of atmospheric circulation and impacts on air temperature variation on James Ross Island, Antarctic Peninsula. Int J Climatol 40(3):1526–1541. https://doi.org/10.1002/joc.6285
Andreas EL, Claffey KJ, Mahshtas AP (2000) Low-level atmospheric jets and inversions over the western Weddell Sea. Boun- Lay Meteorol 97(3):459–486. https://doi.org/10.1023/A:1002793831076
Astapenko PD (1964) Atmospheric process in the high latitudes of the Southern Hemisphere. Israel Program for Scientific Translations, Jerusalem
Baas P, Van de Wiel BJH, Van Meijgaard E, Vignon E, Genthon C, Van der Linden SJA, De Roode SR (2019) Transitions in the wintertime near-surface temperature inversion at Dome C. Antarctica Q J R Meteorol Soc 145(720):930–946. https://doi.org/10.1002/qj.3450
Bintanja R, Graversen RG, Hazeleger W (2011) Arctic winter warming amplified by the thermal inversion and consequent low infrared cooling to space. Nat Geosci 4(11):758–761. https://doi.org/10.1038/ngeo1285
British Antarctic Survey (2016) British Antarctic Survey geodata portal: Antarctic Digital Database. https://add.data.bas.ac.uk/repository/entry/show?entryid=f477219b-9121-44d6-afa6-d8552762dc45. Accessed 30 June 2019
Bromwich DH, Otieno FO, Hines KM, Manning KW, Shilo E (2013) Comprehensive evaluation of polar weather research and forecasting model performance in the Antarctic. J Geophys Res Atmos 118:274–279. https://doi.org/10.1029/2012JD018139
Claremar B, Obleitner F, Reijmer C, Pohjola V, Waxegård A, Karner F, Rutgersson A (2012) Applying a mesoscale atmospheric model to Svalbard glaciers. Adv Meteorol, 321649. https://doi.org/10.1155/2012/321649
Copernicus Climate Change Service (2017) ERA5: Fifth generation of ECMWF atmospheric reanalyses of the global climate. Copernicus Climate Change Service Climate Data Store (CDS). https://cds.climate.copernicus.eu/cdsapp#!/home. Accessed 25 May 2019
Czech Geological Survey (2009) JRI—northern part. In: Topographic Map 1: 25 000, 1st edition. Czech Geological Survey, Prague
Deb P, Orr A, Scott Hosking J, Phillips T, Turner J, Bannister D, Pope JO, Colwell S (2016) An assessment of the Polar Weather Research and Forecasting (WRF) model representation of near-surface meteorological variables over West Antarctica. Geophys Res Atmos 121(4):1532–1548. https://doi.org/10.1002/2015JD024037
Elvidge DE, Kuipers Munneke P, King JC, Renfrew IA, Gilbert E (2020) Atmospheric drivers of melt on Larsen C ice shelf: surface energy budget regimes and the impact of foehn. J Geophys Res Atmos 125(17):1–25. https://doi.org/10.1029/2020JD032463
Elvidge AD, Renfrew IA, King JC, Orr A, Lachlan-Cope T, Weeks M, Gray S (2015) Foehn jets over the Larsen C ice shelf, Antarctica. Q J R Meteorol Soc 141:698–713. https://doi.org/10.1002/qj.2382
Esau I, Sorokina S (2010) Climatology of the Arctic planetary boundary layer In: Lang, PR, Lombargo, FS (eds) atmospheric turbulence, meteorological modeling and aerodynamics. Nova Science Publishers Inc, New York
Howat I, Morin P, Porter C, Noh M-J (2019) The reference elevation model of Antarctica. Cryosphere 13:665–674. https://doi.org/10.5194/tc-13-665-2019
Hrbacek F, Laska K, Engel Z (2016) Effect of snow cover on the active-layer thermal regime—a case study from JRI, Antarctic Peninsula. Permafrost Periglac 27:307–315. https://doi.org/10.1002/ppp.1871
Iacono MJ, Delamere JS, Mlawer EJ, Shephard MW, Clough SA, Collins WD (2008) Radiative forcing by longlived greenhouse gases: calculations with the AER radiative transfer models. J Geophys Res 113:D13103. https://doi.org/10.1029/2008JD009944
Kavan J, Nývlt D, Láska K, Engel Z, Kňažková M (2020) High-latitude dust deposition in snow on the glaciers of James Ross Island. Antarctica Earth Surf Proc Land 45(7):1569–1578. https://doi.org/10.1002/esp.4831
Kavan J, Ondruch J, Nyvlt D, Hrbacek F, Carrivick JL, Laska K (2017) Seasonal hydrological and suspended sediment transport dynamics in proglacial streams, JRI. Antarctica Geogr Ann A 99(1):38–55. https://doi.org/10.1080/04353676.2016.1257914
Kejna M (2008) Topoclimatic conditions in the vicinity of the Arctowski Station (King George Island, Antarctica) during the summer season of 2006/2007. Pol Polar Res 29(2):95–116
King JC, Lachlan-Cope TA, Ladkin RS, Weiss A (2008) Airborne measurements in the stable boundary layer over the Larsen Ice Shelf, Antarctica. Bou-Lay Meteorol 127(413). https://doi.org/10.1007/s10546-008-9271-4
King JC, Turner J (1997) Antarctic Meteorology and Climatology. Cambridge University Press, Cambridge
King JC, Turner J, Marshall GJ, Connolley WM, Lachlan-Cope TA (2013) Antarctic Peninsula climate variability and its causes as revealed by analysis of instrumental records. In: Domack EW, Burnett A, Leventer A, Conley P, Kirby M, Bindschadler R (eds) Antarctic Peninsula climate variability: a historical and paleoenvironmental perspective. American Geophysical Union, Washington, DC
Kuipers Munneke P, Luckman AJ, Bevan SL, Smeets CJPP, Gilbert E, Van den Broeke MR, Wang W, Zender C, Hubbard B, Ashmore D, Orr A, King JC, Kulessa B (2018) Intense winter surface melt on an Antarctic Ice Shelf. Geophys Res Lett 45(15):1–9. https://doi.org/10.1029/2018GL077899
Láska K, Chládová Z, Hošek J (2017) High-resolution numerical simulation of summer wind field comparing WRF boundary-layer parametrizations over complex Arctic topography: case study from central Spitsbergen. Meteorol Z 26(4):391–408. https://doi.org/10.1127/metz/2017/0796
Matsuoka K, Skoglund A, Roth G (2018) Quantarctica, Norwegian Polar Institute. https://doi.org/10.21334/npolar.2018.8516e9,1. Accessed 1 Aug 2020
McClave JT, Dietrich FH (1991) Statistics. Dellon, San Francisco
Melsheimer C, Spreen G (2019) AMSR2 ASI sea ice concentration data, Antarctic, version 5.4 (NetCDF) (July 2012 - December 2018) PANGAEA. https://doi.org/10.1594/PANGAEA.898400. Accessed 15 July 2019
Mernild SH, Liston GE (2010) The influence of air temperature inversions on snowmelt and glacier mass balance simulations, Ammassalik Island, Southeast Greenland. J Appl Meteorol Climatol 49:47–67. https://doi.org/10.1175/2009JAMC2065.1
Niu G-Y, Yang Z-L, Mitchell KE, Chen F, Ek MB, Barlage M, Kumar A, Manning K, Niyogi D, Rosero E, Tewari M, Xia Y (2011) The community Noah land surface model with multiparameterization options (Noah-MP): 1. Model description and evaluation with local-scale measurements. Geophys Res Atmos 116(12):12109. https://doi.org/10.1029/2010JD015139
Nygård T, Tisler P, Vihma T, Pirazzini R, Palo T, Kouznetsov R (2017) Properties and temporal variability of summertime temperature inversions over Dronning Maud Land, Antarctica. Q J R Meteorol Soc 143:582–595. https://doi.org/10.1002/qj.2951
Pietroni I, Argentini S, Petenko I (2014) One year of surface-based temperature inversions at Dome C, Antarctica. Bou-Lay Meteorol 150:131–151. https://doi.org/10.1007/s10546-013-9861-7
Pithan F, Mauritsen T (2014) Arctic amplification dominated by temperature feedbacks in contemporary climate models. Nat Geosci 7(2014):181–184. https://doi.org/10.1038/ngeo2071
Rau F (2004) Schneeeigenschaften und Gletscherzonen der Antarktischen Halbinsel im Radarbild: thermische Phänomene der Schnee- und Firndecken im Hinterland der großen Schelfeisabbrüche. Dissertation, University of Freiburg
Schwerdtfeger W (1970) Die Temperaturinversion über dem antarktischen Plateau und die Struktur ihres Windfeldes (The temperature inversion over the Antarctic Plateau and the structure of its windfield). Meteorol R 23:164–171
Serreze MC, Barry RG (2005) The Arctic climate system. Cambridge University Press, Cambridge
Spreen G, Kaleschke L, Heygster G (2008) Sea ice remote sensing using AMSR-E 89 GHz channels. J Geophys Res Oceans 113:C02S03. https://doi.org/10.1029/2005JC003384
Skamarock WC, Klemp JB, Dudhia J, Gill DO, Barker DM, Huang X-Y, Wang W, Powers JG (2008) NCAR TECHNICAL NOTE: A description of the advanced research WRF Version 3. 125
Soares J, Alves M, Dutra Ribeiro FN, Codato G (2019) Surface radiation balance and weather conditions on a non-glaciated coastal area in the Antarctic region. Polar Sci 20(2):117–128. https://doi.org/10.1016/j.polar.2019.04.001
Sukoriansky S, Galperin B, Perov V (2005a) Application of a new spectral theory of stably stratified turbulence to the atmospheric boundary layer over sea ice. Bou- Lay Meteorol 117(2):231–257. https://doi.org/10.1007/s10546-004-6848-4
Sukoriansky S, Galperin B, Staroselsky I (2005b) A quasinormal scale elimination model of turbulent flows with stable stratification. Phys Fluids 17(8):1–28. https://doi.org/10.1063/1.2009010
Stull RB (1988) An introduction to boundary layer meteorology. Kluwer Academic Publishers, Dordrecht
Tastula E-M, Galperin B, Dudhia J, Lemone MA, Sukoriansky S, Vihma T (2015) Methodical assessment of the differences between the QNSE and MYJ PBL schemes for stable conditions. Q J R Meteorol Soc 141(691):2077–2089. https://doi.org/10.1002/qj.2503
Tastula E-M, Vihma T (2011) WRF model experiments on the Antarctic atmosphere in winter. Mon Weather Rev 139(4):1279–1291. https://doi.org/10.1175/2010MWR3478.1
Thompson G, Rasmussen RM, Manning K (2004) Explicit forecasts of winter precipitation using an improved bulk microphysics scheme. Part I: description and sensitivity analysis. Mon Weather Rev 132(2): 519–542. https://doi.org/10.1175/1520-0493(2004)132<0519:EFOWPU>2.0.CO;2
Tomasi C, Petkov BH, Benedetti E (2012) Annual cycles of pressure, temperature, absolute humidity and precipitable water from the radiosoundings performed at Dome C, Antarctica, over the 2005–2009 period. Antarct Sci 24(6):637–658. https://doi.org/10.1017/S0954102012000405
Van den Broeke M, Reijmer C, van den Wal, R (2004) Surface radiation balance in Antarctica as measured with automatic weather stations. J Geophys Res, 109(D09103). https://doi.org/10.1029/2003JD004394
Vihma T, Johansson, MM, Launiainen J (2009) Radiative and turbulent surface heat fluxes over sea ice in the western Weddell Sea in early summer, J Geophys Res, 114(C4). https://doi.org/10.1029/2008JC004995
Wang D, Guo J, Xu H, Li J, Lv Y, Solanki R, Guo X, Han Y, Chen T, Ding M, Chen A, Bian L, Rikne A (2021) Vertical structures of temperature inversions and clouds derived from high-resolution radiosonde measurements at Ny-Ålesund. Svalbard Atm Res 254(2021):105530. https://doi.org/10.1016/j.atmosres.2021.105530
Zhang T, Osterkamp TE, Stamnes K (1997) Effects of climate on the active layer and permafrost on the North Slope of Alaska, U.S.A. Permafrost Periglac 8:45–67. https://doi.org/10.1002/(SICI)1099-1530(199701)8:1%3c45::AID-PPP240%3e3.0.CO;2-K
Zhang Y, Seidel D, Golaz J-C, Deser C, Tomas RA (2011) Climatological characteristics of Arctic and Antarctic surface-based inversions. J Clim 24(19):5167–5168. https://doi.org/10.1175/2011JCLI4004.1
Acknowledgements
The authors are grateful to members of the Czech summer expeditions 2004–2018 to James Ross Island for their field assistance and service of meteorological stations on James Ross Island. Long-term support of EMS Brno (Czech Republic) and sharing the knowledge on instrumentation and measuring devices is very much appreciated. This study was supported by Erasmus + Europe: Staff Mobility for Training within Key Activity 1 (KA 103), the Czech Science Foundation project (GA20-20240S) and the Czech Polar Research Infrastructure project (LM2015078) funded by the Ministry of Education, Youth and Sports of the Czech Republic. Access to the CERIT-SC computing and storage facilities provided by the CERIT-SC Center, under the programme “Projects of Large Research, Development, and Innovations Infrastructures” (CERIT Scientific Cloud LM2015085) and to the UNINETT Sigma2 within the project NN9506K (Investigating the Atmospheric Boundary Layer with LES) is greatly appreciated.
Funding
Open access funding provided by University of Bergen (incl Haukeland University Hospital). Erasmus + Europe: Staff Mobility for Training within Key Activity 1 (KA 103).
Czech Science Foundation project (GA20-20240S).
Czech Polar Research Infrastructure project (LM2015078).
MUNI/A/1356/2019.
ECOPOLARIS project (CZ.02.1.01/0.0/0.0/16_013/0001708).
Projects of Large Research, Development, and Innovations Infrastructures (CERIT Scientific Cloud LM2015085).
NN9506K (Investigating the Atmospheric Boundary Layer with LES).
Author information
Authors and Affiliations
Contributions
KA: Writing-original draft, data curation, formal analysis; KL: conceptualization, supervision, writing-review and editing; MM: methodology, software, writing-review and editing; JR: conceptualization, supervision, writing-review and editing.
Corresponding author
Ethics declarations
Ethics approval
Not applicable.
Consent to participate
Not applicable.
Consent for publication
Not applicable.
Conflict of interest
The authors declare no competing interest.
Additional information
Publisher's note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Ambrožová, K., Láska, K., Matějka, M. et al. Interannual variability of air temperature inversions in ice-free area of northern James Ross Island, Antarctica. Theor Appl Climatol 148, 967–983 (2022). https://doi.org/10.1007/s00704-021-03912-6
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00704-021-03912-6