1 Introduction

The net radiation flux is the most important for land surface energy transformations, such as sensible heat, soil heat flux, and evapotranspiration (ET). It is an important quantity for research into land–atmosphere interactions (Blad et al. 1998; Monteith 1965; Niemelä et al. 2001; Nishida et al. 2003; Priestley and Taylor 1972; Rosenberg et al. 1983; Su 2002; Zeng et al. 2015; Zhao et al. 2018), and it is, therefore, important to parameterize net radiation flux appropriately for hydrology and climate modeling studies (Bisht et al. 2005; Ryu et al. 2008). Net radiation is usually measured at specific locations using net radiometers, but it is difficult to generalize from these point measurements to other locations because the net radiation varies spatially and is strongly influenced by the characteristics of the surface over which it is measured, particularly if the surface is highly heterogeneous (Blad et al. 1998; Chen et al. 2013). Moreover, in many countries, instruments suitable for making direct measurements over a reasonable spatial range are often not available, or are inaccurate, because of technical and financial constraints (Kjærsgaard et al. 2007; Sozzi et al. 1999; Washington et al. 2004).

Alternative methods of estimating net radiation have recently been proposed, using input datasets from radiation modeling and combining field measurements with remote sensing data (Amatya et al. 2015a; Wang et al. 2005). Numerous studies have estimated the instantaneous net radiation flux from data collected by different satellite sensors, including moderate resolution imaging spectroradiometer (MODIS) (Bisht et al. 2005; Cai et al. 2007; Feng and Wang 2017; Hwang et al. 2013; Jia et al. 2013; Peng et al. 2019; Ryu et al. 2008; Slater 2016). However, most of these studies have been limited to flat areas and lack consideration of topography effects. Downward shortwave radiation varies spatially over large and heterogeneous topography, and estimations of radiation that neglect topographic effects can be inaccurate as variations in altitude, slope, orientation (aspect), and shadows cast by topographic features create strong local gradients in solar radiation (Tovar-Pescador et al. 2006; Wang et al. 2005). Many researchers have proposed models that take into account topographic effects (Chen et al. 2013; Dozier 1980; Dubayah 1992; Duguay 1995; Flint and Childs 1987; Gratton et al. 1993; Kumar et al. Pro 1997; Long et al. 2010; Proy et al. 1989) and solar radiation extinction processes (Gueymard 2003a, b; Leckner 1978; Yang et al. 2001; Yang and Koike 2005; Yang et al. 2006) and have used these to estimate net radiation fluxes in mountainous areas. More recently, Chen et al. (2013) have developed a topographically enhanced surface energy balance system (TESEBS) model that combines the effects of topography and solar radiation extinction processes in the atmosphere and have used this to estimate the net radiation flux over the complex topography of Mt. Qomolangma (Everest) areas in China. Amatya et al. (2015a) and Han et al. (2016) have used the TESEBS model to estimate the net radiation flux distribution, and other land surface heat fluxes, on the southern side of the central Himalayas in Nepal and in the Mt. Qomolangma region over the Tibetan Plateau, respectively. The TESEBS model includes atmospheric attenuation and topographic effects while estimating downward shortwave radiation, and so is an important advance for mountainous areas where solar radiation measurements from meteorological stations are totally absent, or are insufficient for reliable spatial interpolation. However, surface radiation calculated by the TESEBS model cannot be as accurate or reliable as direct measurements of radiation made by weather stations distributed evenly over the area of interest.

The Upper Blue Nile (UBN) River in Northwestern Ethiopia is one of the two major tributaries of the Nile River. ET is a major mechanism for surface water loss and accounts over 90% of the annual precipitation in the dry lowland areas of the river basin (Alemu et al. 2014; Glenn et al. 2007; Kurc and Small 2004; Molden et al. 2007; Morillas et al. 2013; Sun et al. 2019; Wilcox et al. 2003). Even in the wettest parts of the Ethiopian Plateau regions, ET accounts for around 70% of the basin water balance (NBI 2014). The strength of ET primarily depends on the local energy balance, and most ET estimation methods require the net radiation as an input variable. Hydrologists and water resource managers focused on the UBN basin should therefore implement the latest state-of-the-art methods for estimating the net radiation estimation flux. For this reason, several attempts have been made to estimate ET in the UBN basin, but these have not fully addressed the spatial and temporal variability of the flux, and validation of the calculated ET and net radiation through comparison with ground truth measurements was incomplete in most of the studies (Abreham 2009; Anderson et al. 2011; Enku 2009; Gieske et al. 2008; Mohamed et al. 2005; Senay et al. 2009; Yilmaz et al. 2014).

The main objective of this study is to estimate and characterize the instantaneous net radiation flux distribution in the UBN River basin using Automatic weather stations (AWS) and MODIS data and considering topographic effects. AWS data are recorded and stored automatically and are then transmitted from the stations to a data receiver system via a telemetry system (Ahmad et al. 2017; Sharan 2014; Słownik 1992). Since meteorological data from AWS are recorded and transferred automatically, they are less erroneous than data from conventional stations and have many applications in hydrological studies. The UBN River basin is very important in terms of economic development, and so the Ethiopian government is expanding the AWS network across the basin to enhance the quality of meteorological data available to hydrological studies (Sabatini 2017; Shanko 2015). We hypothesize that the use of AWS data and consideration of topographic effects will result in estimates of net radiation that are more robust than any previous estimates for this part of Africa.

2 Materials and methods

2.1 Study area

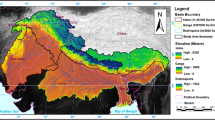
The UBN River basin is located in Northwestern Ethiopia between latitudes 7°40′ and 12°51′ N and between longitudes 34°25′ and 39°49′ E (Fig. 1a and b). It drains through large parts of the Central and Southwestern Ethiopian Highlands, the Central Ethiopian Plateau, Lake Tana, and the western arid lowlands of the country. The river has cut a deep and circuitous course. The gorge is 1 km deep in some places and flows around 900 km from Lake Tana before leaving Ethiopia and crossing into the vast plains of Sudan (Conway 1997). The basin has a total drainage area of 199,912 km2 (Yilma and Awulachew 2009) and comprises the following two topographically distinct areas: the central and eastern parts of the basin are rugged mountainous areas and the western parts are lowlands. Altitude varies significantly across the basin, from below 500 m above sea level in the lowlands to greater than 4000 m a.s.l. in the mountains (Fig. 1b).

Fig. 1
figure 1

(a) Location of Nile River Basin with its riparian countries and two major tributaries (WN, White Nile; BN, Blue Nile). Green-shaded portion of the figure is Nile River watershed, the red dashed rectangle is the study area (Upper Blue Nile). (b) Elevation (m) map of the study area delineated by the black-lined shape file, automatic weather station (AWS) distributions (black up-pointing triangle), and location of eddy covariance (EC) tower (+); (c) picture of installed EC instrument and its surrounding area

Full size image

The climate of the UBN River basin is mainly tropical and is strongly influenced by the movement of air masses associated with the Inter-Tropical Convergence Zone (ITCZ) (Conway 2000; Mohamed et al. 2005). During the months of November to March, dry continental air masses flow over the Ethiopian Highlands from the Northeast. From March to May, the ITCZ brings a small amount of rainfall, known locally as “Belg,” to the northeastern part of the basin, while the rest part of the basin is dry. From June to October, the southwestern air stream extends over the entire basin, bringing the rainy season. Both temperature and precipitation vary significantly with altitude in the basin. Lowland areas are warmer and drier than highland areas (Abtew et al. 2009; Conway 2005; Zeleke et al. 2013), and the mean maximum and minimum temperatures both vary seasonally, although the range is not as great as in the high latitude regions.

Land cover also varies in the UBN River basin. Woodland and shrub cover large parts of the basin (~ 28%), followed by sedentary rain-fed cropping, which covers nearly 26% of the basin, mainly in the highlands areas, and includes different crop types, such as Eragrosist (Teff), barley, and wheat. Grasslands cover around 25% of the basin and are concentrated along the main river course and tributary rivers, and shrubs and bushes cover the remaining 21%. This latter land cover type is mainly located along the river gorges and in the vast western parts of the basin (ENTRO 2007; Lemann et al. 2019; Medhin 2011; Roth et al. 2018).

2.2 Input datasets

2.2.1 Meteorological forcing data

We used in situ meteorological AWS data (air temperature, global radiation, and relative humidity) from the National Meteorological Agency database for Ethiopia (Shanko 2015). Data measured at 2 m height were selected for times coincident with satellite overpass times. We chose to use AWS data because they provide a continuous times series and so can be matched to instantaneous remote sensing measurements.

Surface pressure is usually recorded at meteorological stations and is important for estimating net radiation (Yang et al. 2006); however, surface pressure data were not included in our AWS datasets and so instead it is estimated from the relationship between sea level pressure (p0) and elevation. As elevation in our study area varies from 420 m to higher than 4200 m (Fig. 1b), the estimated surface pressure also varies significantly. The surface pressure is estimated from ps = p0 exp(− Z/H), following Chen et al. (2013) and others, where p0 = 101,325 Pa, and H = 8430 m is scale height, and Z is altitude (in m), read for each location from a digital elevation model (DEM) of the study area. Data were initially taken from 56 AWSs located in the basin and its immediate vicinity, but after vigorous quality control checks for internal consistency and technical sensor problems, based on procedures in Estévez et al. (2011) and WMO (2007, 2017), stations with spurious data and inaccurate measurements were excluded and data from 43 stations were retained for our study. To convert meteorological station data into surface data, appropriate spatial interpolation techniques were implemented for each data type as briefly discussed in Section 2.

2.2.2 Remote sensing data

MODIS multispectral sensors on board the National Aerodynamic and Space Administration’s (NASA) Earth Observation System (EOS) Terra and Aqua satellites have continuously monitored the Earth’s land, atmosphere, and ocean since December 1999 and May 2002, respectively (Amatya et al. 2015b). In this study, we used MODIS products from the Terra satellite as an input to the TESEBS model. MODIS observations are recorded in 36 wide spectral bands that cover the solar reflectivity and thermal emissivity regions of the spectrum (Xiong et al. 2009). These data have been used to improve our understanding of global dynamics and of processes occurring on land, in the oceans, and in the lower atmosphere (Masuoka et al. 1998; Rosenberg et al. 1983). MODIS data provide a consistent and wide range of simultaneous measurements for the land surface, biosphere, and atmosphere, including skin temperature, land cover, and the normalized difference vegetation index (NDVI) (Jin and Dickinson 2010; Jin and Mullens 2012). Analyzing these variables is useful for research into land surface–biosphere–atmosphere interactions, such as the work presented here. We used surface reflectance from bands 1 to 7 at a spatial resolution of 500 m from the land product MOD09GA. Land surface temperature (LST) with a spatial resolution of 1 km was taken from the land product MOD11A1 (Table 1). The surface reflectance data were resampled to 1 km resolution for consistency with the LST data so that both datasets could be used as model inputs. We selected cloud-free MODIS scenes over the study area; however, MODIS data are strongly susceptible to cloud contamination over tropical Africa (Hansen et al. 2008; Roy et al. 2006). This study was carried out during the precipitous period that precedes the main rainy season, when boundary layer atmospheric processes may enhance local cloud formations over the south and southwestern parts of the study area. This meant that cloud-free Terra satellite scenes were only available for 11 dates (Table 2). Land surface parameters, such as albedo, emissivity, fractional vegetation cover, and NDVI, were calculated using the equations presented in Section 2.

Table 1. MODIS products used in this study
Full size table
Table 2. MODIS data dates with their respective acquisition local times (year, 2019).
Full size table

2.2.3 Digital elevation model

Shuttle Radar Topography Mission (SRTM) digital elevation model (DEM) data with a spatial resolution of 1 arc-second were obtained from the United States Geological Survey (USGS) website (http://earthexplorer.usgs.gov/). This dataset has a spatial resolution of 30 m and was resampled to 1 km grid. The coordinate system and map projection used for the DEM are WGS-1984-UTM-Zone 37N. The DEM allows us to include the effects of topography (elevation, slope, and aspect) in our estimates of the spatial distributions for air temperature and for the downward shortwave radiative flux.

2.3 Theory and scheme

The net radiation flux is the algebraic sum of all radiative energy fluxes that leave, or are incident upon, a given surface. In this study, we used equations from the TESEBS model to parameterize the upward shortwave, upward longwave, and downward longwave components of the net radiation flux. The downward shortwave component of the flux, SWd, was read from the spatially interpolated AWS data. For a detailed description of the parameterizations in the TESEBS model, we refer the reader to Chen et al. (2013) and Han et al. (2016). In this work, we used only the equations needed to parameterize the stated fluxes. The net radiation flux can be estimated at various spatial scales using different approaches. Detailed ground observations or high-resolution satellite data, for example, from Landsat (e.g. Chen et al. 2013), can be used to estimate the net radiation flux at the micro- and meso-scales. Our aim was to estimate the regional net radiation flux at a basin level, using the MODIS data products and AWS data as described subsequently.

The net radiation flux (Rn) can be obtained from Eq. (1)

$$ {\displaystyle \begin{array}{l}{R}_{\mathrm{n}}\left(\mathrm{x},\mathrm{y}\right)= SWd\left(\mathrm{x},\mathrm{y}\right)- SWu\left(\mathrm{x},\mathrm{y}\right)+ LWd\left(\mathrm{x},\mathrm{y}\right)- LWu\left(\mathrm{x},\mathrm{y}\right)\\ {}{R}_n\left(\mathrm{x},\mathrm{y}\right)=\left(1-{\mathrm{r}}_0\left(\mathrm{x},\mathrm{y}\right)\right)\ S\mathrm{Wd}\left(\mathrm{x},\mathrm{y}\right)+ LWd\left(\mathrm{x},\mathrm{y}\right)-\updelta {\upvarepsilon}_0\left(\mathrm{x},\mathrm{y}\right) LST\ {\left(\mathrm{x},\mathrm{y}\right)}^4\ \end{array}} $$
(1)

where SWd and SWu are the incoming and outgoing shortwave radiation fluxes and LWd and LWu are the incoming and outgoing longwave radiation fluxes, respectively. r0 is the surface albedo, calculated from the narrow band spectral value (e.g. Liang 2001); LST is the surface temperature (K) that may be derived differently to the method used to retrieve it from the satellite data; ε0 is the surface emissivity, which can be estimated from NDVI or from the fractional vegetation cover using the model described in Valor and Caselles (1996); and δ is the Stefan-Boltzmann constant (= 5.676 × 10−8 W m−2 k4).

Over homogeneous terrain, surface meteorological variables can be easily estimated from point weather station data, using either inverse distance or ordinary kriging interpolation techniques. However, these techniques provide less reliable estimates over more complex topography and/or more heterogeneous land surfaces (Alsamamra et al. 2009; Daly et al. 2002; Marquínez et al. 2003). The topography in the UBN River basin is rugged and varies considerably in altitude (Melesse et al. 2014; Jury 2011). Variations in the topography (elevation, slope, and aspect) can influence the accuracy of interpolated surface meteorological variables when either inverse distance or ordinary kriging methods are applied. To overcome this, there is a need for new procedures to be proposed that include topographical information in the interpolation procedure. Various studies state that the residual kriging (RK) procedure is the easiest and most appropriate technique (e.g., Eldeiry and Garcia 2009; Prudhomme and Reed 1999). RK is a spatial interpolation technique that combines regression of the dependent variable on the explanatory variables (in this case, elevation, aspect, and slope) with kriging for the regression residuals (Pebesma 2006). As solar radiation and air temperature vary across heterogeneous terrain, we use RK when we convert the AWS solar radiation and air temperature point location data to spatially distributed surface data. Details of the procedures we followed for this are discussed in Sections 2.3.1 and 2.3.2. An overview of the general concepts governing our method for estimating the net radiation flux is presented in Fig. 2.

Fig. 2
figure 2

Flow chart showing the details of data processing and net radiation flux estimation procedures

Full size image

2.3.1 Air temperature (T air) and vapor pressure (e a)

Air temperature was taken from a limited number of AWSs, and so the data represent the temperature at specific point locations and may not be representative of the wider study area (Li and Heap 2011; Ninyerola et al. 2000). We therefore interpolated our air temperature dataset from point-scale measurements to the regional scale using appropriate methods (Liu et al. 2016). Our study area is mountainous and air temperature changes with elevation, so we implemented an interpolation that considers the effects of elevation on air temperature (Dodson and Marks 1997). Since LST largely controls the air temperature spatial distribution, it is also possible to obtain air temperature at regional scales from LST, as has been demonstrated in various studies (Colombi et al. 2007; Flores and Lillo 2010; Gallo et al. 2011; Hachem et al. 2012; Hadria et al. 2018; Shen and Leptoukh 2011; Sun et al. 2005; Vancutsem et al. 2010; Tadesse et al. 2015). We postulated that using both LST and elevation to estimate air temperature would increase the accuracy of the estimated air temperature spatial distribution. We applied residual kriging (RK) to estimate the surface air temperature from LST and elevation following the process described subsequently:

  1. 1.

    Let the AWS air temperature be denoted by Tair(x, y), where (x, y) is the position of each AW station. The elevation and LST for each AWS location were extracted from the DEM and from the MODIS LST, respectively. The extracted point values were treated as explanatory variables, and robust fitting was carried out between Tair(x, y), elevation, and LST using Eqs. (2a) and (2b).

$$ {T}_{\mathrm{a}\mathrm{ir}}\left(\mathrm{x},\mathrm{y}\right)={T_{\mathrm{a}\mathrm{ir}}}^{\ast}\left(\mathrm{x},\mathrm{y}\right)+\mathrm{r}\left(\mathrm{x},\mathrm{y}\right)=\sum \left({\upbeta}_{\mathrm{i}}{\mathrm{a}}_{\mathrm{i}}\left(\mathrm{x},\mathrm{y}\right)\right)+\mathrm{r}\left(\mathrm{x},\mathrm{y}\right) $$
(2a)
$$ {T}_{air}\left(\mathrm{x},\mathrm{y}\right)\kern0.75em ={\upbeta}_0+{\upbeta}_1\mathrm{elevation}\left(\mathrm{x},\mathrm{y}\right)+{\upbeta}_2 LST\left(\mathrm{x},\mathrm{y}\right)+r\left(\mathrm{x},\mathrm{y}\right) $$
(2b)

where βi = β0, β1, and β2 are the constant and coefficients for the robust regression; ai(x, y) is the elevation and LST at an AWS location; and r(x, y) is the residual error. Tair∗(x, y) is the deterministic (regressed) part of the model. The residual error, r(x, y), is the difference between the AWS value for Tair(x,y) and the regressed value Tair∗(x, y) used in Eq. (2a):

$$ r\left(\mathrm{x},\mathrm{y}\right)= Tair\left(\mathrm{x},\mathrm{y}\right)-{T_{air}}^{\ast}\left(\mathrm{x},\mathrm{y}\right) $$
(3)
  1. 2.

    We apply the regression model to all points on a grid covering the study area (except the AWS locations). Some parts of Tair can be estimated at all grid points using the regression part of Eq. (2b), the gridded elevation values (DEM), and LST:

$$ {{\mathrm{T}}^{\ast}}_{\mathrm{grids}}={\upbeta}_0+{\upbeta}_1\mathrm{DEM}+{\upbeta}_2\mathrm{LST} $$
(4)

Where T∗grids is the gridded Tair, with a spatial resolution equal to that of the grids for LST and DEM, DEM are the gridded elevation values, and LST is the gridded land surface temperature.

  1. 3.

    A separate kriging procedure was applied to the residual, r(x, y). Finally, a map of \( {\hat{\mathrm{T}}}_{\mathsf{grids}} \) was obtained by combining \( {{\mathit{\mathsf{T}}}^{\ast}}_{\mathsf{grids}} \) and \( {\hat{\mathit{\mathsf{r}}}}_{\mathsf{grid}\mathit{\mathsf{s}}} \) as:

$$ {\hat{\mathrm{T}}}_{\mathrm{grids}}={{\mathrm{T}}^{\ast}}_{\mathrm{grids}}+{\hat{\mathrm{r}}}_{\mathrm{grids}} $$
(5)

where Tgrids is the estimated air temperature and T∗grids and \( {\hat{\mathrm{r}}}_{\mathrm{grids}} \) are the trend and residual part of the regression, respectively, at the grid spatial scale.

Atmospheric water vapor is recorded in the AWS data as relative humidity (Rh), which we interpolated spatially to obtain values on the same surface grid as for the other variables.

Relative humidity has nonlinear function with topographic variables (Liston and Elder 2006), and its spatial distribution is largely constant over areas which are a long way from major water sources, such as our study area (Beek 1991). This makes ordinary kriging an appropriate method for spatial interpolation, and we applied it in here. The spatially interpolated relative humidity (Rh-interp) was then converted to vapor pressure (ea) using the standard conversion methods for saturated vapor pressure (WMO C 2008) found in the TESEBS model. The spatially interpolated Tair and ea were validated using 32 (74%) of the AWS datasets as a training dataset, and the other 11 (26%) independent, randomly selected AWS datasets as a test dataset (Fig. 3a and b). Though the biases and RMSE were small for Tair and ei, these statistical metrics were relatively large for the downward longwave radiation flux that was calculated from them (Fig. 3c). This was due to the sensitivity of downward longwave radiation calculation to both air temperature and water vapor pressures.

Fig. 3
figure 3

Graphs of cross-validation results: (a) air temperature (Kelvin), (b) vapor pressure (hPa), (c) downward longwave radiation (W m−2), and (d) downward shortwave radiation (W m−2)

Full size image

2.3.2 Downward shortwave radiation (SWd)

Shortwave radiation comprises about 85% of the incident solar radiation flux (Sardar et al. 2017), and it is the largest term in the surface energy balance (Cuffey and Paterson 2010). SWd varies both spatially and temporally over the Earth’s surface. Terrain characteristics (elevation, slope, and orientation of terrain features/aspects) drive variability in SWd at the surface in mountainous areas (Olson et al. 2019). Elevated surfaces have a lower atmospheric thickness than lower lying land surfaces, and the SWd incident on these surfaces has therefore been subject to lower atmospheric attenuation. The increase in SWd with elevation makes elevation an important explanatory variable for regression-based interpolation (Alsamamra et al. 2009; Martínez-Durbán et al. 2009). The distribution of incident solar radiation is also influenced by both slope and aspect in mountainous areas. In the Northern Hemisphere, south-facing slopes and ridges receive high levels of SWd, while canyon bottoms and north-facing slopes receive less (Rich et al. 1995; Charabi and Gastli 2010; Li 2013). Moreover, depending on the solar zenith angle, areas with steep slopes can block direct solar radiation that would otherwise reach opposing sun-facing slopes. Interpolation over areas of rugged terrain should therefore take terrain characteristics into account.

Estimates of SWd over large spatial areas are needed in the fields of agriculture, renewable energy, and hydrological studies and can be obtained through interpolation of meteorological station data. In mountainous areas, SWd varies with altitude, surface gradient, and orientation (Dozier 1980; Dubayah 1992; Duguay 1995; Flint and Childs 1987), making RK the most appropriate interpolation method because it accounts for topography (Alsamamra et al. 2009; Dobesch et al. 2013; Dyras and Ustrnul 2007; Hengl 2009; Holdaway 1996; Liao and Li 2004; Prudhomme and Reed 1999; Sluiter 2009; Wu and Li 2013).

The UBN River basin is characterized by highly rugged topography and a considerable range of altitudes (Melesse et al. 2014; Jury 2011). The ruggedness of the basin topography suggests that both steepness and slope orientation are highly variable (Mukherjee et al. 2013). The incident solar radiation is strongly influenced by variations in elevation, slope, and aspect across the region (Hoch and Whiteman 2010; Vico and Porporato 2009). Any spatial interpolation of SWd in the UBN River basin should therefore account for the effects of elevation, slope, and aspect, for example by using RK techniques. We used this method to interpolate SWd values from the AWS data as follows:

  1. 1.

    Let AWS global radiation be denoted by S(x, y), where (x, y) is the location of each AWS station. The environmental variables, elevation, slope, and aspect, were read from the DEM for each AWS location, and a robust liner regression was implemented. Robust fitting was carried out for S(x, y) and the extracted variables using Eqs. (6a) and (6b).

$$ S\left(\mathrm{x},\mathrm{y}\right)={S}^{\ast}\left(\mathrm{x},\mathrm{y}\right)+r\left(\mathrm{x},\mathrm{y}\right)=\sum \left({\upbeta}_{\mathrm{i}}{\mathrm{a}}_{\mathrm{i}}\left(\mathrm{x},\mathrm{y}\right)\right)+r\left(\mathrm{x},\mathrm{y}\right) $$
(6a)
$$ \mathrm{S}\left(\mathrm{x},\mathrm{y}\right)={\upbeta}_0+{\upbeta}_1\mathrm{elevation}+{\upbeta}_2\mathrm{slope}+{\upbeta}_3\mathrm{aspect}\left(\mathrm{x},\mathrm{y}\right)+\mathrm{r}\left(\mathrm{x},\mathrm{y}\right) $$
(6b)

Where β0, β1 , β2and β3are the constant and coefficients for the robust regression; ai(x, y) are the values of environmental variables at each AWS location; r(x, y) is the residual error; and S∗(x, y) is the deterministic (regressed) part of the model.

  1. 2.

    The residual error, r(x, y), is the difference between the AWS values for S(x, y) and the regressed value \( {\mathit{\mathsf{S}}}^{\ast}\left(\mathsf{x},\mathsf{y}\right) \) from Eq. (6):

$$ r\left(\mathrm{x},\mathrm{y}\right)=S\left(\mathrm{x},\mathrm{y}\right)-{S}^{\ast}\left(\mathrm{x},\mathrm{y}\right) $$
(7)
  1. 3.

    The regression model is implemented for all points in a grid covering the study area (except the AWS locations). Some parts of SWd can be estimated at all grid points using the regression part of Eq. (6b).

$$ {S}^{\ast}\left(\mathrm{grid}\mathrm{s}\right)={\upbeta}_0+{\upbeta}_1 Elevation\left(\mathrm{grid}\mathrm{s}\right)+{\upbeta}_2 Slope\left(\mathrm{grid}\right)+{\upbeta}_3 Aspect\left(\mathrm{grid}\mathrm{s}\right) $$
(8)

where Elevation, Slope, and Aspect are the gridded values of elevation, slope, and aspect, respectively.

  1. 4.

    A separate kriging procedure was implemented for the residual part, \( \mathsf{r}\left(\mathsf{x},\mathsf{y}\right), \) which was then converted to \( \hat{\mathit{\mathsf{r}}}\ \left(\mathsf{grids}\right). \) Finally, a map of \( \hat{\mathit{\mathsf{S}}\ }\left(\mathsf{grids}\right) \)was obtained by combining \( {\mathit{\mathsf{S}}}^{\ast}\left(\mathsf{grids}\right) \) and \( \hat{\mathit{\mathsf{r}}}\ \left(\mathsf{grids}\right) \):

$$ \hat{S}\left(\mathrm{grids}\right)={S}^{\ast}\left(\mathrm{grids}\right)+\hat{r}\left(\mathrm{grids}\right) $$
(9)

where S∗grids is the regressed model output for all grid points except the AWS locations; r∗grids is spatially interpolated residual; and \( {\hat{S}}_{\mathrm{grids}} \) is the total downward solar radiation at the spatial scale of the grid. These results were validated as for Tair and ea, and the result (Fig. 3d) shows that the RK spatial interpolation technique is promising for estimating SWd with a relatively small MB and RMSE.

2.3.3 Upward shortwave radiation (SWu)

The SWu flux is solar radiation that is reflected back to space from the land surface. The ratio of SWu to the total incident solar radiation is the planetary albedo (r0), which is a property of the land surface (Stephens et al. 2015). SWu can therefore be estimated from the downward solar radiation and the surface albedo:

$$ SWu={r}_0 SWd $$
(10)

The surface albedo (r0) was calculated from MODIS narrow spectral reflectance bands using a linear combination equation from Liang (2001):

$$ {\mathrm{r}}_0=0.160{\upalpha}_1+0.291{\upalpha}_2+0.243{\upalpha}_3+0.116{\upalpha}_4+0.112{\upalpha}_5+0.081{\upalpha}_7-0.0015 $$
(11)

where \( {\mathsf{\alpha}}_{\mathsf{1}} \)–\( {\mathsf{\alpha}}_{\mathsf{7}} \) are the reflectivity values for MODIS bands 1–7, respectively.

2.3.4 Downward longwave radiation (LWd)

The LWd flux is radiation emitted from aerosols, water vapor, and other gaseous molecules and depends mainly on temperature and water vapor concentration in the lower atmosphere (Schmetz 1989; Wang and Dickinson 2013). It is an important component of the energy flux across the land–atmosphere interface, and its absence would result in mean global surface temperature being 30 to 40 °C cooler than it is (Sellers 1965; Trigo et al. 2010). The method used most frequently to parameterize LWd is from Brutsaert (1975), expressed in its original form in Eq. (12) (Amatya et al. 2016; Chen et al. 2013; Han et al. 2013; Kjærsgaard et al. 2007; Long et al. 2010). We recalibrated this original method to be more appropriate to our study area, as is described in more detail in Section 3.

$$ LWd={\upvarepsilon}_{\mathrm{a}}\updelta\ {T_{air}}^4 $$
(12)

Where δ is the Stefan-Boltzmann constant (= 5.67 × 10−8 W m−2 K−4), Tair (in K) is the near surface air temperature, ea (in hPa) is the actual vapor pressure, and εa is the clear sky air emissivity, obtained using an empirical formula:

$$ {\upvarepsilon}_{\mathrm{a}}=1.24{\left(\frac{{\mathrm{e}}_{\mathrm{a}}}{T_{air}}\right)}^{1/7} $$
(13)

2.3.5 Upward longwave radiation (LWu)

The Earth absorbs shortwave radiation from the sun, after it has passed through the atmosphere and radiates at an equilibrium temperature that is close to the surface temperature. This process is described by the Stefan-Boltzmann law, which we used to parameterize the LWu flux:

$$ LWu={\upvarepsilon}_0{\updelta LST}^4 $$
(14)

Where δ is Stefan Boltzmann constant; LST is the land surface temperature from the MOD11A1 product; and εo is the surface emissivity. The surface emissivity εowas calculated following Valor and Caselles (1996):

$$ {\upvarepsilon}_{\mathrm{o}}={\upvarepsilon}_{\mathrm{v}}{\mathrm{f}}_{\mathrm{c}}+{\upvarepsilon}_{\mathrm{g}}\left(1-{\mathrm{f}}_{\mathrm{c}}\right)+\left\langle \mathrm{d}\upvarepsilon \right\rangle \left(1-{\mathrm{f}}_{\mathrm{c}}\right) $$
(15)

where εv = 0.985(±0.007) is the surface emissivity for full vegetation cover; εg = 0.96(±0.010) is the surface emissivity of the bare soil; <dε >  = 0.015(±0.008) is the error; and fc is the fractional vegetation coverage, estimated following Carlson and Ripley (1997):

$$ {\mathrm{f}}_{\mathrm{c}}={\left(\frac{\mathrm{NDVI}-{\mathrm{NDVI}}_{\mathrm{min}}}{{\mathrm{NDVI}}_{\mathrm{max}}-{\mathrm{NDVI}}_{\mathrm{min}}}\right)}^2 $$
(16)

where NDVImax = 0.8 and NDVImin = 0.2 are the NDVI values for full vegetation and bare soil, respectively (Gandhi et al. 2015).

3 Results and discussion

3.1 Validation

In surface energy balance studies, mean bias (MB) and root mean square error (RMSE) are the statistical tools most commonly used for validation. In this work, in situ measurements of eddy covariance radiation fluxes were averaged over 30 min intervals, and the model data were compared with the in situ radiation flux for the same time, allowing MB and RMSE to be found:

$$ \mathrm{MB}=\sum \limits_{\mathrm{i}=1}^{\mathrm{n}}\left({\mathrm{x}}_{\mathrm{i}}-{\mathrm{obs}}_{\mathrm{i}}\right) $$
(17)
$$ \mathrm{RMSE}=\sqrt{\frac{\sum_{\mathrm{i}=1}^{\mathrm{n}}{\mathrm{x}}_{\mathrm{i}}-{\mathrm{obs}}_{\mathrm{i}}}{\mathrm{N}}} $$
(18)

where xi is the model value, obsi is the observed (measured) value for the same time, and N is number of sample observations.

3.2 Calibration for downward longwave radiation (LWd)

Despite much research into LWd estimation methods for the lower atmosphere, an accurate, universally appropriate method has not yet been found. There is growing interest in finding alternative techniques for estimation of LWd at specific locations (Iziomon et al. 2003). Most scholars choose to implement the Brutsaert (1975) method to parameterize LWd because it is based on a physically precise approach. Initially, we also chose to follow this method. However, in our study, the original Brutsaert (1975) parameterization scheme underestimated both the net LWd flux and the total net radiation (Rn) when compared with ground truth measurements. This could be attributable to low atmospheric density and highly variable humidity at the high altitude (4000 m) setting for our eddy covariance measurement station, relative to the lower elevation area for which the Brutsaert (1975) method was initially designed. The Brutsaert (1975) method was found to similarly underestimate fluxes for the Andean Altiplano Plateau, which are at a similar elevation to our study area (Lhomme et al. 2007).

To address this, we adapted the Brutsaert (1975) method to be more appropriate to the atmospheric conditions of our study area. We re-calibrated the method by iteratively adjusting the coefficients and comparing the results to air temperature and vapor pressure measured at the Choke Mountain Flux Tower. The recalibrated model is written as:

$$ {\varepsilon}_a=1.24{\left(2\ \frac{e_a}{T_{air}}\right)}^{1/7}{{\updelta T}_{\mathrm{air}}}^4 $$
(19)

Implementing our recalibrated Brutsaert (1975) method (named the Bruts-Choke method) improved the accuracy of the calculated LWd and net radiation fluxes significantly, as shown in the Table 3.

Table 3. Comparisons of validation results among Brutsaert (1975) and Brutsaert-Choke methods
Full size table

The original Brutsaert (1975) method is not appropriate for all parts of the world, and several studies have implemented similar recalibrations to ours, for example Culf and Gash (1993) adjusted the method for the dry season in Niger, and Crawford and Duchon (1999) adjusted it for Oklahoma in the USA. In all cases, implementation of the recalibrated Brutsaert (1975) method resulted in a more accurate parameterization than other methods. Sridhar and Elliott (2002) also adapted Brutsaet’s original equation by adjusting the coefficient, based on one year of data from different parts of Oklahoma. Our adjustment to the method adapted it be appropriate for the highlands of Ethiopia. However, our recalibration was made using only data from the pre-monsoon season in the central highlands of Ethiopia and we recommend further research to assess the appropriateness of the method over all seasons and for lowland parts of the country.

3.3 Case study and overall validations

The UBN River basin covers a vast area and several satellite image tiles were needed to create a composite image of the whole basin. In this study, a mosaic was created from four satellite image tiles each day, and mosaics from eleven days were used for our analysis (Table 2). The downward and upward shortwave and longwave radiative fluxes and the net total radiation were estimated from the satellite data and from the AWS observations made at the satellite overpass time. The estimated radiative fluxes were validated through comparison with ground truth flux measurements made at Choke Mountain (37.84° E, 10.65° N). The eddy covariance tower at Choke Mountain is the first tower in the UBN River basin to be used for land–atmosphere interaction studies. It was established through a collaboration between then Institute of Tibetan Plateau Research, Chinese Academy of Sciences and the Center for Environmental Sciences, Addis Ababa University and is located in the central part of the basin (Fig. 1b). For the validation, gridded radiative flux estimates from the model were selected to match both the satellite acquisition times and the location of the eddy covariance observation site. These selected model outputs were compared with the tower measurements. The RMSE values for SWd, SWu, LWd, and LWu were 72.93, 25.31, 31.29, and 18.35 W m−2, respectively. The corresponding MB values were, − 14.36, 0.48, − 11.3, and − 5.61 W m−2, respectively (Fig. 4). Our estimation method successfully retrieved all components of the total radiative flux. The RMSE and MB values for SWd and SWu are lower than those reported in similar studies that have used MODIS data (Gusain et al. 2014; Hwang et al. 2013; Jacobs et al. 2002; Kim 2008; Roupioz et al. 2016). Moreover, RMSE and MB values of SWu, LWd, and Rn in our results are smaller than the values reported in Chen et al. (2013), which were derived from high-resolution Landsat data using the TESEBS model. However, our validation is based on a single ground truth measurement site in the central part of our study area and may not be representative of the effectiveness of the method for other parts of the study area. For future validation to cover the whole study area, more eddy covariance turbulent measurement systems are required in mid- and low-altitude areas. In the absence of eddy covariance measurements, datasets with fine spatial resolution can be used as complementary data for validation.

Fig. 4
figure 4

Comparison of derived results with field measurements for the net radiation flux components: (a) downward shortwave radiation flux (Swd) in W m−2; (b) shortwave upward radiation flux (SWu) in W m−2; (c) net shortwave radiation flux (Net-SW) in W m−2; (d) upward long wave radiation flux (LWu) in W m−2; (e) downward long wave radiation flux (LWd) in W m−2; (f) net long wave radiation flux (Net-LW) in W m−2; (g) overall net radiation flux (Rn) in W m−2

Full size image

The spatial distribution maps of the radiation components (SWd, SWu, LWd, and LWu) from 10 February 2019, 11:12 am (local time), show the physiographic heterogeneity of the study area (Fig. 5). The eastern, and most central, parts of the basin are at high elevation, where turbidity in the atmosphere is low and the atmospheric attenuation of SWd is small. As a result, the maximum values for SWd occur in these parts of the basin. Rain-fed agriculture is common practice in the highlands of the basin and February is the driest month. With little artificial irrigation over most of the area, vast areas in the basin had an albedo of less than 0.25 for the study period. This is a typical albedo value for soil or dry vegetation. Dry vegetation could include agricultural field residues, left after crop harvesting (Hartmann 2015). The SWu flux was therefore very low and most of the SWd flux may have been converted to a soil heat flux and to available energy in the atmosphere (sensible and latent heat fluxes). Looking at parameterizations for soil heat flux and for the available energy flux will be the next focus of our work. Longwave radiation fluxes were strongest over the extensive northwestern lowlands and along the river gorges, which are areas that are warmer than the surrounding plateau. This is because both the upward and downward longwave radiation fluxes depend mainly on the land surface and atmospheric temperature distributions.

Fig. 5
figure 5

Spatial distribution maps of components of net radiation flux in W m−2 over the UBN basin on 10 February 2019, 11:12 am local time: (a) downward shortwave radiation flux (SWd); (b) upward shortwave radiation flux (SWu); (c) upward long wave radiation flux (LWu); (d) downward long wave radiation flux; (e) net radiation flux (Rn); location of eddy covariance (EC) tower is designated by (+) ; white scattered regions represent where no information was available due to cloud cover

Full size image

Figure 6a–d shows the frequency distribution for the net radiation flux at four sample dates within the study period. This study was carried out in the dry season for the basin (February, March, April, and May), when the net radiation flux is large and varies little month to month. This could be related to the clear sky conditions over most parts of the basin since these promote the transfer of large amounts of solar radiation to the surface. The range between the minimum and maximum values for the net radiation flux was large during the study period, which could be due to the heterogeneous landscape and the rugged mountains in the basin. There was also some variability in the shape of the distributions and the spread around the mean. The total net radiation flux ranged from 242.84 to 833.74 W m−2 in February, from 40.13 to 867.92 W m−2 in March, from 75.63 to 957.75 W m−2 in April, and from 150.20 to 738.60 W m−2 in May (Table 4 and Fig. 6a–d). The net radiation flux has a negatively skewed distribution for the first three months. The majority of values therefore fall to the right of the mean (to the maximum side) and cluster at the upper end of the distribution, while the tail extends to smaller values.

Fig. 6
figure 6

Frequency distributions of net radiation over the UBN basin area on 10 February, 2019 (a), 20 March, 2019 (b), 26 April, 2019 (c), and 14 May, 2019 (d)

Full size image
Table 4. Statistical summary of net radiation distributions
Full size table

The main rainy season usually starts in early June in most parts of the UBN River basin, and May is the hottest month before the onset of the major rains (Abera et al. 2016; Conway 200). Our work has shown that basin-wide surface warming in May was more homogeneous and fluxes were more closely concentrated around their mean value than in the preceding months. This can be seen from the smallest standard deviation (Table 4) and leptokurtic frequency distributions (Fig. 6d). This uniform warming could trigger unstable atmospheric conditions, causing air to rise upwards over the study area, promoting cloud formation (Ahrens 2007). However, the upward rising air is unlikely to condense and form precipitation in May as it contains insufficient water vapor. Other studies (Block and Rajagopalan 2007; Gamachu 1977; Griffiths 1972; Mellander et al. 2013) have confirmed that warming extends north beyond the study area, and moist air from the southwest starts to invade the UBN River basin in June. Previous studies of the main rain-bearing processes in the UBN River basin, however, were carried out in terms of synoptic weather systems (Seleshi and Zanke 2004; Jury 2010 ). The uniform local surface warming and related thermal low conditions in May can be considered a background condition that precedes further warming and the atmospheric processes responsible for the main rain season, which occurs from June to August over most of the UBN River basin.

4 Conclusions

In this study, the regional distribution of the component parts of the total net radiation flux (i.e., SWd, SWu, LWd, and LWu) were parameterized over the heterogeneous landscapes of the UBN River basin using DEM, MODIS, and AWS data. The parameterized net radiation flux components were compared with simultaneous, co-located field measurements recorded at the eddy covariance site. The results show that the estimated net radiation flux components are in good agreement with the in situ measurements. The statistical metrics (MB and RMSE) used to characterize the performance of the net radiation parameterization were lower than those reported from similar research carried out using MODIS data in other parts of the world. This is likely to be attributable to the spatial interpolation methods applied in this study, and to the quality of the AWS forcing input data that were used in our estimation processes. The RMSE and MB values for LWd, SWu, and Rn were smaller than for a similar study that used Landsat data, which have a very fine spatial resolution. This shows that our methodology and study procedures could provide improved and operationally useful results for satellite data with a finer spatial resolution than MODIS.

In this study, the LWd flux parameterization needed to be recalibrated since it was standardized for an environment that was quite different from the atmospheric conditions of our study area. Our recalibrated method drastically improved our estimate of both the LWd flux and the total net radiation flux. The net radiation flux is key to heat exchange and water management studies. Research into Ethiopia in these fields is developing, and the findings of this study provide a springboard to improved understanding of land–atmosphere interactions and will be useful for the science of water resource management, such as ET estimation.