1 Introduction

Marked variations in regional climate patterns arise as a response to persistent changes of the climate system. Identifying these patterns is therefore fundamental for a better understanding of past climate changes at local and regional scales. Thus, with increasing computational power, the number of classification methodologies providing robust characterizations of regional climates has quickly escalated in the climate community, becoming a common tool for the study of past climatic patterns (Abatzoglou et al. 2009; Srivastava et al. 2012; Perdinan 2015; Horton et al. 2015).

Within this framework, classical clustering techniques, such as the k-means algorithm (Hartigan and Wong 1979; Phillips 2002), have become widespread in the past few years as dimensionality reduction methods are able to extract relevant information from extensive climate databases (Bernard et al. 2013; Bador et al. 2015; Zhang et al. 2016). These methodologies can arrange data according to their internal structure by defining spatial regions for datasets with geolocated climate information (Rao and Srinivas 2006). Therefore, clustering algorithms have been used in several studies such as the identification of regional climates (Aliaga et al. 2017), air pollution (Gao et al. 2011; Wang et al. 2015), and ecology (Miele et al. 2014; Cheruvelil et al. 2017). These clusterings have usually been applied to spatially resolved climate variables obtained from model simulations or instrumental observations, or a combination of both. Moreover, pattern recognition of climate trends has also been explored by cluster analysis of individual samples (DeGaetano 2001), which provided valuable information about the evolution of regionally located climate variables (Scherrer et al. 2016).

These classical clustering techniques often require complete datasets, limiting regional analyses to series without time gaps. Unfortunately, most available climate archives (Klein Tank et al. 2002; Glaser and Riemann 2009; PAGES2k Consortium et al. 2017) contain missing values which must be properly handled prior to clustering. Most straightforward approaches consist of removing data points (deletion) that do not cover the requested time period (Dixon 1979), whereas more sophisticated methods intend to estimate missing values (imputation) by means of statistical procedures (Henn et al. 2013). This limitation restricts cluster analyses to periods with complete information, disregarding earlier climate imprints contained in longer time series. In turn, there are only a few methods designed to work with inhomogeneities in climate datasets. Such is the case of k-POD (Chi et al. 2016), an algorithm that instead of relying on deletion and imputation uses a majorization-minimization algorithm (Lange et al. 2000) to clusterize observed data with a certain level of missingness. It is however difficult to find a method that performs well with sparse climate datasets.

In this paper, we show a new clustering method to classify sets of time series with a significant number of missing values. Its structure is similar to those employed in classical methods of clusterization such as the k-means algorithm, but with some key changes that allow for the selection and attachment of records with different temporal lengths. k-Gaps has also been validated with a series of statistical tests that ensure the consistency of its clustering skill, making it suitable for the analysis of regional climates from historical and paleoclimate datasets.

The paper is structured as follows: In the first place, a thorough description of the k-gaps algorithm is provided in the methodology (Section 2), whereas the experimental setting regarding the generation of synthetic data, the validation tests, and the comparison with other clustering techniques are shown in the experiments section (Section 3), together with a discussion of possible applications. Final conclusions are shown in Section 4.

2 The k-gaps algorithm: clustering incomplete temporal datasets

2.1 Assumptions and definitions

Let us assume we have a dataset of climate records at different locations, and maybe with different temporal lengths, which together describes the climatology of a specific zone (Europe in our case) for a given period T := [n1,n2,⋯ ,nT], where ni stands for the time step at which a certain climate variable has been measured, and T represents the total number of time steps. Thus, a given climate record A is defined for a subset of T, and may (or may not) overlap with other climate records included in the dataset (i.e., incomplete records are considered).

Generally, clustering climate records implies computing distances between some centroids (in our case, temperature series that are representative of certain regions) and the records, by considering a pre-defined metric (the root-mean-square deviation, for example). However, note that for incomplete datasets, these distances can only be estimated during the time intervals with available information. Therefore, to identify periods where some time series overlap, a vector mask ranging from the oldest to the most recent time step in the dataset has been defined for each time series. These record masks can be defined as indicator functions (Eq. 1), filled with 1’s when their associated time series have available data, and 0’s for the remaining period.

$$ \begin{array}{@{}rcl@{}} \text{Mask}_{A}(n_{i}):= \begin{cases} 1, & \text{if $n_{i}$\ $\in$ \textit{A}}\\ 0, & \text{if $n_{i}$\ $\notin$ \textit{A}} \end{cases}\ \forall \ n_{i} \in \mathrm{\mathbf{T}} \end{array} $$
(1)

For instance, Fig. 1 illustrates two randomly generated records (signals A and B with no specific units) with different temporal lengths, and the subsequent time series obtained when these two records are merged (Fig. 1c), for example in a centroid calculation procedure. In our case, signals A and B were combined by averaging them in the time range where there are data available in both series (i.e., during the overlapping interval). Otherwise, when only one of the signals is available, its values are included to the merged series. Note that the mask in Fig. 1c contains the number of time series with available data at each time step and, although the resulting period is defined from 50 to 325 (i.e., the time interval in which there is at least one time series available), the overlapping interval used to combine them is in between 200 and 300. Thus, the resulting series has data of signal A from time 50 to time 199, the averaged information of signal A and signal B from time 200 to time 300, and the information of signal B from time 301 to time 325. Note that the use of vector masks allows merging of records with different temporal lengths (e.g., temperature observations, or historical archives), and provides information about the number of time series used to calculate a resulting centroid. Moreover, these masks are important because keeping the number of series available at each time step allows us to discern between periods with robust mean values (i.e., time steps with a high number of temperature series available) and those time intervals with data scarcity.

Fig. 1
figure 1

Data records considered (a and b), and the resulting series obtained by merging them (c). All the records are presented with their respective masks

Full size image

It is noteworthy to mention that clustering techniques can help identify regional climates by grouping together instrumental time series with similar mean temperatures or correlated variability. While the former can be achieved by using series with absolute values, clusterizing time series focused on their variability requires normalizing the series first. For instance, Fig. 2 depicts two records with different means (Fig. 2a and b), but correlated variability (Fig. 2c), that would be clustered together if they were normalized. Frequently, it is an interesting clustering series according to their similar variability. The k-gaps algorithm has therefore been designed to clusterize time series with similar mean (“basic” mode hereafter) and also with correlated variability (“normalization” mode). While the basic mode is directly applied over temperature records, the normalization mode requires a workaround because homogeneous normalizations cannot be calculated from records with different temporal lengths. This issue has been tackled by applying an adjustment of the climate data to calculate the centroids (Section 2.3) and a linear fitting to properly reclassify the time series (Section 2.4).

Fig. 2
figure 2

Representations of two synthetic records. Series with different mean values (a and b), but with correlated variabilty (c)

Full size image

2.2 k-Gaps

Taken into account these previous definitions, we can now describe the k-gaps algorithm for clustering records of incomplete time series. The general structure of k-gaps is similar to the well-known k-means algorithm (Hartigan and Wong 1979), which is an iterative method whose main purpose is to classify series of data within clusters represented by central vectors known as centroids (Cj). In k-means, these centroids are calculated by averaging the series associated with previous clusters, and subsequently reassigning the records to the nearest centroid for the next iteration. The proposed k-gaps algorithm follows the same idea, but including some extra steps to treat the problematic case of having incomplete records in the database. Figure 3 shows a flowchart of the k-gaps implementation, which can be summarized in the following steps:

  1. 1.

    Randomly assign the existing records (time series) over k initial clusters.

  2. 2.

    Proceed to centroid calculation, following the procedure described in Section 2.3.

  3. 3.

    Reassign records to clusters by similarity with the centroids (Section 2.4).

  4. 4.

    Count the number of records for each cluster.

    For empty clusters, proceed to step 5. Otherwise, jump to step 6.

  5. 5.

    Generation of new clusters by applying random Gaussian noise to existent groups, and restart from step 2.

  6. 6.

    Check whether the stopping condition has been fulfilled (Section 2.5). If it is not, go to step 2.

Fig. 3
figure 3

k-Gaps flowchart. Circles contain general clustering procedures, and squares describe specific k-gaps operations. The algorithm’s conditions are represented as diamonds in the flowchart

Full size image

2.3 k-Gaps centroid calculation

In clustering algorithms requiring complete datasets such as the k-means, centroids are usually calculated by averaging the time series associated with a certain cluster at each time step. However, this procedure can debase the robustness of the regionalization when applied over incomplete datasets (i.e., sets of records defined for different time periods) by producing unrealistic clusters when some time series do not overlap. This bias will be propagated for the subsequent iterations, clusterizing artificially mixed regions. To circumvent this problem, centroids have been estimated by only averaging records that overlap for at least a minimum time interval. This minimum overlapping must be estimated in each case depending on the temporal resolution and the number of time steps that characterize the dataset aimed to clusterize. For the case in Section 3, after trying different parametrizations, we found that the k-gaps algorithm could not converge for values lower than 90 days, yielding significantly different clusterings over successive runs. This indicates that clusters are barely robust and their results must not be trusted. We tackled this issue by setting a minimum overlap of 90 days. The procedure to calculate the centroids in the algorithm will be described next. Note that it is different depending whether we consider k-gaps in basic mode or in normalization mode:

Procedure for k-gaps basic mode (i.e., clustering records with similar means):

  1. 1.

    Set the longest time series as the new centroid (Cj).

  2. 2.

    Select the records (Si) with the longest overlap with the centroid (Ovi, j) using Eq. (2).

    $$ \begin{array}{@{}rcl@{}} Ov_{i,j} &=& \sum\limits_{n=0}^{n_{T}} F_{i,j}(n) \rightarrow F_{i,j}(n)\\ &:=& \left\{\begin{array}{l}0 \quad \text{if} \quad \text{Mask}_{i}(n) \cdot \text{Mask}_{j}(n) = 0 \\ 1 \quad \text{if} \quad \text{Mask}_{i}(n) \cdot \text{Mask}_{j}(n) >0 \end{array}\right. \end{array} $$
    (2)

    where j ∈ [0,k) represents a certain cluster (of a total of k clusters), n is the time, nT is the last time step, Maski is the mask associated with Si, and Maskj is the centroid mask.

  3. 3.

    Combine the centroid (Cj) and Si following Eq. 3:

    $$ C_{j} = C_{j} + S_{i} \cdot \text{Mask}_{i} $$
    (3)

    Centroids are firstly calculated by adding at each time step the temperatures of their associated series.

  4. 4.

    Update the centroid mask using Eq. 4:

    $$ \text{Mask}_{j} = \text{Mask}_{j} + \text{Mask}_{i} $$
    (4)
  5. 5.

    Get back to Step 2 until all records are checked out or overlapping is below a predefined threshold.

  6. 6.

    Divide the centroids in Step 3 by their respective Maskj to obtain their average temperature at each time step (note that centroid masks are defined as the number of series available at each time step).

For each cluster in normalization mode (i.e., clustering time series with similar variability):

  1. 1.

    Set the longest series as the new centroid (Cj).

  2. 2.

    Select the time series (Si) with the longest overlap with the centroid (Ovi, j) using Eq. 2.

  3. 3.

    Adjust the centroid using a linear regression estimated in the overlapping section between the centroid and the series (Eq. 5):

    $$ S_{i}=c_{1} \cdot C_{j} + c_{0} \rightarrow {S}_{i}^{\prime} = \frac{S_{i}-c_{0}}{c_{1}} $$
    (5)

    where c0 and c1 are two constants known as the intercept and slope of the regression line respectively. Note that while the centroid Cj (which is a time series that determines a certain cluster) is generated by combining normalized series (\({S}_{i}^{\prime }\)), it is adjusted by linear regression to the original series Si, preventing c1 from being 0. (The intercept (c0) is subtracted from the original series (Si) and the result is divided by the slope (c1), obtaining \(S^{\prime }_{i}\).)

  4. 4.

    Combine the centroid and \(S_{i}^{\prime }\) following Eq. 3.

  5. 5.

    Update the centroid mask using Eq. 4.

  6. 6.

    Divide the centroid by its mask. This process is undertaken for each time series considered, since it is necessary to estimate the centroid to apply Step 3 for the forthcoming record.

  7. 7.

    Back to Step 2 until all records are checked out or overlapping is below a predefined threshold.

2.4 Assignment of records to clusters in k-gaps

Clustering algorithms associate records with different clusters by means of a certain metric. In its basic mode, k-gaps assigns each record to the cluster whose mean squared error (MSE) is minimum, following Eq. 6.

$$ \text{MSE}(i,j)={Ov}_{i,j}^{-1}\sum\limits_{n=0}^{Ov_{i,j}} F_{i,j}(n)\left[S_{i}(n)-C_{j}(n)\right]^{2} + P $$
(6)

where Ovi, j is the overlapping length and P is a penalty associated with short overlapping intervals between two time series. Note that the number of superimposed values should be long enough to ensure that the metric used for the classification of time series into clusters (MSE) is significative, because otherwise time series with a good fit during a short overlapping interval could be assigned to the wrong cluster (that is why it is important to add the value P in Eq. 6). Clusterizations of this sort are considered barely robust because they show very different classification patterns each time the algorithm is run. Hence, the procedure to find the right value for P is by tuning different parametrizations until robust clusterings are obtained. We used series of daily temperatures and found that by setting this parameter to 30 days and a penalty of 100, the final pattern of the clusterization did not significantly change over successive runs of the k-gaps algorithm.

In the normalization mode, the assignment process is different: in this case, linear regressions are computed between time series (Si) and clusters (Cj) to find the centroid that best fits each record. In our case, cluster assignment is performed by minimization of mean quadratic errors (\({\epsilon _{j}^{2}}\)) obtained from residuals of the linear fit estimated using Eq. 7.

$$ S_{i} = c_{1} \cdot C_{j}\!+c_{0}+\epsilon_{j} \!\rightarrow\! \text{Error}_{i,j} = Ov_{i,j}^{-1} \sum\limits_{n=0}^{Ov_{i,j}} {\epsilon^{2}_{j}}(n) + P $$
(7)

where c0 and c1 are once again the intercept and slope of the linear fit, respectively. Note that the linear regression is performed in the overlapping section between each centroid and the time series.

2.5 k-Gaps stop conditions

In the classic k-means algorithm, the stop condition is usually reached when convergence is detected (no change of the solution in a number of iterations), or after a given number of iterations that ensures the algorithm has obtained a “good enough” solution. However, additional criteria are required in the k-gaps to handle incomplete records. For instance, since centroids are based on compositions of uneven time series, they might be affected by adding and removing records from their corresponding clusters; therefore, total convergence cannot be ensured. Furthermore, looping assignation may occur when some series move cyclically from one cluster to another during consecutive iterations, affecting the convergence of the algorithm. Therefore, to provide a general stop condition for k-gaps, a detector of clustering changes (D) has been defined (Eq. 8) as the summation of absolute values obtained from differences between the number of time series in each cluster at a given step (s), and the number of time series in those clusters for the next iteration (s + 1).

$$ D = \sum\limits_{j=0}^{k} |\text{Size}_{j}(s)-\text{Size}_{j}(s+1)| $$
(8)

where k is the total number of clusters, and Sizej(s) represents the number of records in cluster j during step s.

Hence, when the value of D tends to 0, we assume that the algorithm has converged, and the stop condition has been reached. On the other hand, when D values are repeated over successive iterations, it indicates that the algorithm entered in one of the aforementioned loops, and a halting procedure should be applied, starting again the algorithm with a different initial condition.

3 Computational experiments and results

3.1 Experimental setting

The main goal of this study is to evaluate the performance of k-gaps in the clusterization of daily summer European temperatures since 1950 to 2016 when data availability is constrained to a few locations. For this purpose, 500 synthetic datasets have been elaborated with incomplete time series extracted from the E-Obs grid of temperatures (version 14.0) (Haylock et al. 2008). The E-Obs dataset provides daily spatially resolved European field temperatures with a spatial resolution of 0.25∘× 0.25∘. However, due to the presence of missing values, locations with less than 6000 days were removed, as well as time periods when any of the remaining data points presented missing values. In this way, there were enough time series to generate a complete set (in space and time) of 17,452 grid points with 5569 days of summer mean temperatures contained in between latitudes 35∘ S and 72∘ N, and longitudes 20∘ W and 42∘ E, for a time span of 66 years since 1950. As uncertainty estimations arising from thermometer exposure and urbanization are reduced to 0 by 1930, they were neglected for this study. The synthetic datasets were then extracted from this complete grid of temperatures as detailed in Section 3.2.

To obtain the “ideal” case scenario where complete data is available for regionalization, two k-means clusterings have been performed using this initial (complete) dataset (Fig. 4). Thus, absolute temperatures have been used to provide the clusterization of areas with similar temperature means (k-gaps basic mode), whereas standardized temperatures have been employed for the clusterization of records with correlated variability (the normalization mode). Note that, while the former (Fig. 4a) associates Northern regions with high-altitude locations such as the Alps (Rubel et al. 2017) (as expected due to their similar lower mean temperatures), the latter (Fig. 4b) yields coherent patterns in terms of regional climate variability. Interestingly, the regionalization of Fig. 4a has certain similarities with the Köppen-Geiger classification (Köppen 1884), especially in the aforementioned association of high-altitude temperatures with northernmost climates. However, it is not possible to directly compare against these Köppen-Geiger climate classifications because their classification system also takes into account precipitation patterns that are beyond the scope of this study. The regions obtained using k-means with the entire grid of European temperatures (k-means[EObs], hereafter) will be assigned as target to test the skill of k-gaps and other clustering techniques by comparison. The closer the regionalization to k-mean[EObs] regions, the higher the skill of the method.

Fig. 4
figure 4

k-Means clusterization of the E-Obs grid of daily summer temperatures since 1950 to 2016 (k-means[EObs]) using absolute (a) and standardized (b) temperatures

Full size image

3.2 Generation of synthetic data

The considered synthetic datasets are generated from the complete E-Obs temperature grid using three main parameters: the number of synthetic records, their spatial distribution, and their time length. These parameters can be interrelated since sampling networks and measuring campaigns have usually been conducted by organizations at regional scales. So most sampling collections are regionally related in time, leading to changes in the spatial coverage of the zone at different time periods. Synthetic data are therefore generated using Gaussian models (Fig. 5) that imitate the distribution and time intervals of real measuring campaigns. These models are spatially conformed by marked centers where there is a higher concentration of records, and a sparser coverage of their surroundings. On the other hand, different temporal lengths for synthetic time series are obtained by randomly altering the start and end times (inset of Fig. 5) of complete temporal records from the E-Obs temperature dataset.

Fig. 5
figure 5

General representation of the spatial distribution of a Gaussian model (blue shade) employed to generate sample-starved datasets (with incomplete temperature series) where “×” demarcates the center. Darker blues indicate a higher concentration of time series, whereas lighter blues depict fewer time series. Inset: Time lengths of synthetic series generated with random variations of predefined initial (tini) and final (tend) days

Full size image

Hence, 500 synthetic datasets of temperature records were generated to assess the performance of k-gaps, combining 20 Gaussian models with different centers, distributions, and time periods. Each one of them presents fewer than 1100 time series, containing from 55 to 90% of missing values within their chronologies (Fig. 6). These reduced number of records and data missing level are similar to real historical (Küttel et al. 2010) and paleoclimate (PAGES2k Consortium et al. 2017) databases, and will serve as a test bed to validate the method for future studies. For example, Fig. 7 illustrates one of these case studies. It is composed of 815 time series with a higher density of temperature records over Central Europe, while large territories of Southern Europe such as Italy, Spain, and Portugal remain almost uncovered. Moreover, the number of available records is not constant and decreases back in time since 1980, restricting the information of past temperature changes. These features are different for each synthetic dataset and, therefore, provide a good framework to assess the robustness of clustering algorithms.

Fig. 6
figure 6

Distributions of the number of time series per dataset (left) and level of missing values related to the temporal length of the records (right) associated with 500 synthetic datasets generated to validate the k-gaps algorithm

Full size image
Fig. 7
figure 7

Temporal (a) and spatial (b) distribution of a sample study composed of 20 Gaussian models centered at different points in Europe

Full size image

3.3 Results

A statistical analysis has been carried out using the adjusted Rand Index (de Vargas and Bedregal 2013), a metric that is used in data analysis to assess the similarity between clusterings. The index is constructed to detect whether two clusters obtained from different methods have the same associated time series, indicating how much those clusters look alike. In this sense, it can be seen as an accuracy measure, as well as a comparison test for clustering methods. In our case, the Rand Index was employed to compare the k-gaps results with the ideally perfect k-means[EObs] clustering. The index ranges from 0 to 1, and serves to quantify the similarity between two clustering processes. While a Rand Index value of 0 means that all data points correspond to completely different clusters, a Rand Index value of 1 would indicate that both clusterings are the same. The performance of k-gaps has been compared with that of two other clustering techniques: the k-POD algorithm (Chi et al. 2016) and the k-means algorithm (from now onwards k-means[rs], where rs stands for reduced set, indicating that it is only applied over a few time series, in contraposition with k-means[EObs] which uses the entire grid of temperatures). Note that, whereas k-gaps and k-POD clusterize incomplete time series (i.e., series with different temporal lengths that lead to gaps of missing information for some time intervals), k-means[rs] clusterized the same 500 datasets but with complete records (i.e., series covering the entire time period since 1950 CE). Thus, the comparison of k-gaps and k-POD with k-means[rs] provides information about the skill of these techniques to reproduce robust spatial patterns with fragmentary temporal data.

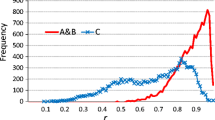
Table 1 shows the adjusted Rand Index means and standard deviations associated with these three methods for both modes. k-Gaps exhibited good results for most datasets with index values close enough to k-means[rs]’s indices, outperforming the skill of k-POD to clusterize uneven time series. In fact, k-gaps clusterings obtained higher Rand indices than k-POD counterparts for all synthetic datasets. Moreover, all clustering techniques yielded higher indices once the time series were normalized, indicating that these methods achieve better skill when records are clusterized in terms of their climate variability. Note that the capability to generate robust clusterings with these methodologies depends on two main factors: the temporal lengths of the time series, and their respective locations. To see which factor is predominant, let us examine Fig. 8, where k-means[rs] index distributions (blue bars) illustrate the impact of sparse sampling locations on the skill to reproduce perfect clusterings. In turn, differences between the k-gaps (red bars) and k-means[rs] indices can be explained due to the loss of temporal information (shorter time series). As a matter of fact, k-gaps and k-means[rs] performances are quite similar, indicating that clusterings are more sensitive to the distribution of sampling locations rather than to differences in the temporal length of records.

Table 1 Adjusted Rand Index means of 500 synthetic case studies within 95% confidence interval for three clustering techniques
Full size table
Fig. 8
figure 8

Comparison of clustering techniques using adjusted Rand Index for absolute (a) and normalized (b) temperatures. The adjusted Rand Index is calculated with respect to the clusterization obtained by applying k-means to the complete E-Obs gridded dataset

Full size image

The skill of the method has also been assessed as a function of the number of records used in the clustering process. Table 2 exhibits Rand indices for 3 different-sized datasets without any clear correspondence between size and performance (for instance, P404 is the biggest dataset with 875 time series, and its clustering has the worst performance in the normalized mode), suggesting that the efficiency of k-gaps does not strongly rely on the number of time series employed. Note that in these examples, the average amount of missing data per series is above 80%, and the loss of information (i.e., the distribution of missing data) is different for each dataset as shown in Fig. 9. This implies that the algorithm is able to clusterize time series that are almost empty, as long as the entire period of study is covered by the sum of the different series included in the dataset. It is also shown that different performances can be obtained for the same dataset depending on the clustering mode (i.e., P280 and P404), which indicates that a robust regionalization with absolute temperature series requires different locations than clusterings with normalized series. This is consistent with the fact that regions with similar mean temperatures are not the same as regions with similar climate variability, as shown in Fig. 4.

Table 2 Adjusted Rand Index for k-gaps clusters with 3 synthetic datasets with different numbers of time series (size), and an averaged missing data (per series) above 80%
Full size table
Fig. 9
figure 9

Distribution of missing data for each one of the series included in datasets P191, P280, and P404. Days without temperature values are depicted in blue, and available daily temperatures are shown in yellow

Full size image

To visualize the spatial patterns obtained in a regionalization with the k-gaps algorithm, we have clusterized a dataset with an intermediate Rand Index value (the clustering performance with P191 from Table 2 is not the best nor the worst, and therefore it is representative of what can be expected from the regionalization of the 500 synthetic datasets). Figure 10 displays the resulting clusterings of these series of temperature together with their locations. Note that to facilitate the comparison with Fig. 4, once P191 has been clusterized, we have interpolated the clustering in the remaining grid points where temperatures are not available by using the k-nearest neighbors algorithm (Cover and Hart 1967). The adjusted Rand indices for basic and normalization modes are 0.52 and 0.69, respectively. These values indicate that k-gaps has similar performance with k-means (which needs complete temporal information) using sample-starved climate datasets with different temporal lengths.

Fig. 10
figure 10

k-Gaps clusterization of a study case with 815 time series (black dots), for basic (a) and normalization (b) modes

Full size image

On the other hand, lower Rand indices are related to irregular spatial distributions, where small regions are well characterized by a disproportioned number of climate records, while large extensions of land remain unsampled. Such is the case of dataset P404 in Table 2, chosen as a data clustering with low Rand Index (0.38 for normalization mode as seen in Table 2), and whose regionalization using the normalization mode is depicted in Fig. 11. In this case, the difference between the number of time series in Central Europe and Southern Europe has altered the formation of clusters by associating regions in the Iberian Peninsula with the big aggregation of temperature records in France as seen in Fig. 11 (black dots depict the spatial distribution of dataset P404). At the same time, the concentration of points in Ireland produced a new cluster for the British Isles which is not present in k-means[EObs]. This indicates that special attention should be paid to disparities in the coverage of the territory because they play an important role in the final structure of the clustering, and an uneven distribution of time series can debase the analysis of regional climates. However, while non-homogeneous distributions force the splitting and merging of some clusters, some of the spatial patterns from Fig. 4 can be identified, proving that realistic information about temperature variability can still be extracted from low-quality datasets such as P404.

Fig. 11
figure 11

k-Gaps clusterization for P404 in Table 2 using the normalization mode. The dataset is composed of 875 time series (black dots) unevenly distributed over Europe

Full size image

3.4 Discussion

The full potential of k-gaps is evidenced in Fig. 10 where the resulting spatial patterns for both modes exhibit important similarities with those obtained for k-means[EObs] (Fig. 4). This is quite remarkable because k-gaps is applied over an incomplete dataset whose size is 21 times smaller than the homogeneous grid of temperatures (which has complete temperature information for the entire time period in all grid points). It is also noteworthy to mention that although synthetic records are sparsely distributed across Europe, clusters are defined for almost the same regions as for the gridded dataset, confirming the robustness of the spatial clustering. For instance, spatial patterns over Iberia and the UK are well reconstructed with the method even when there is a lack of sampling records (black dots in Fig. 10 represent the locations with temperature series) in the southern part of their territory. This suggests that only a few number of locations are necessary to reproduce most of the climatology within these areas. Moreover, while absolute temperatures are classified by their means (e.g., high latitude points are related with high-altitude locations), normalized temperatures are grouped by their variability, indicating that clusterings are as climatically consistent as those obtained with classical algorithms and complete datasets.

Furthermore, k-gaps cluster analyses provide a useful framework for the study of past climate trends and the detection of extreme events at regional scales. For instance, the linear regression of centroids can be utilized to estimate regional temperature trends for periods beyond the scope of complete datasets. Figure 12 shows that trend differences between k-means[EObs] and k-gaps are below 0.03 ∘C/year for 75% of our synthetic datasets. This indicates that although there could be small biases induced by the irregular distribution of uneven (and scarce) time series, the temperature trends obtained from k-gaps centroids are similar to those ideally obtained from the clusterization of complete gridded datasets (i.e., k-means[EObs]). Therefore, these k-gaps centroids can be used to study changes in past temperature trends from incomplete datasets.

Fig. 12
figure 12

Histogram of trend errors estimated from differences between k-gaps centroids and ideal centroids retrieved from k-means[EObs]. Temperature trends have been calculated for 500 synthetic datasets

Full size image

On the other hand, as the normalization mode of k-gaps associates time series with correlated variability, extreme temperature events can be detected for each cluster of these series. Note that extreme events have been defined for values above the 95 percentile of temperatures on record for at least 95% of the time series available at each cluster (Demuzere et al. 2011). Thus, we can estimate the probability of detection by comparing extreme events detected with 500 synthetic datasets (i.e., incomplete series) and those detected with the complete E-Obs grid. Figure 13 shows that the probability of capturing these extreme events is high for most regions (i.e., clusters defined by time series with correlated variability), even when the number of temperature records per day is reduced down to a few tens. For example, clusters with only 20 time series have, on average, between 60 and 80% chances of detecting temperature extremes. This probability increases above 90% for clusters with at least 30 time series, indicating that the detection of extreme events within regions defined by the k-gaps algorithm is possible with sets of just a few time series per cluster.

Fig. 13
figure 13

Probability distribution of detecting extreme events for 500 synthetic datasets. The color of each grid point represents the number of clusterized regions with a certain detection probability and a mean number of time series

Full size image

4 Conclusions

In this paper, we have presented a novel clustering technique for incomplete datasets known as k-gaps. This algorithm is an iterative technique that allows for the clustering of heterogeneous datasets using most of the information contained in incomplete time series (where at least 55% of the information is unavailable). The method is fully based on the structure of the well-known k-means algorithm, but including different procedures in order to adapt the algorithm to the case of having time series of different temporal lengths. Thus, the k-gaps algorithm is ideal for obtaining robust regionalizations of different climate fields such as temperature, precipitation, or sea level pressure from datasets whose sampling records are only available for certain time periods.

k-Gaps exhibited a good performance with most of the 500 synthetic datasets of daily temperatures (with an average of around 80% of missing data per record) employed for its validation, yielding similar patterns in terms of temperature mean and variability to traditional clusterings with complete time series, including k-means. Moreover, consistent climatic clusterings have been achieved even when the number of time series in these datasets was 21 times smaller than the original grid of temperatures (synthetic datasets are composed of around 800 time series, while the gridded dataset has more than 17,000 grid points). This indicates that cluster areas obtained with the k-gaps algorithm are appropriate for the analysis of regional climates using observations unevenly distributed in space and time.

On the other hand, additional experiments with synthetic datasets showed no clear correspondence between the number of time series and the skill of the clustering, indicating that the spatial distribution of sampling records over the region of interest plays a more important role than the size of the dataset.

Furthermore, it has been shown that k-gaps is well suited for the reconstruction of regional climate trends, and the detection of extreme events. These trends and extremes are obtained from time series contained in clusters defined by the k-gaps algorithm. If the clusterization is performed in basic mode, the resulting centroids can provide an estimation of the temperature trends of each cluster, whereas if it is done in normalization mode, time series with correlated variability will be grouped together, allowing for the detection of extreme events at regional scale.

Therefore, this classification algorithm allows for the regionalization of uneven time series (with the same temporal resolution), and makes a good performance with datasets containing high levels of temporal missing values and a reduced number of climate records. Although further research should be carried out to test the robustness of the algorithm under records with significant amounts of noise, the k-gaps algorithm also paves the way for future applications on regional analyses of past climate changes based on historical and paleoclimate archives.