Abstract
A 2-month (August–September) regime of the year 2007 West African monsoon (WAM) was simulated with 27 physics combinations using the Weather Research and Forecasting model at 20-km horizontal grid. The objective is to examine WAM sensitivity to parameterization of microphysical, convective, and boundary layer processes for long-term simulation. The model precipitation was evaluated against the TRMM, CMORPH, and GPCP satellite rainfall products. The surface temperature was compared against the ERA-Interim, NCEP, MERRA, and global surface air temperature, an ensemble of the three reanalysis datasets. Model skill score (MSS) computed from a synthesis of the normalized correlation coefficient, mean bias, and mean absolute error was used to rank the model performance. Results show the model adequately simulates the diurnal cycles of surface temperature than precipitation, as well as the westward propagation of intense precipitation associated with the African easterly waves. The new Grell-Freitas (nGF) cumulus parameterization scheme (CPS) outperforms its predecessor especially when combined with the Mellor-Yamada-Nakanishi-Niino 2.5 (MYNN) planetary boundary layer scheme. The new simplified Arakawa-Schubert (nSAS) and Tiedtke CPSs produced better simulation of precipitation and surface temperature, respectively. The simulation of observed peak of diurnal precipitation in nSAS and nGF highlights success made towards a more realistic representation of convective processes by the schemes. Goddard microphysics and MYNN performed better for both variables. Based on the MSS, some relatively good and poorly performing combinations for precipitation and surface temperature were identified. The optimal combinations are however not separated in a statistically significant way and, thus, could be used for long-term simulation of WAM.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
West African rainfall season is dominated by the West African monsoon (WAM) system. The WAM provides most of the precipitation in the region as it transports abundant moisture into the monsoon domain by the warm and moist south-westerlies from the Atlantic Ocean (Redelsperger et al. 2002). The precipitation produced by the monsoon serves as a major source of water supply for rain-fed agriculture and could also determine food availability and sustainability over the region. On the other hand, torrential and severe rainfall events during the WAM season could lead to flood events that can have a negative impact on economic activities from loss of cultivated croplands, lives, and properties. Another critical threat is reduced amount of monsoon rainfall that can lead to meteorological drought with dire consequences for agricultural production, food security, and potable water supply. This makes WAM of economic importance to policy makers, stakeholders, and the scientific community. It is therefore necessary to better understand the WAM dynamics for improved onset and cessation forecast as well as its rainfall delivery potential.
The WAM is a complex large-scale circulation system defined by changes in surface and lower-level wind direction. Its initiation is associated with meridional horizontal temperature gradient between the Atlantic Ocean and continent. The WAM involves interactions of many multi-scale atmospheric circulation components such as monsoon flow, e.g. African Easterly Jet (AEJ), Tropical Easterly Jet (TEJ), African Easterly Waves (AEW), and Mesoscale Convective Systems (MCS). This makes the simulation of regional climate over this area and its surroundings quite challenging.
Previous studies have shown varying performances with different parameterized physical atmospheric processes in regional climate simulations. For example, Flaounas et al. (2011) examined the impact of some physical schemes using Weather Research and Forecasting (WRF) model in regional climate mode. They highlighted the effect of planetary boundary layer (PBL) schemes to be strongest on temperature, humidity vertical distribution, and rainfall amount while the cumulus parameterization schemes (CPSs) strongly influenced the dynamics and precipitation variability. Furthermore, the Mellor-Yamada-Janjic (MYJ) PBL was found to produce more realistic humidity, temperature, and WAM onset when combined with Kain-Fritsch (KF). The different combinations, used in Flaounas et al. however, revealed the role of different regional climate features in the dynamics of WAM.
Hagos et al. (2014) studied the response of the African monsoon system and Sahel precipitation to land use land cover (LULC) change in WRF model. Their study emphasized the role of land-atmosphere interactions on WAM, that is, normal (wet/dry) seasons have significantly stronger (weaker) response to changes in LULC because there is moisture/limited energy during the wet/dry years. An important conclusion of Hagos et al. is that changes in precipitation are related to changes in circulation, the intensity, and latitudinal position of the AEJ, which varies with the changes in meridional surface temperature gradients. Klein et al. (2017) also investigated the feedback of observed interannual vegetation change on the WAM using WRF model. They identified a feedback process that led to higher (lower) rainfall amounts during nighttime (daytime) for higher vegetation fraction (and the opposite for lower vegetation fractions) in both water and energy-limited regions of West Africa. Thus, the coupling between the WAM dynamics and land surface processes cannot be over emphasized.
A more recent study by Li et al. (2015) reported that biases in radiation fluxes that originated from radiation physics influence radiative forcing and the spatial distribution and intensity of WAM precipitation. Likewise, different radiation treatments reproduced different meridional surface temperature gradients between the Sahel and Guinea coast, a major driver of the WAM. This variation affects the position of both the AEJ and low-level monsoon inflow from the Gulf of Guinea coast. Noble et al. (2014) showed that Grell-Devenyi CPS has a stronger linear relationship than KF CPS in its ability to reproduce vorticity maxima associated with the AEW. The Grell-Devenyi scheme was also shown to perform relatively well in simulating the westward-propagating precipitation maxima associated with AEW (Noble et al. 2017). Klein et al. (2015) used a multi-physics ensemble approach to reproduce the WAM and purported that both microphysics (MP) and PBL have significant contributions to the ensemble spread of monsoon precipitation over West Africa. Moreover, the PBL was found to impact more on cloud fraction and thus have stronger influence on the movement of the monsoon rainband. These studies underscored the crucial role of physical parameterization in the simulation of WAM and the difficulty in the model setup giving that there are numerous available parameterization schemes in WRF model. The complexity in the model setup raises an issue of having the best physics combination as presented in earlier studies (Flaounas et al. 2011; Noble et al. 2014). Further, conclusions from these studies however stressed that any kind of physics evaluation is subjective and depends on the verification techniques, region of focus, and variables of interest.
The goal of this study is to complement previous studies by further quantifying the dependency of WAM simulations on the choice of physics parameterizations with focus on newly improved schemes. The motivation behind the approach is to identify optimal combinations of various physics schemes for long-term regional climate simulation over the monsoon region. This is intended to provide guidance for the model community in making selection of optimal sets of physics parameterization for WAM simulations and applications and will be used as a basis for follow-on studies over longer periods and for regional climate projection. The study focuses and presents the inter-comparison of some selected regional physics from choices of MP, PBL, and cumulus (CU) parameterization schemes. Section 2 gives a detailed description of the WRF model, the data used, and the experimental design. Section 3 presents and discusses the results, and conclusions are drawn in Section 4.
2 Data and methods
2.1 WRF model configuration
This study used the WRF model (version 3.8.1 released in 2016) to simulate a 2-month regime of WAM from August to September in 2007, which was observed to be a normal monsoon year. During this regime, the WAM is fully developed in August and consistent with the Saharan heat low over land and the highest pressures in southern tropical Atlantic, thereby bringing about widespread of rainfall in the monsoon domain; thereafter, the westerly wind speed drastically decrease with no significant change in the area of westerly wind in September (Janicot et al. 2008). Another set of simulations was done using the later version 3.9 of the WRF model to test the newly modified Grell-Freitas CU scheme (hereafter, nGF).
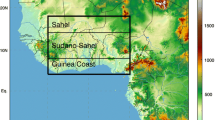
The domain is centered on the West African region (0°–20° N, 20° W–20° E; outer red box in Fig. 1) and also has an area of the Atlantic Ocean, which serves as the major source of moisture carried into the region by the monsoon flow. The horizontal grid size is 20 km and the center is at 12.5° N and longitude 0°. The initial and lateral boundary conditions are from ECMWF Interim Re-Analysis (ERA-Interim) at horizontal resolution of 0.75° (Dee et al. 2011) and 1° resolution National Centers for Environmental Protection (NCEP) final analysis (FNL) initial soil data (sea surface temperature, soil moisture, and temperature) from the NCAR’s Computational and Information Systems Laboratory Research Data Archive (CISL RDA) (NCEP FNL 2000). The reason for using the FNL soil data is because it is more consistent with the soil layers and scheme of the unified Noah land-surface model used. In this study, the first 5 days were used as spin-up, so only 6 August to 30 September 2007 was analyzed.
2.2 Model validation datasets
West Africa is one of the data sparse regions where the conventional rain gauge and synoptic weather station network remain inadequate for validating the spatiotemporal distribution of the model results. Therefore, the skill of precipitation simulation is assessed using satellite rainfall products (SRPs) from Tropical Rainfall Measurement Mission (TRMM; Huffman et al. 2007), Climate Prediction Center (CPC) MORPHing technique (CMORPH; Joyce et al. 2004), and GPCP (Huffman et al. 2009, 2016). The SRP was interpolated at 1° × 1° resolution using the first-order conservative remapping method (Jones 1999). The reliance on the precipitation verification analysis has to be made with caution because of the differences between SRPs (Noble et al. 2017) as a result of their observation platforms and different algorithms used in producing them. However, the high temporal and spatial (3 hourly and 0.25°) resolution TRMM 3B42 product is one of the reliable sources for merged high-quality precipitation estimates (Huffman et al. 2007) and it is therefore used as the standard for evaluating the model outputs. Global Precipitation Climatology Project 1° Daily (GPCP 1dd) is another reliable SRP produced from optimized merged estimates computed from microwave, infrared, and sounder data observed by the international constellation of precipitation-related satellites and precipitation gauge analysis (Huffman et al. 2009, 2016). Also, the model results are compared with the CMORPH global precipitation analyses produced at high spatial and temporal resolution similar to that of TRMM.
Reanalyzed surface air temperature products including ERA-Interim, NCEP, Modern-Era Retrospective analysis for Research and Applications (MERRA; Rienecker et al. 2011), and global surface air temperature (GSAT; ensemble of ERA, NCEP, and MERRA), interpolated at 0.5° × 0.5° resolution, are used to validate the model surface temperature. The bias correction of both monthly mean maximum (Tmax) and minimum (Tmin) GSAT was performed using the Climate Research Unit Time Series version 3.10 (CRU TS3.10) data (Wang and Zeng 2014).
2.3 Physics options
A total of 27 runs were produced from the combinations of two microphysics, six cumulus convections, and three planetary boundary layer schemes (see Table 1 for references). The WRF model has quite a number of options with varying levels of complexities for each physics process. These three physics play important roles to modify the atmospheric moisture and heat distribution, and thus, their proper treatment is critical to realistic simulation and prediction of the WAM and its associated dynamics. The selected schemes are widely used within the WRF community and have been shown to perform well over different regions. Other physics like the unified Noah land-surface model scheme (Chen and Dudhia 2001) and Rapid Radiative Transfer Mdel (RRTMG) schemes (Iacono et al. 2008) were kept constant in all simulations.
The WSM5 MP scheme allows no supercooled water and has immediate melting of snow below the melting layer, whereas the Goddard (GD) MP scheme is a six-class microphysics with graupel and modifications for ice/water saturation based on Lin et al. (1983). The YSU is a planetary boundary layer (PBL) scheme with stronger boundary layer top entrainment and boundary layer inner mixing than MYJ (Zhang et al. 2012). MYJ is a local closure scheme that predicts turbulent kinetic energy (TKE). MYNN PBL uses local TKE-based vertical mixing in boundary layer and free atmosphere. KF is a mass flux type CU parameterization scheme with updrafts and downdrafts, entrainment, and detrainment of cloud, rain, ice, and snow. It has both deep and shallow convections and uses a convective available potential energy (CAPE) removal time-scale closure. BMJ is a profile adjustment scheme that relaxes both deep and shallow profiles to a reference profile without explicit updraft, downdraft, or cloud entrainment. Both GF and nGF are mass flux schemes that have multiple closures, including CAPE removal, quasi-equilibrium, moisture convergence, and cloud-base ascent. The difference in both schemes is that nGF has the capability to trigger mid-level convection and its shallow convection also produces rainfall. Similar to the KF, the new Tiedtke (nTDK; Tiedtke 1989; Zhang et al. 2011) is a mass flux scheme with updrafts and downdrafts. Another newly modified scheme is a CAPE removal time-scale simplified Arakawa-Schubert (nSAS) scheme that has momentum transport with a pressure term and new mass flux type shallow convection that is different from the earlier SAS CU. The 27 physics scheme combinations tested are shown in Fig. 13. Based on the WSM5 microphysics test results, three less CU schemes were tested with GD microphysics.
2.4 Model evaluation method
There are various evaluation statistics that can be used to assess model performance. However, there is no single statistic that encapsulates all aspects of interest. It is therefore important to consider different performance statistics and also to understand the type of information they might provide. In this study, a few statistics of the model outputs are computed in order to find the optimal physics combinations for long-term simulations. These statistics examine the strength of correlation, systematic error, and accuracy of the model in comparison to observation and are detailed below.
One of the statistics used is correlation coefficient (r), a measure of the strength of the linear relationship between model and observations.
where O represents observation or reanalysis, M model output, σ standard deviation, and n number of data points in the series.
The mean bias (B) is an indication of the mean over- or underestimate of predictions. It has the same units as the quantities being considered.
The mean absolute error (MAE) determines the mean error between model and observation regardless of whether it is an over- or underestimate. It also has the same units as the quantities being considered:
Furthermore, to compare and rank the physics performance based on their statistics, a new comparative model skill score (MSS) is defined and computed. The first step in computing MSS is to calculate the time and space statistics. The space statistics were derived from the time average of the evaluation area (in Fig. 1) and quantify the error in the mean patterns. The time statistics are based on comparing the time series of space-averaged values within the same area and quantify errors in phase. Thereafter, the MSS is calculated from the sum of the normalized (Xnorm) values of time (t) and space (S) correlation coefficient (r), bias (B), and mean absolute error (MAE).
where X could be either time or space averaged r, |B|, and MAE, and Xmin and Xmax are defined by the worst and best of the 27 compared simulations.
where |B|norm = S|B|norm = t|B|norm
Simulations with higher MSS values perform better while those with lower values have poorer performance. Each of the five normalized terms has values ranging from 0 for the worst to 1 for the best, so the scores for a given variable range between 0 and 5.
3 Results and discussion
3.1 Precipitation analysis
Figure 2 shows the diurnal cycle of precipitation rate averaged over latitudes 5°–15° N and longitudes 10° W–10° E for 6 August to 30 September 2007. Each of the stacked plots (Fig. 2a–f) displays the combinations of MP and PBL physics. The black and colored lines are the SRPs and CU simulations, respectively. Both TRMM (reference) and CMORPH SRPs are analyzed and compared with the individual simulations. The peak of diurnal precipitation of the two SRPs occurred at 18 h (Fig. 2) in agreement with the findings of Klein et al. (2015). Some of the simulations reproduced early diurnal precipitation peak at 15 h relative to the reference peak. The peak of nTDK, BMJ, and KF occurred at 15 h whereas that of nSAS, GF, and nGF occurred same time with TRMM and CMORPH, suggesting that some CU schemes trigger earlier convective activity. The right peak simulated by some CUs underscores some success made towards a more realistic parameterization of convective process in nSAS and nGF. However, the differences in model diurnal precipitation peaks lay emphasis on some of the uncertainties inherent in the representation of sub-grid scale convective processes and thus suggest the need to explicitly represent deep convection with a more realistic model dynamics (Prein et al. 2013). Further results show that nGF simulated a delay in the minimum rainfall compared with observed. In addition, KF and nGF produced more precipitation during the daytime and nighttime, respectively, than other CU schemes.
Figure 3 shows the daily precipitation amount averaged over latitudes 5°–15° N and longitudes 10° W–10° E for 6 August to 30 September 2007. The stack plot is the same as that described in Fig. 2. In Fig. 3, the SRP, including GPCP, daily precipitation phase quite agrees with each other while some model outputs simulated different phases. For example, combinations of KF and nGFs with WSM5-YSU produced excess daily precipitation amounts for some cases. Other model runs give similar daily precipitation patterns as TRMM but with varying magnitudes. Also, the simulations reproduced the observed wet period in August and dry period in September.
a–f Time series of daily precipitation amount (mm/day) averaged over 5°–15° N and 10° W–10° E. The stack plot is the same as described in Fig. 2
The averaged spatial distribution of daily precipitation is presented in Fig. 4. Only few of the combinations that performed best relative to the CU schemes are displayed. The SRP daily precipitation patterns agree with each other. They all showed precipitation maximum cores around the west coast of the region between latitudes 5°–15° N and also around the Cameroun Mountain. This pattern was also found in most of the model simulations. From the results in Fig. 4, it can be inferred that the orographic effect of the Cameroun Mountain caused the model to produce intense precipitation maximum around the area. Another agreement is evident in the reduced precipitation amount between longitudes 0°–10° W and northward of latitude 7° N. This is pronounced in some runs with nTDK, GF, nGF, and KF. The KF CU triggered strong convection and usually unrealistic precipitation events with rotational features that looked like tropical cyclones over land (not shown). This behavior in the KF runs resulted in overestimated daily precipitation amounts.
There were noticeable spatial systematic errors in all simulations (e.g., in Fig. 5). The error however varies in location and magnitude. For example, KF in Fig. 5a produced wet precipitation bias > 10 mm/day between 10°–15° N latitude band and dry bias around coastal regions. Other cumulus schemes had moderately wet and dry precipitation biases.
Figure 6 shows the time-longitude cross section (Hovmöller) of daily precipitation that describes the westward propagation of precipitation maxima linked to the activity of the AEWs. Some studies have shown a tight coupling of convective rainfall activity with the African Easterly Waves (AEWs: Duvel 1990; Thorncroft and Blackburn 1999; Diedhiou et al. 1999; Noble et al. 2017). All SRPs showed more active westward-propagating maxima associated with AEWs in August and less in September. Also inherent in the models is the westward movement of the precipitation maxima but the phase may differ. The AEWs are found to be active all through the considered period in KF and GF but the reduced activity later was more realistic in nTDK, BMJ, and nGF. In BMJ, the waves are less organized and appear more like episodic events but nTDK, nSAS, and nGF show well-structured linear westward propagation of the precipitation maxima. Similar patterns of well-defined active westward propagation of precipitation maxima in August occur for TRMM, GPCP, and CMORPH data.
3.2 Evaluation of precipitation
As emphasized earlier in Section 2 of this study, the information of interest in this study is the correlation, systematic error, and accuracy of the model outputs relative to reference observations.
Figure 7 presents the scatter plots of precipitation for both time- and space-averaged statistics. TRMM was used as the reference observed data to evaluate other SRPs and model precipitation. GPCP and CMORPH agree with TRMM in terms of lesser MAE and stronger correlation both at spatial and temporal scales. Combinations with nTDK, BMJ, and nSAS show high skill with correlations between 0.4–0.65 and MAE of < 3 mm/day in space and time (Table 2). Most simulations with KF or old GF performed poorly. However, the old GF combined with WSM5-MYNN performed fairly in WRFV3.8.1 while the modified nGF in WRFV3.9 produces a much better simulation when combined with the same MP and PBL schemes, that is, WSM5-MYNN. The improved performance of the nGF underlines the positive effects of its modification.
Scatter plots of precipitation statistics for a time MAE against time correlation, b space MAE against space correlation, and c space against time correlation; the best bar indicates the direction of the best model and observation. The shapes represent PBL schemes, size of the shapes represents the microphysics, and the colors are the CUs
Furthermore, the MSS of the individual model simulations were ranked from the highest to the lowest in Table 3. It can be seen from the table that runs with BMJ, nTDK, and nSAS had high MSS compared with the KF, GF, and nGF with low MSS. However, the nGF improved much with WSM5-MYNN highlighting its advantage over the old version. It is also possible to group the simulations sharing a particular parameterization. For instance, the average group score with GD MP has better skill than that with WSM5 while MYNN PBL group score is found to be higher than other PBLs (not shown). Also, the average group score of nSAS CU runs produces the highest MSS among the selected CU schemes.
3.3 Surface temperature analysis
Similar to the precipitation, the diurnal cycle of surface temperature at 2 meters (T2m) are computed for each of the 27 member runs in Table 2 and compared with ERA (reference), MERRA, NCEP, and GSAT. Figure 8 shows the diurnal cycle of T2m with and without differencing relative to ERA, that is, Fig. 8a, b, respectively. Figure 8b displays the biases inherent in model outputs and other data sets relative to ERA. In Fig. 8a, the surface temperatures for both model and reanalysis reach their minimum and peak at 06 and 15 h, respectively. However, with the observed minimum and maximum reproduced in all simulations, it is less clear to observe the latent systematic error in Fig. 8a.
Stack plot of a diurnal circle of surface temperature and b difference with respect to ERA reanalysis for Aug–Sep 2007. The stack plot is the same as described in Fig. 2 and the bias plot was made to clearly see the difference between the model and reference datasets
It is evident in Fig. 8b that the magnitude of peak in MERRA is earlier at 12 h compared with other reanalyses. Combinations with YSU produce the highest difference ranging between 0.4 and 0.8 °C during early daytime and nighttime, being warm-biased at night. The simulations of MYNN MP are closer to ERA in the early hours of the day than MYJ; however, both show cooling during evening and nighttime. Also, T2m responds differently to the combination of CU schemes with MP and PBL. For example, nSAS mostly simulates a warm bias in all combinations while GF reproduces cooling. The cooling in nTDK is obviously stronger with GD than with WSM5, and this cumulus scheme seems to vary more with the selected microphysics than other cumulus options. At night, the nGF is warmer than GF but cooler during the daytime.
Figure 9, displaying the daily average 2 m temperature in the region over the 2-month period, shows the existence of bias between ERA and NCEP, MERRA, and GSAT, that is, ERA is mostly cooler than the other reanalysis products. However, the models and reanalysis products have the same pattern of daily T2m. On average, all series tend to fluctuate between 298 and 299 K (~ 25–26 °C) in August and thereafter warmed by 1–2 °C in September. The warming marks the end of the monsoon season when the rainband, which tightly couples with the movement of the Inter-Tropical Discontinuity (ITD), retreats southwards such that cloud cover and precipitation decrease and insolation increases. The magnitude of the daily surface temperature series is higher in YSU PBL simulations but consistently more realistic in MYJ and MYNN. One distinguishing difference between GF and nGF is that GF is more out of phase with ERA compared with nGF. This behavior is more pronounced in the month of September where the T2m by GF is found to be cooler than the reference data.
a–f Time series of daily 2 m surface temperature averaged over 5°–15° N and 10° W–10° E. The stack plot is the same as described in Fig. 2
Unlike the highly variable precipitation, the model simulates a more realistic spatial distribution of surface temperature (as shown in Fig. 10). The increasing temperature gradient in the Sahel (above 10° N) was well captured in the model. The cooling over higher grounds such as that of the Cameroun Mountain, Jos plateau, and Guinea highland is also seen clearly. The temperature over the ocean is better simulated in runs shown here with BMJ and nSAS when compared with ERA.
The spatial biases in Fig. 11 show that T2m in the model and reanalysis differs from ERA within the range of − 3 to 3 °C. All reanalyses show a cool bias over the Sahel and warming around the Guinea coast relative to ERA. Similarly, the models simulate relative coolness in some parts of the Sahel and warmth near the Guinea coast where, as seen in Fig. 10, the hot area extends further south. nSAS with WSM5-YSU simulates a general warming over a large land area and some parts of the ocean near the equator. nTDK and GF combined with WSM5-MYNN simulate about 1 °C cooling over the ocean while KF, BMJ, and nGF reproduce warming of the same magnitude around the equatorial region of the Atlantic Ocean.
3.4 Evaluation of surface temperature
A similar approach as for precipitation is used to evaluate the surface temperature. Figure 12 shows that both reanalysis and model simulations are comparable with ERA (reference data). The models perform better in time MAE than in space MAE but better in space correlation than time correlation. The role of the MP scheme is not clearly seen with T2m as both WSM5 (big shapes) and GD (small shapes) MP cluster together in the plot. However, some combinations with YSU (squares) perform poorly both in space and time statistics. For example, in Fig. 12b, two of nSAS and BMJ simulations combined with YSU produced the highest MAE (> 0.7 °C). Some MYJ and MYNN have the lowest MAE and stronger r in space and time average, respectively. Furthermore, KF or GF CUs perform poorly in the overall simulation (as was seen in precipitation). The nGF and nTDK compete favorably with each other and simulate T2m better. This again underscores the significant improvement in the modified nGF CU, most especially when combined with MYNN PBL.
Scatter plots of surface temperature at 2 m for a time MAE against time correlation, b space MAE against space correlation, and c space against time correlation; similar to precipitation scatter plots, the best bar indicates the direction of the best model and observation. The shapes represent PBL schemes, size of the shapes represents the microphysics, and the colors are the CUs
The MSS, computed from the normalized model statistics in Table 4, is used to rank the model’s performance based on how well each simulation reproduced T2m. The relative average group score of GD, MYNN, and nTDK show higher skill. But the combinations with WSM5-MYNN-nTDK and GD-MYJ-BMJ are found to rank within the top 3 (Table 5) combinations as was seen in the precipitation ranking.
The physics combinations of WSM5-MYNN-nTDK and GD-MYJ-BMJ are ranked highest (Table 6) with the combined statistics of precipitation and surface temperature equally weighted to give a score out of 10. Based on the model rankings, some combinations are however found to have good performance (subjectively defined as MSS > 7.5), others moderate, and some performed poorly (MSS < 5) with precipitation and surface temperature. This corroborates the conclusion of Flaounas et al. (2011) and Noble et al. (2014) that any evaluation adopted is subjective and could depend on the variable of interest. However, it is notable that the good scheme combinations are probably not separated in a statistically significant way. A comprehensive summary of results in Table 6 is further presented in Fig. 13. This figure shows no significant difference between the MP used as their combinations with the same CU and PBL schemes fall within the same performance category based on the overall MSS. For the CU schemes, all nTDK combinations produce good simulations while KF, on the contrary, performs moderately with MYNN and poorly with YSU and MYJ combinations. BMJ and nSAS combinations are both good with MYJ and MYNN and moderate with YSU. Both GF and nGF as stated earlier produce a better simulation only when combined with MYNN. Furthermore, the simulations with MYNN PBL, when combined with CU and MP schemes, have a general advantage over the other two PBL schemes; however, its skill is also reduced when used with the KF CU scheme. On the other hand, MYJ only performs well with BMJ, nSAS, and nTDK CU. And the YSU PBL performance is good only when combined with nTDK.
The 27 different WRF model physics combinations included in the sensitivity analysis. The combinations containing the asterisked CU scheme are runs from the newly modified Grell-Freitas in WRFV3.9. The figure shows a summary of results in Table 6. Green highlights are good combinations while yellow and red are moderate and poor combinations, respectively
However, it is quite important to note that factors such as the initial and lateral boundary conditions may influence the performance of the identified good physics combinations for longer simulations of the WAM regime. This may affect the skill scores of the identified best-performing regional physics combination. The effect appears however to be less than one standard deviation from the 2-month test when compared with the mean of some 8-month (March–October 2007) tests (not shown). This implies that the model skill score (MSS) of the long-term runs lies within the variability of that found using the same 2-month regime from the 8-month runs. Furthermore, the results of this study also point out the schemes that are developed together tend to perform better (e.g., MYJ-BMJ; MYNN-nGF; but less so YSU-nSAS) even though their primary tuning has not been for West Africa.
4 Conclusion
A total of 27 WRF simulations of the August–September 2007 monsoon regime, run on a 20-km grid over West Africa, were evaluated to investigate the sensitivity of the WAM regime to three model physics (i.e., cumulus (CU), microphysics (MP), and planetary boundary layer (PBL) parameterization schemes). This study focuses on hourly and daily precipitation and surface temperature at 2 m during a period of widely spread convective activity over the West African region. The 27 WRF runs are derived from the combinations of two (2) MP, six (6) CU, and three (3) PBL schemes, three of which were done from the latest WRF version 3.9 to test the advantage of the improved nGF CU over the old one in WRF version 3.8.1. The model’s precipitation was evaluated against the TRMM (reference), CMORPH, and GPCP SRPs. Also, the surface temperature was evaluated against the ERA (reference), NCEP, MERRA, and GSAT, which is an ensemble of the three corresponding reanalysis products.
All model physics combinations simulated the diurnal cycles of surface temperature more adequately than precipitation, however, with some biases. Some combinations simulated realistic westward propagation of precipitation maxima associated with the AEWs. Correlations found in surface temperature are higher than for precipitation, which depicts that the simulations have higher skill in simulating temperature as may be expected because of the variation of surface characteristics over the area. This also suggests that any form of evaluation is subjective and varies with respect to the variable of interest. Based on the overall MSS, the best-performing physics combinations in both surface temperature and precipitation for the period of study are WSM5-MYNN-nTDK and GD-MYJ-BMJ. However, the good combinations are rather clustered in our overall skill scores and any combinations highlighted in green in Fig. 13 should be considered not significantly different within our error margins and equally adequate for use to investigate the seasonal, annual, and decadal variability of WAM as well as its future (climate) outlook.
References
Chen F, Dudhia J (2001) Coupling an advanced land surface–hydrology model with the Penn State–NCAR MM5 modeling system. Part I: model implementation and sensitivity. Mon Weather Rev 129(4):569–585
Dee DP, Uppala SM, Simmons AJ, Berrisford P, Poli P, Kobayashi S, Andrae U, Balmaseda MA, Balsamo G, Bauer P, Bechtold P, Beljaars ACM, van de Berg L, Bidlot J, Bormann N, Delsol C, Dragani R, Fuentes M, Geer AJ, Haimberger L, Healy SB, Hersbach H, Hólm EV, Isaksen L, Kållberg P, Köhler M, Matricardi M, McNally AP, Monge-Sanz BM, Morcrette JJ, Park BK, Peubey C, De Rosnay P, Tavolato C, Thépaut JN, Vitart F (2011) The ERA-Interim reanalysis: configuration and performance of the data assimilation system. QJR Meteorol Soc 137:553–597. https://doi.org/10.1002/qj.828
Diedhiou A, Janicot S, Viltard A, De Felice P, Laurent H (1999) Easterly wave regimes and associated convection over West Africa and tropical Atlantic: results from NCEP/NCAR and ECMWF reanalyses. Clim Dyn 15:795–822
Duvel JP (1990) Convection over tropical Africa and the Atlantic Ocean during northern summer. Part II: modulation by easterly waves. Mon Weather Rev 118:1855–1868
Flaounas E, Bastin S, Janicot S (2011) Regional climate modelling of the 2006 West African monsoon: sensitivity to convection and planetary boundary layer parameterization using WRF. Clim Dyn 36:1083–1105. https://doi.org/10.1007/s00382-010-0785-3
Grell GA, Freitas SR (2013) A scale and aerosol aware stochastic convective parameterization for weather and air quality modeling. Atmos Chem Phys Discuss 13(9):23845–23893
Hagos S, Leung LR, Xue Y, Boone A, De Sales F, Neupane N, Huang M, Yoon JH (2014) Assessment of uncertainties in the response of the African monsoon precipitation to land use change simulated by a regional model. Clim Dyn 43(9–10):2765–2775
Han J, Pan HL (2011) Revision of convection and vertical diffusion schemes in the NCEP global forecast system. Weather Forecast 26(4):520–533
Hong SY, Dudhia J, Chen SH (2004) A revised approach to ice microphysical processes for the bulk parameterization of clouds and precipitation. Mon Weather Rev 132(1):103–120
Hong SY, Noh Y, Dudhia J (2006) A new vertical diffusion package with an explicit treatment of entrainment processes. Mon Weather Rev 134(9):2318–2341
Huffman GJ, Bolvin DT, Nelkin EJ, Wolff DB, Adler RF, Gu G, Hong Y, Bowman KP, Stocker EF (2007) The TRMM multisatellite precipitation analysis (TMPA): quasi-global, multiyear, combined-sensor precipitation estimates at fine scales. J Hydrometeorol 8(1):38–55
Huffman GJ, Adler RF, Bolvin DT, Gu G (2009) Improving the global precipitation record: GPCP version 2.1. Geophys Res Lett 36(17). https://doi.org/10.1029/2009GL040000
Huffman GJ, Bolvin DT, Adler RF (2016) GPCP Version 1.2 One-Degree Daily Precipitation Data Set. Research Data Archive at the National Center for Atmospheric Research, Computational and Information Systems Laboratory. doi:https://doi.org/10.5065/D6D50K46
Iacono MJ, Delamere JS, Mlawer EJ, Shephard MW, Clough SA, Collins WD (2008) Radiative forcing by long-lived greenhouse gases: calculations with the AER radiative transfer models. J Geophys Res Atmos 113(D13). https://doi.org/10.1029/2008JD009944
Janicot S, Thorncroft CD, Ali A, Asencio N, Berry G, Bock O, Bourles B, Caniaux G, Chauvin F, Deme A, Kergoat L, Lafore JP, Lavaysse C, Lebel T, Marticorena B, Mounier F, Nedelec P, Redelsperger JL, Ravegnani F, Reeves CE, Roca R, de Rosnay P, Schlager H, Sultan B, Tomasini M, Ulanovsky A, ACMAD forecasters team (2008) Large-scale overview of the summer monsoon over West Africa during the AMMA field experiment in 2006. Ann Geophys 26:2569–2595
Janjić ZI (1994) The step-mountain eta coordinate model: further developments of the convection, viscous sublayer, and turbulence closure schemes. Mon Weather Rev 122(5):927–945
Janjić ZI (2000) Comments on “Development and evaluation of a convection scheme for use in climate models”. J Atmos Sci 57(21):3686–3686
Jones PW (1999) First-and second-order conservative remapping schemes for grids in spherical coordinates. Mon Weather Rev 127(9):2204–2210
Joyce RJ, Janowiak JE, Arkin PA, Xie P (2004) CMORPH: a method that produces global precipitation estimates from data at high spatial and temporal resolution. J Hydrometeorol 5:487–503
Kain JS (2004) The Kain–Fritsch convective parameterization: an update. J Appl Meteorol 43:170–181. https://doi.org/10.1175/1520-0450(2004)043,0170:TKCPAU.2.0.CO;2
Klein C, Heinzeller D, Bliefernicht J, Kunstmann H (2015) Variability of West African monsoon patterns generated by a WRF multi-physics ensemble. Clim Dyn 45(9–10):2733–2755
Klein C, Bliefernicht J, Heinzeller D, Gessner U, Klien I, Kunstmann H (2017) Feedback of observed interannual vegetation change: a regional climate model analysis for the West African monsoon. Clim Dyn 48:2837–2858. https://doi.org/10.1007/s00382-016-3237-x
Li R, Jin J, Wang SY, Gillies RR (2015) Significant impacts of radiation physics in the weather research and forecasting model on the precipitation and dynamics of the West African monsoon. Clim Dyn 44(5–6):1583–1594
Lin YL, Farley RD, Orville HD (1983) Bulk parameterization of the snow field in a cloud model. J Clim Appl Meteorol 22(6):1065–1092
Nakanishi M, Niino H (2004) An improved Mellor–Yamada level-3 model with condensation physics: its design and verification. Bound-Layer Meteorol 112(1):1–31
Nakanishi M, Niino H (2006) An improved Mellor–Yamada level-3 model: its numerical stability and application to a regional prediction of advection fog. Bound-Layer Meteorol 119(2):397–407
National Centers for Environmental Prediction/National Weather Service/NOAA/U.S. Department of Commerce (2000) updated daily. NCEP FNL Operational Model Global Tropospheric Analyses, continuing from July 1999. Research Data Archive at the National Center for Atmospheric Research, Computational and Information Systems Laboratory. doi:https://doi.org/10.5065/D6M043C6. Accessed 09 March 2017
Noble E, Druyan LM, Fulakeza M (2014) The sensitivity of WRF daily summertime simulations over West Africa to alternative parameterizations. Part I: African wave circulation. Mon Weather Rev 142(4):1588–1608
Noble E, Druyan LM, Fulakeza M (2017) The sensitivity of WRF daily summertime simulations over West Africa to alternative parameterizations. Part II: precipitation. Mon Weather Rev 145(1):215–233
Prein AF, Gobiet A, Suklitsch M, Truhetz H, Awan NK, Keuler K, Georgievski G (2013) Added value of convection permitting seasonal simulations. Clim Dyn 41:2655–2677
Redelsperger JL, Diongue A, Diedhiou A, Ceron JP, Diop M, Gueremy JF, Lafore JP (2002) Multi-scale description of a Sahelian synoptic weather system representative of the West African monsoon. Q J R Meteorol Soc 128(582):1229–1257
Rienecker MM, Suarez MJ, Gelaro R, Todling R, Bacmeister J, Liu E, Bosilovich MG, Schubert SD, Takacs L, Kim GK, Bloom S (2011) NASA’s modern-era retrospective analysis for research and applications (MERRA). J Clim 24(14):3624–3648
Tao WK, Simpson J, McCumber M (1989) An ice-water saturation adjustment. Mon Weather Rev 117(1):231–235
Thorncroft CD, Blackburn M (1999) Maintenance of the African easterly jet. Q J R Meteorol Soc 125:763–786
Tiedtke MICHAEL (1989) A comprehensive mass flux scheme for cumulus parameterization in large-scale models. Mon Weather Rev 117(8):1779–1800
Wang A, Zeng X (2014) Global hourly 0.5-degree land surface air temperature datasets. Research Data Archive at the National Center for Atmospheric Research, Computational and Information Systems Laboratory. doi:https://doi.org/10.5065/D6PR7SZF. Accessed 05 April 2017
Zhang C, Wang Y, Hamilton K (2011) Improved representation of boundary layer clouds over the Southeast Pacific in ARW-WRF using a modified Tiedtke cumulus parameterization scheme. Mon Weather Rev 139(11):3489–3513
Zhang C, Wang Y, Lauer A, Hamilton K (2012) Configuration and evaluation of the WRF model for the study of Hawaiian regional climate. Mon Weather Rev 140(10):3259–3277
Acknowledgements
Many thanks to NCAR’s MMM Laboratory for supporting the research work. Also thanks to Wei Wang and Changhai Liu for comments, and Ming Chen and Michael Duda for technical supports. The initial model configuration was done on the WACS-GRP FUTA cluster unit. We would like to acknowledge high-performance computing support from Yellowstone and Cheyenne (doi:https://doi.org/10.5065/D6RX99HX) provided by NCAR’s Computational and Information Systems Laboratory, sponsored by the National Science Foundation. Special thanks goes to the anonymous reviewers who greatly helped to improve the quality of this manuscript.
Funding
The German Federal Ministry of Education and Research (BMBF) primarily funded this research through the WACS-GRP FUTA.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Gbode, I.E., Dudhia, J., Ogunjobi, K.O. et al. Sensitivity of different physics schemes in the WRF model during a West African monsoon regime. Theor Appl Climatol 136, 733–751 (2019). https://doi.org/10.1007/s00704-018-2538-x
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00704-018-2538-x