Spatio-temporal modelling of wind speed variations and extremes in the Caribbean and the Gulf of Mexico

Abstract

The wind speed variability in the North Atlantic has been successfully modelled using a spatio-temporal transformed Gaussian field. However, this type of model does not correctly describe the extreme wind speeds attributed to tropical storms and hurricanes. In this study, the transformed Gaussian model is further developed to include the occurrence of severe storms. In this new model, random components are added to the transformed Gaussian field to model rare events with extreme wind speeds. The resulting random field is locally stationary and homogeneous. The localized dependence structure is described by time- and space-dependent parameters. The parameters have a natural physical interpretation. To exemplify its application, the model is fitted to the ECMWF ERA-Interim reanalysis data set. The model is applied to compute long-term wind speed distributions and return values, e.g., 100- or 1000-year extreme wind speeds, and to simulate random wind speed time series at a fixed location or spatio-temporal wind fields around that location.

1 Introduction

Due to the increased regulation pressure on maritime transport in terms of energy efficiency and emission control (DNV 2015), there is a growing interest in the study of the characteristics of wind/wave variation at sea. To develop solutions for utilizing renewable wind energy in ship propulsion (ABS 2013), it is greatly important to have access to reliable wind statistics along arbitrary ship routes. These statistics are used to estimate the average performance of a ship/offshore renewable energy unit and to assess the risk of extreme winds. Furthermore, extreme winds (and waves) in coastal areas can destroy infrastructures, cause human loss leading to great economical damages. Therefore, accurate modelling of wind speed variations is important for addressing related engineering problems.

Typically, the variation in wind speed at a certain location or in a certain region is described by its Cumulative Distribution Function (CDF). The long-term CDF of the wind speed, i.e., fraction of time when wind speed is below a threshold during one year, is often fitted with Weibull distributions; e.g., see DNV (2010) and Morgan et al. (2011). However, in the Caribbean sea, the Weibull model does not fit well with the observed data, particularly for regions where extreme wind speeds can arise during hurricanes or tropical storms (see, e.g., Mao and Rychlik (2016)). The limitation may compromise engineering safety when the Weibull model is used to determine the extreme design condition, i.e., the so-called 100/1000-year extreme wind speeds, for engineering structures in such regions.

However, the rarity of the high winds caused by, e.g., hurricanes and other storms, makes empirical estimation of extreme wind speeds difficult; instead, estimates of such extreme winds can be derived from stochastic models of wind speeds variability. In this study, a new model (named as the hybrid model) for wind speed variability is proposed. The proposed model is used to estimate the frequencies of extreme winds, i.e., winds exceeding a fixed high threshold, by means of the so-called Rice’s method, which was presented in details in, e.g., Azais and Wschebor (2009). Particular applications of this method were presented in, e.g., Baxevani and Rychlik (2006), Rychlik et al. (2011).

Methods based on the univariate extreme value theory (Coles 2001) are used to validate the proposed approach. For example, by fitting the generalized extreme value (GEV) distribution to yearly maximum wind speeds at a fixed location, the extreme wind speed estimated from the fitted GEV distribution is used as a reference value to validate the Rice’s method that uses the proposed spatio-temporal wind model. Alternatively, Peak over Threshold (POT) method (Davison and Smith 1990) could be employed. However, strong seasonal wind speed variation and correlation make the POT method very complex to use, and less suitable for our validation purpose. Methods of modelling extreme wind speeds due to hurricanes or tropical storms have been investigated by many researchers (see, e.g., Jagger and Elsner (2006) and Reich and Fuentes (2007) and references therein). An extensive publication list can be also found in Larsén et al. (2016). Recently, a large focus is also put on the modelling of multivariate extremes, spatial extremes (max-stable processes), and spatio-temporal extremes (see, e.g., Coles (1993)). In this study, an example of applying the proposed model to derive the distribution of maximum wind speeds in August in a region south of Haiti is presented in Section 7. However, more detailed studies of this problem are outside of the scope of this paper.

Spatio-temporal models are often based on well understood Gaussian models, but real data seldom follow Gaussian distributions perfectly. Hence, transformed Gaussian processes (fields) are often used for the modelling. Popular transformations proposed by Brown et al. (1984), Winterstein et al. (1994) etc. are frequently used in engineering literature. For example, the exponential transformation proposed by Brown et al. (1984) was successfully used in Mao and Rychlik (2016) to model wind speed distributions in the Northern Atlantic. However, for the Caribbean sea, the kurtosis of exponentially transformed wind speeds is often significantly exceeding the Gaussian threshold (three), and hence, this model underestimates the frequencies of high wind speeds. Consequently, the Hermite transformation proposed by Winterstein et al. (1994) was also tested. This transformation is a monotonic cubic polynomial, which is calibrated such that the first four moments (mean, variance, skewness, and kurtosis) of the transformed model are equivalent to the moments of the data. The following example shows that the Hermite transformed Gaussian model is overestimating frequencies of high wind speeds in the Caribbean sea. The reason is that the extreme storms are very rare.

Example

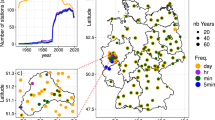
Wind speeds in August (2000–2015) at the location (72.75 W, 17.25 N) as shown in Fig. 1 are used for the investigation. Firstly, frequencies of upcrossing of level u and empirical probabilities that wind speeds exceed a threshold u have been estimated from the extracted data set. Those empirical characteristics are shown in Fig. 2, together with the expected characteristics, which are evaluated using the fitted transformed Gaussian models based on Brown’s exponential transformation and Winterstein’s Hermite polynomial transformation. The two models either underestimates or overestimates the empirical frequencies and wind speed distribution at the tail. Finally, the expected characteristics evaluated by the proposed hybrid model are also presented. They agree well with the empirical values.

Fig. 1

Upper plot: Sixteen years of hindcast hindcast wind speeds W(t) at the three locations. Lower plot: Movement (shown in the hindcast data) of hurricane Dean close to the coast of Haiti

Fig. 2

Comparison of the distribution and expected upcrossing rates of wind speeds in August at the location (72.75 W, 17.25 N) computed by transformed Gaussian models based on Brown’s exponential and Winterstein’s Hermite Polynomials transformations. The characteristics are compared with the empirical values and that evaluated using the proposed hybrid model

In this paper, the exponentially transformed Gaussian model is used to model wind speeds at locations, where extraordinary meteorological events like extreme storms or lulls may rarely occur. Examples of such events can be seen in the time series shown in Fig. 1. The newly proposed model for W^a is a sum of a Gaussian field and several non-Gaussian random fields (with Laplace distributed amplitudes), which are independent and randomly spread in time and space. This type of model (named as the Hybrid model here) was used in Bogsjö et al. (2012) and Kvarnström et al. (2013) for signals with rarely occurring transients.

The paper is organized as follows. First, the transformed wind speeds X = W^a and methods of estimating the parameter a and the mean, variance and correlation structure of X are presented in Section 2. Then, Section 3 briefly introduces three types of random fields: Gaussian, Laplace, and the hybrid model. In particular, methods of estimating the parameters in the hybrid model are also discussed here and in Section 4. The technical details of the procedures are moved to appendices. Subsequently, Section 5 presents procedures for using the hybrid model in three practical applications, i.e., to derive the long-term wind speed distribution, to estimate the expected number of wind speeds that cross arbitrary values, and to simulate local wind speeds. In Section 6, the hybrid model is validated by three examples/locations, one in the Caribbean sea and two in the Gulf of Mexico, with respect to long-term wind distribution and 100/1000-year extreme wind prediction. Examples illustrating the hybrid model are given in Section 7. The estimation of spatio-temporal extreme wind speeds are also discussed, the Matlab code to simulate the spatio-temporal maximums using the hybrid model is given in the Appendix C.

2 Spatio-temporal modelling of the transformed wind speed X = W ^a

In this study, the term wind speed refers to the 10-min average wind speed (in the unit of m/s at 10 meters above ground level) taken from the ECMWF hindcast database. Let W(p) = W(t_p, x_p, y_p) denote the wind speed at a spatial-temporal location p = (t_p, x_p, y_p). Obviously, the average characteristics of wind speed variation change with seasons t_p ∈ [0,1] (unit: year), and geographical locations (x_p, y_p). However, on shorter spatial and temporal scales, these characteristics can be considered to be constant. More precisely, within a small neighbourhood of p with a spatial radius of several degrees and a time interval of a month, the variability of the wind speed is assumed to be homogeneous and stationary:

$$\begin{array}{@{}rcl@{}} &&W^{a}(\textbf{p}+\textbf{q}) =W^{a}(t_{p} + t, x_{p} + x, y_{p} + y) = X_{\textbf{p}}(t, x, y)\\ &&0.4<a<2, \end{array} $$

(1)

where X_p is a homogeneous field with a mean of m_p, a variance of ${\sigma }_{\textbf {p}}^{2}$ and a correlation function of ρ_p(t,x,y), all of which depend on the location p. In some cases, the index p in X_p(t,x,y), m_p, ${\sigma }^{2}_{\textbf {p}}$ and ρ_p(t,x,y) will be neglected in order to simplify the notation.

The parameters a_p, m_p and ${\sigma }_{\textbf {p}}^{2}$ are estimated by the method of moments. First, the transformation exponent a is estimated to fulfill the criteria that the skewness of W^a is zero, and m,σ² are equal to the mean and variance (monthly) of the transformed wind speeds. All parameters defining the model of Eq. 1 depend on the location p and are estimated “pointwise.” It should be noted that for the applications of predicting extreme wind speeds by the model, the parameters are smoothed over a spatial neighbourhood of about 3 degrees radius.

Furthermore, a non-homogeneous and non-stationary correlation function ρ of a spatio-temporal transformed wind speed $W^{a_{\textbf {p}}}(\textbf {p})$ was presented in Rychlik and Mao (2014) and Rychlik (2015), and a global wind model for large regions was also established. In this study, only local non-Gaussian models of similar correlation functions are presented and validated. The case of a global model will be considered in the future work.

2.1 Correlation function ρ(t,x,y)

Similarly to our previous studies (Rychlik and Mao 2014; Mao and Rychlik 2016), the following Gaussian correlation function is used in this paper. For a location p, the correlation of wind speeds around the surrounding homogeneous region q is written as

$$ \rho(\textbf{q})= \rho(t,x,y) =\,\exp\left( -\pi^{2}\textbf{q}\,{\Lambda}\, \textbf{q}^{T}/2\right), $$

(2)

where Λ = [λ_ij] is a positive-definite matrix. Equation 2 defines the spatio-temporal correlation of transformed wind speeds in the neighbourhood of the location p.

2.2 The kernel f constructed from ρ(t,x,y)

For a wind speed field of the correlation function ρ, a kernel f can be constructed to describe the characteristics of wind speed time series and the shape of extreme wind speeds. It is defined such that f ∗ f(q) = ρ(q), where ∗ defines a convolution operation. For a correlation function ρ as in Eq. 2, the kernel f is defined by

$$ f(\textbf{q}) \,=\,(2\pi)^{3/4}\,|\!\det {\Lambda}|^{1/4}\exp\!\left( \!-\pi^{2}\textbf{q}\,{\Lambda}\, \textbf{q}^{T}\!\right),\!\!\quad \textbf{q}\,=\,(t,x,y). $$

(3)

In this study, the kernel of Eq. 3 is used to approximate various types of X_p as in Eq. 1 by discretizing a spatio-temporal region S as presented in the following Section 3. It can be shown that as the discretization steps tend to zero and S grows without bounds, the approximation converges to a homogeneous standardized Gaussian field X_G of correlation ρ defined in Eq. 2.

2.3 Estimation of Λ in the kernel

If the transformed wind speed X is a locally stationary Gaussian field such as wind speeds in the North Atlantic, the matrix Λ could be estimated by the maximum likelihood method. However, for locations in the Caribbean Sea and the Gulf of Mexico, where tropical storms are rarely occurring, the Gaussian assumption to model X fails. Consequently, a crude method, i.e., the method of moments, is used to estimate the matrix Λ. The property that Λ is proportional to the covariance matrix of the X-gradient is employed here. More precisely, let X(t) = X(t,0,0), X(x) = X(0,x,0) and X(y) = X(0,0,y). The following derivatives can be defined as

$$X_{t}(t)\,=\,d\,\!X(t)/dt,\!\!\!\!\quad \!X_{x}(x)\,=\,d\,\!X\!(x)\!/dx, \!\!\!\quad \!\!X_{y}(y)\,=\,d\,\!X\!(y)/d\!y. $$

The difference quotient is used here to evaluate the above derivatives. And the terms

$$(X,X_{1},X_{2},X_{3})(t_{\textbf{p}},x_{\textbf{p}},y_{\textbf{p}})=(X(0),X_{t}(0),X_{x}(0),X_{y}(0)) $$

are the values and the gradients of the transformed wind speed fields W^a at a geographical location (x_p, y_p) and a time t_p. Then, let the position (x_p, y_p) be fixed and only the time t_p vary, the above terms become four time series denoted by (X,X₁, X₂, X₃)(t_p).

Let the covariance matrix of the gradient components (X₁, X₂, X₃)(t_p) at the position p be denoted by Σ = [λ_ij], i,j = 1,2,3. Using the Theorem 7.6 as in Lindgren (2013), it can be shown that

$$ {\Lambda}=\frac{{\Sigma}}{\pi^{2}\sigma^{2}}, $$

(4)

where as before σ² = V (X). It is assumed that at any geographical location (x_p, y_p), the above four wind time series can be considered to be stationary for a period of approximately one month. Consequently, for p = (x_p, y_p), t_p = j/12 + 1/24 (t with unit year), mean and variance m_p, ${\sigma }_{\textbf {p}}^{2}$ and Σ_p of the transformed wind speeds W^a(p) can be estimated by standard statistical methods.

3 Stochastic models for the transformed wind speed field X

In the neighbourhood of p, the transformed wind speed field is modeled by a homogeneous random field X(t,x,y) as in Eq. 1 with mean m_p, variance ${\sigma }_{\textbf {p}}^{2}$ and the correlation function ρ_p defined in Eq. 2. For locations in the Northern part of the North Atlantic, the variable X(t,x,y) can be modelled by a stationary Gaussian field, which is uniquely defined by a mean m, a variance σ² and the correlation function ρ given in Eq. 2. For locations in the Caribbean Sea and the Gulf of Mexico with rarely occuring tropical storms, non Gaussian models requiring additional parameters should be used to model the transformed wind speeds, but keep using the same correlation ρ.

In this paper, three standardized random fields X_M (of mean zero, variance one and the same correlation ρ) will be investigated to describe the random wind fields X, which is modelled by scaling one of these standardized fields by σ_p and adding m_p:

$$ X(t,x,y)=m_{\textbf{p}}+ \sigma_{\textbf{p}} X_{M}(t,x,y). $$

(5)

where X_M represents the Gaussian field X_G, the Laplace field X_LMA and the hybrid field X_H, respectively. Furthermore, these fields X_M are symmetrical with skewness zero. Hence, the same estimates of the parameters a, m, σ, and ρ can be used in Eq. 1 for any model of X_M.

3.1 Gaussian moving average model X _G

For a fixed position p = (t_p, x_p, y_p), the transformed Gaussian model is given by X(t,x,y) = m_p + σ_pX_G(t,x,y), where the Gaussian field X_G is approximated by a moving average of Gaussian noise as follows:

$$ X_{G}(t,x,y)\approx \sum\limits_{i,j,k} f(t-t_{k},x-x_{i},y-y_{j})Z_{ijk}\sqrt{dx\,dy\,dt}, $$

(6)

where Z_ijk are independent zero mean, variance one, Gaussian variables and f is a deterministic kernel function defined by Eq. 3. For the approximation, a stationary and homogeneous wind region S ⊂ R³ has to be chosen first. Choice of region S is discussed in Section 4.2. The region S is dicretized using a grid, i.e. S ∋ (t_k, x_i, y_j). The discretization steps of S are dt, dx, dy. (The detailed definition of S will be given later.)

The discretizations steps dt, dx, dy are chosen such that

$$dx\,dy\,dt\,\sum\limits_{i,j,k} f(t_{k},x_{i},y_{j})^{2} \approx \int f(t,x,y)^{2} dx\,dy\,dt= 1. $$

It should be noted that the kernel used here is very simple and cannot describe real wind field structures and dynamics in great detail. More complex models could be constructed to describe the wind speed variability on different time scales; see e.g., Rychlik and Mao (2014), Rychlik (2015), where the wind speeds in the North Atlantic were modelled using four kernels of various scales but of a similar type to that in Eq. 3: a diurnal pattern due to different temperatures at day and night, a pattern considering the frequency of depressions and anti-cyclones, an annual pattern and a pattern of fast variability (noise).

3.2 Laplace moving average model (LMA) X _LMA

The Laplace moving average field was introduced in Åberg and Podgórski (2011). It can be also constructed using Eq. 6 but to allow the Gaussian noise Z_ijk to have variable variance. More precisely, Z_ijk is multiplied by the square root of independent gamma distributed random factor K_ijk as follows:

$$ X_{LMA}(\textbf{q})\!\!\approx\! \!\sum\limits_{i,j,k} f(t-t_{k},x-x_{i},\!y-y_{j})\sqrt{K_{ijk}}Z_{ijk}\sqrt{dx\,\!dy\,\!dt}. $$

(7)

The parameters of the gamma-distributed random variable K_ijk are defined to fulfill two conditions: the mean value of K_ijk has to be one and the kurtosis of X_LMA should be equal to the kurtosis of the observed wind speeds. Obviously, many other possible models are available to construct stationary non-Gaussian fields using the moving average method, e.g., to replace the Gaussian field in Eq. 6 by other infinitely divisible noises. The infinite divisibility assumption is convenient to allow for a variable discretization step while still keeping the same noise type (see, e.g., Feller (1966) for basic properties of infinite divisible distributions).

Moving averages of Laplace noise $\sqrt {K_{ijk}}Z_{ijk}$ have many attractive mathematical properties (see, e.g., Cambanis et al. (1995) and Podgórski and Wallin (2016)). For example, conditionally on values of factors $\sqrt {K_{ijk}}$, the LMA field becomes a zero mean nonstationary Gaussian field. In particular, the very large factors K_ijk will result in unusual high variability of the wind speed field. Intuitively, it would be convenient to reorder the factors K_ijk in such a way that larger factors can be considered first. This is achieved through an alternative definition of LMA using series expansions of infinitely divisible distributions (see, e.g., in Bondesson (1982)). In this study, this definition is used to model X_LMA.

The kernel f defined in Eq. 3 will be used again, along with a large region S ∋ (0,0,0) to define X_LMA. The size of S depends on f through the matrix Λ (the choice of S will be discussed in Section 4). Here, a symmetrical Laplace field will be used, and hence, only one additional parameter, 𝜗 > 0, is needed to define its distribution. Now, the Laplace moving average field at q = (t,x,y) is approximated by the following sum of random functions modelling weather events with extreme values equal to $Z_{i}\sqrt {R_{i}}$ and located at U_i ∈S:

$$ X_{LMA}(\textbf{q})\approx \sum\limits_{i = 1}^{\infty} X_{i}(\textbf{q}), \qquad X_{i}(\textbf{q})=Z_{i}\sqrt{R_{i}}f(\textbf{q} - \textbf{U}_{i}). $$

(8)

Here, random variables Z_i, R_i and U_i are independent. The Z_i have a standard normal distribution, whereas the U_i are uniformly spread in S. The distribution of R_i depends on the parameter 𝜗. They are independent but not equally distributed. Given the parameter 𝜗 and the region S, R_i can be simulated as follows:

$$R_{i}= \vartheta|\textbf{S}|\,\zeta_{i}\,e^{-\vartheta\gamma_{i}} $$

where ζ_i are i.i.d. standard exponential random variables independent of γ_i, which are locations of the i-th point in a Poisson process, i.e., ${\gamma }_{i}={\sum }_{j = 1}^{i} G_{j}$, where G_j are independent standard exponential distributed random variables. Note that $Y_{i}=Z_{i}\sqrt {\zeta _{i}}$ forms a sequence of independent standard Laplace distributed random variables (Kotz et al. 2001), i.e., of probability density f(y) = 0.25exp(−|y|/2). This motivates the name Laplace moving average. The random functions X_i have the following amplitudes,

$$ Z_{i}\sqrt{R_{i}}\,=\,\sqrt{\vartheta|\textbf{S}|\exp(-\vartheta{\gamma}_{i})}\cdot Y_{i}\,=\, \sqrt{|\textbf{S}|}\,\sqrt{\vartheta}(V_{1}\cdot{\ldots} \cdot V_{i})^{\vartheta/2}\,Y_{i}, $$

(9)

where V₁,…,V_N are independent uniformly on [0,1] distributed variables and also independent of Y₁,…,Y_N.

It can be shown that mean of X_LMA is zero, variance $\mathbb V(X_{LMA})\approx 1$, skewness zero and the correlation is approximately equal to ρ as in Eq. 2. Note that the sum in Eq. refLMA approaches the LMA field as the region S grows to R³ having variance one and correlation as in Eq. 2.

3.3 The Hybrid model X _H

The hybrid model is a combination of the Laplace and Gaussian models. Let us start with Eq. 8, where the random terms X_i(q) have mean zero and decreasing variances

$$ \mathbb V(X_{i}(\textbf{q}))\approx\frac{\vartheta}{\left( 1+\vartheta\right)^{i}}. $$

(10)

Since the random functions X_i in Eq. 8 appears in order of decreasing variance, only the first N terms will be used to model “weather anomalies,” e.g., large storms or lengthy wind lulls. Furthermore, since the variability of transformed wind speeds under the “normal” conditions is very well described using Gaussian fields, X_G, as defined in Eq. 6, is adopted to approximate ${\sum }_{i=N + 1}^{\infty } X_{i}(\textbf {q})$ in Eq. 8. This leads to the following definition of the hybrid model:

$$ X_{H}(\textbf{q})= p\,X_{G}(\textbf{q}) + \sum\limits_{i = 1}^{N} X_{i}(\textbf{q}),\qquad \textbf{q}=(t,x,y). $$

(11)

where X_G is the Gaussian field in Eq. 6 and X_i are defined in Eq. 8. The parameters N and 𝜗 are related to frequency of storms and kurtosis of the transformed wind speeds.

Both the Gaussian field X_G and the weather anomalies X_i are defined using the same kernel f presented in Eq. 3. The value of p, 0 ≤ p ≤ 1, is chosen such that variance of X_H within the homogeneity region (S) is one. This causes the correlation function ρ of X_H to coincide with that given in Eq. 2. Obviously, if N = 0, then X_H = X_G, whereas X_H tends to X_LMA as N tends to infinity. By introducing the two extra parameters p and N, the hybrid model will significantly better model the actual wind speeds. It is demonstrated by the following example.

Example

Main difference between wind speed statistics in the North Atlantic and the Caribbean region are the frequencies of extreme speeds. Wind speeds in August during 2000–2015 at the location (72.75 W, 16.5 N) are extracted from ERA Interim reanalysis data set. The time series are shown in Fig. 3, along with the yearly frequencies of upcrossing of level u. The expected upcrossing frequencies were evaluated for transformed Gaussian (N = 0, hybrid N = 6 and LMA (N = 1000)). It is shown that the transformed Gaussian model underestimates, while LMA overestimates the frequencies of high wind speeds events. The frequencies computed using transformed hybrid model agree very well with the observed ones. Actually, the value N = 6 is estimated by minimizing a distance between the observed and computed upcrossing frequencies (see Appendix B for details).

Fig. 3

Comparison of expected upcrossing rates of wind speeds in August at the location (72.75 W, 16.5 N) computed by the transformed Gaussian model, the hybrid model, the Laplace moving average model as in Eq. 8 (right plot) and the upcrossing rates found in the time series of wind speeds presented in the (left plot)

Finally, the Gaussian, LMA and the hybrid models predict the 1000-year extreme wind speeds to be 16.5, 33, and 46 m/s, respectively. Since during years 2000–2015, a maximum wind of 27 m/s was recorded, it seems that the 1000-year wind predicted by the Gaussian and LMA models are very likely too low, and the hybrid model gives better fit than the Gaussian and LMA models.

3.4 Estimation of parameters in the hybrid model

As mentioned before the transformed Gaussian model works well for North Atlantic where W^a have skewness zero and kurtosis about three. Estimation of parameters a, m_p, ${\sigma }^{2}_{\textbf {p}}$ in Eq. 1 and correlation ρ has been discussed in Section 2. Figures 4 and 5 present the estimation of these parameters for the Caribbean Sea.

Fig. 4

Parameter a defining transformed wind speed X = W^a for January and August (upper plots). Estimated skewness of W for January and August (lower plots)

Fig. 5

Median wind speed $m_{\textbf {p}}^{1/a}$ (upper plots) and logarithm of standard deviation of transformed wind speeds ln(σ_p) (lower plots) in February and August, respectively

However, in the Caribbean and the Gulf of Mexico, the kurtosis of transformed wind speeds may significantly exceed three in hurricane season. Hence, the hybrid model is used here. In this model, the parameter N, i.e., the number of storms and lulls in the stationary region S, is one of the most important parameter. If N = 0, the hybrid model becomes the transformed Gaussian model, while for very large N it is equivalent to the transformed LMA model. In addition to N, the other two more parameters are p and 𝜗. Given the values of N, they are estimated by solving the condition that the kurtosis of X_H is equal to the kurtosis of the observed transformed wind speeds, while p is used to ensure that variance of X_H is one.

The difficult part of constructing the hybrid model is to find an appropriate value of N. It is estimated by setting that frequencies of crossings of high wind levels given by the hybrid model have to well agree with the observed crossing frequencies in the wind data. This is an important requirement for engineering safety assessment (Rychlik et al. 1997). Algorithms to estimate N, p and 𝜗 are given in the Appendix B. Finally, it should be noted that the hybrid models are fitted point-wise and monthly, i.e., the parameters vary in terms of geographical locations and months. However, in applications, the parameters are smoothed over suitable neighbourhood of a location of interest.

Remark

The hybrid model and the proposed algorithm to estimate parameters are working very well at various locations, where wind speeds have positive skewness. At such locations, the transformation parameter, i.e., the exponent a < 1. However, there are locations with negative skewness of W and hence a > 1, as shown in the bottom plots of Fig. 4. At those locations, the hybrid model gives lighter tails of wind speed distributions than what the standard extreme value analysis would suggest. Consequently, when skewness is negative, it is proposed to change methods to estimate N and 𝜗 by requiring that only crossings of high wind levels are well approximated; see the Appendix B for more details.

4 Stationary and homogeneous wind region S

The region S depends on the shape of the kernel f defined in Eq. 3. It should contain (0,0,0) and should be at least large enough that ${\int }_{\textbf {S}} f(\textbf {q})^{2}\,d\textbf {q}\approx 1$. In this study, S is defined using the average geometry (size) of a spatio-temporal windy weather region. The geometry parameters are defined as follows.

4.1 Size of windy weather region

In the Caribbean and the Gulf of Mexico, wind speeds are modelled by the transformed hybrid model. The model consists of a Gaussian part describing the “every day” variability of wind and a number of random functions X_i modelling storms and lulls occurring in the region S. At a location p, let a windy weather be defined as X(t,x,y) > m. Furthermore, let τ be the average duration of uninterrupted windy weather at location p = (t_p, x_p, y_p), where t_p is discretized by month for the estimation.

Similarly, let the average spatial extents of windy weather in the longitudinal and latitudinal directions be denoted by L_x and L_y, respectively. More precisely, τ, L_x and L_y are the average length of excursions above the median wind speed (i.e., W ≥ m^1/a) in the processes X(t) = X(t,0,0), X(x) = X(0,x,0) and X(y) = X(0,0,y), respectively. If X(t), X(x) and X(y) were stationary Gaussian processes, then by Rice’s formula Eq. 22 and the Theorem 7.6 given in Lindgren (2013), the following relations can be obtained:

$$\begin{array}{@{}rcl@{}} \tau&=&\pi\sqrt{\frac{V(X(t))}{ V(\dot{X}(t))}}=\lambda_{11}^{-1/2},\,\, L_{x} =\pi\sqrt{\frac{ V(X(x))}{ V(\dot{X}(x))}}\\&=&\lambda_{22}^{-1/2}, \,\, L_{y} =\pi\sqrt{\frac{ V(X(y))}{ V(\dot{X}(y))}}=\lambda_{33}^{-1/2}, \end{array} $$

(12)

where V (X) denotes the variance of the random variable X. When wind speeds should be described by the hybrid model, i.e., N > 0, the above parameters τ, L_x and L_y should be seen as spectral parameters. The parameters can be fair approximations of the observed average sizes of windy weather regions since most of the time the hybrid model is generated using a Gaussian field X_G. The parameters τ,L_x, L_y depend on a, which varies with season/month (t_p) and geographical position (x_p, y_p) of the location p; see Fig. 6 for an illustration.

Fig. 6

Comparison of spatial variability of τ, defined in Eq. 12, in February and August, respectively

4.2 Choice of S

For the accurate estimation of long-term distributions or crossing rates at a fixed location p, the region

$$\begin{array}{@{}rcl@{}} \textbf{S}&=&[-1.75\tau, 1.75\tau]\times[-1.75L_{x}, 1.75L_{x}]\\&&\times[-1.75L_{y}, 1.75L_{y}] \end{array} $$

(13)

is used. The typical value of |S| is approximately 8 ⋅10⁴ [hour⋅deg²]. If the spatio-temporally homogeneous properties of W in a neighbourhood field of p are needed, S must be enlarged to contain the neighbourhood. For example, to simulate time series of wind speeds during one month, i.e., 720 h, the size of S has to be enlarged to

$$\begin{array}{@{}rcl@{}} \tilde{\textbf{S}}&=&[-360-1.75\tau, 360 + 1.75\tau]\times[-1.75L_{x}, 1.75L_{x}]\\ &&\times[-1.75L_{y}, 1.75L_{y}]. \end{array} $$

(14)

Note that N must also be increased by a factor of $|\tilde {\textbf {S}}|/|\textbf {S}|= 1+\frac {360}{1.75\tau }$. The new value of N is the number of wind anomalies placed at random in $\tilde {\textbf {S}}$ in order to describe the wind fields in the larger region. The intensity of extraordinary wind events N/|S| is presented in Fig. 7. However, the value of 𝜗 presented in Fig. 8 and |S| used in Eq. 9 to define amplitudes $Z_{i}\sqrt {R_{i}}$ of X_i do not change.

Fig. 7

Intensity of extraordinary wind events in a region of 25 deg² during one month 31 × 25 × N/|S| computed for transformed wind speeds in July, August, and September, respectively

Fig. 8

Parameter 𝜗 in July, August, and September, respectively

The wind field in the neighbourhood of p for the period of time within a month can be simulated by the hybrid model in Eq. 11, where the Gaussian part can be simulated on any grid using some standard methods, e.g., Cholesky decomposition of the covariance matrix. Here, the size of the field matrix is the limiting factor. Since the estimated values of N in the Caribbean and the Gulf of Mexico are small, for example for a region as in Eq. 14 and a time period of 1 month it would not exceed 100, simulations of ${\sum }_{i = 1}^{N} X_{i}(\textbf {q})$ is numerically very simple task for any grid.

Note that only local models are considered in this study. If more than one region are considered, the simulations of wind speed fields in these regions are independent, even if these regions are overlapped.

5 Validation statistics and practical applications of the hybrid model

In the following, three statistics of wind speeds are presented: (1) the long-term wind speed distribution at a fixed location, (2) the crossing rates for the prediction of 100/1000-year extreme wind speeds using the Rice’s method, and (3) the simulation of local fields and time series of wind speeds at specific locations. These statistics are used to validate the proposed hybrid model, as well as to demonstrate the practical applications of the hybrid model.

5.1 Long-term wind speed distributions

Since the variability of W depends on the season, to avoid ambiguity when discussing the distribution of W, the time span and region from which the wind observations were gathered need to be clearly specified. The long-term CDF at p can be retrieved by averaging W(p) distributions. For example, the yearly distribution of W at (x_p, y_p) is given by

$$ \mathbb P(W\le w)={{\int}_{0}^{1}} \mathbb P(W(t_{p},x_{p},y_{p})\le w)\,dt_{p}. $$

(15)

Similarly the yearly long-term CDF over a region A is given by

$$\mathbb P(W\le w)=|\textbf{A}|^{-1} {\int}_{\textbf{A}}{{\int}_{0}^{1}} \mathbb P(W(t,x,y)\le w)\,dt\,dx\,dy, $$

where |A| is the area of the region A. If W is described by the transformed Gaussian model then

$$\mathbb P(W(\textbf{p})\le w) = {\Phi}\left( \frac{w^{a(\textbf{p})}-m_{\textbf{p}}}{\sigma_{\textbf{p}}}\right),\qquad \textbf{p}=(t_{p},x_{p},y_{p}), $$

where Φ(x) is the cumulative distribution of a standard Gaussian variable. However, if the transformed W^a is described by the hybrid model, then the computations of $\mathbb {P}(W(\textbf {p})\le w)$ is slightly more complicated. The detailed calculation procedure is given in the Appendix A.

5.2 Estimation of 100/1000-year extreme wind speeds

The long-term distribution of W is commonly used to describe the variability of wind speeds. An important applications of the distribution is to estimate expected values of various functions of wind speed, e.g., the average available wind energy for harvesting at a particular wind farm. Another category of wind characteristics consists of the extreme wind speed statistics, and such characteristics are relevant to, e.g., maritime-safety-related activities. For such purposes, the statistical wind characteristics are most often described in terms of the distribution of the maximum wind speeds over a given period of time T, e.g., one year.

Let M_T denote the maximum wind speed during a period T, where T is usually one year, 1 month or one hurricane season. The probability distribution of M_T describes the long-term variability of M_T. Somewhat simpler statistics are the so-called 100/1000-year extreme (return) wind speeds denoted by w₁₀₀ and w₁₀₀₀, respectively. These extreme values are quantiles of the M_T distribution; e.g., the 100-year extreme wind is defined by

$$\mathbb P(M_{T}\ge w_{100})=\frac{1}{100}. $$

The name is motivated by the heuristics that for T = 1 year, the wind speed level of w₁₀₀ will be exceeded in average once per 100 years.

In this study, the so-called Rice’s method is used to estimate $\mathbb P(M_{T}\ge w)$ (see, e.g., Rice (1944, 1945), Baxevani and Rychlik (2006), and Mao and Rychlik (2013)). This method employs the concept of level crossing defined as follows. For a time series denoted by W(t), let N_T(u) be the number of level crossings in a time interval T, i.e., the number of times t at which W(t) = u for t ∈T = [t₁, t₂]. The Rice’s method uses the following bound:

$$ \mathbb P(M_{T}\ge u)\le \mathbb P(W(t_{1})\ge u)+\mathbb E[N_{T}(u)]/2, \quad T=[t_{1},t_{2}]. $$

(16)

The bound becomes very accurate when the level u reaches very high values, e.g., extreme values. The means to evaluate $\mathbb E[N_{T}(u)]$ are given in the Appendix A.

The transformed Gaussian and the hybrid model can be used to evaluate the frequencies/distributions of extreme wind speeds by the generalized Rice’s formula (Azais and Wschebor 2009) (see, e.g., Brodtkorb et al. (2000)). The estimation of the maximum distribution as in Eq. 16 is the typical/simplest application of this methodology to study the frequencies of extreme events. Furthermore, the so-called Slepian models (Lindgren and Rychlik 1991; Podgórski et al. 2015) allow for simulating time series of wind or wind surfaces in the vicinity of an extreme event. With the simulated wind information, physical interaction between wind and an engineering structure can be modelled to estimate the frequencies of potentially harmful events, which can trigger undesired/dangerous responses.

5.3 Simulation of local fields and time series of wind speeds

An important feature of the stochastic field models proposed here is that they can be used to generate artificial wind speeds on the time series and fields scales. The use of the hybrid model defined in Eq. 11 to simulate those two types of wind speed, i.e., local fields and time series of wind speed, will be demonstrated here, viz.

$$W(t_{\textbf{p}}+t,x_{\textbf{p}}+x,y_{\textbf{p}}+y) \,=\, \left( m_{\textbf{p}}\,+\,\sigma_{\textbf{p}}\left( \!p\,X_{G}(\textbf{q}) \,+\, \sum\limits_{i = 1}^{N} X_{i}(\textbf{q})\right)\!\right)^{1/a}. $$

First, the generation of time series at three fixed locations will be demonstrate to validate the hybrid model in the following Section 6. Then, the simulation of temporal wind speed fields of 4-h interval in a neighbourhood of a fix location will be demonstrated by the model in Section 7. Such simulations could be used to study the responses of engineering structures to wind loads. For example, this model can be used to estimate the long-term (e.g., 30 years) distribution of wind speeds along arbitrary ship routes. Then, Rice’s method can be employed to get the maximum wind speed during those 30-year sailing routes. The obtained wind information is essential for estimating the pay-back times of wind-assisted propulsion devices (Nelissen et al. 2016) to be installed onboard ships and for assessing the safety of the ships after installation. Based on such simulated wind information, a ship could also choose to sail in a more economic way so as to encounter more beneficial wind conditions along its routes. Furthermore, wind speed field simulations provide important information regarding the choice/design of wind farms in specific regions. The wind correlations provided by this model could also be used for conditional prediction of wind speeds when some spatial or temporal wind information is known for given areas of interest.

6 Validation of the hybrid model for wind in the caribbean and the gulf of Mexico

Here, the hybrid models are estimated using 16 years ERA-Interim wind data (Dee et al. 2011) from ECMWF for the years 2000–2015. The parameters of the models are estimated for each month, and they also vary in space. The spatio-temporal variability of the transformation exponent a, the mean m, the standard deviations σ and the duration of windy weather τ are shown in Figs. 4, 5, and 6. An additional important parameter N, which describes the frequency of storms, is shown in Fig. 7. The wind speeds at the three locations represented in Fig. 1 (upper plot) will be used to illustrate and validate the accuracy of the hybrid model.

In the following, the accuracy of the fitted hybrid models will be investigated by comparing the yearly exceedance probabilities $\mathbb P(W>u)$, and the expected number of upcrossings during one year $\mathbb E[N^{+}(u)]=\mathbb E[N(u)]/2$. For model validation, the theoretical long-term distribution $\mathbb P(W>u)$ is computed using Eq. 30, and the upcrossing rate $\mathbb E[N^{+}(u)]$ is estimated using Eqs. 27–29 based on the fitted hybrid models; see the Appendix A for more details. These estimates are then compared with the empirical values based on 16 years of hindcast wind data.

6.1 Validation at the location west of Haiti coast (72 W, 17.25 N)

At this location, the transformation exponents a during the hurricane and winter seasons are very different, as shown in Fig. 4. In winter, a is far above 1.2, whereas in summer, it is far below 0.7. In addition, a highest wind speed of 47 m/s (due to the hurricane Dean) has been observed at this location; see the lower plot in Fig. 1. Data of this type present a challenge for automatic estimation procedures.

Figure 9 presents the comparison results for the location west of the coast of Haiti. It is shown that the hybrid model describe the yearly wind speed variability/probability very well. Very good agreement between the theoretically computed $\mathbb E[N^{+}(u)]$ (obtained using the fitted hybrid model) and the observed yearly crossing frequencies is also observed. In the figure, the thin (blue) lines represent the empirical yearly wind speed distributions obtained from simulations of the transformed hybrid model. Furthermore, the empirical yearly wind speed probabilities based on the simulated wind speeds are also presented, and very extreme (outliers) wind speeds can be found in the simulated wind speeds.

Fig. 9

Comparison of the expected number of upcrossings during one year $\mathbb E[N^{+}(u)]$ and yearly probabilities $\mathbb P(W>u)$ from different models, at the location west of Haiti (72.75 W, 17.25 N)

6.2 Validation at the location south of New Orleans (90 W,28.50 N)

At this location, the transformation exponents a are also distinctly different between the hurricane and winter seasons. However, in the winter, a is approximately equal to 1, i.e., no transformation is needed. It is well-known that the coasts of Louisiana and Mississippi often experience extreme winds when hurricanes are passing this region. For example, in 2005, the passage of Hurricane Katrina through this region produced maximum wind speeds above 50 m/s. However, no such extreme wind speeds are recorded in the 2000–2015 ERA-Interim data; a highest wind speed of only 25 m/s was recorded on 2008-09-12. (One possible reason for this is that wind speeds are given every 6 h in the dataset.) Thus, an interesting question is whether the proposed hybrid model for estimating the 100/1000-year extreme wind speeds will result in a higher wind speed.

Figure 10 shows similar results to those in Fig. 9 but for the location at (90W, 28.5N). It is shown that the theoretically computed quantities agree very well with observed values except for wind speeds of approximately 20 m/s.

Fig. 10

Comparison of the expected number of upcrossings during one year $\mathbb E[N^{+}(u)]$ and yearly probabilities $\mathbb P(W>u)$ from different models, at the location south of New Orleans (90W, 28.5N)

6.3 Validation at the location west of the Florida coast (84W, 28.5N)

Here, wind speeds vary in a similar way as in the North Atlantic; i.e., there is no significant difference between the values of a in the hurricane and winter seasons. However, since the kurtosis of the transformed wind speeds X = W^a for the months of June and July is greater than four, the hybrid model should nevertheless be used for this location. (In the North Atlantic, the kurtosis of X is approximately 3.)

Figure 11 presents results for the location west of the coast of Florida. The theoretically computed quantities obtained using the hybrid model agree very well with the observed values. The wind speeds simulated based on the hybrid wind model are also presented. It should be noted that the hybrid model can generate very high wind speeds, far above the values observed in the data (at this location, approximately 23 m/s). Hurricanes do sometimes hit the northwest coast of Florida, e.g., in the years 2005 and 2016. Such rarely occurring “outliers” cannot be generated using transformed Gaussian models.

Fig. 11

Comparison of the expected number of upcrossings during one year $\mathbb E[N^{+}(u)]$ and yearly probabilities $\mathbb P(W>u)$ from different models, at the location west of Florida (84W, 28.5N)

7 Extreme prediction and simulation of wind speeds by the hybrid model

In this section, three examples illustrating the utilization of the hybrid model will be presented. The first example is the extreme wind prediction in the regions of the Caribbean sea and the Gulf of Mexico, and the second example is the simulation of wind speeds as local fields and time series. In the third example, simulating wind speed fields will be used to estimate spatio-temporal wind extremes of the fields. The examples have quite practical applications within the maritime community.

7.1 Estimation of 100/1000-year extreme winds speed

Various methods are available for statistical extreme value prediction. For example, in Walshaw (2000), the parameters in a GEV distribution were assumed to be random, and a Bayesian approach was used to estimate the extreme wind speeds. By contrast, in Payer and Kuchenhoff (2004), not only the yearly maximum but also the r highest values during each year were used to fit the GEV distribution. This approach is particularly useful if there are only a few years of data available. When only very limited data are available, an alternative approach is to compute the probability $\mathbb P(M_{T}>u)$ from a parametric wind speed variability model, e.g., a transformed Gaussian or the hybrid model; see Rychlik et al. (2011). Obviously, extrapolation beyond the range of the available data can lead to severely biased estimates if the assumed model does not hold in the region of extrapolation. This is why a careful validation of the accuracy of proposed models is always needed.

For the application considered here, the transformed hybrid model is used, and the parameters of the hybrid model for the Caribbean sea are estimated as before, using 16-year ERA-Interim wind data. First, the extreme wind speeds have been estimated for each geographical location. Then these point-wise estimates are smoothed by means of a Gaussian kernel. The 100/1000-year extreme wind speeds computed by the Rice’s method based on the hybrid model are presented in Fig. 12, together with that derived from fitted GEV distributions. As can be seen that the risk for severe winds is highest in the region south of Mississippi coast. Hence, high extreme wind speeds should be expected in location close to New Orleans.

Fig. 12

Estimates of 100/1000-year extreme wind speeds [m/s] using Rice’s method based on the hybrid model (left plots) and GEV method (right plots). The estimates are obtained by smoothing point-wise estimates using a Gaussian kernel

However, it should be noted that the smoothing strategy will significantly reduce the strong variability of estimated extreme wind speeds at surrounding locations. The variability is illustrated in Table 1, where the predicted wind speeds at locations 0.75 degrees apart are significantly different. (Note that those are point-wise estimate and hence not smoothed using estimates at the neighbouring locations.) The fact can be also seen from Fig. 13, which presents the maximum wind speeds during the years of 2000–2015. Furthermore, Table 1 also illustrates the difference of extreme wind speed predictions between derived from fitted GEV distributions and estimated by the Rice’s method based on the hybrid and transformed Gaussian models. The predictions based on transformed Gaussian models systematically underestimate the 100/1000-year extreme wind speeds at the three locations. Estimates computed using the Rice’s method and transformed hybrid model agrees fairly with the estimates derived using the GEV method.

Table 1 Estimation of 100/1000-year extreme wind speeds (denoted by W₁₀₀ and W₁₀₀₀) at three locations

Fig. 13

The maximum wind speeds during the years of 2000-2015. The white cross represents the location (72.75W, 16.5N), and the black circle represents the location (72.75W, 17.25N), respectively

7.2 Simulation of time series of wind speeds using the hybrid model

Here and in the following subsections, the wind speeds in the neighbourhood of the location (72.75W, 16.5N) will be simulated using hybrid model. The fitted parameters for the August are a = 0.6, m = 6.8, σ = 1.5, and p = 0.92, which means that 84% of variance is modelled by Gaussian component. Furthermore N = 6, 𝜗 = 0.03. The parameters defining the spatio-temporal dependence are τ = 1.08 day, L_x = 10.1,L_y = 6.2 degree, defined in Eq. 12, and drift speed v_x = − 0.11,v_y = 0.02 [deg/hour], defined in Section 7.3.1, while correlation between the spatial derivatives of transformed wind speed 0.04 is negligible.

The parameters τ, L_x, L_y and velocities v_x, v_y describe average geometry of extreme wind speed regions and their dynamics. The estimated values are in terms of the covariance matrix of the gradients. The values given above are quite typical for these parameters at this region. The parameter N describes the average number of weather anomalies, which are about 1.6 per month in a region of 25 deg². For example, Fig. 7 presents the variability of this parameter for various months. It should be noted that the intensity of extraordinary wind events is higher than intensity of cyclones. The parameters σ, 𝜗 and a influence the tails of wind speed distribution, and hence the frequencies of extreme wind speeds. The low value of the parameter a makes tails heavier. For example, if a hybrid model predicts an extreme value of x_max, it is corresponding to the extreme wind speed of (m + σx_max)^1/a. (Note that using models with very low a is questionable for extreme wind prediction.) Furthermore, 𝜗 is the scale parameter to determine the highest value of X_i(q) components. It can be deduced, by combining Eqs. 3, 9, and 36. The highest value of X_i(q) is about $c\sqrt {\vartheta } Y_{i}$, where c is a constant and Y_i is Laplace distributed variables.

For the location (72.75W, 16.5N), 500 independent time series of wind speeds in August are simulated by the hybrid model. The time step is 6 h and the region S has been increased using Eq. 14. The parameter N = 6 is also increased by a factor of 1 + 360/(1.75 × 30) giving the new value of N ≈ 50. Figure 14 presents 16 (out of 500) simulated time series. The simulations are compared with wind speeds extracted from the ECMWF hindcast data. It demonstrates that the hybrid model can generate extreme windy episodes as observed in the data. In order to compare the time series for low and moderately high speeds, these plots have been zoomed and presented in the right plots of Fig. 14. It is shown that the simulated time series of wind speeds are smoother than the observed values. This is caused by simplicity of the chosen kernel. In Rychlik (2015) and Rychlik and Mao (2014), a more complex kernel was presented and could be used even here.

Fig. 14

Comparison of wind speed time series between simulated and extracted from hindcast at the position (72.75 W, 17.25 N) in August during the years of years 2000–2015. Right plots: Zoomed left plots

Consequently, based on the 500 simulated wind time series, the upcrossing frequencies are also estimated and compared with that computed from the hybrid model and empirical values from the hindcast data. These comparisons are presented in Fig. 15. Agreement between the simulated, observed and computed frequencies is fair.

Fig. 15

Upcrossing frequencies of wind speeds in August evaluated by the hybrid model are compared with those estimated using 500 simulated wind time series and hindcast data during the years 2000-2015

Finally, the problem of uncertainties in predicting extreme wind speeds can be illustrated by the simulation study. The hybrid model is used to simulate wind speed time series in August for 500 years. The wind speed that is exceeded once in 500 years is taken as an empirical estimate of the 500-year extreme wind speed. This procedure has been repeated ten times. The estimated 500-year extreme wind speeds vary between 38 and 102 m/s. Note that 500-year extreme wind speed evaluated by the hybrid model at the location is 51 m/s.

7.3 Spatio-temporal simulation of local wind speeds using the hybrid model

In this section, a local spatio-temporal hybrid model will be used to simulate wind speed fields in a small region of about 6 × 6 degrees square and a time period of 8 h. Obviously, observed wind speeds at a fixed position does not reflect dynamics of wind moving systems. The joint spatial and temporal data are needed to investigate movements of wind systems. Here, the gradient is used to define local spatio-temporal dependence. However, such a local information is not sufficient to investigate the movement of cyclones. For this type of dynamics, a global spatio-temporal model is needed. Development of such a model is planned but not discussed here.

The location south of the coast of Haiti in August is chosen for the local wind field simulations. Two types of procedures have been used to simulate the wind fields. First, only the Gaussian fields X_G(q) in Eq. 11 are simulated, and then transformed into wind speed fields, which are presented in the left plots (with 4-h interval) of Fig. 16. The other approach is to employ the hybrid model as in Eq. 11, i.e., multiplying the above simulated X_G(q) by a factor p, adding the ${\sum }_{i = 1}^{N} X_{i}(\textbf {q})$ and transforming them into wind speed fields as follows:

$$W(t_{\textbf{p}}+t,x_{\textbf{p}}+x,y_{\textbf{p}}+y) \,=\, \left( m_{\textbf{p}}\,+\,\sigma_{\textbf{p}}\left( p\,X_{G}(\textbf{q}) \,+\, \sum\limits_{i = 1}^{N} X_{i}(\textbf{q})\right)\!\right)^{1/a}. $$

In the second simulation, storms are modelled by random functions X_i with the kernel f defined in Eq. 3. And then the amplitudes and the tops of these storms are generated and placed at random in this region. The amplitudes of the storms change in time and the tops of the storms are moving with constant velocity. The simulation results are presented in the right plots of Fig. 16.

Fig. 16

Simulated wind fields 4 hours apart in August from the transformed Gaussian model (left plots), and wind fields (right plots) simulated from the hybrid model that is estimated at the location (72.75 W, 16.5 N) in August

If the components of gradients X_x, X_y are uncorrelated (as in the current example), the velocity of X_i movement is equal to median propagation velocity of the wind speed field given in Eq. 18. It will be briefly reviewed in Section 7.3.1. Obviously, the storms move in variable velocities and usually faster than (v_x, v_y) (see, e.g., Dorst (2014)). Development of more realistic models for the storm dynamics is planned in future.

7.3.1 Velocities of a wind speed field

In the classical paper by Longuet-Higgins (1957), velocities were introduced to study the movements of random surfaces. Alternative definitions can be found in, e.g., Baxevani et al. (2003). Here, the so-called velocity in a fixed direction will be defined below and used throughout this paper.

Consider a wind field surrounding location p, i.e., W(t,x,y) = W(t_p + t,x_p + x,y_p + y). The velocities V_x and V_y in the x and y directions, respectively, are defined by

$$ V_{x}=-\frac{W_{t}}{W_{x}}, \qquad V_{y}=-\frac{W_{t}}{W_{y}}, $$

(17)

where W_t, W_x, and W_y are the partial derivatives of W. Some simple calculus is needed to show that

$$\frac{W_{t}}{W_{x}}=\frac{X_{t}}{X_{x}},\qquad \frac{W_{t}}{W_{y}}=\frac{X_{t}}{X_{y}} $$

which means that the velocities are independent of the transformation exponent a. The median velocities V_x and V_y will be denoted by v_x and v_y, respectively. Now, if X is a homogeneous Gaussian field, then the medians of the velocities V_x and V_y are given by

$$ v_{x}=-\frac{\lambda_{12}}{\lambda_{22}},\qquad v_{y}=-\frac{\lambda_{13}}{\lambda_{33}}, $$

(18)

see Baxevani et al. (2003) for the proof. Here λ_ij is the i,j element of the matrix Λ of Eq. 4, which defines the correlation structure of the wind field X.

The drift speeds v_x and v_y are approximately half of the average speed of cyclone movements at this region; see, Dorst (2014) for the movement speeds statistics of cyclones. When cyclones are not present in the region, most likely v_x and v_y could describe the movement of windy weather. In the Appendix C, some MATLAB code is given and can be used (after small adaptations) to simulate the wind speed fields.

7.3.2 Estimation of spatio-temporal extremes by means of simulated wind speeds fields

In this section, an example is presented to demonstrate the application of wind speed simulations by the hybrid model for the spatio-temporal extreme predictions. A spatial region of longitude between 68.5W and 76.5W, latitude between 14.5N and 20.5N, is chosen for wind simulations in August. The wind speed variability in this region is assumed to be homogeneous and stationary (The assumption might be not accurate because of islands in this region.) The hybrid model is fitted at the location (72.25W, 16.5N) in August. Wind speeds have been simulated based on the hybrid model over the region on a mesh resolution of 0.5 degree and 2 hours. Then, maximum wind speeds are picked up from the simulated spatio-temporal wind speed fields. In total, 500 spatio-temporal maximum wind speeds are simulated and the GEV distribution is also fitted to the data.

For the extreme wind prediction in the spatial region, the probability of maximum wind speeds is estimated by fitting GEV distribution, Rice’s method based on the hybrid model and presented in the left plot of Fig. 17, as well as the empirical probability based on the hindcast data and the 500 simulations. Similar results for a single location (72.75W, 16.5N) marked as the cross are presented in the right plot of Fig. 17, where the result obtained from Rice’s method based on transformed Gaussian model replaces the probability based on the 500 simulations.

Fig. 17

Probabilities that maximum wind speeds exceed a threshold u [m/s] estimated by various approaches. Left plot: Estimates of the probability in a spatial region shown in Fig. 13 in August. The empirical probabilities are estimated based on both 15 years hindcast data, and 500 simulations of spatio-temporal wind speed fields by the hybrid model. Right plot: Estimates of the probability of wind speeds at the location (72.5W, 16.5N) in August by various methods

The figure shows that the spatio-temporal maximums are considerably higher than the one observed at a fixed location. It should be noted that the hybrid model at the location (72.75W, 16.5N) is used instead of the location (72.75W, 17.25N), where the maximum wind speed in the whole data set was observed. For practical applications, smoothed over region model for simulations of spatio-temporal wind maximums should be used.

Some MATLAB scripts to simulate spatio-temporal extreme wind speeds is given in the Appendix C. In the program, the zero mean variance one Gaussian field X_G(q) is replaced by a standard Gaussian variable (X_G(0,0,0)). This approximation is used because simulations of Gaussian field on a large number of positions are very time consuming. Since X_G and X_i are independent and the size of extreme maximums is defined by the sum ${\sum }_{i = 1}^{N} X_{i}(\textbf {q})$ (easy and fast to simulate), this leads to fast and accurate simulations of spatio-temporal maximums.

8 Conclusions

Due to the strong tropical storms and hurricanes that can occur in the Caribbean sea and the Gulf of Mexico, the spatio-temporal wind model used in the North Atlantic, which is based on a transformed Gaussian field, cannot properly describe the wind variability in this region. Therefore, a hybrid spatio-temporal model, combining a transformed Gaussian field with Laplace moving averages, is proposed to describe the wind speed variability in this region. The hybrid model encompasses the Gaussian and Laplace models as limiting cases.

The capability of the hybrid model has been demonstrated through the estimation of the yearly long-term distribution and the distributions of yearly maximum wind speeds at three locations in the Caribbean sea and the Gulf of Mexico. The wind speed distributions computed using the hybrid models agree well with the empirical distributions estimated from the ECMWF hindcast wind database. The application of Rice’s method to the fitted hybrid models yields 100/1000-year extreme wind speed predictions, which agree well with those derived using generalized extreme value (GEV) distributions fitted to 16 consecutive yearly maximum wind speeds.

The proposed model can be used to evaluate the available wind energy at a fixed location. It provides a means of predicting frequencies of extreme wind speeds, which are needed in safety analysis for maritime operations and for planning of coastline protection, at locations where there are no long time series of measured wind speeds available. The model can be also used to estimate the long-term distribution of wind speeds and upcrossing frequencies of extreme wind speeds along arbitrary ship routes. Those are essential for a ship’s safety and route planning considering relevant responses due to wind loads. It can be used to estimate the spatio-temporal extreme/maximum wind speeds as well.

In addition, further research is needed for the future development of the hybrid model, which could allow for variable (more realistic) cyclones movements in the chosen regions. Furthermore, a global non-homogeneous and non-stationary hybrid model could be developed, in which the parameter N will be random (Poisson distributed).

Appendices

Appendix A: Computation of $\mathbb {E}[N(w)]$ and $\mathbb {P}(W(t,x,y)\le w)$ for the hybrid model

1.1 A.1 Rice’s formula for expected number of u crossings

Consider a fixed location p = (t_p, x_p, y_p). For simplicity of notation, let t = t_p, and consider W(t) = W(t,x_p, y_p). The expected number of crossings of level u is given by the well-known Rice’s formula (Rice 1944, 1945)

$$ \mathbb E[N_{T}(u)]={\int}_{T} {\int}_{-\infty}^{+\infty} |z| f_{\dot{W}(t),W(t)}(z,u)\,dz\,dt, $$

(19)

where $\dot {W}$ is the derivative of W(t) with respect to t. The integral

$$ \mu_{\textbf{p}}(u)={\int}_{-\infty}^{+\infty} |z| f_{\dot{W}(t),W(t)}(z,u)\,dz $$

(20)

is called crossing intensity. According to Eq. 19, μ_p(u) dt is equal to the expected number of crossings in the neighbourhood of t of infinitesimal length dt.

1.2 A.2 Transformed Gaussian case

The assumption of local stationarity of the transformed Gaussian model for wind speed means that locally,

$$W(t_{p}+t,x_{p}+x,\!y_{p}+y)\,=\,\left( m_{\textbf{p}}\,+\,\sigma_{\textbf{p}}X_{G}(\textbf{q})\!\right)^{1/a}\!, \quad\! \!\!\textbf{q}\,=\,(t,\!x,\!y), $$

where p = (t_p, x_p, y_p). Since W crosses u at time t_p only if X_G(t) = X_G(t, 0, 0), as defined in Eq. 6, crosses (u^a − m)/σ at zero,

$$ \mu_{\textbf{p}}(u)={\int}_{-\infty}^{+\infty} |z| f_{\dot{X}_{G}(0),X_{G}(0)}(z,(u^{a}-m)/\sigma)\,dz. $$

(21)

Finally, since X_G is a stationary Gaussian process,

$$ \mu_{\textbf{p}}(u)=\frac{1}{\tau_{\textbf{p}}} e^{-\frac{(u^{a}-m_{\textbf{p}})^{2}}{2\sigma_{\textbf{p}}^{2}}}. $$

(22)

The parameters τ_p is defined in Eq. 12, and m_p, $\sigma ^{2}_{\textbf {p}}$ are considered to be constant on a time scale of approximately one month.

1.3 A.3 Estimation of crossing intensity for the hybrid model X _H

The wind speed variability in the surroundings of p = (t_p, x_p, y_p) is modelled by Eq. 11 as follows:

$$W\!(t_{p}+t,x_{p}+x,y_{p}+y\!)\,=\,\left( m_{\textbf{p}}\,+\,\sigma_{\textbf{p}}X_{\!H}\!(\textbf{q})\right)^{\!1/a}\!, \quad \textbf{\!\!q}\,=\,(t,x,\!y). $$

The time series of wind speeds collected at p is represented by W(t) = W(t_p + t,x_p, y_p), and hence

$$\begin{array}{@{}rcl@{}} &&W(t)=\left( m+\sigma\,X_{H}(t)\right)^{1/a}, \quad \text{where}\\ &&X_{H}(t)= p\,X_{G}(t,0,0) + \sum\limits_{i = 1}^{N} X_{i}(t,0,0), \end{array} $$

as before, m = m_p and σ = σ_p. Note that X_H(t) is a stationary process of zero mean and variance one. Now, the same reasoning that motivated Eq. 21 yields the following formula for the expected number of crossings of level u based on the hybrid model of W(t) for t ∈ T = [t₁, t₂], viz.

$$\mathbb E[N_{T}(u)]\!\!={\int}_{t_{1}}^{t_{2}} \!{\int}_{-\infty}^{+\infty}|z| f_{\dot{X}_{H}(0), X_{H}(0)}(z,w)\,dz\,dt,\quad \!\!w\,=\,(u^{a}-m)/\sigma. $$

Thus, the crossing intensity can be computed as the following integral:

$$ \mu_{\textbf{p}}(u)={\int}_{-\infty}^{+\infty}|z| f_{\dot{X}_{H}(0), X_{H}(0)}(z,w)\,dz. $$

(23)

1.4 A.4 Estimation of μ _p(u)

Considering K simulations of the amplitudes R_i and the locations of the highest (or lowest) points in the wind anomalies (U_1i, U_2i, U_3i), i = 1,…,N. Each simulation k, where k = 1,…,K, results in 4 ⋅ N values, denoted by r_k, u_k, containing r_i and u_i = (u_1i, u_2i, u_3i), i = 1,…,N. Furthermore, let μ_k(u|r,u) be the integral of Eq. 23 as evaluated for the conditional density of $\dot {X}_{H}(0)$ and X_H(0) given storm sizes r_k and storm locations u_k. Then, the intensity μ_p(u) can be estimated by averaging the values μ_k(u|r,u) as follows:

$$ \bar{\mu}_{\textbf{p}}(u)=\frac{1}{K}\sum\limits_{k = 1}^{K} \mu_{k}(u|\textbf{r},\textbf{u}). $$

(24)

In examples K = 50000. The computation of the conditional intensity of w level crossings μ_k(u|r,u) will be presented next. The intensity μ_k(u|r,u) can be given in almost analytical form, since conditionally on (r,u), $\dot {X}_{H}(0), X_{H}(0)$ are correlated zero mean Gaussian variables with the variances given below.

The hybrid model is defined by the Gaussian kernel in Eq. 3, i.e.,

$$f(\textbf{q}) =(2\pi)^{3/4}\,|\det {\Lambda}|^{1/4}\exp\left( -\pi^{2}\textbf{q}\,{\Lambda}\, \textbf{q}^{T}\right), $$

where q = (t,x,y). Let $\dot {f}(\textbf {q})$ be the following partial derivative:

$$\dot{f}(\textbf{q})=\frac{\partial f(t,x,y)}{\partial t}, \qquad \textbf{q}=(t,x,y). $$

Given storm amplitudes of r_i and with corresponding centre locations of u_i, i = 1,…,N, the conditional variances and the covariance matrix of the variables $(X_{H}(0),\dot {X}_{H}(0))$ are given by

$$ \begin{array}{ll} V(X_{H}(0)|\textbf{r},\textbf{u}) &{}= p^{2}+{\sum}_{i = 1}^{N} r_{i} f(\textbf{u}_{i})^{2}, \\ V(\dot{X}_{H}(0)|\textbf{r},\textbf{u}) &{}= p^{2}\pi^{2}\lambda_{11}+{\sum}_{i = 1}^{N} r_{i} \dot{f}(\textbf{u}_{i})^{2},\\ Cov(X_{H}(0),\dot{X}_{H}(0)|\textbf{r},\textbf{u}) &{}= {\sum}_{i = 1}^{N} r_{i} f(\textbf{u}_{i})\dot{f}(\textbf{u}_{i}). \end{array} $$

(25)

1.5 A.5 Computation of the conditional crossing intensity μ _k(u|r,u)

For simplicity of notation, let us use X and $\dot {X}$ to denote random variables distributed as X_H and $\dot {X}_{H}$ under the condition that storms amplitudes are r_i and their centres are located at u_i, i = 1,…,N. Hence, X, $\dot {X}$ are zero mean Gaussian with variances and covariance given by Eq. 25. Consequently, by Eq. 23

$$\begin{array}{@{}rcl@{}} \mu_{k}(u|\textbf{r,}\textbf{u})&=&{\int}_{-\infty}^{+\infty}|z|f_{\dot{X}, X}(z,w)\,dz\\ &=&f_{X}(w){\int}_{-\infty}^{+\infty}|z|f(z|w)\,dz,, \quad w=(u^{a}-m)/\sigma, \end{array} $$

(26)

where f(z|w) is the conditional probability density of $\dot {X}$ given that X takes a value of w. The density f(z|w) is normally distributed with a mean and variance given by

$$\begin{array}{@{}rcl@{}} &&\mathbb E[\dot{X}|X=w]= \frac{Cov(\dot{X},X)}{\mathbb V(X)}\,w,\\ &&V(\dot{X}|X)= V(\dot{X})-Cov(\dot{X},X)^{2}/ V(X). \end{array} $$

Then, integration by parts yields

$$ {\int}_{-\infty}^{+\infty}|z|f(z|w)\,dz=\sqrt{ V(\dot{X}|X)}\,{\kern-.5pt}\left( \psi(c(w)){\kern-.5pt}+{\kern-.5pt}\psi(-c(w))\right){\kern-.5pt}, $$

(27)

where $c(w)=\mathbb E[\dot {X}|X=w]/\sqrt { V(\dot {X}|X)}$ and

$$ \psi(y)=\phi(y)+ y\,{\Phi}(y). $$

(28)

Here, ϕ and Φ are the standard Gaussian density and distribution function, receptively. Finally,

$$ f_{X}(w)=\phi\left( w/\sqrt{\mathbb V(X)}\right)/\sqrt{ V(X)}. $$

(29)

1.6 A.6 Computation of the long-term distribution $\mathbb {P}(W(t,x,y)\le w)$

Equations 1 and 11 can be combined to obtain

$$\mathbb P(W_{\textbf{p}}\le w)=\mathbb P\left( p\,X_{\textbf{p}}+\sum\limits_{i = 1}^{N} X_{i}\le\frac{w^{a}-m_{\textbf{p}}}{\sigma_{\textbf{p}}}\right), $$

where X₀ = X_G(0, 0, 0) is the standard Gaussian variable and p = (t_p, x_p, y_p). For i ≥ 1,

$$X_{i}=X_{i}(0,0,0)=Z_{i}\sqrt{R_{i}}f(- \textbf{U}_{i}), $$

where the U_i are uniformly distributed locations of storms in a region S ⊂ R³. (Note that p, a and the kernel f depend on the location p.)

Since X₀, Z₁, Z₂,…,Z_N are i.i.d. standard Gaussian random variables, independent of U_i and R_i, if the value of R_if(−U_i)² is known, then $p\,X_{0}+{\sum }_{i = 1}^{N} X_{i}$ is a Gaussian random variable with a variance equal to $p^{2}+{\sum }_{i = 1}^{N} R_{i}\,f(-\textbf {U}_{i})^{2}$. Therefore, if the variance $p^{2}+{\sum }_{i = 1}^{N}$R_if(−U_i)² is independently simulated K times (K = 50000 in this study), then for each simulation, the following probability is computed:

$$\begin{array}{@{}rcl@{}} p_{j}(w)\!&=&\!{\Phi}\left( \!\frac{w^{a}\,-\,m}{\sigma\sqrt{p^{2}\,+\,{\sum}_{i = 1}^{N} r_{ij}f(-u_{1ij},-u_{2ij},-u_{3ij})^{2}}}\!\right),\\ &&sj\,=\,1,{\ldots} K, \end{array} $$

where Φ(x) is the probability distribution of a standard normal random variable. Now, the average of the p_j is an estimate of the local distribution of W_p:

$$ \mathbb P(W_{\textbf{p}}\le w)\approx \frac{1}{K}\sum\limits_{j = 1}^{K} p_{j}(w). $$

(30)

Appendix B: Estimation of the parameters N, p and 𝜗

Given the parameter N and the region S, the parameters p and 𝜗 can be estimated by requiring that the variance and the kurtosis of X_H are equal to the variance and kurtosis of the observed wind speeds. Furthermore, the crossing intensities μ_N(u) [unit: number per month] can be found using methods presented in the Appendix A for a given position p = (t_p, x_p, y_p), where t_p = j/12 − 1/24, j = 1,…, 12, represents the j th month. Similarly, the observed crossing intensities μ^emp(u) can be estimated from the hindcast wind data at the position p. Finally, the parameter N ≥ 0 is the location of the first local minimum of the distance d_N as in Eq. 31 between μ_N and μ^emp.

Definition of d _N

Let us introduce the normalized crossing rates

$$\begin{array}{@{}rcl@{}} f_{N}(u)&=&\mu_{N}(u)/{\int}_{D} \mu_{N}(u)\,du,\\ f^{emp}(u)&=&\mu^{emp}(u))/{\int}_{D} \mu^{emp}(u)\,du,\quad u\in D. \end{array} $$

where D = {u : f^emp(u) > 0} if the skewness of the wind time series is positive, otherwise, D = {u > u₀ : f^emp(u) > 0}. Here, the threshold u₀ > 0 is used to focus on the crossings of high levels. Then, the distance between μ_N(u) and μ^emp(u) is defined by

$$ d_{N}={\int}_{D} f^{emp}(u)\left|\log(f^{emp}(u))-\log(f_{N}(u))\right|\,du. $$

(31)

The distance is a modification of the Kullback-Leibler divergence, which measures the amount of information lost when f_N(u) is used to approximate f^emp(u).

Appendix C: MATLAB scripts to simulate spatio-temporal extremes

In this appendix, some MATLAB scripts to simulate spatio-temporal extremes are provided. First, a hybrid model has to be defined. Here, the proposed model is derived using physical parameters describing a possible wind speed climate. Then, the parameters a, m and σ of the wind speed field should be estimated, and they are given here in the script. For simplicity, the wind field is assumed to be symmetrical, i.e., skewness of W is zero, and hence parameter a = 1. The mean speed m is 9 m/s, whereas the standard deviation of W, σ = 3 m/s. Consequently, the Gaussian model for W postulates that most of the wind speeds at the location vary between 0 and 18 m/s.

3.1 C.1 Choose the matrix Λ

Next, the kernel function f(q) as in Eq. 3 should be defined. It is a function of the matrix Λ as in Eq. 4. Let assume that the excursion sets of extreme wind speeds are ellipses with major axis coinciding with south-north direction. Consequently, the correlation between the partial derivatives W_x and W_y is zero, and hence λ₂₃ = 0. The reminding components of the Λ matrix are chosen using the average sizes of windy regions L_x, L_y, the duration τ defined in Eq. 12, and the velocities v_x, v_y as in Eq. 18.

Let L_x = 7 degrees represent the windy region in longitude, L_y = 8 degrees represent the windy region in latitude, and let τ = 24 hours represent the windy time period, respectively. Then, by Eq. 12λ₂₂ = 1/49, λ₃₃ = 1/64 and λ₁₁ = 1/24². The remaining parameters λ₁₂ and λ₁₃ will be chosen by Eq. 18. Using the correlation matrix of the gradient X_t, X_x, X_y, and under the assumption that W_x and W_y are uncorrelated, it can be shown that,

$$ v_{x} = \rho_{tx}\frac{L_{x}}{\tau},\qquad v_{y}=\rho_{ty}\frac{L_{y}}{\tau}, $$

(32)

where ρ_tx, ρ_ty are the correlations between W_t and W_x, W_y, respectively. Consequently, the maximal average speed that a windy weather can move is 10/24 degree/hour in longitude direction and 1/3 degree/hour in the latitude direction. Let choose ρ_tx = 0.3 and ρ_ty = 0.5, it gives v_x ≈ 10 km/h and v_x ≈ 18 km/h, which are reasonable values for the Caribbean region (see, e.g., Dorst (2014)).

In the following MATLAB script, the parameters a,m,σ and the matrix Λ will be defined:

3.2 C.2 Select the region S and parameters N,𝜗,p

The region S has to be defined first. According to Eq. 13:

$$\textbf{S}=[-1.75\tau, 1.75\tau]\times[-1.75L_{x}, 1.75L_{x}]\times[-1.75L_{y}, 1.75L_{y}]. $$

For the above chosen region, |S| is calculated as 3.5³τL_xL_y = 57624 [hour⋅deg²]. The model will be specified when the parameters N, 𝜗 and p are given.

The method of moments is used to estimate p and 𝜗. The parameter is chosen in such a way that the variance of X_H is equal to one, and the kurtosis κ(X_H) is equal to the kurtosis of the transformed wind speeds X = W^a from the ECMWF hindcast dataset. (Here κ(X) = 12 will be chosen.) Consequently, as shown in Kvarnström et al. (2013), 𝜗 satisfies the following equality

$$ \kappa(X)= 3+\left( \sum\limits_{i = 1}^{N} \frac{\vartheta}{\left( 1+\vartheta\right)^{i}}\right)^{2}\left( \kappa\left( \sum\limits_{i = 1}^{N} X_{i}\right)-3\right). $$

(33)

Finally, the parameter p² is calculated by the following equation

$$ p^{2}= 1-\sum\limits_{i = 1}^{N} \frac{\vartheta}{\left( 1+\vartheta\right)^{i}}. $$

(34)

3.2.1 C.2.1 The case N = 1

For simplicity, N = 1 is chosen for the demonstration. As mentioned before, the kurtosis $\kappa ({\sum }_{i = 1}^{N} X_{i})$, where X_i are defined in Eq. 8, depends only on 𝜗. This relation can be used to estimate 𝜗. However, the computation of κ(X_Nn is very tedious; see the Appendix in Kvarnström et al. (2013). Only for N = 1, there is a simple formula for κ(X₁) as follows:

$$\begin{array}{@{}rcl@{}} \kappa(X_{1})&=&6|\textbf{S}|\,{\int}_{\textbf{S}} f(\textbf{p})^{4}\,d\textbf{p}\,\cdot \frac{(1+\vartheta)^{2}}{1 + 2\vartheta}\\ &=&6|\textbf{S}|\pi^{3/2}\sqrt{\det ({\Lambda})}\cdot \frac{(1+\vartheta)^{2}}{1 + 2\vartheta}. \end{array} $$

(35)

If ρ_xy = 0, which can be always achieved by rotating the coordinate system, and the region S is given in Eq. 13, the following equation can be obtained:

$$ |\textbf{S}|\sqrt{\det ({\Lambda})}=(3.5)^{3}\sqrt{1 -\rho_{tx}^{2}-\rho_{ty}^{2}}. $$

(36)

The value of 𝜗 is obtained by numerically solving the Eq. 33. Then p is computed by Eq. 34. Estimates of 𝜗 and p are evaluated using the following MATLAB script:

For N = 1 and κ(X) = 12, the program gives 𝜗 = 0.096 and p = 0.955.

3.2.2 C.2.2 Simulations of spatio-temporal maximums

Let us choose a spatial region of 6 by 6 degrees and period one month (31 days). The variable POS contains the discretized region while (Y) contains (Nsim= 500) of maximums. The discretization steps are half degree and two hours.

Using the code, three time series of 200 independent spatio-temporal maximums have been simulated and presented in Fig. 18.

Fig. 18

Three simulations of 200 independent spatio-temporal maximums of wind speeds over a region of 6 by 6 degrees and the time period of one month using hybrid model defined in Section A