Abstract
Located in northern Quebec, Canada, eight hydroelectric reservoirs of a 9782-km2 maximal area cover 6.4% of the La Grande watershed. This study investigates the changes brought by the impoundment of these reservoirs on seasonal climate and precipitation recycling. Two 30-year climate simulations, corresponding to pre- and post-impoundment conditions, were used. They were generated with the fifth-generation Canadian Regional Climate Model (CRCM5), fully coupled to a 1D lake model (FLake). Seasonal temperatures and annual energy budget were generally well reproduced by the model, except in spring when a cold bias, probably related to the overestimation of snow cover, was seen. The difference in 2-m temperature shows that reservoirs induce localized warming in winter (+0.7 ± 0.02 °C) and cooling in the summer (−0.3 ± 0.02 °C). The available energy at the surface increases throughout the year, mostly due to a decrease in surface albedo. Fall latent and sensible heat fluxes are enhanced due to additional energy storage and availability in summer and spring. The changes in precipitation and runoff are within the model internal variability. At the watershed scale, reservoirs induce an additional evaporation of only 5.9 mm year−1 (2%). We use Brubaker’s precipitation recycling model to estimate how much of the precipitation is recycled within the watershed. In both simulations, the maximal precipitation recycling occurs in July (less than 6%), indicating weak land-atmosphere coupling. Reservoirs do not seem to affect this coupling, as precipitation recycling only decreased by 0.6% in July.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Hydroelectric production globally continues to increase in terms of number of dams and capacity. Over 50,000 large dams can be found around the world (Dahir 2006), and as of March 2014, 3700 more were planned or under construction (Zarfl et al. 2015). These new infrastructures are expected to increase the global electricity production capacity by 720 GW within the next 20 years (Zarfl et al. 2015). The impoundment of hydropower reservoirs is known to induce changes to the regional climate that may vary in magnitude, spatial and temporal scales, depending on the reservoir size and its geographic location.
At high latitudes, several studies have reported that lakes and reservoirs absorb heat in summer, and release it partially in autumn, resulting in the damping of air temperature diurnal and annual cycles (Dutra et al. 2010; Eaton et al. 2001; Nordbo et al. 2011; Samuelsson et al. 2010; Subin et al. 2012). For example, based on field observations over and around the Great Bear and Great Slave Lakes (Northwest Territories, Canada), Rouse et al. (2008, 2005) evaluated the impacts of adding lakes to a region composed of uplands and wetlands. In part, due to their smaller surface albedo and greater heat capacity, lakes caused a fourfold increase of the maximum seasonal heat storage. Using regional climate simulations over the same region, Long et al. (2007) found that skin temperatures decreased by up to 10 °C in July and August, and increased by as much in October owing to the presence of the two lakes. The effect of the Laurentian Great Lakes on seasonal climatic conditions has been well-documented using not only field data (Robert and Floyd 1997), but also modeling experiments (Bates et al. 1993; Lofgren 1997; Martynov et al. 2012; Notaro et al. 2013; Wilson 1977). Over Lake Superior, Martynov et al. (2012) reported an average warming of 6 °C in January and an average cooling of 2 °C in June when multidecadal regional climate simulations with and without lakes were compared. Following a similar approach, Huziy and Sushama (2016) used the fifth generation of the Canadian Regional Climate Model (CRCM5; Martynov et al. (2013)), coupled to the Hostetler 1D lake model (Hostetler et al. 1993), to investigate the influence of lakes on regional climate and hydrology. Over northern Quebec, they reported that lakes were responsible for a warming in fall, winter, and spring (maximum in winter and under 4 °C) and a cooling in summer (under 2 °C). While several studies have investigated the impacts of large water bodies on the regional energy balance and local climate in northwestern Canada (Long et al. 2007; Rouse et al. 2008; Rouse et al. 2005) and northern Europe (Nordbo et al. 2011; Samuelsson et al. 2010), very few have focused on northern Quebec, where some of the world largest hydropower reservoirs can be found.
There is debate in the scientific community about the water use through hydropower production —mostly due to the diversity of water consumption definitions. First introduced by Hoekstra (2003), the water footprint is the most commonly used water consumption indicator. The blue water footprint of hydroelectricity is defined as the annual volume of water that is evaporated from a reservoir, normalized by its energy production. It is often referred to as the gross water consumption. When using this definition, some studies reported that hydropower production has a large water consumption (Gerbens-Leenes et al. 2009; Mekonnen and Hoekstra 2012). Another frequently used indicator is the net water consumption (Herath et al. 2011), where evapotranspiration (ET) from pre-impoundment landscapes is subtracted from the reservoirs annual evaporation. The estimated water loss is thus significantly reduced. For example, Strachan et al. (2016b), who investigated water consumption of the Eastmain-1 reservoir in northern Quebec, reported net water consumption to be within 19 to 34% of the gross water consumption. More recent studies also allocate the gross or net water consumption to the different uses of multi-purpose reservoirs (Zhao and Liu 2015). However, a problem still arises in all methods described above: they consider all the evaporated water as a loss. This is true to a limited extent, since the evaporated water may return to the watershed as precipitation. This phenomenon is called precipitation recycling.
The concept of precipitation recycling has been explored in many studies focusing on land surface-atmosphere interactions (e.g., Eltahir and Bras 1994; Kunstmann and Jung 2007; Lettau et al. 1979; Szeto et al. 2008). The so-called precipitation-recycling ratio is used to quantify the contribution of local evaporation to precipitation in the same region. At the planetary scale, the precipitation-recycling ratio equals one and at a single point, it equals zero. To quantify the precipitation-recycling ratio at the regional scale (from a large catchment to a continent), several methods have been developed. Many of them are based on the atmospheric water balance (Brubaker et al. 1993; Budyko 1974; Eltahir and Bras 1994), which usually assumes vertically well-mixed atmospheric moisture and neglects monthly variations of atmospheric moisture content, as they are normally much smaller than the evaporated and advected moisture fluxes. Alternative methods trace evaporated water molecules as they are advected in the atmosphere and later precipitate inside or outside the delimited domain (Bosilovich and Chern 2006; Dirmeyer and Brubaker 1999; Koster et al. 1986); these water-vapor tracers are generally imbedded within global climate models.
In this study, the CRCM5 is used to quantify the effects of northern Quebec reservoirs on local climate and to estimate their impact on precipitation recycling. The sensitivity analyses were carried out using two simulations: “no reservoir” and “with reservoirs”. The goal is to bring a better understanding of the impacts of reservoirs on regional water resources availability and hydroelectricity water consumption. In section 2, the CRCM5 and the experimental configuration are described. In section 3, the CRCM5 simulations are validated using field observations and are compared to each other. A summary of the main findings is presented in section 4.
2 Models, methods, and data
2.1 Climate model: CRCM5
The CRCM5 was developed at the Centre pour l’Étude et la simulation du climat à l’echelle régionale (ESCER) at the Université du Québec à Montréal (UQAM) with the collaboration of Environment and Climate Change Canada. Based on the dynamic core and physical parameterization of the limited-area version of the Global Environment Multiscale model (GEM; Côté et al. (1998)), the CRCM5 solves primitive non-hydrostatic Eulerian equations using a semi-Lagrangian transport equation and a semi-implicit time-step resolution scheme. Type-C Arakawa grids are used for horizontal discretization. In the vertical, the multilevel coordinates follow topography and are based on hydrostatic pressure. Physical parameterizations from GEM include: Kain and Fritsch (1990) for deep convection, Kuo-Transient for small-scale convection (Bélair et al. 2005), Sundqvist et al. (1989) for large-scale condensation, and k-correlated scheme for shortwave and longwave radiation (Li and Barker 2005). Interactively coupled with the atmospheric module, land surface processes are described by the Canadian Land Surface Scheme (CLASS V3.6, see section 2.2). Compared to earlier versions, the CRCM5 offers physical parameterizations adapted for a finer spatial resolution. In addition, to represent water and energy exchanges between the atmosphere and inland water bodies, the CRCM5 was fully coupled to a 1D lake model (FLake, see section 2.3). To resolve the dynamic and thermodynamic equations, the CRCM5 requires lateral boundary conditions: multi-level air temperature, horizontal winds, specific humidity, and sea level pressure. For a detailed description of the CRCM5, the reader is referred to Šeparović et al. (2013) and to Hernandez-Diaz et al. (2013).
2.2 Land surface model: CLASS V3.6.
CLASS (Verseghy 1991; Verseghy et al. 1993) solves the energy and water budgets separately for the following land covers: bare soil, snow over bare soil, snow over vegetation, and vegetation alone. Four vegetation groups can coexist: needleleaf trees, broadleaf trees, crops, and grass. For each vegetation group, canopy properties are calculated as weighed averages over the subclasses represented in that group; 22 different vegetation subclasses are available. Surface fluxes are averaged considering the proportion of each land cover in a given model grid cell; this method is known as the mosaic approach. The soil is discretized in 17 layers, with a maximum total depth of 15 m. Infiltration is described with the Green and Ampt (1911) model, in which water moves between vertical layers as a wetting front. Snow is considered as a single layer and snow cover is complete when the snow depth reaches or exceeds 10 cm. Compared to the previous versions, the amount of snowfall needed to reset the snow albedo value to that of fresh snow, the snow thermal conductivity parameterization and the ponding depth over organic soils have all been revised. For a description of the runoff generation modeling, the reader is referred to Verseghy (1991).
The ability of CLASS to simulate summer energy balance has been confirmed for various types of terrain (Bartlett et al. 2002; Bellisario et al. 2000; Comer et al. 2000; Lafleur et al. 2000). For example, for a boreal forest in north-central Manitoba, Bartlett et al. (2002) showed that CLASS V2.6. could reproduce diurnal net radiation and turbulent fluxes. However, many studies have reported a tendency for CLASS to overestimate snow cover duration (Brown et al. 2006; Langlois et al. 2014; Langlois et al. 2004).
2.3 Lake model: FLake
FLake is a one-dimensional model designed to predict freshwater lakes thermal regimes (Kheyrollah Pour et al. 2012; Kourzeneva and Braslavsky 2005; Mironov et al. 2010; Stepanenko et al. 2010). The energy budget is solved for each of the following layers: bottom sediments, water, ice, and snow. In all layers, the temperature profiles are described with the concept of self-similarity, analogous to the ocean active layer (Kitaigorodskii and Miropolski 1970). Only two layers are considered in the water column, namely, the mixed layer and the thermocline. In the mixed layer, the temperature is constant with depth. In the thermocline, it varies with depth as a polynomial function and depends on a dimensionless shape factor. Within the ice and snow layers above the water column, the temperature profiles are linear. The model is fully described in Mironov (2008).
FLake has previously been coupled with many RCMs and weather prediction models (Mallard et al. 2014; Martynov et al. 2010; Martynov et al. 2012; Mironov et al. 2010). For shallow and freezing lakes, several studies showed that FLake could reproduce lake surface temperatures (LST) with and without an ice cover, as well as freeze-up and breakup dates (Kheyrollah Pour et al. 2012; Martynov et al. 2010; Samuelsson et al. 2010). When running FLake off-line, Kourzeneva and Braslavsky (2005) reported that FLake had low sensitivity to initial conditions, as well as fetch and optical parameters. However, LST showed strong sensitivity to lake depth. This is in agreement with the study conducted by Martynov et al. (2010).
2.4 CRCM5 experimental configuration and simulation datasets
As mentioned above, regional climate models require lateral boundary conditions at each integration time step. For this study, the CRCM5 is nested within the ERA-Interim reanalysis over the period of 1979–2014. Along the lateral boundaries, a halo zone of ten grid points allows for the semi-Lagrangian interpolation, which is followed by an equivalent sponge zone, where physical variables are relaxed toward the driving fields (Davies 1976). Centered on the province of Quebec, the 300 × 300 grid points free domain is discretized at a 0.11° horizontal resolution. In the vertical, 56 levels are used. Calculations are performed at 5-min time steps. Ocean surface temperatures and ocean ice-cover fraction are prescribed with the ERA-Interim dataset (Dee et al. 2011).
Table 1 describes the numerical simulations run in this study. Two CRCM5 simulations, without hydropower reservoirs (NoRes), corresponding to the pre-impoundment conditions (before 1979), and including hydropower reservoirs (WithRes), corresponding to the post-impoundment conditions (after 2006), are performed by adjusting the water/land fraction on the reservoir grids. The simulation outputs are then compared to address our research objectives.
Regional climate models present their own internal variability (IV; see for instance, Alexandru et al. 2007; Braun et al. 2012; Caya and Biner 2004; de Elía and Côté 2010). Because of truncation errors in numerical integration and the non-linearity of feedback mechanisms represented in a model, even two simulations run on the same domain and with similar driving data will provide slightly different outputs (Christensen et al. 2001). Due to computational constraints, we carried out a basic IV analysis, using an ensemble of two CRCM5 simulations that started a year apart (IV-I and IV-II). A change due to the presence of reservoirs is considered significant only when it exceeds the model internal variability.
2.5 Precipitation recycling model
The precipitation recycling model from Brubaker (1991) is used. This model was chosen for its simplicity and its ability to include the direction of the advected water vapor in the domain. The 2D precipitation recycling model from Brubaker (1991) is an extension of the Budyko (1974) 1D model. Both models represent the precipitation P over a chosen domain as the sum of precipitation originating from atmospheric moisture advected into the domain P adv and originating from evapotranspiration P evap within the domain:
Over a linear domain oriented along the advected water vapor, Budyko (1974) defines the precipitation recycling ratio as:
where E is the evaporation averaged along the water vapor flux streamline, L, domain length and I the moisture influx.
In Brubaker (1991) precipitation recycling model, the advection of water vapor is not necessarily assumed to be parallel to a linear domain. This adjustment is achieved by using an effective domain length (L eff, see Eq. 7) and an effective moisture influx (I eff, see Eq. 8) rather than using L and I. The precipitation recycling ratio ρ p is therefore calculated as
where 〈E〉 is the mean evapotranspiration over the 2D domain. This method assumes mean regional precipitation and evaporation to be representative of the local conditions.
First, the monthly zonal and meridional water vapor fluxes are calculated for each grid point inside and around the domain using the 3-h pressure levels’ specific humidity (q), zonal wind (u) and meridional wind (v). These are vertically integrated over the atmospheric column (from the surface p o, to the lowest pressure level p top):
where g is the gravitational constant. The vertically integrated water vapor fluxes (VIWVF), Qu and Qv, are expressed in kg m−1 s−1. The mean flow and the transient eddies are represented, respectively, by the first and second terms on the right-hand side of the Eq. 4.
Then, from the meridional and zonal VIWVF, the part of the perimeter on which inflow occurs is identified (γ A to γ B ), and influx vectors \( \overrightarrow{\mathrm{Q}}\left(\upgamma \right) \) are calculated (blue arrows in Fig. 1):
Schematic of the precipitation recycling model components for an arbitrary domain, adapted from Brubaker (1991). Only \( \overrightarrow{\mathrm{Q}\left(\upgamma \right)} \) , 1(γ), and α(γ) vary along the influx borders
Next, the direction of the area mean VIWVF, the unit vector \( \overrightarrow{u} \) , is evaluated:
where 〈〉 represents spatial averages over the domain.
Refer to Fig. 1 for an illustration of the important terms in the following equations.
The expression for the effective domain length L eff (in m) is given by
where A is the domain area, θ the angle between \( \overrightarrow{u} \) and the x-direction, ∆y the domain width and ∆x the domain length.
The effective influx I eff, expressed in kg m−1 s−1, is calculated as
where 1(γ) represents the path of an influx vector (along the direction of \( \overrightarrow{u} \)) from its entry point until it exits the domain (in m); γ the distance along the influx border (in m) and α(γ) the angle between \( \overrightarrow{u} \) and its adjacent side of the domain (see Fig. 1).
First introduced by van der Ent et al. (2010), the concept of evaporation recycling was used to determine which part of evapotranspiration is recycled as continental precipitation. In this study, we define the evaporation recycling ratio ρ e as the fraction of evapotranspiration that returns to the watershed as precipitation, namely,
It is derived from monthly precipitation recycling ratios ρ p, as well as spatially-averaged precipitation 〈P〉 and evapotranspiration 〈E〉. This indicator provides additional information of water loss through evapotranspiration.
2.6 La Grande River watershed and its hydropower reservoirs
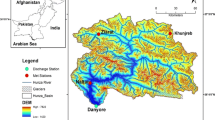
The study area is the La Grande River watershed, in northern Quebec, Canada (Fig. 2). In the period 1979 to 2006, eight hydropower reservoirs were progressively impounded, covering 6.4% of the watershed area (153,798 km2). As of today, this basin hosts 11 hydropower plants for a total installed capacity of 16.9 GW.
Note that our analysis extends from the reservoir scale (∼103 km2), hereby defined as the local scale, to the watershed scale (∼105 km2), defined as the regional scale. Table 2 presents some characteristics of the reservoirs in the watershed. For each reservoir, we only considered model grid points where the water fraction increased by at least 10%; therefore, the run-of-river LG1 reservoir was excluded from the analysis. The Eastmain-1 reservoir (Fig. 2) also had to be excluded due to inconsistencies in the model outputs from the WithRes simulation. Even after changing the land and water fractions over Eastmain-1 reservoir, the grid points at this location were still not recognized as lakes.
As can be seen from Table 2, lake depths in the CRCM5 geophysical database may differ from the actual lake depths. When the lake depth is not included in the database, a basic lake depth parameterization is used: 60 m when the water fraction exceeds 50% and 10 m otherwise. The same parametrization was also used by Martynov et al. (2012). At most locations, the modeled and actual reservoir depths are close (typically within ±4.5 m), except at the LG3 reservoir. Pre- and post-impoundment lake fractions are derived from Hydro-Quebec archives and the Base de Données pour l’Aménagement du Territoire (BDAT; Ministère de l’Énergie et des Ressources Naturelles 2015), respectively. Since many islands can be found over the reservoirs, their mean water fractions remain under 55%.
Vegetation fractions in the CRCM5 geophysical database were derived from the U.S. Geological Survey’s Global Land Cover Characteristics database (USGS-GLCC; Anderson et al. 1976; Brown et al. 1999). It is the land cover dataset currently used in GEM and in many other meteorological and climate models (e.g., Hübener et al. 2005; Huziy and Sushama 2016; Paeth et al. 2009; Winter and Eltahir 2010). In the late stages of our analysis, we found that the position of the needleleaf treeline within USGS-GLCC had a bias to the south, resulting in an underestimation of needleleaf coverage inside the watershed. Although this is certainly a limitation of the study, we believe that this should not affect the main conclusions of our analysis. A thorough discussion of this issue can be found in section 4.
2.7 Observations used for model validation
To evaluate the CRCM5 ability to adequately simulate land-atmosphere water and energy exchanges, outputs from the NoRes and the WithRes simulation are compared to a detailed set of in situ observations, from a network of weather stations, and from local eddy flux tower data (Strachan et al. 2016a; Wang et al. 2016) (see Fig. 2).
A total of 38 weather stations were deployed within the La Grande River watershed between 1979 and 2014. These stations were managed by local governmental authorities, namely Hydro-Québec, Natural Resources Canada (NRCan), and the Ministère du Développement Durable, de l’Environnement et de la Lutte contre les Changements Climatiques (MDDELCC). Their daily time series vary in length between 3 and 30 years. We compared temperature and precipitation observations to the closest model grid point. Years with 10% or more of missing data were excluded from the analysis. Since the weather station located near the Robert-Bourassa reservoir (53.63° N, 77.8° W) was operational for 30 years, it was used to validate the mean annual precipitation cycle (see section 3.1.2.).
The reservoirs were not impounded simultaneously (Table 1). The first reservoir (Robert-Bourrassa) was created in 1978, and the latest one (Eastmain-1), in 2006. Thus, the NoRes and WithRes simulations correspond to the landscape before 1978 and after 2006, respectively. Since the landscape evolved between 1978 and 2006, validating the modeled temperature and precipitation using in situ observations during this period is not trivial, as weather stations in the vicinity of the reservoirs may be affected by the impoundment. To take this effect into account, we used the following approach. When a weather station was located within 120 km from the shore of a nearby reservoir, we separated its time series into three periods: pre-impoundment, impoundment, and post-impoundment. Data from the pre- and post-impoundment periods were compared with outputs from the NoRes and WithRes simulations, respectively, whereas data from the impoundment period were simply rejected. Weather stations outside this radius were compared to the WithRes simulation. Note that the value of 120 km was carefully selected following a sensitivity analysis of mean seasonal temperature biases.
Long-term datasets of energy budget terms in northern regions are scarce, particularly in remote areas like the La Grande River watershed. The closest FLUXNET sites (Baldocchi et al. 2001) were ∼280 km south of the watershed and were exclusively taken over forested surfaces (Grant et al. 2009). Fortunately, radiative and turbulent flux measurements were taken during the period 2008–2012 at three eddy covariance towers in the southwestern portion of the watershed (Fig. 2), as part of a study on greenhouse gas emissions from boreal hydropower reservoirs (Teodoru et al. 2012). One of the towers was located over the Eastmain-1 reservoir (52° 07′ 30″ N, 75° 55′ 51″ W), the second one, over an ombrotrophic bog (52°17′25″N, 75°50′25″W), and the third one, in a black spruce forest (52° 06′ 16″ N, 76° 11′ 48″ W). No data were collected over bare soil, which covers less than 10% of the La Grande watershed. Note that the upwelling shortwave (SW) and longwave (LW) radiation from the tower located over the reservoir were only available from May to September 2008.
Validation data of the energy balance at the watershed scale were computed using an area-weighted average of tower observations following the fractions of water, grass and needleleaf in the CRCM5 geophysical database for the WithRes simulation. Flux measurements collected over the Eastmain-1 reservoir were assumed to be representative of those observed over water bodies across the entire watershed. Similarly, fluxes measured over a bog and over black spruces were assumed to be representative of low vegetative cover and forests at the catchment scale (corresponding to the grass/tundra and needleleaf land covers in CLASS), respectively.
3 Results and discussion
3.1 Model validation
3.1.1 Seasonal 2-m air temperature
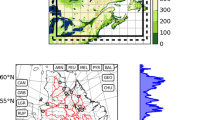
Figure 3 compares observed 2-m air temperatures from each weather station within the La Grande watershed to the CRCM5 closest grid point temperature. Given that biases are smaller than 1.2 °C, mean winter, fall, and summer temperatures are relatively well captured by the CRCM5. Mean spring 2-m temperatures show slightly larger cold bias of approximately −1.9 °C (Fig. 3a). For daily minimum temperatures (Fig. 3b), higher negative biases were found in transitional seasons, −1.2 °C in fall, and −1.0 °C in spring (all stations averaged). In winter and summer, depending on the weather station, minimum temperatures are either underestimated or overestimated, leading to a warm bias of approximately +0.2 °C and +0.3 °C, respectively. The CRCM5 underestimates daily maximum temperatures during all seasons (Fig. 3c); the largest mean bias (at all stations) is seen in spring (−3.1 °C). Comparing CRCM5 simulated mean 2-m air temperatures with that of ERA-Interim, CRU 3.1 and UDel datasets, Martynov et al. (2013) reported similar biases in JJA and DJF (i.e. under −3 °C).
Observed and simulated seasonal a mean, b minimum, and c maximum air temperature. Observations from each weather station are compared to the temperature simulated at the closest model grid point. See section 2.7 for more details on how this comparison is performed
3.1.2 Precipitation
Simulated and observed annual total precipitation are compared in Fig. 4. Note that most weather stations have time series of 5 to 10 years. As shown in Fig. 4a, the CRCM5 annual precipitation is overestimated at all stations. Overall bias of annual precipitation over the La Grande River watershed is approximately 315 mm per year (48%). It is interesting to note that the station with the largest time series (>20 years) shows the smallest bias (111 mm per year, 18%). This dataset is used to validate the precipitation annual cycle (Fig. 4b). CRCM5 captures the precipitation annual cycle relatively well despite the large annual bias; the root mean square error is of 0.4 mm day−1. Using multiple gridded precipitation datasets, over their boreal and arctic land subdomains, Martynov et al. (2013) reported annual wet biases that could reach 0.5 mm day−1. These errors might not be exclusively related to the model since measuring snowfall accurately is very challenging (snow typically accounts for 40% of annual precipitation at these latitudes (Groisman and Easterling 1994)). Fortin et al. (2008) found that catch ratios of an automatic gauge (similar to those deployed over the watershed) to a double fence intercomparison reference (DFIR) located in northern Quebec were under 80% when wind speed exceeded 2 m s−1, which is the case most of winter (data not shown). No correction was applied to account for wind-induced bias in precipitation measurements.
a Observed annual mean precipitation for weather stations spread over the La Grande River watershed versus the CRCM5 precipitation at the closest model grid point; b observed precipitation annual cycle for the period 1982–2014 at the station with the longest time series (55.36° N, 77.7° W) and its closest corresponding CRCM5 grid point
3.1.3 Energy budget at the watershed scale
Neglecting the heat flux into the bottom sediments, the energy balance for a soil or water column is expressed as
where \( \frac{\Delta \mathrm{S}}{\Delta \mathrm{t}} \) represents the rate of heat storage, Net SW the net shortwave radiation (positive downward), Net LW the net longwave radiation (positive downward), SH the sensible heat flux (positive upward) and LH the latent heat flux (positive upward). All terms are expressed in W m−2.
Annual cycles of simulated and observed energy fluxes at the watershed scale are shown in Fig. 5. Since upwelling shortwave and longwave radiation data over the reservoir were not available most of the year, we only plotted the annual cycles of each tower separately. The upwelling shortwave radiation (Fig. 5a) seems largely overestimated by the model from April to May, with a bias exceeding 50 W m−2 at the monthly scale. This agrees with the cold bias observed in spring (Fig. 3a). We think that these biases are due to the fact that the snow module within our land surface scheme (CLASS V3.6) tends to overestimate both the maximum snow depth and the snow cover duration in northern Quebec, as reported by Langlois et al. (2014). The upwelling longwave radiation is underestimated from February to June (Fig. 5b). In general, the downwelling shortwave and longwave radiation annual cycles are well represented by the CRCM5, although simulated downwelling longwave radiation tends to be somewhat underestimated throughout the year (Fig. 5d). During June, July, August, and September, the regional net radiation is well reproduced with a 4-month bias under 0.5 W m−2 (not shown).
Annual cycles of simulated and observed energy fluxes at the watershed scale and at each eddy flux tower for a upwelling shortwave radiation, b upwelling longwave radiation, c downwelling shortwave radiation, d downwelling longwave radiation, e sensible heat flux, and f latent heat flux for the La Grande River watershed for the years 2008, 2009, 2011, and 2012. In c–f, observations (OBS) are calculated as area-weighted averages of energy fluxes measured in the bog, the spruce forest and over the reservoir as discussed in section 2.7
Over each reservoir in the WithRes simulation, ice forms in the second half of October and disappears in the first half of June. Yet, estimations from Wang et al. (2016) indicate that ice over Eastmain-1 reservoir typically forms in the second half of November and disappears in May. Spring energy input (Fig. 5a) and air temperature (Fig. 3) are underestimated by the model, which is associated with the slightly delayed breakup dates compared to observations―causing reduced maximum heat storage. Consequently, the freeze-up dates occur earlier in the model than in the observations.
Figure 5 shows that the CRCM5 reproduces sensible heat fluxes over most of the year quite well; although negative bias occurs from April to June. For the same period, simulated latent heat fluxes (Fig. 5f) also tend to be smaller than the observations. These underestimations may be explained by two phenomena: the energy deficit (net radiation being underestimated by the model) at the same period and the assumption made to extrapolate the energy budget terms at the watershed scale. As mentioned in section 2.7, the observed surface heat fluxes were averaged based on the fraction of each surface type represented in the model. The observations taken in the bog were associated to the grass fraction—mainly composed of tundra. However, the evaporative patterns of bogs and tundra are different. In bogs, the peat soil has a high water content and water table close to the surface. Therefore, energy input is the principal driver of ET (Price 1991), leading to an early increase of ET (as the snow cover decreases) and strong summer daily ET rates. This is not the case in tundra-dominated surfaces, where water availability typically limits daily ET (Isard and Belding 1989). Given the large spatiotemporal heterogeneity of surface fluxes one can find even at small scales (Brutsaert 1998), the assumption that the eddy covariance observations—with a footprint area in the black spruce forest estimated to be ∼0.02 km2 under unstable atmospheric conditions (Schmid 1994)—were representative of fluxes observed over an area of 153,798 km2 also has its limitations. In light of these considerations, the model performance appears sufficiently good to proceed with the sensitivity analysis.
3.2 Sensitivity analysis
3.2.1 Impacts of reservoirs on local air temperatures
Figure 6 presents the changes on seasonal maximum, minimum, and mean 2-m air temperatures and the corresponding IV maxima induced by the reservoir impoundment. Figure 6a shows that, over all reservoirs, summer daily maximum temperatures are sensitive to the increasing surface water fraction, since the changes on this variable exceed the internal variability of the model. Following impoundment, summer days become significantly colder (−1.1 °C, approximately) as water has significantly different thermal properties compared to land surfaces. During daytime, over land, surface radiative forcing combined with the small thermal conductivity and small heat capacity results in important surface warming. This leads to increasing unstable stratification in the atmospheric boundary layer (ABL) and thus to transport of heat upwards through the action of convective eddies. As for the lakes, the situation is different: wind-driven mixing (and thus heat transport through the water column) and high heat capacity result in reduced surface warming. Smaller temperature gradients lead to weaker surface sensible heat fluxes, which explain colder air daily maximum temperature over the reservoirs during summer. Throughout the year, nights are significantly warmer when reservoirs are present. This is reflected in higher daily minimum temperatures (Fig. 6b). Averaged over all reservoirs, increases of daily minimum temperatures of 1.4, 1.2, and 1 °C, are seen in winter, spring, and fall, respectively. At night, ice-free reservoirs are warmer than the atmosphere, resulting in sensible heat losses. Excluding summer, changes in mean daily temperature are greater than the model internal variability (Fig. 6c). A slight warming is observed in DJF, MAM, SON and a cooling is observed in JJA. These changes in local air temperatures associated with the presence of reservoirs are smaller than those reported by Huziy and Sushama (2016) (in winter, a warming over 4 °C was reported over the Robert-Bourassa reservoir), who compared regional climate simulations with and without lakes over the province of Quebec. This is expected, as in the case of their simulation without lakes, the latter were replaced by bare soil, whereas in the case of our NoRes simulation, reservoirs were replaced by pre-impoundment land covers (e.g., forest, tundra, and swamp). The outcome is a more realistic diagnostic of the impact of reservoirs on local climate.
Modeled seasonal changes in 2-m air temperatures due to the presence of reservoirs for a daily maximum temperature, b daily minimum temperature, c daily mean temperature over each reservoir and averaged over all reservoirs for the period 1982–2014. The bars represent the maximal seasonal internal variability
3.2.2 Impacts of reservoirs on local energy balance
Changes over each reservoir and the corresponding IV maxima of energy budget terms are shown in Fig. 7.
Same as in Fig. 6 but for a net shortwave radiation (positive downward), b net longwave radiation (positive downward), c rate of heat storage, d sensible heat flux, and e latent heat flux
For nearly all seasons and sites, the impacts of reservoirs on the seasonal energy budget exceed the internal variability (Fig. 7). In winter, no significant change in downwelling radiation is observed (not shown). However, the net shortwave radiation increases by 9.4% (Fig. 7a). Ice cover is mostly constant throughout the season, with the smallest ice coverage over the Laforge 1 reservoir (83%) and the largest over Laforge 2 reservoir (100%). The magnitude of net longwave radiation is increased by 11% (Fig. 7b), resulting in a decrease of the available net energy at the surface. Since the sensible heat flux increase (+210%) is larger than the increase in latent heat flux (+36%) and thus evaporative cooling, the seasonal 2-m air temperatures increase.
In spring, the 11% increase of net shortwave radiation exceeds the internal variability and is therefore significant (Fig. 7a). Again, the change in net shortwave radiation is exclusively due to the decrease of surface albedo (−2.7% averaged over all reservoirs). This additional energy is heating the reservoirs rather than being transferred back to the atmosphere (Fig. 7c), which is typical of temperate freezing lakes. In fact, from energy flux measurements, Nordbo et al. (2011) have also reported small daily latent heat flux and even negative daily sensible heat fluxes from a shallow boreal lake in April and May.
In summer, the water bodies induce colder surface temperatures and the net longwave radiation increases by 4% (Fig. 7b). The downwelling shortwave radiation increases by 2% (not shown), suggesting a decrease in cloud cover presumably brought by a more stable atmosphere. As a matter of fact, Rouse et al. (2005) reported that afternoon summer clear-skies conditions over Great Slave Lake occurred around 25% more often than over near terrestrial areas. Depending on the reservoir, the albedo decreased between 2.5% and 9.3%. Less sensible heat (−21.6%) is transferred to the atmosphere and the changes in latent heat fluxes are small. Since LSTs increases slowly compared to land (not shown), significant turbulent fluxes transfer from water bodies to the atmosphere tends to begins later in the year (Fig. 5e, f). For example, Rouse et al. (2005) reported that turbulent heat transfer onset occurred 40 days later over a medium lake (12.1 m deep) in northwestern Canada than over uplands. The rate of heat storage is increased by 8% with the presence of reservoirs (Fig. 7c). As reported by Spence et al. (2003), shallow boreal lakes act as heat sinks in the open water season (June to mid-August) and as heat sources later on (Sept. to Nov.).
In fall, slightly more net shortwave radiation is absorbed at the surface (5.6%). The net LW radiation decreases, since skin temperatures are increased when reservoirs are present at the surface (Fig. 7b). This enhances thermal ABL instabilities. This instability, stronger winds, and the accumulation of energy in the reservoirs will lead to more turbulent energy transfer from the surface to the overlaying air: +7.4 W m−2 (60%) sensible heat flux and +8.2 W m−2 (25%) latent heat flux. During the first half of fall, the reservoirs are still ice-free—maximum ice coverage is reached by the end of November. Maximum changes on turbulent fluxes remain below 15 W m−2 (Fig. 7d, e). After all, water fraction increases over each reservoir remain under 44% and the reservoirs are not very deep (Table 2); therefore, maximum energy storage and turbulent heat transfer are limited.
A few limitations of the analysis should be re-emphasized here. The parameterized reservoirs depths within the FLake model differed from their real values. This induces biases in simulated water surface temperatures, energy partitioning at the surface and lake ice formation/breakup timing. Depending on the amount of precipitation and the reservoir management practices, it is known that the depth of a hydroelectric reservoir varies during the year. According to Hydro-Québec (Schetagne and Therrien 2013), depending on the reservoir, water levels vary typically between 1 and 8 m throughout the year. Considering these changes on reservoir levels and that error on 10-m deep reservoirs is generally under 4.5 m, we think that the assumed averaged value of 10 m is acceptable for this study. As well, we found an underestimation of needleleaf trees coverage over the La Grande River watershed. With a needleleaf tree dominated land cover (instead of tundra dominated), we think that the presence of reservoirs would not cause as much additional available energy since coniferous forests already have low albedo. Since coniferous trees have a larger surface contact area from which sublimation can occur, replacing them by water should induce a decrease in latent heat flux during winter (see Fig. 5f). Also, a decrease of sensible heat should be seen in the beginning of the year. In fact, from January to August, observed sensible heat flux from the forest far exceeds that from the Eastmain-1 reservoir (Fig. 5e). This is consistent with observations of Harding and Pomeroy (1996), who reported that needleleaf canopies tend to have lower albedos and release more sensible heat than ice-covered lakes.
3.2.3 Impacts of reservoirs on regional water resources
The changes on seasonal precipitation following impoundment are shown in Fig. 8. Averaged over all reservoirs, the model shows a slight increase of precipitation in winter (+0.8%) and a slight increase in summer (+1%). As shown by the small difference between the grouped bars in Fig. 8a, c, those changes are mostly attributed to the model internal variability rather than the presence of reservoirs. In spring, the all-reservoirs change in precipitation exceeds the IV. However, they vary from one reservoir to another: precipitation decreases over four reservoirs and increases over two reservoirs (Fig. 8b). In fall, the signal is clearer: reservoir-averaged precipitation increases by 1.5% (more thermal instability). Changes on seasonal runoff generally follow those on seasonal precipitation (data not shown).
Annually, precipitation and runoff are slightly higher when reservoirs are present. Again, these increases cannot be considered significant because they are smaller than the internal variability. With pre-impoundment conditions, regional evaporative losses sum up to 269.3 ± 0.3 mm per year. The presence of reservoirs causes a very minor additional evaporation of 5.9 ± 0.3 mm per year (2%).
Note that changes in precipitation are seen over the whole simulation domain (due to the model IV) and those related to latent heat fluxes occur strictly over the reservoirs (not shown); therefore, the increase in ET is not simply due to the additional precipitation.
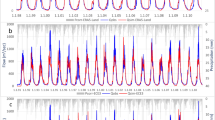
As previously mentioned, most hydropower water consumption studies quantify the gross and net evaporation. Here, we are interested in understanding how precipitation and evaporation are recycled in the watershed and how the presence of reservoirs impacts these ratios. Note that our study is the first one to evaluate the sensitivity of precipitation recycling to a land cover change. Monthly precipitation and evaporation ratios are shown in Fig. 9.
In both simulations, the monthly precipitation recycling ratio remains under 6% and peaks in July, when the evapotranspiration is high (Fig. 9). This result indicates weak coupling between the evaporation happening at the surface and the generation of precipitation in the atmosphere. Some small change is found in April and July, as the presence of reservoirs decreases the precipitation recycling ratio by 0.6%. Therefore, reservoirs do not significantly affect the coupling between evaporation and precipitation within the watershed; mostly because the watershed is so large that regional monthly ET rates are similar from one simulation to the other (only 6.4% of the watershed is covered by reservoirs). Note that monthly precipitation recycling ratios of the watersheds located at the northern and eastern limits of the La Grande watershed are also small and not affected by the presence of reservoirs. Depending on the season, 4 to 19% of the evaporation returns to the watershed as precipitation. The evaporation recycling is greater in cold months as the ratio of P to ET is high (Eq. 9). Again, the presence of reservoirs does not seem to affect the rate of evaporation recycling.
Given the multiple assumptions lying behind the precipitation recycling model of Brubaker (1991), several limitations of these results should be noted. The first assumption is that the moisture fluxes are horizontally well mixed, with minor spatial changes in monthly water vapor fluxes. Since different surface types can be found across the watershed, the spatial changes in monthly evaporation appear more important than initially assumed. Nonetheless, it is important to note that previous studies have used a similar recycling model on much larger scales, where ET varied even more throughout the domain (Brubaker et al. 1993). The second assumption states that the monthly change in moisture storage is smaller than the changes in the other water vapor fluxes, as put forward by Eltahir and Bras (1996). The third assumption implies that the atmospheric moisture is vertically well mixed, which might not be a good representation of the actual processes. Burde and Zangvil (2001) showed that this assumption leads to the underestimation of precipitation recycling over North America. Even if the precipitation recycling model used here is one of the simplest, a weak evaporation-precipitation coupling at the catchment scale seems realistic. However, for an improved understanding of the impacts of reservoirs on precipitation recycling, additional analyses based on distributed precipitation recycling models, which do not rely upon the assumptions cited above, should be done.
4 Conclusions
This study aimed to evaluate the impacts that northern Quebec’s hydroelectric reservoirs have on local climate and regional water resources using climate simulations generated by the CRCM5. The validation analysis carried out within this study shows that the CRCM5 driven with the ERA-Interim reanalysis is, in general, capable of reproducing seasonal 2-m air temperatures over the La Grande River watershed in northern Quebec, Canada. However, a cold bias (−1.9 °C), probably related to the overestimation of snow cover (and thus of surface albedo), is observed in spring throughout the watershed. For precipitation, even if the annual cycle is relatively well captured, the model tends to overestimate precipitation amounts throughout the year. The downwelling shortwave and longwave radiation are well reproduced, while upwelling shortwave and longwave radiation are underestimated due to an abnormally persistent snowpack.
Analysis of pre- (NoRes) and post-impoundment (WithRes) simulations led to the conclusion that the effects of reservoirs on temperature and on some of the energy budget components may be important on local and seasonal time scale; sensitivity to change in surface water fraction was generally greater than the change related to internal variability. Overall, the increase of daily minimum temperatures induces a warming in fall, winter, and spring. In summer, a cooling is observed as the daily maximum temperatures decrease. The presence of reservoirs decreases latent heat flux in summer (1.4%) and increases this flux in fall (25%). Sensible heat fluxes decrease in summer (21.6%) and increase in winter and fall (210 and 60%, respectively). In general, more energy is available over the reservoirs throughout the year due to a reduced surface albedo (−3.5%). We have evaluated the increase in ET at the scale of the watershed. On an annual scale, the presence of reservoirs increased ET by only 5.9 mm year−1 (2%): reservoirs only cover 6.4% of the watershed area. Precipitation and runoff changes are usually within the model internal variability on both annual and seasonal time scales.
A precipitation recycling analysis seems to point toward a weak coupling between the surface (through evaporation) and the atmosphere (through precipitation generation) at the watershed scale (monthly maximum: 5% recycling ratio), with reservoirs having limited impact on the coupling. We recommend using multiple and more sophisticated precipitation recycling models for future analysis.
Change history
03 May 2017
An erratum to this article has been published.
References
Alexandru A, de Elía R, Laprise R (2007) Internal variability in regional climate downscaling at the seasonal scale. Mon Weather Rev 135:3221–3238. doi:10.1175/mwr3456.1
Anderson JR, Hardy EE, Roach JT, Witmer RE (1976) A land use and land cover classification system for use with remote sensor data vol 964. US Government Printing Office, Arlington
Baldocchi D et al (2001) FLUXNET: a new tool to study the temporal and spatial variability of ecosystem-scale carbon dioxide, water vapor, and energy flux densities. B Am Meteorol Soc 82:2415–2434. doi:10.1175/1520-0477(2001)082<2415:FANTTS>2.3.CO;2
Bartlett PA, McCaughey JH, Lafleur PM, Verseghy DL (2002) A comparison of the mosaic and aggregated canopy frameworks for representing surface heterogeneity in the Canadian boreal forest using CLASS: a soil perspective. J Hydrol 266:15–39. doi:10.1016/S0022-1694(02)00090-2
Bates GT, Giorgi F, Hostetler SW (1993) Toward the simulation of the effects of the Great Lakes on regional climate. Mon Weather Rev 121:1373–1387. doi:10.1175/1520-0493(1993)121<1373:ttsote>2.0.co;2
Bélair S, Mailhot J, Girard C, Vaillancourt P (2005) Boundary layer and shallow cumulus clouds in a medium-range forecast of a large-scale weather system. Mon Weather Rev 133:1938–1960. doi:10.1175/MWR2958.1
Bellisario LM, Boudreau LD, Verseghy DL, Rouse WR, Blanken PD (2000) Comparing the performance of the Canadian land surface scheme @class for two subarctic terrain types. Atmosphere-Ocean 38:181–204. doi:10.1080/07055900.2000.9649645
Bosilovich MG, Chern J-D (2006) Simulation of water sources and precipitation recycling for the Mackenzie, Mississippi, and Amazon River basins. J Hydrometeorol 7:312–329. doi:10.1175/JHM501.1
Braun M, Caya D, Frigon A, Slivitzky M (2012) Internal variability of the Canadian RCM’s hydrological variables at the basin scale in Quebec and Labrador. J Hydrometeorol 13:443–462. doi:10.1175/JHM-D-11-051.1
Brown JF, Loveland TR, Ohlen DO, Zhu Z-L (1999) The global land-cover characteristics database: the users’ perspective Photogramm Eng Rem S 65:1069–1074
Brown R, Bartlett P, MacKay M, Verseghy D (2006) Evaluation of snow cover in CLASS for snow MIP. Atmosphere-Ocean 44:223–238. doi:10.3137/ao.440302
Brubaker KL (1991) Atmospheric water vapor transport: estimation of continental precipitation recycling and parameterization of a simple climate model. M.Sc., Massachusetts Institute of Technology
Brubaker KL, Entekhabi D, Eagleson PS (1993) Estimation of continental precipitation recycling. J Clim 6:1077–1089. doi:10.1175/1520-0442(1993)006<1077:EOCPR>2.0.CO;2
Brutsaert W (1998) Land-surface water vapor and sensible heat flux: spatial variability, homogeneity, and measurement scales. Water Resour Res 34:2433–2442. doi:10.1029/98WR01340
Budyko MI (1974) Climate and life vol 18. International Geophysics Series. Elsevier Science, New York
Burde GI, Zangvil A (2001) The estimation of regional precipitation recycling. Part II: a new recycling model. J Clim 14:2509–2527. doi:10.1175/1520-0442(2001)014<2509:TEORPR>2.0.CO;2
Caya D, Biner S (2004) Internal variability of RCM simulations over an annual cycle. Clim Dynam 22:33–46. doi:10.1007/s00382-003-0360-2
Christensen BO, Gaertner AM, Prego AJ, Polcher J (2001) Internal variability of regional climate models. Clim Dynam 17:875–887. doi:10.1007/s003820100154
Comer NT, Lafleur PM, Roulet NT, Letts MG, Skarupa M, Verseghy D (2000) A test of the Canadian Land Surface Scheme (CLASS) for a variety of wetland types. Atmosphere-Ocean 38:161–179. doi:10.1080/07055900.2000.9649644
Côté J, Gravel S, Méthot A, Patoine A, Roch M, Staniforth A (1998) The operational CMC-MRB global environmental multiscale (GEM) model. Part I: design considerations and formulation. Mon Weather Rev 126:1373–1395
Dahir AH (2006) Badoosh dam-break hypothetical using HEC-RAS. In: Dams and Reservoirs, Societies and Environment in the twenty-first Century, Two Volume Set. CRC Press, pp 967–970. doi:10.1201/b16818-150
Davies HC (1976) A lateral boundary formulation for multi-level prediction models. Q J Roy Meteor Soc 102:405–418
de Elía R, Côté H (2010) Climate and climate change sensitivity to model configuration in the Canadian RCM over North America. Meteorol Z 19:325–339. doi:10.1127/0941-2948/2010/0469
Dee DP et al (2011) The ERA-Interim reanalysis: configuration and performance of the data assimilation system. Q J Roy Meteor Soc 137:553–597. doi:10.1002/qj.828
Dirmeyer PA, Brubaker KL (1999) Contrasting evaporative moisture sources during the drought of 1988 and the flood of 1993. J Geophys Res: Atmos 104:19383–19397. doi:10.1029/1999JD900222
Dutra E, Stepanenko VM, Balsamo G, Viterbo P, Miranda P, Mironov D, Schär C (2010) An offline study of the impact of lakes in the performance of the ECMWF surface scheme boreal. Environ Res 15:100–112
Eaton AK, Rouse WR, Lafleur PM, Marsh P, Blanken PD (2001) Surface energy balance of the western and central Canadian subarctic: variations in the energy balance among five major terrain types. J Clim 14:3692–3703. doi:10.1175/1520-0442(2001)014<3692:sebotw>2.0.co;2
Eltahir EA, Bras RL (1994) Precipitation recycling in the Amazon basin. Q J Roy Meteor Soc 120:861–880. doi:10.1002/qj.49712051806
Eltahir EAB, Bras RL (1996) Precipitation recycling. Rev Geophys 34:367–378. doi:10.1029/96RG01927
Fortin V, Therrien C, Anctil F (2008) Correcting wind-induced bias in solid precipitation measurements in case of limited and uncertain data. Hydrol Process 22:3393–3402. doi:10.1002/hyp.6959
Gerbens-Leenes PW, Hoekstra AY, Van der Meer T (2009) The water footprint of energy from biomass: a quantitative assessment and consequences of an increasing share of bio-energy in energy supply. Ecol Econ 68:1052–1060. doi:10.1016/j.ecolecon.2008.07.013
Grant RF et al (2009) Interannual variation in net ecosystem productivity of Canadian forests as affected by regional weather patterns—a FLUXNET-Canada synthesis. Agric For Meteorol 149:2022–2039. doi:10.1016/j.agrformet.2009.07.010
Green WH, Ampt GA (1911) Studies on soil Phyics. J Agr Sci 4:1–24. doi:10.1017/S0021859600001441
Groisman PY, Easterling DR (1994) Variability and trends of total precipitation and snowfall over the United States and Canada. J Clim 7:184–205. doi:10.1175/1520-0442(1994)007<0184:VATOTP>2.0.CO;2
Harding RJ, Pomeroy JW (1996) The energy balance of the winter boreal landscape. J Clim 9:2778–2787. doi:10.1175/1520-0442(1996)009<2778:tebotw>2.0.co;2
Herath I, Deurer M, Horne D, Singh R, Clothier B (2011) The water footprint of hydroelectricity: a methodological comparison from a case study in New Zealand. J Clean Prod 19:1582–1589. doi:10.1016/j.jclepro.2011.05.007
Hernandez-Diaz L, Laprise R, Sushama L, Martynov A, Winger K, Dugas B (2013) Climate simulation over CORDEX Africa domain using the fifth-generation Canadian regional climate model (CRCM5). Clim Dynam 40:1415–1433. doi:10.1007/s00382-012-1387-z
Hoekstra AY (2003) Virtual water trade. Proceedings of the International Expert Meeting on Virtual Water Trade Value of Water Research Report Series No. 12
Hostetler SW, Bates GT, Giorgi F (1993) Interactive coupling of a lake thermal model with a regional climate model. J Geophys Res-Atmos 98:5045–5057. doi:10.1029/92JD02843
Hübener H, Schmidt M, Sogalla M, Kerschgens M (2005) Simulating evapotranspiration in a semi-arid environment. Theor Appl Climatol 80:153–167. doi:10.1007/s00704-004-0097-9
Huziy O, Sushama L (2016) Impact of lake–river connectivity and interflow on the Canadian RCM simulated regional climate and hydrology for Northeast Canada. Clim Dynam:1–17. doi:10.1007/s00382-016-3104-9
Isard SA, Belding MJ (1989) Evapotranspiration from the alpine tundra of Colorado, U.S.A Arct Alp Res 21:71–82 doi:10.2307/1551518
Kain JS, Fritsch JM (1990) A one-dimensional entraining/detraining plume model and its application in convective parameterization. J Atmos Sci 47:2784–2802. doi:10.1175/1520-0469(1990)047<2784:AODEPM>2.0.CO;2
Kheyrollah Pour H, Duguay C, Martynov A, Brown LC (2012) Simulation of surface temperature and ice cover of large northern lakes with 1-D models: a comparison with MODIS satellite data and in situ measurements. Tellus A: Dyn Meteorol Oceanogr 64. doi:10.3402/tellusa.v64i0.17614
Kitaigorodskii SA, Miropolski YZ (1970) On the theory of the open ocean active layer. Atmos Oceanic Phys 6:177–188
Koster R, Jouzel J, Suozzo R, Russell G, Broecker W, Rind D, Eagleson P (1986) Global sources of local precipitation as determined by the NASA/GISS GCM. Geophys Res Lett 13:121–124. doi:10.1029/GL013i002p00121
Kourzeneva K, Braslavsky D (2005) Lake model FLake, coupling with atmospheric model: first steps. In: Fourth SRNWP/HIRLAM Workshop on Surface Processes and Assimilation of Surface Variables jointly with HIRLAM Workshop on Turbulence pp 43–53
Kunstmann H, Jung G (2007) Influence of soil-moisture and land use change on precipitation in the Volta Basin of West Africa. Int J Riv Bas Manage 5:9–16. doi:10.1080/15715124.2007.9635301
Lafleur PM, Skarupa MR, Verseghy DL (2000) Validation of the Canadian Land Surface Scheme (CLASS) for a subarctic open woodland. Atmosphere-Ocean 38:205–225. doi:10.1080/07055900.2000.9649646
Langlois A, Royer A, Fillol E, Frigon A, Laprise R (2004) Evaluation of the snow cover variation in the Canadian regional climate model over eastern Canada using passive microwave satellite data. Hydrol Process 18:1127–1138. doi:10.1002/hyp.5514
Langlois A et al (2014) Evaluation of CLASS 2.7 and 3.5 simulations of snow properties from the Canadian regional climate model (CRCM4) over Québec. Canada J Hydrometeorol 15:1325–1343. doi:10.1175/JHM-D-13-055.1
Lettau H, Lettau K, Molion LCB (1979) Amazonia’s hydrologic cycle and the role of atmospheric recycling in assessing deforestation effects. Mon Weather Rev 107:227–238. doi:10.1175/1520-0493(1979)107<0227:AHCATR>2.0.CO;2
Li J, Barker HW (2005) A radiation algorithm with correlated-k distribution. Part I: local thermal equilibrium. J Atmos Sci 62:286–309. doi:10.1175/JAS-3396.1
Lofgren BM (1997) Simulated effects of idealized Laurentian Great Lakes on regional and large-scale climate. J Clim 10:2847–2858. doi:10.1175/1520-0442(1997)010<2847:SEOILG>2.0.CO;2
Long Z, Perrie W, Gyakum J, Caya D, Laprise R (2007) Northern lake impacts on local seasonal climate. J Hydrometeorol 8:881–896. doi:10.1175/jhm591.1
Mallard MS, Nolte CG, Bullock OR, Spero TL, Gula J (2014) Using a coupled lake model with WRF for dynamical downscaling. J Geophys Res-Atmos 119:7193–7208. doi:10.1002/2014jd021785
Martynov A, Sushama L, Laprise R (2010) Simulation of temperate freezing lakes by one-dimensional lake models: performance assessment for interactive coupling with regional climate models Boreal Environ Res 15:143–164
Martynov A, Sushama L, Laprise R, Winger K, Dugas B (2012) Interactive lakes in the Canadian Regional Climate Model, version 5: the role of lakes in the regional climate of North America Tellus A 64 doi:10.3402/tellusa.v64i0.16226
Martynov A, Laprise R, Sushama L, Winger K, Separovic L, Dugas B (2013) Reanalysis-driven climate simulation over CORDEX North America domain using the Canadian Regional Climate Model, version 5: model performance evaluation. Clim Dynam 41:2973–3005. doi:10.1007/s00382-013-1778-9
Mekonnen MM, Hoekstra AY (2012) The blue water footprint of electricity from hydropower. Hydrol Earth Syst Sc 16:179–187. doi:10.5194/hess-16-179-2012
Ministère de l’Énergie et des Ressources Naturelles Base de données pour l’aménagement du territoire à l’échelle de 1/100 000, 2015. 1.0. edn. Centre d’information géographique et statistique, Québec
Mironov DV (2008) Parametrization of lakes in numerical weather prediction. Description of a lake model vol 11. Deutscher Wetterdienst. Offenbach am Main, Germany
Mironov D, Heise E, Kourzeneva E, Ritter B, Schneider N, Terzhevik A (2010) Implementation of the lake parameterisation scheme FLake into the numerical weather prediction model COSMO Boreal Environ Res 15:218–230
Nordbo A, Launiainen S, Mammarella I, Leppäranta M, Huotari J, Ojala A, Vesala T (2011) Long-term energy flux measurements and energy balance over a small boreal lake using eddy covariance technique. J Geophys Res-Atmos:116. doi:10.1029/2010JD014542
Notaro M, Holman K, Zarrin A, Fluck E, Vavrus S, Bennington V (2013) Influence of the Laurentian Great Lakes on regional climate. J Clim 26:789–804. doi:10.1175/JCLI-D-12-00140.1
Paeth H, Born K, Girmes R, Podzun R, Jacob D (2009) Regional climate change in tropical and northern Africa due to greenhouse forcing and land use changes. J Clim 22:114–132. doi:10.1175/2008JCLI2390.1
Price JS (1991) Evaporation from a blanket bog in a foggy coastal environment. Bound-Layer Meteorol 57:391–406. doi:10.1007/bf00120056
Robert S, Floyd H (1997) Lake effects on climatic conditions in the Great Lakes basin. Illinois Department of Natural Ressources, Champaign
Rouse WR et al (2005) The role of northern lakes in a regional energy balance. J Hydrometeorol 6:291–305. doi:10.1175/jhm421.1
Rouse WR, Blanken PD, Bussieres N, Oswald CJ, Schertzer WM, Spence C, Walker AE (2008) Investigation of the thermal and energy balance regimes of Great Slave and Great Bear Lakes. J Hydrometeorol 9:1318–1333. doi:10.1175/2008jhm977.1
Samuelsson P, Kourzeneva E, Mironov D (2010) The impact of lakes on the European climate as simulated by a regional climate model Boreal. Environ Res 15:113–129
Schetagne R, Therrien J (2013) Suivi environnemental du complexe La Grande. Évolution des teneurs en mercure dans les poissons. GENIVAR inc. et Hydro-Québec Production
Schmid HP (1994) Source areas for scalars and scalar fluxes. Bound-Layer Meteorol 67:293–318. doi:10.1007/bf00713146
Šeparović L et al (2013) Present climate and climate change over North America as simulated by the fifth-generation Canadian regional climate model. Clim Dynam 41:3167–3201. doi:10.1007/s00382-013-1737-5
Spence C, Rouse WR, Worth D, Oswald C (2003) Energy budget processes of a small northern lake. J Hydrometeorol 4:694–701. doi:10.1175/1525-7541(2003)004<0694:EBPOAS>2.0.CO;2
Stepanenko VM, Goyette S, Martynov A, Perroud M, Fang X, Mironov D (2010) First steps of a lake model intercomparison project: LakeMIP Boreal Environ Res 15:191–202
Strachan IB, Pelletier L, Bonneville M-C (2016a) Inter-annual variability in water table depth controls net ecosystem carbon dioxide exchange in a boreal bog. Biogeochemistry 127:99–111. doi:10.1007/s10533-015-0170-8
Strachan IB, Tremblay A, Pelletier L, Tardif S, Turpin C, Nugent KA (2016b) Does the creation of a boreal hydroelectric reservoir result in a net change in evaporation? J Hydrol 540:886–899. doi:10.1016/j.jhydrol.2016.06.067
Subin ZM, Murphy LN, Li F, Bonfils C, Riley WJ (2012) Boreal lakes moderate seasonal and diurnal temperature variation and perturb atmospheric circulation: analyses in the Community Earth System Model 1 (CESM1) Tellus A 64 doi:10.3402/tellusa.v64i0.15639
Sundqvist H, Berge E, Kristjánsson JE (1989) Condensation and cloud parameterization studies with a mesoscale numerical weather prediction model. Mon Weather Rev 117:1641–1657. doi:10.1175/1520-0493(1989)117<1641:CACPSW>2.0.CO;2
Szeto KK, Liu J, Wong A (2008) Precipitation recycling in the Mackenzie and three other major river basins. In: Cold region atmospheric and hydrologic studies. The Mackenzie GEWEX experience. Springer, pp 137–154
Teodoru CR et al (2012) The net carbon footprint of a newly created boreal hydroelectric reservoir. Glob Biogeochem Cycles:26. doi:10.1029/2011gb004187
van der Ent RJ, Savenije HHG, Schaefli B, Steele-Dunne SC (2010) Origin and fate of atmospheric moisture over continents. Water Resour Res:46. doi:10.1029/2010WR009127
Verseghy DL (1991) CLASS—A Canadian land surface scheme for GCMs. I Soil model Int J Climatol 11:111–133. doi:10.1002/joc.3370110202
Verseghy DL, McFarlane NA, Lazare M (1993) CLASS—A Canadian land surface scheme for GCMs, II. Vegetation model and coupled runs. Int J Climatol 13:347–370. doi:10.1002/joc.3370130402
Wang W, Roulet NT, Strachan IB, Tremblay A (2016) Modeling surface energy fluxes and thermal dynamics of a seasonally ice-covered hydroelectric reservoir. Sci Total Environ 550:793–805. doi:10.1016/j.scitotenv.2016.01.101
Wilson JW (1977) Effect of Lake Ontario on precipitation. Mon Weather Rev 105:207–214. doi:10.1175/1520-0493(1977)105<0207:EOLOOP>2.0.CO;2
Winter JM, Eltahir EAB (2010) The sensitivity of latent heat flux to changes in the radiative forcing: a framework for comparing models and observations. J Clim 23:2345–2356. doi:10.1175/2009JCLI3158.1
Zarfl C, Lumsdon A, Berlekamp J, Tydecks L, Tockner K (2015) A global boom in hydropower dam construction. Aquat Sci 77:161–170. doi:10.1007/s00027-014-0377-0
Zhao D, Liu J (2015) A new approach to assessing the water footprint of hydroelectric power based on allocation of water footprints among reservoir ecosystem services. Phys Chem Earth, Parts A/B/C 79–82:40–46. doi:10.1016/j.pce.2015.03.005
Acknowledgements
This project was funded by MITACS, Hydro-Québec and the Ouranos Consortium under grant IT04933. Simulation outputs used in this study were generated and provided by the Climate Simulation and Analysis group at Ouranos. Computations were made on the supercomputer Guillimin from McGill University, managed by Calcul Québec and Compute Canada. The operation of this supercomputer is funded by the Canada Foundation for Innovation (CFI), the Ministère de l’Économie, de la Science et de l’Innovation du Québec (MESI), and the Fonds de recherche du Québec-Nature et technologies (FRQNT). We would like to acknowledge the contribution of ESCER, UQÀM, and Environment and Climate Change Canada for the development of the CRCM5. Field observations used in this paper were collected during campaigns supported by a NSERC-CRD grant awarded to Prof. Ian Strachan. We would like to recognize the logistical support from Hydro-Québec—production and particularly from Dr. Alain Tremblay during the field campaign. Special thanks go to Anne Frigon for her valuable help during the study, as well as Michel Giguère, Hélène Côté, Dominique Paquin and Sébastien Biner for their technical support.
• Land fraction used in the WithRes simulation are derived from a database provided by the Ministère de l’Énergie et des Ressources Naturelles (URL: http://mern.gouv.qc.ca/territoire/portrait/portrait-donnees.jsp).
• Eastmain-1 data requests may be sent to Professor Ian Strachan (ian.strachan@mcgill.ca).
• Requests to access simulation outputs may be sent directly to Ouranos.
• Weather station datasets may be requested to Climat-Québec and Hydro-Québec.
Author information
Authors and Affiliations
Corresponding author
Additional information
The original version of this article was revised due to a retrospective Open Access order.
An erratum to this article is available at https://doi.org/10.1007/s00704-017-2128-3.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Irambona, C., Music, B., Nadeau, D.F. et al. Impacts of boreal hydroelectric reservoirs on seasonal climate and precipitation recycling as simulated by the CRCM5: a case study of the La Grande River watershed, Canada. Theor Appl Climatol 131, 1529–1544 (2018). https://doi.org/10.1007/s00704-016-2010-8
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00704-016-2010-8