1 Introduction

The slipperiness of winter roads is of great interest to winter road maintenance engineers, road weather researchers and road users. As an important indicator of road slipperiness, the road surface temperature (RST) is influenced by both meteorological and geographical parameters. Previously, geographical data are usually collected through field measurements or low resolution digital elevation model (DEM). The availability of the high resolution digital surface model (DSM) derived by light detection and ranging (Lidar) provides a new, cheaper, less time-consuming and more convenient opportunity to model the influence of geographical parameters on RST. Currently, the Lidar-derived high resolution DSM data is available in, e.g. the UK, Finland and Sweden. Such data has recently been applied in the meteorological field, e.g. identification of buildings shape, size, location and tree classification (Goodwin et al. 2009) and identification of sunlit surface areas of urban facets (Lindberg et al. 2015). With the high resolution DSM data, parameters that influence the radiation fluxes at the road surface can also be calculated, e.g. shading effects. Shading effects occur when the supply of direct solar radiation to the road surface is blocked by buildings, trees or the topography of the surrounding land (White et al. 2006). There are usually appreciable temperature differences between sun-exposed and shaded sites, so shading affects the spatial RST distribution because of its influence on the road’s thermal regime (Rosema and Welleman 1977). Specifically, shaded locations typically have lower RST values than their sun-exposed counterparts. Slipperiness can occur under clear conditions—for example, the gradual warming of the air during winter mornings when the road surface is cold can induce hoar-frost formation. Similarly, freezing dew can form during clear and calm weather, or water cover may freeze under clear conditions after a rainy period (Lindqvist 1979). Norrman et al. (2000) showed that around 34 % of all accidents are caused by these types of slippery conditions. Furthermore, 78.2 % of road accidents occur in fine weather without high winds (a description that covers any weather condition that doesn’t affect driving or involve precipitation in the form of hail, drizzle or sleet), which is considered to be non-hazardous for driving (Department of Transport 1996). Solar glare can also be a major problem for drivers in winter months when the solar elevation is much lower than in other seasons (Satterthwaite 1976). Finally, differences in RST due to daytime shading are known to have significant effects on the RST at the screened site after sunset (Bogren 1991). Improved shading models that enable more accurate prediction of daytime RST values will make it possible to account for these factors in order to improve traffic safety. Another phenomenon that can be calculated from the high resolution DSM is hemisphere blocking. Hemisphere blocking is usually quantified using a geographical parameter known as the sky-view factor (ψ s ) that ranges from 0 to 1 and measures the degree to which the sky is obscured by the surroundings at a given location. Watson and Johnson (1987) define ψ s as the ratio of radiation received by a planar surface to that received from the entire hemispheric radiating environment. Hemisphere blocking affects both short- and long-wave radiation fluxes at the road surface. It is often discussed in the context of its influence on nocturnal radiation budgets (Thornes 1991; White et al. 2006). However, hemisphere blocking also affects the daytime RST distribution by influencing the incident solar radiation at any given site. Shading objects thus influence the direct shortwave radiation flux at the road surface, the downward long-wave radiation flux, and the flux of diffuse radiation. Consequently, it is important to consider both shading effects and ψ s when attempting to model daytime RST distributions. In this study, the term ‘screening effects’ is used to describe the combined impact of shading effects and ψ s .

1.1 Shading effects

As an important geographical parameter that affects RST distributions, the shading effect has attracted research interest for over 40 years. Shaded areas are more likely to experience ice-forming conditions, and the danger of ice formation increases with the degree of shading (Milloy and Humphreys 1969). Studies examining the effects of various shadow obstacles have shown that rock cuts formed when roads are built through hills are particularly strongly linked to low RST values (Lindqvist 1982; Gustavsson and Bogren 1991). As noted above, road surfaces are primarily warmed by solar radiation. The intensities of both direct and diffuse shortwave radiation increase with increasing solar elevation under clear sky conditions (Paltridge and Platt 1977). Bogren (1991) found that the greatest RST differences between shaded and sun-exposed sites occur under clear conditions when the solar elevation is at its daily maximum. Gustavsson and Bogren (1993) subsequently used this finding while developing a local climatological model for Sweden.

Empirical formulae describing the relationships between solar elevation and daily maximum RST differences between shaded and unshaded sites have been presented by Bogren et al. (2000a). These expressions have terms that account for ‘lag effects’, whereby daytime RST differences influence RST differences after sunset, using the time after sunset and the day of the year as variables. Bogren et al. (2000b) subsequently extended their model to account for the influence of clouds under partly cloudy conditions, revealing that shading has a significant influence on the RST distribution even in the presence of partial cloud cover.

The shading-dependent RST differences predicted using these empirical formulae were compared to thermal mapping data for a length of road with both shaded and exposed regions (Bogren et al. 2000a). While the predicted values were generally in agreement with the measured temperature differences, it was not possible to completely reproduce the experimental variation in RST over the entire stretch of road. Chapman et al. (2001b) developed an alternative method for calculating shading effects from fish-eye images and used it to perform route-based modelling of nocturnal RST distributions. Their results indicated that nocturnal RST distributions are negatively correlated with shading effects and that the proportion of variance in RST that can be attributed to shading effects is consistently below 25 %.

To properly describe the effects of shading on RST, it is important to model the underlying physical processes. To this end, the shading effect was accounted by terrain analysis (accounting for factors such as slope and aspect) to calculate local sunrise and sunset times in Icebreak model (Shao and Lister 1995), by inclusion of a fixed wall in the Deutscher Wetterdienst (DWD) model (Jacobs and Raatz 1996), by plotting sun-tracks on fish-eye images in IceMiser energy balance model (Chapman et al. 2001b) or by creating a representative artificial horizon for every km2 from all the site-based fish-eye images in the West Midlands Grid model (WMG) (Bradley et al. 2002). In the current version of Model of the Environment and Temperature of Roads (METRo) (Crevier and Delage 2001) 3.3.0 (http://documentation.wikia.com/wiki/Changelog_%28METRo%29#Version_3.3.0), the shading effect is accounted by adding a sun-shadow algorithm for the road based on the sky-view information of stations. Other numerical models (Rayer 1987; Sass 1992; Best 1998; Greenfield and Takle 2006; Bouris et al. 2010; Chapman et al. 2010; Feng and Feng 2012) didn’t consider influence of shading effect on RST.

1.2 Sky-view factor

The sky-view factor, ψ s , is often considered when modelling nocturnal RST distributions (e.g. Bärring et al. 1985; Eliasson 1996; Upmanis 1999; Chapman et al. 2001a, b; Bradley et al. 2002; Chapman and Thornes 2006; Brown et al. 2008), due to the influence of hemisphere blocking on the nocturnal radiation budget. During daytime, ψ s is often used as a surrogate for the shading effect (Chapman et al. 2001a) but the influence of hemisphere blocking on other radiation fluxes at the road surface has not yet been fully investigated.

Methods for calculating ψ s have been developed and refined for some time. Approaches introduced before the year 2000 were reviewed by Chapman et al. (2001c). A wide range of methods are currently used to estimate ψ s ; among other things, it can be computed by analysing fish-eye images (Steyn 1980) or GPS data (Chapman et al. 2002), using high resolution DSM (Ratti and Richens 1999, 2004) based on geodata supplied by local governments (Lindberg 2007), or by analysing Lidar data (Lindberg and Grimmond 2011b; Kidd and Chapman 2012). ψ s values derived from Lidar data, which can be collected in a very time-efficient manner, were found to be in good agreement with values obtained by analysing fish-eye images (Kidd and Chapman 2012).

1.3 Route-based RST mapping

Route-based RST prediction is a type of spatial forecast that provides predictions of RST and road condition across the road network. In recent years, there is growing interest in route-based RST prediction (e.g. Chapman et al. 2001a; Chapman and Thornes 2004, 2006, 2011; Thornes et al. 2005; Brown et al. 2008; Hammond et al. 2010, 2011). Therefore, it would be desirable to be able to fully explain the influence of screening effects along specific road routes during daytime conditions. The previously reported empirical relationships (Bogren et al. 2000a) only predict RST differences between fully exposed and fully shaded sites; they cannot be applied when dealing with partially shaded sites or account for the effects of variation in the degree of shading. Most previous studies on shading effects were site-based or relied on fish-eye images taken from vehicles. This is a time-consuming data gathering process as it involves driving over a large road network. However, the availability of Lidar data makes it possible to quickly calculate route-based shading effects over large areas. This has only recently become realistically possible to investigate in detail. Similarly, most previous attempts to model daytime RST distributions have relied on site-based shading effects, and there has been little work using route-based shading effects and ψ s values.

Therefore, the objective of this work was to evaluate the use of high resolution DSM in conjunction with geographical information system (GIS) in modelling the influence of route-based screening effects on daytime RST distributions.

2 Study area and data

2.1 Study area

As shown in Fig. 1, data were gathered from two different areas in Sweden. One is located in the vicinity of Borås (henceforth referred to as the country road area), in which three country roads were examined. The other is part of the E6 highway between Kungälv and the Nordbymotet overpass (henceforth referred to as the highway area). The main difference between the roads in these two areas is their width. Roads in the country road area are normally 5–7 m wide, whereas the highway is normally more than 20 m wide because it has twice as many lanes and a safety fence between lanes for traffic moving in different directions. In addition, the highway is flanked on either side by a vegetation-free corridor, meaning that potential screening objects are much further from the road border than is the case for the country roads, where screening objects may be directly adjacent to the border. The two study areas were chosen to represent different types of roads and land use contexts.

Fig. 1
figure 1

Location of the study areas and road weather information system stations

Full size image

2.2 Datasets

Multiple data sets were used in this study. The first was derived from Sweden’s road weather information system (RWIS), which was developed in the 1970s and has since been used to monitor weather conditions along Sweden’s road network (Lindqvist and Mattsson 1979). Currently there are more than 700 RWIS stations in Sweden. This study used data on the RST, air temperature at a height of 2 m and relative humidity from eight RWIS stations in the highway area and six in the country road area (Fig. 1).

The second data set examined in this work was generated by using vehicle-mounted infrared thermometers to measure RST values for the roads of interest. During 2012, measurements were acquired at 30 m intervals while the vehicle was moving at a maximum speed of 60 km/h. In later years, the vehicle’s GPS coordinates were recorded at the time each measurement was taken. The process of measuring RST values in this way is known as thermal mapping. A total of 16 daytime thermal mapping exercises (henceforth referred to as mobile measurements) were conducted in this study, 9 in the country road area and 7 in the highway area. Table 1 provides further details of the thermal mapping measurements, each one of which was assigned an ID number for future reference. To reduce the influence of time trends, the E6 highway was divided into two sections for the purposes of measurement, with the dividing line passing through the city of Uddevalla. Two of the highway area measurements were conducted south of Uddevalla, and the remainder was conducted to the north of the city.

Table 1 Thermal mapping measurements used in this study
Full size table

Two different infrared thermometers were used in this study. Measurements M1-M7 and M10-M12 were conducted using a Heimann KT 15 SMD thermometer with a reaction time of 1000 ms and a precision of \( \pm \)0.3 °C at temperatures below 0 °C and \( \pm \)0.1 °C between 0 and 20 °C. Measurements M8-M9 and M13-M16 were conducted with a MetTempMobile thermometer having a typical reaction time of 1000 ms and a precision of \( \pm 1 \)°C plus 0.6 % of the difference between the target and sensor head temperatures.

Lidar-generated DSM data were generated by the Swedish mapping, cadastral and land registration authority (Lantmäteriet) between 2009 and 2013. The data cover almost the entirety of Sweden’s surface; only data gathered outside the growing season were used in this work. Both DSM and road vector data were obtained from Lantmäteriet. DSMs are rasterised surface models that include information on the elevation of the ground as well as the presence of objects such as buildings, trees, bridges and so on. The Lidar data examined in this work has a spatial resolution of 2 m and a vertical resolution of 0.2 m, which is sufficient to enable the easy identification of trees, buildings and other large structures. A representative Lidar image of a residential area in Sweden is shown in Fig. 2 together with the shading pattern derived from the Lidar data and an aerial photograph of the area. Various shading objects and the corresponding shading patterns are readily visible in the Lidar image. One advantage of using Lidar data is that it allows large areas to be rapidly surveyed in considerable detail. In this work, Lidar data were used to predict the shadow patterns generated by trees and buildings. It should be noted that buildings and trees differ in their transmissivity of shortwave radiation: buildings block all incoming shortwave radiation whereas the gaps between trees’ branches allow some shortwave radiation to pass through. In previous studies, the shortwave transmissivity of trees was assumed to be 20 % (Oke 1987; Robitu et al. 2006). However, subsequent investigations by Lindberg and Grimmond (2011a) showed that a value of 0.07 is more appropriate for isolated urban trees during summer months, and even lower values should be used for forest canopies. A more recent study by Konarska et al. (2014) showed that the transmissivity of shortwave radiation through vegetation is very small in summer time and also much lower than expected during winter time. Therefore, the transmissivity of shortwave radiation by forests was not considered when calculating shadow patterns. It was however examined in more detail when analysing different land use types.

Fig. 2
figure 2

An example of the Lidar data used in this study (©Lantmäteriet I2014/00696)

Full size image

Land use data with a spatial resolution of 25 m and DEM data with a spatial resolution of 2 m were also provided by Lantmäteriet. The land use data were gathered in the year 2000 and used to classify land usage. The DEM data were used to identify rock cuts in the highway area.

STRÅNG (Landelius et al. 2001) is a mesoscale model for solar radiation developed by the Swedish Meteorological and Hydrological Institute (SMHI). It is based on observations from 12 stations covering the whole of Sweden and uses cloud data from the analytical model MESAN, water vapour levels and geographical ozone distribution data as inputs. It predicts solar radiation levels with a resolution of 11 × 11 km for all periods after June 2006 and 22 × 22 km before then, with a time resolution of 1 hour. The output of the STRÅNG model has been used in research fields including biology (e.g. Lappalainen et al. 2010), ocean geography (e.g. Hansson and Håkansson 2007) and human health (e.g. Nilson et al. 2014). In this work, hourly global and direct shortwave radiation predictions from STRÅNG (SMHI, http://strang.smhi.se) were used to calculate the radiation reaching the road surface.

3 Methods

3.1 Segment-based data analysis

Most of the data processing was conducted in a geographical information system (GIS) environment. The road vector data were divided into 50-m segments and the mobile RST measurements, re-classified land use data and predicted radiation levels were spatially related to the segmented scaled road vertices. This segment-based approach facilitated quantitative analysis of the relationship between radiation and RST. A segment length of 50 m was chosen to match the scale of the mobile RST measurements.

3.2 Modelling of the radiation fluxes at road surface

To model the road surface radiation fluxes, it was necessary to calculate segment-scale values for two geographical parameters: \( {\psi}_s \) and the shading ratio (\( {S}_r \)), which measures the proportion of a segment that is shaded. Both parameters were computed using Lidar data. \( {\psi}_s \) was calculated using the solar long-wave environmental irradiance geometry (SOLWEIG) model. In SOLWEIG, \( {\psi}_s \) is derived using a shadow casting algorithm whose inputs are the altitude and azimuth of a distant light source (the sun) together with a rasterised DSM. To generate shadow volumes, a new DEM is created by sequentially moving a raster DSM at the azimuth angle of the sun, while reducing the height for each iteration on sun elevation angle. A \( {\psi}_s \) value is calculated for each pixel of the DSM by using annulus weighting (Steyn 1980) to generate an appropriate altitude and azimuth. For further details, see Lindberg and Grimmond (2010).

\( {S}_r \) was calculated using the Spatial Analyst Toolbox in ArcGIS for Desktop. By setting the solar elevation and solar azimuth value, it was possible to compute the shading effect at a given moment from the Lidar data. \( {S}_r \) was calculated hourly from sunrise to the moment when a mobile measurement was carried out. Average \( {\psi}_s \) and shading ratios were calculated separately for each segment of the studied routes.

As shown in Fig. 3, multiple radiation fluxes were computed for each segment to analyse the influence of different levels of screening on the RST distribution.

Fig. 3
figure 3

Radiation fluxes and geographical parameters considered in this study. K↓: incoming shortwave radiation, L↓: incoming long-wave radiation, K↑: reflected shortwave radiation from the road surface, OLR: outgoing long-wave radiation, ψ s : sky-view factor, \( {S}_r \): shading ratio. K↓ is composed of radD (diffuse radiation), radI (direct radiation) and reflected diffuse and direct radiation. L↓ is composed of \( {L}_{sky} \) (long-wave radiation from the sky), long-wave radiation reflected by the surroundings and \( {L}_{obj} \) (long-wave radiation from the surroundings)

Full size image

3.2.1 Shortwave radiation fluxes

The incoming shortwave radiation (K↓) has three components and is expressed as:

$$ K\downarrow =\left(1-{S}_r\right)\times {I}_{\mathrm{strang}}+{\psi}_s{D}_{\mathrm{strang}}+{\alpha}_{\mathrm{surr}}\times \left(1-{\psi}_s\right)\left({I}_{\mathrm{strang}}+{D}_{\mathrm{strang}}\right) $$
(1)

The first term on the right hand side of this expression is the incoming direct shortwave radiation, the second is the incoming diffuse radiation, and the third is the direct and diffuse radiation reflected from the surroundings to the road surface. \( {S}_r \) represents the shading ratio; \( {I}_{\mathrm{strang}} \) and \( {D}_{\mathrm{strang}} \) represent the direct and diffuse radiation outputs from the STRÅNG model, respectively; and \( {\alpha}_{\mathrm{surr}} \) represents the average albedo of trees and buildings, which was set to 0.15.

The outgoing shortwave radiation (K↑) is the shortwave radiation reflected from the road surface back to the sky. It is estimated as:

$$ K\uparrow ={\alpha}_{\mathrm{road}}\times K\downarrow $$
(2)

where \( {\alpha}_{\mathrm{road}} \) is an average road surface albedo. The albedo of road asphalt ranges from 0.05 to 0.2 (Oke 1987); an average of 0.1 was assumed in this work.

3.2.2 Long-wave radiation fluxes

The incoming long-wave radiation (L↓) also has three components:

$$ L\downarrow ={\psi}_s{\varepsilon}_{\mathrm{sky}}\sigma {T_{\mathrm{air}}}^4+\left(1-{\psi}_s\right)\left(1-{\varepsilon}_{\mathrm{tree}}\right)\times {\varepsilon}_{\mathrm{sky}}\sigma {T_{\mathrm{air}}}^4+\left(1-{\psi}_s\right)\times {\varepsilon}_{\mathrm{tree}}\sigma {T_{\mathrm{air}}}^4 $$
(3)

where the first term on the right hand side is the long-wave radiation from the sky, the second is the long-wave radiation reflected from the surroundings to the road surface, and the third is the long-wave radiation emitted from the surroundings to the road surface. To simplify the modelling of long-wave radiation from the surroundings, the emissivity and temperature of buildings and trees are assumed to be the same. \( {\varepsilon}_{\mathrm{tree}} \) usually ranges from 0.97–0.98 for deciduous and 0.97–0.99 for coniferous trees (Oke 1987). In this study, \( {\varepsilon}_{\mathrm{tree}} \) was set to 0.98 because the forests in the studied areas were mixed deciduous and coniferous. The temperature of a sunlit building is usually higher than that of a tree. However, the roads in both study areas are mainly in rural areas and have few nearby buildings. To simplify the simulation process, the air temperature at a height of 2 m was assumed to be identical for buildings and trees. \( {\varepsilon}_{\mathrm{sky}} \) is the emissivity of the sky, \( \sigma \) is the Stefan-Boltzmann constant and \( {T}_{\mathrm{air}} \) is the air temperature at a height of 2 m. \( {\varepsilon}_{\mathrm{sky}} \) is assumed to equal the atmospheric emissivity given cloudless skies, which was estimated using the method of Brutsaert (1975):

$$ {\varepsilon}_{a(0)}=0.575\times {e_a}^{1/7} $$
(4)

where \( {\varepsilon}_{a(0)} \) is the atmospheric emissivity with cloudless skies and \( {e}_a \) is the vapour pressure in millibars.

The vapour pressure \( {e}_a \) is a function of the relative humidity and saturation vapour pressure, which is calculated using Tetens’ formula (Tetens 1930).

The long-wave radiation emitted from the road surface (L↑) is modelled using interpolated RST data from RWIS stations. The temperature measured at the closest station with a similar shading pattern to the road stretch is assumed to equal the corresponding surface temperature, and the long-wave radiation is modelled as:

$$ L\uparrow ={e}_{\mathrm{road}}\sigma {\mathrm{RST}}^4 $$
(5)

where \( {e}_{\mathrm{road}} \) is the average road surface emissivity, which was set to 0.95.

3.3 Derivation of radiation flux indexes

Equations 1 to 5 were used to calculate a set of different radiation fluxes for each measurement. Because most of the measurements were conducted over a period of 1 hour, it was necessary to ensure that the radiation fluxes for each segment were calculated for the time when its RST was recorded in order to avoid discrepancies between the timing of the RST measurement and the corresponding radiation flux calculation. This was done by simple time-based interpolation, which was also used to interpolate the RST data from the RWIS stations prior to computing L↑. To determine how detailed the model needed to be in order to adequately describe the RST distribution along the road, the total incoming radiation, net radiation (Q*) and incoming direct shortwave radiation (I) were calculated for each road segment and measurement timing and compared to the measured RST values.

4 Results

4.1 The influence of shading effects in RST modelling

Two examples of the relationship between the measured RST and the simulated instantaneous \( I \) are shown in Fig. 4. Both examples were from measurement M2 but cover different parts of the route. Figure 4a is based on the measurements of the northernmost road 182 with mostly dense forest at both sides, whereas Fig. 4b is based on measurements over a part of road 42 close to the city centre of Borås. As shown in Fig. 1, the road orientation of the examples is nearly perpendicular to each other. In the first case, the measured RST distribution correlates strongly with the calculated instantaneous I values while in the second the correlation is lower. Even though the same method was used to measure RST in all cases, the variation in the correlation between the measured RST and the simulated instantaneous radiation is quite substantial. This suggests that models based on instantaneous shading effects may be more difficult to apply in certain road environments. When using GIS to simulate shading effects, both the land use type and the angle (θgs) between the geographical orientation of the road segment and the solar azimuth may influence the results obtained. The influence of both parameters on the relationship between the distribution of RST and radiation was therefore investigated.

Fig. 4
figure 4

Two examples (from the same mobile measurement M2) of the relationship between measured RST and the simulated direct shortwave radiation at the measurement time (sample number 260). a an example with high correlation, b an example with low correlation

Full size image

4.1.1 The influence of land use

Three land use types were defined for each study area. Those for the country road area were urban, coniferous forest and other. Urban was defined as area with dense urban structure, area with more than 200 inhabitants including green area or industry, commercial and public service area, as defined by Lantmäteriet (2015). Other land use included open, deciduous forest, farm land and area with less than 200 inhabitants. For the highway area, the urban category was replaced with rock cut because the highway did not pass through any built up regions. The country road area did not contain any rock cut stretches.

The influence of different land use types on the relationship between the simulated instantaneous \( I \) and the RST distribution is shown in Table 2. The correlation between the RST distribution and the shading pattern is slightly different for the different land use types, and the land use type with the strongest correlation is not always the same for each measurement.

Table 2 The influence of land use and the angle between the road’s direction and the solar azimuth on the correlation between RST and the simulated instantaneous direct shortwave radiation. n denotes the number of samples for each category. Measurements M1-M9 were conducted in urban areas while M10-M16 were conducted in rock cut areas
Full size table

4.1.2 The influence of direction

Table 2 also shows the influence of θgs on the correlation coefficient for the relationship between the simulated instantaneous \( I \) and the RST distribution. Three θgs ranges were considered: 0–30°, 30–60° and 60–90°. As shown in Table 2, the correlation coefficient differs between road segments and varies with θgs; the strongest correlations usually occur when θgs is between 60 and 90°.

4.2 The influence of hemisphere blocking and different radiation fluxes

4.2.1 The accumulated radiation

The correlation coefficients for the relationships between various radiation flux indices and the RST distribution are shown in Table 3. The instantaneous radiation indexes generally explained the RST distribution quite well other than for measurements made close to sunset. It may thus be necessary to consider accumulated radiation (i.e. the cumulative road surface radiation flux prior to measurement) as well as instantaneous radiation fluxes in such cases. Ideally, the entire energy balance should be considered when studying how incoming solar radiation influences the RST distribution; in particular, it may be helpful to consider heat storage in the road and the sensible heat flux. However, because the uncertainties associated with estimating these quantities are large, the accumulated radiation was chosen as a more practical estimate of the prior energy input into the road, i.e. heat storage.

Table 3 The correlation coefficient between different instantaneous radiation fluxes and the distribution of RST
Full size table

Separate radiation fluxes were calculated for each hour from sunrise to the measurement moment. These hourly fluxes were then used to calculate cumulative radiation fluxes over defined periods of time, and the correlation between these cumulative fluxes and the measured RST distribution was characterized using the Pearson correlation coefficient (R). Multiple accumulation periods were considered for each RST measurement, starting with the 1-hour period immediately prior to the measurement and then increasing the duration of the accumulation period in hourly increments back to sunrise. Figure 5 shows that varying the length of the accumulation period affected the correlation coefficient (R) for the relationship of the spatial RST distribution with the cumulative total incoming radiation, Q*, and I. In all cases, the measured RST distribution correlates more strongly with the cumulative radiation indices than the corresponding instantaneous radiation fluxes and the explained variance is improved by up to 30 % in the best cases. While the different radiation indices generally responded similarly to increases in the length of the accumulation period, the accumulation period length required to maximize R depended on both the study area and the timing of the measurement occasion relative to sunset.

Fig. 5
figure 5

Changes in the correlation coefficient (R) for the relationship between the accumulated radiation and the RST distribution as the accumulation period is varied. On the x-axis, zero represents the time at which the measurement was taken and negative values indicate the length of the accumulation period considered (TBS: time before sunset)

Full size image

In order to better understand how the timing of the measurement affects the optimal accumulation period, the length of accumulation period required to maximize R was plotted against the timing of the measurement relative to sunset for the country road and highway areas (see Fig. 6a, b, respectively). For measurements in the country road area, the relationship was linear, and the timing of the measurement explained 48 % of the variance in the R-maximizing accumulation period. It thus seems that the later the RST measurement is conducted, the greater the accumulation period required to maximize R. However, for measurements in the highway area, the relationship becomes polynomial and explains 40 % of the variance in the R-maximizing accumulation period. This suggests that for measurements in the highway area, the accumulation time required to maximize R increases as the measurement timing gets closer to noon.

Fig. 6
figure 6

The relationship between the time before sunset (when each measurement was conducted) and the duration of the accumulation period required to maximize R (see Fig. 5) in a the country road area and b the highway area

Full size image

4.2.2 Net radiation and all incoming radiation

The RST distribution was generally well explained by the cumulative I values calculated using the shading effect model. However, comparatively weak correlations were observed for measurements M1, M4, M7 and M10 (Fig. 5). Three of these measurements were conducted when the solar elevation and the incoming \( I \) were quite low. The scope for improving the model’s performance in such cases by including ψ s in the simulation of radiation fluxes was therefore investigated. Figure 7 shows the variance of the RST distribution that is explained by using the cumulative \( I \), total incoming radiation and Q* when ψ s is accounted for. The amount of variance explained by the cumulative I is generally somewhat lower than that explained by the cumulative total incoming radiation or Q*. The amount of variance explained by the models based on the cumulative total incoming radiation and Q* is more than 5 % greater than that explained by the model based on the cumulative I for 6 out of 16 measurements. For all of the other measurements, all three radiation flux models explained similar amounts of the observed variation in RST. The greatest improvements due to the inclusion of ψ s were achieved for measurements M1, M4 and M7, which were conducted in the country road area during the early morning or late afternoon. It should be noted that including ψ s significantly complicates the simulation process because the calculation of ψ s and other radiation fluxes is substantially more time-consuming than that of the shading effect and \( I \).

Fig. 7
figure 7

The proportion of the variance in the RST distribution explained using models based on different cumulative radiation fluxes

Full size image

4.3 Development of a general radiation model

As shown previously, the accumulated radiation models describe the RST distribution better than instantaneous radiation models. It would therefore be useful to develop a general accumulated radiation model for predicting RST distributions. The cumulative I was selected as the basis for such a model because it is simple to compute and explained the variation in the measured RST distributions reasonably well. Because the relationship between the measurement timing and the optimal length of the radiation accumulation period differed between the country road and highway (Fig. 6), it was necessary to build separate models for each area. For the country road area, the optimal accumulation period was calculated from the results presented in Fig. 6a and used to create a separate linear regression radiation model for each measurement. In each model, the independent variable is the accumulated radiation in W/m2, the dependent variable is the measured RST in Celsius and y-intercepts is the RST when the cumulative radiation is zero, i.e. the environmental temperature when each measurement in question was conducted. To build a general radiation model, all these models had to be standardized to the same environmental temperature. This was done by removing the y-intercepts value for each measurement, so that the RST is always zero when the accumulated \( I \) is zero. By combining all of the standardized radiation models in this way, a general radiation model was built for the country road area as shown in Fig. 8a, where the standardized RST is the difference between the measured RST along the road and the environmental RST. As shown, the model can explain 57 % of the spatial variation in the RST for the country road area.

Fig. 8
figure 8

a The relationship between the accumulated direct radiation predicted by the general model for the country road area and the corresponding standardized RST values. Radiation denotes the accumulated direct radiation, and the standardized RST is the difference between the actual RST along the road and the environmental RST. Subfigure b shows the equivalent results for the highway area

Full size image

The same method was used to construct a general model for the highway area based on the seven measurements acquired in this region and the data presented in Fig. 6b. As shown in Fig. 8b, the resulting general model explained 51 % of the variation in RST for the highway measurements.

As mentioned before, predicted shading effects are sensitive to both land use and θgs. The influence of these parameters on the output of the general radiation models (Fig. 8) was therefore investigated. Variants of the general models for different land use types were constructed for each study area; their output is shown in Fig. 9. Figure 9a shows the results obtained using the country road area models for urban areas, coniferous forest areas and other land types, while Fig. 9b shows the highway area models for coniferous forest areas, rock cut regions and other land types. In both cases, the models for different land types have different slopes and y-intercepts.

Fig. 9
figure 9

a The relationship between the output of the land use radiation model and the standardized RST in the country road area. Radiation represents the accumulated direct radiation, and standardized RST is the difference between the actual RST along the road and the environmental RST. Subfigure b shows the corresponding results for the highway area

Full size image

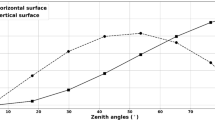
Radiation models that account for changes in θgs cannot be based on cumulative radiation estimates because θgs changes over time. Therefore, instantaneous \( I \) values were used when constructing the direction models. The environmental temperature was calculated for each measurement based on the corresponding instantaneous \( I \) and then removed to build the general direction model. Figure 10 shows the output of the general direction models for the two study areas. Their slopes are steepest when θgs is between 60 and 90° and lowest when it is 0–30°.

Fig. 10
figure 10

a The relationship between the standardized RST and the output of the model based on the angle between the road direction and the solar azimuth for the country road area. Radiation represents the instantaneous direct radiation and the standardized RST is the difference between the actual RST along the road and the environmental RST. Subfigure b shows the corresponding results for the highway area

Full size image

In reality, the environmental temperature can be estimated using average RST values from RWIS stations. The equations for the general radiation models, land use models and direction models for the two study areas are presented in Table 4 and can be used to calculate estimated environmental temperatures for each measurement. Note that the explained variance for the highway area direction model with θgs values of 60–90° is not significant because few of the measurements have many samples with θgs values in this range.

Table 4 Relationship between the b value (the background environmental temperature) in different radiation-based RST models and the average RST from RWIS stations
Full size table

4.4 Cross-validation

The performance of each model discussed above was assessed by leave-one-out cross-validation. In this technique, one measurement from the set initially used to construct the model to be validated is excluded, and the model is rebuilt using only the non-excluded measurements. The rebuilt model is then used to predict the RST of the omitted measurement, and the agreement between the prediction and measurement is assessed. This process is then repeated for each measurement of the original set in succession to estimate the model’s overall validity. The environmental temperature for each measurement was estimated using the data in Table 4. The system bias, root mean square error (RMSE) and explained variance for each model are listed in Tables 5 and 6. In the best cases, the general radiation models explained 65 % of the RST variation in the country road area and 71 % in the highway area.

Table 5 Cross-validation results for the country road area models
Full size table
Table 6 Cross-validation results for the highway area models
Full size table

5 Discussion

5.1 Modelling RST distribution by shadow pattern

At present, daytime RST modelling is in many cases done by interpolating data gathered from adjacent RWIS stations. However, the close correlation between the I values computed using Lidar-derived shading effects and experimentally measured RST distributions (Fig. 4) suggest that Lidar data may be generally useful for estimating shading patterns, offering a significant increase in the accuracy of RST modelling relative to simple interpolation. Figure 4a showed remarkably high correlation 0.86. Figure 4b showed lower correlation but still as seen in Fig. 7, the explained variance of RST distribution by the general radiation model is up to 70 %. The cross-validation results (Tables 5 and 6) also showed that the general radiation model could explain the distribution of RST to a very large extent. Such good agreement between the model output and the observation is remarkable and proves the method is physically reliable; therefore, it can be applied on a national scale by using GIS in conjunction with DSM data.

5.2 The influence of land use and θgs on the RST distribution

This approach becomes less reliable when it is necessary to account for both shading and urban heat island effects because the shading effect tends to cool the road surface, whereas the road surface tends to be warmer in the urban area. This is consistent with the output of the land use models presented herein: the urban area model (for the country road area) generates a shallower slope and a much higher y-intercept than the other land use models. Coniferous forests and rock cuts are usually very effective at obstructing I, so roads passing through such terrain usually have lower RST values than other road segments. This was observed in the output of the coniferous forest model for the country road area. However, the effect was less pronounced in the highway area due to the geographical orientation of the studied highway; this finding is discussed more extensively in section 5.5. θgs influences both the position and size of shaded areas. For a given solar elevation, increases in the value of θgs cause progressively more extensive road surface shading in road segments surrounded by shading objects. Extreme cases occur when θgs is either 0 or 90. When θgs is zero, i.e. the road segment is parallel to the solar azimuth; there are no shaded spots on the road even if shading objects are present. On the other hand, when θgs is 90, shading objects by the side of the road create the strongest possible shading effect. Due to the large temperature difference between road segments that are maximally shaded and sun-exposed, the direction model for θgs values of 60–90° always produces the steepest slopes while that for θgs values of 0–30 always produces the shallowest slopes.

5.3 The influence of the accumulated radiation on the RST distribution

The strong correlation between the accumulated radiation and the RST distribution (Fig. 5) is caused by differences in heat storage on different road segments. Under clear conditions, sun-exposed road surfaces receive more radiation than shaded ones. This creates temperature differences that persist and influence later RST distributions.

In the country road area, the length of the radiation accumulation period that had to be taken into account to achieve an optimal correlation with the measured RST distribution increased as the time of measurement got closer to sunset (Fig. 6a). Around sunset, incoming direct shortwave radiation becomes less intense and the RST distribution is mainly determined by heat stored earlier on in the day. After sunset, the road surface starts to cool down and the heat is released to the atmosphere, which is replenished by conduction from the ground (Oke 1987). An earlier study by Bogren (1991) similarly showed that RST differences between shaded sites and sun-exposed sites that developed during daytime persisted even after sunset. A similar effect occurs between sunrise and noon: longer accumulation periods are required for measurements conducted closer to noon because of the progressively greater influence of incoming direct shortwave radiation from the atmosphere over the course of the morning. A study conducted by Shao and Lister (1995) also showed that the shading simulation is especially important for improving the prediction of afternoon RSTs, when the prediction error for models that do not account for shading was much greater than at other time periods.

In the highway area, the longest radiation accumulation periods were required for measurements taken at around noon (Fig. 6b). This was due to the road’s geographical orientation and width, as well as the large gap between the road’s border and the nearest shading objects. Most of the studied route has a north–south orientation, which means that most of the road surface is not shaded and experiences intense incoming radiation during the middle of the day. This unshaded period is extended by the substantial width of the highway and the distance between shading objects and the road border. Consequently, much of the variation in the RST is actually caused by shadow patterns that were present in the hours leading up to noon rather than the midday period of intense insolation. Similarly, the spatial variation in RST around sunset is mainly due to shading effects in the late afternoon rather than the relatively evenly distributed strong insolation that occurs around noon. The accumulation time required to achieve the best correlations for afternoon measurements is shorter than for midday measurements because the period of intense insolation extends some way into the afternoon. In contrast to the highway area, shading objects are quite evenly distributed along the length of the country road and its geographical orientation varies. Consequently, the shadow patterns change continuously over time along the road’s length and there is no one time during which most of the road’s segments are sun-exposed. The relationship between the accumulated radiation and the RST distribution in the country road area is therefore likely to be applicable in many of Sweden’s road environments, which feature changing road orientations and shading objects close to the road border. On the other hand, the models developed for the highway area may be applicable in other highway environments in which the road’s orientation rarely changes.

5.4 The influence of different radiation fluxes in RST modelling

The models based on the cumulative total incoming radiation and Q* explained the early morning and late afternoon RST distributions in the country road area better than the cumulative \( I \) model due to the weak incoming \( I \) during these periods. The dominant fluxes in the early morning and late afternoon are long-wave and diffuse radiation. It was proposed that the inclusion of ψ s might improve the agreement of the RST models with the experimental measurements during these periods and also that the low explained variance achieved with the I model might be due to cloud cover. Under partly cloudy conditions, diffuse and long-wave radiation dominate and hemisphere blocking becomes more important. While no measurements were taken at around sunset time in the highway area, it is likely that the cumulative total incoming radiation and Q* models would similarly outperform the I model in this environment too. The Q* model, which used RST as a major input, did not generally outperform the total incoming radiation model, probably because the RST values used in its derivation were obtained by spatial interpolation of measurements made at widely separated locations. The number of RWIS stations on the studied roads was quite low given their length, and real RST values can vary quite substantially even over rather short distances (Chapman and Thornes 2011). Consequently, it would have been very difficult to accurately capture the variation in RST along the road simply by using information from the few available stations. Nevertheless, the three different radiation models that were developed explained quite similar proportions of the overall variation in RST for most of the measurements, especially under clear conditions. This is notable because as mentioned previously, the models are constructed in rather different ways. For the \( I \) model, only \( {S}_r \) needs to be considered whereas the other two both require the calculation of \( {\psi}_s \) (which adds complexity to the model as calculation of \( {\psi}_s \) is time-consuming when dealing with large areas) and that of several other radiation fluxes. In addition, the Q* model requires the spatial interpolation of RST data. Therefore, there is a trade-off between the higher explained variance achieved with the total incoming radiation or Q* models and the much simpler \( I \) model. For clear conditions, when the influence of \( I \) is strong, the \( I \) model is recommended.

5.5 The influence of road types on the general radiation model

Due to the regional difference between the country road area and the highway area, separate general radiation models were built for each. Figure 8 shows that the slopes of the two linear models are quite different. For the country road area, the level of shading varies over the length of the road and the course of the day, creating large differences in RST between sun-exposed and screened sites. This produces relatively steep slopes. For the highway area, there is quite a long period during the day when almost the entire length of the road is sun-exposed, which diminishes the RST difference between sun-exposed and screened sites. Consequently, the slope of the general radiation model for the highway area is shallower than that for the country road area. This is consistent with the findings of Bogren et al. (2000a), which indicated that the greatest RST differences occurred between sites that are always sun-exposed and those that are always shaded. This again highlights the fundamental difference between the highway and country road areas.

Cross-validation of the two general direct radiation models suggested that the accumulated radiation model can explain the RST distribution to a large extent. The explained variance is influenced by both the solar elevation and extent of cloud cover. Usually, the higher the solar elevation is, the greater the explained variance under clear conditions. Cloud cover reduces model performance, which is again consistent with the findings of Bogren (1991). The explained variance is usually low around sunset because the I-based model disregards other radiation fluxes such as long-wave and diffuse radiation for instance. This can be regarded as an acceptable trade-off for simplifying the simulation. As shown in Fig. 8, both models produce a wide range of predicted RST value for a given radiation intensity. This is largely due to variation in land use patterns and θgs values. However, performance is not improved by adopting land use-specific models or direction models. The direction models performed worse than the general radiation models because they were based on the instantaneous\( I \), which correlates less strongly with the RST distribution than does the cumulative I. The difference between the land use models and the general radiation model is quite small and in some cases, the land use model provided worse results. These results suggest that separating measurements across different land use groups does not substantially differentiate the results (Table 2). However, Fig. 9a shows that it is important to consider urban heat island effects when building radiation models. More studies will be required to determine how land use data can be applied in conjunction with LIDAR data and information on other factors in order to best calculate the relationship between radiation and RST.

5.6 Uncertainties and errors

Despite the general models’ ability to explain a large amount of the observed variation in RST, there were some measurements for which they afforded relatively high bias and RMSE values. This may be due to various sources of uncertainty and error.

First of all, the precision of the mobile measurements must be considered. There are two potential sources of error in the mobile measurements: errors caused by using different infrared sensors and errors caused by the limited spatial precision of the mobile measurements. Two different infrared sensor models were used during the measurements in both the country road area and the highway area. Differences in the performance of the sensors may lead to errors in the general radiation models. Spatial errors may arise due to the method used to determine the position of the vehicle carrying the infrared sensors. As mentioned previously, the vehicle’s position during measurements M1-M7 was determined on the basis of its velocity whereas GPS data were used for all other measurements. While the mobile measurements were resampled to a scale of 50 m, the possible spatial error should not be neglected. Another type of spatial error is caused by the spatial difference between the digitized road segments in the GIS environment and the actual driving route. In GIS, it is assumed that the driver always travels down the centre of a road. However, in reality, the mobile measurement route is influenced by traffic conditions and the actions of individual drivers, which means there may be minor spatial discrepancies between the digitized routes and those actually travelled during measurements. Furthermore, changes in the weather and cloud cover during mobile measurements may create shadow patterns that differ from those predicted by the screening models; this is another potential source of error. All of the shadow patterns used in this work were derived from Lidar data, so another potential source of error is the precision of these data. As noted in the data section, the Lidar data were acquired between 2009 and 2013, whereas the mobile measurements were conducted between 2012 and 2014. It is possible that the land use types along different sections of each route may have changed after the Lidar data were obtained. It is therefore important to use recently acquired Lidar data when simulating shadow patterns. A final potential source of modelling error is the STRÅNG data used in this work, which is based on observations from 12 stations that cover the entirety of Sweden. The low density of stations may lead to modelling errors in the STRÅNG data and therefore errors in the general radiation models. It may be possible to develop general models with lower error levels by maintaining up-to-date Lidar databases, performing mobile measurements with the same type of infrared sensors and using high-precision GPS position data during all measurements.

6 Conclusion and future research

The availability of high resolution Lidar data covering entire countries offers new opportunities in RST modelling. By using GIS to derive shading patterns based on Lidar data, it becomes possible to accurately simulate radiation fluxes at the road surface and thus the spatial RST distribution during daytime. The results presented herein have a high explained variance and the underlying physics is sound. The simulations are sensitive to land use types, angle (θgs) between the road direction and solar azimuth and various radiation fluxes. While it is often sufficient to use models that only account for instantaneous radiation when modelling the RST distribution, the results presented herein demonstrated that the accumulated radiation can better explain the RST distribution in some cases, for instance, close to sunset. Of the various models presented in this work, the cumulative \( I \) model is recommended due to its simplicity and time-efficiency. However, the importance of \( {\psi}_s \) when predicting shading during the early morning, late afternoon or the effects of cloud cover should not be neglected. Two different general radiation models were built for country roads and a highway region due to their environmental differences. These general radiation models will be incorporated into a numerical energy balance model and used to improve the precision of RST predictions.

Future planned research is to apply the technique to the distribution of nocturnal RST and examine the lagged effect of the accumulated shading. In the current study, buildings and trees in the Lidar data were treated in the same way in simulation of the shading pattern. In the future research, they will be separated and different transmissivity will be applied to get a better view of the shading effect.