Effect of data homogenization on estimate of temperature trend: a case of Huairou station in Beijing Municipality

Lei Zhang; Guo-Yu Ren; Yu-Yu Ren; Ai-Ying Zhang; Zi-Ying Chu; Ya-Qing Zhou

doi:10.1007/s00704-013-0894-0

Download PDF

Theoretical and Applied Climatology

February 2014, Volume 115, Issue 3–4, pp 365–373

Effect of data homogenization on estimate of temperature trend: a case of Huairou station in Beijing Municipality

Authors
Authors and affiliations

Lei Zhang
Guo-Yu RenEmail author
Yu-Yu Ren
Ai-Ying Zhang
Zi-Ying Chu
Ya-Qing Zhou

Open Access

Original Paper

First Online:: 25 April 2013

Received:: 16 February 2013
Accepted:: 27 March 2013

DOI: 10.1007/s00704-013-0894-0

Cite this article as:: Zhang, L., Ren, GY., Ren, YY. et al. Theor Appl Climatol (2014) 115: 365. doi:10.1007/s00704-013-0894-0

Abstract

Daily minimum temperature (Tmin) and maximum temperature (Tmax) data of Huairou station in Beijing from 1960 to 2008 are examined and adjusted for inhomogeneities by applying the data of two nearby reference stations. Urban effects on the linear trends of the original and adjusted temperature series are estimated and compared. Results show that relocations of station cause obvious discontinuities in the data series, and one of the discontinuities for Tmin are highly significant when the station was moved from downtown to suburb in 1996. The daily Tmin and Tmax data are adjusted for the inhomogeneities. The mean annual Tmin and Tmax at Huairou station drop by 1.377°C and 0.271°C respectively after homogenization. The adjustments for Tmin are larger than those for Tmax, especially in winter, and the seasonal differences of the adjustments are generally more obvious for Tmin than for Tmax. Urban effects on annual mean Tmin and Tmax trends are −0.004°C/10 year and −0.035°C/10 year respectively for the original data, but they increase to 0.388°C/10 year and 0.096°C/10 year respectively for the adjusted data. The increase is more significant for the annual mean Tmin series. Urban contributions to the overall trends of annual mean Tmin and Tmax reach 100% and 28.8% respectively for the adjusted data. Our analysis shows that data homogenization for the stations moved from downtowns to suburbs can lead to a significant overestimate of rising trends of surface air temperature, and this necessitates a careful evaluation and adjustment for urban biases before the data are applied in analyses of local and regional climate change.

1 Introduction

The homogeneous time series of climate variables are defined as those which contain only climatic variation and regional trend information. It is generally recognized that only by using homogenized data series can the long-term climatic trends be accurately detected. However, due to changes in observing sites, instruments, observing schedule, observing habits and micro-environment around the observational grounds, discontinuous points in the observational records can be created, especially for surface air temperature (SAT) records. The inhomogeneous data may bring certain deviation for estimating climatic trends, leading to inaccurate analyses for regional climate change detection in some circumstances (Jones et al. 1986; Easterling and Peterson 1995a; Yan et al. 2001; Ren et al. 2005; Menne et al. 2010). Therefore, researchers commonly examine and adjust the inhomogeneities before going to analyze long-term SAT trends at single sites or on regional scales, by combining varied mathematical methods and station metadata (e.g., Jones et al. 1986; Easterling and Peterson 1995a, b; Alexandersson and Moberg 1997; Aguilar et al. 2003; Menne and Williams 2005).

The inhomogeneities caused by observing schedule, instrumentation, and relocation were adjusted in SAT data of the United States USHCN (US Historical Climate Network) (Karl and Williams 1987; Quayle et al. 1991; Easterling and Peterson 1995a, b; Menne and Williams 2009). Vincent (1998) and Vincent et al. (2002) adjusted the Canadian Tmin and Tmax series using multiple linear regression method. Researchers from other countries and regions also created their own homogeneous SAT dataset using methods such as Easterling and Peterson method, Standard Normal Homogeneity Test, Two-Phase Regression, Penalized Maximal t Test, and Multiple Analysis of Series for Homogenization (MASH) (Wang et al. 2007a; Aguilar et al. 2003; Reeves et al. 2007).

Chinese researchers made studies of SAT data homogenization (Song et al. 1995; Zhai and Eskridge 1996; Liu 2000; Yan et al. 2001; Yan and Jones 2008; Li et al. 2004; Li and Dong 2009; Li and Yan 2010). Using three different tests for undocumented change points, for example, Li et al. (2009) estimated the artificial discontinuities in annual mean daily Tmin and Tmax in southeastern China and found that there are more discontinuity points in annual mean Tmin series; Li and Yan (2010) apply MASH method to detect and to adjust inhomogeneities for daily SAT series of 1960–2006 at Beijing station.

Given the adjustments are accurate and applicable for monitoring and detecting regional climate change, however, there remain still a few of issues to be solved. One is what effect the homogenization will have on the estimated long-term SAT trends at a single station or in a large region. If the SAT trends are significantly different between the prior and aft adjusted data series, then what are the underlying causes? Does the adjustment for inhomogeneities significantly recover the urban bias when the breakpoints are mostly caused by the moves of stations from urban areas to rural areas, as previously suggested by Winkler et al. (1981) and Hansen et al. (2001) for the United States and recently by Ren et al. (2010) for mainland China? To answer these questions will certainly deepen our understanding of the systematic biases of the SAT data and their influences on the estimates of magnitude and rate of local and regional temperature change.

In this paper, we examine the effect of data homogenization on the estimate of Tmin and Tmax trends at Huairou station of Beijing Municipality (BM). We first make an examination of inhomogeneities of temperature data and adjust the breakpoints identified to obtain a homogenized SAT data; we then compare the linear trends of the original and adjusted SAT series and analyze the urban effects on the linear trends of the original and adjusted SAT series using the temperature data of the same reference stations.

2 Data and methods

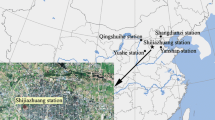
The original daily Tmin and Tmax data of Huairou, Xiayunling, and Shangdianzi stations from 1960 to 2008 are obtained from the National Meteorological Information Center of the China Meteorological Administration. The locations of the stations are shown in Fig. 1, and the basic information of the stations is listed in Table 1. The station history records are from the Beijing Meteorological Bureau (BMB) (2009), and the population data for the residential areas near the stations are from the China Statistic Bureau (2002).

Fig. 1
Locations of the weather stations used in the study. a Huairou station and reference stations in present; b present and historical locations of Huairou station. Numbers 1, 2, and 3 in b indicate the locations before 1964, 1964–1996, and after 1996

Table 1

Information of the weather stations used in this study

Station code	Station name	Longitude (°E)	Latitude (°N)	Altitude (m)	Start time of record	Relocation (d/m/y)	Population in 2000 (10³)
54419	Huairou	116.62	40.37	76	1959	1/8/1964	74.6
						1/7/1996
54597	Xiayunling	115.72	39.72	408	1959		0
54421	Shangdianzi	117.12	40.65	293	1958	1/9/1989	Less than 1.0

As a rapidly grown small city, Huairou is located in the northern mountainous areas of the BM, with a population of ~75 thousands in the urban area in 2000 (Fig. 1a). Huairou weather station is a typical urban station (Fig. 1b), and the recent 49-year records from the station are evaluated in this paper for the data inhomogeneities and urbanization effects on the SAT trends as a target observational site. Although Xiayunling and Shangdianzi stations are also located in the mountainous areas, they are both far from larger residential areas, with the former being on a valley in the southwest and the latter on a slope near a small village having a population of no more than a thousand in the northeast (Fig. 1a). The two observational sites are chosen as the reference stations from 20 weather stations with over 30-year records in the BM. In addition to the small population of the residential areas near stations and the similar physiographic characteristics to the target station, the reference stations are also required to have the continuous observation records with as possible as less the missing observational values. The two weather stations were ever used as reference stations in previous studies of urbanization effect on the SAT trends of Beijing station (Chu and Ren 2005; Ren et al. 2007).

Inhomogeneities of SAT data can be caused by such factors as instrumentation, relocation, change in observational time, and modified statistical methods for daily averages. The introduction of the Autonomous Weather Stations (AWS) to operational observations around 2004 in mainland China may in certain extent have resulted in additional inhomogeneities in SAT records. Wang et al. (2007b) indicated, however, that the SAT of AWS has certain difference from that of manual weather stations, but overall the difference is small and not significant. No change in observational time and statistical methods of daily mean SAT occurred during the last 50 years, and these will not cause any detectable inhomogeneities of the SAT data. It has been realized that the most important factor causing the inhomogeneities of SAT data is the frequent relocations of stations in mainland China (Yan et al. 2001; Li et al. 2004; Ren et al. 2005).

Huairou station experienced relocation twice. It was moved for the first time from West Gate of the old town (Site 1 in Fig. 1b) to Beitumenzi (Site 2 in Fig. 1b) at the East Gate Road outside the old town on 1 August 1964. The second move occurred on 1 July 1996, from Beitumenzi to a suburban village called Liugezhang (Site 3 in Fig. 1b), about 5.5 km from the center of the old town (BMB 2009). For the two reference stations, on the other hand, the only move occurred for Shangdianzi station on 1 September 1989, but the horizontal distance of the movement was 750 m, and the observational grounds changed from 255 m above sea level (ASL) to 293 m ASL, increasing by 38 m in altitude.

The data are quality-controlled with the following steps: (1) if the maximum temperature (Tmax) values are lower than the minimum temperature (Tmin) values, they are registered as unreasonable readings. There is no unreasonable record in the SAT dataset of Huairou station; (2) the values beyond four times of standard deviation are marked as outliers. If outliers are detected, the reasonable records are retained, and unreasonable ones are corrected or regarded as missing values, based on the comparison to the records of the neighboring stations. There is only one outlier found in the dataset, but it is not unreasonable; (3) missing values, which account for less than 0.25% of the total records, are filled in by using the means of the same stations for the reference time period 1971–2000.

The monthly mean Tmin and Tmax series T_i,j are calculated based on the daily records, and the monthly change-in-temperature time series dT/dt for Huairou station are then created referring to Easterling and Peterson (1995a). The i and j indicate number of year and month respectively.

$$ {{\left( {\mathrm{d}T/\mathrm{d}t} \right)}_{i,j }}={T_{i+1,j }}-{T_{i,j }} $$

(1)

The monthly reference change-in-temperature time series $ \left( {\mathrm{d}T/\mathrm{d}t} \right)\prime $ are constructed by averaging the two reference station data with squares of correlation coefficients with Huairou station series as weights. We thus get the reference series $ T\prime $.

$$ T{\prime_{i+1,j }}=T{\prime_{i,j }} + \left( {\mathrm{d}T/\mathrm{d}t} \right){\prime_{i,j }} $$

(2)

Discontinuous points in annual difference series of the target station and the reference stations are detected by using method of moving t test. As mentioned above, Huairou station was moved in 1964 and 1996. In order to effectively identify the discontinuities due to the relocations, the son series length is set as 3 years since the dataset started in 1960. Therefore, the series length n = 49, the son series length n1 = n2 = 3, and the significance level α = 0.01. The metadata are used to validate the existence of the inhomogeneous points, and they are adjusted if proved to be real and caused by relocation. Otherwise, the original records are kept as they were.

The 5-year averages of monthly mean SAT difference between the target station and the reference series is taken as the adjustment values. If the records are less than 5 years before or after discontinuous points, then all the years of record available are used to determine the adjustment values. The adjustments for inhomogeneities are made on basis of daily SAT data. The daily adjustment values are obtained by a linear interpolation method, with the monthly mean adjustment values being assigned to the mid-month days (15th or 14th) of the neighboring months.

The sections of data after the last documented inhomogeneous points are taken as the base series, and they remain unchanged. Before the inhomogeneous points, the adjustment values are added to the original records for every day.

Urban effect (ΔT_ur) is defined as the SAT trends caused by the changing Urban Heat Island (UHI) intensity and/or other factors (such as aerosols) related to urbanization near the specific locations of urban weather stations (Chu and Ren 2005; Ren et al. 2008). It is estimated by formula:

$$ \varDelta {T_{ur }}={T_u}-{T_r} $$

(3)

where T_u is the SAT trend of urban station and T_r is the SAT trend of reference (rural) station (series). ΔT_ur is larger than 0 if the urbanization raises the SAT trend at urban station, and it is smaller than 0 if the urbanization reduces the SAT trend at urban station.

ΔT_ur can also be estimated by calculating the annual and monthly mean SAT differences between urban station and reference series and the linear trend of the difference series over the time period analyzed. In this paper, the annual mean SAT difference series of Tmin and Tmax between Huairou station and the average reference series are constructed, and their linear trends for the time period 1960–2008 are estimated by using least-square method and are examined for statistical significance by t test.

Urban contribution (E_u) is defined as a proportion that the statistically significant urban effect accounts for the total SAT trend at urban station (Chu and Ren 2005; Ren et al. 2008). It can be expressed as:

$$ {E_u}=\left| {\frac{{\Delta {T_{ur }}}}{{{T_u}}}} \right|\times 100\%=\left| {\frac{{{T_u}-{T_r}}}{{{T_u}}}} \right|\times 100\% $$

(4)

Generally, ΔT_ur/T_u is a positive value less than 100% (0 ≤ E_u ≤ 100%); absolute value is taken because it, in certain circumstances, assumes negative value due to the effects other than increasing UHI intensity. If E_u = 100%, then it shows that the SAT trend of the urban station is entirely caused by urbanization; if E_u is more than 100%, it implies that the extra trend might have been caused by other local factors not yet identified or the errors of data, but it is regarded as 100% in this study. As the definition implies, urban contribution is not calculated if the urban effect is not statistically significant.

3 The results

3.1 Detection and adjustment of data inhomogeneities

There is no discontinuous point detected in the SAT data series of the two reference stations, despite the relocation of Shangdianzi station in September 1989. This happens mainly due to the relatively small change in the altitude and the environment. No adjustment is done, therefore, and the quality-controlled data are used for producing a single and average reference series.

However, the inhomogeneities are more evident in the SAT data series of Huairou station. Figure 2 shows curves of the moving t statistics of Tmin and Tmax at Huairou station. There are three discontinuous points in the Tmin series in 1963, 1991, and 1996, respectively, and three discontinuous points in the Tmax series in 1974, 1996, and 2000, respectively. By checking the metadata, the discontinuous points in 1963 and 1996 occurred most probably due to the station moves of 1 August 1964 and 1 July 1996 (Table 1). The two discontinuous points are more significant statistically for the Tmin series than those for Tmax series, and they have to be adjusted for homogeneity. However, the discontinuous points statistically detected for Tmin in 1991 and for Tmax in 1974 and 2000 cannot be validated by the station historical records and have been kept as they are.

Fig. 2
The moving t statistics of Tmin (a), Tmax (b) at Huairou station (the *dotted straight lines* denote that the values are statistically significant at 0.01 confidence level)

The daily mean adjustment values of Tmin and Tmax for the two discontinuous points validated are shown in Fig. 3. The monthly and daily mean adjustment values are all positive in 1964 and 1996. For the discontinuous point in 1996, however, the Tmin adjustment values are significantly larger than the Tmax adjustment values, and the Tmin adjustment values are significantly larger in winter than those in summer. It suggests that the daily Tmin and Tmax all dropped when the station was moved from within the town to outside the town, with the drop in Tmin more significant. There are also obvious seasonal differences in the Tmin adjustment values, with those in winter larger than in summer. The seasonal differences for Tmax adjustment values are smaller.

Fig. 3
The daily mean adjustment values of Tmin and Tmax at Huairou station in 1964 and 1996

Figure 4 gives the annual mean Tmin and Tmax of the original and the homogeneity-adjusted data series at Huairou station and of the average reference data series. It is obvious that the adjusted temperature series, especially for Tmin, are more homogeneous and continuous than the original ones, and they are more consistent with the average reference series in inter-annual variability. The annual mean Tmin for the whole period analyzed decreases by 1.377°C after the adjustment, while the annual mean Tmax decreases by 0.271°C (Table 2). The average adjustment magnitudes of mean Tmin are significantly larger than those of mean Tmax.

Fig. 4
The annual mean Tmax (a) and Tmin (b) of original and adjusted data series at Huairou station and of reference series during 1960–2008. The *solid straight lines* denote linear trends

Table 2

The mean and variance of annual Tmin and Tmax of Huairou station before and after adjustment during 1960–2008 (degrees Centigrade)

		Before adjustment	After adjustment	Difference
Tmin	Mean	6.683	5.306	−1.377
Tmin	Variance	0.339	0.577	0.238
Tmax	Mean	17.561	17.290	−0.271
Tmax	Variance	0.542	0.629	0.087

A notable phenomenon is that the linear trends of the original annual mean Tmin and Tmax series of Huairou station are −0.006°C/10 year and 0.204°C/10 year, respectively, while the linear trends of the adjusted annual mean Tmin and Tmax series are increased to 0.385°C/10 year and 0.335°C/10 year, respectively (Table 3 and Fig. 4). The trends of annual mean Tmin and Tmax both increase obviously after the adjustment, with the former regaining 0.391°C/10 year and the latter 0.131°C/10 year, respectively. It is obvious that the increase of annual mean Tmin trend is larger and more significant, indicating that Tmin records are more sensitive to the station relocations and the data homogenizations than Tmax records. The reasons for the regains of the SAT trends will be discussed below.

Table 3

Urban effects on the Tmin and Tmax trends of the Huairou station (degrees Centigrade per 10 years) and the urban contribution to the overall temperature trends (percent) for the data series before and after adjustment for period 1960–2008

		Before adjustment	After adjustment	Difference
Tmin	Linear trend	−0.006	0.385^a	0.391
	Urban effect	−0.004	0.388 ^a	0.392
	Urban contribution		100
Tmax	Linear trend	0.204 ^a	0.335 ^a	0.131
	Urban effect	−0.035	0.096 ^a	0.131
	Urban contribution		28.8

^aSignificant at the 0.01 confidence level

The annual mean Tmin and Tmax values are all reduced after the adjustments, and the reasons for the decrease are that the adjustments are made with the section of data series at the present location of observation as baseline, and also the sections of data series adjusted before the last relocation are longer in combination than the latest section of records. Once again, the reduction of the annual mean Tmin is significantly larger than that of the annual mean Tmax.

3.2 Urban biases in adjusted and original data series

Figure 5 shows changes in annual mean SAT difference values between Huairou station and the average reference series. The two SAT difference series of annual mean Tmin and Tmax for the original and homogeneity-adjusted data have highly similar inter-annual variability, but their linear trends are obviously different, with those for the adjusted data witnessing larger increasing trends, especially for Tmin series. Therefore, the relocations of Huairou station from the downtown to the suburb produced breakpoints or inhomogeneities, but they at the same time also largely reduced the urban warming trends, as seen in the original temperature series, while the data homogenization performed for welding the breakpoints now results in a recovery of the urban effect as shown in the adjusted temperature series.

Fig. 5
The differences of annual mean Tmax (a) and Tmin (b) between Huairou station and reference data for original (dotted lines) and adjusted (solid lines) data series during 1960–2008. The *solid straight lines* denote linear trends

Table 3 gives the urban effects and urban contributions of Huairou station for the time period 1960–2008 for the data series before and after the data adjustments. The urban effects are −0.004°C/10 year and −0.035°C/10 year, respectively, for the Tmin and Tmax before the adjustments, all non-significant statistically, but they increase to 0.388°C/10 year and 0.096°C/10 year, respectively, after the adjustments, both statistically significant at the 0.01 confidence level. The adjusted Tmin series witnesses a more significant increase in the annual mean urban warming trend.

Urban contributions to the overall temperature trends for Huairou station are not estimated for the original annual mean Tmin and Tmax series due to the non-significance of the urban effects, but they reach 100% and 28.8% for the adjusted annual mean Tmin and Tmax series, respectively. After the data adjustment for inhomogeneities, the positive trend of annual mean Tmin at Huairou station during 1960–2008 can be totally explained by the urban effect, and almost a third of the warming trend observed for annual mean Tmax at the station can be attributed to the urban effect.

4 Discussion

Relocations of weather stations from downtowns to suburbs are a common practice in mainland China during the past decades, especially for the national reference climate stations and national basic meteorological stations (Li et al. 2004; Ren et al. 2010), which have been mostly frequently applied for analyses of regional climate change. This occurs mainly due to the closeness of the weather stations to built-up areas of cities and towns and the unprecedented urbanization process over the past decades in mainland China under the rapid growth of economy (Ren et al. 2008). Our analysis and the findings of Huairou station in this paper therefore are in some extent of representativeness to the SAT datasets commonly used in studies for the country.

The frequent relocations of stations usually cause obvious inhomogeneities in SAT data, which require a homogenization before long-term trends of temperature can be analyzed. However, the adjustment may change the estimates of mean SAT trends at single stations or even in regional scale and may lead to an overestimate of the warming rates for the stations or the regions. This phenomenon were pointed out in previous studies (Hansen et al. 2001; Menne et al. 2009; Ren et al. 2010) but have not been exclusively examined. Winkler et al. (1981) found, however, that the homogeneity-adjusted SAT data depict a larger UHI intensity and UHI extent in the urban area of Minneapolis–St. Paul, Minnesota. They adjusted the data inhomogeneities induced by changes in observational time and station location. Our analysis for Huairou station in this paper shows that the increased warming rates as estimated from the homogeneity-adjusted data series compared with the original data series mainly result from the recovery of the urban warming trends. The regained warming trends, especially for the annual mean Tmin, are caused by enhanced urban effect near the first location of the city station, which now has been located in the center of the built-up areas due to the urbanization. The overall trend and the urban effect in the annual mean Tmax series also increase after the homogenization, but the changes are much smaller.

Figure 6 gives a conceptual illustration of the effects of homogenization on estimates of SAT trends with those occurred at Huairou station as a case. The first move of the station from West Gate of the old town to Beitumenzi of East Gate Road in 1964 resulted in a relatively small drop of annual mean Tmin due to the short distance between the two sites, but the second move from Beitumenzi to Liugezhang in 1996 caused a tremendous drop of annual mean Tmin due to the long distance of the relocation and the radically different settings around the two sites (also see Fig. 1b). The positive linear trend of annual mean Tmin for the unadjusted data series, as shown by the black dotted line, is small and statistically insignificant as a result of the two plunges caused by the relocations. When the SAT data is adjusted for the inhomogeneities, however, the larger positive trend of annual Tmin at the station has been recovered, as shown by the red dotted line, because the annual mean Tmin values before the two breakpoints are successively lowered by subtracting the adjustment values from the original data series.

Fig. 6
A sketch of effects of Huairou station relocations on annual mean minimum temperature trends of the adjusted and unadjusted data series

Further investigations are needed to understand to what extent the data homogenization of the national reference climate stations and national basic meteorological stations in mainland China has affected the estimates of the large scale SAT trends. It is reasonable to assume that the effect of the data homogenization on the estimates of SAT trends and urban biases for the country on a whole would be more moderate than that reported for Huairou station in this paper, but it would not be overlooked considering that a common practice is to relocate the weather stations within built-up areas to suburbs or countryside when they are regarded as being less representative for monitoring baseline climate, and this will result in obvious inhomogeneities in the SAT data series in mainland China, which has been consensually regarded as improper for applications in studies of climate change and requires a homogeneity-adjustment before they could be used in studies. If the homogenization significantly affects the SAT trends for part or even majority of the stations in the country, the urban biases in the homogenized SAT data series of the stations have to be more carefully assessed and adjusted before they are to be confidently used in analyses of climate change.

The issue is also relevant to a few of questions baffling the researchers of climate change. One is the understanding of the different trends of Tmin and Tmax in continents. The “asymmetry” in increases of Tmin and Tmax series and the resulting decline of the Diurnal Temperature Range (DTR) were reported for many regions (e.g., Karl et al. 1993; Xie and Cao 1996; Zhai and Pan 2003; Qian and Lin 2004; Choi et al. 2009; Zhou and Ren 2011). The changes were related to the increase in cloud coverage and precipitation worldwide and aerosols over some regions (Dai et al. 1999; Easterling et al. 2000). However, Zhou and Ren (2009, 2011) found a larger urban contribution to the “asymmetry” in the Tmin and Tmax increases and in the decrease of the DTR in North China. The analysis result based on the homogeneity-adjusted data in this paper also shows that the significant increase in annual mean Tmin at Huairou station might have been completely explained by urbanization, and the increase in annual mean Tmax might have been partially caused by urbanization, generally consistent with the conclusions drawn by Zhou and Ren (2009, 2011) for North China and by Zhang et al. (2011) for Beijing station.

5 Conclusions

In this paper, the daily Tmin and Tmax data at Huairou station, Beijing Municipality, from 1960 to 2008 are examined and adjusted for inhomogeneities caused by relocations of station, and the temperature trends before and after the adjustments are compared. Following conclusions are drawn:

1.
The adjusted annual mean Tmin and Tmax drop by 1.377°C and 0.271°C, respectively, and the adjustment values for Tmin are significantly larger than those for Tmax. The location changes of Huairou station from downtown to the suburb, especially the second move in 1996, cause more significant drop in annual mean Tmin. The drops in monthly mean Tmin values are larger during winter than those during summer.
2.
The data homogenization for the station relocations from downtown to suburb at Huairou station leads to an increase in mean SAT trends, and the increase is more significant for Tmin than for Tmax. The urban effects on annual mean Tmin and Tmax trends are statistically insignificant (−0.004°C/10 year and −0.035°C/10 year, respectively) for the original data series, but they reach 0.388°C/10 year and 0.096°C/10 year, respectively, for the homogeneity-adjusted data series. The urban contributions to the overall positive SAT trends are 100% and 28.8%, respectively, for Tmin and Tmax for the homogeneity-adjusted data.
3.
The larger effects of relocations, homogenization, and urbanization on Tmin data series than on Tmax data series in a larger extent explain the "asymmetry" in daytime and nighttime SAT trends at Huairou station, and the urban effect is also a major contributor to the DTR decline as implied in the "asymmetry" changes of the annual mean Tmin and Tmax for the homogeneity-adjusted data at the station.

Acknowledgments

This work is financially supported by the Ministry of Science and Technology of China (GYHY201206012). Thanks are also due to Mr. G.H. Li. at the Huairou Meteorological Bureau, Beijing Municipality, for providing the information of station history.

References

Aguilar E, Auer I, Brunet M, Peterson TC, Wieringa J (2003) Guidelines on climate metadata and homogenization. WMO-TD No.1186, WCDMP No.53. Geneva, Switzerland: World Meteorological Organization, 55
Alexandersson H, Moberg A (1997) Homogenization of Swedish temperature data. Part I: homogeneity test for linear trends. Int J Climatol 17:25–34CrossRefGoogle Scholar
Beijing Meteorological Bureau (2009) The history of meteorological stations in Beijing. 147 pp., China Meteorological Press, Beijing, China (in Chinese)
China Statistic Bureau (2002) Population data of China towns and city districts. 949 pp., China Statistic Press, Beijing, China (in Chinese)
Choi G, Collins D, Ren GY, Trewin B, Baldi M, Fukuda Y, Afzaal M, Pianmana T, Gomboluudev P, Huong PTT, Lias N, Kwon WT, Boo KO, Cha YM, Zhou YQ (2009) Changes in means and extreme events of temperature and precipitation in the Asia-Pacific Network region, 1955–2007. Int J Climatol 29:1960–1925Google Scholar
Chu ZY, Ren GY (2005) Chang in urban heat island magnitude and its effect on mean air temperature record in Beijing region. Acta Meteor Sin 63(4):534–540 (in Chinese)Google Scholar
Dai A, Trenberth KE, Karl TR (1999) Effects of clouds, soil moisture, precipitation, and water vapor on diurnal temperature range. J Climate 12:2451–2473CrossRefGoogle Scholar
Easterling DR, Peterson TC (1995a) A new method for detecting undocumented discontinuities in climatological time series. Int J Climatol 15:369–377CrossRefGoogle Scholar
Easterling DR, Peterson TC (1995b) The effect of artificial discontinuities on recent trends in minimum and maximum temperatures. Atmos Res 37:19–26CrossRefGoogle Scholar
Easterling DR, Evans JL, Groisman PY, Karl TR, Kunkel KE, Ambenje P (2000) Observed variability and trends in extreme climate events: a brief review. Bull Amer Meteor Soc 81:417–425CrossRefGoogle Scholar
Hansen J, Ruedy R, Sato M, Imhoff M, Lawrence W, Easterling D, Peterson T, Karl T (2001) A closer look at United States and global surface temperature change. J Geophys Res 106(D20):23947–23963CrossRefGoogle Scholar
Jones PD, Raper SCB, Bradley RS, Diaz HF, Kelly PM, Wigley TML (1986) Northern Hemisphere surface air temperature variations: 1851–1984. J Climate Appl Meteor 25(2):161–179CrossRefGoogle Scholar
Karl TR, Williams CN (1987) An approach to adjusting climatological time series for discontinuous inhomogeneities. J Climate Appl Meteor 26:1744–1763CrossRefGoogle Scholar
Karl TR, Jones PD, Knight RW, Kukla G, Plummer N (1993) A new perspective on recent global warming: asymmetric trends of daily maximum and minimum temperature. Bull Amer Meteor Soc 74(6):1007–1023CrossRefGoogle Scholar
Li QX, Liu XN, Zhang HZ, Peterson TC, Easterling DR (2004) Detecting and adjusting on temporal inhomogeneity in Chinese mean surface air temperature data. Adv Atmos Sci 21(2):260–268CrossRefGoogle Scholar
Li QX, Dong WJ (2009) Detection and adjustment of undocumented discontinuities in Chinese temperature series using a composite approach. Adv Atmos Sci 26(1):143–153CrossRefGoogle Scholar
Li Z, Yan ZW (2010) Application of multiple analysis of series for homogenization to Beijing daily temperature series 1960–2006. Adv Atmos Sci 27(4):777–787CrossRefGoogle Scholar
Liu XN (2000) The homogeneity test on mean annual wind speed over China. Quart J Appl Meteor 11(1):27–34 (in Chinese)Google Scholar
Menne MJ, Williams CN (2005) Detection of undocumented changepoints using multiple test statistics and composite reference series. J Climate 18:4271–4286CrossRefGoogle Scholar
Menne MJ, Williams CN (2009) Homogenization of temperature series via pairwise comparisons. J Climate 22:1700–1717CrossRefGoogle Scholar
Menne MJ, Williams CN, Palecki MA (2010) On the reliability of the U.S. surface temperature record. J Geophys Res 115, D11108CrossRefGoogle Scholar
Qian WH, Lin X (2004) Regional trends in recent temperature indices in China. Clim Res 27:119–134CrossRefGoogle Scholar
Quayle RG, Easterling DR, Karl TR, Hughes PY (1991) Effects of recent thermometer changes in the cooperative station network. Bull Amer Meteor Soc 72(11):1718–1723CrossRefGoogle Scholar
Ren GY, Zhang AY, Chu ZY, Zhou JX, Ren YY, Zhou YQ (2010) Principles and procedures for selecting reference surface air temperature stations in China. Meteorol Sci Technol 38(1):78–85 (in Chinese)Google Scholar
Ren GY, Xu MZ, Chu ZY, Guo J, Li QX, Liu XN, Wang Y (2005) Changes of surface air temperature in China during 1951–2004. Clim Environ Res 10(4):717–727 (in Chinese)Google Scholar
Ren GY, Zhou YQ, Chu ZY, Zhou JX, Zhang AY, Guo J, Liu XF (2008) Urbanization effects on observed surface air temperature trends in north China. J Climate 21:1333–1348CrossRefGoogle Scholar
Ren GY, Chu ZY, Chen ZH, Ren YY (2007) Implications of temporal change in urban heat island intensity observed at Beijing and Wuhan stations. Geophys Res Lett 34, L05711. doi:10.1029/2006GL027927 Google Scholar
Reeves J, Chen J, Wang XL, Lund R, Lu QQ (2007) A review and comparison of changepoint detection techniques for climate data. J Appl Meteor Climatol 46:900–915CrossRefGoogle Scholar
Song CH, Liu XN, Li JM (1995) A study of testing methods on inhomogeneity of temperature sequences. Quart J Appl Meteor 6(3):289–296 (in Chinese)Google Scholar
Vincent LA (1998) A technique for the identification of inhomogeneities Canadian temperature series. J Climate 11:1094–1104CrossRefGoogle Scholar
Vincent LA, Zhang X, Bonsal BR, Hogg WD (2002) Homogenization of daily temperatures over Canada. J Climate 15:1322–1334CrossRefGoogle Scholar
Wang XL, Wen QH, Wu Y (2007a) Penalized maximal t test for detecting undocumented mean change in climate data series. J Appl Meteor Climatol 46:916–931CrossRefGoogle Scholar
Wang Y, Liu XN, Ju XH (2007b) Differences between automatic and manual observation. J Appl Meteorol Sci 18(6):849–855 (in Chinese)Google Scholar
Winkler JA, Skaggs RH, Baker DG (1981) Effect of temperature adjustments on the Minneapolis–St. Paul urban heat island. J Appl Meteor 20:1295–1300CrossRefGoogle Scholar
Xie Z, Cao HX (1996) Asymmetric changes in maximum and minimum temperature in Beijing. Theor Appl Climatol 55:151–156CrossRefGoogle Scholar
Yan ZW, Yang C, Jones P (2001) Influence of inhomogeneity on the estimation of mean and extreme temperature trends in Beijing and Shanghai. Adv Atmos Sci 18(3):309–322CrossRefGoogle Scholar
Yan ZW, Jones PD (2008) Detecting inhomogeneity in daily climate series using wavelet analysis. Adv Atmos Sci 25(2):157–163CrossRefGoogle Scholar
Zhai PM, Eskridge RE (1996) Analyses of inhomogeneities in radiosonde temperature and humidity time series. Int J Climatol 9:884–894CrossRefGoogle Scholar
Zhai PM, Pan XH (2003) Trends in temperature extremes during 1951–1999 in China. Geophys Res Lett 30(17):1913. doi:10.1029/2003GL018004 CrossRefGoogle Scholar
Zhang L, Ren GY, Liu J, Zhou YQ, Ren YY (2011) Urban effect on trends of extreme temperature indices at Beijing Station. Chin J Geophys 54(5):1150–1159 (in Chinese)CrossRefGoogle Scholar
Zhou YQ, Ren GY (2009) The effect of urbanization on maximum, minimum temperatures and daily temperature range in north China. Plateau meteorology 28(5):1158–1166 (in Chinese)Google Scholar
Zhou YQ, Ren GY (2011) Change in extreme temperature events frequency over mainland China during 1961–2008. Clim Res 50:125–139CrossRefGoogle Scholar

Copyright information

Open Access This article is distributed under the terms of the Creative Commons Attribution License which permits any use, distribution, and reproduction in any medium, provided the original author(s) and the source are credited.

Authors and Affiliations

Lei Zhang
- 1
Guo-Yu Ren
- 2
Email author
Yu-Yu Ren
- 2
Ai-Ying Zhang
- 3
Zi-Ying Chu
- 3
Ya-Qing Zhou
- 4

1.College of Atmospheric ScienceNanjing University of Information Science & TechnologyNanjingChina
2.Laboratory for Climate StudiesNational Climate Center, CMABeijingChina
3.Beijing Meteorological Bureau, CMABeijingChina
4.Jinzhong Meteorological Bureau of Shanxi Province, CMAJinzhongChina

Effect of data homogenization on estimate of temperature trend: a case of Huairou station in Beijing Municipality

Abstract

1 Introduction

2 Data and methods

3 The results

3.1 Detection and adjustment of data inhomogeneities

3.2 Urban biases in adjusted and original data series

4 Discussion

5 Conclusions

Acknowledgments

Copyright information

Authors and Affiliations

Personalised recommendations

Cookies