Spectral analysis of unevenly spaced climatological time series

Abstract

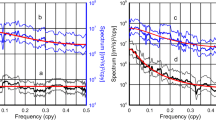
Spectral analysis is often based on the periodogram and on fitting a first-order autoregressive [AR(1)] process to data as climatological time series generally exhibit red noise spectra that can be well approximated by AR(1) models. When the periodogram exceeds some threshold at a frequency, the spectrum is said to differ from the AR(1) spectrum, and the frequency is generally taken as a member of the discrete spectrum. This traditional technique, however, must not be used without modifications for unevenly spaced data. Our purpose is to provide an AR(1) modeling tool that is more accurate than the TAUEST procedure commonly used for unevenly spaced paleoclimatical records. A periodogram based on an entire least square fit to unevenly spaced data is also introduced instead of the well-known Lomb–Scargle periodogram. The methodology is applied to two paleoclimatological records. Our results compared to those of a frequently used procedure (consisting of TAUEST and Lomb–Scargle periodogram) show some interesting differences.

Appendix

It is known (e.g., p. 248 in Priestley 1981) that a stationary stochastic process can be approximated with arbitrary accuracy with a finite set of random amplitude periodic components. Evidently, higher accuracy requires higher number of periodic components. A time series of length n can also be approximated with periodic components, and the highest accuracy of this approximation is achieved when the number of sinusoid and cosinusoid components is $J = \left\lceil {n/2} \right\rceil$, the feasible highest integer.

Preserving notations used in the previous sections the vector x should be approximated with 2J covariates corresponding to the J number of frequencies satisfying

$$ E\left[ {\underline x } \right] = \underline{\underline Z} \underline c $$

(9)

The least square procedure to estimate c results in the system of linear equations

$$ \left( {{{\underline{\underline Z} }^T}\underline{\underline Z} } \right)\underline c = {\underline{\underline Z}^T}\underline x, $$

(10)

and has the solution

$$ \underline {\widehat{c}} = {\left( {{{\underline{\underline Z} }^T}\underline{\underline Z} } \right)^{{ - 1}}}{\underline{\underline Z}^T}\underline x . $$

(11)

This is an unbiased estimate of c as

$$ E\left[ {\underline {\widehat{c}} } \right] = E\left[ {{{\left( {{{\underline{\underline Z} }^T}\underline{\underline Z} } \right)}^{{ - 1}}}{{\underline{\underline Z} }^T}\underline x } \right] = E\left[ {{{\left( {{{\underline{\underline Z} }^T}\underline{\underline Z} } \right)}^{{ - 1}}}\left( {{{\underline{\underline Z} }^T}\underline{\underline Z} } \right)\underline c } \right] = \underline c $$

(12)

The last equality in Eq. (12) utilizes Eq. (9). These equations hold for the periodogram and ELS periodogram. In the case of the L-S periodogram, only two covariates are used for the J number of frequencies separately. For the jth frequency, the solution of the least square problem is

$$ {\widehat{{\underline c }}_{{2,j}}} = {\left( {\underline{\underline Z}_{{2,j}}^T{{\underline{\underline Z} }_{{2,j}}}} \right)^{{ - 1}}}\underline{\underline Z}_{{2,j}}^T\underline x, j = 1, \ldots, J $$

where subscript 2 refers to the number of covariates, while j refers to the jth frequency. Let ${\underline {\widehat{c}}_2} = {\left( {\underline c_{{2,1}}^T, \ldots, \underline c_{{2,J}}^T} \right)^T}$ be the L-S estimate of c. Taking the expectation of ĉ ₂, similar operations used in Eq. (12) results in $E\left[ {{{\underline {\widehat{c}} }_2}} \right] \ne \underline c$ (except for evenly spaced data). Hence, the frequency-wise estimation (L-S periodogram) of the sinusoid and cosinusoid coefficients is biased in contrast to the case when the entire set (ELS periodogram) of the sinusoid and cosinusoid coefficients is estimated.

As it was mentioned earlier, every frequency λ _j is affected by frequencies not involved in the estimation procedure. Specifically, the right hand side of Eq. (10) is associated not solely with frequencies λ _j , but is influenced by the rest of frequencies. Therefore, although ĉ in Eq. (11) would be unbiased if the right-hand side of Eq. (10) were accurate, the ELS periodogram will be biased. The L-S periodogram, however, will introduce an additional bias as shown above.