1 Introduction

Short-time heavy rainfall is an important meteorological disaster, and the accurate forecast will help to prevent and reduce such disasters and ensure the safety of people’'s lives and property. However, due to the short forecast lead-time and strong rainfall intensity, the accuracy of short-time heavy precipitation forecast is still a huge challenge in operational forecast. At present, the forecasts of short-time heavy precipitation are mainly made by meso- and small-scale numerical models, whose accuracy mainly depends on improving the accuracy of the initial field. The data assimilation is one of the methods to effectively improve the initial conditions in the numerical weather prediction (NWP) model. And the Doppler weather radar is one of the important observation platforms for meso- and small-scale weather systems. Therefore, the effective assimilation of Doppler weather radar observations is of great significance for improving the accuracy of short-time heavy rainfall forecasts.

In the past 30 years, great progresses have been made in assimilating the remote sensing observations. meanwhile experts and scholars have developed a variety of advanced data assimilation methods, mainly including variational data assimilation (Parrish and Derber 1992; Courtier et al. 1994; Gauthier et al. 1999; Lorenc and Coauthors 2000; Huang et al. 2009; Meng Zhang et al. 2011; Xu et al. 2013, 2019a, b; Honda et al. 2005; Zupanski et al. 2005; Huang et al.2009; Shen et al. 2019a), ensemble Kalman filter (En KF) data assimilation and hybrid data assimilation (Wang et al. 2008a, b; Wang 2011; Xu et al. 2015a, b, 2016a, Zhang and Zhang 2012; Li et al. 2012; Shen and Min 2015, 2016; Shen et al. 2017a, b, 2019b).

The variational data assimilation method includes three-dimensional variational (3DVAR) and four-dimensional variational (4DVAR) methods, which are widely used in the simulation of convective storms and the improvement of precipitation prediction. For example, Sun and Crook (1997) applied the 3DVAR method to the assimilation of radial velocity and reflectivity from the Doppler radar in a cloud model and its adjoint model; thus, the structural characteristics of wind field, thermal field and micro-physical field in convective storms can be retrieved. Kuo et al. (2005) used the 3DVAR method to assimilate the radial velocity and reflectivity of the Doppler radar in the MM5 model, improving the quantitative precipitation forecast. Gao et al. (2004,2012) used the 3DVAR method to assimilate the reflectivity of Doppler radar and achieved good results in simulating super storms. Montmerle and Faccani (2009) also used the 3DVAR assimilation technique to assimilate radial velocity from Doppler radars of the French ARAMIS (Application Radar la Météorologie Infra Synoptique) network. They found a positive impact of radar wind data on the analysis and forecast of precipitation. Soichirow et al. (2009) improved the quantitative precipitation prediction by assimilating the Doppler radar data through the cloud analysis in the 3DVAR assimilation system of WRF. Wang et al. (2013a) indirectly assimilated the radar reflectivity using 3DVAR method in WRF. It was concluded that the assimilation of reflectivity increases the humidity, rainwater, and convective available potential energy (CAPE) in the convective region. At the same time, they also developed a 4DVAR assimilation scheme for assimilating the radar reflectivity and radial velocity in WRF (Wang et al. 2013b). Sun and Wang (2013) used 4DVAR method to assimilate the radial velocity and reflectivity of the Doppler radar for more accurately analyzing the low-level cold pools, leading-edge convergence and mid-level latent heat of squall line systems.

In recent years, the assimilation method of EnKF has been also widely used. The use of EnKF to assimilate radar observation data and radial velocities can improve the forecast of convections and the simulation of severe storms, respectively (Zhang et al. 2004; Tong and Xue 2005; Dowell et al. 2011; Tanamachi et al. 2013;). Assimilating the Doppler radial velocity through EnKF can improve the forecast accuracy of typhoon intensity and moving-track (Zhang et al. 2009). In the National Severe Storms Laboratory (NSSL) Collaborative Model for Multi-scale Atmospheric Simulation (NCOMMAS), the EnKF method is used to assimilate the radar data. The third method is the hybrid data assimilation method. Many scholars have confirmed that using the variational and ensemble methods to assimilate the Doppler radar data can improve the initial field of the model (Wang et al. 2013a, b, c; Gao and Stensrud 2014; Gao et al. 2016; Wang and Wang 2017).

Many studies have demonstrated that temperature and humidity in the initial field of the model play an important role in the analysis and prediction of the storm scale (Ge et al. 2013). However, Doppler weather radars cannot directly observe the model variables, because the radar radial velocity only represents partial information about the wind field. Besides, there are no direct observations of water vapor mass mixing ratio and the content of hydrometeors from radar data. Thereby, it is necessary to assimilate radar reflectivity data using the corresponding relation between water vapor and the reflectivity factor, and this method is more and more used. For example, the 3DVAR method assimilates the retrieved one-dimensional relative humidity profile (Caumont et al. 2010; Wattrelot et al. 2014); 3DVAR method assimilates the rainwater and water vapor retrieved from radar reflectivity factor data (Wang et al. 2013a, b); during the cloud analysis process, the relative humidity, water vapor mixing ratio and temperature of the model are adjusted based on radar, satellite and ground observation data (Xue et al. 2003; Zhang 1999; Brewster 2015; Hu et al. 2006; Schenkman et al. 2011). According to the vertical integrated liquid (VIL) water content of radar, 3DVAR assimilation is used to retrieve the water vapor (Lai et al. 2019). In this study, the statistical relationship between the radar reflectivity factor and relative humidity is used to retrieve water vapor content in the initial field. Combined with the 3DVAR of Weather Research and Forecasting model assimilation system (hereinafter referred to as WRF-3DVAR), the radar data assimilation experiments with retrieved water vapor and hydrometer in the initial field are carried out. The effect of assimilating the retrieved water vapor and hydrometer in the initial field on the simulation of short-time heavy rainfall is studied.

2 Methods

2.1 WRF-3DVAR

WRF-3DVAR is used to solve a quadratic functional minimization problem (Lorenc) for the deviation between the analysis field and observation field and that between the analysis field and background field. The functional is defined as follows.

$$J(x) = \frac{1}{2}\left[ {(x - x_{b} )^{T} B^{ - 1} (x - x_{b} ) + (H(x) - y_{0} )^{T} O^{ - 1} (H(x) - y_{0} )} \right],$$
(1)

where \(x\) represents the analysis field; \({x}_{b}\) represents the background field; \({y}_{0}\) represents the observation field; \(B\) is the covariance matrix of background errors; \(O\) is the covariance matrix of observation errors; \(\mathrm{y}=H(x)\) is observation equivalence of analysis variables; \(H\) is the observation operator, which may be a simple interpolation operator or a complex one. For the radial velocity data from radar observations, the observation operators include the spatial interpolation operators and the physical conversion process. The primary goal of the 3DVAR system is to solve the minimum value of the above objective function through an iterative method, so as to obtain an estimate value close to the true state of the atmosphere as possible. In the calculation process of variational minimization, the inverse matrixes of the observation-error covariance and the background-error covariance are used. It is generally considered that the observations are uncorrelated, and \(O\) is a diagonal matrix or a near-diagonal matrix, whose inverse matrix is not difficult to find.

2.2 2.2 Observation operator for assimilating the radar radial velocity

The radar radial velocity is not a direct observation variable in the model. An observation operator needs to be established to link the horizontal and vertical velocity in the model with the radial wind velocity from the radar. The observation operator for the Doppler radar radial velocity in WRF-3DVAR is calculated as follows (Sun et al. 1997; Sun et al. 1998).

$$V_{r} = u\frac{{x - x_{i} }}{{r_{i} }} + v\frac{{y - y_{i} }}{{r_{i} }} + \left( {w - v_{T} } \right)\frac{{z - z_{i} }}{{r_{i} }},$$
(2)

where \(u\), \(v\) and \(w\) are the model wind components; x, y and z represent the location of radar station; \({x}_{i}\), \({y}_{i}\) and \({z}_{i}\) denote the location of radar observation; \({r}_{i}\) is the distance between the observation site and the location of radar; \({v}_{T}\) (m s−1) is the terminal velocity, and \({v}_{T}\) of precipitation particles must be considered during the radar volume scanning at each angle of elevation. The calculation of \({v}_{T}\) takes the following form.

$$v_{T} = 5.40\upsilon q_{r\alpha }^{0.125}$$
(3)

where \(q_{r\alpha },\) is the mixing ratio of rainwater, and υ is the correction factor, which is defined as follows.

$$\upsilon = \left( {\frac{{p_{0} }}{{\overline{p}}}} \right)^{0.4} ,$$
(4)

where \(\overline{p},\) is the background pressure, and \(p_{0},\) is the surface pressure (1000 hPa). To make it possible to assimilate the radar radial velocity in the WRF-3DVAR system, the horizontal wind can be decomposed into a potential function and a stream function.

2.3 Forward operator for assimilating the radar reflectivity

The forward operator of radar reflectivity factor in WRF-3DVAR is obtained by calculating the mixing ratios of three hydrometeors, including rain (\(q_{ra}\)), snow (\(q_{sn}\)) and graupel (\(q_{gr}\)) (Lin et al. 1983; Gilmore et al. 2004; Dowell et al. 2011). And the equivalent radar reflectivity (\(Z_{e} )\) is the reflectivity sum of these three hydrometeors. The formula is as follows,

$$Z_{e} = Z(q_{ra} ) + Z(q_{sn} ) + Z(q_{gr} ).$$
(5)

Since the reflectivity factor in Eq. (5) is assumed to be a function of the three hydrometeors' mixing ratios, the assimilation of the reflectivity may make the mixing ratios of hydrometeors more uncertain (e.g., the rainwater mixing ratio may appear at the upper level in the initial field of model). To reduce the uncertainty, the forward operators based on the temperature in the background field are applied (Gao and Stensrud 2012) with the following formula.

$${Z}_{e}=\left\{\begin{array}{l} {T}_{b}>5^\circ C\\ {Z(q}_{sn})+ {Z(q}_{gr}) {T}_{b}<-5^\circ C\\ \alpha {Z(q}_{ra})+\left(1-\alpha \right)[{Z(q}_{sn})+ {Z(q}_{gr})] -5^\circ C< {T}_{b}<5^\circ C\end{array}\right.$$
(6)

where \(T_{b}\) is the background temperature, while it varies in the range from − 5 °C to 5 °C, α varies linearly between 0 and 1. Gao and Stensrud (2012) found that while assimilating the radar reflectivity, the correction of Eq. (6) is more accurate and the hydrometeor profile can be effectively obtained.

2.4 Water vapor retrieval

2.4.1 Retrieval method

In previous stues, for adjusting the water vapor, a common method is to set the background relative humidity (RH) as a fixed threshold (RH = 95, RH = 100, etc.) in the model, and to calculate the water vapor with qv = qs × RH. Among them, qs is the saturation specific humidity of the atmosphere, which is calculated with the functional relationship between the air pressure and temperature at the model levels, while qv is the water vapor (g kg−1). However, actual meteorological observations show that when precipitation occurs, the relative humidity is not necessarily 100%, which can change from 80 to 100%. Only in the heavy fog, the air relative humidity near the ground can reach saturation. Therefore, based on the statistical relationship between the radar reflectivity factor (Z;dBZ) and the relative humidity (RH; %) in East China, the relative humidity in the model is calculated and the water vapor is adjusted, as shown in Table 1. To distinguish the effective precipitation echo from the clear-air echo, this study selects the echo exceeding 25 dBZ as the effective precipitation echo, and the clear-air echo is considered below 20 dBZ. For the region with reflectivity factor exceeding 25  dBZ, the relative humidity is calculated with RH = f (Z) and f (Z) is given in Table 1. For the region with reflectivity below 20 dBZ, the relative humidity is calculated with RH = min (RHb, 50) (RHb is the relative humidity of the background field). While adjusting the water vapor, Eq. (5) and Eq. (6) need to be used to retrieve the hydrometeor content. To distinguish the hydrometeor content in the precipitation area and the clear-air area, we set that for the observation stations with reflectivity exceeding 25  dBZ, the retrieved hydrometeor in the model initial field is obtained according to Eq. (5) and Eq. (6). For the observation stations with reflectivity lower than 20 dBZ, the hydrometeor content(qhydrometer) is determined by qhydrometer = min (qhydrometer, qhydrometer_b). qhydrometer is the retrieved hydrometeor content according to Eq. (5) and Eq. (6), and qhydrometer_b is the hydrometeor content in the model background field.

Table 1 Statistical relationship between Z (dBZ) and RH (%)
Full size table

2.4.2 Evaluation of retrieval the scheme

The vertical water vapor profile at the point (115.57oE, 32.67oN) is retrieved at 1200 UTC on July 26th, 2018. In the Fig. 1, comparing with the vertical water vapor profile of sounding observations at neighboring point, it can be seen that the water vapor adjustment area in our current study is mainly about 850–500 hPa.

Fig. 1
figure 1

The vertical water vapor profile at 1200 UTC on July 26th, 2018 at the point (115.57oE,32.67oN)

Full size image

The water vapor content from 850 to 500 hPa in the retrieval experiment is larger than the observation, the average error is 1.41 g/kg and the standard deviation of 5.45 g/kg. Then the water vapor content of the no retrieval experiment is smaller than the observation, The average error is −2.13 g/kg, and the standard deviation is 5.52 g/kg from 850 to 500 hPa.

3 Case selection, data and numerical experiments

3.1 The rainstorm on July 26th, 2018 and radar data processing

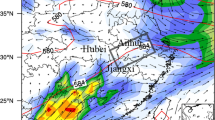
A rainstorm in the warm sector occurred in Anhui on July 26th, 2018. The torrential rainfall mainly occurred during 1200 UTC–1500 UTC on July 26th with the hourly accumulated precipitation of nearly 100 mm, causing urban water accumulation and traffic congestion. From the analysis of the weather situation chart (Fig. 2), the Anhui area was controlled by the subtropical high at 1200 UTC on July 26th, and ordinarily, precipitation is not easy to occur. Therefore, neither the global-scale numerical forecast nor the regional mesoscale numerical forecast could predict this precipitation process.

Fig. 2
figure 2

500-hPa geopotential height field at 1200 UTC on July 26th, 2018

Full size image

In this study, the radar observation data are from the Doppler weather radars in Hefei of Anhui Province and Nanjing of Jiangsu Province. This is a new-generation S-band Doppler weather radar independently developed by China, and its performance is close to the WSR-88D radar in the U.S. Considering that the Doppler radar network is still constructing in China, there is no unified software or platform to process the radar-based observation data. Therefore, it is necessary to carry out the quality control before inputting the radar observation data to numerical models. The quality control mainly includes the following steps. (1) Since the gradient of the ground clutter echo intensity (GdBZ) is strong in the vertical direction, it can be used to remove the ground clutter. GdBZ= ZLOW–ZUP (ZLOW is the radar reflectivity at a certain elevation and position, and ZUP is the reflectivity at this position corresponding to the upper elevation). The threshold is determined as 30dBZ, and if GdBZ > 30dBZ, the observations are eliminated. (2) The points with the isolated reflectivity factor or the radial velocity are removed: when the number of valid observations in the range of 3° × 3 km around this point is counted, if the number is less than 4, the observation at this point is eliminated. (3) The average value and the standard deviation of each observation in the range of 3° × 3 km around this point on the same cone are calculated. When the standard deviation is larger than 20 (m s−1 or dBZ), the observation data at this point are considered as discontinuous and then eliminated. (4) Observations of radar radial wind less than 2 m s−1 are eliminated. (5) Observations of the reflectivity factor less than 25 dBZ are eliminated.

3.2 Experimental design

The experiments use the WRFV3.8, which is a compressible non-hydrostatic mesoscale model, with 50 hPa as the top layer. The model adopts double-domain nesting, with the grids of 193 × 193 in the outer domain and the grids of 289 × 289 in the inner domain. The horizontal resolution is 9 km and 3 km, respectively. The number of vertical layers is 35, and the integration time-step is 45 s. The range of the simulation area is shown in Fig. 3. Since the inner domain has been refined to the cloud scale, the cumulus convection parameterization scheme is not selected. The main physical parameterization schemes include Mellor–Yamada–Janjic (MYJ) boundary layer scheme, the WRF Single-Moment 6-class (WSM6) microphysics scheme, Rapid Radiative Transfer Model (RRTM) long-wave radiation scheme and Dudhia short-wave radiation scheme. The initial field and lateral boundary conditions in the model are from the reanalysis data with a resolution of 0.25° × 0.25° provided by the European Centre for Medium-Range Weather Forecasts (ECWMF). The covariance of the background error is calculated by the National Meteorological Center (NMC) method. The experimental design and flowchart are shown in Table 2; Figs. 4, 5, respectively.

Fig. 3
figure 3

Simulation domain and radar locations

Full size image
Table 2 Experimental design
Full size table
Fig. 4
figure 4

Flow chart of qv retrieval

Full size image
Fig. 5
figure 5

Flow chart of cycling assimilation

Full size image

The five experiments used for the comparative research in this study are CTRL experiment, RV_RF_S experiment, RV_RF_QV_S experiment, RV_RF_Cycle experiment and RV_RF_QV_Cycle experiment. The CTRL experiment is a benchmark experiment without assimilating any observation data. In the RV_RF_S experiment, the Doppler radar radial wind observation data are directly assimilated and the radar reflectivity factor observation data is single indirectly assimilated through the single WRF-3DVAR. Configuration of the RV_RF_QV_S experiment is similar to that of the RV_RF_S experiment. The only difference is that at the initial time of the analysis, before assimilating the radar radial velocity and reflectivity factors, the QV was adjusted based on the observed radar reflectivity factors. CTRL experiment, RV_RF_S experiment, RV_RF_QV_S experiment are cold start from 12:00 to 15:00. The RV_RF_Cycle experiment and RV_RF_QV_Cycle experiment are used to discuss the effect of water vapor adjustment for the assimilation and forecasts after the hot start of the model, so as to evaluate the influence of the water vapor adjustment scheme on the simulation results in the assimilation cycling of radar data. The RV_RF_Cycle experiment takes the time of 1200 UTC on July 26th, 2018 as the initial analysis time, and the observation data (radar radial velocity and reflectance factor) is assimilated every hour until 1400 UTC on July 26, 2018. The analysis field at the last time is taken as the background field for the 3-h deterministic prediction. The RV_RF_QV_Cycle experiment adds water vapor adjustment based on the RV_RF_Cycle experiment, and then assimilates the observation data of radar radial velocity and reflectivity factor every hour, so that the water vapor in the initial field of model corresponds to the observed reflectivity factor as much as possible.

The RV + RF + QV assimilation cycling experiment designed here is to verify the effect of water vapor adjustment cycling and assimilating radar radial velocity and radar reflectivity factor for the rainfall simulation. Figure 5 shows a flowchart of this scheme.

4 Results

As can be seen from the above sections, a single cold start assimilation and assimilation cycling are designed in this study to evaluate the influence of water vapor adjustment in the initial field and the different assimilation methods of radar reflectivity factors on the analysis and forecast of this rainstorm. Chapters are arranged as follows. In Sects. 4.1.1–4.1.4, the effects of the single assimilation at 1200 UTC on July 26th, 2018 in the CTRL, RV_RF_S and RV_RF_QV_S experiments are analyzed. And in Sects. 4.2.1–4.2.4, the effects of hourly assimilation cycling in the RV_RF_Cycle and RV_RF_QV_Cycle experiments are analyzed.

4.1 Analysis of assimilation experiment with single cold start

4.1.1 Water vapor content in the initial field

The humidity information in the initial field of the numerical model often plays a key role in the accurate prediction of the rainstorm system. In this section, we analyze the effects of the single assimilation in the cold start model after the water vapor adjustment. Figure 6 shows the distribution of water vapor increments in the 11th level of the model on July 26th, 2018. It can be found that in the RV_RF_QV_S experiment after adjusting the water vapor based on the radar reflectivity factor, the water vapor content in the key area of convection increases significantly, and the area of increase is roughly consistent with the actually observed convection area, with a maximum value of 11.8 g kg−1. While the water vapor increment in the RV_RF_S experiment is about 7.8 g kg−1, which has a phase deviation from the actual observed convection area.

Fig. 6
figure 6

Water vapor increment on the 11th level at 1200 UTC on July 26th, 2018. a Maximum reflectivity observed at 1200 UTC, (b) RV_RF_S-CTRL and (c) RV_RF_QV_S-CTRL

Full size image

4.1.2 Simulation based on the single assimilation of radar reflectivity

To some extent, the echo intensity reflects the distribution of water vapor in the atmosphere that has not landed on the ground. Therefore, the accuracy of echo intensity analysis plays a very important role in the forecast of short-time heavy precipitation. Figure 7 shows the hourly composite reflectivity factor from the analysis and prediction of each experiment. First, from Fig. 7b1 to b4, it can be found that the CNTL experiment could hardly predict the heavy precipitation process. Compared with the CNTL experiment, the RV_RF_S experiment successfully analyzed some heavy rainbands, but compared with the observation, the position of them still showed a large deviation. Then, by comparing Fig. 7a1 and d1, it can be seen that the composite reflectivity factor analyzed by the RV_RF_QV_S experiment after the water vapor adjustment is substantially the same as the observed reflectivity factor. For the forecast in the following 3 h, the composite reflectivity factor analyzed by the RV_RF_QV_S experiment is consistent with the observation, but the magnitude is larger. Third, from the comparison between Fig. 7a2 and d2, we can see that the positions of simulated convection echoes at A, B, C, and D in RV_RF_QV_S experiment are consistent with the observations, while the simulated intensity is stronger than the observations. But the new-generated isolated echoes at E and F are not successfully predicted, and false echoes are predicted at G. Fourth, by comparing Fig. 7a3 and d3, the analysis region of echoes greater than 25 dBZ is wider than observed, the strong echo at A is further east and stronger, and the strong echo at B is not generated. Finally, from the comparison between Fig. 7a4 and d4, it can be easily concluded that for the region of echoes greater than 25 dBZ, the range of maximum reflectivity factor analyzed by the RV_RF_QV_S experiment is larger than that observed, the strong echo at A is further north, and the strong echo at B is not generated.

Fig. 7
figure 7

Observations and forecasts of hourly maximum reflectivity. (1, 2, 3 and 4 denote the reflectivity at 1200 UTC, 1300 UTC, 1400 UTC and 1500 UTC, respectively. a, b, c and d denote the observation, CNTL experiment, RV_RF_S experiment and RV_RF_QV_S, respectively)

Full size image

4.1.3 Forecast performance of single assimilation for precipitation

The previous section has analyzed the water vapor field and composite reflectivity factors. In this section, we will further evaluate the impact of water vapor adjustment and radar data assimilation on the analysis and prediction of this precipitation process. Seen from Fig. 8a1–c3, the CNTL and RV_RF_S experiments did not simulate the heavy precipitation process successfully; thus, they may have no ability to predict heavy precipitation. However, by comparing Fig. 8a1, d1, we can see that for the accumulated precipitation forecast at 12:00–13:00 on July 26th, 2018 from the RV_RF_QV_S experiment, the predicted regions of heavy rainfall are basically consistent with the actual observation precipitation for the three convective systems, but the predicted intensity is significantly stronger; for the accumulated precipitation forecast at 13:00–14:00 on July 26th, 2018, Fig. 8a2, d2 show that the heavy rainfall region coincides with the actual observation, but the predicted intensity is significantly stronger; and for the accumulated precipitation forecast at 13:00–14:00 on July 26th, 2018, seen from Fig. 8a3, d3, the north–south rainband predicted by the RV_RF_QV_S experiment is slightly further east than the observation, and the intensity is equivalent. However, the forecast of east–west rainband is of low accuracy.

Fig. 8
figure 8

Observed precipitation and simulated hourly rainfall in each experiment. (1, 2, and 3 denote the reflectivity at 1300 UTC, 1400 UTC, and 1500 UTC, respectively. a, b, c and d denote observation, CNTL experiment, RV_RF_S experiment and RV_RF_QV_S, respectively)

Full size image

4.1.4 Objective verification of precipitation forecast

4.1.4.1 a Verification method

In this section, we use the fraction skill score (FSS), threat score (TS) and bias score (BIAS) to quantitatively verify the simulation results of the three groups of experiments (Roberts and Lean 2008). The basic principle is to calculate the probability value of the central grid point of the window region in the study area, that is, the ratio of grid points exceeding a certain threshold to the total grid points in the window region, thereby transforming the prediction field and the observation field into a probability distribution field of grids. The FSS is then defined as follows.

$$F = 1 - \frac{{\frac{1}{N}\mathop \sum \nolimits_{i - 1}^{N} \left( {p_{fi} - p_{oi} } \right)^{2} }}{{\frac{1}{N}[\mathop \sum \nolimits_{i - 1}^{N} p_{fi}^{2} + \mathop \sum \nolimits_{i - 1}^{N} p_{oi}^{2} ]}},$$
(7)

where F is the value of FSS, \(P_{fi}\) and \(P_{oi}\) are, respectively, the forecast probability and observation probability in the window region, and N is the number of neighborhood windows in the study area. The FSS value is between 0 and 1. If FSS is 1, it means that forecast is perfect. If FSS is 0, it means a complete mismatch. When the width of the neighborhood window increases from 1 (the resolution of model) to (2n–1) (n is the number of grid points along the long axis of the window region), the FSS tends to be 1. Under a certain threshold, the variation curve of the FSS with the window size can be obtained by taking the window size as the X-axis and FSS as the Y-axis. By comparing different forecasting systems, the closer the FSS variation curve is to the upper left corner, the closer it is to one1 in a smaller window region, that is, the better the forecast performance of this system will be.

$${\text{TS } = \text{ }}\frac{{{\text{NA}}}}{{\text{NA + NB + NC}}},$$
(8)
$${\text{BIAS } = \text{ }}\frac{{\text{NA } + \text{ NB}}}{{\text{NA } + \text{ NC}}} ,$$
(9)

where TS is the value of threat score, BIAS is the value of bias score. NA represents the number of stations (times) with correct forecast, NB represents the number of stronger stations (times), and NC represents the number of missing stations (times). The larger the TS value, the better the forecast effect.

4.1.4.2 b Evaluation and analysis of precipitation forecast results

In this study, the thresholds selected for the hourly precipitation FSS are 0.1 mm, 5 mm, 10 mm and 25 mm, respectively. Seen from Fig. 9, the FSS of the RV_RF_QV_S experiment is significantly better than those of the CNTL and RV_RF_S experiment, and the precipitation FSS in each period is significantly improved. The results mean that after adjusting the water vapor, the precipitation FSS of the radar data assimilation is better than that without adjusting the water vapor in each period.

Fig. 9
figure 9

Precipitation FSS of a single assimilation at different times under different thresholds. (a1–a4, b1–b4, and c1–c4 show the FSS at 1200–1300 UTC, 1300–1400 UTC, and 1400–1500 UTC, respectively, while 1, 2, 3 and 4 correspond to the precipitation thresholds of 0.1 mm, 5 mm, 10 mm and 25 mm, respectively. Red line represents the RV_RF_QV_S experiment, blue line represents the RV_RF_S experiment, and green line represents the CNTL experiment)

Full size image

Seen from Fig. 10, by comparing the TS and BIAS scores from the RV_RF_QV_S experiment, RV_RF_S experiment, and CTRL experiment, the TS scores of the RV_RF_QV_S experiment are significantly improved. It should be pointed out the BIAS of the RV_RF_QV_S experiment is a bit higher when the 6-h precipitation is more than 30 mm. The possible reason is that the retrieval water vapor content between 850 and 500 hPa is larger than the observation, which is shown in Fig. 1. In the meanwhile, the RV_RF_S experiment and the CTRL experiment do not have the capacity to predict the heavy precipitation.

Fig. 10
figure 10

6-h Precipitation forecast skills of a single assimilation. a The TS and (b) the BIAS for the accumulated precipitation at 1200–1800UTC

Full size image

4.2 Analysis of cycling assimilation

4.2.1 Reflectivity in the analysis field after cycling assimilation

From Fig. 11a1–a3, by comparing the different experiments at 1300 UTC, the reflectivity in the analysis field of the RV_RF_QV_Cycle experiment is closer to the observation, and it makes a better simulation of the new-born convection echo. In addition, by comparing (Fig. 11b1–b3), we find the same result at 1400 UTC as at 1300 UTC.

Fig. 11
figure 11

The Maximum reflectivity in observation and analysis fields. (1, 2 and 3 denote observation, RV_RF_Cycle, and RV_RF_QV_Cycle, respectively. a and b denote 1300 UTC and 1400 UTC, respectively)

Full size image

4.2.2 Reflectivity in the forecast field after cycling assimilation

The impact of cycling assimilation on the reflectivity forecast is analyzed. Figures 12, 13 show the forecast reflectivity at different leading times by the RV_RF_QV_Cycle experiment and RV_RF_ Cycle experiment, as well as their comparisons with observations. The conclusions from Fig. 7 are similar. It can be concluded that during this precipitation process, the RV_RF_Cycle experiment has a weaker ability to predict the reflectivity. The maximum reflectivity at the leading time of 10 min forecasted by the RV_RF_QV_Cycle experiment is close to the observation, but with the increase of leading time, its forecasting ability also obviously weakens. After 30 min, the forecast echo shows a lag compared with the observation. At the same time, the forecast echoes in Figs. 12 and 13 are stronger than the observations.

Fig. 12
figure 12

The maximum reflectivity every 10 min initialized at 1300 UTC from cycling assimilation experiments. (1, 2 and 3 denote observation, RV_RF_Cycle and RV_RF_QV_Cycle, respectively. a, b and c Denote 1310 UTC, 1320 UTC and 1330 UTC, respectively)

Full size image
Fig. 13
figure 13

The maximum reflectivity every 10 min initialized at 1400 UTC from assimilation cycling experiments. (1, 2 and 3 denote observation, RV_RF_Cycle and RV_RF_QV_Cycle, respectively. a, b and c Denote 1410 UTC, 1420 UTC and 1430 UTC, respectively)

Full size image

4.2.3 Precipitation forecast after cycling assimilation

In the previous section, it has been found that the simulation result of water vapor retrieval in a single assimilation can maintain good for about 3 h. Next, the effects of rapid cycling assimilation for the model prediction will be discussed.

By comparing and analyzing the accumulated precipitation during 1300–1400 UTC in Fig. 14a (observation), 14b (RV_RF_Cycle experiment) and 14c (RV_RF_QV_Cycle experiment), it is found that the RV_RF_Cycle experiment does not successfully predict the precipitation at 1300–1400 UTC. However, the area of heavy precipitation forecasted by the RV_RF_QV_Cycle experiment is closer to the observation, especially its forecast for the isolated precipitation area is better, while the forecast magnitude of the heavy rainfall is stronger than the observation.

Fig. 14
figure 14

a Observation and forecast of 1-h accumulated precipitation (the observation precipitation during 1300–1400 UTC; b the forecast rainfall during 1300–1400 UTC initialized at 1300 UTC by RV_RF_Cycle experiment; c the forecast rainfall during 1300–1400 UTC initialized at 1300 UTC by RV_RF_QV_Cycle experiment; d the observation precipitation precipitation during 1300–1400 UTC; e the forecast rainfall during 1400–1500 UTC initialized at 1400 UTC by RV_RF_Cycle experiment; f the forecast rainfall during 1400–1500 UTC initialized at 1400 UTC by RV_RF_QV_Cycle experiment)

Full size image

By comparing and analyzing the accumulated precipitation during 1400–1500 UTC in Fig. 14d (observation),14e (RV_RF_Cycle experiment) and 14f (RV_RF_QV_Cycle experiment), it can be found that the simulation results of the RV_RF_Cycle experiment are similar to the observations at the beginning, but the intensity and rainfall region are smaller. The RV_RF_QV_Cycle experiment is significantly better than the RV_RF_Cycle experiment for predicting the rainfall region and is closer to the observation, but the forecast rainfall intensity is still stronger than the observation.

4.2.4 Evaluation and analysis of precipitation forecast results after cycling assimilation

The precipitation thresholds are 0.1 mm, 5 mm, 10 mm, and 25 mm, respectively, and the FSS is performed on the hourly precipitation. In Fig. 15, there is not much difference in the FSS between RV_RF_QV_Cycle experiment and RV_RF_Cycle experiment when the precipitation is no more than 0.1 mm. When the precipitation is greater than 5 mm, the FSS of RV_RF_QV_Cycle experiment is significantly better than that of the RV_RF_Cycle experiment, especially in a small-scale area. This shows that cycling adjustment of water vapor and radar data assimilation can effectively improve the result of hourly precipitation prediction Fig. 16.

Fig. 15
figure 15

FSSs of precipitation with different thresholds at different times after cycling assimilation. (1, 2, 3 and 4 denote precipitation thresholds of 0.1 mm, 5 mm, 10 mm and 25 mm, a denotes the forecast precipitation in 1300–1400 UTC initialized at 13:00 UTC, b denotes the forecast precipitation in 1400–1500 initialized at 1300 UTC, and c denotes the forecast precipitation in 1400–1500 initialized at 1400 UTC. The red line denotes the RV_RF_QV_Cycle experiment, and the blue line denotes the RV_RF_Cycle experiment)

Full size image
Fig. 16
figure 16

TSs and BIAS of precipitation with different thresholds at different times after cycling assimilation for the accumulated precipitation (a1) from 1300 to 1800UTC initialized at 1300 UTC, a2) from 1400 to 1900UTC initialized at 1400 UTC. b1–b2 same as a1-a2, but for BIAS

Full size image

Figure 16 shows that the TS and BIAS scores from the the RV_RF_QV_Cycle experiment and RV_RF_Cycle experiment. It seems that the TS scores at different forecast leading times from the RV_RF_QV_Cycle experiment are significantly improved. Also note that the BIAS of the RV_RF_QV_Cycle experiment is less than RV_RF_Cycle experiment. Similar to the results from Song et al. 2019, Rodrigo et al. 2018, and Maiello et al. 2014.

5 Summary and conclusion

In this study, the radar radial velocity, reflectivity data are assimilated in the WRF-3DVAR assimilation system with retrieved water vapor by reflectivity data in the initial field. A convection process on July 26th, 2018 is selected for numerical simulation experiments. And the conclusions are as follows.

(1) The experiment results show that the assimilation of radar data after adjusting the water vapor field can significantly increase the water vapor content at the model level in the analysis field, and it has a good corresponding relationship with the convection area, which can better simulate the distribution of rainbands. Therefore, the prediction of short-time heavy rainfall can be improved.

(2) During this convection process, when the radar data are assimilated after adjusting the water vapor, the simulated reflectivity reflects the meso-scale characteristics more significantly, especially the new-born echo can be simulated clearly. The forecast of short-time heavy rainfall region is closer to the observation, and the forecast result can maintain good for about 3 h.

(3) After the assimilation cycling of retrieved water vapor data, the analysis reflectivity field is closer to the observation than the forecast reflectivity field, and false echoes and false precipitation can be partially decreased. After the assimilation cycling, the forecast of the 1-h rainfall region is closer to the observation. However, the forecast precipitation intensity in the strong echo area is stronger than that of the observation.

In this study, it can be found the BIAS is a bit higher. The reasons may be that key fields such as temperature and humidity are harder to modify only using radar data assimilation and this retrieval algorithm only includes the statistical relationship between radar reflectivity and relative humidity at different temperatures. In fact, the reflectivity is the sum of the reflectivity of rain, snow water and graupel. Therefore, it is not perfect to retrieve relative humidity only by Doppler radar reflectivity. For example, the reflectivity is larger in the hail in summer convection, but the corresponding precipitation is not stronger any time. Thus, the water vapor content QV of WRF model is adjusted higher in the strong echo area, and the precipitation predicted by the model is stronger, and the false alarm (NB) is higher, which makes the bias score higher.

Meanwhile, only one case was used for the assimilation of retrieved water vapor. Due to different factors such as different seasons, different elements affected by different weather processes and the difference of the initial value error, more cases are needed to verify the reasonability of the water vapor retrieval. Meanwhile, in the strong echo region, the intensity of the simulated reflectivity and the short-time heavy rainfall are stronger.

Therefore, in the future, using the dual polarization radar data, the relationship between radar reflectivity (Z), differential reflectivity ZDR and relative humidity at different phase states will be calculated, the local heavy rainfall forecast will be improved. The variation of vertical velocity and temperature in the strong echo region must be considered in the initial filed. Further experiments with more cases over extended periods and assimilating more observations (as well as other remote sensing observations such as radiance by satellite; e.g., Xu et al. 2014, 2015a, b, 2016a) are needed to verify the generality of the results.