1 Introduction

Land-surface processes affect warm-season precipitating systems through heat and moisture exchanges between the surface and overlying atmosphere. During the past few decades, a number of land-surface schemes of various degrees of sophistication have been developed, such as single-layer force-restore (Blackadar 1976), multi-layer thermal diffusion (Dudhia 1996), and land-surface models with soil moisture prediction and vegetation effects (e.g., Chen and Dudhia 2001). Because of the wide variety of schemes currently being used, a natural concern is the sensitivity of the prediction and simulation of warm-season precipitation in high-resolution numerical models to the land-surface parameterization. Another important issue is whether realism is consistently improved with increasingly sophisticated land-surface processes. Addressing these problems is not only of practical significance, but also helpful in guiding the future improvement and development of land-surface parameterizations.

The present study focuses on the diurnal regeneration and propagation characteristics of warm-season precipitating systems. This important climatological aspect of midsummer convection over the Continental United States has been comprehensively documented from radar-based observations (Carbone et al. 2002). Herein, we evaluate the sensitivity of multi-day cloud-system-resolving explicit simulations to two land-surface schemes with emphasis on the precipitation characteristics.

For short-range simulations of up to about 2 days, the land-surface model’s main value is in modulating diurnal effects based on the soil properties. The primary sensitivity is to the initial soil moisture that determines the Bowen ratio partitioning between sensible and latent heat flux and induces mesoscale circulations in response to horizontal gradients of sensible heat fluxes, which in turn helps in determining boundary layer properties that might influence the timing and location of convective development (e.g., Zhang and Anthes 1982; Lanicci et al. 1987; Segal et al. 1995; Shaw et al. 1997). On the other hand, for long-range simulations, such as in regional climate multi-month simulations, the value of the land-surface model is in the prediction of the temporal evolution of surface properties, mainly that of the soil moisture which is likely to be a key component of interannual variability in a given season (e.g., Zhang et al. 2008). However, in the multi-day range, it is still less clear that the time variability in the soil is critical. A recent case study for a 12-day warm-season period demonstrated that the initial soil wetness and land surface scheme have more significant impacts on the mean regional-scale near-surface thermodynamics than evolving soil moisture (Trier et al. 2008). The purpose of this study is to investigate whether multi-day convective studies are sensitive to the temporal soil variation given by sophisticated land-surface models.

2 Numerical model and experimental setup

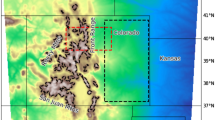
We use the latest nonhydrostatic version of the Pennsylvania State University/National Center for Atmospheric Research mesoscale model (MM5) (Dudhia et al. 2003). The 2,400 × 1,800 km2 computational domain encompasses approximately two-thirds of the continental US with 3-km grid spacing (Fig. 1). There are 40 vertical levels unevenly spaced from ∼2.5 hPa near the surface to 50 hPa. All simulations employ the planetary boundary layer scheme adapted from that in the National Centers for Environmental Prediction (NCEP) medium-range forecast model (Hong and Pan 1996), the Goddard Space Flight Center five-class mixed-phase microphysics scheme (Tao and Simpson 1993), and the longwave and shortwave parameterization based on Dudhia (1989).

Fig. 1
figure 1

Terrain of the computational domain

Full size image

Two land surface schemes are tested to investigate how the warm-season precipitation forecasts depend on the treatment of land-surface processes. The first is the five-layer soil model (hereafter FLSM) developed by Dudhia (1996). This model provides an improvement in the ground temperature prediction over that produced by the two-layer force-restore method (Blackadar 1976) at minimal computational cost. However, it retains the simplicity of predicting just the thermal budget of the soil layers, ignoring soil moisture and vegetation effects. The surface latent heat flux is determined based on the moisture availability that has only land-use and summer/winter dependencies, so there is no soil water budget. The second scheme is the Noah land-surface model (hereafter NLSM), which is a modified after the Oregon State University land surface model (Chen and Dudhia 2001) and closely related to that used in the NCEP global and regional forecast models. This scheme has four layers of soil temperature and soil moisture, and also predicts canopy moisture and snow cover. It has land-use-dependent vegetation effects accounting for stomatal and root zone effects on evapotranspiration soil-type-dependent sedimentation and run-off effects in the soil moisture budget.

The case selected for study is a 7-day warm season heavy precipitation episode over the central United States from 0000 UTC 3 July to 0000 UTC 10 July 2003. During this 1-week period, a nearly zonal westerly flow prevails in the upper troposphere over the northern US, superimposed upon with east-traveling short wave activities (Liu et al. 2006; Trier et al. 2006). A regular daily regeneration of eastward-propagating mesoscale convective systems (MCSs) occurs in the lee of the Rockies. This multi-day pattern has previously been simulated: (1) to evaluate the capabilities of explicit convection-permitting models in predictions of summertime precipitation (Liu et al. 2006), (2) to address the parameterization issue relevant to the mesoscale organization of precipitating convection (Moncrieff and Liu 2006), (3) to examine the mechanisms associated with long-lived propagating convection (Trier et al. 2006), and (4) to quantify the effects of cloud microphysics parameterizations (Liu and Moncrieff 2007). Herein, a total of three numerical experiments are conducted that differ only in the treatment of land surface processes, corresponding to the application of NLSM, FLSM, and NLSM excluding precipitation feedbacks (hereafter referred to as NLNF), respectively. NLNF differs from the full land-surface run (NLSM) only in that it keeps the soil moisture constant at its initial value, excluding the effects of moistening, mostly due to precipitation, and drying due to surface evaporation and drainage. The purpose of NLNF is to evaluate the time dependence of soil moisture and particularly the short-term effect of the water cycle between precipitation events. As in our aforementioned previous studies of this case, the initial conditions, including those for soil moisture for the NLSM and NLNF experiments, and lateral boundary conditions are obtained from the 3-hourly, 40-km grid spacing NCEP operational ETA model analyses.

3 Results

Figure 2 compares the 7-day accumulative rainfall distributions in the three simulations with radar analysis. The radar-derived rainfall in Fig. 2a is based on a reflectivity-rain relationship, Z = 300 R 1.5, where Z and R are the radar reflectivity and rainrate, respectively (Carbone et al. 2002). Although it has desirable spatial and temporal resolution (∼2 km in space and 15 min in time), this dataset features significant uncertainty with regard to quantitative precipitation estimation. The observed heavy precipitation has a largely zonally oriented distribution contained within a narrow zone, extending from the lee of the Rockies across the Great Plains. The heaviest rainfall is located in Iowa, stretching east-south-eastward into Indiana and Ohio. All simulations (Fig. 2b–d) produce an approximately WNW-ESE concentrated precipitation band, bearing a strong resemblance to the radar analysis except for the too-far southward-tilted distributions as compared to the nearly east–west orientation in the radar observations. This meridional position error is associated with the tendency of the forecasted organized convective systems to travel to the right (southern flank) of their observed counterparts. Interestingly, a similar bias in the propagation direction was reported in explicit forecasts with the weather research and forecasting (WRF) model at 4-km grid spacing (Done et al. 2004). Because this deficiency appeared in both MM5 and WRF simulations, it is possibly attributable to the errors in the forcing data, the ETA forecast, which was used to provide initial and boundary conditions for the two models. Another common discrepancy among these simulations is the too-weak intensity and too-widespread distribution in the east portion of the precipitation corridor. In addition, the model misses or underpredicts (overpredicts) the weak rainfall near the southwest (northeast) corner of the computational domain. Visually, NLSM and NLNF are comparable, and the influence of precipitation feedbacks in NLSM is minimal. The domain-averaged accumulated rainfall is 34.7 mm for radar estimate, and is 33.4, 29.8 and 33.2 mm for simulations using NLSM, FLSM and NLNF, respectively. Both NLSM and NLNF produce about 12% more rainfall than FLSM and are also closer to the radar-derived value.

Fig. 2
figure 2

Accumulated rainfall amount during the 7 days. a Radar estimate, and b–d simulations applying Noah land surface model, five-layer soil model, and Noah land surface model without precipitation feedback, respectively

Full size image

Figure 3 details the spatial distribution of differential rainfall amount between each pair of simulations. Even though the accumulative rainfall displays similar spatial patterns among the three simulations, the local difference can still be more than 50 mm inside the concentrated precipitation corridor. The difference is relatively small outside the heavy precipitation region. Careful inspection shows that NLSM generates stronger rainfall than FLSM over a majority of grid points, especially, over the light rainfall regions (Fig. 3a) (the ratio of grid boxes with a positive and negative rainfall anomaly is 1.32). This is in agreement with the aforementioned larger domain-averaged value for the simulation using NLSM. As indicated in Fig. 3b, heavy rainfall shifts southward when precipitation feedback is excluded, but the numbers of grid points with a positive or negative anomaly are almost identical.

Fig. 3
figure 3

Differential accumulative rainfall between a simulations using Noah land surface model and five-layer soil model and b simulations using Noah land surface model with and without precipitation feedback

Full size image

All simulations reasonably capture the temporal and spatial sequences of propagating convection as displayed in the time-longitude depiction of meridionally-averaged rainfall rate (not shown). Figure 4 displays the corresponding diurnal Hovmoller diagrams of rain rate averaged over the 7-day period. Two parallel concentrated downward-sloping rainfall signatures (streaks) in the radar composite (Fig. 4a) originate in the neighborhood of the Continental Divide about 21 UTC. Spanning a sizable fraction of the continent with propagation speed of roughly 21 ms−1, they represent the week-long mean behavior of successive zonally propagating precipitation episodes. On the whole, the surface schemes have equal skill in predicting these coherent rainfall patterns and have similar discrepancies too. The most noticeable deficiency is the dearth of heavy rainfall near the eastern boundary because the modeled rainfall is located too far west. This is especially problematic in the simulation operating FLSM. A similar problem is encountered with a 4-km-resolution simulation with the WRF model (Trier et al. 2006), likely attributable to the too-coarse grid spacing (Moncrieff and Liu 2006).

Fig. 4
figure 4

The 7-day composite diurnal Hovmoller diagrams of meridionally averaged surface rainfall rate. a Radar observations, and b–d simulations using Noah land-surface model, five-layer soil model, and Noah land-surface model without precipitation feedback, respectively

Full size image

Figure 5 compares the evolution of the simulated domain-averaged rainfall rate and fractional area with the respective observation counterpart. The temporal variations in rainfall amount resemble each other and show distinct diurnal oscillations with a late-afternoon (around 00 UTC) maximum and early morning (around 12 UTC) minimum during most of the 1-week period (Fig. 5a). Qualitatively, the results are in agreement with the radar estimate except for the first day during which the rainfall is overpredicted. The 7-day means are about 4.8, 4.3 and 4.7 mm day−1 for simulations using NLSM, FLSM and NLNF, respectively, slightly smaller than the observed value of 5 mm day−1. Consistent with the differential accumulative rainfall discussed above, there is a roughly 12% difference in rain rate between the two land-surface schemes. Similarly, the variability in rainfall area (Fig. 5b) is insensitive to the land-surface parameterization, but show more discrepancies from radar observations. In calculating rainfall areal fraction, it is assumed that precipitation occurs over a grid box when the 30-min accumulated rainfall exceeds an intensity of 0.1 mm h−1. All simulations underpredict the observed values, but overpredict the diurnal amplitudes. This deficiency is likely associated with insufficient resolution to correctly represent convective initiation under weakly forced conditions. On an average, the rain areal coverage is 5, 4, 3.6 and 4% for radar estimates, NLSM, FLSM and NLNF, respectively, equating to a difference of about 11% between the two land-surface parameterizations. The similarity between the NLSM and NLNF simulations also gives a measure of the magnitude of random internal model variability, demonstrating that these differences from FLSM are probably robust in a statistical sense.

Fig. 5
figure 5

Evolution of a domain-averaged rainfall rate and b rainfall areal fraction for radar estimate (thick solid) and simulations using Noah land-surface model (solid), five-layer soil model (dashed), and Noah land-surface model without precipitation feedback (dotted), respectively

Full size image

Figure 6 presents the evolution of the domain-averaged surface sensible and latent heat fluxes. As expected, the sensible heat fluxes exhibit strong upward transport from the underlying warm surface during the daytime and weak downward transport during the nighttime, synchronous with the solar radiation. The daytime maximum occurs around 18 UTC, whereas the nocturnal negative flux is rather small and uniform. In general, FLSM consistently produces a greater (slightly smaller) sensible heat flux than NLSM during the daytime (night) with a temporally averaged difference of about 17 W m−2. In contrast, NLSM produces more (less) latent heat fluxes during the daytime (nighttime) and thus more salient daily variabilities. Additionally, there is a minor timing difference in the maximum. The 7-day mean value is roughly 8.3 W m−2 larger in NLSM than in FLSM. This moisture flux difference is equivalent to a difference of about 0.26 mm day−1 precipitation difference had all the differential moisture rained out: about half the precipitation difference between the two schemes. The mean Bowen ratio is 2.3 and 1.6 for NLSM and FLSM, respectively.

Fig. 6
figure 6

Evolution of a domain-averaged surface sensible heat fluxes and b latent heat fluxes for simulations using Noah land-surface model (solid), five-layer soil model (dashed), and Noah land-surface model without precipitation feedback (dotted), respectively

Full size image

Figure 7 displays the evolution of the temperature and water vapor mixing ratio at the lowest model level (about 25 m above ground level). In response to the surface energy uptake, the near-surface temperature undergoes a significant diurnal oscillation with a peak around 21.5 UTC and a minimum around 11.5 UTC. Obviously, FLSM corresponds to consistently warmer temperature than both NLSM and NLNF, with an averaged difference of approximately 0.8 K, consistent with the differential sensible heat transports (Fig. 6a). The maximum difference occurs in the late afternoon and evening, which, as expected, lags the corresponding maximum difference in sensible heat flux by a few hours. The near-surface water vapor also experiences significant daily fluctuation, but the variational pattern differs considerably between the two surface schemes. A striking diurnal cycle is present in FLSM, whereas NLSM or NLNF generates a less-pronounced daily maximum. In all the simulations, the lowest-level water vapor dries as the boundary layer grows in the morning, presumably due to the PBL scheme mixing drier air downwards. The water vapor recovers later as the surface moisture restores it to an equilibrium value. NLSM has a much reduced diurnal cycle, and additionally has a diurnal cycle in soil moisture (not shown) with a minimum at dusk. NLNF shows that the NLSM diurnal cycle is influenced little by the soil moisture variation, in agreement with Trier et al.’s finding that the soil moisture evolution has negligible effects on near-surface thermodynamics for a 12-day period. The morning drying is less with the NLSM probably due to the higher latent heat flux, and possibly because the reduced sensible heat flux leads to reduced boundary-layer growth and entrainment of drier air from the top of the PBL. The nighttime moistening is also less which is consistent with the reduced latent heat flux. Nevertheless, the temporal averages show not much difference among the simulations.

Fig. 7
figure 7

Evolution of a domain-averaged temperature and b water vapor mixing ratio at the lowest model level (∼25 m above the ground) for simulations using Noah land-surface model (solid), five-layer soil model (dashed), and Noah land-surface model without precipitation feedback (dotted), respectively

Full size image

4 Concluding discussion

We investigated the dependence of cloud-system-resolving simulations of warm season convection on the choice of land-surface schemes in a multi-day case study. The selected case is a 7-day episode in midsummer and characterized by daily genesis of convection east of the Rocky Mountain and, thereafter, upscale development and propagation toward the plains.

For the most part, the successive heavy rainfall sequences and the spatial distribution of accumulated rainfall are insensitive to the surface scheme. The two schemes perform comparably in capturing the rainfall corridor: daily convective generation near the continental divide and subsequent eastward propagation. They also display similar deficiencies, such as the too-weak and too-widespread precipitation over the eastern portion of the computational domain compared to radar observations.

In comparison, the NLSM produces about 12% more rainfall and a similarly larger rainfall areal fraction. The differential rainfall amount is consistent with the differential moisture transport from the land surface, specifically an 8% greater latent heat flux. On the other hand, the FLSM generates greater sensible heat fluxes, which contributes to the warmer temperature near the surface. It is also noted that the precipitation feedback to latent heat fluxes has little impact on the surface water vapor fluxes and thus the boundary-layer properties and overall rainfall intensity, but does affect the detailed precipitation distribution. The FLSM used a specified moisture availability that made its average behavior emulate a drier surface than the LSM. A larger moisture availability could give a closer domain-averaged result, as discussed for the MM5 model’s two-layer Blackadar scheme by Oncley and Dudhia (1995); however, it is not clear how to tune moisture availability as a spatial function, because it likely depends on both soil moisture and vegetation type.

The above conclusions are obtained from a single week-long simulation. Without question, multiple cases under various synoptic conditions are required before these findings can be properly generalized. In particular, the one-week period in the present study corresponds to moderate large-scale forcing (Liu et al. 2006). We anticipate that under weaker synoptic forcing, typical during the summertime, the convective activity might be more dependent on the interactions between the land surface and the overlying planetary boundary layer and, therefore, more sensitive to the treatment of land surface processes. Furthermore, interannual variability likely depends on the large-scale soil moisture distribution dependent on precipitation over several months prior to the season of interest. Our study focused on a single season and the short time-scale variability of the soil moisture.

The weak sensitivity of propagating organized convection to land-surface parameterization as well as the comparable level of sensitivity to cloud-microphysics parameterization shown in Liu and Moncrieff (2007) was anticipated. However, this does not mean that these parameterizations are unimportant in short-range weather forecasting. As demonstrated, they have non-negligible impacts on the simulated cloud and precipitation properties, such as cloudiness, rainfall spectrum, rainfall rate and areal coverage, and therefore are important for quantitative precipitation forecasting. The anticipation of weak sensitivity was based on how convective dynamics is controlled and modulated by environmental wind shear and scale interaction effects embraced by the concept of convective organization (see Moncrieff and Liu 2006 and papers cited therein). Note that the representation of convective organization is incomplete in regional prediction models, inadequate in global weather prediction models and virtually absent from contemporary climate models. Because convective organization directly affects the processing of water not only within the atmosphere (dynamics–microphysics interaction), but also with the underlying surface (atmosphere surface exchange), a systematic investigation of the coupling among moist convective dynamics, cloud-microphysics and atmosphere-surface exchange is required.