Abstract
COVID - 19 affected severely worldwide. The pandemic has caused many causalities in a very short span. The IoT-cloud-based healthcare model requirement is utmost in this situation to provide a better decision in the covid-19 pandemic. In this paper, an attempt has been made to perform predictive analytics regarding the disease using a machine learning classifier. This research proposed an enhanced KNN (k NearestNeighbor) algorithm eKNN, which did not randomly choose the value of k. However, it used a mathematical function of the dataset’s sample size while determining the k value. The enhanced KNN algorithm eKNN has experimented on 7 benchmark COVID-19 datasets of different size, which has been gathered from standard data cloud of different countries (Brazil, Mexico, etc.). It appeared that the enhanced KNN classifier performs significantly better than ordinary KNN. The second research question augmented the enhanced KNN algorithm with feature selection using ACO (Ant Colony Optimization). Results indicated that the enhanced KNN classifier along with the feature selection mechanism performed way better than enhanced KNN without feature selection. This paper involves proposing an improved KNN attempting to find an optimal value of k and studying IoT-cloud-based COVID - 19 detection.
Similar content being viewed by others
Explore related subjects
Find the latest articles, discoveries, and news in related topics.Avoid common mistakes on your manuscript.
1 Introduction
IoT-Cloud based healthcare predictive models play an important role in the detection of several diseases and provide better decisions to the users. It is necessary to propose such an IoT-cloud-based healthcare model for the detection of COVID-19. COVID-19 is mainly caused by Severe Acute Respiratory Syndrome Coronavirus 2 (SARS-CoV-2). It has been declared as a pandemic since March 2020, and according to WHO (World Health Organization), there are 21,409,133 active cases worldwide (December 2020). The virus mainly spreads by respiratory precipitations while coughing, sneezing, etc., and gets transmitted from person to person. While fever, cough is the primary symptoms of the disease, certain pre-existing medical conditions
(heart disease/diabetes/COPD/cancer) actually aggravate the disease’s outcome. Towards an effort to curb this disease and build a pandemic prepared healthcare system, this paper applies predictive data mining techniques on COVID - 19 data to understand the disease better.
Several researchers [5, 6, 8, 33, 35, 42, 43] have applied machine learning as well as deep learning algorithms on COVID - 19 data and derived fruitful insights. While some researchers used neural networks [5,6,7] or deep learning methods, others used regression [12], or classification algorithms [21, 24] to predict the prognosis of the disease. In this paper, we have explored the supervised learning algorithm KNN (k Nearest Neighbor) [14, 16,17,18] on seven COVID - 19 cloud datasets gathered across the world (Asia, Brazil, Mexico, etc.). The dataset sample size ranged from 5000 to 1.5 million. KNN algorithm was opted for because of its simplicity and ease of use. The experimentation demonstrated an enhanced KNN (k Nearest Neighbor) algorithm, which uses a radical mathematical function (square root / cube root / fourth root etc.) of the sample size of the dataset as the k value. The k is represented as (\(\root n \of {N}\)) where the radicand N is actually the sample size of the dataset (number of records present in the dataset) and \(n~=~2,~3,~4\), etc. Thus, the k value is chosen dynamically during the runtime depending on the dataset size. In traditional KNN, the value of k is chosen arbitrarily or randomly [20, 25]. The enhanced KNN (eKNN) overcomes this shortcoming. Several performances indicating parameters (accuracy, precision, F1- score, error rate, etc.) [26, 27, 31, 32] were calculated to show the effectiveness of the proposed eKNN. The performance of eKNN algorithm was improved when used with ACO (Ant Colony Optimization) based feature selection mechanism [30]. For a fair comparison, C4.5 based FS mechanism was also investigated. The parameters were recalculated and compared with enhanced KNN without feature selection. Several graphical representations were shown for better performance visualization.
1.1 Contribution
The paper contributed two noteworthy research questions -
RQ1 - How can the KNN classifier choose the optimal value of k?
The conducted literature survey did not show any experimentation regarding this shortcoming. To bridge this gap, this research proposed eKNN (Enhanced KNN) and overcame the limitations of traditional KNN. The newly proposed eKNN was applied on seven benchmark datasets gathered from the COVID cloud repository of different countries (Brazil, Mexico, etc.). This data analysis can act as a back-end of a healthcare model where IoT is used to develop the front-end interface.
RQ2 - What is the effect of using the KNN classifier with feature selection mechanism?
The proposed eKNN algorithm is used with a feature selection mechanism and made robust. Apart from leveraging ACO based feature selection mechanism, C4.5 based FS mechanism is also explored for a fair comparison. All the datasets were retested. Graphical illustrations are shown to visualize the effect.
1.2 Organization
The paper is organized as follows: Section 2 underlines the related work, while Sect. 3 discusses the proposed methodology and working principle of the proposed eKNN algorithm. Section 4 describes the used dataset. Section 5 demonstrates the experimental setup and proves the fair comparison of the traditional KNN, eKNN with feature selection, and eKNN without feature selection. Finally, a conclusion is provided in Sect. 6 with future directions.
2 Related work
Many researchers [22, 23, 36, 37, 39, 47,48,49] have been exploring machine learning techniques as well as deep learning techniques for health monitoring and tracking COVID - 19 over the cloud and IoT platforms. These studies can help in effective prediction and decision-making regarding the deadly disease. These experiments can help in early intervention, and thus it can eventually reduce the mortality rate.
Khanday et al. used traditional and ensemble machine learning classifiers for classifying textual clinical reports [14]. The authors found out that logistic regression and Naïve Bayes performed better than other ML algorithms by reaching 96.2% testing accuracy. Tiwari et al. [28] also proposed an unsupervised terminformer model to mine terms from the biomedical literature for COVID-19. Flesia et al. studied 2053 individuals with 18 socio-psychological variables and identified participants with elevated stress levels using a predictive machine learning approach [13]. Randhawa et al. focused on the COVID - 19 virus genome signature [15]. The authors combined machine learning and digital signal processing (MLDSP) for classifying COVID - 19 virus genomic sequence. Souza et al. applied several supervised ML algorithms (linear regression, decision tree, SVM, Gradient Boosting, etc.) on COVID positive patients and compared the outcome of each method [12]. Yan et al. studied 2799 patients of Wuhan and designed a prediction model using XGBoost to predict mortality [11]. SIR (Susceptible, Infected, and Recovered) model and machine learning were used for COVID - 19 pandemic forecasting by Ndiaye et al. [10]. Castelnuovo et al. studied Random Forest and indicated that decreased renal function is a potential cause of death in COVID patients [5]. Lalmuanawmaa et al. showed how AI could create less human interference in medical diagnosis [34]. Somasekar et al. applied neural networks for image classification of Chest X-ray [7, 45, 46]. Amar et al. applied regression on COVID data and predicted a number of infected people [8]. The authors collected data from Egypt. The average discharge time of COVID patients from the hospital was analyzed by Nemati et al., and this study [9] helped the hospital professionals to stay better prepared for the disease.
The application of KNN [19, 38, 41] and feature selection mechanism [1, 2] for medical diagnosis is also not new. In 2016, Li et al. conducted a study with EEG graphs regarding depression and found out that optimal performance is achieved using a combination of CFS (Correlation Features Selection) and KNN [3]. Remeseiro et al. applied the feature selection technique for medical applications. A case study was conducted on two medical applications with real-life patient data [4].
Inspired by this background work, this research gained motivation to pursue the implementation of machine learning approaches on COVID - 19 detection.
3 Proposed methodology
In the first setup, the eKNN algorithm was applied without a feature selection mechanism on several datasets obtained from the COVID cloud. This back-end data analysis can be utilized to build an IoT-based front-end Covid screening system.
3.1 Enhanced KNN (eKNN)
In the next step, the eKNN classifier was also applied on all seven datasets. Classification is a supervised ML method, and the role of a classifier is to map the input data into classes. Each object is classified into one group only. The KNN classifier was developed by Fix and Hodges in 1951 [19] and is an example of the simple classification algorithm. It can be used for both classification and regression. In KNN, distances (Manhattan, Euclidean, Minkowsky, Chebyshev, etc.) are calculated between the test sample and training data samples, and thus nearest neighbors are obtained. The neighbors are chosen from a set of training objects whose classes are already available. The test sample is assigned to the class of its nearest neighbor only.
3.2 KNN representation
The KNN join of two sets P and Q is represented by \(\{(p, \text {kNN}(p, Q)), \forall p \in P\}\) where p and q are two elements as \(p \in P\) and \(q \in Q\). k points (which are closest to p) are found from set Q in a dimensional space d.
The KNN algorithm suffers from a limitation and that is its dependency in choosing a proper value of parameter k (number of nearest neighbors). The performance of KNN algorithm hugely depends on this factor as the k value elects the number of neighbours which determines the class. In most of the cases, the k value is chosen randomly and this paper attempts to overcome this drawback.
In this research, the radical mathematical function (square root, cube root, fourth root etc.) is used to determine the k value dynamically during the computation time depending on the size of the dataset. The k is represented as (\(\root n \of {N}\) ) where the radicand N is actually sample size of the dataset (number of records present in the dataset) and \(n = 2, 3, 4\) etc. For example
-
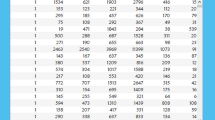
When the dataset contains around 5000 records (Dataset 1 in Table 1), the k value is set to \(\root 2 \of {5000} \approx 71\). A small k value does not produce expected output because of noise/outlier (presented in Table 3) and because of that reason k value was not set to \(\root 3 \of {5000} \approx 17\).
-
But, when the dataset increases in size and contains 0.1 million (Dataset 3) / 0.25 million (Dataset 4) /0.5 million (Dataset 5) records, the k value is set to \(\root 3 \of {N}\) . The value of n is increased from 2 to 3 because too high k value increased computation time heavily. For example, for Dataset 3, if k value is chosen as \(\root 2 \of {100000} \approx 317\), then it costs huge increase in KNN algorithm running time (almost 2 times as presented in Table 3) and thus it creates poor performance. So, to avoid this performance degradation, the k value is set to \(\root 3 \of {100000} \approx 47\) and the estimated computation time of KNN becomes manageable.
-
Again, when the dataset becomes bigger with around 1 million (Dataset 6) or 1.5 million (Dataset 7) records, the k value is set to \(\root 4 \of {N}\) . For example, for Dataset 6 the k value is set to \(\root 4 \of {1000000} \approx 31\).
-
In this eKNN, the value of k is kept odd, to avoid equal voting.
This choice of k is analytical and forms a basis of fair judgement, rather than choosing the k value arbitrarily. The data volume plays an important role is setting the k value and deciding the value of k in this manner will support application of KNN for large datasets. The previous steps are summarized below -

As the proposed eKNN classifier was applied on all the seven datasets under experimentation and obtained a confusion matrix. The matrix contains info about the actual and predicted value on classification. For each eKNN run, the accuracy, precision, recall, specificity, error rate, F1-score parameters were calculated from the confusion matrix. The resultant values are tabulated in Sect. 5.
3.3 eKNN with ACO-based feature selection
In this second phase of implementation, the KNN algorithm was used with ACO based feature selection mechanism. Table 1 Dataset 1 has 8 features; Dataset 2, Dataset 6, and Dataset 7 each have 15 features; Dataset 3 and Dataset 4 each have 18 features while Dataset 5 has 19 features. It is explored whether ACO-based FS (Feature Selection) will bias the implementation potential of the proposed eKNN. If the original feature space is represented by size S, then the feature selection process’s goal is to select the optimal subset of features of size s (\(s \le S\)).
Ant colony optimization replicates ant’s food searching behavior pattern. As the ants move from one node to another, a chemical substance (pheromone) is deposited along the path. The pheromone trail helps other ants to find the food source following the shortest path. The pheromone evaporates at a certain rate resulting in the decay of less traversed paths. ACO is a probabilistic technique that ensures convergence and promotes rapid solution-finding. Because of these traits, ACO was given preference over others.
-
The edges between the nodes guide the choice of next feature
-
Amount of pheromone level is indicated by \(\tau \)
-
The features which belong to the route with high level of pheromone are treated as the selected features.
-
Selected feature subset is governed by -
$$\begin{aligned} P_{ij}^n (t) = \frac{[\tau _{ij}(t)]^{\alpha } * [\eta _{ij}(t)]^{\beta }}{\sum _{u \in j}n[\tau _u(t)]^{\alpha } * [\eta _u(t)]^{\beta }} ~~~ if~i \in j^n \end{aligned}$$(1)-
Where \(P_{ij}^n(t)\) is the probability of an ant at feature i moving to feature j at time instant t
-
n is number of ants / number of features
-
\(j^n\) is set of potential features that can be present in temporal solution
-
\(\tau _{ij}\) indicates amount of pheromone in edge (i, j)
-
\(\eta _{ij}\) indicates heuristic value associated with edge (i, j)
-
All features have same value of \(\tau ,~\eta \) initially
-
\(\alpha> 0,~\beta > 0\) (\(\alpha ,~\beta \) is determined experimentally and taken as \(\alpha = 2,~\beta = 0.5\) in this study)
-
Pheromone evaporation rate is 5% in this study.
-
Stopping criteria is maximum number of iterations.
-
The basic operation of this ACO-based feature selection mechanism is depicted in Fig. 4. After applying the ACO-based FS technique, among 8 features of Dataset 1, 5 features were selected (detailed in Table 2). Dataset 2, Dataset 6, and Dataset 7 have the same features, and 10 features were selected out of 15. Dataset 3 and Dataset 4 have the same features, and 11 out of those 18 features got selected. Dataset 5 initially had 19 features, and after the FS mechanism, 11 got selected. The selected features are tabulated in Table 2. The eKNN algorithm was applied on the reduced datasets, and accuracy, precision, recall, specificity, error rate, F1-score parameters were recalculated for each dataset. The calculated values are summarized in Sect. 5. After applying the eKNN classifier with ACO-based FS mechanism, C4.5 based FS mechanism was also explored to evaluate which FS mechanism is a better performer. The result comparison is tabulated in the next section.
4 Dataset description
The experimentation involved seven standard COVID datasets of different sizes and origins. Table 1 represents the datasets in ascending order of their size. For convenience, we named the datasets with Dataset 1, Dataset 2, and Dataset 3, etc.
The first dataset is collected from Kaggle, and it has 5000 records (both COVID positive and COVID negative cases). The second dataset is a cross-country dataset (Our World in Data COVID-19 cloud dataset [29]) focusing on COVID - 19 testing data obtained from https://ourworldindata.org/ till March 2020 starting from Jan 22, 2020. Dataset 6 and Dataset 7 are also gathered from ’Our World in Data COVID-19 dataset’ [29], but they represent different time frames. Dataset 6 is from April 1, 2020, to April 7, 2020, and it contains 1 million records indicating massive outbreaks across the world rapidly. Dataset 7 is collected based on August 1, 2020, to August 7, 2020, and it contains 1.5 million records. Dataset 3 is obtained from the Brazilian government’s cloud (https://coronavirus.es.gov.br/painel-covid-19-es), and it contains 0.1 million records from 6/1/2020 to 10/8/2020. Dataset 4 is also from Brazil, and it contains a total of 0.25 million cases reported from 6/1/2020 to 24/12/2020. Dataset 5 contains 0.5 million records and is released by Mexican government (https://www.gob.mx/salud/documentos/datos-abiertos-152127).
All the datasets contain several features like age, gender, country, heart disease, COPD, diabetes, pregnancy, smoking habits, etc. Three random datasets (Dataset 2, Dataset 3, and Dataset 4) were chosen to measure the presence of comorbidity, and Fig. 1 represents the count of patients with Comorbidity and Non-Comorbidity. One random dataset (Dataset 4) was chosen to judge the age and gender distribution. Figure 2 depicts the gender distribution and Fig. 3 portrays the age group distribution from Dataset 4 for COVID positive and negative patients. The count of COVID positive male patients was slightly higher than COVID positive female patients, according to Fig.2 as obtained from Dataset 4.
5 Experimental results and discussion
5.1 Data preprocessing
The transformation of raw data into a meaningful format is known as data preprocessing. Data Quality plays a vital role in determining the experimental results. All the seven subject datasets were pre-processed and cleaned. As part of the data cleaning activity, duplicate records were deleted. Several records had certain fields as NULL (age in Dataset 2, Serology Result in Dataset 4, Blood Pressure in Dataset 5, etc.). The NULL values were replaced with an average value of that particular field. Only very few records had inconsistent/junk characters in many fields, so such records are discarded.
For all the 7 datasets, the KNN algorithm was initially implemented using random values of k. The choice of the k parameter is made arbitrarily, and the confusion matrix is obtained for each case.
5.2 Evaluation measures
The confusion matrix helps to measure the performance of a classifier. It is a matrix of two dimensions (Actual and Predicted), and the dimensions have TP(True Positive), TN(True Negative), FP(False Positive), and False Negative(FN) as presented in Fig. 5. True positive are the cases where the predicted value is yes (having the disease), and the patients really have the disease. True negative is when the predicted value is no (not having the disease), and the patients really do not have the disease. False-positive are the cases where the predicted value is yes (having the disease), but the patients actually do not have the disease. False-negative are the cases where the predicted value is no (not having the disease), but the patients have the disease. Several performance indicators of a classifier are derived from this matrix. For example -
The existing KNN algorithm was experimented (with random k value) on all the datasets, and the resultant confusion matrix yielded several performance parameters. The calculated performance metrics are - Accuracy, Precision, Specificity, Recall, F1 score, Error Rate. In each case, the computational time to validate the algorithm is also noted. The results are listed in Table 3 for respective k values for corresponding datasets. After this initial experiment, the proposed eKNN algorithm is validated, and the k value is chosen based on a radical mathematical function. Table 3 contains all the recalculated performance parameters after the eKNN implementation of each dataset.
Figure 6 contains a graphical depiction of these parameters for different k values.
5.3 Experimental analysis and findings
From the obtained experimental results (Table 3), it can be summarized -
-
In terms of Accuracy, F1 score, Error Rate, Computation time, etc., performance indicator, the eKNN algorithm performed significantly better than the ordinary KNN algorithm.
-
Results indicated that for Dataset 1, when k was chosen randomly (k = 37), the obtained accuracy was only 75.6%. But by the use of eKNN, when k was chosen as \(\root 2 \of {N}\) (in this case N = 5000, so k = 71), the obtained accuracy increased to 87.9%. It was also observed that the computation time of eKNN (8.2 seconds) was negligibly higher than ordinary KNN (computation time of 6.45 seconds). Also, the error rate became lower (5.6%) in comparison to normal KNN (an error rate of 9.5%). So, eKNN showed manifold improvement.
-
For Dataset 1, k value was chosen as \(\root 2 \of {N}\) , instead of \(\root 3 \of {N}\) because too low k value cannot handle outliers/noise. Results indicated severe damage in accuracy (only 68.1%), when k value became too small (\(k = \root 3 \of {N} = 17\)).
-
The essence of this eKNN algorithm is that it dynamically chooses the k value depending on the dataset’s size. While k is presented as \(\root n \of {N}\), the radical mathematical function (square root / cube root / fourth root etc.) varies according to sample size (N) of the dataset and thus n = 2, 3, 4 etc. This became very useful when the dataset size increased compared to Dataset 1 (only 5000 records). Dataset 2 and Dataset 3 have 50,000 and 0.1 million records, respectively. So for both of these datasets, k was chosen as \(\root 3 \of {N}\) resulting in high accuracy of 89.9% and 91.5%, respectively (Table 3).
-
For both Dataset 2 and Dataset 3, if k value was taken as \(\root 2 \of {N}\), instead of \(\root 3 \of {N}\) then the k value became very high, resulting in approximately double computation time while showing a very slight increase in accuracy and a minor decrease in error rate. For example, for Dataset 3, when \(k = \root 2 \of {N} = 317\) was chosen, accuracy turned out as 92.5%, error rate appeared as 6.2% and the computation time became 25.4 seconds. But for the same dataset, when \(k = \root 3 \of {N} = 47\) was chosen, accuracy turned out as 91.5% (very negligible decrease), error rate appeared as 7.5% (very minor increase) and the computation time became 11.5 seconds (less than half). So, high accuracy is preserved with very reasonable computation time, and thus these results supported the avoidance of too high a k value.
-
For Dataset 4 (0.25 million) and Dataset 5 (0.5 million), the k value of \(\root 3 \of {N}\) gave very high accuracy of 86.9% and 87.8% respectively. Even though the Precision parameter varied very slightly, the Recall and F1 score parameters also improved both datasets (Table 3).
-
Results also indicated that if k value is taken too small, then accuracy decreases drastically. For example, for Dataset 5 (sample size 0.5 million), if the k value is set to 27, (\(k = \root 4 \of {N} = 27\)), then the obtained accuracy falls down to 69.4%. It was 87.8% when k was set to 79 (\(k = \root 3 \of {N} = 79\)).
-
However, as the datasets became larger in size, the fourth root of radicand usage became necessary. Because too high a k-value will increase the computation time of the algorithm while showing minor accuracy improvement. Results of Dataset 6 (1 million) and Dataset 7 (1.5 million) indicated this. In both cases, high accuracy was obtained at \(k =\root 4 \of {N}\). While Dataset 4 yielded an accuracy of 89.5%, Dataset 7 generated an accuracy of 90.6%. The algorithm’s computation time was also reasonable for both datasets (20.45 seconds and 30.5 seconds, respectively). But slight increment in accuracy (Dataset 6: 89.78%, Dataset 7: 91.2%) and a huge increment in computation time (Dataset 6: 30.6 seconds, Dataset 7: 40.3 seconds) were observed if the cube root of radicand was used to determine k value. Thus, the necessity of using \(k =\root 4 \of {N}\) instead of \(k =\root 3 \of {N}\) is reinforced for larger datasets.
Thus, the eKNN algorithm showed a judicial approach in choosing the k value instead of choosing it randomly. The k value was dynamically determined from the sample size of the dataset using the sample size as radicand, and this formed a logical-mathematical construct instead of arbitrarily chosen k value.
5.4 Results on eKNN with feature selection
In the second phase of experimentation, as the eKNN algorithm was augmented with ACO-based feature selection mechanism, number of feature selected by each subject dataset got reduced. As described in Sect. 4, the features which belong to the route with a high level of pheromone were treated as selected features. According to Table 2, after applying ACO-based FS for maximum iterations, 5 features are selected of Dataset 1, while Dataset 2, Dataset 6, and Dataset 7 are reduced to 10 features each. On the other hand, Dataset 3, Dataset 4, and Dataset 5 selected 11 features from the initial 19 features. Table 2 enlists the names of all the selected features per dataset. For a fair comparison, the eKNN was also tested with C4.5 based FS. The performance parameters were computed.
The eKNN algorithm was applied on all the reduced datasets, and significant improvement in accuracy value was observed. There was a negligible increase in computation time because of feature selection implementation. However, the benefit in terms of accuracy was significant. Table 4 presents the findings. From the results as detailed in Table 4, it is evident that -
-
In all the datasets, eKNN with FS showed improved accuracy over eKNN without FS. The improvement is in the range of 5% to 7% (see Table 4).
-
Among 7 datasets, in 5 cases eKNN with ACO-based FS mechanism showed significant improvement in accuracy value over eKNN without FS mechanism.
-
In the case of two datasets (Dataset 4 and Dataset 5), eKNN with C4.5 based FS mechanism showed the highest accuracy values.
-
The computation time of eKNN with FS mechanism was negligibly higher than eKNN without FS. The increment time was remarkably minor (in the range of 0.3 seconds to 6 seconds only)(Table 4). Only in one exceptional case for Dataset 6, the computation time of KNN was higher than eKNN (maybe because of the high k value chosen randomly).
-
In two datasets (Dataset 2 and Dataset 7), eKNN with ACO-based FS mechanism showed higher computation time than eKNN with C4.5 based FS. In the rest of the datasets, eKNN with C4.5 based FS took a higher time to compute.
Thus, from the results, it is very much clear that eKNN with ACO-based FS performed consistently better than all other experimented techniques. The performance parameter comparison is depicted in Figs. 7 and 8 for better visualization.
Comparison of results with previous studies also showed a very promising prospect. While the mean accuracy value for eKNN with ACO based FS mechanism came as 95.75%, studies conducted by De Souza et al. produced an accuracy of 85% [12] after the application of KNN classifier on the same COVID datasets. Also, it is noteworthy that while CPDS (COVID-19 Patients Detection Strategy) (developed in October 2020) based on a hybrid feature selection mechanism (HFSM) gave a promising result (93% accuracy), this eKNN based on ACO based feature selection mechanism produced higher accuracy of (95.75%). So, it is obvious that the proposed eKNN algorithm can be applied for COVID - 19 data analysis with very high performance.
6 Conclusion
COVID - 19 is a highly contagious disease caused by the newly found coronavirus, and it has jolted our healthcare system. Even though most of the people infected by this disease recover without hospitalization or special medical attention, it has become fatal in many cases. While some people recovered from the disease soon, some people with an underlying health condition (diabetes, heart condition) had passed away. Towards an effort to navigate this enigma, this paper attempts to build an IoT-cloud-based healthcare model for COVID-19 detection using several datasets.
In this paper, we tried to propose an IoT-cloud-based healthcare predictive model to detect COVID-19 using eKNN. A novel enhanced KNN classifier (eKNN) is proposed, which chooses the k value using a radical mathematical function instead of choosing it randomly. The newly designed eKNN algorithm has been experimented on seven COVID - 19 benchmark cloud datasets from different countries (Brazil, Mexico, etc.). This classifier can act as a backend to an IoT-based frontend COVID screening system, and it can promote the processing of large datasets in reasonable time with high computational accuracy. The experiment showed that the eKNN algorithm with an ACO-based FS mechanism generated the best performance. The proposed eKNN can be beneficial to predict the outcome of the disease.
In the future, the work can be extended using weighted KNN or some other feature selection mechanism apart from ACO or C4.5 based mechanism. The work can also be extended for larger COVID datasets (gathered cumulatively over a wide time frame) in the big data domain using Hadoop / Map Reduce approach. This proposed classifier can perform better for disease detection to fight the disease and forecast possible outcomes.
References
Wang L, Wang Y, Chang Q (2016) Feature selection methods for big data bioinformatics: a survey from the search perspective. Methods 111(August):21–31. https://doi.org/10.1016/j.ymeth.2016.08.014
Bolón-Canedo V, Rego-Fernández D, Peteiro-Barral D, Alonso-Betanzos A, Guijarro-Berdiñas B, Sánchez-Maroño N (2018) On the scalability of feature selection methods on high-dimensional data. Knowl Inf Syst 56(2):395–442. https://doi.org/10.1007/s10115-017-1140-3
Li X, Hu B, Sun S, Cai H (2016) EEG-based mild depressive detection using feature selection methods and classifiers. Comput Methods Programs Biomed 136:151–161. https://doi.org/10.1016/j.cmpb.2016.08.010
Remeseiro B, Bolon-Canedo V (2019) A review of feature selection methods in medical applications. Comput Biol Med 112(February):103375. https://doi.org/10.1016/j.compbiomed.2019.103375
Hossain MS, Muhammad G, Guizani N (2020) Explainable AI and mass surveillance system-based healthcare framework to combat COVID-I9 like pandemics. IEEE Network 34(4):126–132
Shorfuzzaman M, Hossain MS (2021) MetaCOVID: a Siamese neural network framework with contrastive loss for n-shot diagnosis of COVID-19 patients. Pattern Recogn 113(2021):107700
Somasekar J, Pavan Kumar P, Sharma A, Ramesh G (2020) Machine learning and image analysis applications in the fight against COVID-19 pandemic: Datasets, research directions, challenges and opportunities. Materials Today: Proceedings 3–6. https://doi.org/10.1016/j.matpr.2020.09.352
Amar LA, Taha AA, Mohamed MY (2020) Prediction of the final size for COVID-19 epidemic using machine learning: a case study of Egypt. Infect Diseas Model 5:622–634. https://doi.org/10.1016/j.idm.2020.08.008
Nemati M, Ansary J, Nemati N (2020) Machine-learning approaches in covid-19 survival analysis and discharge-time likelihood prediction using clinical data. Patterns 1(5):100074. https://doi.org/10.1016/j.patter.2020.100074
Ndiaye BM, Tendeng L, Seck D (2020) Analysis of the COVID-19 pandemic by SIR model and machine learning technics for forecasting. ArXiv
Yan et al. (2020) Prediction of criticality in patients with severe Covid-19 infection using three clinical features: a machine learning-based prognostic model with clinical data in Wuhan. MedRxiv, 2020.02.27.20028027
Souza FSH, Hojo-Souza NS, Santos EB, Silva CM, Guidoni DL (2020) Predicting the disease outcome in COVID-19 positive patients through Machine Learning: a retrospective cohort study with Brazilian data. 2, 1-20. https://doi.org/10.1101/2020.06.26.20140764
Flesia L, Monaro M, Mazza C, Fietta V, Colicino E, Segatto B, Roma P (2020) Predicting perceived stress related to the Covid-19 outbreak through stable psychological traits and machine learning models. J Clin Med 9(10):3350. https://doi.org/10.3390/jcm9103350
Hossain MS (2017) Cloud-supported cyber-physical localization framework for patients monitoring. IEEE Syst J 11(1):118–127
Randhawa GS, Soltysiak MPM, El Roz H, de Souza CPE, Hill KA, Kari L (2020) Machine learning using intrinsic genomic signatures for rapid classification of novel pathogens: COVID-19 case study. PLoS ONE 15(4):1–24. https://doi.org/10.1371/journal.pone.0232391
Cosenza DN, Korhonen L, Maltamo M, Packalen P, Strunk J L, Næsset E, Gobakken T, Soares P, Tomé M (2020) Comparison of linear regression, k-nearest neighbour and random forest methods in airborne laser-scanning-based prediction of growing stock. Forestry. An International Journal of Forest Research, 1-13. https://doi.org/10.1093/forestry/cpaa034
Guo G, Wang H, Bell D, Bi Y, Greer K (2003) KNN model-based approach in classification. Lecture Notes Comput Sci 2888:986–996. https://doi.org/10.1007/978-3-540-39964-3_62
Ali N, Neagu D, Trundle P (2019) Evaluation of k-nearest neighbour classifier performance for heterogeneous data sets. SN Appl Sci, 1(12). https://doi.org/10.1007/s42452-019-1356-9
Sowmiya C, Sumitra P (2020) A hybrid approach for mortality prediction for heart patients using ACO-HKNN. J Ambient Intell Humanized Comput 0123456789. https://doi.org/10.1007/s12652-020-02027-6
Mateos-García D, García-Gutiérrez J, Riquelme-Santos JC (2019) On the evolutionary weighting of neighbours and features in the k-nearest neighbour rule. Neurocomputing 326–327:54–60. https://doi.org/10.1016/j.neucom.2016.08.159
Tiwari P, Melucci M (2018) Towards a quantum-inspired framework for binary classification. In Proceedings of the 27th ACM international conference on information and knowledge management (pp. 1815-1818)
Muhammad G, Hossain MS, Kumar N (2020) EEG-based pathology detection for home health monitoring. IEEE J Sel Areas Commun 39(2):603–610. https://doi.org/10.1109/JSAC.2020.3020654
Rahman MA, Hossain MS (2021) An Internet of Medical Things-Enabled Edge Computing Framework for Tackling COVID-19. IEEE Intern Things J. https://doi.org/10.1109/JIOT.2021.3051080
Tiwari P, Melucci M (2019) Towards a quantum-inspired binary classifier. IEEE Access 7:42354–42372
Van MT, van Tuan N, Son TT, Le-Minh H, Burton A (2017) Weighted k-nearest neighbour model for indoor VLC positioning. IET Commun 11(6):864–871. https://doi.org/10.1049/iet-com.2016.0961
Okfalisa, Gazalba, I, Mustakim, Reza NGI (2018) Comparative analysis of k-nearest neighbor and modified k-nearest neighbor algorithm for data classification. Proceedings - 2017 2nd International Conferences on Information Technology, Information Systems and Electrical Engineering, ICITISEE 2017, 2018-January, 294-298. https://doi.org/10.1109/ICITISEE.2017.8285514
Song G, Rochas J, El Beze LE, Huet F, Magoulès F (2016) K Nearest Neighbour Joins for Big Data on MapReduce: A Theoretical and Experimental Analysis. IEEE Transac Knowled Data Eng, 28(9), 2376-2392. https://doi.org/10.1109/TKDE.2016.2562627
Uprety S, Dehdashti S, Hossain MS (2020) TermInformer: unsupervised term mining and analysis in biomedical literature. Neural Comput Appl 1–14
Hasell J, Mathieu E, Beltekian D et al (2020) A cross-country database of COVID-19 testing. Sci Data 7:345
Menghour K, Souici-Meslati L (2016) Hybrid ACO-PSO based approaches for feature selection. Int J Intell Eng Syst 9:65–79
Vincent, Pascal, Bengio Y (2002) K-Local hyperplane and convex distance nearest neighbor algorithms. Adv Neural Inf Proc Syst
Sowmiya C, Sumitra P (2020) A hybrid approach for mortality prediction for heart patients using ACO-HKNN. J Ambient Intell Humanized Comput
Abdulsalam Y. Hossain, MS. (2020) COVID-19 Networking demand: an auction-based mechanism for automated selection of edge computing services. IEEE Transac Net Sci Eng. https://doi.org/10.1109/TNSE.2020.3026637
Lalmuanawma S, Hussain J, Chhakchhuak L (2020) Applications of machine learning and artificial intelligence for Covid-19 (SARS-CoV-2) pandemic: a review. Chaos, Solitons Fractals 139:110059. https://doi.org/10.1016/j.chaos.2020.110059
Khanday AMUD, Rabani ST, Khan QR, Rouf N, Din Mohi Ud, M. (2020) Machine learning based approaches for detecting COVID-19 using clinical text data. Int J Inf Technol (Singapore) 12(3):731–739. https://doi.org/10.1007/s41870-020-00495-9
Case Study for Epileptic Seizure Detection and Monitoring (2018) Alhussein, M. et al. (2018). Cognitive IoT-Cloud Integration for Smart Healthcare. Mobile Netw Appl 23:1624–1635. https://doi.org/10.1007/s11036-018-1113-0A
Hossain MS. Muhammad, G. (2020) Deep learning based pathology detection for smart connected healthcares. IEEE Netw 34(6):120–125. https://doi.org/10.1109/MNET.011.2000064
Jabbar MA, Deekshatulu BL, Chandra P (2013) Classification of heart disease using K- Nearest Neighbor and genetic algorithm. Procedia Technol 10:85–94. https://doi.org/10.1016/j.protcy.2013.12.340
Amin UA et al. (2019) Multilevel weighted feature fusion using convolutional neural networks for eeg motor imagery classification. IEEE Access.7, 18940-18950 https://doi.org/10.1109/ACCESS.2019.2895688.
Tan W, et al (2020) Multimodal medical image fusion algorithm in the era of big data. Neural Comput Appl, 1-21
ahmedMedjahed, S., Ait Saadi, T., & Benyettou, A. (2013) Breast cancer diagnosis by using k-nearest neighbor with different distances and classification rules. Int J Comput Appl 62(1):1–5. https://doi.org/10.5120/10041-4635
Lin H et al (2020) Privacy-enhanced data fusion for COVID-19 applications in intelligent internet of medical things. IEEE Inter Things J. https://doi.org/10.1109/JIOT.2020.3033129
Jaiswal AK, et al. (2020) Covidpen: A novel covid-19 detection model using chest x-rays and ct scans. medRxiv
Shaban WM, et al (2020) A new COVID-19 patients detection strategy (CPDS) based on hybrid feature selection and enhanced KNN classifier. Knowled Based Syst.205(1), https://doi.org/10.1016/j.knosys.2020.106270
Chouhan V, et al (2020) A novel transfer learning based approach for pneumonia detection in chest X-ray images. Appl Sci, 10(2), 559
Jaiswal AK et al (2019) Identifying pneumonia in chest X-rays: a deep learning approach. Measurement 145:511–518
Min W et al (2015) Cross-platform multi-modal topic modeling for personalized inter-platform recommendation. IEEE Trans Multimedia 17(10):1787–1801
Muhammad G, Hossain MS (2021) COVID-19 and non-COVID-19 classification using multi-layers fusion from lung ultrasound images. Inform Fusion 72:80–88
Alanazi S et al. (2020) Measuring and preventing COVID-19 using the SIR model and machine learning in smart health care. J Healthcare Eng, Article ID 8857346
Acknowledgements
This work was supported by the Taif University Researchers Supporting Project number (TURSP-2020/79), Taif University, Taif, Saudi Arabia.
Funding
Open access funding provided by Aalto University.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Mukherjee, R., Kundu, A., Mukherjee, I. et al. IoT-cloud based healthcare model for COVID-19 detection: an enhanced k-Nearest Neighbour classifier based approach. Computing 105, 849–869 (2023). https://doi.org/10.1007/s00607-021-00951-9
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00607-021-00951-9