1 Introduction

Wavelet analysis involves interesting mathematical properties such as function approximation and applications in signal processing through the discrete wavelet transform which can be implemented with perfect reconstruction filters [1, 2].

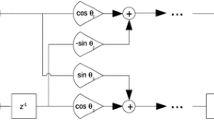
Compactly supported orthogonal wavelets can be used to implement the non-redundant discrete wavelet transform throughout lowpass and highpass filters that satisfy the quadrature mirror properties [3]. The compactly supported orthogonal wavelets can be obtained from scaling functions through the dyadic dilation equation:

$$\begin{aligned} \varphi (t)= \sum _{k=0}^{N-1} h_k \varphi (2t-k) \end{aligned}$$
(1)

where \(N \in \mathbb {N}\), \(h_k \in \mathbb {R}\), and \(h_k=0\) for \(k<0\) and \(k \ge N\). The sequences \(h_k\) and \(g_k=(-1)^{k}h_{N-1-k}\), for \(k=0, 1, \dots , N-1\) represent the impulse response of the filter bank conformed by the low pass filter and the high pass filter respectively. From this point of view, the design of orthogonal wavelets can be viewed as a filter design problem.

Several design criteria have been proposed based on the smoothness, differentiability, or compact support, such as those presented by Daubechies [4] that maximizes the vanishing moments of the wavelets.

An algebraic methodology to construct wavelets appeals to the parameterization of the \(h_k\) coefficients (see [3, 5,6,7,8]) once it reduces the search space of solutions at the same time it provides flexibility of the characteristics of the wavelets.

There are several works related to the construction of optimal wavelets for specific tasks. For example, in [9], an electrocardiogram compressor is proposed based on the optimal selection of wavelet filters and threshold levels in different subbands, to achieve maximum data volume reduction while guaranteeing the reconstruction quality. However, the computational complexity of the proposed technique is the price paid for the improvement in the compression performance measures. In [10], a secret key is implemented using parameterized wavelet filters to improve the security of digital watermarking, and is highlighted the importance of the security as a priority to protect the location of the watermark information. In [11], the researchers support the utility of exploring wavelet parameterizations to maximize the classification accuracy in the development of biomarkers of psychiatric disease and neurological disorders, and report that the length of the wavelet filter has a greater impact on the estimated values of graph metrics than the type of the chosen wavelet. Since one of the main drawbacks of constructing wavelets is the computational cost required to optimize large parameterized filters, we contribute with an approach based on inverse parameterizations, and we expect that other research areas could be benefit with them.

In this work, we review the parameterization of length 4, 6, 8, and 10 filters given in [12,13,14], and present their inverse formulas to get the parameter values from a set of valid \(h_k\) coefficients. We also present an application of these inverse formulas in image compression, throughout the optimization of the parameters to maximize the number of negligible wavelet coefficients.

The article is organized in sections as follows: in Sect. 2 we review the parameterization of filters and obtain their inverse formulas. In Sect. 3, we present several computational experiments to validate the inverse formulas, discuss some properties related to their domain, and present some results with applications in image processing. Finally, in Sect. 4, we present some conclusions.

2 Parameterization of filter coefficients

In this section we review the orthogonality conditions, the parameterization of filters with length 4, 6, 8, and 10, and present their inverse formulas.

From [12,13,14,15] we consider the orthonormality conditions:

$$\begin{aligned} \vert H(z) \vert ^2 + \vert H(-z) \vert ^2= & {} 1, \quad z=e^{i\omega }, and \omega \in \mathbb {R} \end{aligned}$$
(2)
$$\begin{aligned} H(z=1)= & {} 1 \end{aligned}$$
(3)

and the zero moment condition:

$$\begin{aligned} H(z=-1) = 0 \end{aligned}$$
(4)

where H(z) is the trigonometric polynomial expressed as \(H(z)= \sum _k h_k z^k\).

For a filter of length N we have:

$$\begin{aligned} H{(z)}= \sum _{k=0}^{k=N-1}\ _Nh_{k} z^k,\end{aligned}$$
(5)

where we use the notation \(_Nh_{k}\) to represent the k-th coefficient of a filter of length N. Also, we will use parameters with sub-indices to indicate the filter length, for example, \(_4h_{0}\), \(_4h_{1}\), \(_4h_{2}\), and \(_4h_{3}\) are the coefficients of the length four filter, and \(\alpha _4\) the free parameter.

2.1 Parameterization of the length four filters

The parameterization of a perfect reconstruction filter is not unique (see for example [3, 6, 12,13,14]). For our purposes, we will use the parameterizations of [12,13,14]. In particular, for the length four case, we have:Footnote 1

$$\begin{aligned} _4h_{0}= & {} \frac{1}{4} +\frac{1}{2\sqrt{2}}\cos \alpha _4 \end{aligned}$$
(6)
$$\begin{aligned} _4h_{1}= & {} \frac{1}{4} +\frac{1}{2\sqrt{2}}\sin \alpha _4 \end{aligned}$$
(7)
$$\begin{aligned} _4h_{2}= & {} \frac{1}{4} -\frac{1}{2\sqrt{2}}\cos \alpha _4 \end{aligned}$$
(8)
$$\begin{aligned} _4h_{3}= & {} \frac{1}{4} -\frac{1}{2\sqrt{2}}\sin \alpha _4 \end{aligned}$$
(9)

And, from Eqs. (6) to (9), we proceed to calculate the inverse parameterizations, that consist in the determination of the parameter \(\alpha _4\) in terms of the \(_4h_k\) coefficients.

2.2 Inverse parameterization of the length four filters

It should be noted that, the parameterization of a given filter is not unique and moreover, given a single parameterization it is possible to get several inverse equations for the parameters. For example, it is possible to calculate the \(\alpha _4\) parameter in terms of the filter coefficients \(_4h_{0}\), \(_4h_{1}\), \(_4h_{2}\), and \(_4h_{3}\) by considering Eqs. (6)–(9), as follows:

$$\begin{aligned} \alpha _4= & {} \arccos \left( 2\sqrt{2} \left( _4h_0 - \frac{1}{4} \right) \right) \end{aligned}$$
(10)
$$\begin{aligned} \alpha _4= & {} \arcsin \left( 2\sqrt{2} \left( _4h_1 - \frac{1}{4} \right) \right) \end{aligned}$$
(11)
$$\begin{aligned} \alpha _4= & {} \arccos \left( 2\sqrt{2} \left( \frac{1}{4} -_4h_2 \right) \right) \end{aligned}$$
(12)
$$\begin{aligned} \alpha _4= & {} \arcsin \left( 2\sqrt{2} \left( \frac{1}{4} -_4h_3 \right) \right) \end{aligned}$$
(13)

Additional formulas for \(\alpha _4\) can be obtained. For example, subtracting Eq. (8) from (6) we get:

$$\begin{aligned} \alpha _4 = \arccos \left( \sqrt{2} \left( _4h_{0} - _4h_{2} \right) \right) \end{aligned}$$
(14)

and, subtracting Eq. (9) from (7) we get:

$$\begin{aligned} \alpha _4 = \arcsin \left( \sqrt{2} \left( _4h_{1} - _4h_{3} \right) \right) \end{aligned}$$
(15)

In Eqs. (10)–(13) the \(\alpha _4\) parameter depends on a single coefficient, whereas in Eqs. (14) and (15) it depends on two coefficients.

2.3 Parameterization of the length sixth filters

The parameterizations of Eqs. (16)–(21) for length sixth coefficients can be obtained following an algebraic approach, as described in detail in [12]:

$$\begin{aligned} _6h_0= & {} \frac{1}{8} + \frac{1}{4\sqrt{2}}\cos \alpha _6 + \frac{p_6}{2}\cos \beta _6 \end{aligned}$$
(16)
$$\begin{aligned} _6h_1= & {} \frac{1}{8} + \frac{1}{4\sqrt{2}}\sin \alpha _6 + \frac{p_6}{2}\sin \beta _6 \end{aligned}$$
(17)
$$\begin{aligned} _6h_2= & {} \frac{1}{4}-\frac{1}{2\sqrt{2}} \cos \alpha _6 \end{aligned}$$
(18)
$$\begin{aligned} _6h_3= & {} \frac{1}{4}-\frac{1}{2\sqrt{2}} \sin \alpha _6 \end{aligned}$$
(19)
$$\begin{aligned} _6h_4= & {} \frac{1}{8} + \frac{1}{4\sqrt{2}}\cos \alpha _6 - \frac{p_6}{2}\cos \beta _6 \end{aligned}$$
(20)
$$\begin{aligned} _6h_5= & {} \frac{1}{8} + \frac{1}{4\sqrt{2}}\sin \alpha _6 - \frac{p_6}{2}\sin \beta _6 \end{aligned}$$
(21)

where \(p_6=\frac{1}{2}\sqrt{1+\sin (\alpha _6+\frac{\pi }{4})}\), for \(\alpha _6, \beta _6 \in \mathbb {R}\).

Now, with an algebraic approach we get the inverse formulas for \(\alpha _6\) and \(\beta _6\) from the \(_6h_k\) coefficients.

2.4 Inverse parameterization of the length sixth filters

From Eq. (18) we get:

$$\begin{aligned} \alpha _6 = \arccos \left( 2 \sqrt{2}\left( \frac{1}{4} - _6h_{2}\right) \right) \end{aligned}$$
(22)

but, other alternative is to use Eq. (19), so:

$$\begin{aligned} \alpha _6 = \arcsin \left( 2 \sqrt{2}\left( \frac{1}{4}-_6h_{3}\right) \right) \end{aligned}$$
(23)

In case of the \(\beta _6\) parameter, we subtract Eqs. (21) from (17), and (20) from (16). Then, these partial results are divided to get \(\tan \beta _6\) in terms of \(_6h_{0}, _6h_{1}, _6h_{4}\) and \(_6h_{5}\), from which \(\beta _6\) can be expressed as:

$$\begin{aligned} \beta _6 = \arctan \left( \frac{_6h_{1}-_6h_{5}}{_6h_{0}-_6h_{4}}\right) \end{aligned}$$
(24)

2.5 Parameterization of the length eight filters with constraints

We identify two kinds of parameterizations for the length eight filters, namely, with and without parameter constraints. First, we will work with the constrained case.

In the case of the constrained parameterization of the length eight filters (see [12]) the formulas depend on parameters \(\alpha _8\), \(\beta _8\), \(\gamma _8\), and \(\theta _8\) as follows:

$$\begin{aligned} _8h_0= & {} \frac{1}{8}+\frac{1}{4\sqrt{2}}\cos \alpha _8 + \frac{1}{2\sqrt{2}}\cos \beta _8 \cos \gamma _8 \end{aligned}$$
(25)
$$\begin{aligned} _8h_1= & {} \frac{1}{8}+\frac{1}{4\sqrt{2}}\sin \alpha _8 + \frac{1}{2\sqrt{2}}\sin \beta _8 \cos \theta _8 \end{aligned}$$
(26)
$$\begin{aligned} _8h_2= & {} \frac{1}{8}-\frac{1}{4\sqrt{2}}\cos \alpha _8+\frac{1}{2\sqrt{2}} \cos \beta _8 \sin \gamma _8 \end{aligned}$$
(27)
$$\begin{aligned} _8h_3= & {} \frac{1}{8}-\frac{1}{4\sqrt{2}}\sin \alpha _8 + \frac{1}{2\sqrt{2}}\sin \beta _8 \sin \theta _8 \end{aligned}$$
(28)
$$\begin{aligned} _8h_4= & {} \frac{1}{8}+\frac{1}{4\sqrt{2}}\cos \alpha _8 - \frac{1}{2\sqrt{2}}\cos \beta _8 \cos \gamma _8 \end{aligned}$$
(29)
$$\begin{aligned} _8h_5= & {} \frac{1}{8}+\frac{1}{4\sqrt{2}}\sin \alpha _8 - \frac{1}{2\sqrt{2}}\sin \beta _8 \cos \theta _8 \end{aligned}$$
(30)
$$\begin{aligned} _8h_6= & {} \frac{1}{8}-\frac{1}{4\sqrt{2}}\cos \alpha _8 - \frac{1}{2\sqrt{2}}\cos \beta _8 \sin \gamma _8 \end{aligned}$$
(31)
$$\begin{aligned} _8h_7= & {} \frac{1}{8}-\frac{1}{4\sqrt{2}}\sin \alpha _8 - \frac{1}{2\sqrt{2}}\sin \beta _8 \sin \theta _8 \end{aligned}$$
(32)

Subject to the constraint:

$$\begin{aligned}&\sqrt{2}\cos \theta _8 \sin \beta _8 - 2cos\theta _8 \sin \alpha _8 \sin \beta _8 + \sqrt{2}\cos \beta _8 (\cos \gamma _8 -\sin \gamma _8)\nonumber \\&\quad -\,4 \cos ^2 \beta _8 \cos \gamma _8 \sin \gamma _8 -2 \cos \alpha _8 \cos \beta _8 (\cos \gamma _8 + \sin \gamma _8)\nonumber \\&\quad -\,\sqrt{2} \sin \beta _8 \sin \theta _8 -2 \sin \alpha _8 \sin \beta _8 \sin \theta _8 -4 \cos \theta _8 \sin ^2 \beta _8 \sin \theta _8=0 \end{aligned}$$
(33)

In Sect. 2.6, we calculate the inverse formulas for \(\alpha _8\), \(\beta _8\), \(\gamma _8\) and \(\theta _8\).

2.6 Inverse parameterization of the length eight filters with constraints

To obtain \(\alpha _8\), the addition of Eqs. (25)–(29) yields to:

$$\begin{aligned} \alpha _8 = \arccos \left( 2 \sqrt{2} (_8h_{0}+ _8h_{4}-\frac{1}{4})\right) \end{aligned}$$
(34)

and, once \(\alpha _8\) is known, the \(\gamma _8\) can be calculated from Eq. (31) as follows:

$$\begin{aligned} \sin \gamma _8 = \frac{2 \sqrt{2}}{\cos \beta _8} \left( - _8h_6 + \frac{1}{8} - \frac{\cos \alpha _8}{4\sqrt{2}} \right) \end{aligned}$$
(35)

and, from Eq. (25), we get:

$$\begin{aligned} \cos \gamma _8 = \frac{2 \sqrt{2}}{\cos \beta _8} \left( _8h_0 -\frac{1}{8} - \frac{\cos \alpha _8}{4\sqrt{2}} \right) \end{aligned}$$
(36)

Then, taken the division between Eqs. (35) and (36), and solving for \(\gamma _8\) we get:

$$\begin{aligned} \gamma _8 = \arctan \left( \frac{-_8h_{6}+\frac{1}{8}-\frac{\cos \alpha _8}{4\sqrt{2}} }{ _8h_{0}-\frac{1}{8}-\frac{\cos \alpha _8}{4\sqrt{2}}}\right) \end{aligned}$$
(37)

Now, since \(\alpha _8\) and \(\gamma _8\) are known, \(\beta _8\) can be solved from Eq. (25) as follows:

$$\begin{aligned} \beta _8 = \arccos \left( 2\sqrt{2} \frac{_8h_{0}-\frac{1}{8}-\frac{\cos \alpha _8}{4\sqrt{2}}}{\cos \gamma _8}\right) \end{aligned}$$
(38)

Since Eq. (26) involves \(\alpha _8\), \(\beta _8\) and \(\theta _8\), and the first two parameters are known, we can solve for \(\theta _8\) as follows:

$$\begin{aligned} \theta _8 = \arccos \left( 2\sqrt{2} \frac{_8h_{1}-\frac{1}{8}-\frac{\sin \alpha _8}{4\sqrt{2}}}{\sin \beta _8}\right) \end{aligned}$$
(39)

The constraint given in Eq. (33) must be satisfied for valid filter coefficients.

2.7 Parameterization of the length eight filters with no constraints

An improved version of the constrained parameterizations for length eight filters (see [13]) depends only on three parameters \(\alpha _8\), \(\beta _8\) and \(\gamma _8\), as is shown in Eqs. (40)–(48):

$$\begin{aligned} q_8= & {} \frac{1}{2} \cos (\alpha _8 - \gamma _8) (\cos (\alpha _8 +\beta _8-\gamma _8) + \sin (\alpha _8 + \beta _8 - \gamma _8)) \end{aligned}$$
(40)
$$\begin{aligned} _8h_0= & {} q_8 \cos (\beta _8 - \gamma _8) \cos \gamma _8 \end{aligned}$$
(41)
$$\begin{aligned} _8h_1= & {} q_8 \cos (\beta _8 - \gamma _8) \sin \gamma _8 \end{aligned}$$
(42)
$$\begin{aligned} _8h_2= & {} \frac{1}{2} (-\cos \alpha _8 + \sin \alpha _8) \sin \alpha _8 + q_8 \sin (\beta _8 - \gamma _8) \sin \gamma _8 \end{aligned}$$
(43)
$$\begin{aligned} _8h_3= & {} \frac{1}{2} (\cos \alpha _8 - \sin \alpha _8) \cos \alpha _8 - q_8 \sin (\beta _8 - \gamma _8) \cos \gamma _8 \end{aligned}$$
(44)
$$\begin{aligned} _8h_4= & {} \frac{1}{2} (\cos \alpha _8 + \sin \alpha _8) \cos \alpha _8 - q_8 \cos (\beta _8 - \gamma _8) \cos \gamma _8 \end{aligned}$$
(45)
$$\begin{aligned} _8h_5= & {} \frac{1}{2} (\cos \alpha _8 + \sin \alpha _8) \sin \alpha _8 - q_8 \cos (\beta _8 - \gamma _8) \sin \gamma _8 \end{aligned}$$
(46)
$$\begin{aligned} _8h_6= & {} -q_8 \sin (\beta _8 - \gamma _8) \sin \gamma _8 \end{aligned}$$
(47)
$$\begin{aligned} _8h_7= & {} q_8 \sin (\beta _8 - \gamma _8) \cos \gamma _8 \end{aligned}$$
(48)

From which we solve for \(\alpha _8, \beta _8\) and \(\gamma _8\) in Sect. 2.8.

2.8 Inverse parameterization of the length eight filters with no constraints

By adding Eq. (42) to Eq. (46), Eq. (41) to Eq. (45), taking the quotient of these partial results, and after applying the inverse of the tangent function we get:

$$\begin{aligned} \alpha _8 = \arctan \left( \frac{_8h_1+ _8h_5}{_8h_0+_8h_4}\right) \end{aligned}$$
(49)

Also, by adding Eq. (42) to Eq. (48) and applying the two trigonometric identities \(\cos (x-y)= \cos x \cos y + \sin x \sin y\) and \(\sin (x-y)= \sin x \cos y - \cos x \sin y\) we get:

$$\begin{aligned} _8h_1 + _8h_7 = q_8 \sin \beta _8 \end{aligned}$$
(50)

and

$$\begin{aligned} _8h_0 + _8h_6 = q_8 \cos \beta _8 \end{aligned}$$
(51)

thus,

$$\begin{aligned} \beta _8 = \arctan \left( \frac{_8h_1+ _8h_7}{_8h_0+_8h_6}\right) \end{aligned}$$
(52)

For the \(\gamma _8\) parameter, we divide \(_8h_6\) by \(_8h_7\), and applying the inverse of the tangent function, we get:

$$\begin{aligned} \gamma _8 = \arctan \left( -\frac{_8h_6}{_8h_7}\right) \end{aligned}$$
(53)

or, alternatively dividing Eq. (42) by (41) it takes to:

$$\begin{aligned} \gamma _8 = \arctan \left( \frac{_8h_1}{_8h_0}\right) \end{aligned}$$
(54)

In this case, there are no constraints for \(\alpha _8\), \(\beta _8\) and \(\gamma _8\).

Note that, in contrast with the constrained length eight case, the inverse formulas of Eqs. (49)–(53) depend on the filter coefficients exclusively, and not on the other parameters as in Eqs. (37), (38) and (39) of Sect. 2.6.

2.9 Parameterization of the length ten filters with constraints

According to [13], a constrained parameterization for the length ten coefficients is:

$$\begin{aligned} _{10}h_0= & {} \frac{1}{16}+\frac{1}{8\sqrt{2}}\cos \alpha _{10} + \frac{1}{4\sqrt{2}} \cos \beta _{10} \cos \gamma _{10} +\frac{r_{10}}{2}\cos \delta _{10} \end{aligned}$$
(55)
$$\begin{aligned} _{10}h_1= & {} \frac{1}{16}+\frac{1}{8\sqrt{2}}\sin \alpha _{10} + \frac{1}{4\sqrt{2}} \sin \beta _{10} \cos \theta _{10} +\frac{r_{10}}{2}\sin \delta _{10} \end{aligned}$$
(56)
$$\begin{aligned} _{10}h_2= & {} \frac{1}{8} -\frac{1}{4\sqrt{2}}\cos \alpha _{10} + \frac{1}{2\sqrt{2}} \cos \beta _{10} \sin \gamma _{10} \end{aligned}$$
(57)
$$\begin{aligned} _{10}h_3= & {} \frac{1}{8} -\frac{1}{4\sqrt{2}}\sin \alpha _{10} + \frac{1}{2\sqrt{2}} \sin \beta _{10} \sin \theta _{10} \end{aligned}$$
(58)
$$\begin{aligned} _{10}h_4= & {} \frac{1}{8} +\frac{1}{4\sqrt{2}}\cos \alpha _{10} - \frac{1}{2\sqrt{2}} \cos \beta _{10} \cos \gamma _{10} \end{aligned}$$
(59)
$$\begin{aligned} _{10}h_5= & {} \frac{1}{8} +\frac{1}{4\sqrt{2}}\sin \alpha _{10} - \frac{1}{2\sqrt{2}} \sin \beta _{10} \cos \theta _{10} \end{aligned}$$
(60)
$$\begin{aligned} _{10}h_6= & {} \frac{1}{8} -\frac{1}{4\sqrt{2}}\cos \alpha _{10} - \frac{1}{2\sqrt{2}} \cos \beta _{10} \sin \gamma _{10} \end{aligned}$$
(61)
$$\begin{aligned} _{10}h_7= & {} \frac{1}{8} -\frac{1}{4\sqrt{2}}\sin \alpha _{10} - \frac{1}{2\sqrt{2}} \sin \beta _{10} \sin \theta _{10} \end{aligned}$$
(62)
$$\begin{aligned} _{10}h_8= & {} \frac{1}{16}+\frac{1}{8\sqrt{2}}\cos \alpha _{10} + \frac{1}{4\sqrt{2}} \cos \beta _{10} \cos \gamma _{10} -\frac{r_{10}}{2}\cos \delta _{10} \end{aligned}$$
(63)
$$\begin{aligned} _{10}h_9= & {} \frac{1}{16}+\frac{1}{8\sqrt{2}}\sin \alpha _{10} + \frac{1}{4\sqrt{2}} \sin \beta _{10} \cos \theta _{10} -\frac{r_{10}}{2}\sin \delta _{10} \end{aligned}$$
(64)

where \(r_{10}=\sqrt{\frac{1}{2}-a_1^2-a_2^2-a_3^2-b_1^2-b_2^2-b_3^2}\), and subject to the constraint:

$$\begin{aligned}&\cos \beta _{10}(\cos \gamma _{10}(\sqrt{2}-2cos \alpha _{10})-8\sqrt{2}r_{10}\cos \delta _{10} \sin \gamma _{10}) \nonumber \\&\quad +\sin \beta _{10}(\cos \theta _{10}(\sqrt{2}-2 \sin \alpha _{10})-8\sqrt{2}r_{10} \sin \delta _{10} \sin \theta _{10})=0 \end{aligned}$$
(65)

From which we will obtain the inverse formulas for \(\alpha _{10}, \beta _{10}, \gamma _{10}, \theta _{10},\) and \(\delta _{10}\).

2.10 Inverse parameterization of the length ten filters with constraints

For \(\alpha _{10}\) note that the signed summation of Eqs. (55), (57), (59), (61), and (63) produces:

$$\begin{aligned} \frac{1}{\sqrt{2}}\cos \alpha _{10} = _{10}h_0 - _{10}h_2 + _{10}h_4 - _{10}h_6 + _{10}h_8 \end{aligned}$$
(66)

hence,

$$\begin{aligned} \alpha _{10} = \arccos (\sqrt{2} (_{10}h_0 - _{10}h_2 + _{10}h_4 - _{10}h_6 + _{10}h_8)) \end{aligned}$$
(67)

For \(\gamma _{10}\), the signed summation of Eqs. (55), (59), and (63) gives place to:

$$\begin{aligned} \frac{1}{\sqrt{2}}\cos \beta _{10} \cos \gamma _{10}= _{10}h_0 - _{10}h_4 + _{10}h_8 \end{aligned}$$
(68)

and, subtracting Eqs. (61) to (57) it yields to:

$$\begin{aligned} \frac{1}{\sqrt{2}}\cos \beta _{10} \sin \gamma _{10} = _{10}h_2 - _{10}h_6 \end{aligned}$$
(69)

Then, dividing Eq. (69) by (68) and solving for \(\gamma _{10}\) we get:

$$\begin{aligned} \gamma _{10} = \arctan \left( \frac{_{10}h_2 - _{10}h_6}{_{10}h_0 - _{10}h_4 + _{10}h_8}\right) \end{aligned}$$
(70)

For \(\beta _{10}\), once \(\gamma _{10}\) is known, it can be calculated from Eq. (68) as follows:

$$\begin{aligned} \beta _{10} = \arccos \left( \frac{\sqrt{2} (_{10}h_2 - _{10}h_6)}{\sin \gamma _{10}} \right) \end{aligned}$$
(71)

For \(\theta _{10}\) note that

$$\begin{aligned} \frac{1}{\sqrt{2}} \sin \beta _{10} \sin \theta _{10} = _{10}h_3 - _{10}h_7 \end{aligned}$$
(72)

and

$$\begin{aligned} \frac{1}{\sqrt{2}} \sin \beta _{10} \cos \theta _{10} = _{10}h_1 - _{10}h_5 + _{10}h_9 \end{aligned}$$
(73)

then, dividing Eq. (72) by (73) and solving for \(\theta _{10}\) we get:

$$\begin{aligned} \theta _{10} = \arctan \left( \frac{_{10}h_3 - _{10}h_7}{_{10}h_1 - _{10}h_5 + _{10}h_9}\right) \end{aligned}$$
(74)

Finally, since

$$\begin{aligned} r_{10} \sin \delta _{10} = _{10}h_1 - _{10}h_9 \end{aligned}$$
(75)

and

$$\begin{aligned} r_{10} \cos \delta _{10} = _{10}h_0 - _{10}h_8 \end{aligned}$$
(76)

we obtain:

$$\begin{aligned} \delta _{10} = \arctan \left( \frac{_{10}h_1 - _{10}h_9}{_{10}h_0 - _{10}h_8}\right) \end{aligned}$$
(77)

The constraint for the five parameters \(\alpha _{10}, \beta _{10}, \gamma _{10}, \delta _{10}\) and \(\theta _{10}\) given in Eq. (65) must be fulfilled.

2.11 Parameterization of the length ten filters with no constraints

An alternative parameterization to those of Sect. 2.9 was presented in [14] with no parameter constraints and depending on four parameters \(\alpha _{10}\), \(\beta _{10}\), \(\gamma _{10}\), and \(\delta _{10}\), as is shown in Eqs. (78)–(90):

$$\begin{aligned} p_{10}= & {} \frac{1}{4} \sin (\alpha _{10} + \beta _{10}) (\cos \alpha _{10} + \sin \alpha _{10} - \sqrt{2} \sin \delta _{10}) \end{aligned}$$
(78)
$$\begin{aligned} q_{10}= & {} \frac{1}{2} ( \cos \alpha _{10} - \sin \alpha _{10}) \cos (\alpha _{10} + \beta _{10}) \end{aligned}$$
(79)
$$\begin{aligned} r_{10}= & {} \frac{1}{\sqrt{2}} \cos \delta _{10} \sin (\alpha _{10} + \beta _{10}) \end{aligned}$$
(80)
$$\begin{aligned} _{10}h_0= & {} \frac{p_{10}}{2} (\cos \beta _{10} + \cos \gamma _{10}) \end{aligned}$$
(81)
$$\begin{aligned} _{10}h_1= & {} \frac{p_{10}}{2} (\sin \beta _{10} + \sin \gamma _{10}) \end{aligned}$$
(82)
$$\begin{aligned} _{10}h_2= & {} \frac{1}{8} (1+ \cos 2\alpha _{10} - \sin 2\alpha _{10} ) + \frac{1}{2} (q_{10} \cos \gamma _{10} - r \sin \gamma _{10} ) \end{aligned}$$
(83)
$$\begin{aligned} _{10}h_3= & {} \frac{1}{8} (1- \cos 2\alpha _{10} - \sin 2\alpha _{10} ) + \frac{1}{2} (q_{10} \sin \gamma _{10} + r \cos \gamma _{10} ) \end{aligned}$$
(84)
$$\begin{aligned} _{10}h_4= & {} \frac{1}{4} (1 - \cos 2\alpha _{10} + \sin 2\alpha _{10} ) - p_{10} \cos \beta _{10} \end{aligned}$$
(85)
$$\begin{aligned} _{10}h_5= & {} \frac{1}{4} (1 + \cos 2\alpha _{10} + \sin 2\alpha _{10} ) - p_{10} \sin \beta _{10} \end{aligned}$$
(86)
$$\begin{aligned} _{10}h_6= & {} \frac{1}{8} (1+ \cos 2\alpha _{10} - \sin 2\alpha _{10} ) - \frac{1}{2} (q_{10} \cos \gamma _{10} - r \sin \gamma _{10} ) \end{aligned}$$
(87)
$$\begin{aligned} _{10}h_7= & {} \frac{1}{8} (1- \cos 2\alpha _{10} - \sin 2\alpha _{10} ) - \frac{1}{2} (q_{10} \sin \gamma _{10} + r \cos \gamma _{10} ) \end{aligned}$$
(88)
$$\begin{aligned} _{10}h_8= & {} \frac{p}{2} (\cos \beta _{10} - \cos \gamma _{10} ) \end{aligned}$$
(89)
$$\begin{aligned} _{10}h_9= & {} \frac{p}{2} (\sin \beta _{10} - \sin \gamma _{10} ) \end{aligned}$$
(90)

From Eq. (78) to (90) we obtain the inverse formulas for \(\alpha _{10}\), \(\beta _{10}\), \(\gamma _{10}\), and \(\delta _{10}\).

2.12 Inverse parameterization of the length ten filters with no constraints

To solve for \(\alpha _{10}\) see that

$$\begin{aligned} \frac{1}{4} \left( 1+ \cos 2\alpha _{10} - \sin 2\alpha _{10} \right) = _{10}h_2 + _{10}h_6 \end{aligned}$$
(91)

and since \( \cos 2\alpha _{10} - \sin 2\alpha _{10} = \sqrt{2} \cos (2\alpha + \frac{\pi }{4})\) hence

$$\begin{aligned} \alpha _{10} = \frac{1}{2} \left( \arccos \left( \frac{4 (_{10}h_2 + _{10}h_6) -1}{\sqrt{2}} \right) - \frac{\pi }{4}\right) \end{aligned}$$
(92)

To solve for \(\beta _{10}\) see that

$$\begin{aligned} p_{10} \sin \beta _{10} = _{10}h_1+_{10}h_9 \end{aligned}$$
(93)

and,

$$\begin{aligned} p_{10} \cos \beta _{10} = _{10}h_0 + _{10}h_8 \end{aligned}$$
(94)

hence

$$\begin{aligned} \beta _{10} = \arctan \left( \frac{_{10}h_1+_{10}h_9}{_{10}h_0 + _{10}h_8}\right) \end{aligned}$$
(95)

To solve for \(\gamma _{10}\) see that

$$\begin{aligned} p_{10} \sin \gamma _{10} = _{10}h_1-_{10}h_9 \end{aligned}$$
(96)

and,

$$\begin{aligned} p_{10} \cos \gamma _{10} = _{10}h_0-_{10}h_8 \end{aligned}$$
(97)

hence

$$\begin{aligned} \gamma _{10} = \arctan \left( \frac{_{10}h_1-_{10}h_9}{_{10}h_0-_{10}h_8}\right) \end{aligned}$$
(98)

To solve for \(\delta _{10}\), the \(p_{10}\) value is required, so we use Eq. (81) to get:

$$\begin{aligned} p_{10} = \frac{2_{10}h_{0}}{\cos \beta _{10} + \cos \gamma _{10}} \end{aligned}$$
(99)

And, from Eq. (78), we have for \(\delta _{10}\):

$$\begin{aligned} \delta _{10} = \arcsin \left( \frac{1}{\sqrt{2}} \left( \cos \alpha _{10} + \sin \alpha _{10}- \frac{4p_{10}}{\sin (\alpha _{10} + \beta _{10})} \right) \right) \end{aligned}$$
(100)

where there are no constraints for the four parameters \(\alpha _{10}, \beta _{10}, \gamma _{10}\) and \(\theta _{10}\) as in Sect. 2.9.

3 Experiments

In this section, we develop five experiments to validate the inverse formulas and present a parameter repair technique. We also include an application in image compression.

3.1 Experiment 1

In Experiment 1, we deal with the problem of mismatching between the domain and the range of the parameters for which the filter parameterizations and their inverse formulas are defined.

Note that the filter parameterizations are defined in the \(\mathbb {R}\) domain but, in practical applications such as language programming implementations, it is convenient to use a finite interval, such as \([0, 2\pi )\) by appealing to the periodicity of the involved trigonometric functions.

Additionally, note that the range of the arcsin, arccos and arctan trigonometric functions involved in the inverse formulas, does not match the \([0, 2\pi )\) interval, so it is impossible to recover an original value of the parameters. To deal with this case, we propose a repair technique described next.

To repair a parameter we proceed to explore several alternatives by considering the symmetry and periodicity of the trigonometric functions. For example, given the \(\alpha \) parameter obtained from an inverse formula, the next alternatives are considered:

$$\begin{aligned} A=\{ MOD(\pm \alpha \pm n * \pi / 4) \} \quad for \quad n=\{0, 1, 2, 3, 4, 5 , 6, 7, 8\} \end{aligned}$$
(101)

where \({\textit{MOD}}(x)\) is a function from \(x \in R \rightarrow [0, 2\pi )\) described in Algorithm 1.

figure a

The same applies for each parameter. The number of parameter combinations is \(C=\vert A \vert ^P\), where P is the number of free parameters involved in the corresponding filter parameterization.

In our experiments, we consider filters of length four and six for constrained and length eight and ten for unconstrained optimization. So, we do not include the constrained cases for length eight and ten filters because a random generation of their parameters in \([0, 2\pi )\) does not necessarily satisfy the restrictions of Eqs. (33) and (65). However, for further information about the optimization of constrained parameterizations, see for example [16].

We executed an exhaustive search algorithm to determine the repaired value of each parameter obtained from the inverse formulas following the steps of Algorithm 2.

figure b

With MAX=27000 iterations, and \(\epsilon < 10^{-10}\) we got the results of Table 1, where we can observe that a reduced number of parameter alternatives (column marked with *) are required to repair the parameters with an efficiency of \(100\%\).

The most notable time and space search saving is for the length ten case, where the elapsed time was reduced from 99.167 s to 0.562 s, and the space search was reduced from \(34^4\) to 135. The experiments were executed on a Linux based system with 4 Intel Xeon CPU @2.53GHz and 16GBRAM.

Table 1 Exhaustive search to identify alternatives for parameter repair
Full size table

3.2 Experiment 2

In Experiment 2, we apply the inverse equations and the repair technique of Experiment 1 to calculate parameters of well known filters.

In Table 2 we report the parameters for the Daubechies filters, and in Table 3, we report the parameters for Coiflets and Symlets (see [17]). Of course, all the parameters are in \([0, 2 \pi )\).

We remark the importance of detecting the cases where the inverse equations are not defined, for example, in the Haar filter the denominator of Eq. (53) is zero, but we apply Eq. (54) instead.

Table 2 Parameters for Daubechies filters (vanishing moments in the wavelet function)
Full size table
Table 3 Parameters for Coiflets and Symlets (vanishing moments in the scaling and wavelet functions)
Full size table

3.3 Experiment 3

In Experiment 3, we illustrate the nesting property of parameterized filters: shorter filters can be seen as special cases of larger filters.

The nesting property can be useful for optimization purposes because shorter filters have a lower number of parameters than larger filters. Therefore, once the parameters of a shorter filter are optimized, the coefficients can be exported to larger filters via the inverse formulas (see [16, 18]).

In Table 2, it is possible to see that the named parameters \((\alpha , \beta , \gamma \) or \(\delta )\) of shorter filters does not always correspond to those of larger filters for the same nested filter, and the inversion formulas make possible to export the \(h_k\) coefficients to larger filters to get the right parameter values.

As part of Experiment 3, we apply the nesting property to image compression by comparing two approaches: (1) Nesting optimization: the optimization of parameters of shorter filters and exporting the coefficients to larger filters via the inverse formulas, and (2) Direct optimization: the optimization of the length ten filter parameters with no parameter exportation. Note that we refer to image compression although we do not apply any encoding step, since we have studied the relation between compressibility and the energy concentration in the lowest number of wavelet coefficients [16].

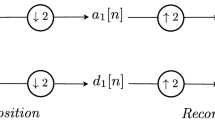
We recall that the discrete wavelet transform of an image with dimensions width (w) and height (h) can be calculated with horizontal and vertical transformation steps [19] which generates a pyramidal effect that gives place to four sub-bands HH, HL, LH and LL, with \(\frac{w}{2} \times \frac{h}{2}\) wavelet coefficients. The HH sub-band stores the most detailed information of the image, whereas the LL sub-band stores the coarser information. When a second transformation level is applied to the LL sub-band, it generates the other four sub-bands, and the process continues while the width and height of the new sub-bands are larger than the parameterized filter.

As we have already mentioned, we estimate the image compressibility in terms of the concentration of energy in the lowest number of wavelet coefficients that minimizes the entropy in the wavelet domain [16, 20]. The energy of a gray-scale image with \(w \times h\) pixels (in the time domain) is given by:

$$\begin{aligned} E=\sum _{i=0}^{w-1} \sum _{j=0} ^{h-1} p_i^2, \quad \text {for} \quad 0 \le p_i \le 255 \end{aligned}$$
(102)

where the \(p_i\) is a pixel value.

After applying the discrete wavelet transform, the wavelet coefficients \(W_i\) conserve the energy,Footnote 2 so the energy in the time-frequency domain is:

$$\begin{aligned} E= \sum _{i=0}^{w-1} \sum _{j=0} ^{h-1} W_i^2 \end{aligned}$$
(103)

By sorting the \(w\times h\) wavelet coefficients in descendent order, we define the cumulative energy of the signal as follows:

$$\begin{aligned} E_c= \sum _{k=0}^{r} W_i^2,\ \ \ 0 \le r < w \times h \end{aligned}$$
(104)
Table 4 Negligible coefficients for Lena image (\(64 \times 64\) and \(128 \times 128\) pixels)
Full size table

Then, we use a genetic algorithm to optimize the filter parameters that maximizes the number of negligible wavelet coefficients (NC) that are less than a threshold value (Th). The threshold Th is automatically calculated when the percentage of cumulative energy \(PE = \frac{E_c}{E}\) reaches a predetermined value.

The fitness function for the genetic algorithm is:

$$\begin{aligned} MAX \quad fitness(PE) = NC \end{aligned}$$
(105)

and the genetic algorithm is characterized by [21]:

  • A population of even size P, with a temporal population of size 2P.

  • Pair wise for crossover between the i-th and the (\(P-1-i\))-th sorted individuals, \(i \in [0, P -1]\).

  • Deterministic selection, the best P individuals from the temporal population.

  • Annular crossover.

Each individual encodes the values of the parameters in the interval \([0, 2\pi )\) and \(PE=0.999999\). The parameters for the genetic algorithm were \(Pm=0.03\), \(Pc=0.97\), and \(P=8\) individuals, with 30 bits of precision.

3.4 Results of Experiment 3

Table 4 shows the results for the Lena image with \(64 \times 64\) pixels. The first column is the genetic algorithm generation, the second column corresponds to the length four filter (F4), the third column to the length sixth filter (F6), the fourth column to the length eight filter (F8), and the fifth column to the length ten filter (F10) exporting their best individual to the next larger filter (\(F4 \rightarrow F6 \rightarrow F8 \rightarrow F10\)). The sixth column corresponds to the direct optimization of the length ten filter (F10*).

Fig. 1
figure 1

Negligible coefficients for the Lena image with \(64 \times 64\) pixels (left) and \(128 \times 128\) pixels (right)

Full size image

Note that the nesting property provides an acceleration in the convergence, and maintains the number of negligible coefficients above the counterpart, along 20 generations. For each generation, the larger filters dominate to shorter filters, taking advantage of their best individuals.

Also, in Table 4, a similar result was obtained for the Lena image of \(128 \times 128\) pixels. The seventh column corresponds to the length four filter (F4), the eight column to the length sixth filter (F6), the ninth column to the length eight filter (F8), and the tenth column to the length ten filter (F10) exporting their best individual to the next larger filter (\(F4 \rightarrow F6 \rightarrow F8 \rightarrow F10\)). The last column corresponds to the direct optimization of the length ten filter (\(F10*\)).

Figure 1 illustrates the data of Table 4: a) for the Lena image with \(64 \times 64\) pixels that reaches \(11.7\%\) of negligible coefficients (left side), and b) for the Lena image of \(128 \times 128\) pixels that reaches \(13.9\%\) of negligible coefficients (right side), with an almost perfect reconstruction preserving \(99.9999\%\) of the energy.

Comparing the percentage of F4 with the percentage of F10 after 20 generations, we have a difference of \(0.53\%\) for Lena \(64\times 64\) and \(1.39\%\) for Lena \(128\times 128\).

For the Lena image with \(64 \times 64\) pixels, the optimized parameters for F10 were \(\alpha _{10}=0.43752732136\), \(\beta _{10}=1.11193750642\), \(\gamma _{10}=1.11193750642\), and \(\delta _{10}=4.35859793125\) (cf. Table 2).

For the Lena image with \(128 \times 128\) pixels, the optimized parameters for F10 were \(\alpha _{10}=0.57094882076\), \(\beta _{10}=0.99754652901\), \(\gamma _{10}=0.99754652901\), and \(\delta _{10}=4.49793963189\) (cf. Table 2).

3.5 Experiment 4

In Experiment 4, we processed the Lena image with \(512 \times 512\) pixels, and let the genetic algorithm to execute \(G=100\) generations to get a better perspective of the convergence towards the optimal value. We tested with an energy conservation \(PE=0.999999\) and \(PE=0.999995\).

3.6 Results of Experiment 4

Table 5 shows the results for the Lena image with \(512 \times 512\) pixels every 5 generations. Figure 2 illustrates the Table 5 data with the results of all the 100 generations.

On one hand, note that for a cumulative energy \(PE=0.999999\), the filter F10 produced \(NC=40160\) negligible coefficients (\(15.3\%\)) with an \(RMSE=0.137444\), and for \(PE=0.999995\) the number of negligible coefficients increased to \(NC=67702\) (\(25.8\%\)) with an \(RMSE=0.307334\), so we have considered that PE can be used as a quality factor.

For the Lena image with \(512\times 512\) pixeles, the optimized parameters for F10 were \(\alpha _{10}=2.77460611264\), \(\beta _{10}=1.54593953461\), \(\gamma _{10}=1.53378153259\), and \(\delta _{10}=0.58070206633\) (cf. Table 2).

On the other hand, note that the smallest filter F4 almost reaches its maximum in 10 generations, but its outperformed by the nested filters (\(F4 \rightarrow F6 \rightarrow F8 \rightarrow F10\)) from the beginning. In fact, F10 is better than F4 in \(1.16\%\) from the first generation even though they were randomly initialized.

Also, note that the \(F10*\) with no inverse parameterizations follows a similar behavior to F4 in the first 40 generations.

It is possible to see that the application of the inverse parameterizations allows F10 to reach \(0.99\%\) of the global value in the first 10 generations, which is never reached by the direct optimization \(F10*\).

As additional information, consider that the average time for each generation was 5.96 s.

Experiment 4 supports the advantages of the inverse parameterizations and the nesting property, by guaranteeing that a larger filter will not be overtaken by a shorter filter and, at the same time, by providing a better flexibility in the search of additional solutions without a demerit of the convergence acceleration to the global solution.

Table 5 Negligible coefficients for Lena image (\(512 \times 512\) pixels)
Full size table

3.7 Experiment 5

In Experiment 5, we processed 28 face images from a repository (see [22]). The images were resized to \(1024 \times 1024\) pixels in grayscale that correspond to unique people.

To see the convergence towards the optimal value, we executed the genetic algorithm with \(G=100\) generations and a population of \(P=4\) individuals, that spent an average of 23 s for each generation.

In this case, we calculated the average of the negligible coefficients over the 28 images for each filter F4, F6, F8, F10 with nesting optimization, and \(F10*\) with direct optimization.

In Table 6, we show these average results for 28 images every 5 generations, and in Fig. 3 (left subfigure) we illustrate the performance of each filter F4, F6, F8, F10 and \(F10*\) for \(G=100\) generations.

In Fig. 3 (right subfigure) we illustrate a box plot with the performance of each filter F4, F6, F8, F10 and \(F10*\).

Fig. 2
figure 2

Negligible coefficients for the Lena image with \(512 \times 512\) pixels: energy conservation \(PE=0.999999\) (left) and \(PE=0.999995\) (right)

Full size image

3.8 Results of Experiment 5

In Fig. 3 (left subfigure) and Table 6, we can see that F10 outperforms all the filters, from the first generation.

Note that both filters, F10 and \(F10*\), converge to the same result in a large number of generations.

After 85 generations \(F10*\) follows, but does not overcome, F10. It shows how the inverse formulas and the nesting property allow to accelerate the convergence towards the global optimum, even from the first generation.

Although the small filter F4 has a fast convergence, it almost reaches its maximum value in a few generations (bold values in Table 6) but it follows an asymptotical convergence to a sub-optimal solution. Moreover, F4 never reaches the worst case of F10 (first generation).

In the box plot of Fig. 3, we can see that, effectively, F10 outperforms the other filters and provides a consistent improvement of \(3.4\%\) while conserving \(99.9999\%\) of the energy.

Also, in the box plot of Fig. 3, we can see that all the boxes are placed under the F10 box, and it corroborates the utility of the the parameter repair, the nesting property and the inverse parameterizations.

As the size of the images increases, the difference in the percentage of negligible wavelet coefficients between small and large filters also increases, so we consider that it can lead to applications with higher resolution images.

Table 6 Average percentage of negligible coefficients for 28 images from a repository (resize to \(1024 \times 1024\) pixels)
Full size table
Fig. 3
figure 3

Average percentage of negligible coefficients for face images (\(1024 \times 1024\) pixels)

Full size image

4 Conclusions

The parameterization of orthogonal filters have been widely studied motivated for the problem of filter design and the construction of wavelet based systems. In this sense, we contribute with the inverse formulas to determine the parameters from valid filter coefficients.

One of the main drawbacks of personalizing the filters is the slowness to calculate them. However, since there is evidence that standard wavelets can be outperformed by personalized wavelets and that short filters yield to sub-optimal solutions, we present a nesting property of parametric filters where the optimization of shorter filters can be used to improve the performance of larger filters by exporting the best coefficients throughout the inverse formulas. This property can be useful in the optimization of larger filters for several applications where is justified the use of these filters. For example, in digital watermarking to enhance the security, since optimized filters allow to protect the location of the watermark information. Also, in classification of neurological signals to enhance the accuracy, and in applications of image compression where we have show some advantages of using the inverse parameterizations. So, we expect that other research areas could be benefit of the inverse parameterizations.