Abstract
This article is a natural continuation of the paper Tiwari, D., Giordano, P., Hyperseries in the non-Archimedean ring of Colombeau generalized numbers in this journal. We study one variable hyper-power series by analyzing the notion of radius of convergence and proving classical results such as algebraic operations, composition and reciprocal of hyper-power series. We then define and study one variable generalized real analytic functions, considering their derivation, integration, a suitable formulation of the identity theorem and the characterization by local uniform upper bounds of derivatives. On the contrary with respect to the classical use of series in the theory of Colombeau real analytic functions, we can recover several classical examples in a non-infinitesimal set of convergence. The notion of generalized real analytic function reveals to be less rigid both with respect to the classical one and to Colombeau theory, e.g. including classical non-analytic smooth functions with flat points and several distributions such as the Dirac delta. On the other hand, each Colombeau real analytic function is also a generalized real analytic function.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
In this article, the study of hyperseries in the non-Archimedean ring of Colombeau generalized numbers (CGN), as carried out in [25], is applied to the corresponding notion of hyper-power series. As we will see, this yields results which are more closely related to classical ones, such as, e.g. the equality  that holds for all
that holds for all  where the exponential is moderate, i.e. if \(|x|\le \log \left( \textrm{d}{\rho }^{-R}\right) \) for some \(R\in \mathbb {N}\). On the other hand, we will see that classical smooth but non-analytic functions, e.g. smooth functions with flat points, and Schwartz distributions like the Dirac delta, are now included in the related notion of generalized real analytic function (GRAF). This implies that necessarily we cannot have a trivial generalization of the identity theorem (see e.g. [20, Corollary 1.2.6, 1.2.7]) but, on the contrary, only a suitable sufficient condition (see Theorem 40 below). The notion of generalized real analytic function hence reveals to be less rigid than the classical concept, by including a large family of non-trivial generalized functions (e.g. Dirac delta \(\delta \), Heaviside function H, but also powers \(\delta ^{k}\), \(k\in \mathbb {N}\), and compositions \(\delta \circ \delta \), \(\delta ^{k}\circ H^{h}\), \(H^{h}\circ \delta ^{k}\), etc., for h, \(k\in \mathbb {N}\).
where the exponential is moderate, i.e. if \(|x|\le \log \left( \textrm{d}{\rho }^{-R}\right) \) for some \(R\in \mathbb {N}\). On the other hand, we will see that classical smooth but non-analytic functions, e.g. smooth functions with flat points, and Schwartz distributions like the Dirac delta, are now included in the related notion of generalized real analytic function (GRAF). This implies that necessarily we cannot have a trivial generalization of the identity theorem (see e.g. [20, Corollary 1.2.6, 1.2.7]) but, on the contrary, only a suitable sufficient condition (see Theorem 40 below). The notion of generalized real analytic function hence reveals to be less rigid than the classical concept, by including a large family of non-trivial generalized functions (e.g. Dirac delta \(\delta \), Heaviside function H, but also powers \(\delta ^{k}\), \(k\in \mathbb {N}\), and compositions \(\delta \circ \delta \), \(\delta ^{k}\circ H^{h}\), \(H^{h}\circ \delta ^{k}\), etc., for h, \(k\in \mathbb {N}\).
Conversely, GRAF preserve a lot of classical results: they can be thought of as infinitely long polynomials  , with uniquely determined coefficient \(a_{n}=\frac{f^{(n)}(c)}{n!}\), they can be added, multiplied, composed, differentiated, integrated term by term, are closed with respect to inverse function, etc. This lays the foundation for a potential interesting generalization of the Cauchy-Kowalevski theorem which is able to include many non-analytic (but generalized real analytic) generalized functions.
, with uniquely determined coefficient \(a_{n}=\frac{f^{(n)}(c)}{n!}\), they can be added, multiplied, composed, differentiated, integrated term by term, are closed with respect to inverse function, etc. This lays the foundation for a potential interesting generalization of the Cauchy-Kowalevski theorem which is able to include many non-analytic (but generalized real analytic) generalized functions.
Concerning the theory of analytic Colombeau generalized functions, as developed in [23] for the real case and in [1, 2, 5,6,7, 18, 22, 26] for the complex one, it is worth to mention that several properties have been proved in both cases: closure with respect to composition, integration over homotopic paths, Cauchy integral theorem, existence of analytic representatives, identity theorem on a set of positive Lebesgue measure, etc. (cf. [23, 26] and references therein). On the other hand, even if in [26] it is also proved that each complex analytic Colombeau generalized functions can be written as a Taylor series, necessarily this result holds only in an infinitesimal neighborhood of each point. The impossibility to extend this property to a finite neighborhood is a general drawback of the use of ordinary series in a (Cauchy complete) non-Archimedean framework instead of hyperseries, as explained in details in [25].
We refer to [21] for basic notions such as the ring of Robinson-Colombeau, subpoints, hypernatural numbers, supremum, infimum and hyperlimits, and [25] for the notion of hyperseries as well as their notations and properties. Once again, the ideas presented in the present article can be useful to explore similar ideas in other non-Archimedean settings, such as [3, 4, 15,16,17, 19, 24].
2 Hyper-power series and its basic properties
2.1 Definition of hyper-power series
In the entire paper, \(\rho \) and \(\sigma \) are two arbitrary gauges; only when it will be needed, we will assume a relation between them, such as \(\sigma \le \rho ^{*}\) or \(\sigma \ge \rho ^{*}\) (see [25]).
A power series of real numbers is usually simply defined as “a series of the form \(\sum _{n\in \mathbb {N}}a_{n}(x-c)^{n}\), where x, c, \(a_{n}\in \mathbb {R}\) for all \(n\in \mathbb {N}\)”. Actually, this (informal) definition does not state explicitly whether a non-convergent series is included or not. However, unlike the real case where finite sums can always be considered, this does not hold for hyperfinite sums in the ring  , see [25]. For this reason, we consider the
, see [25]. For this reason, we consider the  -module
-module  of sequences for hyperseries exactly as the space where we can consider hyperfinite sums regardless of convergence. This is the idea to define the space
of sequences for hyperseries exactly as the space where we can consider hyperfinite sums regardless of convergence. This is the idea to define the space  of formal hyper-power series (HPS):
of formal hyper-power series (HPS):
Definition 1
Let x,  . We say
. We say  if and only if there exist \(\left( a_{n\varepsilon }\right) _{n,\varepsilon }\in \mathbb {R}^{\mathbb {N}\times I}\) and representatives \([x_{\varepsilon }]=x\), \([c_{\varepsilon }]=c\) such that
if and only if there exist \(\left( a_{n\varepsilon }\right) _{n,\varepsilon }\in \mathbb {R}^{\mathbb {N}\times I}\) and representatives \([x_{\varepsilon }]=x\), \([c_{\varepsilon }]=c\) such that

For the notation \(\left[ -\right] _{\text {s}}\), see [25, Defi 1]. Elements of  are called formal HPS because here we are not considering their convergence. In other words, a formal HPS is a hyper series (i.e. an equivalence class
are called formal HPS because here we are not considering their convergence. In other words, a formal HPS is a hyper series (i.e. an equivalence class  in the space of sequences for hyperseries) of the form \(\left[ a_{n\varepsilon }\cdot \left( x_{\varepsilon }-c_{\varepsilon }\right) ^{n}\right] _{{\textrm{s}}}\).
in the space of sequences for hyperseries) of the form \(\left[ a_{n\varepsilon }\cdot \left( x_{\varepsilon }-c_{\varepsilon }\right) ^{n}\right] _{{\textrm{s}}}\).
Remark 2
-
i
We explicitly note that \(x-c\) is not an indeterminate, like in the case of formal power series \(\mathbb {R}\llbracket x\rrbracket \), but a generalized number of
 . For example, in Lemma 10 below, we will prove that if \(x-c=y-d\), then
. For example, in Lemma 10 below, we will prove that if \(x-c=y-d\), then  .
. -
ii
On the contrary with respect to the case of real numbers, being a formal HPS, i.e. an element of
 , depends on the interplay of the two gauges \(\rho \) and \(\sigma \): take e.g. \(a_{n}=\frac{1}{n^{2}}\) and \(x-c=2\), so that for all
, depends on the interplay of the two gauges \(\rho \) and \(\sigma \): take e.g. \(a_{n}=\frac{1}{n^{2}}\) and \(x-c=2\), so that for all  we have \(\sum _{n=1}^{N}a_{n}(x-c)^{n}\ge \sum _{n=0}^{N}\frac{1}{n}\sim \log (N)\). Therefore, taking e.g. \(\sigma _{\varepsilon }=\exp \left( -\exp \left( \frac{1}{\rho _{\varepsilon }}\right) \right) \) and \(N_{\varepsilon }:=\text {int}\left( \sigma _{\varepsilon }\right) \), we have that \(\left( \log N_{\varepsilon }\right) \notin \mathbb {R}_{\rho }\) and hence we cannot even consider hyperfinite sums of this form. Informally stated, for this gauge \(\sigma \), we have that
we have \(\sum _{n=1}^{N}a_{n}(x-c)^{n}\ge \sum _{n=0}^{N}\frac{1}{n}\sim \log (N)\). Therefore, taking e.g. \(\sigma _{\varepsilon }=\exp \left( -\exp \left( \frac{1}{\rho _{\varepsilon }}\right) \right) \) and \(N_{\varepsilon }:=\text {int}\left( \sigma _{\varepsilon }\right) \), we have that \(\left( \log N_{\varepsilon }\right) \notin \mathbb {R}_{\rho }\) and hence we cannot even consider hyperfinite sums of this form. Informally stated, for this gauge \(\sigma \), we have that  is not a formal HPS, i.e. even before considering its convergence or not, we cannot compute \(\sigma \)-hyperfinite sums and get a number in
is not a formal HPS, i.e. even before considering its convergence or not, we cannot compute \(\sigma \)-hyperfinite sums and get a number in 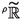 .
. -
iii
In [25], we proved that if x is finite, then
 is a formal HPS for all gauges \(\rho \), \(\sigma \). In Sect. 14, we will prove that
is a formal HPS for all gauges \(\rho \), \(\sigma \). In Sect. 14, we will prove that  ; on the other hand, we will also see that if \(x\le \log \left( \textrm{d}\rho ^{-N}\right) \) and \(\textrm{d}\sigma ^{Q}\le \textrm{d}\rho ^{N}\) for some \(Q\in \mathbb {N}\), then
; on the other hand, we will also see that if \(x\le \log \left( \textrm{d}\rho ^{-N}\right) \) and \(\textrm{d}\sigma ^{Q}\le \textrm{d}\rho ^{N}\) for some \(Q\in \mathbb {N}\), then  is a formal HPS.
is a formal HPS.
The previous Definition 1 sets immediate problems concerning independence of representatives: every time we start from  , for all \(n\in \mathbb {N}\), \([x_{\varepsilon }]=x\), \([c_{\varepsilon }]=c\) and we have that
, for all \(n\in \mathbb {N}\), \([x_{\varepsilon }]=x\), \([c_{\varepsilon }]=c\) and we have that  , we can consider whether the corresponding formal HPS
, we can consider whether the corresponding formal HPS  converges or not. On the other hand, we also have to prove that it is well-defined, i.e. that taking different representatives \(\left[ {\bar{a}}_{n\varepsilon }\right] =\left[ a_{n\varepsilon }\right] \), \([{\bar{x}}_{\varepsilon }]=x\), \([{\bar{c}}_{\varepsilon }]=c\), we have \(\left[ a_{n\varepsilon }\cdot \left( x_{\varepsilon }-c_{\varepsilon }\right) ^{n}\right] _{{\textrm{s}}}=\left[ {\bar{a}}_{n\varepsilon }\cdot \left( {\bar{x}}_{\varepsilon }-{\bar{c}}_{\varepsilon }\right) ^{n}\right] _{{\textrm{s}}}\). However, from [25, Sec. 2] it follows that we can have \(x-c=1\) and \(\left[ a_{n\varepsilon }\right] =\left[ {\bar{a}}_{n\varepsilon }\right] =0\) for all \(n\in \mathbb {N}\), but
converges or not. On the other hand, we also have to prove that it is well-defined, i.e. that taking different representatives \(\left[ {\bar{a}}_{n\varepsilon }\right] =\left[ a_{n\varepsilon }\right] \), \([{\bar{x}}_{\varepsilon }]=x\), \([{\bar{c}}_{\varepsilon }]=c\), we have \(\left[ a_{n\varepsilon }\cdot \left( x_{\varepsilon }-c_{\varepsilon }\right) ^{n}\right] _{{\textrm{s}}}=\left[ {\bar{a}}_{n\varepsilon }\cdot \left( {\bar{x}}_{\varepsilon }-{\bar{c}}_{\varepsilon }\right) ^{n}\right] _{{\textrm{s}}}\). However, from [25, Sec. 2] it follows that we can have \(x-c=1\) and \(\left[ a_{n\varepsilon }\right] =\left[ {\bar{a}}_{n\varepsilon }\right] =0\) for all \(n\in \mathbb {N}\), but
This means that \((b_{n})_{n}:=\left[ a_{n\varepsilon }(x_{\varepsilon }-c_{\varepsilon })^{n}\right] _{\text {s}}\) and \(({\bar{b}}_{n})_{n}:=\left[ {\bar{a}}_{n\varepsilon }(x_{\varepsilon }-c_{\varepsilon })^{n}\right] _{\text {s}}\) yield two different formal HPS (see [25, Theorem 4]) and hence, in general, the operation

is not well-defined.
The problem can also be addressed differently: what notion of equality do we have to set on a suitable subring of \(\mathbb {R}^{\mathbb {N}\times I}\) so as to have independence on representatives? This notion of equality naturally emerges in proving that the following definition of radius of convergence is well-defined (see Lemma 4). What subring we need to consider arises from the idea to include \(\left( \frac{\delta _{\varepsilon }^{(n)}(0)}{n!}\right) _{n,\varepsilon }\)in it, where \(\delta =\left[ \delta _{\varepsilon }(-)\right] \) is a suitable embedding of Dirac’s delta function (see Example 5.(v)).
2.2 Radius of convergence
The idea to define the radius of convergence corresponding to coefficients \((a_{n\varepsilon })_{n,\varepsilon }\in \mathbb {R}^{\mathbb {N}\times I}\) is that it does not matter if
yields a non \(\rho \)-moderate net (for example for \(\varepsilon \in L\subseteq _{0}I\)) because this case would intuitively identify a radius of convergence larger than any infinite number in  :
:
Definition 3
-
(i)
Let \({\overline{\mathbb {R}}}:=\mathbb {R}\cup \{-\infty ,\infty \}\) be the extended real number system with the usual (partially defined) operations but where we define \(\infty -\infty =\infty +(-\infty )=-\infty +\infty =-\infty -(-\infty )=0\). We set
 , where for arbitrary \((x_{\varepsilon })\), \((y_{\varepsilon })\in {\overline{\mathbb {R}}}^{I}\), as usual we define $$\begin{aligned} (x_{\varepsilon })\sim _{\rho }(y_{\varepsilon })\quad :\iff \quad \forall q\in \mathbb {N}\,\forall ^{0}\varepsilon :\ \left| x_{\varepsilon }-y_{\varepsilon }\right| \le \rho _{\varepsilon }^{q}. \end{aligned}$$
, where for arbitrary \((x_{\varepsilon })\), \((y_{\varepsilon })\in {\overline{\mathbb {R}}}^{I}\), as usual we define $$\begin{aligned} (x_{\varepsilon })\sim _{\rho }(y_{\varepsilon })\quad :\iff \quad \forall q\in \mathbb {N}\,\forall ^{0}\varepsilon :\ \left| x_{\varepsilon }-y_{\varepsilon }\right| \le \rho _{\varepsilon }^{q}. \end{aligned}$$Note that, e.g., \((\infty )\sim _{\rho }(\infty )\) because of our definition of \(\infty -\infty \). In
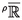 , we can also consider the standard order relation $$\begin{aligned} x\le y\quad :\iff \quad \exists [x_{\varepsilon }]=x,[y_{\varepsilon }]=y\,\forall ^{0}\varepsilon :\ x_{\varepsilon }\le y_{\varepsilon }. \end{aligned}$$
, we can also consider the standard order relation $$\begin{aligned} x\le y\quad :\iff \quad \exists [x_{\varepsilon }]=x,[y_{\varepsilon }]=y\,\forall ^{0}\varepsilon :\ x_{\varepsilon }\le y_{\varepsilon }. \end{aligned}$$Note that
 is an ordered group but, since we are considering arbitrary nets \({\overline{\mathbb {R}}}^{I}\), the set
is an ordered group but, since we are considering arbitrary nets \({\overline{\mathbb {R}}}^{I}\), the set  is not a ring: e.g. \(+\infty \cdot 0\) is still undefined and \(+\infty \cdot [z_{\varepsilon }]=[+\infty ]\) for all \((z_{\varepsilon })\in \mathbb {R}_{>0}^{I}\).
is not a ring: e.g. \(+\infty \cdot 0\) is still undefined and \(+\infty \cdot [z_{\varepsilon }]=[+\infty ]\) for all \((z_{\varepsilon })\in \mathbb {R}_{>0}^{I}\). -
(ii)
Moreover, we denote by
 the quotient ring of coefficients for HPS, where $$\begin{aligned} \left( a_{n\varepsilon }\right) _{n,\varepsilon }\in \left( \mathbb {R}^{\mathbb {N}\times I}\right) _{\rho }:\!\iff \exists Q,R\in \mathbb {N}\,\forall ^{0}\varepsilon \,\forall n\in \mathbb {N}:\ \left| a_{n\varepsilon }\right| \le \rho _{\varepsilon }^{-nQ-R} \nonumber \\ \end{aligned}$$(2.2)
the quotient ring of coefficients for HPS, where $$\begin{aligned} \left( a_{n\varepsilon }\right) _{n,\varepsilon }\in \left( \mathbb {R}^{\mathbb {N}\times I}\right) _{\rho }:\!\iff \exists Q,R\in \mathbb {N}\,\forall ^{0}\varepsilon \,\forall n\in \mathbb {N}:\ \left| a_{n\varepsilon }\right| \le \rho _{\varepsilon }^{-nQ-R} \nonumber \\ \end{aligned}$$(2.2)is the ring of weakly \(\rho \)-moderate nets, and
$$\begin{aligned} \left( a_{n\varepsilon }\right) _{n,\varepsilon }\simeq _{\rho }\left( {\bar{a}}_{n\varepsilon }\right) _{n,\varepsilon }:\!\iff \forall q,r\in \mathbb {N}\,\forall ^{0}\varepsilon \,\forall n\in \mathbb {N}:\ \left| a_{n\varepsilon }-{\bar{a}}_{n\varepsilon }\right| \le \rho _{\varepsilon }^{nq+r},\nonumber \\ \end{aligned}$$(2.3)in this case, we say that these two nets are strongly \(\rho \)-equivalent. Equivalence classes of
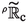 are denoted by
are denoted by  .
. -
(iii)
Finally, if
 , then we set \(\textrm{rad}\left( a_{n}\right) _{\textrm{c}{\varepsilon }}:=r_{\varepsilon }\), and
, then we set \(\textrm{rad}\left( a_{n}\right) _{\textrm{c}{\varepsilon }}:=r_{\varepsilon }\), and  , where $$\begin{aligned} r_{\varepsilon }:=\left( \limsup _{n\rightarrow +\infty }\left| a_{n\varepsilon }\right| ^{1/n}\right) ^{-1}\in \mathbb {R}\cup \{+\infty \}. \end{aligned}$$(2.4)
, where $$\begin{aligned} r_{\varepsilon }:=\left( \limsup _{n\rightarrow +\infty }\left| a_{n\varepsilon }\right| ^{1/n}\right) ^{-1}\in \mathbb {R}\cup \{+\infty \}. \end{aligned}$$(2.4)
In the following lemma, we prove that \(\textrm{rad}\left( a_{n}\right) _\textrm{c}\) is well-defined:
Lemma 4
Let  . Define \(r_{\varepsilon }\) as in (2.4) and similarly define \({\bar{r}}_{\varepsilon }\) using \({\bar{a}}_{n\varepsilon }\). Then \((r_{\varepsilon })\sim _{\rho }({\bar{r}}_{\varepsilon })\), and hence \([r_{\varepsilon }]=[{\bar{r}}_{\varepsilon }]\) in
. Define \(r_{\varepsilon }\) as in (2.4) and similarly define \({\bar{r}}_{\varepsilon }\) using \({\bar{a}}_{n\varepsilon }\). Then \((r_{\varepsilon })\sim _{\rho }({\bar{r}}_{\varepsilon })\), and hence \([r_{\varepsilon }]=[{\bar{r}}_{\varepsilon }]\) in  .
.
Proof
For all \(\varepsilon \in I\) and all \(n\in \mathbb {N}_{>0}\), we have \(\left| {\bar{a}}_{n\varepsilon }\right| ^{1/n}\le \left( \left| {\bar{a}}_{n\varepsilon } -a_{n\varepsilon }\right| +\left| a_{n\varepsilon }\right| \right) ^{1/n}\). The binomial formula yields \((x+y)\le \left( x^{1/n}+y^{1/n}\right) ^{n}\) for all x, \(y\in \mathbb {R}_{\ge 0}\), so that \(\left| {\bar{a}}_{n\varepsilon }\right| ^{1/n}\le \left| {\bar{a}}_{n\varepsilon } -a_{n\varepsilon }\right| ^{1/n}+\left| a_{n\varepsilon }\right| ^{1/n}\). Setting \(r=0\) in (2.3), for all \(q\in \mathbb {N}\) and for \(\varepsilon \) small we have
Therefore, for the same \(\varepsilon \) we get \(\left| {\bar{a}}_{n\varepsilon }\right| ^{1/n}\le \rho _{\varepsilon }^{q}+\left| a_{n\varepsilon }\right| ^{1/n}\). Taking the limit superior we obtain \(\limsup _{n\rightarrow +\infty }\left| {\bar{a}}_{n\varepsilon }\right| ^{1/n} \le \rho _{\varepsilon }^{q}+\limsup _{n\rightarrow +\infty }\left| a_{n\varepsilon }\right| ^{1/n}\). Inverting the role of \((a_{n\varepsilon })_{n,\varepsilon }\) and \(({\bar{a}}_{n\varepsilon })_{n,\varepsilon }\) we finally obtain
which proves the claim. \(\square \)
Remark 5
-
(i)
If
 , then for each fixed \(n\in \mathbb {N}\), we have that
, then for each fixed \(n\in \mathbb {N}\), we have that  , i.e. the net \(\left( a_{n\varepsilon }\right) _{\varepsilon }\) is \(\rho \)-moderate. This is the main motivation to consider the exponent “\(-R\)” in (2.2) (recall that in our notation \(0\in \mathbb {N}\)): without the term “\(-R\)”, the only possibility to have
, i.e. the net \(\left( a_{n\varepsilon }\right) _{\varepsilon }\) is \(\rho \)-moderate. This is the main motivation to consider the exponent “\(-R\)” in (2.2) (recall that in our notation \(0\in \mathbb {N}\)): without the term “\(-R\)”, the only possibility to have  is that \(|a_{0}|\le 1\), which is an unnecessary limitation. Similarly, we can motivate why we are considering the quantifier “\(\forall n\in \mathbb {N}\)” in the same formula (instead of, e.g., “\(\exists N\in \mathbb {N}\,\forall n\in \mathbb {N}_{\ge N}\)”). The proof of the next Lemma 10 will motivate why in (2.2) we consider the uniform property “\(\forall ^{0}\varepsilon \,\forall n\in \mathbb {N}\)” and not “\(\forall n\in \mathbb {N}\,\forall ^{0}\varepsilon \)”.
is that \(|a_{0}|\le 1\), which is an unnecessary limitation. Similarly, we can motivate why we are considering the quantifier “\(\forall n\in \mathbb {N}\)” in the same formula (instead of, e.g., “\(\exists N\in \mathbb {N}\,\forall n\in \mathbb {N}_{\ge N}\)”). The proof of the next Lemma 10 will motivate why in (2.2) we consider the uniform property “\(\forall ^{0}\varepsilon \,\forall n\in \mathbb {N}\)” and not “\(\forall n\in \mathbb {N}\,\forall ^{0}\varepsilon \)”. -
(ii)
Note that
 because the notion of equality \(\sim _{\rho }\) in the two quotient sets is the same and because if \((x_{\varepsilon })\) is \(\rho \)-moderate and \((x_{\varepsilon })\sim _{\rho }(y_{\varepsilon })\), then also \((y_{\varepsilon })\) is \(\rho \)-moderate.
because the notion of equality \(\sim _{\rho }\) in the two quotient sets is the same and because if \((x_{\varepsilon })\) is \(\rho \)-moderate and \((x_{\varepsilon })\sim _{\rho }(y_{\varepsilon })\), then also \((y_{\varepsilon })\) is \(\rho \)-moderate. -
(iii)
Condition (2.2) of being weakly \(\rho \)-moderate represents a constrain on what coefficients \(a_{n}\) we can consider in a hyperseries. For example, if \((a_{n})_{n\in \mathbb {N}}\) is a sequence of real numbers satisfying \(|a_{n}|\le p(n)\), where \(p\in \mathbb {R}[x]\) is a polynomial, then \(p(n)\le \rho _{\varepsilon }^{-nQ}\) for all \(\varepsilon \) sufficiently small and for all \(n\in \mathbb {N}\) if \(Q\ge \max \left( 1,\max \left\{ -\frac{\log n}{p(n)\log \rho _{\varepsilon }}\mid n<N_{1}\right\} \right) \), where \(\frac{\log n}{P(n)}\le 1\) for all \(n\ge N_{1}\) and \(-\frac{1}{\log \rho _{\varepsilon }}\le 1\). Hence \(\left( a_{n}\right) _{n,\varepsilon }\in \left( \mathbb {R}^{\mathbb {N}\times I}\right) _{\rho }\) is weakly \(\rho \)-moderate. On the contrary, we cannot have \(n^{n}\le \rho _{\varepsilon }^{-nQ-R}=\rho _{\varepsilon }^{-R}\left( \frac{1}{\rho _{\varepsilon }^{Q}}\right) ^{n}\) for all \(n\in \mathbb {N}\). Similarly \((n!)_{n\in \mathbb {N}}\) is not weakly \(\rho \)-moderate and hence our theory does not apply to a “hyperseries” of the form
 . On the other hand, in Lemma 7.(i) we will show that, as a consequence of considering only weakly moderate coefficients, the radius of convergence of our hyperseries is always strictly positive.
. On the other hand, in Lemma 7.(i) we will show that, as a consequence of considering only weakly moderate coefficients, the radius of convergence of our hyperseries is always strictly positive. -
iv
Let \(a_{n\varepsilon }=\rho _{\varepsilon }^{\frac{n+1}{\varepsilon }}\), so that \(\left[ a_{n\varepsilon }\right] _{\text {c}}=0\). The corresponding radius of convergence is \(r_{\varepsilon }=\lim _{n\rightarrow +\infty }|a_{n\varepsilon }|^{1/n}=\rho _{\varepsilon }^{1/\varepsilon }\) which is not \(\rho \)-moderate. In general, if
 , we can have different behavior on different subpoints, e.g. \(r|_{L_{1}}=+\infty \),
, we can have different behavior on different subpoints, e.g. \(r|_{L_{1}}=+\infty \),  , \(r|_{L_{3}}\) non \(\rho \)-moderate, etc., where \(L_{i}\subseteq _{0}I\). This behavior is studied in Lemma 7 below.
, \(r|_{L_{3}}\) non \(\rho \)-moderate, etc., where \(L_{i}\subseteq _{0}I\). This behavior is studied in Lemma 7 below. -
v
Let \(\mu :=\mathcal {F}^{-1}(\beta )\in \mathcal {S}(\mathbb {R})\) be a Colombeau mollifier defined as the inverse Fourier transform of a smooth, supported in \([-1,1]_{\mathbb {R}}\), even bump function \(0\le \beta \le 1\) which identically equals 1 in a neighborhood of 0 (see e.g. [14]). Let \(i_{\mathbb {R}}^{b}\) be the embedding of Schwartz distributions into generalized smooth functions (GSF) defined by \(\mu \) and by the infinite number
 (see e.g. [12]). The Schwartz’s Paley-Wiener theorem implies that \(\mu \) is an entire function and we know that if \(\textrm{d}\rho ^{-Q}\ge b=[b_{\varepsilon }]\ge \textrm{d}\rho ^{-R}\), for some Q, \(R\in \mathbb {R}_{>0}\), then the embedding of Dirac delta
(see e.g. [12]). The Schwartz’s Paley-Wiener theorem implies that \(\mu \) is an entire function and we know that if \(\textrm{d}\rho ^{-Q}\ge b=[b_{\varepsilon }]\ge \textrm{d}\rho ^{-R}\), for some Q, \(R\in \mathbb {R}_{>0}\), then the embedding of Dirac delta  is defined by the net \(\delta _{\varepsilon }(x)=b_{\varepsilon }\mu (b_{\varepsilon }x)\) (see e.g. [12]). For \(n\in \mathbb {N}\), we have \(\mu ^{(n)}(0)=\frac{1}{2\pi }\int \beta (x)(ix)^{n}\,\textrm{d} x=0\) if n is odd and \(\left| \mu ^{(n)}(0)\right| \le \frac{1}{2\pi }\left[ \frac{x^{n+1}}{n+1}\right] _{-1}^{1}\le 1\) if n if even. Thereby \(\left| \frac{\delta _{\varepsilon }^{(n)}(0)}{n!}\right| =\left| \frac{\mu ^{(n)}(0)}{n!}b_{\varepsilon }^{n+1}\right| \le \frac{1}{n!}\rho _{\varepsilon }^{-nQ-Q}\le \rho _{\varepsilon }^{-nQ-Q}\). This inequality shows that
is defined by the net \(\delta _{\varepsilon }(x)=b_{\varepsilon }\mu (b_{\varepsilon }x)\) (see e.g. [12]). For \(n\in \mathbb {N}\), we have \(\mu ^{(n)}(0)=\frac{1}{2\pi }\int \beta (x)(ix)^{n}\,\textrm{d} x=0\) if n is odd and \(\left| \mu ^{(n)}(0)\right| \le \frac{1}{2\pi }\left[ \frac{x^{n+1}}{n+1}\right] _{-1}^{1}\le 1\) if n if even. Thereby \(\left| \frac{\delta _{\varepsilon }^{(n)}(0)}{n!}\right| =\left| \frac{\mu ^{(n)}(0)}{n!}b_{\varepsilon }^{n+1}\right| \le \frac{1}{n!}\rho _{\varepsilon }^{-nQ-Q}\le \rho _{\varepsilon }^{-nQ-Q}\). This inequality shows that  and motivates our definition of weakly \(\rho \)-moderate nets. The corresponding radius of convergence is \(r_{\varepsilon }^{-1}=\limsup _{n\rightarrow +\infty }\left| \frac{\delta _{\varepsilon }^{(n)}(0)}{n!}\right| ^{1/n} =\limsup _{n\rightarrow +\infty }b_{\varepsilon }^{1+1/n}\left| \frac{\mu ^{(n)}(0)}{n!}\right| ^{1/n}=b_{\varepsilon }\cdot 0=0\), i.e. \(\textrm{rad}\left( \frac{\delta ^{(n)}(0)}{n!}\right) _\textrm{c}=+\infty \).
and motivates our definition of weakly \(\rho \)-moderate nets. The corresponding radius of convergence is \(r_{\varepsilon }^{-1}=\limsup _{n\rightarrow +\infty }\left| \frac{\delta _{\varepsilon }^{(n)}(0)}{n!}\right| ^{1/n} =\limsup _{n\rightarrow +\infty }b_{\varepsilon }^{1+1/n}\left| \frac{\mu ^{(n)}(0)}{n!}\right| ^{1/n}=b_{\varepsilon }\cdot 0=0\), i.e. \(\textrm{rad}\left( \frac{\delta ^{(n)}(0)}{n!}\right) _\textrm{c}=+\infty \). -
vi
et
 , and assume that for all \(\varepsilon \) there exists \(r_{\varepsilon }:=\left( \lim _{n\rightarrow +\infty }|a_{n\varepsilon }|^{1/n}\right) ^{-1}\) such that
, and assume that for all \(\varepsilon \) there exists \(r_{\varepsilon }:=\left( \lim _{n\rightarrow +\infty }|a_{n\varepsilon }|^{1/n}\right) ^{-1}\) such that  . Then from [21, Theorem 28], for some gauge \(\sigma \le \rho \) we have
. Then from [21, Theorem 28], for some gauge \(\sigma \le \rho \) we have 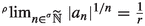 and
and 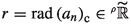 . In Corollary 17, we will see the relationship between our definition of radius of convergence and the least upper bound of all the radii where the HPS converges.
. In Corollary 17, we will see the relationship between our definition of radius of convergence and the least upper bound of all the radii where the HPS converges.
In the following lemma, we show that  is a ring:
is a ring:
Lemma 6
With pointwise operations,  is a quotient ring.
is a quotient ring.
Proof
Actually, the result follows from [13, Theorem 3.6] because the set
is an asymptotic gauge with respect to the order \((n,\varepsilon )\le ({\bar{n}},{\bar{\varepsilon }})\) if and only if \(\varepsilon \le {\bar{\varepsilon }}\). However, an independent proof follows the well-known lines of the corresponding proof for the ring  , and depends on the following properties of \(\mathcal {B}\):
, and depends on the following properties of \(\mathcal {B}\):
-
(a)
\(\forall p,q\in \mathcal {B}\,\exists r,s\in \mathcal {B}:\ p+q\le r,\ p\cdot q\le s\);
-
(b)
\(\forall p\in \mathcal {B}\,\exists r,s\in \mathcal {B}:\ r^{-1}+s^{-1}\le p^{-1}\);
-
(c)
\(\forall p,q,r\in \mathcal {B}\,\exists u,v\in \mathcal {B}:\ u^{-1}\cdot q+v^{-1}\cdot r\le p^{-1}\),
where \(p=(p_{n\varepsilon })_{n,\varepsilon }\le (q_{n\varepsilon })_{n,\varepsilon }=q\) means \(\forall ^{0}\varepsilon \,\forall n\in \mathbb {N}:\ p_{n\varepsilon }\le q_{n\varepsilon }\). \(\square \)
The following lemma represents a useful tool to deal with the radius of convergence. It essentially states that the radius of convergence equals \(+\infty \) on some subpoint, or it is moderate on some subpoint or it is greater than any power \(\textrm{d}\rho ^{-P}\).
Theorem 7
Let  and
and  , then we have
, then we have
-
(i)
\(r>0\).
-
(ii)
\(r<+\infty \) or \(r=_{\textrm{s}}+\infty \).
-
(iii)
If \(r<+\infty \), then the following alternatives hold
-
(a)
\(\forall P\in \mathbb {N}:\ r>\textrm{d}\rho ^{-P}\) or
-
(b)
setting
$$\begin{aligned}&\left[ r\le \rho ^{-P}\right] :=\left\{ \varepsilon \mid r_{\varepsilon } \le \rho _{\varepsilon }^{-P}\right\} =:L_{P}\nonumber \\&P_{\text {m}}:=\min \left\{ P\in \mathbb {N}\mid \left[ r\le \rho ^{-P}\right] \subseteq _{0}I\right\} \end{aligned}$$(2.5)we have
-
(b.1)
\(I=\bigcup _{P\in \mathbb {N}}\left[ r\le \rho ^{-P}\right] \);
-
(b.2)
\(\forall P\ge P_{\text {m}}:\ \left[ r\le \rho ^{-P}\right] \subseteq _{0}I,\ r\le _{L_{P}}\textrm{d}\rho ^{-P}\);
-
(b.3)
\(\forall P<P_{\text {m}}:\ \textrm{d}\rho ^{-P}\le r\);
-
(b.4)
If \(P_{\text {m}}=0\) and \(L_{0}^{c}\subseteq _{0}I\), then \(1\le _{L_{0}^{c}}r\); if \(L_{0}^{c}\not \subseteq _{0}I\), then \(r\le 1\).
-
(b.1)
-
(a)
-
(iv)
Assume that for all \(L\subseteq _{0}I\), the following implication holds
$$\begin{aligned} \left( \exists Q\in \mathbb {N}:\ r\le _{L}\textrm{d}\rho ^{-Q}\right) \text { or }\left( \forall Q\in \mathbb {N}:\ r>_{L}\textrm{d}\rho ^{-Q}\right) \ \Rightarrow \ \forall ^{0}\varepsilon \in L:\ \mathcal {P}\left\{ r_{\varepsilon }\right\} .\nonumber \\ \end{aligned}$$(2.6)Then \(\forall ^{0}\varepsilon :\ \mathcal {P}\left\{ r_{\varepsilon }\right\} \), i.e. the property \(\mathcal {P}\left\{ r_{\varepsilon }\right\} \) holds for all sufficiently small \(\varepsilon \).
-
(v)
If
 and \(q<r\), then \(\exists s\).
and \(q<r\), then \(\exists s\).
Proof
(i): Assume that \(\left| a_{n\varepsilon }\right| \le \rho _{\varepsilon }^{-nQ-R}\) for all \(\varepsilon \le \varepsilon _{0}\) and for all \(n\in \mathbb {N}\). Then \(\limsup _{n\rightarrow +\infty }\left| a_{n\varepsilon }\right| ^{1/n}\le \lim _{n\rightarrow +\infty } \rho _{\varepsilon }^{-Q-\frac{R}{n}}=\rho _{\varepsilon }^{-Q}\), i.e. \(r_{\varepsilon }\ge \rho _{\varepsilon }^{Q}\).
(ii): Set \(L:=\left\{ \varepsilon \mid r_{\varepsilon }=+\infty \right\} \). If \(L\subseteq _{0}I\), then \(r=_{L}+\infty \). Otherwise \((0,\varepsilon _{0}]\cap L=\emptyset \) for some \(\varepsilon _{0}\), i.e. \(r_{\varepsilon }<+\infty \) for all \(\varepsilon \le \varepsilon _{0}\).
(iii): Since we assume that \(r<+\infty \), without loss of generality we can take \(r_{\varepsilon }<+\infty \) for all \(\varepsilon \). We also assume that (a) is false, i.e. \(r\le _{M}\textrm{d}\rho ^{-{\bar{P}}}\) for some \({\bar{P}}\in \mathbb {N}\) and some \(M\subseteq _{0}I\). We first prove (b.1): take \(\varepsilon \in \bigcap _{P\in \mathbb {N}}\left[ r>\rho ^{-P}\right] \), then \(r_{\varepsilon }>\rho _{\varepsilon }^{-P}\) for all \(P\in \mathbb {N}\), so that \(r_{\varepsilon }=+\infty \) for \(P\rightarrow +\infty \), and this is not possible. We also note that \(\left[ r\le \rho ^{-P}\right] \subseteq \left[ r\le \rho ^{-Q}\right] \) for all \(Q\ge P\). From \(M\subseteq _{0}I\) and \(r\le _{M}\textrm{d}\rho ^{-{\bar{P}}}\), we have \((0,\varepsilon _{0}]\cap M\subseteq \left[ r\le \rho ^{-({\bar{P}}+1)}\right] \subseteq _{0}I\), and hence definition (2.5) yields \(P_{\text {m}}\in \mathbb {N}\) and also proves (b.2). For all \(P\in \mathbb {N}_{<P_{\text {m}}}\), we hence have \(\left[ r\le \rho ^{-P}\right] \not \subseteq _{0}I\), i.e. \((0,\varepsilon _{P}]\subseteq \left[ r>\rho ^{-P}\right] \) for some \(\varepsilon _{P}\). This implies \(\textrm{d}\rho ^{-P}\le r\) and proves (b.3). Finally, if \(P_{\text {m}}=0\) and \(L_{P_{\text {m}}}^{c}=L_{0}^{c}\subseteq _{0}I\), then \(1\le _{L_{0}^{c}}r\) because \(L_{0}^{c}=\left[ r>1\right] \). If \(L_{0}^{c}\not \subseteq _{0}I\), then \((0,\varepsilon _{0}]\subseteq L_{0}\) for some \(\varepsilon _{0}\), i.e. \(r\le 1\).
(iv): By contradiction, assume that \(\lnot \mathcal {P}\left\{ r_{\varepsilon }\right\} \) for all \(\varepsilon \in L\) and for some \(L\subseteq _{0}I\). As usual, we assume that all the results we proved for  can also be similarly proved for the restriction
can also be similarly proved for the restriction  . From (ii) for
. From (ii) for  , we have \(r<_{L}+\infty \) or \(r=_{K}+\infty \) for some \(K\subseteq _{0}L\). The second case implies \(r>_{L}\textrm{d}\rho ^{-Q}\) for all \(Q\in \mathbb {N}\). Since \(K\subseteq _{0}I\), we can apply the second alternative in the implication (2.6) to get \(\forall ^{0}\varepsilon \in K:\ \mathcal {P}\left\{ r_{\varepsilon }\right\} \), which gives a contradiction because \(K\subseteq L\). We can hence consider the first case \(r<_{L}+\infty \) and apply the subcase (a), i.e. \(r>_{L}\textrm{d}\rho ^{-P}\) for all \(P\in \mathbb {N}\), and we hence proceed as above applying the second alternative of the implication (2.6). In the remaining subcase, we can use (b.2) (with L instead of I). This yields \(L_{P_{\text {m}}}\subseteq _{0}L\) and \(r\le _{L_{P_{\text {m}}}}\textrm{d}\rho ^{-P_{\text {m}}}\). Since \(L_{P_{\text {m}}}\subseteq _{0}I\), we can apply the first alternative in the implication (2.6) to get once again a contradiction.
, we have \(r<_{L}+\infty \) or \(r=_{K}+\infty \) for some \(K\subseteq _{0}L\). The second case implies \(r>_{L}\textrm{d}\rho ^{-Q}\) for all \(Q\in \mathbb {N}\). Since \(K\subseteq _{0}I\), we can apply the second alternative in the implication (2.6) to get \(\forall ^{0}\varepsilon \in K:\ \mathcal {P}\left\{ r_{\varepsilon }\right\} \), which gives a contradiction because \(K\subseteq L\). We can hence consider the first case \(r<_{L}+\infty \) and apply the subcase (a), i.e. \(r>_{L}\textrm{d}\rho ^{-P}\) for all \(P\in \mathbb {N}\), and we hence proceed as above applying the second alternative of the implication (2.6). In the remaining subcase, we can use (b.2) (with L instead of I). This yields \(L_{P_{\text {m}}}\subseteq _{0}L\) and \(r\le _{L_{P_{\text {m}}}}\textrm{d}\rho ^{-P_{\text {m}}}\). Since \(L_{P_{\text {m}}}\subseteq _{0}I\), we can apply the first alternative in the implication (2.6) to get once again a contradiction.
(v): Assume that \(r>q\) and take  . \(\square \)
. \(\square \)
Explicitly note the meaning of Lemma 7(iv): on an arbitrary subpoint \(r|_{L}\) of the radius of convergence \(r=\textrm{rad}\left( a_{n}\right) _\textrm{c}\), we have to consider only two cases: either \(r|_{L}\) is \(\rho \)-moderate or it is greater than any power \(\textrm{d}\rho ^{-Q}\) (the latter case including also the case \(r|_{L}=+\infty \)); if in both cases we are able to prove the property \(\mathcal {P}\left\{ r_{\varepsilon }\right\} \) for \(\varepsilon \in L\) sufficiently small, then this property holds for all \(\varepsilon \) sufficiently small.
2.3 Set of convergence
Even if the radius of convergence of the exponential hyperseries is \(\textrm{rad}\left( \frac{1}{n!}\right) _\textrm{c}=+\infty \), we have that  implies \(|x|\le \log \left( \textrm{d}\rho ^{-R}\right) \) for some \(R\in \mathbb {N}\): in other words, the constraint to get a \(\rho \)-moderate number implies that even if
implies \(|x|\le \log \left( \textrm{d}\rho ^{-R}\right) \) for some \(R\in \mathbb {N}\): in other words, the constraint to get a \(\rho \)-moderate number implies that even if  converges at x, the exponential HPS does not converge in the interval
converges at x, the exponential HPS does not converge in the interval  .
.
Moreover, in all our examples, if the HPS  converges, then it converges exactly to
converges, then it converges exactly to  . The following definition of set of convergence closely recalls the definition of GSF:
. The following definition of set of convergence closely recalls the definition of GSF:
Definition 8
Let  and
and  . The set of convergence
. The set of convergence

is the set of all  satisfying
satisfying
-
(i)
\(\left| x-c\right| <\textrm{rad}\left( a_{n}\right) _\textrm{c}\),
and such that there exist representatives \([x_{\varepsilon }]=x\), \(\left[ a_{n\varepsilon }\right] _{{\textrm{c}}}=\left( a_{n}\right) _{{\textrm{c}}}\) and \([c_{\varepsilon }]=c\) satisfying the following conditions:
-
(ii)
 , i.e. we have a formal HPS;
, i.e. we have a formal HPS; -
(iii)
 ;
; -
(iv)
For all representatives \([{\bar{x}}_{\varepsilon }]=x\) and all \(k\in \mathbb {N}_{>0}\), the k-th derivative net is \(\rho \)-moderate:
$$\begin{aligned} \left( \frac{\textrm{d}{}^{k}}{\textrm{d}{x}^{k}}\left( \sum _{n=0}^{+\infty }a_{n\varepsilon }(x-c_{\varepsilon })^{n}\right) _{x={\bar{x}}_{\varepsilon }}\right) \in \mathbb {R}_{\rho }. \end{aligned}$$
Note that condition (ii) is necessary because in (iii) we use a HPS; on the other hand, conditions (iii) and (iv) state that the function

is a GSF defined by the net of smooth functions \(\left( \sum _{n=0}^{+\infty }a_{n\varepsilon }(x_{\varepsilon }-c_{\varepsilon })^{n}\right) \). As for GSF, see [12, Theorem 16], condition (iv) will be useful to prove that we have independence from representatives of x in all the derivatives. In Corollary 25, we will see that under very general assumptions and if \(\sigma \le \rho ^{*}\), condition (iv) can be omitted.
In Sect. 14 we will show that  (the set of convergence of the exponential HPS at the origin), but \(\textrm{d}\rho ^{-1}\notin \text {conv}\left( \left( \frac{1}{n!}\right) _{n}^{{\textrm{c}}},0\right) \). We immediately note that \(x\in \text {conv}\left( \left( a_{n}\right) _{n}^{\text {c}},c\right) \) if and only if \(x-c\in \text {conv}\left( \left( a_{n}\right) _{n}^{\text {c}},0\right) \), and because of this property without loss of generality we will frequently assume \(c=0\).
(the set of convergence of the exponential HPS at the origin), but \(\textrm{d}\rho ^{-1}\notin \text {conv}\left( \left( \frac{1}{n!}\right) _{n}^{{\textrm{c}}},0\right) \). We immediately note that \(x\in \text {conv}\left( \left( a_{n}\right) _{n}^{\text {c}},c\right) \) if and only if \(x-c\in \text {conv}\left( \left( a_{n}\right) _{n}^{\text {c}},0\right) \), and because of this property without loss of generality we will frequently assume \(c=0\).
We also note that condition (iii) states that the hyperseries  converges, and it does exactly to the generalized number \(\left[ \sum _{n=0}^{+\infty }a_{n\varepsilon }x_{\varepsilon }^{n}\right] \). It is hence natural to wonder whether it is possible that it converges to some different quantity. This is the problem of the relation between hyperlimit and \(\varepsilon \)-wise limit:
converges, and it does exactly to the generalized number \(\left[ \sum _{n=0}^{+\infty }a_{n\varepsilon }x_{\varepsilon }^{n}\right] \). It is hence natural to wonder whether it is possible that it converges to some different quantity. This is the problem of the relation between hyperlimit and \(\varepsilon \)-wise limit:

which has been already addressed in [25, Theorems 12, 13]. Intuitively speaking, if the gauge \((\sigma _{\varepsilon })\) is not sufficiently small, and hence the infinite nets \((\sigma _{\varepsilon }^{-N})\) are not sufficiently large, it can happen that \({ni}{(N)}_{\varepsilon }\rightarrow +\infty \) as \(\varepsilon \rightarrow 0\) only very slowly, whereas the \(\varepsilon \)-wise limit could require \(N\rightarrow +\infty \) at a greater speed to converge. This can be stated more precisely in the following way: Let  be a formal HPS and assume that \(\sum _{n=0}^{+\infty }a_{n\varepsilon }x_{\varepsilon }^{n}<+\infty \) for \(\varepsilon \) small. Then, for all \(q\in \mathbb {N}\) and for all \(\varepsilon \) small, we can find \(N_{\varepsilon }^{q}\in \mathbb {N}\) such that
be a formal HPS and assume that \(\sum _{n=0}^{+\infty }a_{n\varepsilon }x_{\varepsilon }^{n}<+\infty \) for \(\varepsilon \) small. Then, for all \(q\in \mathbb {N}\) and for all \(\varepsilon \) small, we can find \(N_{\varepsilon }^{q}\in \mathbb {N}\) such that
However, only if \(\left( \sum _{n=0}^{+\infty }a_{n\varepsilon }x_{\varepsilon }^{n}\right) \in \mathbb {R}_{\rho }\) and \((N_{\varepsilon }^{q})\in \mathbb {R}_{\sigma }\), i.e.  , then this also implies
, then this also implies  .
.
As expected, for HPS the set of convergence is never a singleton:
Theorem 9
Let  and
and  . Then
. Then

Proof
From Theorem 7(i), we have \(r:=\textrm{rad}\left( a_{n}\right) _\textrm{c}\ge \textrm{d}\rho ^{q_{1}}\) for some \(q_{1}\in \mathbb {N}\). We also have \(|a_{n\varepsilon }|\le \rho _{\varepsilon }^{-nQ-R}\) from (2.2). Assume that \(|x-c|<\textrm{d}\rho ^{q}\): we want to find \(q\in \mathbb {N}_{\ge q_{1}}\) so that  . To prove property Definition 8(ii), for \(N_{\varepsilon }\), \(M_{\varepsilon }\in \mathbb {N}\) and for \(\varepsilon \) small, we estimate
. To prove property Definition 8(ii), for \(N_{\varepsilon }\), \(M_{\varepsilon }\in \mathbb {N}\) and for \(\varepsilon \) small, we estimate
Therefore, taking \(q=\max (1+Q,q_{1})\), we get
and this proves Definition 8(ii). Similarly, we have
Since  , this proves Definition 8(iii). Finally, for all \(k\in \mathbb {N}_{>0}\) and all representatives \([{\bar{x}}_{\varepsilon }]=x\), we have
, this proves Definition 8(iii). Finally, for all \(k\in \mathbb {N}_{>0}\) and all representatives \([{\bar{x}}_{\varepsilon }]=x\), we have
and hence
In the last step we used \(q\ge Q+1\) and the binomial series \(\sum _{n=k}^{+\infty }y^{n-k}\prod _{j=0}^{k-1}(n-j)=k!\sum _{n=k}^{+\infty }{n \atopwithdelims ()k}y^{n-k}=\frac{k!}{(1-y)^{k+1}}\) for \(|y|<1\). \(\square \)
We can now prove independence from representatives both in Definition 8 and in Definition 1:
Lemma 10
Let  , \(x=[x_{\varepsilon }]=[{\bar{x}}_{\varepsilon }]\),
, \(x=[x_{\varepsilon }]=[{\bar{x}}_{\varepsilon }]\),  . Assume that
. Assume that  . Then
. Then
-
(i)
The nets \(\left( a_{n\varepsilon }\right) _{n,\varepsilon }\), \((x_{\varepsilon })\) and \((c_{\varepsilon })\) also satisfy all the conditions of Definition 8 of set of convergence.
-
(ii)
\(\left[ a_{n\varepsilon }\cdot \left( x_{\varepsilon }-c_{\varepsilon }\right) ^{n}\right] _{{\textrm{s}}}=\left[ {\bar{a}}_{n\varepsilon }\cdot \left( {\bar{x}}_{\varepsilon }-{\bar{c}}_{\varepsilon }\right) ^{n}\right] _{{\textrm{s}}}\), where the equality is in
 .
.
Proof
(i): Since we have similar steps for several claims, let \(N_{\varepsilon }\in \mathbb {N}\) and \(M_{\varepsilon }\in \mathbb {N}\cup \{+\infty \}\), so that a term of the form \(\sum _{n=N_{\varepsilon }}^{M_{\varepsilon }}b_{n\varepsilon }\) represents both the ordinary series \(\sum _{n=0}^{+\infty }b_{n\varepsilon }\) or the finite sum \(\sum _{n=N_{\varepsilon }}^{M_{\varepsilon }}b_{n\varepsilon }\). From Definition 8 of set of convergence, we get the existence of representatives  , \(\left[ {\hat{a}}_{n\varepsilon }\right] _{{\textrm{c}}}=\left( a_{n}\right) _{n}^{{\textrm{c}}}\) and \([{\hat{c}}_{\varepsilon }]=c\) satisfying Definition 8. Set \({\hat{y}}_{\varepsilon }:={\hat{x}}_{\varepsilon }-{\hat{c}}_{\varepsilon }\), \({\hat{y}}:=[{\hat{y}}_{\varepsilon }]\). Let \(r:=[r_{\varepsilon }]:=\textrm{rad}\left( a_{n}\right) _\textrm{c}\) be the radius of convergence. From Lemma 7(v), take
, \(\left[ {\hat{a}}_{n\varepsilon }\right] _{{\textrm{c}}}=\left( a_{n}\right) _{n}^{{\textrm{c}}}\) and \([{\hat{c}}_{\varepsilon }]=c\) satisfying Definition 8. Set \({\hat{y}}_{\varepsilon }:={\hat{x}}_{\varepsilon }-{\hat{c}}_{\varepsilon }\), \({\hat{y}}:=[{\hat{y}}_{\varepsilon }]\). Let \(r:=[r_{\varepsilon }]:=\textrm{rad}\left( a_{n}\right) _\textrm{c}\) be the radius of convergence. From Lemma 7(v), take  satisfying \(|{\hat{y}}|<s\le r\) and a representative \([s_{\varepsilon }]=s\) such that \(|{\hat{y}}_{\varepsilon }|<s_{\varepsilon }\le r_{\varepsilon }\) for all \(\varepsilon \) small. Set \(z_{n\varepsilon }:=a_{n\varepsilon }-{\hat{a}}_{n\varepsilon }\) and \({\hat{z}}_{\varepsilon }:=y_{\varepsilon }-{\hat{y}}_{\varepsilon }\). For all \(k\in \mathbb {N}\), we have
satisfying \(|{\hat{y}}|<s\le r\) and a representative \([s_{\varepsilon }]=s\) such that \(|{\hat{y}}_{\varepsilon }|<s_{\varepsilon }\le r_{\varepsilon }\) for all \(\varepsilon \) small. Set \(z_{n\varepsilon }:=a_{n\varepsilon }-{\hat{a}}_{n\varepsilon }\) and \({\hat{z}}_{\varepsilon }:=y_{\varepsilon }-{\hat{y}}_{\varepsilon }\). For all \(k\in \mathbb {N}\), we have
Since \({\hat{z}}=0\), we also have \(|{\hat{y}}_{\varepsilon }|+|{\hat{z}}_{\varepsilon }|<s_{\varepsilon }\le r_{\varepsilon }\) for all \(\varepsilon \) small. For the same \(\varepsilon \), assume that \(|z_{n\varepsilon }|\le \rho _{\varepsilon }^{np+q}\) for fixed arbitrary p, \(q\in \mathbb {N}\). We first consider the second summand in (2.10):
Since  , we can take \(p\in \mathbb {N}\) sufficiently large so that \(\rho _{\varepsilon }^{p}s_{\varepsilon }<1\). This implies
, we can take \(p\in \mathbb {N}\) sufficiently large so that \(\rho _{\varepsilon }^{p}s_{\varepsilon }<1\). This implies
Thereby, for \(q\rightarrow +\infty \), this summand defines a negligible net. For the first summand of (2.10), we can use the mean value theorem to get
for some \(\xi _{\varepsilon }\in [{\hat{y}}_{\varepsilon },{\hat{y}}_{\varepsilon }+{\hat{z}}_{\varepsilon }]\cup [{\hat{y}}_{\varepsilon }+{\hat{z}}_{\varepsilon },{\hat{y}}_{\varepsilon }]\). Thereby, the right hand side of (2.11) is negligible because of Definition 8(iv).
We can hence state that for all \(k\in \mathbb {N}\)
In the case \(M_{\varepsilon }<+\infty \) for all \(\varepsilon \) and \(k=0\), this proves that  because \(({\hat{a}}_{n\varepsilon })_{n,\varepsilon }\) and \(({\hat{y}}_{\varepsilon })\) satisfy Definition 8(ii). In the case \(M_{\varepsilon }=+\infty \) and \(N_{\varepsilon }=0=k\), it proves the moderateness of \(\left( \sum _{n=0}^{+\infty }a_{n\varepsilon }y_{\varepsilon }^{n}\right) \) too, i.e. the implicit moderateness requirement of Definition 8(iii). Finally, for \(k>0\), from property (2.12) we have that Definition 8(iv) holds for \((a_{n\varepsilon })\) and \((y_{\varepsilon })\) because of (2.8). We can apply (2.12) with \(k=0\) to \(\left[ {\bar{a}}_{n\varepsilon }\right] _{{\textrm{c}}}=\left( a_{n}\right) _{{\textrm{c}}}\), \([{\bar{x}}_{\varepsilon }]=x\), \([{\bar{c}}_{\varepsilon }]=c\), \({\bar{y}}_{\varepsilon }:={\bar{x}}_{\varepsilon }-{\bar{c}}_{\varepsilon }\) and with \(M_{\varepsilon }<+\infty \), to get
because \(({\hat{a}}_{n\varepsilon })_{n,\varepsilon }\) and \(({\hat{y}}_{\varepsilon })\) satisfy Definition 8(ii). In the case \(M_{\varepsilon }=+\infty \) and \(N_{\varepsilon }=0=k\), it proves the moderateness of \(\left( \sum _{n=0}^{+\infty }a_{n\varepsilon }y_{\varepsilon }^{n}\right) \) too, i.e. the implicit moderateness requirement of Definition 8(iii). Finally, for \(k>0\), from property (2.12) we have that Definition 8(iv) holds for \((a_{n\varepsilon })\) and \((y_{\varepsilon })\) because of (2.8). We can apply (2.12) with \(k=0\) to \(\left[ {\bar{a}}_{n\varepsilon }\right] _{{\textrm{c}}}=\left( a_{n}\right) _{{\textrm{c}}}\), \([{\bar{x}}_{\varepsilon }]=x\), \([{\bar{c}}_{\varepsilon }]=c\), \({\bar{y}}_{\varepsilon }:={\bar{x}}_{\varepsilon }-{\bar{c}}_{\varepsilon }\) and with \(M_{\varepsilon }<+\infty \), to get
This proves claim (ii) and hence also Definition 8(iii) because  converges to
converges to  from (2.12). \(\square \)
from (2.12). \(\square \)
2.4 Examples
We start studying geometric hyperseries, which in general are convergent HPS if \(\sigma \le \rho ^{*}\):
Example 11
(Geometric hyperseries) Assume that  . We have:
. We have:

This shows that  for all gauges \(\rho \), \(\sigma \). Hence by Definition 1,
for all gauges \(\rho \), \(\sigma \). Hence by Definition 1,  , i.e. the geometric series is a formal hyper-series. Since coefficients \(a_{n\varepsilon }=1\), we have
, i.e. the geometric series is a formal hyper-series. Since coefficients \(a_{n\varepsilon }=1\), we have  (see Definition 3(i)). Now, by Definition 3(iii), \(\textrm{rad}\left( 1\right) _\textrm{c}=1\). From Definition 8(i), we have
(see Definition 3(i)). Now, by Definition 3(iii), \(\textrm{rad}\left( 1\right) _\textrm{c}=1\). From Definition 8(i), we have  . Now, take \(x=[x_{\varepsilon }]\in (-1,1)\), with \(-1<x_{\varepsilon }<1\) for all \(\varepsilon \). From [25, Example 8], if \(\sigma \le \rho ^{*}\) (i.e. if \(\exists Q\in \mathbb {R}_{>0}\,\forall ^{0}\varepsilon :\ \sigma _{\varepsilon }\le \rho _{\varepsilon }^{Q}\)), we have Definition 8(iii). Finally, if \([{\bar{x}}_{\varepsilon }]=x\) is another representative and \(k\in \mathbb {N}_{>0}\), then \(-1<{\bar{x}}_{\varepsilon }<1\) for \(\varepsilon \) small, and from (2.8) we get \(\sum _{n=k}^{+\infty }k!{n \atopwithdelims ()k}{\bar{x}}_{\varepsilon }^{n-k}=\frac{k!}{(1-{\bar{x}}_{\varepsilon })^{k+1}}\in \mathbb {R}_{\rho }\) because \(1-x>0\) is invertible.
. Now, take \(x=[x_{\varepsilon }]\in (-1,1)\), with \(-1<x_{\varepsilon }<1\) for all \(\varepsilon \). From [25, Example 8], if \(\sigma \le \rho ^{*}\) (i.e. if \(\exists Q\in \mathbb {R}_{>0}\,\forall ^{0}\varepsilon :\ \sigma _{\varepsilon }\le \rho _{\varepsilon }^{Q}\)), we have Definition 8(iii). Finally, if \([{\bar{x}}_{\varepsilon }]=x\) is another representative and \(k\in \mathbb {N}_{>0}\), then \(-1<{\bar{x}}_{\varepsilon }<1\) for \(\varepsilon \) small, and from (2.8) we get \(\sum _{n=k}^{+\infty }k!{n \atopwithdelims ()k}{\bar{x}}_{\varepsilon }^{n-k}=\frac{k!}{(1-{\bar{x}}_{\varepsilon })^{k+1}}\in \mathbb {R}_{\rho }\) because \(1-x>0\) is invertible.
Note explicitly that \(\sigma \le \rho ^{*}\) is a sufficient condition ensuring the convergence of any geometric hyperseries with \(|x|<1\). However, we already used (see e.g. Theorem 9) the convergence of the geometric hyperseries  for all gauges \(\rho \), \(\sigma \). More generally, exactly as proved in [25, Example 8], it is easy to see that
for all gauges \(\rho \), \(\sigma \). More generally, exactly as proved in [25, Example 8], it is easy to see that  if \(\sigma _{\varepsilon }\le \left( \frac{\log x_{\varepsilon }}{\log \rho _{\varepsilon }}\right) ^{Q}\) for \(\varepsilon \) small and some \(Q\in \mathbb {R}_{>0}\).
if \(\sigma _{\varepsilon }\le \left( \frac{\log x_{\varepsilon }}{\log \rho _{\varepsilon }}\right) ^{Q}\) for \(\varepsilon \) small and some \(Q\in \mathbb {R}_{>0}\).
Example 12
(A smooth function with a flat point) Consider the GSF corresponding to the ordinary smooth function
It is not hard to prove that \(|f(x)|\le |x|^{q}\) for all \(x\approx 0\) and all \(q\in \mathbb {N}\). Thereby, \(f(x)=0\) for all x such that \(|x|\le \textrm{d}\rho ^{r}\) for some \(r\in \mathbb {R}_{>0}\). Therefore, we trivially have  only for all x in this infinitesimal neighborhood of 0. On the other hand,
only for all x in this infinitesimal neighborhood of 0. On the other hand,  . Moreover, \(\textrm{rad}\left( \frac{f^{(n)}(c)}{n!}\right) _\textrm{c}=+\infty \) and
. Moreover, \(\textrm{rad}\left( \frac{f^{(n)}(c)}{n!}\right) _\textrm{c}=+\infty \) and  for all
for all  such that \(|c|\gg 0\), i.e. satisfying \(|c|\ge r\) for some \(r\in \mathbb {R}_{>0}\), but
such that \(|c|\gg 0\), i.e. satisfying \(|c|\ge r\) for some \(r\in \mathbb {R}_{>0}\), but  only for all
only for all  such that \(|x|\gg 0\), which is a strict subset of
such that \(|x|\gg 0\), which is a strict subset of  . The GSF f is therefore a candidate to be a GRAF, but not an entire GRAF.
. The GSF f is therefore a candidate to be a GRAF, but not an entire GRAF.
Example 13
(A nowhere analytic smooth function)
A classical example of an infinitely differentiable function which is not analytic at any point is \(F(x)=\sum _{k\in 2^{\mathbb {N}}}e^{-\sqrt{k}}\cos (kx)\), where \(2^{\mathbb {N}}:=\left\{ 2^{n}\mid n\in \mathbb {N}\right\} \). Since for all \(x=\pi \frac{p}{q}\), with \(p\in \mathbb {N}\) and \(q\in 2^{\mathbb {N}}\) and for all \(n\in 2^{\mathbb {N}}\), \(n\ge 4\), \(n>q\), we have \(F^{(n)}(x)\ge e^{-2n}(4n^{2})^{n}+O(q^{n})\) as \(n\rightarrow +\infty \), we have that \(\left( \frac{F^{(n)}(x)}{n!}\right) _{n,\varepsilon }\notin \left( \mathbb {R}^{\mathbb {N}\times I}\right) _{\rho }\), i.e. they are not coefficients for a HPS. Note that this also proves that not even all smooth functions can be embedded as GRAF.
Example 14
(Exponential) We clearly have  and \(\textrm{rad}\left( \frac{1}{n!}\right) _\textrm{c}=+\infty \), i.e. we have coefficients for an HPS with infinite radius of convergence. Set
and \(\textrm{rad}\left( \frac{1}{n!}\right) _\textrm{c}=+\infty \), i.e. we have coefficients for an HPS with infinite radius of convergence. Set

For all \(x=[x_{\varepsilon }]\in C\) and all \(N_{\varepsilon }\), \(M_{\varepsilon }\in \mathbb {N}\), we have \(\left| \sum _{n=N_{\varepsilon }}^{M_{\varepsilon }}\frac{x_{\varepsilon }^{n}}{n!}\right| \le e^{|x_{\varepsilon }|}\le \rho _{\varepsilon }^{-K}\) for \(\varepsilon \) small, and this shows that  , i.e. for all \(x\in C\), we have a formal HPS. We finally want to prove that
, i.e. for all \(x\in C\), we have a formal HPS. We finally want to prove that  if \(\sigma \le \rho ^{*}\). The inclusion \(\supseteq \) follows directly from Definition 8(iii). If \(x=[x_{\varepsilon }]\in C\), then condition Definition 8(iv) holds because the k-th derivative HPS \(\left( k!\sum _{n=k}^{+\infty }{n \atopwithdelims ()k}\cdot \frac{x_{\varepsilon }^{n-k}}{n!}\right) =\left( e^{x_{\varepsilon }}\right) \in \mathbb {R}_{\rho }\). To prove Definition 8(iii), assume that \(|x_{\varepsilon }|<-K\log \rho _{\varepsilon }=:M_{\varepsilon }\) for all \(\varepsilon \) and set
if \(\sigma \le \rho ^{*}\). The inclusion \(\supseteq \) follows directly from Definition 8(iii). If \(x=[x_{\varepsilon }]\in C\), then condition Definition 8(iv) holds because the k-th derivative HPS \(\left( k!\sum _{n=k}^{+\infty }{n \atopwithdelims ()k}\cdot \frac{x_{\varepsilon }^{n-k}}{n!}\right) =\left( e^{x_{\varepsilon }}\right) \in \mathbb {R}_{\rho }\). To prove Definition 8(iii), assume that \(|x_{\varepsilon }|<-K\log \rho _{\varepsilon }=:M_{\varepsilon }\) for all \(\varepsilon \) and set  . Take
. Take  such that \(\frac{M}{N+1}<\frac{1}{2}\), so that, exactly as in [25, Example 8], we can prove that \(\frac{M^{n+1}}{(n+1)!}<\frac{1}{2^{n+1}}\) and hence \(\left| \sum _{n=N_{\varepsilon }+1}^{+\infty }\frac{x_{\varepsilon }^{n}}{n!}\right| \le \sum _{n\ge N_{\varepsilon }}\frac{1}{2^{n}}\rightarrow 0\) as \(N\rightarrow +\infty \),
such that \(\frac{M}{N+1}<\frac{1}{2}\), so that, exactly as in [25, Example 8], we can prove that \(\frac{M^{n+1}}{(n+1)!}<\frac{1}{2^{n+1}}\) and hence \(\left| \sum _{n=N_{\varepsilon }+1}^{+\infty }\frac{x_{\varepsilon }^{n}}{n!}\right| \le \sum _{n\ge N_{\varepsilon }}\frac{1}{2^{n}}\rightarrow 0\) as \(N\rightarrow +\infty \),  , if \(\sigma \le \rho ^{*}\). Similarly, we can consider trigonometric functions whose set of convergence is the whole of
, if \(\sigma \le \rho ^{*}\). Similarly, we can consider trigonometric functions whose set of convergence is the whole of  .
.
Example 15
(Dirac delta) In Remark 5(v), we already proved that  and \(\textrm{rad}\left( \frac{\delta ^{(n)}(0)}{n!}\right) _\textrm{c}=+\infty \). For all
and \(\textrm{rad}\left( \frac{\delta ^{(n)}(0)}{n!}\right) _\textrm{c}=+\infty \). For all  and all \(N_{\varepsilon }\), \(M_{\varepsilon }\in \mathbb {N},\) we have \(\left| \sum _{n=N_{\varepsilon }}^{M_{\varepsilon }}\frac{\delta _{\varepsilon }^{(n)}(0)}{n!}x_{\varepsilon }^{n}\right| \le b_{\varepsilon }\cdot \sum _{n=0}^{+\infty }\frac{|\mu ^{(n)}(0)|}{n!}|b_{\varepsilon }x_{\varepsilon }|^{n}\). But \(|\mu ^{(n)}(0)|=i^{n}\mu ^{(n)}(0)\) because \(\mu ^{(n)}(0)=0\) if n is odd, so that \(\left| \sum _{n=N_{\varepsilon }}^{M_{\varepsilon }}\frac{\delta _{\varepsilon }^{(n)}(0)}{n!}x_{\varepsilon }^{n}\right| \le b_{\varepsilon }\cdot \sum _{n=0}^{+\infty }\frac{\mu ^{(n)}(0)}{n!}|ib_{\varepsilon }x_{\varepsilon }|^{n} =b_{\varepsilon }\mu (i|b_{\varepsilon }x_{\varepsilon }|)\in \mathbb {R}_{\rho }\), and this proves that
and all \(N_{\varepsilon }\), \(M_{\varepsilon }\in \mathbb {N},\) we have \(\left| \sum _{n=N_{\varepsilon }}^{M_{\varepsilon }}\frac{\delta _{\varepsilon }^{(n)}(0)}{n!}x_{\varepsilon }^{n}\right| \le b_{\varepsilon }\cdot \sum _{n=0}^{+\infty }\frac{|\mu ^{(n)}(0)|}{n!}|b_{\varepsilon }x_{\varepsilon }|^{n}\). But \(|\mu ^{(n)}(0)|=i^{n}\mu ^{(n)}(0)\) because \(\mu ^{(n)}(0)=0\) if n is odd, so that \(\left| \sum _{n=N_{\varepsilon }}^{M_{\varepsilon }}\frac{\delta _{\varepsilon }^{(n)}(0)}{n!}x_{\varepsilon }^{n}\right| \le b_{\varepsilon }\cdot \sum _{n=0}^{+\infty }\frac{\mu ^{(n)}(0)}{n!}|ib_{\varepsilon }x_{\varepsilon }|^{n} =b_{\varepsilon }\mu (i|b_{\varepsilon }x_{\varepsilon }|)\in \mathbb {R}_{\rho }\), and this proves that  , i.e. we always have a formal HPS. Condition Definition 8(iv) follows because derivatives
, i.e. we always have a formal HPS. Condition Definition 8(iv) follows because derivatives are always moderate. It remains to prove Definition 8(iii) for all
are always moderate. It remains to prove Definition 8(iii) for all  to show that
to show that  :
:
where the existence of \({\bar{x}}_{\varepsilon }\in [0,x_{\varepsilon }]\cup [x_{\varepsilon },0]\) is derived from Taylor’s formula. Since \(|\mu ^{(k)}(y)|\le \frac{1}{2\pi }\int \beta (x)|x|^{k}\,\textrm{d} x=:C\in \mathbb {R}_{>0}\) for all \(k\in \mathbb {N}\) and all \(y\in \mathbb {R}\), we obtain
Using Stirling’s approximation, we have \(\frac{|x_{\varepsilon }|^{N_{\varepsilon }+1}}{(N_{\varepsilon }+1)!}\le 2\left( \frac{|x_{\varepsilon }|e}{N_{\varepsilon }}\right) ^{N}\le \rho _{\varepsilon }^{N_{\varepsilon }}\) for all  such that \(N>|x|e\textrm{d}\rho ^{-1}\), which is always possible if \(\sigma \le \rho ^{*}\). Since
such that \(N>|x|e\textrm{d}\rho ^{-1}\), which is always possible if \(\sigma \le \rho ^{*}\). Since  , this proves the claim.
, this proves the claim.
A different way to include a large class of examples is to use the characterization Theorem 37 by factorial growth of derivatives of GRAF.
When we say that a HPS  is convergent, we already assume that its coefficients are correctly chosen and that the point x is in the set of convergence, as stated in the following
is convergent, we already assume that its coefficients are correctly chosen and that the point x is in the set of convergence, as stated in the following
Definition 16
We say that  is a convergent HPS if
is a convergent HPS if
-
(i)
 are coefficients for HPS.
are coefficients for HPS. -
(ii)
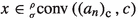 .
.
In all the previous examples, we recognized that dealing with HPS is more involved than working with ordinary series, where we only have to check that the final result is a convergent series “of the form” \(\sum _{n=0}^{\infty }a_{n}(x-c)^{n}\). On the contrary, for HPS we have to control the following steps:
-
(1)
We have to check that the net \((a_{n\varepsilon })_{n,\varepsilon }\) defines coefficients for HPS (Definition 3(i)), i.e. that
$$\begin{aligned} \forall ^{0}\varepsilon \,\forall n\in \mathbb {N}:\ |a_{n\varepsilon }|\le \rho _{\varepsilon }^{-nQ-R} \end{aligned}$$for some Q, \(R\in \mathbb {N}_{>0}\). This allows us to talk about the radius of convergence \(\textrm{rad}\left( a_{n}\right) _\textrm{c}\) and of the set of convergence
 (Definition 8). Because of Theorem 9, this set is always non-trivial
(Definition 8). Because of Theorem 9, this set is always non-trivial 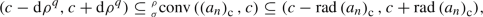 (2.14)
(2.14)but in general is not an interval, like the case of the exponential function clearly shows. This step already allows us to say that the HPS
 is convergent, i.e. Definition 16, if
is convergent, i.e. Definition 16, if  .
. -
(2)
At this point, we can study the set of convergence, e.g. to arrive at an explicit form
 . This depends mainly on three conditions:
. This depends mainly on three conditions: -
(a)
For all \(x\in C\), we must have a formal HPS (Definition 1) because this allows us to talk of any hyperfinite sum \(\sum _{n=N}^{M}a_{n}(x-c)^{n}\) for M,
 . Here, the main step is to prove that the net \(\left( \sum _{n=N_{\varepsilon }}^{M_{\varepsilon }}a_{n\varepsilon }(x_{\varepsilon }-c_{\varepsilon })^{n}\right) \in \mathbb {R}_{\rho }\).
. Here, the main step is to prove that the net \(\left( \sum _{n=N_{\varepsilon }}^{M_{\varepsilon }}a_{n\varepsilon }(x_{\varepsilon }-c_{\varepsilon })^{n}\right) \in \mathbb {R}_{\rho }\). -
(b)
For all \(x\in C\), we have to check Definition 8. (iii), i.e. the equality:
 (2.15)
(2.15) -
(c)
Finally, we have to prove that for all representatives \(x=[{\bar{x}}_{\varepsilon }]\in C\), all the derivatives \(\frac{\textrm{d}{}^{k}}{\textrm{d}{x}^{k}}\left( \sum _{n=0}^{+\infty }a_{n\varepsilon }({\bar{x}}_{\varepsilon }-c_{\varepsilon })^{n}\right) \) are \(\rho \)-moderate.
-
(d)
After the previous three steps, we get
 , and hence it remains to prove the opposite inclusion.
, and hence it remains to prove the opposite inclusion.
See Corollary 25 for sufficiently general conditions under which only (2.15) suffices to prove that x lies in the set of convergence.
-
(a)
Note explicitly that we never formally defined what is a HPS: we have formal HPS (Definition 1), the notion of coefficients for HPS (Definition 3(i)), which always have a strictly positive radius of convergence (Definition 3(iii)) and a non trivial set of convergence (Definition 8 and Theorem 9), and finally convergent HPS (Definition 16).
2.5 Topological properties of the set of convergence
The first consequence of our definition of convergent HPS Definition 16 and radius of convergence Definition 3, is the following
Lemma 17
Let  be a convergent HPS. If the following least upper bound exists
be a convergent HPS. If the following least upper bound exists

then \(r\le \textrm{rad}\left( a_{n}\right) _\textrm{c}\).
Proof
In fact, if  is a convergent HPS, then
is a convergent HPS, then  , and hence \(|{\bar{x}}_{\varepsilon }-c_{\varepsilon }|\le (\limsup _{n}\left| a_{n\varepsilon }\right| ^{1/n})^{-1}\) for all \(\varepsilon \) small, i.e. \(|{\bar{x}}-c|\le \textrm{rad}\left( a_{n}\right) _\textrm{c}\). \(\square \)
, and hence \(|{\bar{x}}_{\varepsilon }-c_{\varepsilon }|\le (\limsup _{n}\left| a_{n\varepsilon }\right| ^{1/n})^{-1}\) for all \(\varepsilon \) small, i.e. \(|{\bar{x}}-c|\le \textrm{rad}\left( a_{n}\right) _\textrm{c}\). \(\square \)
Note that from Example 14, we have that the least upper bound of

does not exist in  , whereas Definition 3 yields the value \(\textrm{rad}\left( \frac{1}{n!}\right) _\textrm{c}=+\infty \). Therefore, Definition 3 allows us to consider the exponential HPS even if the supremum of (2.17) does not exist. It remains an open problem whether \(r=\textrm{rad}\left( a_{n}\right) _\textrm{c}\), at least if the least upper bound (2.16), or the corresponding sharp supremum, exists.
, whereas Definition 3 yields the value \(\textrm{rad}\left( \frac{1}{n!}\right) _\textrm{c}=+\infty \). Therefore, Definition 3 allows us to consider the exponential HPS even if the supremum of (2.17) does not exist. It remains an open problem whether \(r=\textrm{rad}\left( a_{n}\right) _\textrm{c}\), at least if the least upper bound (2.16), or the corresponding sharp supremum, exists.
We now study absolute convergence of HPS, and sharply boundedness of the summands of a HPS. We first show that the hypersequence  of the terms of a HPS is sharply bounded:
of the terms of a HPS is sharply bounded:
Lemma 18
Let x,  . If
. If  is a convergent HPS, then
is a convergent HPS, then

Proof
We recall that because of the definition of formal HPS (Definition 1) and [25, Lemma 7] the term  is well-defined for all
is well-defined for all  . Set \({\bar{x}}:=x-c\), i.e. without loss of generality we can assume \(c=0\). Since
. Set \({\bar{x}}:=x-c\), i.e. without loss of generality we can assume \(c=0\). Since  converges, from [25, Lemma 15] we have
converges, from [25, Lemma 15] we have

Let us consider an arbitrary  . From [21, Lemma 13], we have either \(n\ge N\) or \(n<_{L}N\) for some \(L\subseteq _{0}I\). In the latter case, \(|a_{n}{\bar{x}}^{n}|\le _{L}s:=\sum _{n=0}^{N-1}|a_{n}{\bar{x}}^{n}|<\max (s+1,1)=:K\). From [21, Lemma 7(iii)] and from (2.19), the claim follows. \(\square \)
. From [21, Lemma 13], we have either \(n\ge N\) or \(n<_{L}N\) for some \(L\subseteq _{0}I\). In the latter case, \(|a_{n}{\bar{x}}^{n}|\le _{L}s:=\sum _{n=0}^{N-1}|a_{n}{\bar{x}}^{n}|<\max (s+1,1)=:K\). From [21, Lemma 7(iii)] and from (2.19), the claim follows. \(\square \)
The previous proof is essentially the generalization in our setting of the classical one, see e.g. [20]. However, property (2.18) does not allow us to apply the direct comparison test [25, Theorem 22]. Indeed, let us imagine that we only prove \(\left| a_{n}x^{n}\right| <Kh^{n}\), with \(h<1\), for all  and with K coming from (2.18); as we already explained in [25, Sec. 3.3], this would imply
and with K coming from (2.18); as we already explained in [25, Sec. 3.3], this would imply
and the dependence of \(\varepsilon _{0n}\) from \(n\in \mathbb {N}\) is a problem in estimating inequalities of the form \(\sum _{n=0}^{N_{\varepsilon }}\left| a_{n\varepsilon }x_{\varepsilon }^{n}\right| \le K_{\varepsilon }\sum _{n=0}^{N_{\varepsilon }}h_{\varepsilon }^{n}\), see [25]. A solution of this problem is to consider a uniform property of \(n\in \mathbb {N}\) with respect to \(\varepsilon \):
Definition 19
Let  and x,
and x,  , then we say that \(\left( a_{n}(x-c)^{n}\right) _{n\in \mathbb {N}}\) is eventually
, then we say that \(\left( a_{n}(x-c)^{n}\right) _{n\in \mathbb {N}}\) is eventually  -bounded in
-bounded in  , if there exist representatives \((a_{n})_{\textrm{c}}=\left[ a_{n\varepsilon }\right] _{{\textrm{c}}}\), \([x_{\varepsilon }]=x\), \([c_{\varepsilon }]=c\) such that
, if there exist representatives \((a_{n})_{\textrm{c}}=\left[ a_{n\varepsilon }\right] _{{\textrm{c}}}\), \([x_{\varepsilon }]=x\), \([c_{\varepsilon }]=c\) such that

Remark 20
-
(i)
The adverb eventually clearly refers to the validity of the uniform inequality in (2.20) only for n sufficiently large.
-
(ii)
If for \(\varepsilon \) small, the series \(\sum _{n=0}^{+\infty } \left| a_{n\varepsilon }(x_{\varepsilon }-c_{\varepsilon })^{n}\right| =:R_{\varepsilon }\) of absolute values terms converges to a \(\rho \)-moderate net, then (2.20) holds for \(N=0\). This includes Example 11 of geometric hyperseries, Example 12 of a function with a flat point if both x, c are finite, and Example 14 of the exponential hyperseries at \(c=0\) if x is finite.
-
(iii)
In Example 15 of Dirac delta at \(c=0\), if \(|bx|\le 1\) (therefore, x is an infinitesimal number) we have \(\left| \frac{\delta _{\varepsilon }^{(n)}(0)}{n!}x_{\varepsilon }^{n}\right| =\left| \frac{\mu ^{(n)}(0)}{n!}b_{\varepsilon }^{n+1}x_{\varepsilon }^{n}\right| \le b_{\varepsilon }\) for all \(n\in \mathbb {N}\) such that \(\left| \frac{\mu ^{(n)}(0)}{n!}\right| \le 1\). Therefore, \(\left( \frac{\delta ^{(n)}(0)}{n!}x^{n}\right) _{n\in \mathbb {N}}\) is eventually
 -bounded in
-bounded in  if \(|bx|\le 1\). If \(x\gg 0\), i.e. \(x\ge s\in \mathbb {R}_{>0}\), then \(\left| \frac{\delta _{\varepsilon }^{(n)}(0)}{n!}x_{\varepsilon }^{n}\right| =\left| \frac{\mu ^{(n)}(0)}{n!}b_{\varepsilon }^{n+1}x_{\varepsilon }^{n} \right| \ge \left| \frac{\mu ^{(n)}(0)}{n!}\right| s^{n}b_{\varepsilon }^{n+1}\) and hence condition (2.20) does not hold for any
if \(|bx|\le 1\). If \(x\gg 0\), i.e. \(x\ge s\in \mathbb {R}_{>0}\), then \(\left| \frac{\delta _{\varepsilon }^{(n)}(0)}{n!}x_{\varepsilon }^{n}\right| =\left| \frac{\mu ^{(n)}(0)}{n!}b_{\varepsilon }^{n+1}x_{\varepsilon }^{n} \right| \ge \left| \frac{\mu ^{(n)}(0)}{n!}\right| s^{n}b_{\varepsilon }^{n+1}\) and hence condition (2.20) does not hold for any  because \(b\ge \textrm{d}\rho ^{-a}\) for some \(a\in \mathbb {R}_{>0}\) (see e.g. [12, Sec. 3.0.2]).
because \(b\ge \textrm{d}\rho ^{-a}\) for some \(a\in \mathbb {R}_{>0}\) (see e.g. [12, Sec. 3.0.2]).
The last example also shows that property (2.20) does not hold for all points  . However, it always holds for any c if x is sufficiently near to c:
. However, it always holds for any c if x is sufficiently near to c:
Lemma 21
Let  and
and  , then there exists
, then there exists  such that for all \(x\in B_{\sigma }(c)\), the sequence of summands \(\left( a_{n}(x-c)^{n}\right) _{n\in \mathbb {N}}\) is eventually
such that for all \(x\in B_{\sigma }(c)\), the sequence of summands \(\left( a_{n}(x-c)^{n}\right) _{n\in \mathbb {N}}\) is eventually  -bounded in
-bounded in  .
.
Proof
Using the same notation as above, since  , we have \(\forall ^{0}\varepsilon \,\forall n\in \mathbb {N}:\ |a_{n\varepsilon }|\le \rho _{\varepsilon }^{-nQ-R}\). Therefore, for \(\sigma :=\textrm{d}\rho ^{Q}\), we have \(|a_{n\varepsilon }(x_{\varepsilon }-c_{\varepsilon })^{n}|\le \rho _{\varepsilon }^{-nQ-R}\rho _{\varepsilon }^{nQ}=\rho _{\varepsilon }^{-R}\). \(\square \)
, we have \(\forall ^{0}\varepsilon \,\forall n\in \mathbb {N}:\ |a_{n\varepsilon }|\le \rho _{\varepsilon }^{-nQ-R}\). Therefore, for \(\sigma :=\textrm{d}\rho ^{Q}\), we have \(|a_{n\varepsilon }(x_{\varepsilon }-c_{\varepsilon })^{n}|\le \rho _{\varepsilon }^{-nQ-R}\rho _{\varepsilon }^{nQ}=\rho _{\varepsilon }^{-R}\). \(\square \)
The following result is a stronger version of the previous Lemma 18, and allows us to apply the dominated convergence test:
Lemma 22
Let  , x,
, x,  , and assume that \(\left( a_{n}(x-c)^{n}\right) _{n\in \mathbb {N}}\) is eventually
, and assume that \(\left( a_{n}(x-c)^{n}\right) _{n\in \mathbb {N}}\) is eventually  -bounded in
-bounded in  , then
, then

i.e. for all representatives \((a_{n})_{\textrm{c}}=\left[ a_{n\varepsilon }\right] _{{\textrm{c}}}\), \([x_{\varepsilon }]=x\), \([c_{\varepsilon }]=c\), \([K_{\varepsilon }]=K\), we have
Since  by Remark 5(ii), property (2.21) also shows that Definition 19 does not depend on the representatives involved.
by Remark 5(ii), property (2.21) also shows that Definition 19 does not depend on the representatives involved.
Proof
It suffices to set \(K:=R\vee \max _{n\le N}a_{n}\), where  and \(N\in \mathbb {N}\) come from (2.20). \(\square \)
and \(N\in \mathbb {N}\) come from (2.20). \(\square \)
Even if the case of the exponential HPS (see Example 14) shows that in general the set of convergence is not an interval, it has very similar properties, at least if the gauge \(\sigma \) is sufficiently small:
Theorem 23
Let \(\sigma \le \rho ^{*}\) and  be a convergent HPS whose sequence of summands \(\left( a_{n}({\bar{x}}-c)^{n}\right) _{n\in \mathbb {N}}\) is eventually
be a convergent HPS whose sequence of summands \(\left( a_{n}({\bar{x}}-c)^{n}\right) _{n\in \mathbb {N}}\) is eventually  -bounded in
-bounded in  . Then for all \(x\in B_{|{\bar{x}}-c|}(0)\) we have:
. Then for all \(x\in B_{|{\bar{x}}-c|}(0)\) we have:
-
(i)
The HPS converges absolutely at x, and hence uniformly on every functionally compact \(K\Subset _{\textrm{f}}{\overline{B}}_{|{\bar{x}}-c|}(c)\);
-
(ii)
\(\left( a_{n}(x-c)^{n}\right) _{n\in \mathbb {N}}\) is eventually
 -bounded in
-bounded in  .
. -
(iii
If \(|{\hat{x}}-c|=|{\bar{x}}-c|\), then not necessarily
 converges.
converges.
If  , then:
, then:
-
(iv)
 ;
; -
(v)
x is a sharply interior point, i.e.
 for some
for some 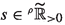 ;
; -
(vi)
 is
is  -convex, i.e. if also
-convex, i.e. if also  , then
, then  ;
; -
(vii)
The set of convergence
 is strongly connected, i.e. it is not possible to write it as union of two non empty strongly disjoint sets, i.e. such that
is strongly connected, i.e. it is not possible to write it as union of two non empty strongly disjoint sets, i.e. such that -
(a)
A,
 , \(A\ne \emptyset \ne B\),
, \(A\ne \emptyset \ne B\), -
(b)
\(\exists \sup (A)\), \(\exists \inf (B)\), \(\sup (A)\le \inf (B)\),
-
(c)
 ,
, -
(d)
\(\exists m\in \mathbb {N}:\ B_{\textrm{d}\rho ^{m}}(A) \cap B_{\textrm{d}\rho ^{m}}(B)=\emptyset \).
-
(a)
Proof
Without loss of generality we can assume \(c=0\). From [21, Lemma 5(ii)], we have either \({\bar{x}}=_{L}0\) or \(|{\bar{x}}|>0\) for some \(L\subseteq _{0}I\). The first case is actually impossible because \(0\le |x|<|{\bar{x}}|=_{L}0\). We can hence work only in the latter case \(|{\bar{x}}|>0\). From Lemma 22, we have \(\forall ^{0}\varepsilon \,\forall n\in \mathbb {N}:\ |a_{n\varepsilon }{\bar{x}}_{\varepsilon }^{n}|\le K_{\varepsilon }\). Setting \(h:=\left| \frac{x}{{\bar{x}}}\right| \), we have \(h<1\) because \(|x|\in B_{|{\bar{x}}|}(0)\), and
Thereby, \(\sum _{n=N}^{M}|a_{n}x^{n}|\le \sum _{n=N}^{M}Kh^{n}\) for all N,  . By the direct comparison test [25, Theorem 22], the HPS
. By the direct comparison test [25, Theorem 22], the HPS  converges absolutely because
converges absolutely because  converges since \(\sigma \le \rho ^{*}\) and \(h<1\). Finally, [12, Theorem 74] yields that pointwise convergence implies uniform convergence on functionally compact sets, see [11]. This proves (i).
converges since \(\sigma \le \rho ^{*}\) and \(h<1\). Finally, [12, Theorem 74] yields that pointwise convergence implies uniform convergence on functionally compact sets, see [11]. This proves (i).
(ii): From (2.23) it follows that \(\sum _{n=0}^{+\infty }|a_{n\varepsilon }x_{\varepsilon }^{n}|=:R_{\varepsilon }\) converges and is \(\rho \)-moderate. This implies condition (2.20).
For (iii), it suffices to consider that  converges (see [25, Sec. 3.6]) whereas
converges (see [25, Sec. 3.6]) whereas  does not by [25, Theorem 18]. Note however, that for \(x=1\), we have \(|x|=\textrm{rad}\left( \frac{1}{n}\right) _\textrm{c}\) so that condition Definition 8(i) does not hold.
does not by [25, Theorem 18]. Note however, that for \(x=1\), we have \(|x|=\textrm{rad}\left( \frac{1}{n}\right) _\textrm{c}\) so that condition Definition 8(i) does not hold.
(iv): From the assumptions, \(x\in B_{|{\bar{x}}-c|}(0)\), \(|{\bar{x}}-c|<\textrm{rad}\left( a_{n}\right) _\textrm{c}\), and hence Definition 8(i) and Definition 8(iii follow. Note that Definition 8(ii) can be proved as above from (2.23). Finally, if \([{\hat{x}}_{\varepsilon }]=x\) and \(k\in \mathbb {N}_{>0}\), we have
where we used Lemma 22, and hence Definition 8(iv) also holds.
(v): For \(s:=|{\bar{x}}|-|x|>0\) and \({\hat{x}}\in B_{s}(x)\), we have \(|{\hat{x}}|\le |{\hat{x}}-x|+|x|<s+|x|=|{\bar{x}}|\), and hence  from (iv).
from (iv).
(vi): Setting \({\hat{x}}:=y+t({\bar{x}}-y)\), we have \(y\le {\hat{x}}\le {\bar{x}}\). We can use trichotomy law [21, Lemma 7(iii)] to distinguish the cases \(y=_{L}0\) or \(y>_{L}0\) or \(y<_{L}0\) for \(L\subseteq _{0}I\). The latter has to be subdivided into the sub-cases \({\hat{x}}>_{M}0\) or \({\hat{x}}=_{M}0\) or \({\hat{x}}<_{M}0\) with \(M\subseteq _{0}L\), i.e. using [21, Lemma 7(iii)] for the ring  . Finally, the latter of these sub-cases has to be further subdivided into \({\hat{x}}>_{K}y\) or \({\hat{x}}<_{K}y\) or \({\hat{x}}=_{K}y\) with \(K\subseteq _{0}M\). In all these cases (clearly, some of these subcases cannot hold simultaneously) we can prove Definition 8 in the corresponding co-final set.
. Finally, the latter of these sub-cases has to be further subdivided into \({\hat{x}}>_{K}y\) or \({\hat{x}}<_{K}y\) or \({\hat{x}}=_{K}y\) with \(K\subseteq _{0}M\). In all these cases (clearly, some of these subcases cannot hold simultaneously) we can prove Definition 8 in the corresponding co-final set.
(vii): By contradiction, if \(a\in A\) and \(b\in B\), then \(x:=\frac{1}{2}\left( \sup (A)+\inf (B)\right) \) lies in the segment  by (vi). But property \(B_{\textrm{d}\rho ^{m}}(A)\cap B_{\textrm{d}\rho ^{m}}(B)\) implies that \(\sup (A)<\inf (B)\) and hence
by (vi). But property \(B_{\textrm{d}\rho ^{m}}(A)\cap B_{\textrm{d}\rho ^{m}}(B)\) implies that \(\sup (A)<\inf (B)\) and hence  . \(\square \)
. \(\square \)
In spite of Theorem 23(v), it remains open the problem whether the set of convergence is always a sharply open set or not. Using the previous theorem, this problem depends, for each point x in the set of convergence, on the existence of a point \({\bar{x}}\) satisfying assumptions of Theorem 23. However, in the case  , Remark 20 (iv) shows that \(\left( \frac{\delta ^{(n)}(0)}{n!}x^{n}\right) _{n\in \mathbb {N}}\) is not eventually
, Remark 20 (iv) shows that \(\left( \frac{\delta ^{(n)}(0)}{n!}x^{n}\right) _{n\in \mathbb {N}}\) is not eventually  -bounded in
-bounded in  , so that such a point \({\bar{x}}\) in this case does not exist and Theorem 23 cannot be applied.
, so that such a point \({\bar{x}}\) in this case does not exist and Theorem 23 cannot be applied.
Corollary 24
Let \(\sigma \le \rho ^{*}\) and let R be the set of all the numbers of the form \(s=|{\bar{x}}-c|\) for some  satisfying:
satisfying:
-
(i)
 is a convergent HPS,
is a convergent HPS, -
(ii)
\((a_{n}({\bar{x}}-c)^{n})_{n\in \mathbb {N}}\) is eventually
 -bounded in
-bounded in  .
.
If  , then
, then  , the HPS
, the HPS  converges absolutely for all \(x\in B_{r}(c)\) and uniformly on every functionally compact \(K\Subset _{\textrm{f}}{\overline{B}}_{r}(c)\).
converges absolutely for all \(x\in B_{r}(c)\) and uniformly on every functionally compact \(K\Subset _{\textrm{f}}{\overline{B}}_{r}(c)\).
Proof
Without loss of generality, we assume \(c=0\), and let \(x\in B_{r}(c)\). Since \(|x|<r\), by the definition of sharp supremum, (see [21]) there exist \(s=\left| {\bar{x}}\right| \) such that \(|x|<\left| {\bar{x}}\right| \le r\) and such that (i) and (ii) hold. The conclusions then follow by Theorem 23. \(\square \)
Property Theorem 23(iv) can also be written as a characterization of the set of convergence:
Corollary 25
Let \(\sigma \le \rho ^{*}\),  ,
,  such that
such that  is a convergent HPS whose sequence of summands \(\left( a_{n}({\bar{x}}-c)^{n}\right) _{n\in \mathbb {N}}\) is eventually
is a convergent HPS whose sequence of summands \(\left( a_{n}({\bar{x}}-c)^{n}\right) _{n\in \mathbb {N}}\) is eventually  -bounded in
-bounded in  . If \(x\in B_{|{\bar{x}}-c|}(0)\), then
. If \(x\in B_{|{\bar{x}}-c|}(0)\), then  if and only if
if and only if

2.6 Algebraic properties of hyper-power series
In this section, we extend to HPS the classical results concerning algebraic operations and composition of power series.
Theorem 26
Assume that  and
and  are two convergent HPS, then:
are two convergent HPS, then:
-
(i)
For all
 , the product
, the product  is a convergent HPS with \(\textrm{rad}\left( ra_{n}\right) _\textrm{c}\ge \textrm{rad}\left( a_{n}\right) _\textrm{c}\), and
is a convergent HPS with \(\textrm{rad}\left( ra_{n}\right) _\textrm{c}\ge \textrm{rad}\left( a_{n}\right) _\textrm{c}\), and 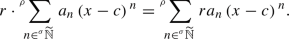 (2.25)
(2.25) -
(ii)
The sum of these HPS is a convergent HPS with
$$\begin{aligned} \textrm{rad}\left( a_{n}+b_{n}\right) _\textrm{c}\ge \min (\textrm{rad}\left( a_{n}\right) _\textrm{c},\textrm{rad}\left( b_{n}\right) _\textrm{c}), \end{aligned}$$and
 (2.26)
(2.26) -
(iii)
For all \({\bar{x}}\in B_{|x-c|}(c)\), the product of these HPS converges to their Cauchy product:
 (2.27)
(2.27)which is still a convergent HPS with radius of convergence greater or equal to \(\min (\textrm{rad}\left( a_{n}\right) _\textrm{c},\textrm{rad}\left( b_{n}\right) _\textrm{c})\).
-
(iv)
Let \(\left[ a_{n\varepsilon }\right] _{\text {c}}=(a_{n})_{\textrm{c}}\) and \(\left[ b_{n\varepsilon }\right] _{\text {c}}=(b_{n})_{\textrm{c}}\) be representatives of the coefficients of the given HPS. Assume that
 is invertible, and recursively define (for \(\varepsilon \) small) \(d_{0\varepsilon }:=\frac{a_{0\varepsilon }}{b_{0\varepsilon }}\), $$\begin{aligned} d_{n\varepsilon }:=\frac{1}{b_{0\varepsilon }}\left( a_{n\varepsilon }-\sum _{l=1}^{n}b_{l\varepsilon }d_{n-l,\varepsilon }\right) \qquad \forall n\in \mathbb {N}_{>0}. \end{aligned}$$(2.28)
is invertible, and recursively define (for \(\varepsilon \) small) \(d_{0\varepsilon }:=\frac{a_{0\varepsilon }}{b_{0\varepsilon }}\), $$\begin{aligned} d_{n\varepsilon }:=\frac{1}{b_{0\varepsilon }}\left( a_{n\varepsilon }-\sum _{l=1}^{n}b_{l\varepsilon }d_{n-l,\varepsilon }\right) \qquad \forall n\in \mathbb {N}_{>0}. \end{aligned}$$(2.28)Then coefficients
 define a convergent HPS with radius of convergence greater or equal to \(\min (\textrm{rad}\left( a_{n}\right) _\textrm{c},\textrm{rad}\left( b_{n}\right) _\textrm{c})\) such that for all \({\bar{x}}\in B_{|x-c|}(c)\), if
define a convergent HPS with radius of convergence greater or equal to \(\min (\textrm{rad}\left( a_{n}\right) _\textrm{c},\textrm{rad}\left( b_{n}\right) _\textrm{c})\) such that for all \({\bar{x}}\in B_{|x-c|}(c)\), if  is invertible, then
is invertible, then  (2.29)
(2.29)
Proof
Equalities (2.25) and (2.26) follow directly from analogous properties of convergent hyperlimits, i.e. [21, Sec. 5.2]. All the inequalities concerning the radius of convergence can be proved in the same way from analogous results of the classical theory, because of Definition (iii) 3. For example, from Definition 8(iii) we have that both the ordinary series \(\sum _{n=0}^{+\infty }a_{n\varepsilon }(x_{\varepsilon }-c_{\varepsilon })^{n}\) and \(\sum _{n=0}^{+\infty }b_{n\varepsilon }(x_{\varepsilon }-c_{\varepsilon })^{n}\) converge. Thereby, their sum \(\sum _{n=0}^{+\infty }\left( a_{n\varepsilon }+b_{n\varepsilon }\right) (x_{\varepsilon }-c_{\varepsilon })^{n}\) converges with radius \(\textrm{rad}\left( a_{n}+b_{n}\right) _{\textrm{c}{\varepsilon }}\ge \min \left( \textrm{rad}\left( a_{n}\right) _{\textrm{c}{\varepsilon }},\textrm{rad}\left( b_{n}\right) _{\textrm{c}{\varepsilon }}\right) \). To prove (2.27) (assuming that \({\bar{x}}\) lies in the convergence set of the product HPS, see below), from Lemma 23 we have that both the series converge absolutely because \({\bar{x}}\in B_{|x-c|}(c)\). We can hence apply the generalization of Mertens’ theorem to hyperseries (see [25, Theorem 37]).
To complete the proof of (iii), we start by showing that the representatives of the product \(\left( \sum _{k=0}^{n}a_{k\varepsilon }b_{n-k,\varepsilon }\right) _{n,\varepsilon }\) defines coefficients for an HPS. Let \((a_{n})_{{\textrm{c}}}=\left[ a_{n\varepsilon }\right] _{{\textrm{c}}}\),  , so that:
, so that:
Without loss of generality we can assume \(Q_{2}>Q_{1}\). We have
We have \(\rho _{\varepsilon }^{Q_{2}-Q_{1}}<1\) because \(Q_{2}>Q_{1}\), and hence
where \(R:=R_{1}+R_{2}\) and for a suitable \(Q\in \mathbb {N}\) (that can be chosen uniformly with respect to \(n\in \mathbb {N}\)). Thereby, the product HPS has well-defined coefficients and hence a suitable set of convergence.
Now, we want to show that \({\bar{x}}\) lies in this set of convergence. Since Definition 8(i) clearly holds and Definition 8(iii) follows from Mertens’ Theorem (both [25, Theorem 37] and the classical version), it remains to prove that we actually have a formal HPS (Definition 8(ii)) and moderateness of derivatives (Definition 8(iv)). The latter follows by the general Leibniz rule for the k-th derivative of a product. For the former one, without loss of generality we can assume \(c=0\); let \(\left( M_{\varepsilon }\right) \), \(\left( N_{\varepsilon }\right) \in \mathbb {N}_{\sigma }\), then for suitable \(\left( {\bar{M}}_{\varepsilon }\right) \), \(\left( {\hat{M}}_{\varepsilon }\right) \in \mathbb {N}_{\sigma }\) and \(\left( {\bar{N}}_{\varepsilon }\right) \), \(\left( {\hat{N}}_{\varepsilon }\right) \in \mathbb {N}_{\sigma }\) such that \(M_{\varepsilon }={\bar{M}}_{\varepsilon }+{\hat{M}}_{\varepsilon }\) and \(N_{\varepsilon }={\bar{N}}_{\varepsilon }+{\hat{N}}_{\varepsilon }\), we have
and thereby Definition 8(ii) follows.
(iv): To prove that  , without loss of generality, we can assume in (2.30) and (2.31) that \(Q_{1}=Q_{2}=:{\hat{Q}}>R_{1}=R_{2}=:{\hat{R}}\) and \({\hat{Q}}>0\). By induction on \(n\in \mathbb {N}\), we want to prove that
, without loss of generality, we can assume in (2.30) and (2.31) that \(Q_{1}=Q_{2}=:{\hat{Q}}>R_{1}=R_{2}=:{\hat{R}}\) and \({\hat{Q}}>0\). By induction on \(n\in \mathbb {N}\), we want to prove that
For \(n=0\), we have \(\left| d_{0\varepsilon }\right| =\left| \frac{a_{0\varepsilon }}{b_{0\varepsilon }} \right| \le \rho _{\varepsilon }^{-{\hat{R}}+{\hat{R}}}\le \rho _{\varepsilon }^{-{\hat{Q}}}\) for all \(\varepsilon \) because \({\hat{Q}}>0\). For the inductive step, we assume (2.34) and use the recursive definition (2.28):
We have \(2\rho _{\varepsilon }^{-n{\hat{Q}}-{\hat{Q}}}\le \rho _{\varepsilon }^{-(n+1){\hat{Q}}-{\hat{Q}}}\) if and only if \(2\le \rho _{\varepsilon }^{-{\hat{Q}}}\), which holds for \(\varepsilon \) small (independently by n).
Finally, equality (2.29) can be proved as we did above for the product because \({\bar{x}}\in B_{|x-c|}(c)\) and

From this equality, it also follows Definition 16(ii) because the product of an invertible non-moderate net (on a co-final set) by a moderate net cannot yield a moderate net. Finally, as above, moderateness of derivatives follows from Mertens’ theorem and the k-th derivative of the quotient. \(\square \)
The following theorem concerns the composition of HPS:
Theorem 27
Let \((a_{n})_{{\textrm{c}}}=\left[ a_{n\varepsilon }\right] _{{\textrm{c}}}\),  be coefficients for HPS. Set
be coefficients for HPS. Set

Set
If  and
and  , then
, then

is a convergent HPS.
Proof
Since \(\left[ a_{n\varepsilon }\right] _{c}\),  , we can assume that both (2.2) and (2.3) hold with \({\hat{Q}}=Q_{1}=Q_{2}>0\) and \({\hat{R}}=R_{1}=R_{2}>0\). We have
, we can assume that both (2.2) and (2.3) hold with \({\hat{Q}}=Q_{1}=Q_{2}>0\) and \({\hat{R}}=R_{1}=R_{2}>0\). We have
For \(\varepsilon \) small, we have \(\frac{4}{\rho _{\varepsilon ^{-1}}}\le 1\), hence \(\frac{2^{2n}}{\rho _{\varepsilon }^{-n}}\le 1\) for the same \(\varepsilon \) and for all \(n\in \mathbb {N}\). Now, take \(\varepsilon \) small so that also \(\frac{1}{1-\rho _{\varepsilon }^{-{\hat{Q}}-{\hat{R}}}}\le 1\), and \(\frac{1}{\rho _{\varepsilon }^{-1}}\le \frac{1}{3}\). We hence have
Since
we finally get
which proves that \((c_{n\varepsilon })_{n,\varepsilon }\) defines coefficients for an HPS.
To prove that  , we can proceed as follows: Definition 8(i) can be proved like in the classical case; Definition 8(ii) is a consequence of composition of polynomials if \(M_{\varepsilon }<+\infty \) or it can be proved proceeding like in the case of composition of GSF if \(M_{\varepsilon }=+\infty \): Definition 8(iii) and Definition 8(iv) can be proved like for GSF (see [12] and Theorem 28 below). \(\square \)
, we can proceed as follows: Definition 8(i) can be proved like in the classical case; Definition 8(ii) is a consequence of composition of polynomials if \(M_{\varepsilon }<+\infty \) or it can be proved proceeding like in the case of composition of GSF if \(M_{\varepsilon }=+\infty \): Definition 8(iii) and Definition 8(iv) can be proved like for GSF (see [12] and Theorem 28 below). \(\square \)
3 Generalized real analytic functions and their calculus
A direct consequence of Definition 8 of set of convergence is the following
Theorem 28
Let  and
and  . Set
. Set

for all  . Then
. Then  is a GSF defined by \(\left( v_{\varepsilon }\right) \).
is a GSF defined by \(\left( v_{\varepsilon }\right) \).
Before defining the notion of GRAF, we need to prove that the derived HPS has the same set of convergence of the original HPS:
Theorem 29
Assume \(\sigma \le \rho ^{*}\),  and
and  . Then the set of convergence of the derived series
. Then the set of convergence of the derived series  is the same as the set of convergence of the original HPS
is the same as the set of convergence of the original HPS  . Thereby, recursively, all the derivatives have the same set of convergence of the original HPS and define a GSF.
. Thereby, recursively, all the derivatives have the same set of convergence of the original HPS and define a GSF.
Proof
By Definition 3(iii) of radius of convergence and the classical theory, we have
so Definition 8(i) for the original HPS and the derived one are equivalent. From the condition  and \(\sigma \le \rho ^{*}\), in the usual way it follows that
and \(\sigma \le \rho ^{*}\), in the usual way it follows that  . Vice versa, from \((n+1)\left| a_{n+1,\varepsilon }\right| \ge \left| a_{n+1,\varepsilon }\right| \) the opposite implication follows. The condition Definition 8(iv) about moderateness of derivatives for the original HPS clearly implies the analogue condition for the derived one. For the opposite inclusion, we can distinguish the case \(x=_{\text {s}}c\) or \(|x-c|>0\), the former one being trivial. We have
. Vice versa, from \((n+1)\left| a_{n+1,\varepsilon }\right| \ge \left| a_{n+1,\varepsilon }\right| \) the opposite implication follows. The condition Definition 8(iv) about moderateness of derivatives for the original HPS clearly implies the analogue condition for the derived one. For the opposite inclusion, we can distinguish the case \(x=_{\text {s}}c\) or \(|x-c|>0\), the former one being trivial. We have
so that also the net \(\left( \sum _{n=0}^{+\infty }a_{n\varepsilon }(x_{\varepsilon }-c_{\varepsilon })^{n}\right) \in \mathbb {R}_{\rho }\) if the derivative is moderate. \(\square \)
Theorem 28 motivates the following definition:
Definition 30
Let \(\sigma \le \rho ^{*}\) and U be a sharply open set of  , then we say that f is a GRAF on U (with respect to \(\rho \), \(\sigma \)), and we write
, then we say that f is a GRAF on U (with respect to \(\rho \), \(\sigma \)), and we write  if
if  and for all \(c\in U\) we can find
and for all \(c\in U\) we can find  ,
,  such that
such that
-
(i)
 ,
, -
(ii)
 for all \(x\in (c-s,c+s)\).
for all \(x\in (c-s,c+s)\).
Moreover, we say that  is an entire function (with respect to \(\rho \), \(\sigma \)) if we can find
is an entire function (with respect to \(\rho \), \(\sigma \)) if we can find  and
and  such that
such that
-
(iii)
 ,
, -
(iv)
 for all
for all  .
.
We also say that f is entire at c if (iii) and (iv) hold.
Example 31
-
(a)
Clearly, if
 ,
,  , and we set
, and we set  , then f is a GRAF on the interior points of the set of convergence
, then f is a GRAF on the interior points of the set of convergence  . Vice versa, if
. Vice versa, if  , then U is contained in the union of all the sharp interior sets
, then U is contained in the union of all the sharp interior sets  , because of condition (i).
, because of condition (i). -
(b)
Example 15 shows that Dirac \(\delta \) is entire at 0 but it is not at any
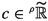 such that \(\left| c\right| \ge s\) for some \(s\in \mathbb {R}_{>0}\).
such that \(\left| c\right| \ge s\) for some \(s\in \mathbb {R}_{>0}\). -
(c)
Example 12 of a function f with a flat point shows that f is a GRAF, but if \(c=0\), then
 satisfying condition (i) is infinitesimal, whereas if \(c\gg 0\), then \(s\gg 0\) is finite, and these two types of set of convergence are always disjoint.
satisfying condition (i) is infinitesimal, whereas if \(c\gg 0\), then \(s\gg 0\) is finite, and these two types of set of convergence are always disjoint.
Corollary 32
Let \(\sigma \le \rho ^{*}\),  be a sharply open set and
be a sharply open set and  , then also
, then also  and it can be computed with the derived HPS i.e.
and it can be computed with the derived HPS i.e.  .
.
Because of our definition Definition 8 of set of convergence, several classical results can be simply translated in our setting considering the real analytic function that defines a given GRAF.
Theorem 33
Let \(\sigma \le \rho ^{*}\),  ,
,  , and set
, and set  for all interior points
for all interior points  , then \(a_{k}=\frac{f^{(k)}(c)}{k!}\) for all \(k\in \mathbb {N}\).
, then \(a_{k}=\frac{f^{(k)}(c)}{k!}\) for all \(k\in \mathbb {N}\).
Proof
From Corollary 32, we have \(f^{(k)}(x)=\left[ \sum _{n=k}^{\infty }a_{n\varepsilon }k!{n \atopwithdelims ()k}(x_{\varepsilon }-c_{\varepsilon })^{n-k}\right] \) for all the interior points  . For \(x=c\) (which is always a sharply interior point because of Theorem 9) this yields the conclusion. \(\square \)
. For \(x=c\) (which is always a sharply interior point because of Theorem 9) this yields the conclusion. \(\square \)
Corollary 34
Let \(\sigma \le \rho ^{*}\), U be a sharply open set of  , and
, and  . Then for all \(c\in U\) the Taylor coefficients
. Then for all \(c\in U\) the Taylor coefficients  .
.
The definition of 1-dimensional integral of GSF by using primitives, allows us to get a simple proof of the term by term integration of GRAF:
Theorem 35
In the assumptions of the previous theorem, set

for all the interior points  . Then \(F(x)=\int _{c}^{x}f(x)\,\textrm{d}{x}\) and F is a GRAF on the interior points of
. Then \(F(x)=\int _{c}^{x}f(x)\,\textrm{d}{x}\) and F is a GRAF on the interior points of  .
.
Proof
The proof that  is a convergent HPS with the same set of convergence of f can be done as in Theorem 29, and hence F is a GRAF on the interior points of
is a convergent HPS with the same set of convergence of f can be done as in Theorem 29, and hence F is a GRAF on the interior points of  . The remaining part of the proof is straightforward by using Corollary 32, so that \(F'(x)=f\left( x\right) \) and \(F(c)=0\). and using [12, Theorem 42, Definition 43]. \(\square \)
. The remaining part of the proof is straightforward by using Corollary 32, so that \(F'(x)=f\left( x\right) \) and \(F(c)=0\). and using [12, Theorem 42, Definition 43]. \(\square \)
We close this section by first noting that, differently with respect to the classical theory, if  for all
for all  , and we take another point
, and we take another point  , we do not have that
, we do not have that  ; in fact for \(c={\bar{c}}\) this would yield the false equality
; in fact for \(c={\bar{c}}\) this would yield the false equality  . On the other hand, in the following result we show that
. On the other hand, in the following result we show that  :
:
Theorem 36
In the assumptions of Theorem 33, if  , then
, then  .
.
Proof
In fact, since  , we have
, we have

Thereby, if  , we have
, we have

Therefore, the usual proof, see e.g. [20], yields
and hence  , which implies the conclusion. \(\square \)
, which implies the conclusion. \(\square \)
4 Characterization of generalized real analytic functions, inversion and identity principle
The classical characterization of real analytic functions by the growth rate of the derivatives establishes a difference between GRAF and Colombeau real analytic functions:
Theorem 37
Let \(\sigma \le \rho ^{*}\), U be a sharply open set of  , and
, and  be a GSF defined by the net \((f_{\varepsilon })\). Then
be a GSF defined by the net \((f_{\varepsilon })\). Then  if and only if for each \(c\in U\) there exist \(s=[s_{\varepsilon }]\), \(C=\left[ C_{\varepsilon }\right] \),
if and only if for each \(c\in U\) there exist \(s=[s_{\varepsilon }]\), \(C=\left[ C_{\varepsilon }\right] \),  such that \(B_{s}(c)\subseteq U\) and
such that \(B_{s}(c)\subseteq U\) and
Proof
We prove that condition (4.1) is necessary. For \(c\in U\), we have  for all \(x\in (c-{\bar{s}},c+{\bar{s}})\) for some \({\bar{s}}>0\) from Definition 30 and Theorem 33. We first note that condition (4.1) can also be formulated as an inequality in
for all \(x\in (c-{\bar{s}},c+{\bar{s}})\) for some \({\bar{s}}>0\) from Definition 30 and Theorem 33. We first note that condition (4.1) can also be formulated as an inequality in  and as such it does not depend on the representatives involved. Therefore, from Theorem 28 and Theorem 33, without loss of generality, we can assume that the given net \((f_{\varepsilon })\) is of real analytic functions satisfying \(f_{\varepsilon }(x)=\sum _{n=0}^{+\infty }\frac{f_{\varepsilon }^{(n)}(c_{\varepsilon })}{n!}(x-c_{\varepsilon })^{n}\) for all \(x\in (c_{\varepsilon }-\textrm{rad}\left( a_{n}\right) _{\textrm{c}{\varepsilon }},c_{\varepsilon }+\textrm{rad}\left( a_{n}\right) _{\textrm{c}{\varepsilon }})\). From Lemma 21, locally the Taylor summands \(\left( \frac{f^{(n)}(c)}{n!}({\bar{x}}-c)^{n}\right) _{n\in \mathbb {N}}\) are eventually
and as such it does not depend on the representatives involved. Therefore, from Theorem 28 and Theorem 33, without loss of generality, we can assume that the given net \((f_{\varepsilon })\) is of real analytic functions satisfying \(f_{\varepsilon }(x)=\sum _{n=0}^{+\infty }\frac{f_{\varepsilon }^{(n)}(c_{\varepsilon })}{n!}(x-c_{\varepsilon })^{n}\) for all \(x\in (c_{\varepsilon }-\textrm{rad}\left( a_{n}\right) _{\textrm{c}{\varepsilon }},c_{\varepsilon }+\textrm{rad}\left( a_{n}\right) _{\textrm{c}{\varepsilon }})\). From Lemma 21, locally the Taylor summands \(\left( \frac{f^{(n)}(c)}{n!}({\bar{x}}-c)^{n}\right) _{n\in \mathbb {N}}\) are eventually  -bounded in
-bounded in  if \({\bar{x}}\) is sufficiently near to \(c=[c_{\varepsilon }]\), i.e. there exists
if \({\bar{x}}\) is sufficiently near to \(c=[c_{\varepsilon }]\), i.e. there exists  such that for each \({\bar{x}}=[{\bar{x}}_{\varepsilon }]\in B_{\sigma }(c)\) we have
such that for each \({\bar{x}}=[{\bar{x}}_{\varepsilon }]\in B_{\sigma }(c)\) we have
for some  . Set \(s:=\frac{1}{2}\min (\sigma ,{\bar{s}})\in \mathbb {R}_{>0}\) and \(S:=|{\bar{x}}-c|\), where \({\bar{x}}\) is any point such that \(s<|{\bar{x}}-c|<\sigma \), so that \(0<\frac{s}{S}<1\) and from (4.2) we obtain
. Set \(s:=\frac{1}{2}\min (\sigma ,{\bar{s}})\in \mathbb {R}_{>0}\) and \(S:=|{\bar{x}}-c|\), where \({\bar{x}}\) is any point such that \(s<|{\bar{x}}-c|<\sigma \), so that \(0<\frac{s}{S}<1\) and from (4.2) we obtain
For each \([x_{\varepsilon }]\in B_{s}(c)\), we have
and hence from (4.3):
which is our claim for \(C:=\frac{K}{1-\frac{s}{S}}\) and \(R:=S\left( 1-\frac{s}{S}\right) \). Note that, differently with respect to the case of Colombeau real analytic functions [23], not necessarily the constant \(\frac{1}{R}\) is finite, e.g. if \(s\approx S\).
We now prove that the condition is sufficient. Let \(c=[c_{\varepsilon }]\in U\) and \(s=[s_{\varepsilon }]\), \(C=[C_{\varepsilon }]\),  be the constants satisfying (4.1). Set \({\bar{s}}:=\frac{1}{2}\min (s,R,\textrm{rad}\left( \frac{f^{(n)}(c)}{n!}\right) _\textrm{c})\) and take \(x\in B_{{\bar{s}}}(c)\). We first prove the equality
be the constants satisfying (4.1). Set \({\bar{s}}:=\frac{1}{2}\min (s,R,\textrm{rad}\left( \frac{f^{(n)}(c)}{n!}\right) _\textrm{c})\) and take \(x\in B_{{\bar{s}}}(c)\). We first prove the equality  . Let
. Let  , with \(N_{\varepsilon }\in \mathbb {N}\). For all \(\varepsilon \), from Taylor’s formula for the smooth \(f_{\varepsilon }\), we have
, with \(N_{\varepsilon }\in \mathbb {N}\). For all \(\varepsilon \), from Taylor’s formula for the smooth \(f_{\varepsilon }\), we have
for some \(t_{\varepsilon }\in [0,1]_{\mathbb {R}}\) and for \(\xi _{\varepsilon }:=(1-t_{\varepsilon })c_{\varepsilon }+t_{\varepsilon }x_{\varepsilon }\). Since \(\left| \xi _{\varepsilon }-c_{\varepsilon }\right| =t_{\varepsilon }\left| x_{\varepsilon } -c_{\varepsilon }\right|<{\bar{s}}_{\varepsilon }<s_{\varepsilon }\), we can apply (4.1) and get \(\forall ^{0}\varepsilon \,\forall n\in \mathbb {N}:\ \left| \frac{f_{\varepsilon }^{(n)}(\xi _{\varepsilon })}{n!}\right| \le \frac{C_{\varepsilon }}{R_{\varepsilon }^{n}}\). Thereby, for these small \(\varepsilon \) and for \(n=N_{\varepsilon }+1\) we obtain
and hence the claim follows by  . Now, we prove that
. Now, we prove that  . In fact, once again from (4.1) we have
. In fact, once again from (4.1) we have

because \({\bar{s}}<R\) and hence  converges. Finally, take \({\bar{x}}\in B_{{\bar{s}}}(c)\) such that \(|x-c|<|{\bar{x}}-c|\). As above, we can prove that
converges. Finally, take \({\bar{x}}\in B_{{\bar{s}}}(c)\) such that \(|x-c|<|{\bar{x}}-c|\). As above, we can prove that  converges; moreover from (4.1) we also have \(\forall ^{0}\varepsilon \,\forall n\in \mathbb {N}:\ \left| \frac{f_{\varepsilon }^{(n)}(c_{\varepsilon })}{n!}({\bar{x}}_{\varepsilon }-c_{\varepsilon })^{n}\right| \le C_{\varepsilon }\left( \frac{{\bar{s}}_{\varepsilon }}{R_{\varepsilon }}\right) ^{n} \le \frac{C_{\varepsilon }}{1-\frac{{\bar{s}}_{\varepsilon }}{R_{\varepsilon }}}\). This proves that \(\left( \frac{f^{(n)}(c)}{n!}({\bar{x}}-c)^{n}\right) _{n\in \mathbb {N}}\) is eventually
converges; moreover from (4.1) we also have \(\forall ^{0}\varepsilon \,\forall n\in \mathbb {N}:\ \left| \frac{f_{\varepsilon }^{(n)}(c_{\varepsilon })}{n!}({\bar{x}}_{\varepsilon }-c_{\varepsilon })^{n}\right| \le C_{\varepsilon }\left( \frac{{\bar{s}}_{\varepsilon }}{R_{\varepsilon }}\right) ^{n} \le \frac{C_{\varepsilon }}{1-\frac{{\bar{s}}_{\varepsilon }}{R_{\varepsilon }}}\). This proves that \(\left( \frac{f^{(n)}(c)}{n!}({\bar{x}}-c)^{n}\right) _{n\in \mathbb {N}}\) is eventually  -bounded in
-bounded in  and hence
and hence  by Corollary 25. \(\square \)
by Corollary 25. \(\square \)
As we have already noted in this proof, differently with respect to the definition of Colombeau real analytic function [23], we have that, generally speaking,  is not finite. For example, for \(f=\delta \) at \(c=0\), we have \(\left| \frac{\delta _{\varepsilon }^{(n)}(x_{\varepsilon })}{n!}\right| =\left| \frac{\mu ^{(n)} (x_{\varepsilon })}{n!}b_{\varepsilon }^{n+1}\right| =\left| \frac{\mu ^{(n)}(x_{\varepsilon })}{n!}b_{\varepsilon } \right| \frac{1}{\left( b_{\varepsilon }^{-1}\right) ^{n}}\le \frac{{\bar{C}}b_{\varepsilon }}{(b_{\varepsilon }^{-1})^{n}}\), where \(\left| \mu ^{(n)}(x_{\varepsilon })\right| \le \int \beta =:{\bar{C}}\) and hence \(\frac{1}{R}=b\) which is an infinite number. Thereby, in the particular case when \(\frac{1}{R}\) is finite, f is a Colombeau real analytic function in a neighborhood of c. Vice versa, any Colombeau real analytic function and any ordinary real analytic function are GRAF.
is not finite. For example, for \(f=\delta \) at \(c=0\), we have \(\left| \frac{\delta _{\varepsilon }^{(n)}(x_{\varepsilon })}{n!}\right| =\left| \frac{\mu ^{(n)} (x_{\varepsilon })}{n!}b_{\varepsilon }^{n+1}\right| =\left| \frac{\mu ^{(n)}(x_{\varepsilon })}{n!}b_{\varepsilon } \right| \frac{1}{\left( b_{\varepsilon }^{-1}\right) ^{n}}\le \frac{{\bar{C}}b_{\varepsilon }}{(b_{\varepsilon }^{-1})^{n}}\), where \(\left| \mu ^{(n)}(x_{\varepsilon })\right| \le \int \beta =:{\bar{C}}\) and hence \(\frac{1}{R}=b\) which is an infinite number. Thereby, in the particular case when \(\frac{1}{R}\) is finite, f is a Colombeau real analytic function in a neighborhood of c. Vice versa, any Colombeau real analytic function and any ordinary real analytic function are GRAF.
This characterization also yields the closure of GRAF with respect to inversion. We first recall that the local inverse function theorem holds for GSF, see [9]. Therefore, if  and at the point \(x_{0}\in U\) the derivative \(f'(x_{0})\) is invertible, we can find open neighborhoods of \(x_{0}\in X\subseteq U\) and of \(y_{0}:=f(x_{0})\in Y\) such that \(f|_{X}:X\rightarrow Y\) is invertible,
and at the point \(x_{0}\in U\) the derivative \(f'(x_{0})\) is invertible, we can find open neighborhoods of \(x_{0}\in X\subseteq U\) and of \(y_{0}:=f(x_{0})\in Y\) such that \(f|_{X}:X\rightarrow Y\) is invertible,  and \(f'(x)\) is invertible for all \(x\in X\).
and \(f'(x)\) is invertible for all \(x\in X\).
Theorem 38
If \(\sigma \le \rho ^{*}\) and we use notations and assumptions introduced above, then  .
.
Proof
For simplicity, set \(g:=\left( f|_{X}\right) ^{-1}\) and \(h(x):=\frac{1}{f'(x)}\) for all \(x\in X\), so that \(g'(y)=h[g(y)]\) for all \(y\in Y\). From Corollary 32 and Theorem 26, we know that h is a GRAF. Therefore, Theorem 37 yields \(\forall ^{0}\varepsilon \,\forall n\in \mathbb {N}:\ \left| h_{\varepsilon }^{(j)}(x_{\varepsilon })\right| \le C_{\varepsilon }\frac{j!}{R_{\varepsilon }^{j}}\) for all \([x_{\varepsilon }]\in B_{s}(x_{0})\) and suitable constants s, C,  . For \([y_{\varepsilon }]\in f\left( B_{s}(x_{0})\right) \) (note that this is an open neighborhood of \(y_{0}\) because f is an open map) and these \(\varepsilon \), formula (1.15) of [20, Theorem 1.5.3] yields \(\left| g_{\varepsilon }^{(j)}(y_{\varepsilon })\right| \le j!(-1)^{j-1}{1/2 \atopwithdelims ()j}\frac{(2C_{\varepsilon })^{j}}{R_{\varepsilon }^{j-1}}\) for all \(j\in \mathbb {N}_{>0}\), and hence
. For \([y_{\varepsilon }]\in f\left( B_{s}(x_{0})\right) \) (note that this is an open neighborhood of \(y_{0}\) because f is an open map) and these \(\varepsilon \), formula (1.15) of [20, Theorem 1.5.3] yields \(\left| g_{\varepsilon }^{(j)}(y_{\varepsilon })\right| \le j!(-1)^{j-1}{1/2 \atopwithdelims ()j}\frac{(2C_{\varepsilon })^{j}}{R_{\varepsilon }^{j-1}}\) for all \(j\in \mathbb {N}_{>0}\), and hence  once again by Theorem 37. \(\square \)
once again by Theorem 37. \(\square \)
Since \(\delta \) is a GRAF, in general the identity principle does not hold for GRAF. From our point of view this is a feature of GRAF because it allows to include as GRAF a large class of interesting generalized functions and hence pave the way to a more general related Cauchy-Kowalevski theorem. The following theorem clearly shows that the identity principle does not hold in our framework exactly because we are in a non-Archimedean setting: every interval is not connected in the sharp topology because the set of all the infinitesimals is a clopen set, see e.g. [8].
Theorem 39
Let  be an open set and f,
be an open set and f,  . Then the set
. Then the set
is clopen in the sharp topology.
Proof
For simplicity, considering \(f-g\), without loss of generality we can assume \(g=0\). We only have to show that \(\mathcal {O}\) is closed in U. Assume that c is in the closure of \(\mathcal {O}\) in U, i.e.

We have to prove that \(c\in \mathcal {O}\). We first note that for each \({\bar{c}}\in \mathcal {O}\), we have \(B_{p}({\bar{c}})\subseteq \mathcal {O}\) for some  and hence
and hence
Now, fix \(n\in \mathbb {N}\) in order to prove that \(f^{(n)}(c)=0\). From (4.4), for all  we can find \({\bar{c}}_{r}\in B_{r}(c)\cap \mathcal {O}\) such that \(f^{(n)}({\bar{c}}_{r})=0\) from (4.5). From sharp continuity of \(f^{(n)}\), we have \(f^{(n)}(c)=\lim _{r\rightarrow 0^{+}}f^{(n)}({\bar{c}}_{r})=0\). Since
we can find \({\bar{c}}_{r}\in B_{r}(c)\cap \mathcal {O}\) such that \(f^{(n)}({\bar{c}}_{r})=0\) from (4.5). From sharp continuity of \(f^{(n)}\), we have \(f^{(n)}(c)=\lim _{r\rightarrow 0^{+}}f^{(n)}({\bar{c}}_{r})=0\). Since  and \(c\in U\), we can hence find \(\sigma >0\) such that
and \(c\in U\), we can hence find \(\sigma >0\) such that  for all \(x\in B_{\sigma }(c)\), i.e. \(c\in \mathcal {O}\). \(\square \)
for all \(x\in B_{\sigma }(c)\), i.e. \(c\in \mathcal {O}\). \(\square \)
For example, if \(f=\delta \) and \(g=0\), the set

is clopen. Thereby, also  is clopen, and we have
is clopen, and we have

If we assume that all the derivatives of f are finite and the neighborhoods of Definition 30 are also finite, then we can repeat the previous proof considering only standard points \(c\in \mathbb {R}\) and radii \(r\in \mathbb {R}_{>0}\), obtaining the following sufficient condition:
Theorem 40
Let  be an open set such that \(U\cap \mathbb {R}\) is connected. Let f,
be an open set such that \(U\cap \mathbb {R}\) is connected. Let f,  be such that \(f|_{V\cap \mathbb {R}}=g|_{V\cap \mathbb {R}}\) for some nonempty subset \(V\subseteq U\) such that \(V\cap \mathbb {R}\) is open in the Fermat topology, i.e.
be such that \(f|_{V\cap \mathbb {R}}=g|_{V\cap \mathbb {R}}\) for some nonempty subset \(V\subseteq U\) such that \(V\cap \mathbb {R}\) is open in the Fermat topology, i.e.
Finally, assume that all the following quantities are finite:
-
(i)
The neighborhood length s in Definition 30 is finite for each \(c\in U\cap \mathbb {R}\),
-
(ii)
\(\forall x\in U\,\forall n\in \mathbb {N}:\ f^{(n)}(x)\) and \(g^{(n)}(x)\) are finite.
Then \(f|_{U\cap \mathbb {R}}=g|_{U\cap \mathbb {R}}\).
Proof
The proof proceeds exactly as in Theorem 39 but considering
where \(\text {int}_{\text {F}}\) is the interior in the Fermat topology (i.e. the topology generated by the balls \(B_{r}(c)\) for  and \(r\in \mathbb {R}_{>0}\), see [8]). We have to note that assumption (ii) implies that all \(f^{(n)}\) are continuous in this topology (see [11]). \(\square \)
and \(r\in \mathbb {R}_{>0}\), see [8]). We have to note that assumption (ii) implies that all \(f^{(n)}\) are continuous in this topology (see [11]). \(\square \)
For example, if \(f\in \mathcal {C}^{\omega }(\mathbb {R})\) is an ordinary real analytic function and K,  are finite numbers, the GRAF
are finite numbers, the GRAF  , where
, where  is the set of compactly supported points, satisfies the assumptions of the last theorem.
is the set of compactly supported points, satisfies the assumptions of the last theorem.
5 Conclusions
Sometimes, e.g. in the study of PDE, the class of real analytic functions is described as a too rigid set of solutions. In spite of their good properties with respect to algebraic operations, composition, differentiation, integration, inversion, etc., this rigidity is essentially well represented by the identity principle that necessarily excludes e.g. solitons with compact support or interesting generalized functions. Thanks to Theorem 39, we can state that this rigidity is due to the banishing of non-Archimedean numbers from mathematical analysis. The use of hyperseries allows one to recover all these features including also interesting non trivial generalized functions and compactly supported functions. This paves the way for an interesting generalization of the Cauchy-Kowalevski theorem for GRAF that we intend to develop in a subsequent work. Its proof can be approached by trying a generalization of the classical method of majorants, or using the Picard-Lindel-f theorem for PDE with GSF and then using characterization Theorem 37 to show that the GSF solution is actually a GRAF.
References
Aragona, J.: On existence theorems for the \({\bar{\partial }}\) operator on generalized differential forms. Proc. Lond. Math. Soc. 53, 474–488 (1986)
Aragona, J.: Some properties of holomorphic generalized functions on \({\bar{C}}\) pseudo-convex domains. Acta Math. Hung. 70, 167–175 (1996)
Benci, V., Luperi Baglini, L.: A non-archimedean algebra and the Schwartz impossibility theorem. Monatsh. Math. 176, 503–520 (2015)
Berarducci, A., Mantova, V.: Transseries as germs of surreal functions. Trans. Am. Math. Soc. 371, 3549–3592 (2019)
Colombeau, J.F.: New Generalized Functions and Multiplication of Distributions. North-Holland, Amsterdam (1984)
Colombeau, J.F., Gale, J.E.: Holomorphic generalized functions. J. Math. Anal. Appl. 103, 117–133 (1984)
Colombeau, J.F., Gale, J.E.: Analytic continuation of generalized functions. Acta Math. Hung. 52, 57–60 (1988)
Giordano, P., Kunzinger, M.: New topologies on Colombeau generalized numbers and the Fermat-Reyes theorem. J. Math. Anal. Appl. 399, 229–238 (2013). https://doi.org/10.1016/j.jmaa.2012.10.005
Giordano, P., Kunzinger, M.: Inverse Function Theorems for Generalized Smooth Functions. Chapter in T1 Generalized Functions and Fourier Analysis T1, Volume 260 of the series Operator Theory: Advances and Applications, pp. 95–114 (2017)
Giordano, P., Kunzinger, M.: A convenient notion of compact sets for generalized functions. Proc. Edinb. Math. Soc. 61(1), 57–92 (2018)
Giordano, P., Kunzinger, M., Vernaeve, H.: Strongly internal sets and generalized smooth functions. J. Math. Anal. Appl. 422(1), 56–71 (2015)
Giordano P., Kunzinger M., Vernaeve H.: A Grothendieck topos of generalized functions I: basic theory. See https://www.mat.univie.ac.at/giordap7/ToposI.pdf
Giordano, P., Luperi Baglini, L.: Asymptotic gauges: generalization of Colombeau type algebras. Math. Nachr. 289(2–3), 247–274 (2016)
Grosser, M., Kunzinger, M., Oberguggenberger, M., Steinbauer, R.: Geometric Theory of Generalized Functions. Kluwer, Dordrecht (2001)
Khalfallah, A., Kosarew, S.: Examples of new nonstandard hulls of topological vector spaces. Proc. Am. Math. Soc. 146, 2723–2739 (2018)
Khalfallah, A., Kosarew, S.: Bounded polynomials and holomorphic mappings between convex subrings of \(^{*}\mathbb{C} \). J. Symb. Log. 83(1), 372–384 (2018)
Keisler, H.J.: Limit ultrapowers. Trans. Am. Math. Soc. 107, 383–408 (1963)
Khelif, A., Scarpalezos, D.: Zeros of generalized holomorphic functions. Monatsh. Math. 149, 323–335 (2006)
Koblitz, N.: p-adic Numbers, p-adic Analysis, and Zeta-Functions. Graduate Texts in Mathematics (Book 58), 2nd edn. Springer, Berlin (1996)
Krantz, S.G., Parks, H.R.: A Primer of Real Analytic Functions. BirkhÁuser, Basel (2002)
Mukhammadiev, A., Tiwari, D., Apaaboah, G., et al.: Supremum, infimum and hyperlimits in the non-Archimedean ring of Colombeau generalized numbers. Monatsh. Math. 196, 163–190 (2021)
Oberguggenberger, M., Pilipovi, S., Valmorin, V.: Global Representatives of Colombeau Holomorphic Generalized Functions. Monatsh. Math. 151, 67–74 (2007)
Pilipoviç, S., Scarpalezos, D., Valmorin, V.: Real analytic generalized functions. Monatsh. Math. 156, 85 (2009)
Shamseddine, K.: A brief survey of the study of power series and analytic functions on the Levi–Civita fields. Contemporary Mathematics, vol. 596 (2013)
Tiwari, D., Giordano, P.: Hyperseries in the non-Archimedean ring of Colombeau generalized numbers. Monatsh. Math. (2021). https://doi.org/10.1007/s00605-021-01647-0
Vernaeve, H.: Generalized analytic functions on generalized domains, arXiv:0811.1521v1 (2008)
Funding
Open access funding provided by Austrian Science Fund (FWF).
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by Michael Kunzinger.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
D. Tiwari has been supported by Grants P30407 and P33538 of the Austrian Science Fund FWF. A. Mukhammadiev has been supported by Grants P30407 and P33538 of the Austrian Science Fund FWF. P. Giordano has been supported by Grants P30407, P34113, P33538 of the Austrian Science Fund FWF
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Tiwari, D., Mukhammadiev, A. & Giordano, P. Hyper-power series and generalized real analytic functions. Monatsh Math 203, 475–508 (2024). https://doi.org/10.1007/s00605-023-01849-8
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00605-023-01849-8




 . For example, in Lemma
. For example, in Lemma  .
. , depends on the interplay of the two gauges
, depends on the interplay of the two gauges  we have
we have  is not a formal HPS, i.e. even before considering its convergence or not, we cannot compute
is not a formal HPS, i.e. even before considering its convergence or not, we cannot compute 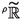 .
. is a formal HPS for all gauges
is a formal HPS for all gauges  ; on the other hand, we will also see that if
; on the other hand, we will also see that if  is a formal HPS.
is a formal HPS. , where for arbitrary
, where for arbitrary 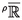 , we can also consider the standard order relation
, we can also consider the standard order relation  is an ordered group but, since we are considering arbitrary nets
is an ordered group but, since we are considering arbitrary nets  is not a ring: e.g.
is not a ring: e.g.  the quotient ring of coefficients for HPS, where
the quotient ring of coefficients for HPS, where 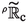 are denoted by
are denoted by  .
. , then we set
, then we set  , where
, where  , then for each fixed
, then for each fixed  , i.e. the net
, i.e. the net  is that
is that  because the notion of equality
because the notion of equality  . On the other hand, in Lemma
. On the other hand, in Lemma  , we can have different behavior on different subpoints, e.g.
, we can have different behavior on different subpoints, e.g.  ,
,  (see e.g. [
(see e.g. [ is defined by the net
is defined by the net  and motivates our definition of weakly
and motivates our definition of weakly  , and assume that for all
, and assume that for all  . Then from [
. Then from [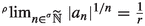 and
and 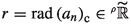 . In Corollary
. In Corollary  and
and  , i.e. we have a formal HPS;
, i.e. we have a formal HPS; ;
; .
. are coefficients for HPS.
are coefficients for HPS.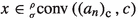 .
. (Definition
(Definition 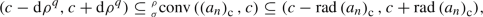
 is convergent, i.e. Definition
is convergent, i.e. Definition  .
. . This depends mainly on three conditions:
. This depends mainly on three conditions:  . Here, the main step is to prove that the net
. Here, the main step is to prove that the net 
 , and hence it remains to prove the opposite inclusion.
, and hence it remains to prove the opposite inclusion. -bounded in
-bounded in  if
if  because
because  -bounded in
-bounded in  .
. converges.
converges. ;
; for some
for some 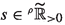 ;
; is
is  -convex, i.e. if also
-convex, i.e. if also  , then
, then  ;
; is strongly connected, i.e. it is not possible to write it as union of two non empty strongly disjoint sets, i.e. such that
is strongly connected, i.e. it is not possible to write it as union of two non empty strongly disjoint sets, i.e. such that  ,
,  ,
, is a convergent HPS,
is a convergent HPS, -bounded in
-bounded in  .
. , the product
, the product  is a convergent HPS with
is a convergent HPS with 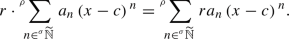


 is invertible, and recursively define (for
is invertible, and recursively define (for  define a convergent HPS with radius of convergence greater or equal to
define a convergent HPS with radius of convergence greater or equal to  is invertible, then
is invertible, then 
 ,
, for all
for all  ,
, for all
for all  .
.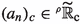 ,
,  , and we set
, and we set  , then f is a GRAF on the interior points of the set of convergence
, then f is a GRAF on the interior points of the set of convergence  . Vice versa, if
. Vice versa, if  , then U is contained in the union of all the sharp interior sets
, then U is contained in the union of all the sharp interior sets  , because of condition (i).
, because of condition (i). such that
such that  satisfying condition (i) is infinitesimal, whereas if
satisfying condition (i) is infinitesimal, whereas if