On volume preserving almost Anosov flows

Abstract

The purpose of this paper is to establish limit laws for volume preserving almost Anosov maps of ${{\mathbb {T}}}^2$ flows on 3-three manifolds having a transversally neutral periodic orbit of cubic saddle type. In the process, we derive estimates for the Dulac maps for neutral saddles in planar vector fields.

1 Introduction

A flow $\phi ^t: {{\mathcal {M}}}\times {{\mathbb {R}}}\rightarrow {{\mathcal {M}}}$ on a (in our setting 3-dimensional) compact differentiable manifold ${{\mathcal {M}}}$ is called Anosov if its tangent bundle has a continuous flow-invariant mutually transversal splitting into a neutral flow direction $E^c$, a hyperbolically stable direction $E^s$ and a hyperbolically unstable direction $E^u$. The uniform hyperbolicity of such flows enables one to show various ergodic and statistical properties, such as ergodicity (if the flow is topologically mixing) and the Central Limit Theorem (CLT) for Hölder continuous observables.

We obtain an almost Anosov flow (see Definition 1.1 below) by inserting a neutral orbit $\Gamma \simeq \{ (0,0)\} \times {{\mathbb {S}}}^1$ near which the flow has the following form in local Euclidean coordinates:

$$\begin{aligned} \begin{pmatrix} \dot{x} \\ \dot{y}\\ \dot{z} \end{pmatrix} = X \begin{pmatrix} x \\ y \\ z \end{pmatrix} = \begin{pmatrix} x(a_0 x^2 + a_1 xy + a_2 y^2) \\ -y(b_0 x^2 + b_1 xy + b_2 y^2) \\ 1 + w(x,y) \end{pmatrix} + {{\mathcal {O}}}(4) \end{aligned}$$

(1)

where the parameters satisfy

$$\begin{aligned}{} & {} a_1, b_1 \in {{\mathbb {R}}},\, a_0, a_2, b_0, b_2 \ge 0 \text { with } \Delta := a_2b_0 - a_0b_2 \ne 0 \text { and } \nonumber \\{} & {} \quad a_1^2< 4a_0a_2,\ b_1^2 < 4b_0b_2. \end{aligned}$$

(2)

The last two conditions of (2) imply that the first component in (1) is non-negative and the second non-positive for $x,y \ge 0$. The term ${{\mathcal {O}}}(4)$ indicates terms of order four and higher, under the condition that they are of the form $x^2 {{\mathcal {O}}}(2)$ near the yz-plane and of the form $y^2 {{\mathcal {O}}}(2)$ near the xz-plane, because otherwise these are not a small perturbation compared to the leading terms of (1). These leading terms are cubic in the direction transversal to $\Gamma$, but this is the only source of non-hyperbolicity. Finally, w is a linear combination of homogeneous functions in x and y, vanishing at (0, 0). Thus the period of $\Gamma$ is its length.

The original motivation to study such systems was to find a class of natural examples of non-uniformly hyperbolic invertible maps where operator renewal theory can be applied to establish precise statistical laws. The map in this context can be the Poincaré map on a section $\Sigma \subset {{\mathbb {R}}}^2 \times \{ 0 \}$ or the time-1 map $f_{hor} = \phi _{hor}^1$ for the horizontal flow where only the x- and y-coordinates are taken into account:

$$\begin{aligned} \begin{pmatrix} \dot{x} \\ \dot{y} \end{pmatrix} = X_{hor}\begin{pmatrix} x \\ y \end{pmatrix} = \begin{pmatrix} x(a_0x^2+a_1xy+a_2y^2) \\ -y(b_0x^2+b_1xy+b_2 y^2) \end{pmatrix} + {{\mathcal {O}}}(4), \end{aligned}$$

(3)

with the restrictions (2).

Initially, in [2] for the parameter range $\beta _2 := \frac{a_2+b_2}{2b_2} \le 1$ where $f_{hor}$ preserves an infinite Sinaĭ-Bowen-Ruelle (SRB) measure, we gave mixing rates for $C^1$ observables. Later [3], and more relevant to this paper, in the parameter range $\beta _2 > 1$ where the flow $\phi ^t$ preserves a finite SRB-measure, we established limit laws (Stable Laws and the CLT with standard or non-standard scaling, depending on whether $\beta _2 \in (1,2)$, $\beta = 2$ or $\beta _2 > 2$).

All these results were obtained in the absence of mixed terms, i.e., $a_1=b_1=0$ in (1). This is of course not a natural assumption, and to our knowledge there is no change of coordinates that allows one to remove the mixed terms. In fact, if $a_1^2 > 4a_0a_2$ or $b_1^2 > 4b_0b_2$, then the dynamics near the saddle is not locally conjugate to the dynamics under the current condition (2).

The purpose of this paper is to perform the analysis when mixed terms are present, and also the treatment of the perturbation terms (see Sect. 3) is substantially different and more straightforward than in [2, 3]. The crux of the analysis is the existence of a local first integral (and its explicit form when ${{\mathcal {O}}}(4)$-terms are absent in (9)), which allows us to reduce the ODE to dimension one. We will show in Lemma 2.1 that the first integral L can be found if

$$\begin{aligned} \frac{b_1}{a_1} = \frac{b_2a_0+a_2+2b_0b_2}{b_2a_0+a_2+2a_0a_2}. \end{aligned}$$

(4)

This is a co-dimension one condition in parameter space. However, if we also stipulate that the flow $\phi ^t$ is volume preserving, we must assume that $\text{ div }\, X = 0$ in (1), which is equivalent to $\text{ div }\, {{\mathcal {O}}}(4) = 0$ together with

$$\begin{aligned} 3a_0 = b_0, a_2 = 3b_2, a_1 = b_1. \end{aligned}$$

(5)

Condition (4) follows automatically from (5), and therefore (1) describes a generic volume preserving almost Anosov flow with a single neutral periodic orbit of cubic saddle type. We present the results on limit laws in the volume preserving setting, see Theorem 1.2.

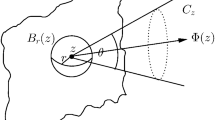
Central to the proof of the main theorem of this paper (as well as precise mixing rates) is the analysis of the Dulac map near the neutral equilibrium of (3). This means that we take an incoming and an outgoing transversal to the flow, in our case an unstable leaf $W^u(0,\eta )$, $\eta \in [\eta _0, \eta _1]$, and a stable leaf $W^s(\zeta _0,0)$, see Fig. . The Dulac map $D:W^u(0,\eta ) \rightarrow W^s(\zeta _0,0)$ assigns to $(\xi ,\eta )$ the first intersection $\phi _{hor}^T(\xi ,\eta )$ of the integral curve through $(\xi ,\eta )$ with the outgoing transversal $W^s(\zeta _0,0)$. The corresponding flow-time is denoted by T. As main technical result of this paper we obtain precise estimates of the Dulac map when (3) contains mixed terms, but using the assumption (4).

Fig. 1

The Dulac map $D:(\xi (\eta _0, T),\eta _0) \mapsto (\zeta _0,\omega (\eta _0, T))$ with Dulac time T

Dulac [5] introduced his map as an ingredient to prove that polynomial vector fields in the plane have at most finitely many limit cycles, thus making a major contribution to the solution of Hilbert’s 16th problem. Il’yashenko [7] corrected some weak parts in Dulac’s arguments, see also the summary in Roussarie’s book [12, Sect. 3.3]. Further contributions are due to e.g. Dumortier and more recently Mardešić and collaborators [4, 8,9,10, 13]. Specifically, polycycles (i.e., heteroclinic saddle connections) are not accumulated upon by limit cycles. Whereas our estimates only concern a single neutral saddle, it is to our knowledge the first estimation of the Dulac times (and hence the Dulac map, see (6)), at cubic saddle of this generality.

1.1 Main results

The crucial estimates here are of the Dulac times, i.e., the times that orbits take to pass from an “incoming” unstable transversal to an “outgoing” unstable transversal to the flow, see Fig. 1.

Theorem 1.1

Consider a $C^3$ vector field of local form (3) with parameters satisfying (2) and (4). Define

$$\begin{aligned} \beta _0 := \frac{a_0+b_0}{2a_0}, \qquad \beta _2 := \frac{a_2+b_2}{2b_2}. \end{aligned}$$

Then there constants¹$\xi _0(\eta ), \omega _0(\eta )$ such that the following asymptotics hold:

$$\begin{aligned} \xi (\eta ,{\tilde{T}}) = \xi _0(\eta ) {\tilde{T}}^{-\beta _2} (1 + O({\tilde{T}}^{-\frac{1}{2}})) \end{aligned}$$

and

$$\begin{aligned} \omega (\eta ,{\tilde{T}}) = \omega _0(\eta ) {\tilde{T}}^{-\beta _0} (1 + O({\tilde{T}}^{-\frac{1}{2}})). \end{aligned}$$

as $T \rightarrow \infty$.

In particular, the functions $\xi$ and $\omega$ are regularly varying of order $-\beta _2$ and $-\beta _0$ in T, respectively. That is: $\lim _{T\rightarrow \infty } \frac{\xi (\eta ,cT)}{\xi (\eta ,T)} = c^{\beta _2}$ for every $c > 0$ and analogous for $\omega (\eta ,T)$. Moreover, the Dulac map $D:W^u(0,\eta ) \rightarrow W^s(\zeta _0,0)$ itself has the form (as $\xi \rightarrow 0$)

$$\begin{aligned} \omega = D(\xi ) = \omega _0(\eta ) \xi _0(\eta )^{-\frac{\beta _0}{\beta _2} } \, \xi ^{\frac{\beta _0}{\beta _2} } \left( 1+{{\mathcal {O}}}(\xi ^{\frac{1}{2\beta _2}}) \right) . \end{aligned}$$

(6)

With assumptions (5) and $c_1^2 < 4c_0 c_2$ in place, we can use the change of coordinates ${\bar{x}} = \sqrt{a_0} x, \ {\bar{y}} = \sqrt{b_2}y$ and ${\bar{\gamma }} = a_1/\sqrt{a_0 b_2} \in (-4,4)$ to transform (1) into the one-parameter family

$$\begin{aligned} \begin{pmatrix} \dot{{\bar{x}}} \\ \dot{{\bar{y}}} \\ \dot{{\bar{x}}} \end{pmatrix} = \begin{pmatrix} {\bar{x}}({\bar{x}}^2+ {\bar{\gamma }} {\bar{x}} {\bar{y}} + 3 {\bar{y}}^2) \\ -{\bar{y}}(3 {\bar{x}}^2 + {\bar{\gamma }} {\bar{x}} {\bar{y}} + {\bar{y}}^2))\\ 1+{\bar{w}}({\bar{x}}, {\bar{y}}) \end{pmatrix} + {{\mathcal {O}}}(4), \end{aligned}$$

(7)

for some transformed function ${\bar{w}}$.

Because of this genericity and reduced number of technicalities that Lebesgue measure gives as opposed to the SRB-measure, we state our statistical result for volume preserving flows. Theorem 1.1 is used to estimate the measures of the strips $\{ \varphi = n\}$, see Fig. , which in turn, together with the spectral properties of an induced Poincaré map ${\hat{f}}$, are crucial ingredients for the analysis required to establish the following stochastic limit properties of the flow $\phi ^t$.

Theorem 1.2

Consider a volume preserving almost Anosov flow (7) on ${{\mathcal {M}}}$ with ${\bar{\gamma }} \in (-4,4)$ and an observables $v:{{\mathcal {M}}}\rightarrow {{\mathbb {R}}}$ that is $C^1$ on ${{\mathcal {M}}}\setminus \Gamma$ and has the form $v = v_0 + o(\rho )$ where $\int _0^{\tau } v_0 \circ \phi ^t \, dt$ is homogeneous of order $\rho > -2$ in local coordinates (x, y) near p and $o(\rho )$ stands for terms of order $> \rho$.

• 1. If $\rho \in (0,\infty )$, then v satisfies the Central Limit Theorem, i.e.,

  $$\begin{aligned} \frac{\int _0^t v \circ \phi ^s \, ds - t \int v \ dVol}{\sigma \sqrt{t}} \Rightarrow _{dist} {{\mathcal {N}}}(0,1) \quad \text { as } t\rightarrow \infty , \end{aligned}$$

  where the variance $\sigma ^2 > 0$ unless $\int _0^\tau v \circ \phi ^t \, dt$ is a coboundary.

• 2. If $\rho = 0$, then v satisfies the Central Limit Theorem with non-standard scaling $\sqrt{t \log t}$, i.e.,

  $$\begin{aligned} \frac{\int _0^t v \circ \phi ^s \, ds - t \int v \ dVol}{\sigma \sqrt{t \log t}} \Rightarrow _{dist} {{\mathcal {N}}}(0,1) \quad \text { as } t\rightarrow \infty , \end{aligned}$$

  and the variance $\sigma ^2 > 0$ unless $\int _0^\tau v \circ \phi ^t \, dt$ is a coboundary.

• 3. If $\rho \in (-\,2, 0)$ then v satisfies a Stable Law of order $\frac{4}{2-\rho } \in (1,2)$.

Theorem 1.1 also allows us to derive other limit theorems such as in the infinite measure setting of [2], but with mixed terms. Since we restrict to flows preserving Lebesgue measure (not just an SRB-measure), we don’t give any further details here.

1.2 Set-up

The set-up here is largely taken over from [3]. Our phase space will be the 3-dimensional compact manifold ${{\mathcal {M}}}$.

Definition 1.1

[6, Definition 1] A diffeomorphism $f:{{{\mathbb {T}}}}^2\rightarrow {{{\mathbb {T}}}}^2$ is called almost Anosov if there exists two continuous families of non-trivial cones $x\rightarrow {{\mathcal {C}}}_x^u, {{\mathcal {C}}}_x^s$ such that except for a finite set S,

• (i) $D f_x{{\mathcal {C}}}_{x}^u\subseteq {{\mathcal {C}}}_{f(x)}^u$ and $D f_x{{\mathcal {C}}}_{x}^s\supseteq {{\mathcal {C}}}_{f(x)}^s$;

• (ii) $|D f_x v|>|v|$ for any $0 \ne v\in {{\mathcal {C}}}_x^u$ and $|D f_x v|<|v|$ for any $0 \ne v\in {{\mathcal {C}}}_x^s$.

For $x \in S$, $Df_x$ is the identity.

A flow $f^t$ on 3-torus ${{\mathbb {T}}}^3$ is called almost Anosov flow if it has a finite set S of neutral periodic orbits, but everywhere else observes the condition of an Anosov flow in that there is a continuous splitting of the tangent bundle into a stable, an unstable and a neutral (flow) direction. For $x \in S$, the derivative at the return time $\tau$ is $Df^\tau _x$ is the identity.

The time-1 map f of the flow $\phi ^t$ of (1) has the form of a skew-product

$$\begin{aligned} f\begin{pmatrix} x \\ y \\ z \end{pmatrix} = \begin{pmatrix} x(1+a_0x^2+a_1 xy + a_2y^2) \\ y(1-b_0x^2-b_1 xy - b_2y^2) \\ z + O(|w(x,y)|) \end{pmatrix} + {{\mathcal {O}}}(4), \end{aligned}$$

(8)

see [2, Sect. 2.1]. Restricted to the (x, y)-coordinates, this restriction $f_{hor}$ of f to the first two coordinates is a smooth almost Anosov map with a single neutral fixed point $p = (0,0)$. Let $\{ P_i \}_{i = 0}^k$ be the Markov partition for $f_{hor}$ (which we can assume to exist since $f_{hor}$ is a local perturbation of a Anosov diffeomorphism on ${{\mathbb {T}}}^2$). We assume that p belongs to the interior of $P_0$. Clearly, the x- and y-axis are the unstable and stable manifolds of p respectively. We assume that the Markov partition element $P_0 \subset U$ is a small rectangle such that $\overline{f_{hor}^{-1}(P_0) \cup P_0 \cup f_{hor}(P_0)} \subset U$. Due to the symmetries $(x,y) \mapsto (\pm x, \pm y)$, it suffices to do the analysis only in the first quadrant $Q = [0,\zeta _0] \times [0,\eta _0]$ of $P_0$, see Fig. 2. Without loss of generality (see [2, Lemma 2.1]) we can think of $[0, \zeta _0] \times \{ \eta _0 \}$ as a local unstable leaf and $\{ \zeta _0\} \times [0, \eta _0]$ as a local stable leaf of the global diffeomorphism.

Fig. 2

The first quadrant Q of the rectangle $P_0$, with stable and unstable foliations drawn vertically and horizontally, respectively

We consider an induced map $F_{hor} = f_{hor}^\varphi : Y \rightarrow Y$ for $Y := {{{\mathbb {T}}}}^2 \setminus P_0$, where

$$\begin{aligned} \varphi (z) = \min \{ n \ge 1 : f_{hor}^n(z) \notin P_0\} \end{aligned}$$

is the first return time to Y. Note that $F_{hor}$ is invertible because $f_{hor}$ is. In the first quadrant of $U \setminus P_0$, the sets $\{ \varphi = n \} := \{ z \in f^{-1}(Q) \setminus Q : \varphi (z) = n\}$, $n \ge 2$, are vertical strips (see Fig. 2) adjacent to the local unstable leaf $[0,\zeta _0] \times \{\eta _0 \}$, and converging to $\{ 0 \} \times [\eta _0, \eta _1]$ as $n \rightarrow \infty$. The images $F_{hor}(\{ \varphi = n\})$ are horizontal strips, adjacent to the local stable leaf $\{ \zeta _0 \} \times [0,\eta _0]$, and converging to $[\zeta _0, \zeta _1] \times \{ 0 \}$ as $n \rightarrow \infty$.

In contrast to $f_{hor}$, the induced map $F_{hor}$ is uniformly hyperbolic, but only piecewise continuous. Indeed, continuity fails at the boundaries of the strips $\{ \varphi = n\}$, $n \ge 2$ (and F is undefined on $W^s(p)$), but these boundaries are local stable and unstable leaves, and it is possible to create a countable Markov partition refining $\{ P_i \}_{i=1}^k$ of Y for F, in which all the strips $\{ \varphi = n \}$ are partition elements.

2 Regular variation of $\mu (\varphi > n)$ with mixed terms

In this section, we allow quadratic mixed terms in (3), but for the moment leave out the ${{\mathcal {O}}}(4)$-terms. That is, we consider

$$\begin{aligned} {\left\{ \begin{array}{ll} \dot{x} = x(a_0x^2+a_1xy+a_2y^2), \\ \dot{y} = -y(b_0x^2+b_1xy+b_2 y^2), \end{array}\right. } \end{aligned}$$

(9)

with the restrictions (2) and (4). The condition $c_1^2 < 4c_0c_2$ avoids the formation of invariant lines $y = px$, but in the below proofs it is used to guarantee that expressions as $c_0 + c_1 M + c_2 M^2$ for $M = y/x$ are positive. Our exposition closely follows [2], but since the mixed terms require adjustments throughout the proof, we will give it in full.

Set $c_i := a_i+b_i,\ i = 0,1,2$. The conditions $a_1^2< 4a_0a_2, b_1^2 < 4b_0b_2$ imply that $a_1^2b_1^2 - 16 a_0a_2b_0b_2 \le 0 \le 4(a_0b_0-a_2b_2)^2$, and thus $a_1^2b_1^2 \le 4(a_0b_2+a_2b_0)^2$. Since $a_0,b_0,a_2,b_2 \ge 0$, we also have $a_1b_1 \le 2(a_0b_2+a_2b_0)$, which implies that $c_1^2 \le 4c_0c_2$. Let $u,v \in {{\mathbb {R}}}$ be the solutions of the linear equations

$$\begin{aligned} {\left\{ \begin{array}{ll} (u+2) a_0 = v b_0 \\ (v+2) b_2 = u a_2 \end{array}\right. } \quad \text { that is:}\quad {\left\{ \begin{array}{ll} u = \frac{2b_2 c_0}{\Delta }, \\ v = \frac{2a_0 c_2}{\Delta }. \end{array}\right. } \end{aligned}$$

(10)

Note that u, v and $\Delta$ (recall $\Delta \ne 0$) all have the same sign and (4) implies that $\frac{b_1}{a_1} = \frac{u+1}{v+1}$. Compute that

$$\begin{aligned} \beta _0:= & {} \frac{a_0+b_0}{2a_0} = \frac{u+v+2}{2 v}, \nonumber \\ \beta _2:= & {} \frac{a_2+b_2}{2b_2} = \frac{u+v+2}{2 u}, \quad \frac{\beta _0}{\beta _2} = \frac{u}{v} = \frac{b_2c_0}{a_0c_2}, \end{aligned}$$

(11)

and note that $\beta _0, \beta _2 > \frac{1}{2}$ (or $=\frac{1}{2}$ if we allow $b_0=0$ or $a_2=0$ respectively). Under the extra assumption (5) we obtain $\beta _0 = \beta _2 = 2$ and $u = v = 1$.

The first estimates is about the Dulac map of (3).

Proposition 2.1

Consider a vector field on the 2-torus with local form (3) for $a_0, a_2, b_0, b_2 \ge 0$ and $\Delta \ne 0$. There are functions $\xi _0(\eta ), \omega _0(\eta ), \xi _1(\eta ), \omega _1(\eta ) > 0$ independent of T (with exact expressions given in the proof) such that

$$\begin{aligned} \xi (\eta , T) = \xi _0(\eta ) T^{-\beta _2} \left( 1 - \xi _1(\eta ) T^{-1} + O(T^{-2}, T^{-2 \beta _2} )\right) \end{aligned}$$

and

$$\begin{aligned} \omega (\eta , T) = \omega _0(\eta ) T^{-\beta _0} \left( 1 - \omega _1(\eta ) T^{-1} + O(T^{-2}, T^{-2 \beta _0} )\right) . \end{aligned}$$

Lemma 2.1

The function

$$\begin{aligned} L(x,y) = {\left\{ \begin{array}{ll} x^u y^v ( \frac{a_0}{v}\ x^2 + \frac{a_1}{v+1} xy + \frac{b_2}{u}\ y^2 ) &{} \text { if } \Delta > 0,\\ x^{-u} y^{-v} ( \frac{a_0}{v}\ x^2 + \frac{a_1}{v+1} xy \frac{b_2}{u}\ y^2 )^{-1} &{} \text { if } \Delta < 0, \end{array}\right. } \end{aligned}$$

(12)

is a first integral of (9).

Proof of Lemma 2.1

First assume $\Delta > 0$, so $u,v > 0$ as well. By (10), we can write L(x, y) as

$$\begin{aligned} L(x,y) = x^u y^v \left( \frac{b_0}{u+2 }\ x^2 + \frac{a_1}{v+1} xy + \frac{b_2}{u}\ y^2 \right) = x^u y^v \left( \frac{a_0}{v}\ x^2 + \frac{b_1}{u+1} xy + \frac{a_2}{v+2 }\ y^2 \right) . \end{aligned}$$

Using these two equivalent expressions we compute the Lie derivative directly

$$\begin{aligned} \dot{L}= & {} \langle \nabla L , X \rangle \\ {}= & {} x^{u-1}y^v\left( \frac{b_0}{u+2}(u+2) x^2 + \frac{a_1}{v+1}xy + \frac{b_2}{u} u x^{u-1} y^2\right) x(a_0 x^2 + a_1 xy + a_2 y^2 )\\{} & {} - x^uy^{v-1}\left( \frac{a_0}{v} x^2 v + \frac{a_1}{v+1}xy+\frac{a_2}{v+2}(v+2)y^2\right) y(b_0 x^2 + b_1 xy + b_2 y^2)\\= & {} 0. \end{aligned}$$

Any function of a first integral is a first integral; in particular this holds for 1/L. Therefore the conclusion is immediate for $\Delta < 0$ too.

Corollary 2.1

Every (x(y), y) on the integral curve from $(\xi ,\eta )$ to $(\delta ,\delta )$ satisfies

$$\begin{aligned} x(y) = U(y) \delta ^{1+\frac{a_2}{b_2} } \eta ^{-\frac{a_2}{b_2}}, \end{aligned}$$

for

$$\begin{aligned} U(y) := \left( c_2+\frac{a_1 u c_2}{b_2 (v+1)}+c_0\right) ^{\frac{1}{u}} \left( c_2+\frac{a_1 uc_2}{b_2 (v+1)} \frac{x}{y} + c_0 \frac{x^2}{y^2}\right) ^{-\frac{1}{u}}. \end{aligned}$$

(13)

In terms $M = y/x$, we have

$$\begin{aligned} x(M)^2= & {} \xi ^{\frac{2 u}{u+v+2 }} \eta ^{\frac{2 v}{u+v+2 }} M^{-\frac{2 v}{u+v+2 }} \left( \frac{c_0\xi ^2 + c_1\xi \eta + c_2\eta ^2 }{c_0+c_1M+c_2M^2 } \right) ^{\frac{2 }{u+v+2 }} \nonumber \\= & {} \xi ^{\frac{1}{\beta _2}} \eta ^{\frac{1}{\beta _0}} M^{-\frac{1}{\beta _0}} \left( \frac{c_0\xi ^2 + c_1\xi \eta + c_2\eta ^2 }{c_0+c_1M+c_2M^2 } \right) ^{1 - \frac{1}{2 \beta _0} - \frac{1}{2 \beta _2}}. \end{aligned}$$

(14)

Proof

We carry out the proof for $\Delta > 0$, so $L(x,y) = x^u y^v ( \frac{a_0}{v}\ x^2 + \frac{a_1}{v+1} xy + \frac{b_2}{u}\ y^2 )$ as in Lemma 2.1. The case $\Delta < 0$ goes likewise.

We solve for x from $L(x, y) = L(\delta , \delta ) = \delta ^{u+v+2}(\frac{a_0}{v}+\frac{a_1}{v+1}+\frac{b_2}{u})$:

$$\begin{aligned} x = x(y)= & {} \delta ^{\frac{u+v+2}{u}} y^{-\frac{v+2}{u}} \left( 1+\frac{a_1 u}{b_1(v+1)} + \frac{u a_0}{v b_2}\right) ^{\frac{1}{u}} \left( 1+\frac{a_1 u}{b_1 (v+1)}\frac{x}{y} + \frac{c_0}{c_2} \frac{x^2}{y^2}\right) ^{-\frac{1}{u}} \\= & {} U(y) \delta ^{1+\frac{a_2}{b_2}} y^{-\frac{a_2}{b_2}}, \end{aligned}$$

giving the required expression with U(y) as in (13). Note that $\lim _{y \rightarrow \delta } U(y) = 1$ (i.e., the limit as (x, y) approaches the diagonal), and U(y) is differentiable.

For the other expression, we use that $L(x,y) = L(\xi ,\eta ) = \xi ^u \eta ^v(\frac{a_0}{v} \xi ^2 +\frac{a_1}{v+1} \xi \eta + \frac{b_2}{u}\eta ^2 )$, and solve for $x^2$:

$$\begin{aligned} \xi ^u\eta ^v \left( \frac{a_0}{v} \xi ^2 + \frac{a_1}{v+1} \xi \eta + \frac{b_2}{u}\eta ^2 \right)= & {} x^u y^v \left( \frac{a_0}{v} x^2 + \frac{a_1}{v+1} xy + \frac{b_2}{u} y^2 \right) \\= & {} x^{u+v+2 } M^v \left( \frac{a_0}{v} + \frac{a_1}{v+1} M + \frac{b_2}{u} M^2 \right) . \end{aligned}$$

Here we used

$$\begin{aligned} \xi ^u\eta ^v \left( \frac{a_0}{v} \xi ^2 + \frac{a_1}{v+1} \xi \eta + \frac{b_2}{u}\eta ^2 \right)= & {} \xi ^u\eta ^v \left( \frac{a_0 \Delta }{2a_0 c_2} \xi ^2 + \frac{a_1 \Delta }{2a_0c_2+\Delta } \xi \eta + \frac{b_2 \Delta }{2b_2c_0}\eta ^2 \right) \nonumber \\= & {} \frac{\Delta }{2c_0c_2} \left( c_0 \xi ^2 + \frac{2a_1 c_0c_2}{2a_0c_2+\Delta } \xi \eta + c_2\eta ^2\right) \nonumber \\= & {} \frac{\Delta }{2c_0c_2} \left( c_0 \xi ^2 + c_1 \xi \eta + c_2\eta ^2\right) , \end{aligned}$$

(15)

(where the last step follows from (4)) and a similar computation for the term with x, y. Use (10) and (11) to obtain

$$\begin{aligned} {\left\{ \begin{array}{ll} \frac{a_0}{v} + \frac{a_1}{v+1} M + \frac{b_2}{u} M^2 = \frac{\Delta }{2 c_0c_2} ( c_0+c_1M+ c_2M^2 ), \\ \frac{a_0 \xi ^2}{v} + \frac{a_1}{v+1} \xi \eta + \frac{b_2 \eta ^2 }{u} = \frac{\Delta }{2 c_0c_2} ( c_0 \xi ^2 + c_1 \xi \eta + c_2 \eta ^2 ). \end{array}\right. } \end{aligned}$$

This gives

$$\begin{aligned} x^2= & {} \xi ^{\frac{2 u}{u+v+2 }} \eta ^{\frac{2 v}{u+v+2 }} M^{-\frac{2 v}{u+v+2 }} \left( \frac{c_0\xi ^2 + c_1\xi \eta + c_2\eta ^2 }{c_0+c_1M+c_2M^2 } \right) ^{\frac{2 }{u+v+2 }} \\= & {} \xi ^{\frac{1}{\beta _2}} \eta ^{\frac{1}{\beta _0}} M^{-\frac{1}{\beta _0}} \left( \frac{c_0\xi ^2 + c_1\xi \eta + c_2\eta ^2 }{c_0+c_1M+c_2M^2 } \right) ^{1 - \frac{1}{2 \beta _0} - \frac{1}{2 \beta _2}}, \end{aligned}$$

where we recall that $\beta _0 = \frac{u+v+2 }{2 v}$ and $\beta _2 = \frac{u+v+2 }{2 u}$ from (11), which also gives $\frac{2 }{u+v+2 } = 1-\frac{1}{2 \beta _0}-\frac{1}{2 \beta _2}$. $\square$

Proof of Proposition 2.1

We carry out the proof for $\Delta > 0$, so $L(x,y) = x^u y^v ( \frac{a_0}{v}\ x^2 + \frac{a_1}{v+1} xy + \frac{b_2}{u}\ y^2 )$ as in Lemma 2.1. The case $\Delta < 0$ goes likewise. Fix $\eta$ such that $(\xi (\eta ,T), \eta ) \in \overline{\phi ^{-1}(Q) \setminus Q}$. We use the variable $M = y/x$, so $y = Mx$ and differentiating gives $\dot{y} = \dot{M} x + M \dot{x}$. Recalling that $c_i = a_i+b_i$ and inserting the values for $\dot{x}$ and $\dot{y}$ from (9), we get

$$\begin{aligned} \dot{M} = -M( c_0 + c_1 M + c_2 M^2 ) x^2 . \end{aligned}$$

(16)

Combined with (14), this gives

$$\begin{aligned} \dot{M} = -G(\xi ,\eta ) M^{1-\frac{1}{\beta _0}} \left( c_0+c_1M+c_2M^2 \right) ^{\frac{1}{2 \beta _0} + \frac{1}{2 \beta _2}} \end{aligned}$$

(17)

with

$$\begin{aligned} G(\xi ,\eta ) := \xi ^{ \frac{1}{\beta _2} } \eta ^{ \frac{1}{\beta _0} } \left( c_0\xi ^2 + c_1\xi \eta + c_2\eta ^2 \right) ^{1-\frac{1}{2 \beta _0}-\frac{1}{2 \beta _2}}. \end{aligned}$$

(18)

For the exit time $T \ge 0$, recall that $\xi (\eta ,T)$ and $\omega (\eta ,T)$ are such that the solution of (3) satisfies $(x(0), y(0)) = (\xi (\eta ,T), \eta )$ and $(x(T), y(T)) = (\zeta _0,\omega (\eta ,T))$. This implies $M(0) = \eta /\xi (\eta ,T)$ and $M(T) = \omega (\eta ,T)/\zeta _0$. Inserting this in (17), separating variables, and integrating we get

$$\begin{aligned} \int _{\omega (\eta ,T)/\zeta _0}^{\eta /\xi (\eta ,T)} \frac{ M^{\frac{1}{\beta _0}-1} \, dM}{ \left( c_0+c_1M+c_2 M^2 \right) ^{ \frac{1}{2 \beta _0} + \frac{1}{2 \beta _2} } } = G(\xi (\eta ,T), \eta ) T. \end{aligned}$$

(19)

In the rest of the proof, we will frequently suppress the dependence on $\eta$ and T in $\xi (\eta ,T)$ and $\omega (\eta ,T)$. We know that $L(\xi (\eta , T), \eta ) = \xi ^u \eta ^v(\frac{a_0}{v} \xi ^2 + \frac{b_2}{u}\eta ^2 ) = \zeta _0^u \omega ^v (\frac{a_0}{v} \zeta _0^2 + \frac{b_2}{u} \omega ^2 ) = L(\eta ,\omega (\eta ,T))$, which gives

$$\begin{aligned} \xi ^u \eta ^v (c_0\xi ^2 +c_1\xi \eta + c_2\eta ^2 ) = \zeta _0^u \omega ^v(c_0\zeta _0^2+c_1\zeta _0\omega +c_2\omega ^2 ). \end{aligned}$$

(20)

From their definition, $\xi (\eta ,T)$ and $\omega (\eta , T)$ are clearly decreasing in T, so their T-derivatives $\xi '(\eta ,T), \omega '(\eta ,T) \le 0$. Since $c_0, c_2 > 0$ (otherwise $\Delta = 0$), the integrand of (19) is $O(M^{\frac{1}{\beta _0}-1})$ as $M \rightarrow 0$ and $O(M^{-\frac{1}{\beta _2}-1})$ as $M \rightarrow \infty$. Hence the integral is increasing and bounded in T. But this means that $G(\xi (\eta ,T), \eta ) T$ is increasing in T and bounded as well. Let $g(\eta ,T) = \xi (\eta ,T) T^{\beta _2}$. Since

$$\begin{aligned} G(\xi (\eta ,T), \eta ) T = g(\eta ,T)^{\frac{1}{\beta _2}} \eta ^{\frac{1}{\beta _0}} (c_0 g(\eta ,T)^2 T^{-2 \beta _2} + c_1 g(\eta ,T) T^{-\beta _2} + c_2 \eta ^2 )^{1-\frac{1}{2 \beta _0} - \frac{1}{2 \beta _2}}, \end{aligned}$$

and $1-\frac{1}{2 \beta _0} - \frac{1}{2 \beta _2} > 0$, we find that $g(\eta ,T)$ converges²:

$$\begin{aligned} \xi _0(\eta ) := \lim _{T\rightarrow \infty } g(\eta ,T) = c_2^{-\frac{1}{u}} \eta ^{- \frac{a_2}{b_2} } \left( \int _0^\infty \frac{ M^{\frac{1}{\beta _0}-1} \, dM }{\left( c_0 + c_1 M + c_2 M^2 \right) ^{ \frac{1}{2 \beta _0} + \frac{1}{2 \beta _2} } }\right) ^{\beta _2} ,\nonumber \\ \end{aligned}$$

(21)

where we have used $-\beta _2(1-\frac{1}{2 \beta _0} - \frac{1}{2 \beta _2}) = -\frac{2 \beta _2}{u+v+2 } = -\frac{1}{u}$ for the exponent of $c_2$, and $\frac{2 }{u} + \frac{\beta _2}{\beta _0} = \frac{v+2 }{u} = \frac{a_2}{b_2}$ for the exponent of $\eta$.

We continue the proof to get higher asymptotics. Differentiating (19) w.r.t. T gives

$$\begin{aligned}{} & {} -\frac{ \eta ^{\frac{1}{\beta _0}} \xi ^{\frac{1}{\beta _2}-1} \xi '}{(c_0 \xi ^2 + c_1\xi \eta + c_2\eta ^2 )^{\frac{1}{2 \beta _0} + \frac{1}{2 \beta _2}}} -\frac{\zeta _0^{\frac{1}{\beta _2}} \omega ^{\frac{1}{\beta _0}-1} \omega '}{(c_0\zeta _0^2 + c_1 \zeta _0\omega + c_2 \omega ^2 )^{\frac{1}{2 \beta _0} + \frac{1}{2 \beta _2}}}\nonumber \\{} & {} \quad = \frac{\partial G(\xi ,\eta )}{\partial \xi } T \xi ' + G(\xi ,\eta ), \end{aligned}$$

(22)

where (by differentiating (18))

$$\begin{aligned} \frac{\partial G(\xi ,\eta )}{\partial \xi } = \left( 2b_0\xi ^2 + c_1\left( \frac{b_0}{c_0}+\frac{a_2}{c_2}\right) \xi \eta + b_2\eta ^2 \right) \xi ^{\frac{1}{\beta _2}-1} \eta ^{\frac{1}{\beta _0}} \left( c_0\xi ^2 + c_1 \xi \eta + c_2 \eta ^2 \right) ^{-\frac{1}{2 \beta _0} - \frac{1}{2 \beta _2}}. \end{aligned}$$

Combined with (18), (20) and (22), this gives

$$\begin{aligned} -\eta ^{\frac{1}{\beta _0}} \xi '&- \zeta _0^{\frac{1}{\beta _2}} \left( \frac{\zeta _0^u \omega ^v}{\xi ^u \eta ^v} \right) ^{\frac{1}{2 \beta _0} + \frac{1}{2 \beta _2}} \frac{\omega ^{\frac{1}{\beta _0}-1}}{\xi ^{\frac{1}{\beta _2}-1}} \omega ' \nonumber \\&=\left( 2b_0\xi ^2 + c_1\left( \frac{b_0}{c_0}+\frac{a_2}{c_2}\right) \xi \eta + b_2\eta ^2 \right) T \eta ^{\frac{1}{\beta _0}} \xi ' + \eta ^{\frac{1}{\beta _0}} \xi \left( c_0 \xi ^2 + c_1 \xi \eta + c_2 \eta ^2 \right) . \end{aligned}$$

(23)

Because $\frac{1}{2 \beta _0} + \frac{1}{2 \beta _2} - 1 = -\frac{2 }{u+v+2 }$, using (11) and dividing by $\eta ^{\frac{1}{\beta _0}}$, we can simplify (23) to

$$\begin{aligned} - \xi ' - \frac{\zeta _0^u}{\eta ^v} \frac{\omega ^{v-1}}{\xi ^{u-1}} \omega '= & {} \left( 2b_0\xi ^2 + c_1\left( \frac{b_0}{c_0}+\frac{a_2}{c_2}\right) \xi \eta + b_2\eta ^2 \right) T \xi ' \nonumber \\{} & {} +\, \xi (c_0 \xi ^2 + c_1 \xi \eta + c_2 \eta ^2 ). \end{aligned}$$

(24)

Taking the derivative of (20) w.r.t. T and multiplying with $\Delta /(c_0c_2)$ gives

$$\begin{aligned}{} & {} \left( 2b_0\xi ^2 + c_1\left( \frac{b_0}{c_0}+\frac{a_2}{c_2}\right) \xi \eta + b_2\eta ^2 \right) \eta ^v \xi ^{u-1} \xi ' \\{} & {} \quad = \left( 2a_0\zeta _0^2 + + c_1\left( \frac{b_0}{c_0}+\frac{a_2}{c_2}\right) \zeta _0\omega + 2a_2 \omega ^2 \right) \zeta _0^u \omega ^{v-1} \omega '. \end{aligned}$$

Hence, we can rewrite (24) as

$$\begin{aligned}&-\left( 1 + \frac{2b_0\xi ^2 + c_1\left( \frac{b_0}{c_0}+\frac{a_2}{c_2}\right) \xi \eta + 2b_2\eta ^2}{2a_0\zeta _0^2 + c_1\left( \frac{b_0}{c_0}+\frac{a_2}{c_2}\right) \zeta _0\omega + 2a_2\omega ^2 }\right) \xi ' \\&\quad =\ \left( 2b_0\xi ^2 + c_1\left( \frac{b_0}{c_0}+\frac{a_2}{c_2}\right) \xi \eta + b_2\eta ^2 \right) T \xi ' + \xi (c_0 \xi ^2 + c_1 \xi \eta + c_2 \eta ^2 ). \end{aligned}$$

We insert $\xi ' = g'(T) T^{-\beta _2} - \beta _2 g(T) T^{-(1+\beta _2)}$ and multiply with $T^{\beta _2}$, which leads to

$$\begin{aligned}&-\left( 1+ \frac{2b_0\xi ^2 + c_1\left( \frac{b_0}{c_0}+\frac{a_2}{c_2}\right) \xi \eta + 2b_2\eta ^2}{2a_0\zeta _0^2 + c_1\left( \frac{b_0}{c_0}+\frac{a_2}{c_2}\right) \zeta _0\omega + 2a_2\omega ^2 }\right) (g'(T) - \beta _2 g(T) T^{-1}) \\&\quad =\ \left( 2b_0\xi ^2 + c_1 \left( \frac{b_0}{c_0}+\frac{a_2}{c_2}\right) \xi \eta + 2b_2\eta ^2\right) g'(T) \ T -\frac{\Delta }{b_2} g(T)^3 T^{-2 \beta _2}. \end{aligned}$$

Since $\xi = O(T^{-\beta _2})$ and $\omega = O(T^{-\beta _0})$, we can write this differential equation as

$$\begin{aligned} \frac{g'}{g} = \frac{1}{T^2} \frac{\beta _2}{2} \frac{\dfrac{a_0\zeta _0^2 +b_2 \eta ^2 + O(T^{-2 \beta _2})}{a_0\zeta _0^2 +O(T^{-2 \beta _0})} -\frac{\Delta }{b_2} g(T)^2 T^{-\frac{a_2}{b_2}} }{b_2 \eta ^2 + O(T^{-2 \beta _2}) + O(T^{-1})}. \end{aligned}$$

Keeping the leading terms only (where we use that $2\beta _2, 2\beta _0 > 1$), we get the differential equation

$$\begin{aligned} \frac{g'}{g} = \left( \xi _1(\eta ) + O\left( \max \{T^{-1}, T^{-\frac{a_2}{b_2}}\} \right) \right) \frac{1}{T^2} \quad \text { for } \xi _1(\eta ) := \frac{\beta _2}{2} \left( \frac{1}{a_0\zeta _0^2}+ \frac{1}{b_2\eta ^2 } \right) . \end{aligned}$$

Using the limit boundary value $\xi _0 = \xi _0(\eta ) = \lim _{T \rightarrow \infty } g(\eta ,T)$, we find the solution

$$\begin{aligned} g(\eta ,T) = \xi _0 e^{-\left( \xi _1 + O\left( \max \{T^{-1}, T^{-\frac{a_2}{b_2}}\} \right) \right) T^{-1} } = \xi _0\left( 1 - \xi _1 T^{-1} + O\left( \max \{T^{-2}, T^{-2 \beta _2}\} \right) \right) \end{aligned}$$

as required. The analogous asymptotics for $\omega$ and the constants $\omega _0$ and $\omega _1$ can be derived by changing the time direction and the roles $(a_0, a_2) \leftrightarrow (b_2, b_0)$, and also by the relation $\xi ^u \eta ^{v+2 }c_2 \sim \zeta _0^{u+2} \omega ^v c_0$ from (20):

$$\begin{aligned} \omega _0(\eta )= & {} c_0^{-\frac{1}{v}} \zeta _0^{-\frac{b_0}{a_0}} \left( \int _0^\infty \frac{ M^{\frac{1}{\beta _2}-1} \, dM }{\left( c_0 M^2 + c_1 M + c_2 \right) ^{ \frac{1}{2 \beta _0} + \frac{1}{2 \beta _2} } } \right) ^{\beta _0}, \nonumber \\ \omega _1(\eta )= & {} \frac{\beta _0}{2 } \left( \frac{1}{b_2\zeta _0^2}+ \frac{1}{a_0\eta ^2 }\right) . \end{aligned}$$

This concludes the proof.

3 Proof of Theorem 1.1

To prove that the regular variation established in Proposition 2.1 is robust under perturbations of the vector field, we put the ${{\mathcal {O}}}(4)$ terms back into (3), but since we consider it as a perturbation of (9), we write ${\tilde{X}}$ instead:

$$\begin{aligned} {\tilde{X}} = \begin{pmatrix} {\tilde{X}}_1 \\ {\tilde{X}}_2 \end{pmatrix} = \begin{pmatrix} x(a_0 x^2 + a_1xy + a_2 y^2) \\ -y(b_0 x^2 + b_1xy + b_2 y^2) \end{pmatrix} + {{\mathcal {O}}}(4), \end{aligned}$$

(25)

so that $|{\tilde{X}} - X| = {{\mathcal {O}}}(4)$. The quantities $\xi (\eta , T), \omega (\eta ,T)$ will be written as ${\tilde{\xi }}(\eta , T), {\tilde{\omega }}(\eta ,T)$ etc., and the goal is to show that ${\tilde{\xi }}(\eta , T)$ is still regularly varying.

As before, let $\xi = \xi ( \eta ,T)$ be such that for the unperturbed flow, $\phi ^T (\xi , \eta ) = (\zeta _0, \omega (\eta ,T))$. Proposition 2.1 gives the asymptotics of $\xi (\eta ,T)$ as $T \rightarrow \infty$. At the same time, under the perturbed flow associated to (25), $\phi ^{{\tilde{T}}} (\xi , \eta ) = (\zeta _0, {\tilde{\omega }}(\eta ,{\tilde{T}}))$ for some ${\tilde{T}}$. Therefore we can write $\xi (\eta ,T) = {\tilde{\xi }}(\eta , {\tilde{T}})$, and once we estimated ${\tilde{T}}$ as function of T, we can express ${\tilde{\xi }}(\eta , {\tilde{T}})$ explicitly as function of ${\tilde{T}}$. We follow the argument of the proof of Proposition 2.1, keeping track of the effect of the higher order terms.

The perturbed first integral To start, we construct a first integral ${\tilde{L}}$ on $Q = [0,\zeta _0] \times [0,\eta _0]$ by defining

$$\begin{aligned} {\tilde{L}}({\tilde{\phi }}^t(\delta , \delta )) = L(\delta ,\delta ) = {\left\{ \begin{array}{ll} \delta ^{u+v+2}\, (\frac{a_0}{v} + \frac{a_1}{v+1} + \frac{b_2}{u}) &{} \text { if } \Delta > 0,\\ \delta ^{-(u+v+2)}\, (\frac{a_0}{v} + \frac{a_1}{v+1} + \frac{b_2}{u})^{-1} &{} \text { if } \Delta < 0, \end{array}\right. } \end{aligned}$$

for $0 < \delta \le \min \{\zeta _0, \eta _0\}$ and $t \in {{\mathbb {R}}}$. (We continue the argument for the case $\Delta > 0$; the other case goes analogously.)

By construction, ${\tilde{L}}$ is constant on integral curves of $\dot{z} = {\tilde{X}}(z)$. Because ${\tilde{X}}$ is $C^3$, the integral curves are $C^3$ curves, and form a $C^3$ foliation of $P_0$, see e.g. [14, Theorem 2.10]. Note that the coordinate axes consist of the stationary point (0, 0) and its stable and unstable manifold; we put ${\tilde{L}}(x,0) = {\tilde{L}}(0,y) = 0$. Then ${\tilde{L}}$ is continuous on Q and $C^{3}$ on the interior of Q.

Now we compare ${\tilde{L}}$ with L on a small neighbourhood U of $\phi _{hor}^{-1}(Q) \cup Q \cup \phi _{hor}^1(Q)$. Take $y_0 = \eta _0$ and $x_0 = x_0(\delta )$ such that the integral curve of $\dot{z} = X(z)$ through $z_0 := (x_0, y_0)$ intersects the diagonal at $(\delta , \delta )$. Then the integral curve of $\dot{z} = {\tilde{X}}(z)$ through $z_0$ intersects the diagonal at $({\tilde{\delta }}, {\tilde{\delta }})$ for some ${\tilde{\delta }} = {\tilde{\delta }}(\delta )$, see Fig. .

For some $z_1$ on this integral curve between $z_0$ and $({\tilde{\delta }},{\tilde{\delta }})$, the integral curve through $z_1$ of the unperturbed system intersects the diagonal in some point $(\delta ', \delta ')$ between $(\delta ,\delta )$ and $({\tilde{\delta }}, {\tilde{\delta }})$. Therefore

$$\begin{aligned} {\tilde{L}}(z_1) \ = \ {\tilde{L}}({\tilde{\delta }}, {\tilde{\delta }})\ =\ L({\tilde{\delta }}, {\tilde{\delta }}) =\ L(\delta ',\delta ') \left( \frac{{\tilde{\delta }}}{\delta '}\right) ^{u+v+2} \ = \ L(z_1) \left( \frac{{\tilde{\delta }}}{\delta '}\right) ^{u+v+2} \!\!\!\!\!\!\! \!\!\!\!\! \!\!\! . \nonumber \\ \end{aligned}$$

(26)

Fig. 3

Solutions of (27) and (28), starting from the same point $z_0 = (x_0, y_0)$

Estimating $|{\tilde{\delta }}-\delta |$: Parametrise the integral curve of X through $z_0$ as (x(y), y) for $\min \{ \delta , {\tilde{\delta }}\} \le y \le y_0$. (So $x \le y$; the case $y \le x$ can be dealt with by switching the roles of x and y.) Then by (9):

$$\begin{aligned} x'(y) = F(x,y) := -\frac{x(a_0 x^2 + a_1xy+ a_2 y^2)}{y(b_0 x^2 + b_1 xy + b_2 y^2)}. \end{aligned}$$

(27)

For the perturbed vector field (25) we parametrise the integral curve through $z_0$ as $({\tilde{x}}(y), y)$ and we have the analogue of (27):

$$\begin{aligned} {\tilde{x}}'(y) = {\tilde{F}}({\tilde{x}},y) := -\frac{{\tilde{x}}(a_0 {\tilde{x}}^2 + a_1 {\tilde{x}} y + a_2 y^2 + \sum _{j=1}^3 {\hat{a}}_j {\tilde{x}}^j y^{3-j})}{y(b_0 {\tilde{x}}^2 + b_1 {\tilde{x}} y+ b_2 y^2 + \sum _{j=1}^3 {\hat{b}}_j {\tilde{x}}^j y^{3-j})}, \end{aligned}$$

(28)

where ${\hat{a}}_j, {\hat{b}}_j$ are bounded functions in ${\tilde{x}}$ and y. The absence of the terms ${\hat{a}}_0 y^3$ and ${\hat{b}}_0 y^3$ is because of the assumption that ${{\mathcal {O}}}(4) = x^2 {{\mathcal {O}}}(2)$ near the yz-plane. For the region ${\tilde{x}} > y$ we need to leave out the terms ${\hat{a}}_3 {\tilde{x}}^3$ and ${\hat{b}}_3 {\tilde{x}}^3$ instead.

Combining (27) and (28) we have

$$\begin{aligned} {\tilde{x}}'(y) = -\frac{{\tilde{x}}(a_0 {\tilde{x}}^2 + a_1 {\tilde{x}} y + a_2 y^2)}{y(b_0{\tilde{x}}^2 + b_1 {\tilde{x}} y + b_2 y^2)} (1+ {\tilde{x}} \, q_0({\tilde{x}}, y)) \end{aligned}$$

(29)

for the bounded function $q_0: [0, \max \{ \delta ,{\tilde{\delta }}\}] \times [\delta ,y_0] \rightarrow {{\mathbb {R}}}$, given by

$$\begin{aligned} q_0({\tilde{x}}, y) = \frac{1}{{\tilde{x}}} \left( \left( 1+\frac{ {\tilde{x}} \sum _{j=1}^3 {\hat{a}}_j {\tilde{x}}^{j-1} y^{3-j}}{a_0 {\tilde{x}}^2 + a_1 {\tilde{x}} y + a_2 y^2} \right) \ \left( 1 + \frac{{\tilde{x}} \sum _{j=1}^3 {\hat{b}}_j {\tilde{x}}^{j-1} y^{3-j}}{b_0 {\tilde{x}}^2 + b_1 {\tilde{x}} y + b_2 y^2} \right) ^{-1} -1 \right) . \end{aligned}$$

From Grönwall’s Lemma, we can bound the speed at which ${\tilde{x}}(y)$ and x(y) diverge from each other, see [14, Theorem 2.8]:

$$\begin{aligned} u(y) := |{\tilde{x}}(y) - x(y)| \le |{\tilde{x}}(y_0) - x(y_0)| e^{(y_0-y){\text {{Lip}}}} + \frac{V}{{\text {{Lip}}}} \left( e^{(y_0-y) {\text {{Lip}}}} - 1 \right) ,\nonumber \\ \end{aligned}$$

(30)

for $y \in [\delta , y_0]$, where ${\text {{Lip}}}$ is the Lipschitz constant of F(x, y) in x maximized over $y \in [\delta ,y_0]$ and

$$\begin{aligned} V = \sup _{y \in [\delta ,y_0]} \sup _{x \in [0, \max \{\delta , {\tilde{\delta }}\}]} |F(x,y)| q_0(x,y) x. \end{aligned}$$

The Lipschitz constant of F is $\sup _{x,y} \frac{\partial }{\partial x} F(x,y)$, which is of order $1/\delta$. Therefore (30) gives a very poor estimate if we apply it at once to the whole interval $[\delta , y_0]$, but we can improve it by partitioning $[\delta ,y_0]$ into smaller intervals.

Proposition 3.1

Assume the equation ${\tilde{x}}'(y) = F({\tilde{x}},y) (1+q_0 {\tilde{x}})$ for some bounded function $q_0 = q_0({\tilde{x}},y)$ and initial value ${\tilde{x}}(y_0)=x(y_0) = x_0$. Then there is a constant K for all $y \in [\delta ,y_0]$ we have $|{\tilde{x}}(y) - x(y)| \le K \delta ^2$.

Proof

We divide the interval $[\delta ,y_0]$ into N interval $[y_{j+1}-y_j]$ of the same length, so $y_j = \delta + \frac{y_0-\delta }{N}(N-j)$ and set $x_j = x(y_j)$. The Lipschitz constant $[y_{j+1}, y_j]$ is $\sup _{y \in [y_{j+1}, y_j]} \sup _{x \in [0,\delta ^2]} \frac{\partial }{\partial x} F(x,y) \le \frac{1}{y} (\gamma + \varepsilon )$ for $\gamma = \frac{a_2}{b_2}$. Therefore

$$\begin{aligned} {\text {{Lip}}}(y_j)(y_j-y_{j+1}) \le \frac{y_0-\delta }{N} \frac{\gamma + \varepsilon }{ \delta + \frac{y_0-\delta }{N}(N-j-1) } = \frac{\gamma + \varepsilon }{(N-(j+1)) + \delta N/(y_0-\delta )} \end{aligned}$$

Recall from (13) that $x(y) = U(y) \delta ^{1+\frac{a_2}{b_2}} y^{-\frac{a_2}{b_2}}$. Let

$$\begin{aligned} C = 2 \sup _{y \in [y_{j+1}, y_j]} \sup _{x \in [0, 2x(y)]} q_0(x,y)\ \frac{a_0x^2 + a_1 xy + a_2 y^2}{b_0x^2 + b_1 xy + b_2 y^2} \ U(y)^2. \end{aligned}$$

Take $K = \frac{2C}{\gamma }y_0^{-2\gamma }$ and assume by induction that $u(y_j) \le K \delta ^2 \le 1$ (so we assume that $\delta$ is sufficiently small). Clearly this induction hypothesis holds for $j=0$ because $u(y_0) = 0$. Then

$$\begin{aligned} V(y_j):= & {} \sup _{y \in [y_{j+1}, y_j]} \sup _{x \in [0, x(y)(1+K \delta ^2)]} q_0(x,y)\, x\, F(x,y) \\\le & {} \sup _{x,y} \frac{a_0x^2 + a_1 xy + a_2 y^2}{b_0x^2 + b_1 xy + b_2 y^2} \ q_0(x,y)\ \sup _{y \in [y_{j+1}, y_j]} \frac{ x(y)^2 (1+K\delta ^2)^2}{y} \\\le & {} \sup _{x,y} \frac{a_0x^2 + a_1 xy + a_2 y^2}{b_0x^2 + b_1 xy + b_2 y^2} \ q_0(x,y)\ 2U(y)^2 \ \sup _{y \in [y_{j+1}, y_j]} \delta ^{2(1+\gamma )} y^{-(1+2\gamma )} \\= & {} C \delta ^{2(1+\gamma )} y_{j+1}^{-(1+2\gamma )}. \end{aligned}$$

The estimate (30) applied to $[y_{j+1}, y_j]$ gives the recursive formula

$$\begin{aligned} u(y_{j+1}) \le u(y_j) e^{ (\gamma +\varepsilon ) \frac{ y_j-y_{j+1} }{ y_{j+1}} } + C \delta ^{2(1+\gamma )} y_{j+1}^{-(1+2\gamma )} (y_j-y_{j+1}). \end{aligned}$$

(31)

Therefore, for $1 \le M < N$,

$$\begin{aligned} u(y_M) \le C \delta ^{2(1+\gamma )} \sum _{j=1}^M y_j^{-(1+2\gamma )} (y_{j-1}-y_j) e^{(\gamma +\varepsilon ) \sum _{k=j}^M \frac{ y_{k-1}-y_k}{y_k} }. \end{aligned}$$

(32)

Then (32) gives for $N = \lceil \delta ^{-1} \rceil$ and $M < N$,

$$\begin{aligned} u(y_M)\le & {} C \delta ^{2(1+\gamma )} y_0^{-2\gamma } N^{2\gamma } \sum _{j=1}^{M} \frac{e^{(\gamma +\varepsilon ) \sum _{k=j}^M 1/(N-k)}}{(N-j)^{1+2\gamma }} \\\le & {} C \delta ^2 y_0^{-2\gamma } \frac{1}{(N-M)^{\gamma +\varepsilon }} \sum _{j=1}^M \frac{1}{(N-j)^{\gamma -\varepsilon +1}} \le \frac{C}{\gamma -\varepsilon } \delta ^2 y_0^{-2\gamma }. \end{aligned}$$

Therefore $|{\tilde{x}}(y_M) - x(y_M)| = u(y_M) \le K \delta ^2$ as claimed. $\square$

By (29) for $y = \delta = {\tilde{x}}(\delta )+ O(\delta ^2)$, the derivative ${\tilde{x}}'(\delta ) = \frac{a_0+a_1+a_2}{b_0+b_1+b_2} + O(\delta )$. Since ${\tilde{\delta }}$ lies between $\delta$ and ${\tilde{x}}(\delta )$ (see Fig. 3), we have by a Taylor approximation

$$\begin{aligned} |{\tilde{x}}(\delta ) - \delta |= & {} |{\tilde{x}}(\delta ) - {\tilde{\delta }}| + |{\tilde{\delta }} - \delta | = \left( 1+ \frac{a_0+a_1+a_2}{b_0+b_1+b_2} + O(\delta )\right) |{\tilde{\delta }} - \delta | \nonumber \\= & {} \frac{c_0+c_1+c_2 + O(\delta ) }{b_0+b_1+b_2}|{\tilde{\delta }} - \delta |. \end{aligned}$$

(33)

and therefore $|{\tilde{\delta }}-\delta | = O(|{\tilde{x}}(\delta )- \delta |) = O(\delta ^2)$. Now that we have this relation between ${\tilde{\delta }}$ and $\delta$, we can estimate ${\tilde{T}}$ in terms of T, and effectively finish of Theorem 1.1.

Proof of Theorem 1.1

Let $z_0 = (x_0, y_0) = (\xi (\eta , T), \eta ) = ({\tilde{\xi }}(\eta , {\tilde{T}}), \eta )$ as in Fig. 3 be the point such that $\phi _{hor}^T(z_0) = (\zeta _0, \omega (\eta ,T))$ under the unperturbed flow and ${\tilde{\phi }}_{hor}^{{\tilde{T}}}(z_0) = (\zeta _0, {\tilde{\omega }}(\eta ,{\tilde{T}}))$ under the perturbed flow. We estimate ${\tilde{T}}$ in terms of T.

Combining the estimate for $\xi (\eta , T)$ from Proposition 2.1 with $L(\delta ,\delta ) = L(\xi (\eta ,T), \eta )$, we can find the relation between $\delta$ and T:

$$\begin{aligned} \delta = \delta _0 T^{-\frac{1}{2}} \left( 1 - \frac{\xi _1}{2\beta _2} T^{-1} + O(T^{-2}, T^{-2 \beta _2})\right) , \end{aligned}$$

(34)

for

$$\begin{aligned} \delta _0 = \xi _0^{\frac{1}{2 \beta _2}} \eta ^{1-\frac{1}{2 \beta _2}} \left( \frac{c_0\frac{\xi ^2}{\eta ^2} + c_1 \frac{\xi }{\eta } + c_2}{c_0+c_1+c_2}\right) ^{\frac{1}{u+v+2}}. \end{aligned}$$

To estimate ${\tilde{T}}$, we divide the trajectory ${\tilde{\phi }}^t(z_0) = ({\tilde{x}}(t), {\tilde{y}}(t))$ of $z_0$ for the region ${\tilde{x}} \le {\tilde{y}}$ into two parts delimited by points in time:

$$\begin{aligned} {\tilde{T}}_1= & {} \min \{ t> 0 : 2{\tilde{x}}(t) = {\tilde{y}}(t) \}, \nonumber \\ {\tilde{T}}_2= & {} \min \{ t > 0 : {\tilde{x}}({\tilde{T}}_1 + t) = {\tilde{y}}({\tilde{T}}_1+t) \}, \end{aligned}$$

(35)

and symmetric quantities for the region ${\tilde{y}} \le {\tilde{x}}$. Let $T_1, T_2$ be the analogous quantities for the unperturbed trajectory. For $y_1 := y(T_1)$ and ${\tilde{y}}_1 := y({\tilde{T}}_1)$, we have $|{\tilde{y}}_1 - y_1| = O(\delta ^2)$. Assume that ${\tilde{y}}_1 \ge y_1$ (the case ${\tilde{y}}_1 < y_1$ goes likewise). We compute

$$\begin{aligned} T_1= & {} \int _{y_1}^{y_0} \frac{dy}{\dot{y}} = \int _{{\tilde{y}}_1}^{y_0} \frac{dy}{\dot{y}} + \int _{y_1}^{{\tilde{y}}_1} \frac{dy}{\dot{y}} \\= & {} \int _{{\tilde{y}}_1}^{y_0} \frac{dy}{-y(b_0 x(y)^2 + b_1 x(y)y + b_2 y^2)} + \int _{y_1}^{{\tilde{y}}_1} \frac{dy}{\dot{y}}. \end{aligned}$$

The first term is $O(\delta ^{-2})$ as $\delta \rightarrow 0$ and the second is O(1) (and therefore small compared to the first term) because $|{\tilde{y}}_1-y_1| = O(\delta ^2)$. Hence $T_1 = O(\delta ^{-2})$. Similarly,

$$\begin{aligned} {\tilde{T}}_1 - T_1 = \int _{{\tilde{y}}_1}^{y_0} \frac{dy}{\dot{{\tilde{y}}}} - \int _{{\tilde{y}}_1}^{y_0} \frac{dy}{\dot{y}} - \int _{y_1}^{{\tilde{y}}_1} \frac{dy}{\dot{y}} = \int _{{\tilde{y}}_1}^{y_0} \frac{1}{\dot{{\tilde{y}}}} - \frac{1}{\dot{y}} \, dy + O(1). \end{aligned}$$

(36)

Using that ${\tilde{x}}(y) - x(y) \le \delta ^2$ and abbreviating $\Sigma = \sum _{j=1}^3 {\hat{b}}_j {\tilde{x}}^j y^{3-j} = O(y^3)$ for ${\tilde{x}} \le {\tilde{y}}$, we compute the last integral of (36) as

$$\begin{aligned} \int _{{\tilde{y}}_1}^{y_0}&\frac{1}{-y(b_0 {\tilde{x}}(y)^2 + b_1{\tilde{x}}(y)y + b_2 y^2 + \Sigma )} - \frac{1}{-y(b_0 x(y)^2 + b_1 x(y)y + b_2 y^2)} \ dy \\ =&\int _{{\tilde{y}}_1}^{y_0}\frac{ ({\tilde{x}} - x)(b_0 ({\tilde{x}}+x) + b_1 y) + \Sigma }{ y(b_0 {\tilde{x}}(y)^2 + b_1{\tilde{x}}(y)y + b_2 y^2 + \Sigma )(b_0 x(y)^2 + b_1 x(y)y + b_2 y^2)} \ dy \\ \le&\ \delta ^2 \int _{{\tilde{y}}_1}^{y_0} \frac{3b_0+2b_1}{\max _i b_i \ y^2} \ dy + \int _{{\tilde{y}}_1}^{y_0} O(y^{-1}) \ dy = O(\delta ^{-1}). \end{aligned}$$

Together with (34) and the fact that $\int _{y_1}^{{\tilde{y}}_1} \frac{dy}{\dot{y}} = O(1)$, this gives

$$\begin{aligned} {\tilde{T}}_1 = T_1(1+ O(\delta )) = T_1(1+ O(T^{-\frac{1}{2}})). \end{aligned}$$

(37)

For ${\tilde{M}} = y/{\tilde{x}}$, computations analogous to (16) show that $\dot{{\tilde{M}}} = -{\tilde{M}} (c_0 + c_1{\tilde{M}} + c_2{\tilde{M}}^2 + {\tilde{x}} \Psi ) {\tilde{x}}^2$ for ${\hat{c}}_j = {\hat{a}}_j + {\hat{b}}_j$ and $\Psi := \sum _{j=0}^2 {\hat{c}}_{3-j} {\tilde{M}}^j$. For every $({\tilde{x}},y) = ({\tilde{x}},{\tilde{x}}{\tilde{M}})$ on the ${\tilde{\phi }}$-trajectory of $z_0$ (which is a level set of ${\tilde{L}}$), we have

$$\begin{aligned} \xi ^u \eta ^v \left( \frac{a_0}{v} \xi ^2 + \frac{a_1}{v+1} \xi \eta + \frac{b_2}{u} \eta ^2\right) \frac{{\tilde{\delta }}}{\delta '} = {\tilde{x}}^{u+v+2} {\tilde{M}}^v \left( \frac{a_0}{v} + \frac{a_1}{v+1} {\tilde{M}} + \frac{b_2}{u} {\tilde{M}}^2\right) , \end{aligned}$$

with $\delta '$ as in (26). This gives the analogue of [2, formula (32)]:

$$\begin{aligned} \dot{{\tilde{M}}} = - G(\xi ,\eta ) {\tilde{M}}^{1-\frac{1}{\beta _0}} \left( c_0+c_1{\tilde{M}} + c_2{\tilde{M}}^2 + {\tilde{x}}\Psi ({\tilde{x}},{\tilde{M}}) \right) ^{\frac{1}{2 \beta _0} + \frac{1}{2 \beta _2}} \left( \frac{{\tilde{\delta }}}{\delta '} \right) ^{1-\frac{1}{2 \beta _0} - \frac{1}{2 \beta _2}}, \end{aligned}$$

(38)

where $G(\xi ,\eta )$ is as in (18). Because $\delta '$ lies between $\delta$ and ${\tilde{\delta }}$, the conclusion $|{\tilde{\delta }}-\delta | = O(\delta ^2)$ of (33) gives

$$\begin{aligned} \frac{{\tilde{\delta }}}{\delta '} \le 1 + \frac{|{\tilde{\delta }}-\delta '|}{\delta '} \le 1 + \frac{|{\tilde{\delta }}-\delta |}{\delta } = 1+O(\delta ). \end{aligned}$$

Note also on the time interval $[{\tilde{T}}_1, {\tilde{T}}_1 + {\tilde{T}}_2]$, we have ${\tilde{x}}(y) \le y \le 2{\tilde{x}}(y) \le 2\max \{\delta , {\tilde{\delta }}\}$ and therefore

$$\begin{aligned} c_0 + c_1 {\tilde{M}} + c_2 {\tilde{M}}^2 + {\tilde{x}} \Psi ({\tilde{x}}, {\tilde{M}})= & {} c_0 (1+O({\tilde{x}})) + c_1 {\tilde{M}} (1+O(y)) + c_2 {\tilde{M}}^2 \\= & {} (c_0 + c_1 {\tilde{M}} + c_2 {\tilde{M}}^2) (1+O(\delta )). \end{aligned}$$

This combined with (38) we find

$$\begin{aligned} \dot{{\tilde{M}}} = - G(\xi ,\eta ) {\tilde{M}}^{1-\frac{1}{\beta _0}} \left( c_0 + c_1{\tilde{M}} + c_2{\tilde{M}}^2\right) ^{\frac{1}{2 \beta _0} + \frac{1}{2 \beta _2}} (1+O(\delta )). \end{aligned}$$

The choice of ${\tilde{T}}_1$ and $T_1$ ensures that ${\tilde{M}}({\tilde{T}}_1) = M(T_1) = 2$ and similarly ${\tilde{M}}({\tilde{T}}_1+{\tilde{T}}_2) = M(T_1+T_2) = 1$. Therefore

$$\begin{aligned} {\tilde{T}}_2= & {} \int _{{\tilde{T}}_1}^{{\tilde{T}}_1 + {\tilde{T}}_2} dt = \int _{{\tilde{M}}({\tilde{T}}_1+{\tilde{T}}_2)}^{{\tilde{M}}({\tilde{T}}_1)} \dot{{\tilde{M}}} ^{-1} \, d{\tilde{M}} \\= & {} \int _1^2 \frac{ {\tilde{M}}^{\frac{1}{\beta _0}-1} (1+O(\delta ))^{-1} }{ G(\xi ,\eta )(c_0+c_1{\tilde{M}}+c_2\tilde{M}^2)^{\frac{1}{2 \beta _0} + \frac{1}{2 \beta _2}} } \, d{\tilde{M}} \\= & {} \int _{M(T_1+T_2)}^{M(T_1)} \frac{M^{\frac{1}{\beta _0}-1} (1+O(\delta ))^{-1} }{ G(\xi ,\eta )(c_0+c_1M+c_2M^2)^{\frac{1}{2 \beta _0} + \frac{1}{2 \beta _2}} } \, dM \\= & {} T_2(1+O(\delta ))^{-1} = T_2(1+O(T^{-\frac{1}{2}} )). \end{aligned}$$

Combining this with (37) gives ${\tilde{T}} = T(1+O(T^{-\frac{1}{2}}))$. The estimate of Proposition 2.1 now gives ${\tilde{\xi }}(\eta , {\tilde{T}}) = \xi _0(\eta ) {\tilde{T}}^{-\beta _2}(1+O({\tilde{T}}^{-\frac{1}{2}}))$ as claimed.

Reversing the roles $(a_0, a_2) \leftrightarrow (b_2, b_0)$ as in the end of the proof of Proposition 2.1 gives ${\tilde{\omega }}(\eta , {\tilde{T}}) = \omega _0(\eta ) {\tilde{T}}^{-\beta _0}(1+O({\tilde{T}}^{-\frac{1}{2}}))$.

The formula (6) for the Dulac maps follows directly from Theorem 1.1 by inverting $T \mapsto \xi (\eta ,T)$ and inserting this in the formula for $\omega (\eta ,T)$. In the special case that $\beta _0=\beta _2$, formula (6) reduces to

$$\begin{aligned} \omega = D(\xi ) = \left( \frac{b_2}{a_0}\right) ^{\frac{1}{\beta _2-1}} \left( \frac{\eta }{\zeta _0} \right) ^{2\beta _2-1} \xi \left( 1+O(\xi ^{\frac{1}{2\beta _2}})\right) . \end{aligned}$$

Reducing further by assuming (5) (i.e., in the volume preserving setting), we get

$$\begin{aligned} \omega = D(\xi ) = \frac{b_2}{a_0}\left( \frac{\eta }{\zeta _0} \right) ^3 \xi \left( 1+O(\xi ^{\frac{1}{4}})\right) . \end{aligned}$$

This coefficient $\frac{b_2}{a_0}\left( \frac{\eta }{\zeta _0} \right) ^3 = \frac{\Vert X_{hor}(0,\eta ) \Vert }{\Vert X_{hor}(\zeta _0,0) \Vert }$ agrees with the fact that for $\omega = D(\xi )$, the flow-boxes $\cup _{t \in [0,\varepsilon ]} \phi _{hor}^t([0,\xi ] \times \{\eta \})$ and $\cup _{t \in [0,\varepsilon ]} \phi _{hor}^t(\{\zeta _0\} \times [0,\omega ])$ must have the same volume. If the neutral saddle p is part of a heteroclinic cycle, then it is accumulated by periodic solutions, but these are not limit cycles of course.

4 Time-1 map versus Poincaré map

First we give an estimate of observables integrated over the flow-lines of $X_{hor}$ of (9).

Proposition 4.1

Let $r = \sqrt{x^2+y^2}$, $\rho > 0$ and W(T) be the integral curve for (9) connecting $(\xi (\eta _0, T), \eta _0))$ to $(\zeta _0, \omega (\eta _0, T))$, see Fig. 1. Then there is a constant $C = C(\rho ) > 0$ such that

$$\begin{aligned} \Theta = \Theta (T) := \int _{W(T)} r(t)^\rho \, dt = {\left\{ \begin{array}{ll} C T^{1-\frac{\rho }{2}} (1+o(1)) &{} \text { if } \rho < 2, \\ C \log (T) (1+o(1)) &{} \text { if } \rho = 2, \\ C (1+o(1)) &{} \text { if } \rho > 2. \end{array}\right. } \end{aligned}$$

(39)

Proof

We build on the proof of Proposition 2.1 (or in fact Theorem 1.1), and in the integral $\Theta$ we change coordinates $M = y/x$. That is, $r^\rho = (x^2+y^2)^{\rho /2} = x^{\rho } (1+M^2)^{\rho /2}$. Use (14) to get

$$\begin{aligned} x = G(T)^{\frac{1}{2}} M^{-\frac{v}{u+v+2 }} (c_0+c_1M+c_2M^2)^{\frac{-1}{u+v+2 }}, \end{aligned}$$

with $G(T) := G(\xi (\eta _0, T)), \eta _0)$ as in (18). Abbreviate $\xi (\eta _0, T) = \xi (T)$ and $\omega (\eta _0, T) = \omega (T)$. Inserting the above in the integral of (19), we obtain

$$\begin{aligned} \Theta = G(T)^{\frac{\rho }{2}-1} \int _{\omega (T)/\zeta _0}^{\eta /\xi (T)} \frac{ M^{-\frac{\rho v}{u+v+2}} (c_0+c_1M+c_2M^2)^{\frac{-\rho }{u+v+2 }} (1+M^2)^{\frac{\rho }{2}}}{ M^{1-\frac{1}{\beta _0}} \left( c_0+c_1M+c_2 M^2 \right) ^{ \frac{1}{2\beta _0} + \frac{1}{2\beta _2} } } \ dM.\nonumber \\ \end{aligned}$$

(40)

For $M \rightarrow 0$, the leading term in the integrand is

$$\begin{aligned} c_0^{-1+(1-\frac{\rho }{2}) \frac{1}{\beta _0}} M^{\frac{1}{\beta _0}-1 - \rho \frac{v}{u+v+2} } = c_0^{-1+(1-\frac{\rho }{2}) \frac{1}{\beta _0}} M^{(1-\frac{\rho }{2})\frac{1}{\beta _0} - 1}, \end{aligned}$$

i.e., the exponent is $> -1$ for $\rho < 2$. For $M \rightarrow \infty$, the leading term in the integrand is

$$\begin{aligned} c_2^{-1+(1-\frac{\rho }{2}) \frac{1}{\beta _0}} M^{-\frac{1}{\beta _2}-1 - \rho (\frac{v}{u+v+2} + \frac{2}{u+v+2} -1) } = c_0^{-1+(1-\frac{\rho }{2}) \frac{1}{\beta _0}} M^{-(1-\frac{\rho }{2})\frac{1}{\beta _2} - 1}, \end{aligned}$$

i.e., the exponent is $< -1$ for $\rho < 2$. This means that the integral in (40) converges to some constant $C_0 = C_0(\rho )$ as $T \rightarrow \infty$, and $\Theta \sim C_0 G(T)^{\frac{\rho }{2}-1} \sim C T^{1-\frac{\rho }{2}}$ for $C = C_0 \left( c_2^{1-\frac{1}{2 \beta _0} - \frac{1}{2 \beta _2}} \xi _0^{\frac{1}{\beta _0}} \eta _0^{1-\frac{1}{\beta _2}} \right) ^{1-\frac{\rho }{2}}$. This finishes the proof for $\rho < 2$.

If $\rho > 2$, then the value of $\Theta$ based on the leading terms of the integrand only, is

$$\begin{aligned} \Theta = G(T)^{\frac{\rho }{2}-1} \frac{c_0^{-1+(1-\frac{\rho }{2}) \frac{1}{\beta _0}} }{\frac{\rho }{2}-1} \left( \beta _2 \left( \frac{\eta _0}{\xi (T)}\right) ^{-(1-\frac{\rho }{2})\frac{1}{\beta _2}} - \beta _0 \left( \frac{\omega (T)}{\zeta _0} \right) ^{(1-\frac{\rho }{2})\frac{1}{\beta _0}} \right) . \end{aligned}$$

Insert the values of $\xi (T)$ and $\omega (T)$ from Proposition 2.1 as well as the leading term of G(T):

$$\begin{aligned} \Theta= & {} \left( c_2^{1-\frac{1}{2 \beta _0} - \frac{1}{2 \beta _2}} \xi _0^{\frac{1}{\beta _0}} \eta _0^{1-\frac{1}{\beta _2}} \right) ^{1-\frac{\rho }{2}} T^{1-\frac{\rho }{2}} \frac{c_0^{-1+(1-\frac{\rho }{2}) \frac{1}{\beta _0}} }{\frac{\rho }{2}-1}\nonumber \\ {}{} & {} \left( \beta _2 {\eta _0}^{(\frac{\rho }{2}-1)\frac{1}{\beta _2}} - \beta _0 \zeta _0^{(\frac{\rho }{2}-1)\frac{1}{\beta _0}} \right) T^{\frac{\rho }{2}-1}. \end{aligned}$$

The powers of T cancel in this expression, proving the case $\rho > 2$. Finally, if $\rho = 2$, then the factor $G(T)^{\frac{\rho }{2}-1}$ in (40) disappears and the leading terms in the integrand (both as $M \rightarrow 0$ and $M \rightarrow \infty$), are $c_0^{-1} M^{-1}$. This gives, due to Proposition 2.1,

$$\begin{aligned} \Theta \sim \frac{1}{c_0} \left( \log \frac{\eta _0}{\xi (T)} - \log \frac{\omega (T)}{\zeta _0} \right) \sim \frac{\beta _2+\beta _0}{c_0} \log T. \end{aligned}$$

$\square$

The 3-dimensional time-1 map $\phi ^1$ preserves no 2-dimensional submanifold of ${{\mathcal {M}}}$. Yet in order to model $\phi ^t$ as a suspension flow over a 2-dimensional map, we need a genuine Poincaré map. For this we choose a section $\Sigma$ transversal to $\Gamma$ and containing a neighbourhood U of p. As an example, $\Sigma$ could be ${{\mathbb {T}}}^2 \times \{ 0 \}$, and the Poincaré map to ${{\mathbb {T}}}^2 \times \{ 0 \}$ could be (a local perturbation of) Arnol’d’s cat map; in this case (and most cases) ${{\mathcal {M}}}$ is not homeomorphic to ${{\mathbb {T}}}^3$ because the homology is more complicated, see [1, 11].

Let $h:\Sigma \rightarrow {{\mathbb {R}}}^+$, $h(q) = \min \{ t > 0 : \phi ^t(q) \in \Sigma \}$ be the first return time. Assuming that $\sup _\Sigma |w(x,y)| < 1$, the first return time h is bounded and bounded away from zero, say $0< \inf _{\Sigma } h < \sup _{\Sigma } h$.

The Poincaré map $f := \phi ^h: \Sigma \rightarrow \Sigma$ has a neutral saddle point p at the origin. Its local stable/unstable manifolds are $W^s_{loc}(p) = \{ 0 \} \times (-\varepsilon ,\varepsilon )$ and $W^u_{loc}(p) = (-\varepsilon ,\varepsilon ) \times \{ 0 \}$. Because the flow $\phi ^t$ is a perturbation of an Anosov flow, and f is a Poincaré map, it has a finite Markov partition $\{P_i\}_{i \ge 0}$ and we can assume that p is in the interior of $P_0$. In the sequel, let U be a neighbourhood of p that is small enough that (1) is valid on $U \times [0,1]$ but also that $f(U) \supset {\hat{P}}_0 \cup P_0$.

In order to regain the hyperbolicity lacking in f, let

$$\begin{aligned} r(q) := \min \{ n \ge 1 : f^n(q) \in Y \} \end{aligned}$$

(41)

be the first return time to $Y := \Sigma \setminus P_0$. Then the Poincaré map $F = f^{r} = \phi ^\tau$ of $\phi ^t$ to $Y \times \{ 0 \}$ is hyperbolic, where

$$\begin{aligned} \tau (q) = \min \{ t > 0 : \phi ^t((q,0)) \in Y \times \{ 0 \} \} = \sum _{j=0}^{r-1} h \circ f^j \end{aligned}$$

is the corresponding first return time.

Consequently, the flow $\phi ^t:{{\mathcal {M}}}\times {{\mathbb {R}}}\rightarrow {{\mathcal {M}}}$ can be modeled as a suspension flow on $Y^\tau = \left( \bigcup _{q \in Y} \{ q \} \times [0,\tau (q)) \right) /(q,\tau (q)) \sim (F(q),0)$. Since the flow and section $Y \times \{ 0 \}$ are $C^1$ smooth, $\tau$ is $C^1$ on each piece $\{r= k\}$.

Lemma 4.1

Let ${\hat{\tau }}(q) = \min \{ t > 0 : \phi ^t_{hor}((q,\eta )) \in W^s(\zeta _0,0) \}$ be the time the horizontal flow needs to reach $\partial Q$. Then $\tau (q) = {\hat{\tau }}(q) + O(1)$ and $r= {\hat{\tau }}(q)+\Theta ({\hat{\tau }}(q))+O(1)$, where $\Theta$ is as in Proposition 4.1.

Fig. 4

The first quadrant of the rectangle $P_0$, with stable and unstable foliations of Poincaré map $f = \phi ^h$ drawn vertically and horizontally, respectively. Also one of the integral curves is drawn

Proof

By the definition of ${\hat{\tau }}$ we have $\phi ^{{\hat{\tau }}}_{hor}(q) \in {\hat{W}}^s$. Therefore it takes a bounded amount of time (positive or negative) for $\phi ^{{\hat{\tau }}}(q,0)$ to hit $Y \times \{ 0 \}$, so $|\tau (q)-{\hat{\tau }}(q)| = O(1)$.

The function w in the vertical component of the local vector field X of (1) is a linear combination of homogeneous functions $C_i \cdot (x^2+y^2)^{\rho _i/2}$. It suffices to take the leading term, i.e., the one with the smallest $\rho _i =: \rho$. Using this term in (39), we obtain that ${\hat{\tau }}(q) + \Theta ({\hat{\tau }}(q))$ indicates the vertical displacement by the flow $\phi ^t$. In particular, it gives the number of times the flow-line intersects $\Sigma$, and hence $r= {\hat{\tau }}(q) + \Theta ({\hat{\tau }}(q)) + O(1)$. $\square$

Assume that $\phi ^t$ and ${\hat{f}}$ preserve Lebesgue measure.

Proposition 4.2

Recall that $\beta _2 = \frac{a_2+b_2}{2b_2} \in (\frac{1}{2}, \infty )$. There exists $C^* > 0$ such that

$$\begin{aligned} \text{ Leb }(\{ \tau > t \}) = C^* t^{-\beta _2} (1+o(1)) \end{aligned}$$

(42)

for the F-invariant SRB-measure $\mu _{{\bar{\phi }}}$.

Proof

The function $\tau$ is defined on $\Sigma {\setminus } P_0$ and $\tau \ge h_2 = h + h \circ f$ on $Y_{\{r\ge 2\}} := f^{-1}(P_0) {\setminus } P_0$. The set $Y_{\{r\ge 2\}}$ is a rectangle with boundaries consisting of two stable and two unstable leaves of the Poincaré map f. Let $W^u(y)$ denote the unstable leaf of f inside $Y_{\{r\ge 2\}}$ with (0, y) as (left) boundary point. Let $y_1 < y_2$ be such that $W^u(y_1)$ and $W^u(y_2)$ are the unstable boundary leaves of $Y_{\{r\ge 2\}}$.

The unstable foliation of ${\hat{f}} = \phi _{hor}^1$ does not entirely coincide with the unstable foliation of f. Let ${\hat{W}}^u(y)$ denote the unstable leaf of ${\hat{f}}$ with (0, y) as (left) boundary point. Both ${\hat{W}}^u(y)$ and $W^u(y)$ are $C^1$ curves emanating from (0, y); let $\gamma (y)$ denote the angle between them. Then the lengths

$$\begin{aligned} \text{ Leb }(W^u(y) \cap \{ \tau> t\})= & {} |\cos \gamma (y)|\ \text{ Leb }({\hat{W}}^u(y) \cap \{ \tau > t\}) (1+o(1)) \\= & {} |\cos \gamma (y)|\ \xi _0(y)\ t^{-\beta _2} (1+o(1)) \end{aligned}$$

as $t\rightarrow \infty$, where the last equality and the notation $\xi _0(y)$ and $\beta _2 = (a_2+b_2)/(2b_2)$ come from Theorem 1.1

We decompose Lebesgue on $Y_{\{r\ge 2\}}$ as

$$\begin{aligned} \int _{Y_{\{r\ge 2\}}} v\, d\mu _{{\bar{\phi }}} = \int _{y_1}^{y_2} \left( \int _{W^u(y) } v\, d\mu ^s_{W^u(y)} \right) d\nu ^u(y). \end{aligned}$$

The conditional measures $\mu _{W^u(y)}$ on $W^u(y)$ equals 1-dimensional Lebesgue $m_{W^u(y)}$ on $W^u(y)$ Therefore, as $t \rightarrow \infty$,

$$\begin{aligned} \mu _{{\bar{\phi }}}(\tau> t)= & {} \int _{y_1}^{y_2} \mu _{W^u(y)}(W^u(y) \cap \{ \tau> t\} ) \, d\nu ^u(y) \\= & {} \int _{y_1}^{y_2} m_{W^u(y)}( W^u(y) \cap \{ \tau> t\} ) \, d\nu ^u(y) \\= & {} \int _{y_1}^{y_2} |\cos \gamma (y)|\ m_{{\hat{W}}^u(y)}({\hat{W}}^u(y) \cap \{ \tau > t\} ) (1+o(1)) \, d\nu ^u(y) \\= & {} \int _{y_1}^{y_2} |\cos \gamma (y)|\ \xi _0(y)\ t^{-\beta _2} (1+o(1)) \, d\nu ^u(y) = C^* t^{-\beta _2}(1+o(1)), \end{aligned}$$

for $C^* = \int _{y_1}^{y_2} |\cos \gamma (y)| \ \xi _0(y) \, d\nu ^u(y)$. This proves the result. $\square$

5 The proof of Theorem 1.2

Proof

The proof of Theorem 1.2 is a direct application of Theorem 2.7 in [3], where ${\bar{v}} = \int _0^\tau v \circ \phi ^t\, dt$ takes the role of ${\bar{\psi }}$ in [3, Theorem 2.7], but the condition that ${\bar{\psi }} = C-\psi _0$ for some positive $\psi _0$ is only important for the results on the shape of the pressure function in [3]. For us, only the tail of ${\bar{v}}$ matters and since v is $C^1$ on ${{\mathcal {M}}}\setminus \Gamma$, ${\bar{v}}$ is $C^1$ on each partition element $\{ \phi = n\}$ of the Markov map F. Since Proposition 4.1 applies to v we get ${\bar{v}}(x,y) \sim C_p T^{1-\frac{\rho }{2}}$ if the Dulac time of (x, y) is T. Since our invariant measure is Lebesgue, and $\beta _2 = 2$, Theorem 1.1 can be immediately used to estimate

$$\begin{aligned} \text{ Leb }({\bar{v}} > t) \sim \frac{\int _{\eta _0}^{\eta _1} \xi _0(\eta ) \, d\eta }{\text{ Vol } (\Sigma \setminus P_0)} \left( \frac{t}{C_p} \right) ^{\frac{-4}{2-\rho } }, \end{aligned}$$

(43)

where $\Sigma$ is the Poincaré section and $\text{ Vol } (\Sigma \setminus P_0)$ is the normalizing constant for Lebesgue restricted to the domain $\Sigma \setminus P_0$ of F. If $\rho \ge 2$, this asymptotic formula should be interpreted as $\text{ Leb }({\bar{v}} > t) = 0$ for t large, that is: ${\bar{v}}$ is bounded.

The exponent of the tail (43) is $-2$ if and only if $\rho = 0$, and in this case [3, Theorem 2.7(a)(ii)] gives the non-Gaussian CLT.

If $-\,2< \rho < 0$, [3, Theorem 2.7(a)(i)] gives a Stable Law of order $4/(2-\rho ) \in (1,2)$.

Finally, if $0< \rho < 2$ (or $\rho \ge 2$ when ${\bar{v}}$ is bounded), then we obtain the CLT provided the variance $\sigma ^2 > 0$, and this follows from ${\bar{v}}$ not being a coboundary. In other words, ${\bar{v}} \ne h - h \circ F$ for any $h \in {{\mathcal {B}}}$, the Banach space used in the proofs of [3], and this we assumed explicitly. $\square$